Практика постоянный ток

1.

Порядок решения задач с помощью
законов Кирхгофа
1.Определить число узлов n и ветвей m схемы.
2. Произвольно расставить направления токов в ветвях.
3. Выбрать (n - 1) узел и записать уравнения для этих
узлов по первому закону Кирхгофа.
4. Выбрать (m - n + 1) взаимно независимых контуров и
задать для этих контуров направления обхода (н.о.).
5. Для выбранных контуров записать уравнения по
второму закону Кирхгофа и решить полученную систему
уравнений.
6. Произвести проверку решения с помощью баланса
мощности.

2.

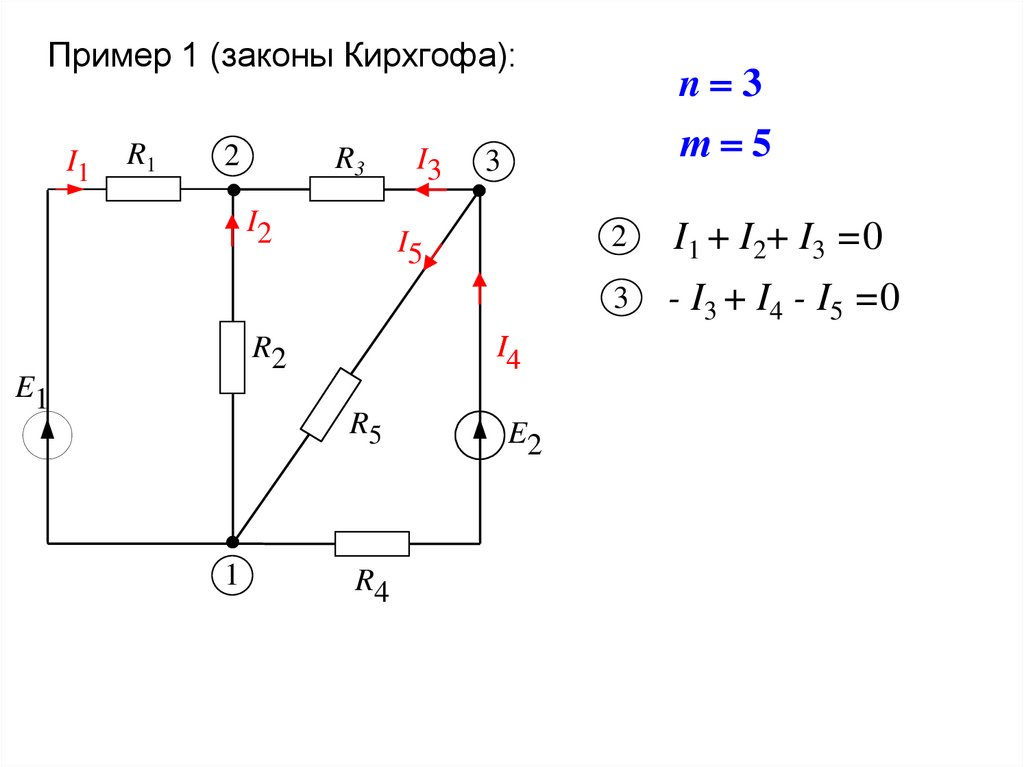
Пример 1 (законы Кирхгофа):
I1
R1
2
R3
I2
I4
R5
1
3
I5
R2
E1
I3
R4
n 3
т 5
E2
2
I1 + I2+ I3 =0
3
- I3 + I4 - I5 =0

3.

I1
R1
2
R3
I2
I3
n 3
т 5
3
2 I1 I 2 I3 0
I5
II
R2
I
E1
III
R5
1
I4
E2
3 I I I 0
3
4
5
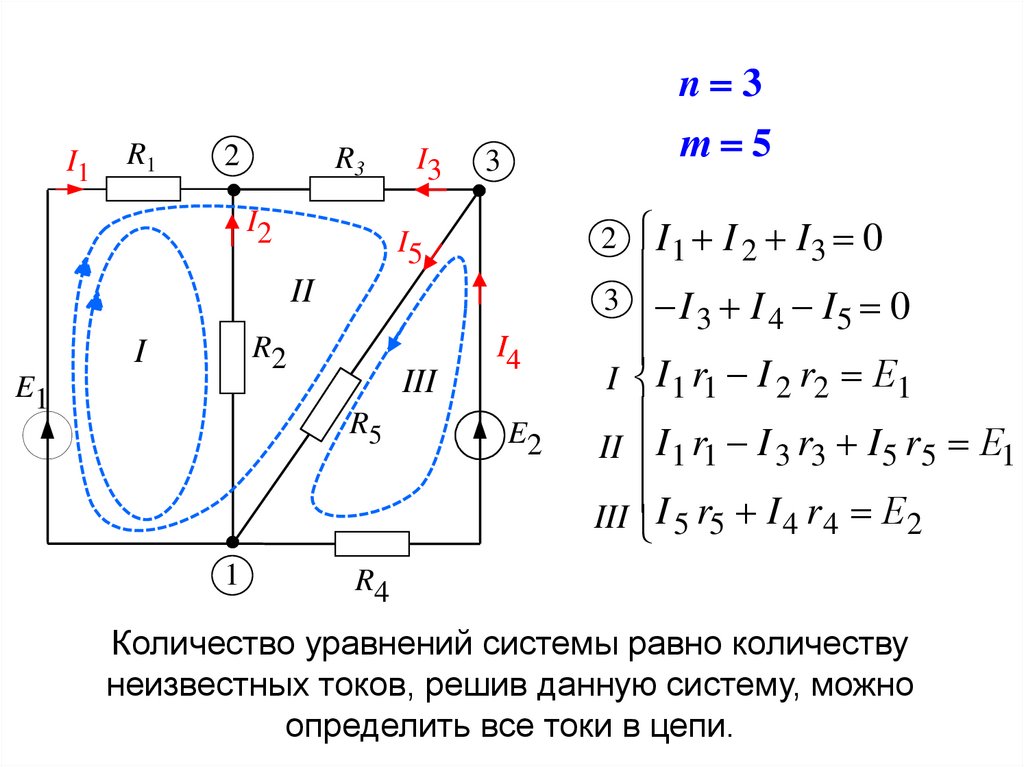
I I 1 r1 I 2 r2 Е1
II I 1 r1 I 3 r3 I 5 r5 Е1
III I 5 r5 I 4 r 4 Е2
R4
Количество уравнений системы равно количеству
неизвестных токов, решив данную систему, можно
определить все токи в цепи.

4.

Порядок решения задач методом наложения
1. Определить число источников энергии в схеме.
Количество источников энергии равно количеству частичных
токов, подлежащих определению.
2. Поочередно рассчитать частичные токи в ветвях, возникающие
от действия каждого источника в отдельности. При этом
остальные источники мысленно удаляются из цепи, но
сохраняются их внутренние сопротивления.
3. Истинные токи определяется алгебраической суммой
частичных токов.
4. Произвести проверку решения с помощью баланса мощности.

5.

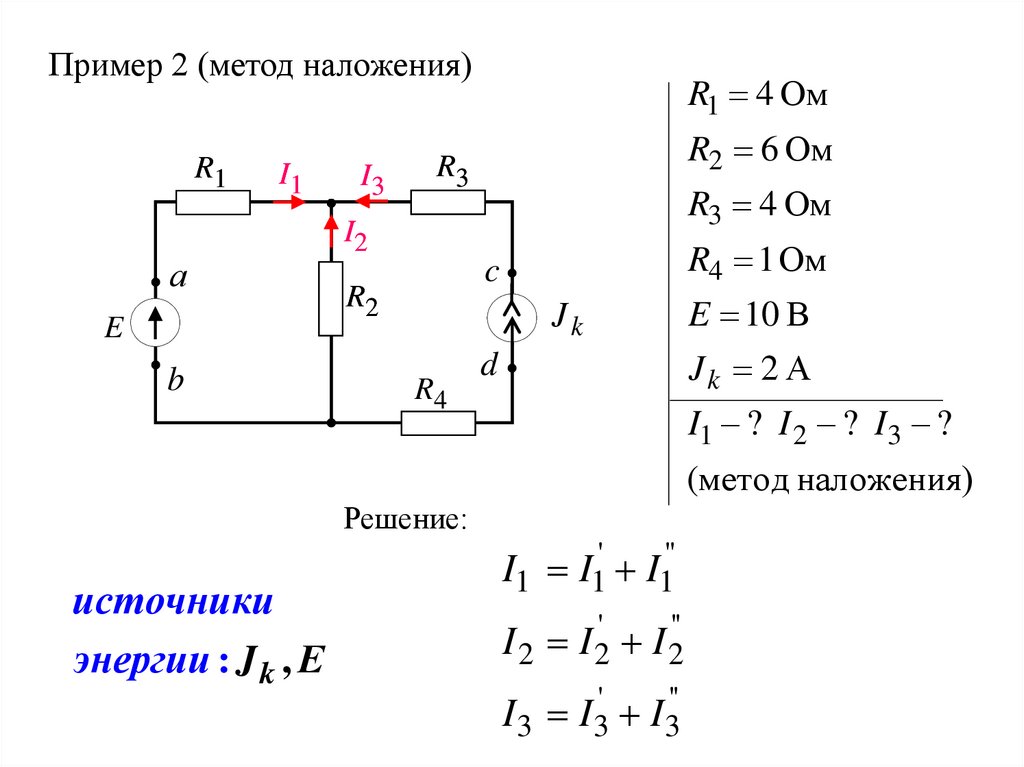
Пример 2 (метод наложения)
R1
I1
а
E
b
I3
R1 4 Ом
R2 6 Ом
R3
R3 4 Ом
I2
R4 1 Ом
c
R2
Jk
R4
d
E 10 В
Jk 2 А
I1 ? I 2 ? I 3 ?
(метод наложения)
Решение:
источники
энергии : J k , Е
'
''
I1 I1 I1
I 2 I 2' I 2''
I 3 I 3' I 3''

6.

R1
I1
а
E
b
I' 1
b
I' 3
c
R2
E
R1
R3
I2
а
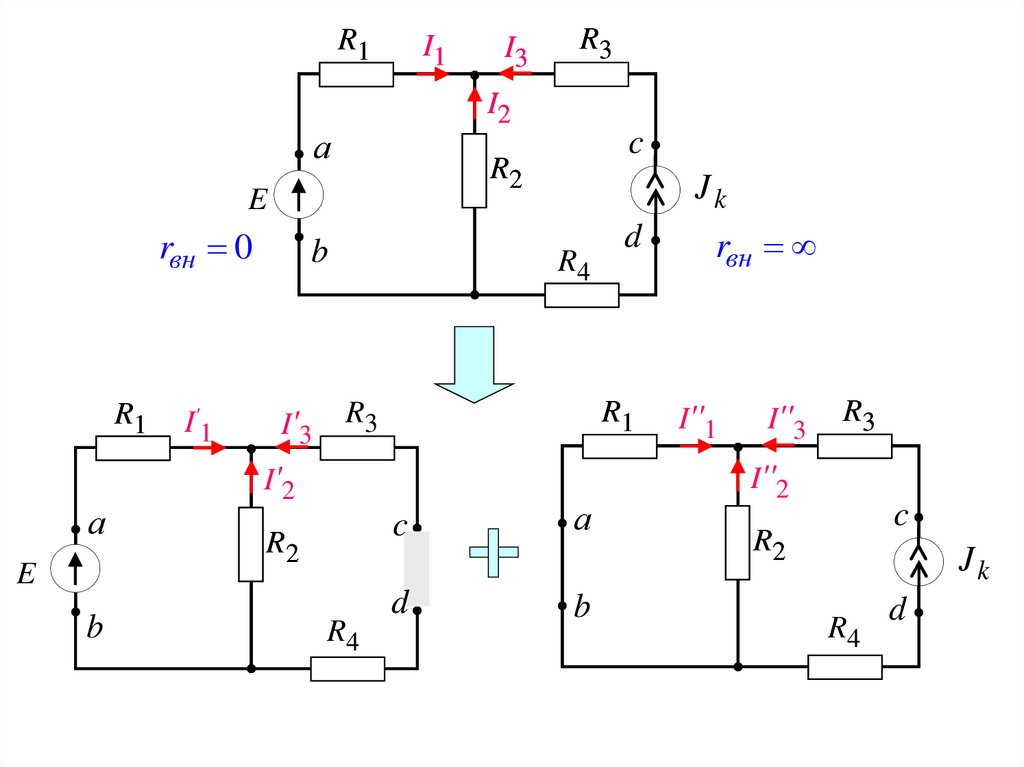
rвн 0
I3
Jk
R4
R1
R3
I '2
c
R2
R4
d
d
а
b
rвн
I''1
I''3
R3
I''2
c
R2
Jk
R4
d

7.

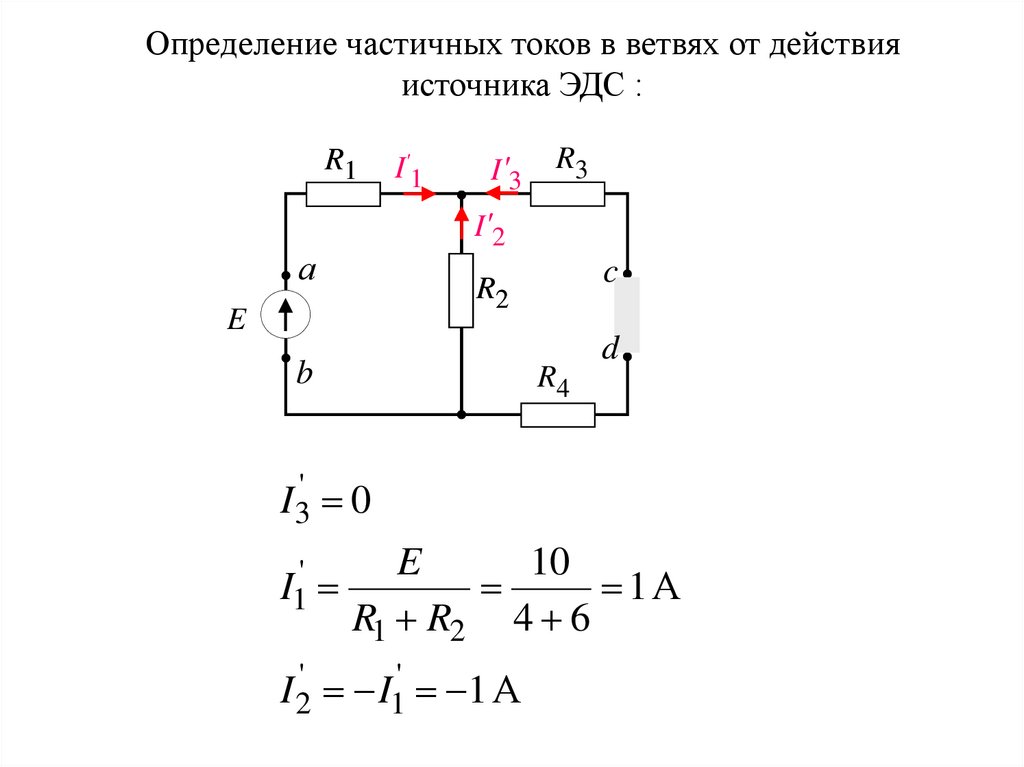
Определение частичных токов в ветвях от действия
источника ЭДС :
R1
I'1
I' 3
R3
I' 2
а
c
R2
E
b
R4
d
'
I3 0
I1'
E
10
1А
R1 R2 4 6
I 2' I1' 1 А

8.

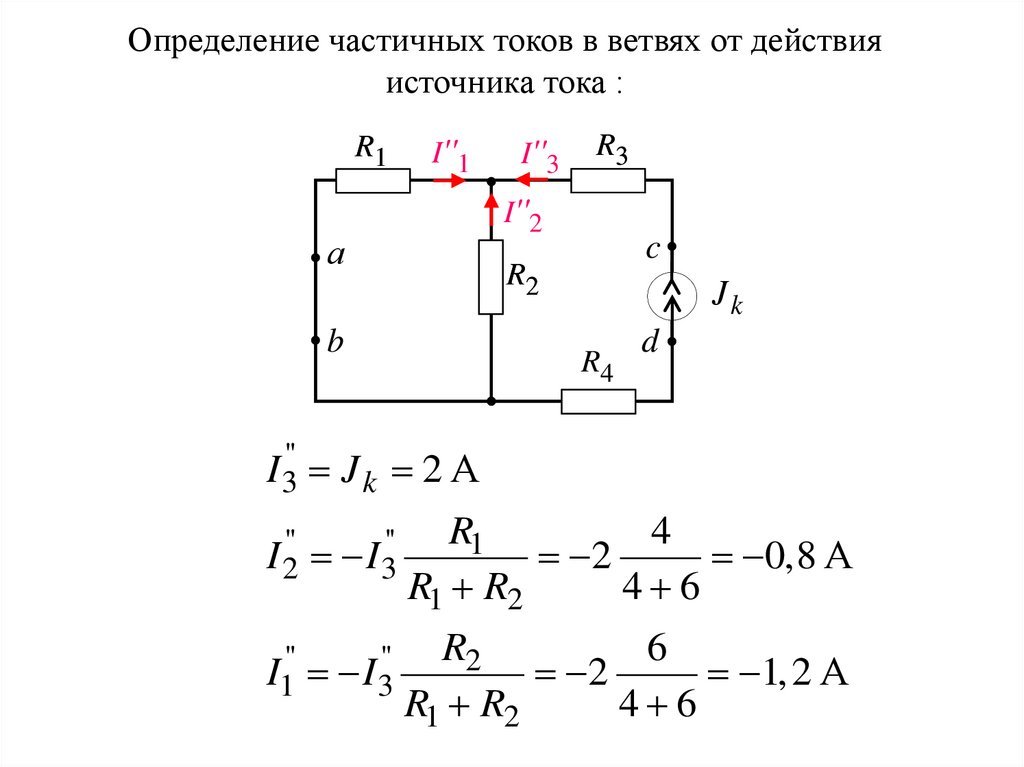
Определение частичных токов в ветвях от действия
источника тока :
R1
I''1
I''3
R3
I''2
а
c
R2
b
Jk
R4
d
I 3'' J k 2 А
I 2'' I 3''
R1
4
2
0,8 А
R1 R2
4 6
I1'' I3''
R2
6
2
1,2 А
R1 R2
4 6

9.

Определение истинных токов в ветвях :
I1 I1' I1'' 1 1,2 0,2 А
I 2 I 2' I 2'' 1 0,8 1,8 А
I3 I 3' I 3'' 0 2 2 А
После определения искомых токов следует сделать
проверку решения одним из известных методов.

10.

Порядок решения задач методом контурных токов
1. Определить число узлов n и ветвей m схемы.
2. Выбрать (m - n + 1) взаимно независимых контуров и
задать для этих контуров направления обхода (н.о.).
3. Принять направления контурных токов совпадающим с
направлением обхода контуров.
4. Для выбранных контуров записать уравнения по МКТ и
решить полученную систему уравнений.
5. Произвольно расставить направления реальных токов в ветвях.
6. Определить реальные токи в ветвях как алгебраическую сумму
контурных токов.
7. Произвести проверку решения с помощью баланса мощности.

11.

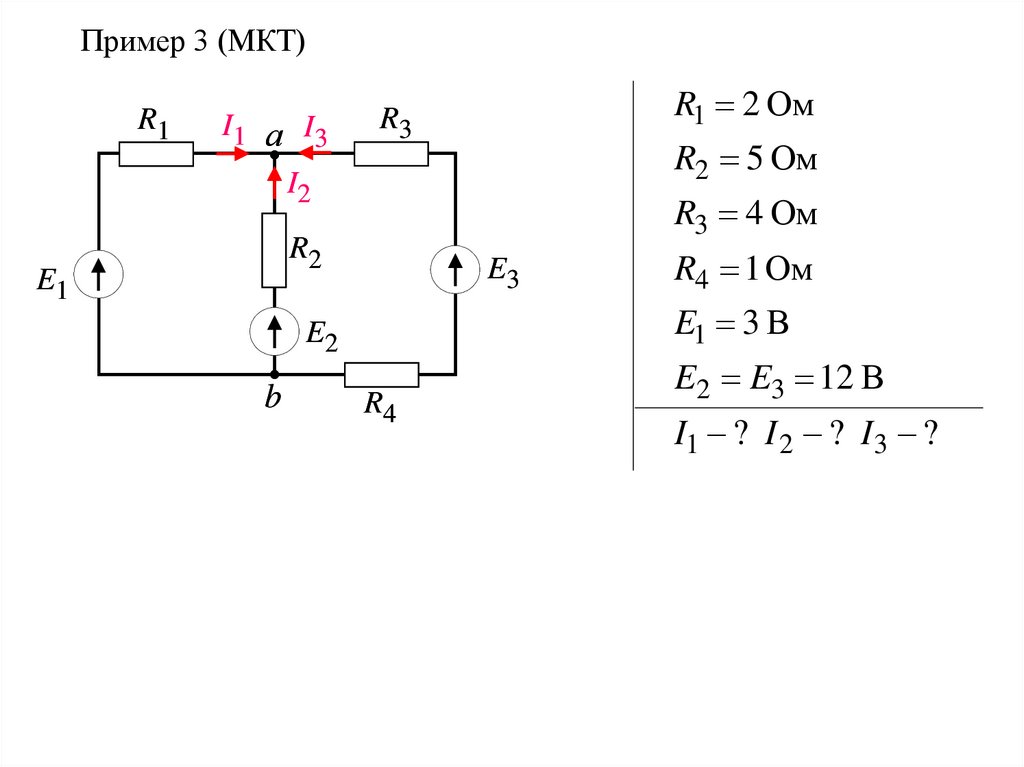
Пример 3 (МКТ)
R1
I1 а I3
R1 2 Ом
R3
R2 5 Ом
I2
R3 4 Ом
R2
E1
E3
E1 3 В
E2
b
R4 1 Ом
R4
E2 E3 12 В
I1 ? I 2 ? I 3 ?

12.

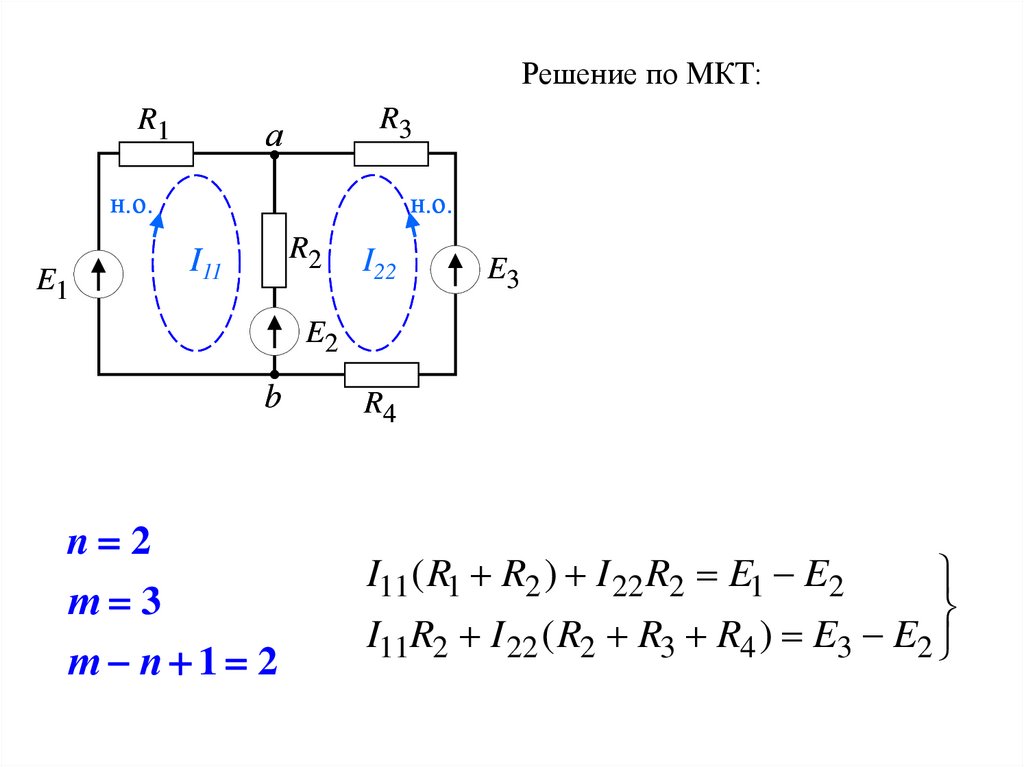
Решение по МКТ:
R1
R3
а
н.о.
н.о.
E1
R2
I11
I22
E3
E2
b
n 2
т 3
т n 1 2
R4
I11( R1 R2 ) I 22 R2 E1 E2
I11R2 I 22 ( R2 R3 R4 ) E3 E2

13.

Решение полученной системы методом подстановки :
7 I11 5 I 22 9
5 I11 10 I 22 0
I11 2 I 22
9 I 22 9
I11 2 Α
I 22 1 Α

14.

Определение реальных токов в ветвях :
E1
R1
I1 а I3
н.о.
I2
R2
I11
R3
I22
E2
b
I1 I11 2 Α
н.о.
R4
E3
I 2 ( I11 I 22 ) 1 Α
I3 I 22 1 Α

15.

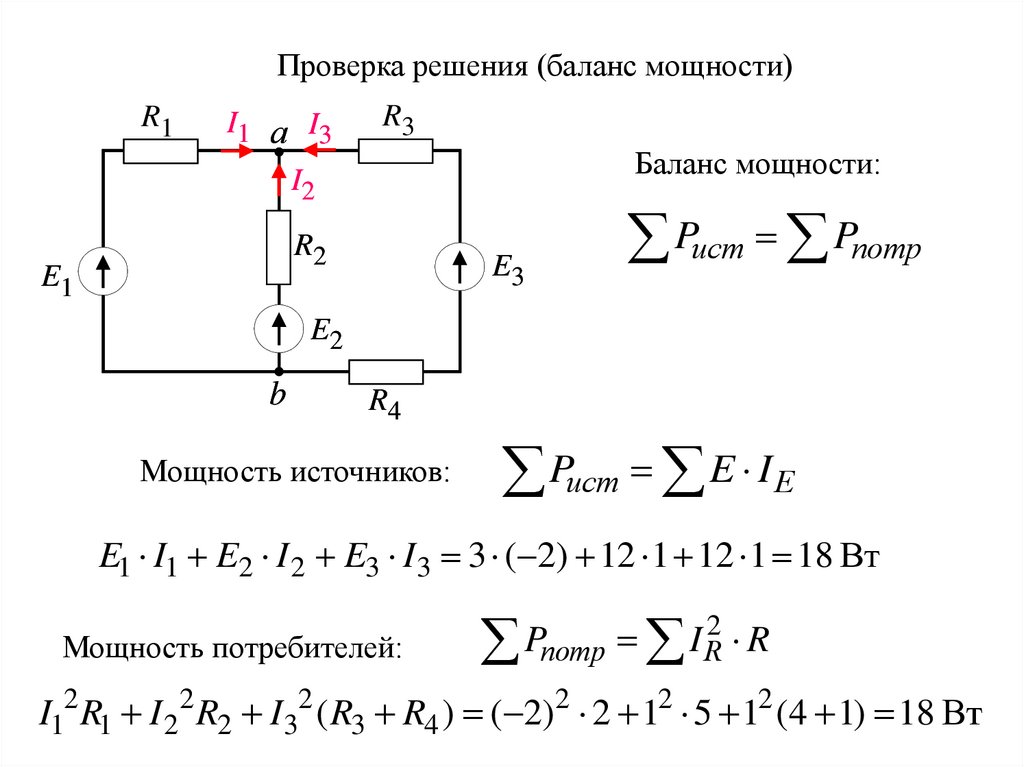
Проверка решения (баланс мощности)
R1
I1 а I3
R3
Баланс мощности:
I2
R2
E1
E3
Pист Pпотр
E2
b
R4
Мощность источников:
Pист E I E
E1 I1 E2 I 2 E3 I3 3 ( 2) 12 1 12 1 18 Вт
Мощность потребителей:
2
P
I
потр R R
I12 R1 I 22 R2 I32 ( R3 R4 ) ( 2)2 2 12 5 12 (4 1) 18 Вт

16.

Порядок решения задач методом узловых потенциалов
1. Определить число узлов n и ветвей m схемы.
2. Выбрать узел, к которому подходит наибольшее количество
ветвей и заземлить этот узел (принять потенциал узла равным
нулю).
3. Для оставшихся узлов записать (n - 1) уравнение по МУП и
решить полученную систему уравнений.
4. Произвольно расставить направления токов в ветвях.
5. Токи в ветвях определить по закону Ома и первому закону
Кирхгофа.
6. Произвести проверку решения с помощью баланса мощности.

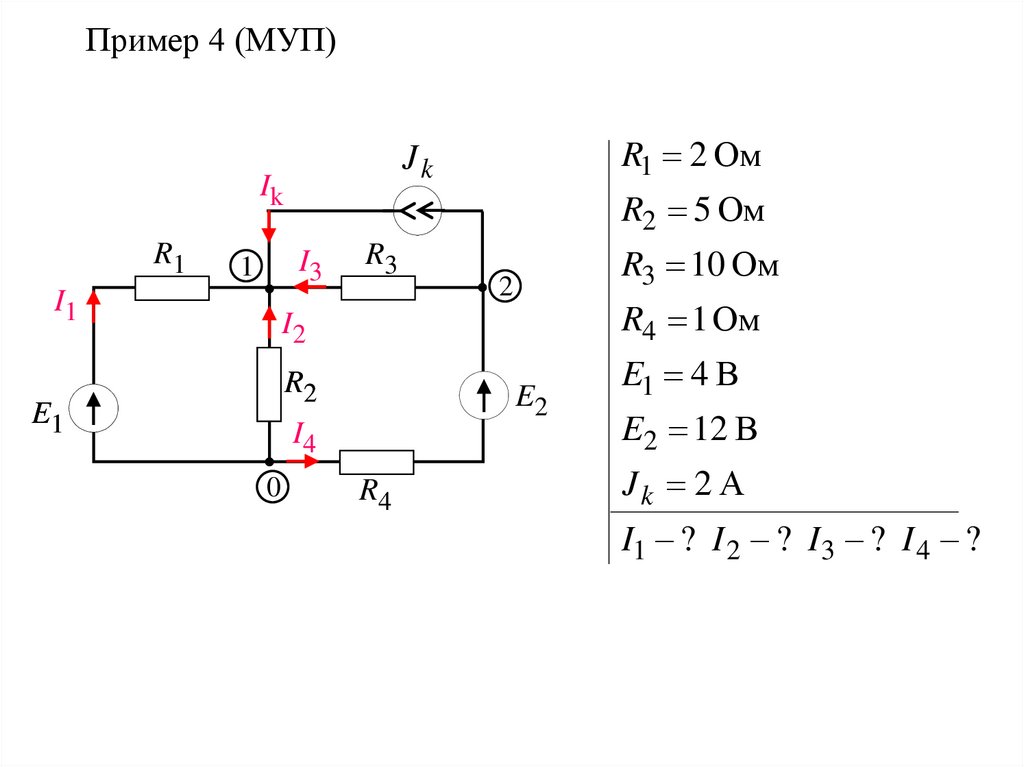
17.

Пример 4 (МУП)
Ik
R1
R2 5 Ом
I3
1
I1
E1
R3
R3 10 Ом
2
I2
R4 1 Ом
R2
E1 4 В
E2
I4
0
R1 2 Ом
Jk
R4
E2 12 В
Jk 2 А
I1 ? I 2 ? I 3 ? I 4 ?

18.

Ik
R
I1
1
I3
1
I2
E
1
0
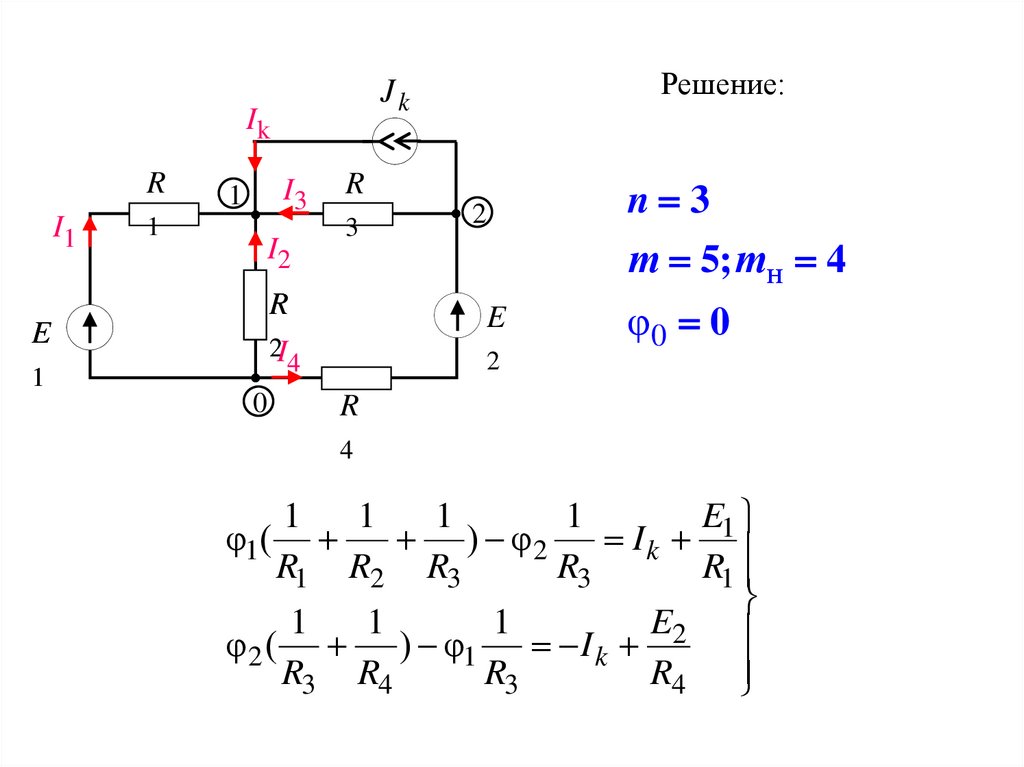
Решение:
Jk
R
3
n 3
2
т 5; тн 4
R
E
2I
2
4
φ0 0
R
4
1
1
1
1
E1
φ1(
) φ2
Ik
R1 R2 R3
R3
R1
1
1
1
E2
φ2 ( ) φ1
Ik
R3 R4
R3
R4

19.

Решение полученной системы методом подстановки :
0,8 φ1 0,1 φ 2 4
0,1 φ1 1,1 φ 2 10
8,7 φ 2 84
φ1 11 φ 2 100
φ 2 9,7 В
φ1 6,2 В

20.

Определение реальных токов в ветвях по :
E1 φ1
1,14 А
I1
R2 R2
φ1
1,24 А
I2
R2
φ 2 φ1
0,35 А
I3
R3 R3
E2 φ 2
2,3 А
I4
R4 R4

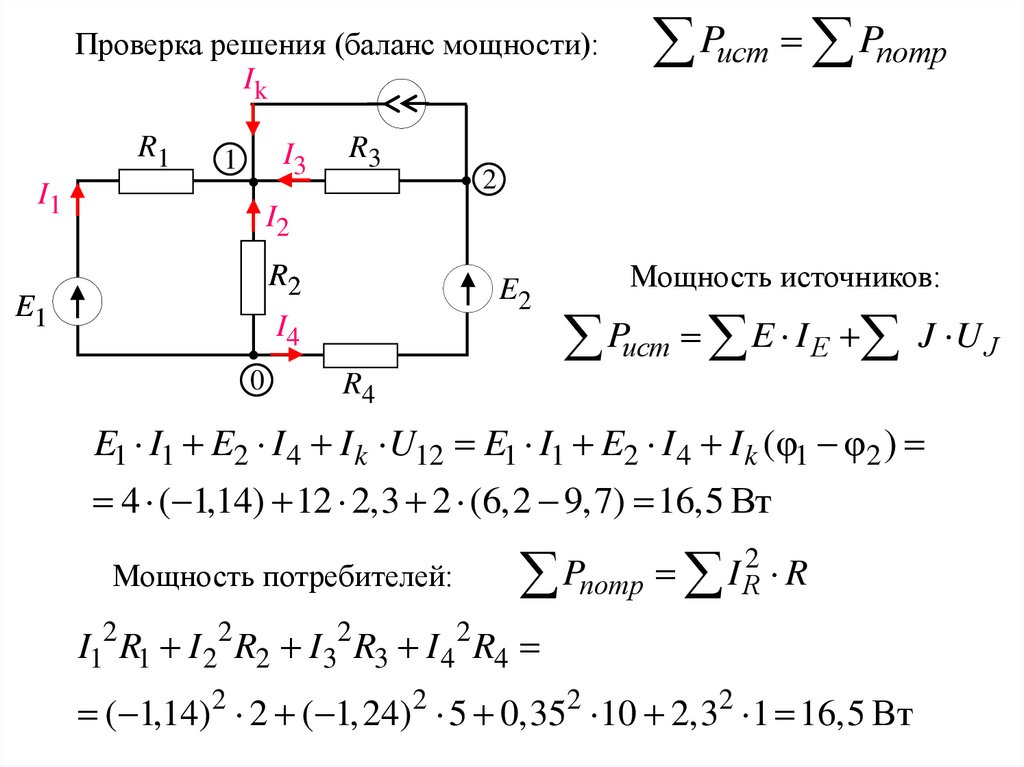
21.

Проверка решения (баланс мощности):
Ik
R1
I3
1
I1
R3
Pист Pпотр
2
I2
R2
E1
E2
I4
0
Мощность источников:
Pист E I E J U J
R4
E1 I1 E2 I 4 I k U12 E1 I1 E2 I 4 I k (φ1 φ2 )
4 ( 1,14) 12 2,3 2 (6,2 9,7) 16,5 Вт
Мощность потребителей:
2
P
I
потр R R
I12 R1 I 22 R2 I32 R3 I 4 2 R4
( 1,14)2 2 ( 1,24) 2 5 0,352 10 2,32 1 16,5 Вт

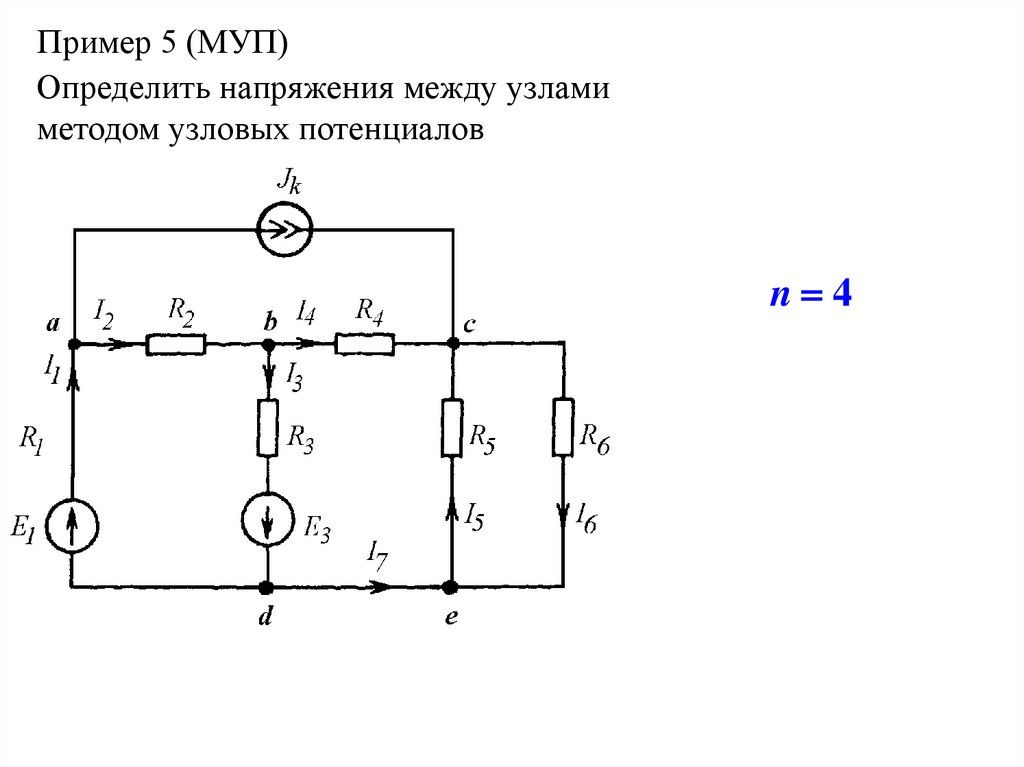
22.

Пример 5 (МУП)
Определить напряжения между узлами
методом узловых потенциалов
n 4

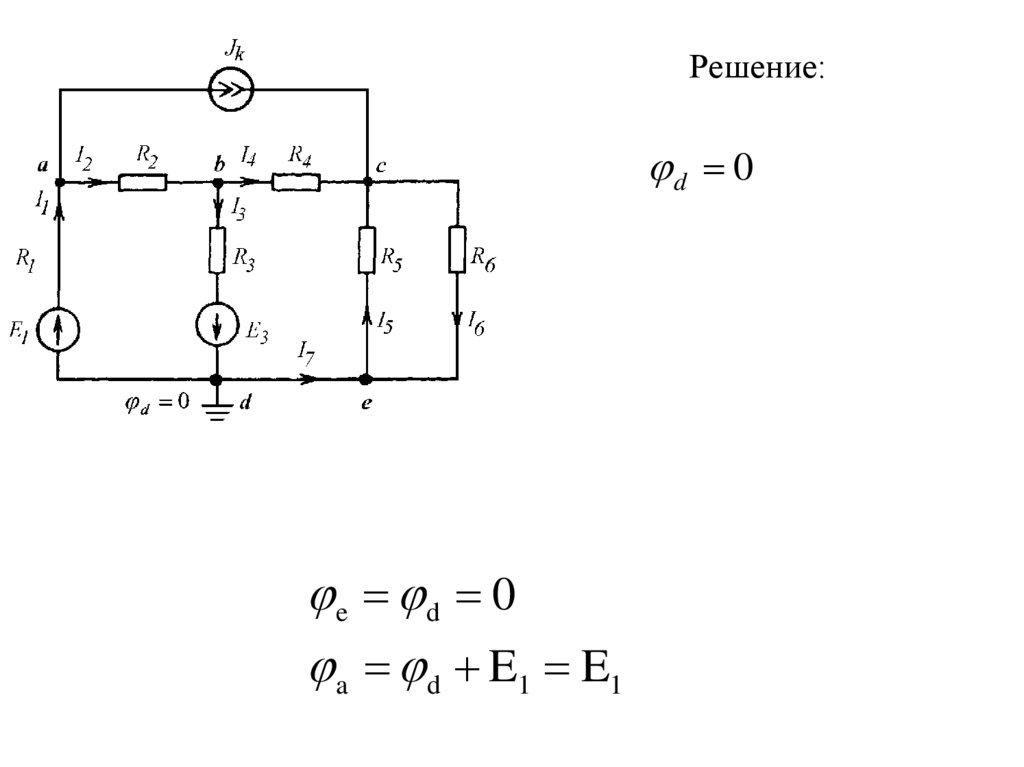
23.

Решение:
d 0
e d 0
a d E1 E1

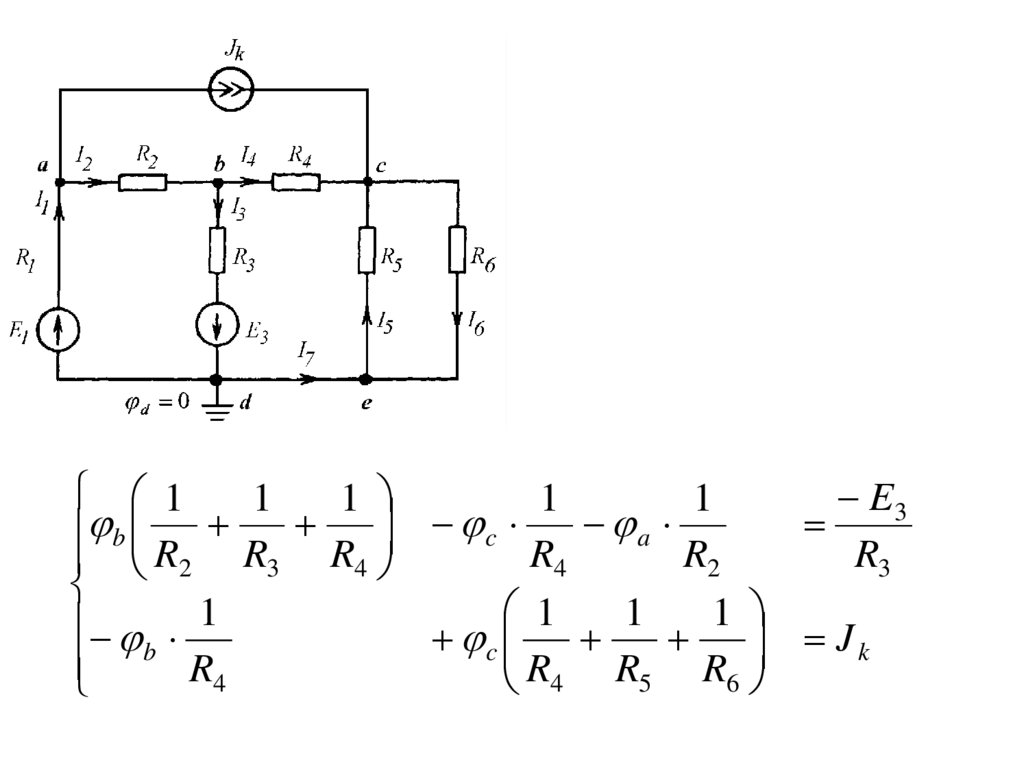
24.

1
E3
1
1
1
1
c
a
b
R4
R2
R3
R2 R3 R4
1
1
1
1
J k
c
b
R4
R4 R5 R6

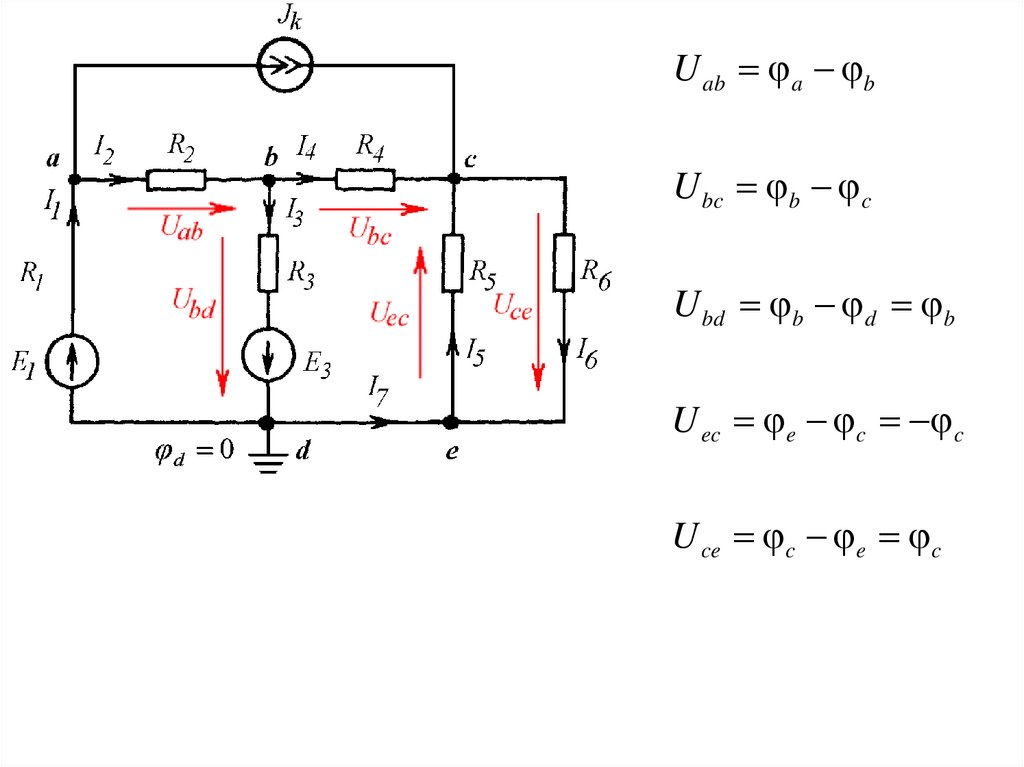
25.

U ab a b
U bc b c
U bd b d b
U ec e c c
U ce c e c

26.

Порядок решения задач методом эквивалентного генератора
1. Представить схему в виде активного (А) и пассивного (П)
двухполюсников, соединенных последовательно. В качестве пассивного
двухполюсника принять ветвь с искомым током.
2. Определить напряжение на зажимах активного двухполюсника в
режиме холостого хода Uхх. Оно направлено в ту же сторону, что и
искомый ток. ЭДС эквивалентного генератора равна этому напряжению
Eг = Uхх .
3. Рассчитать эквивалентное сопротивление активного двухполюсника
относительно его зажимов Rг. Для этого сформировать схему для
расчета сопротивлений, удалив из нее источники энергии, но сохранив
их внутренние сопротивления.
4. Определить искомый ток по закону Ома:
Eг
I
Rг R

27.

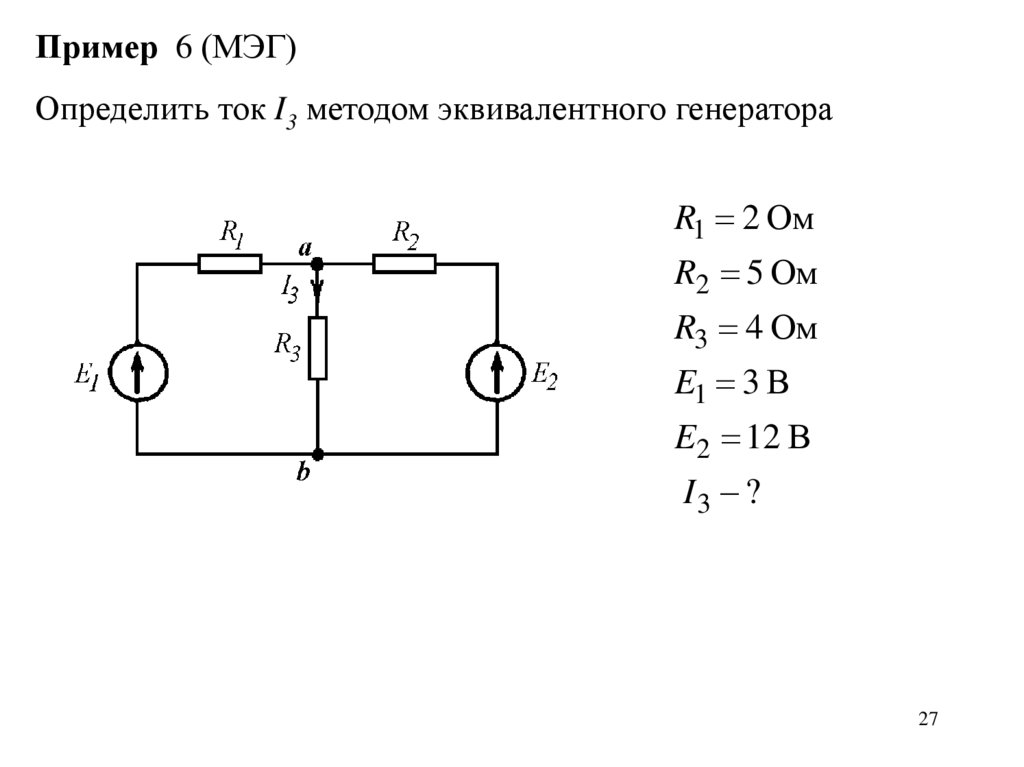
Пример 6 (МЭГ)
Определить ток I3 методом эквивалентного генератора
R1 2 Ом
R2 5 Ом
R3 4 Ом
E1 3 В
E2 12 В
I3 ?
27

28.

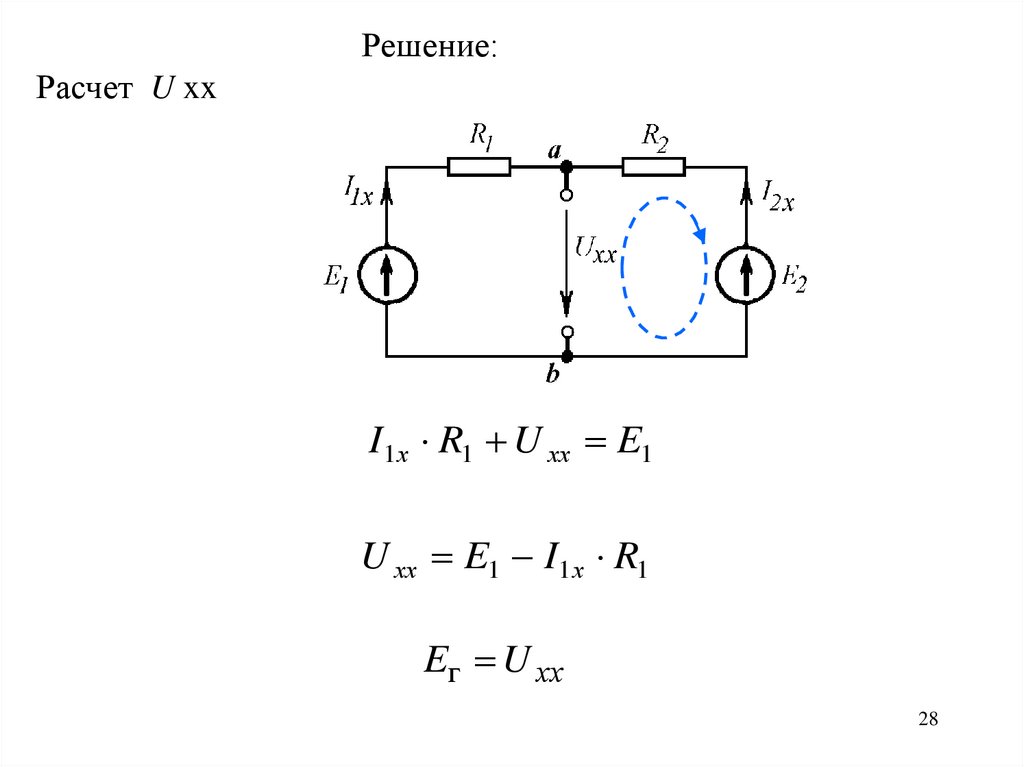
Решение:
Расчет U xx
I1х R1 U хх E1
U хх E1 I1х R1
Eг U хх
28

29.

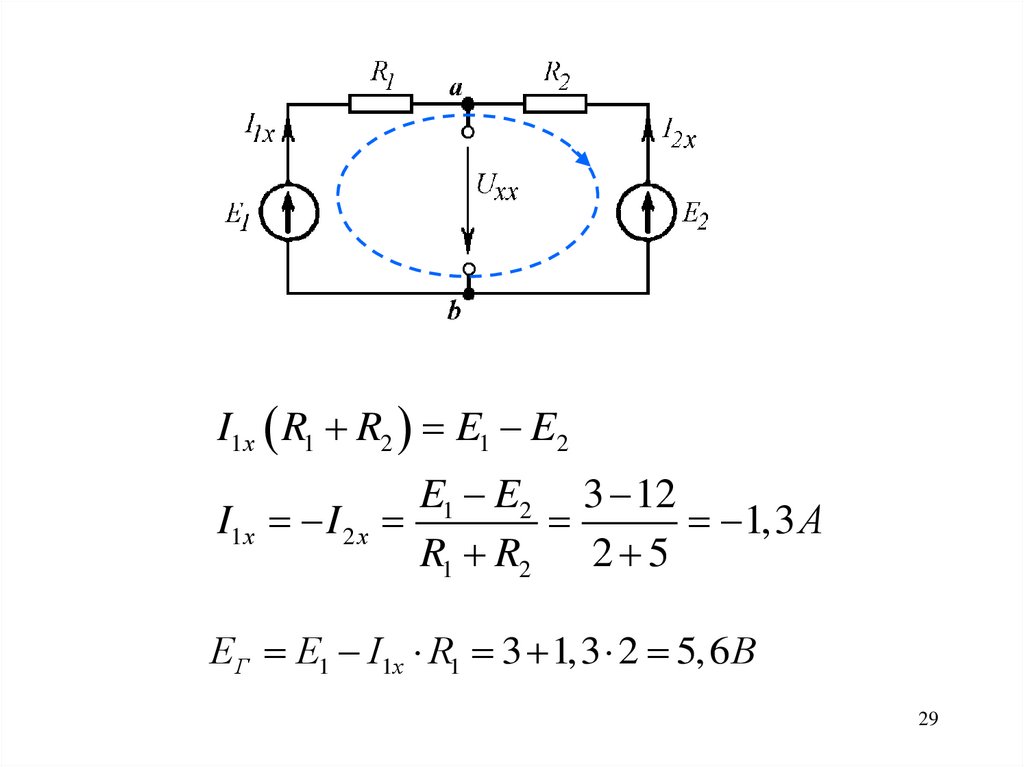
I1х R1 R2 E1 E2
E1 E2 3 12
I1х I 2 х
1,3 А
R1 R2 2 5
ЕГ E1 I1х R1 3 1,3 2 5,6 В
29

30.

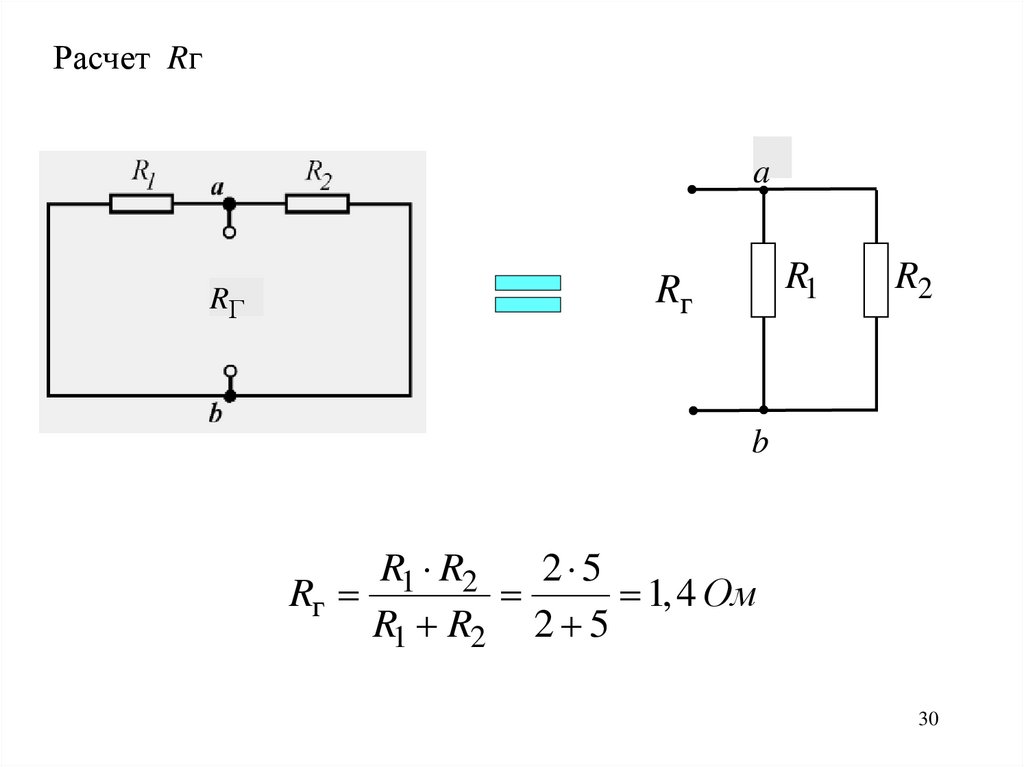
Расчет Rг
a
RГ
R1
Rг
R2
b
R1 R2
2 5
Rг
1,4 Ом
R1 R2 2 5
30

31.

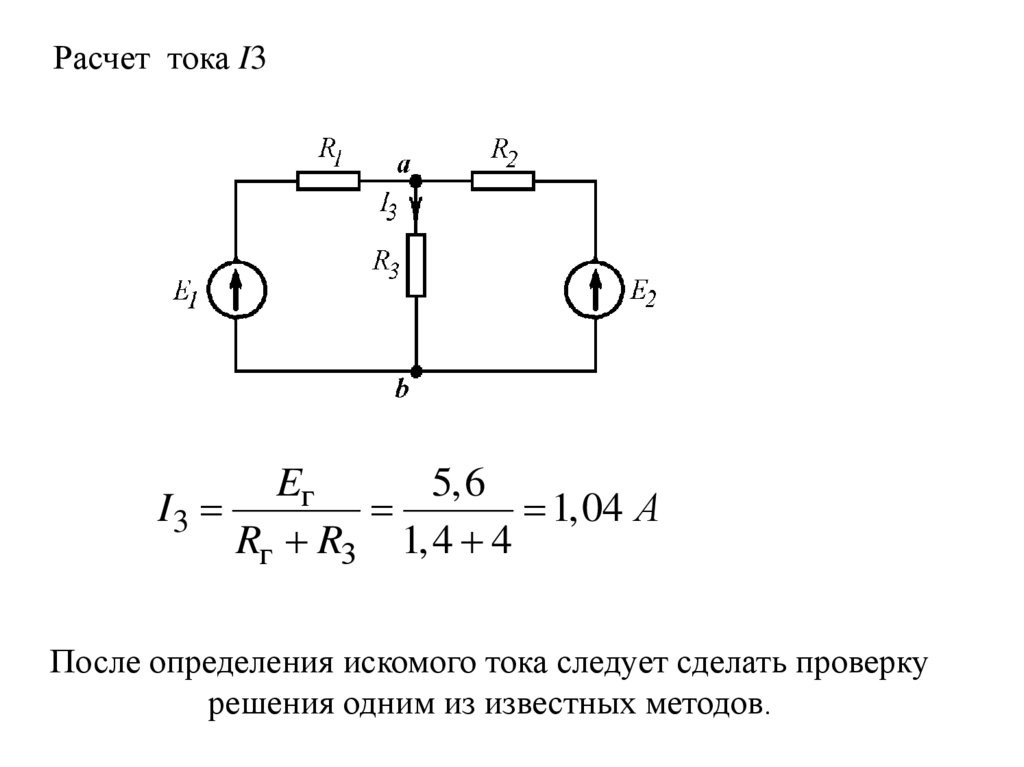
Расчет тока I3
Eг
5,6
I3
1,04 А
Rг R3 1,4 4
После определения искомого тока следует сделать проверку
решения одним из известных методов.

32.

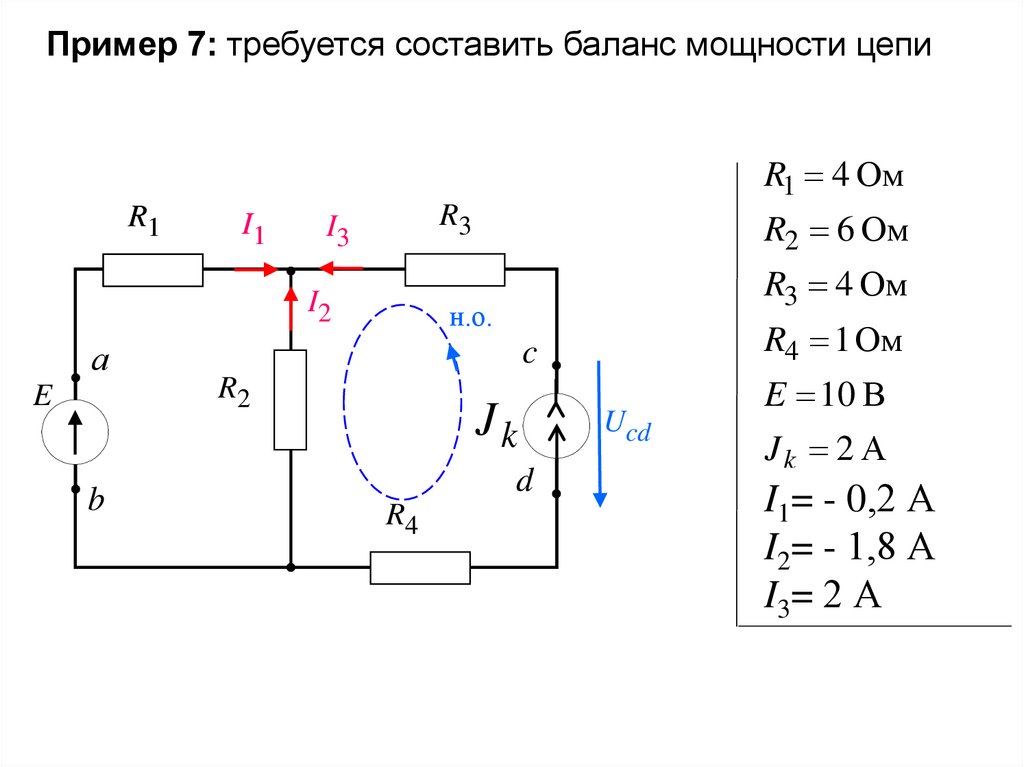
Пример 7: требуется составить баланс мощности цепи
R1 4 Ом
R1
I1
R3
I3
I2
а
E
b
R2 6 Ом
R3 4 Ом
н.о.
R4 1 Ом
c
R2
Jk
d
R4
Ucd
E 10 В
Jk 2 А
I1= ?- 0,2
I 2 А? I 3 ?
I2= - 1,8
А
(метод
наложения
I3= 2 А

33.

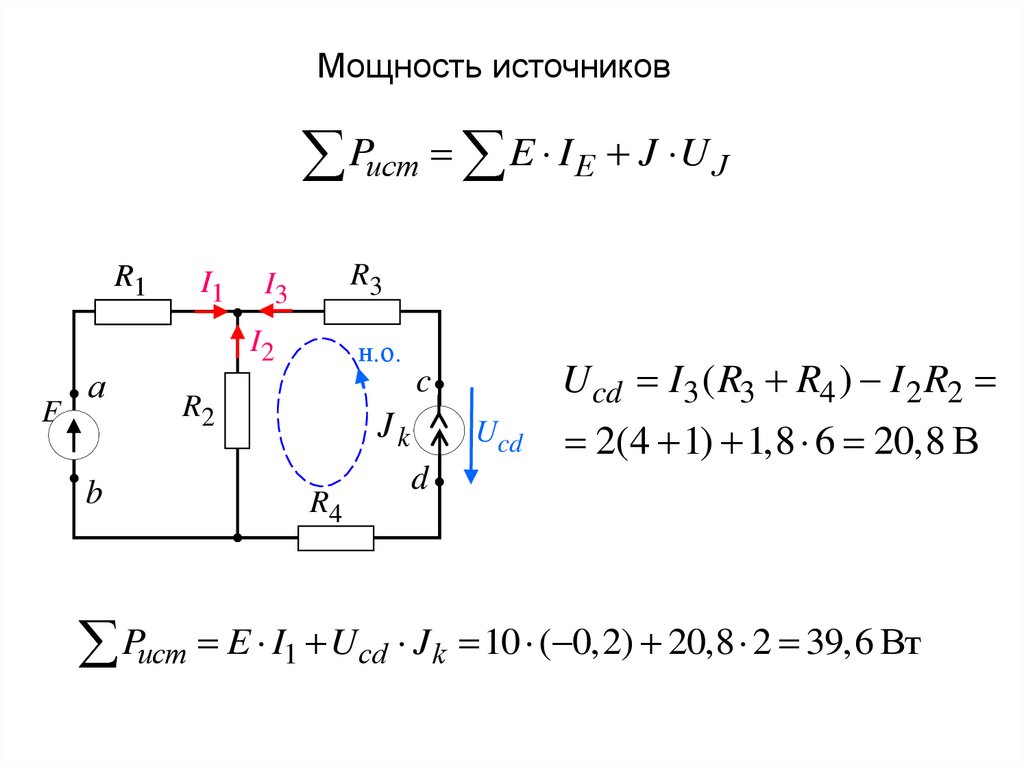
Мощность источников
Pист E I E J U J
R1
E
а
b
I1
I3
R3
I2
н.о.
U cd I3 ( R3 R4 ) I 2 R2
c
R2
Jk
R4
Ucd
2(4 1) 1,8 6 20,8 В
d
Pист E I1 Ucd J k 10 ( 0,2) 20,8 2 39,6 Вт

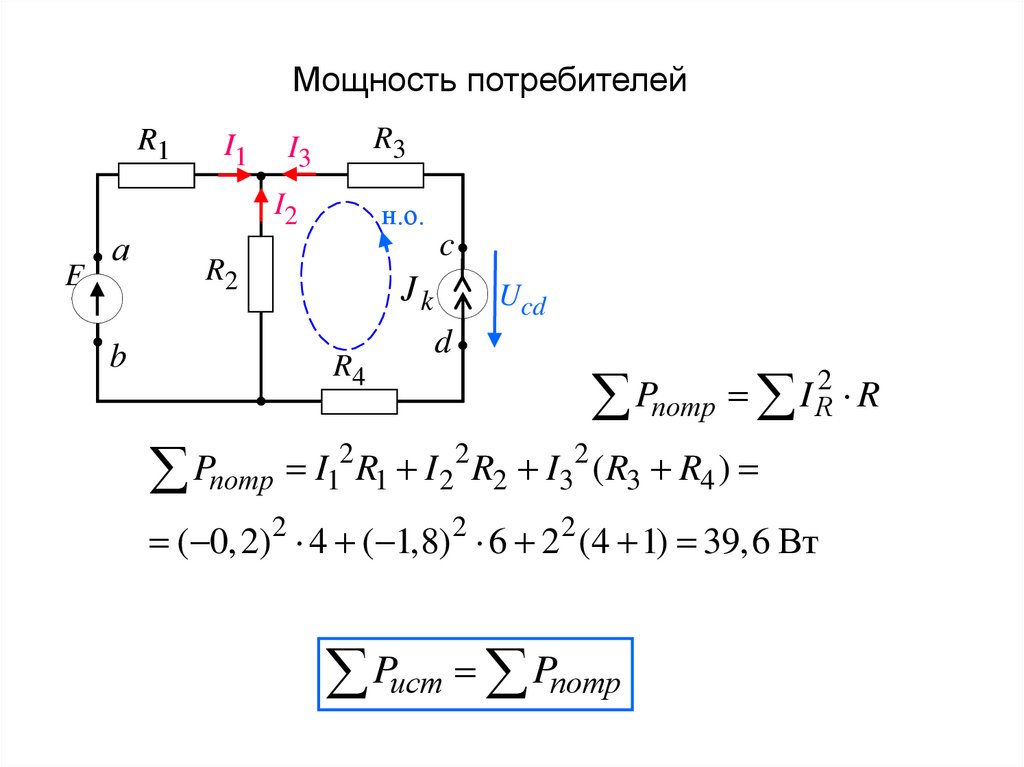
34.

Мощность потребителей
R1
E
а
b
I1
I3
R3
I2
н.о.
c
R2
Jk
R4
Ucd
d
2
P
I
потр R R
2
2
2
P
I
R
I
R
I
потр 1 1 2 2 3 ( R3 R4 )
( 0,2) 2 4 ( 1,8) 2 6 22 (4 1) 39,6 Вт
Pист Pпотр