Законы Кирхгофа

1.

Схема – это графическое изображение
электрической цепи.
Ветвь – это участок схемы, вдоль
которого течет один и тот же ток.
Узел – это место соединения трех или
большего числа ветвей
Контур – это замкнутый путь,
проходящий по нескольким ветвям
Независимый контур – это контур, у
которого хотя бы одна ветвь не
принадлежит другим контурам
1

2.

При последовательном соединении через
все элементы протекает один ток
Rэкв R1 R2 R3 ...Rn
i
R1
R2
R3
…
Rn
Rэкв
2

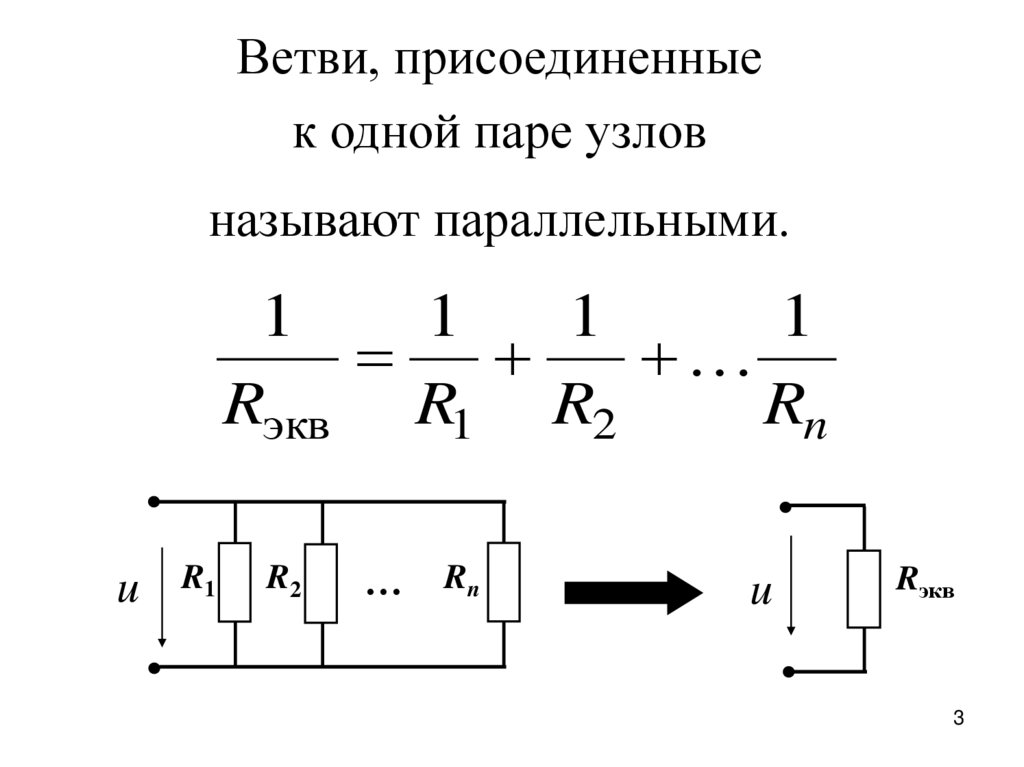
3.

Ветви, присоединенные
к одной паре узлов
называют параллельными.
1
1
1
1
Rэкв R1 R2
Rn
u
R1
R2
…
Rn
u
Rэкв
3

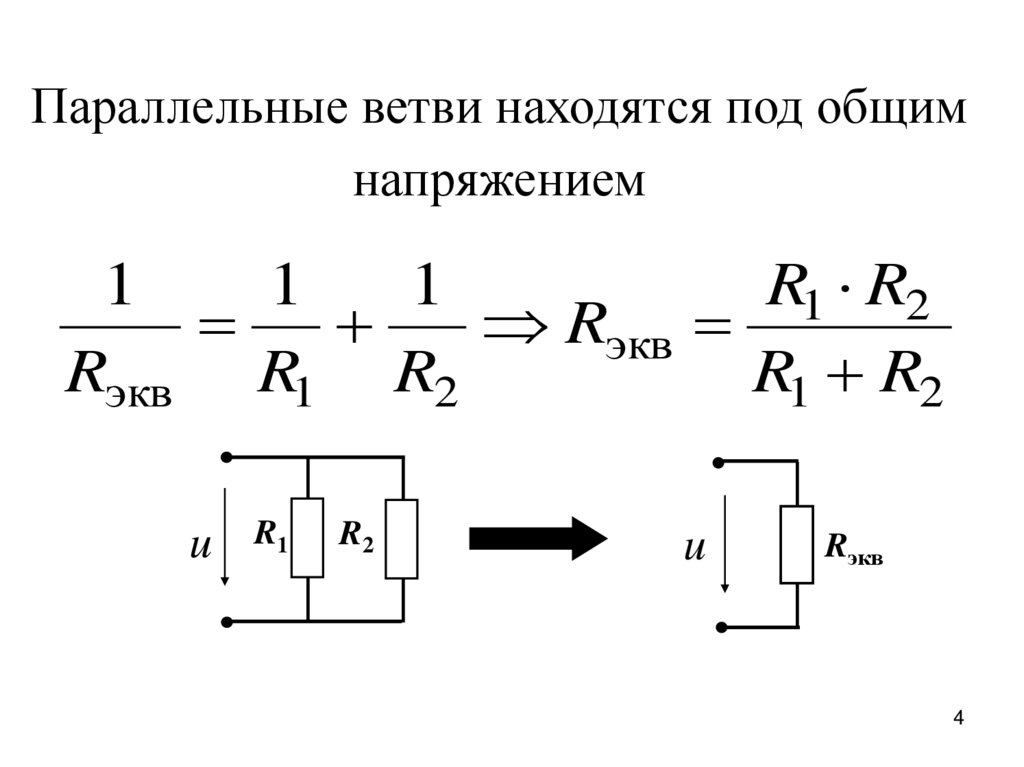
4.

Параллельные ветви находятся под общим
напряжением
1
1
1
R1 R2
Rэкв
Rэкв R1 R2
R1 R2
u
R1
R2
u
Rэкв
4

5.

Схема
N=4 – число узлов
М=6 – число ветвей
L1
R1
i4
i1
1к
e1
a
e2
b
C4
3к
R3
2к
i2
L5
i3
c
i5
d
J
5

6.

Законы Кирхгофа
Кирхгоф (Kirchhoff) Густав Роберт
1824-1887г.
немецкий физик, член Берлинской АН,
член-корреспондент Петербургской АН.
В возрасте двадцати одного года, сформулировал основные
законы для расчета токов и напряжений в электрических
цепях
6

7.

Первый закон Кирхгофа:
алгебраическая сумма токов в узле
равняется нулю (токи, вытекающие из узла,
считаются положительными, а втекающие –
отрицательными):
( ik ) 0
Физический смысл этого закона прост: если бы он
не выполнялся, в узле непрерывно накапливался
бы электрический заряд, а этого никогда не
происходит.
7

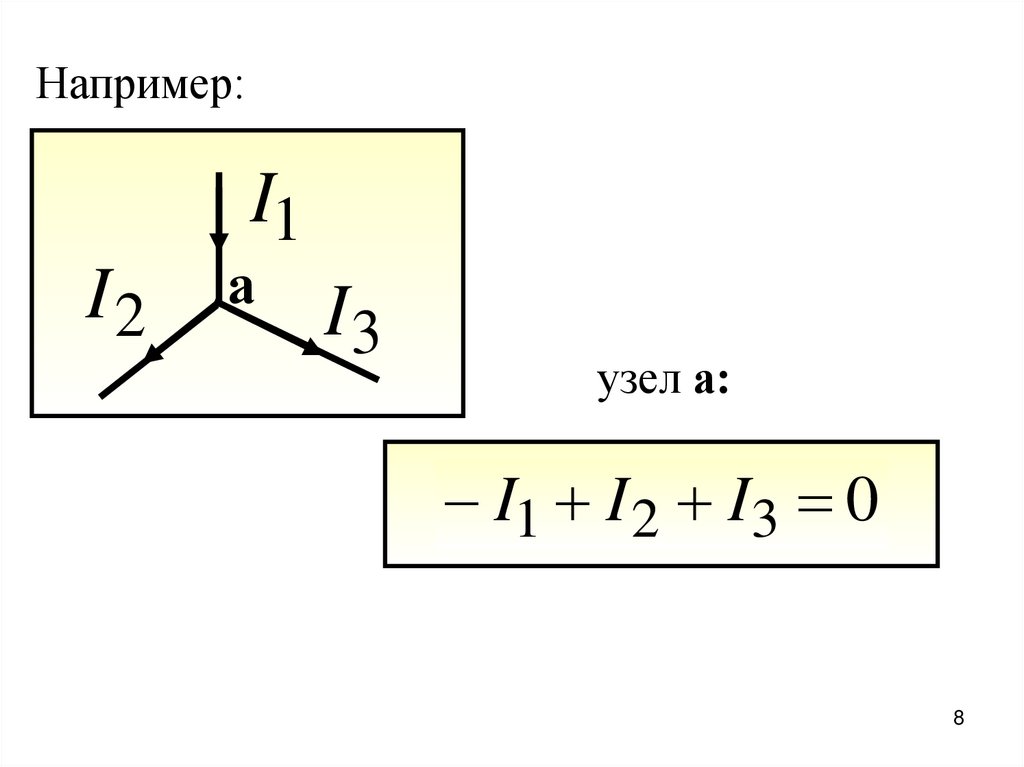
8.

Например:
I1
I2
а
I3
узел а:
I1 I 2 I3 0
8

9.

Второй закон Кирхгофа:
в контуре алгебраическая сумма падений
напряжения на пассивных элементах равна
алгебраической сумме ЭДС и напряжений на
зажимах источников тока.
с “+” берутся все слагаемые, положительное
направление которых совпадает с выбранным
обходом контура:
n
uk
k 1
m
ek
k 1
d
u Jk
k 1
9

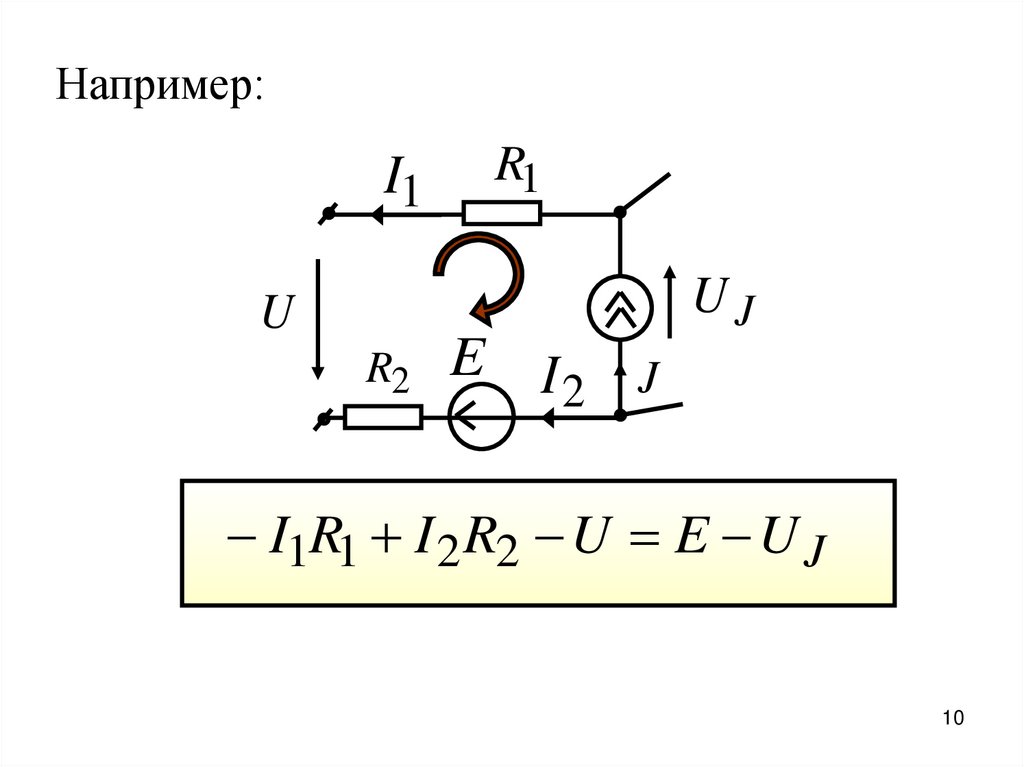
10.

Например:
R1
I1
UJ
U
R2
E
I2 J
I1R1 I 2 R2 U E U J
10

11.

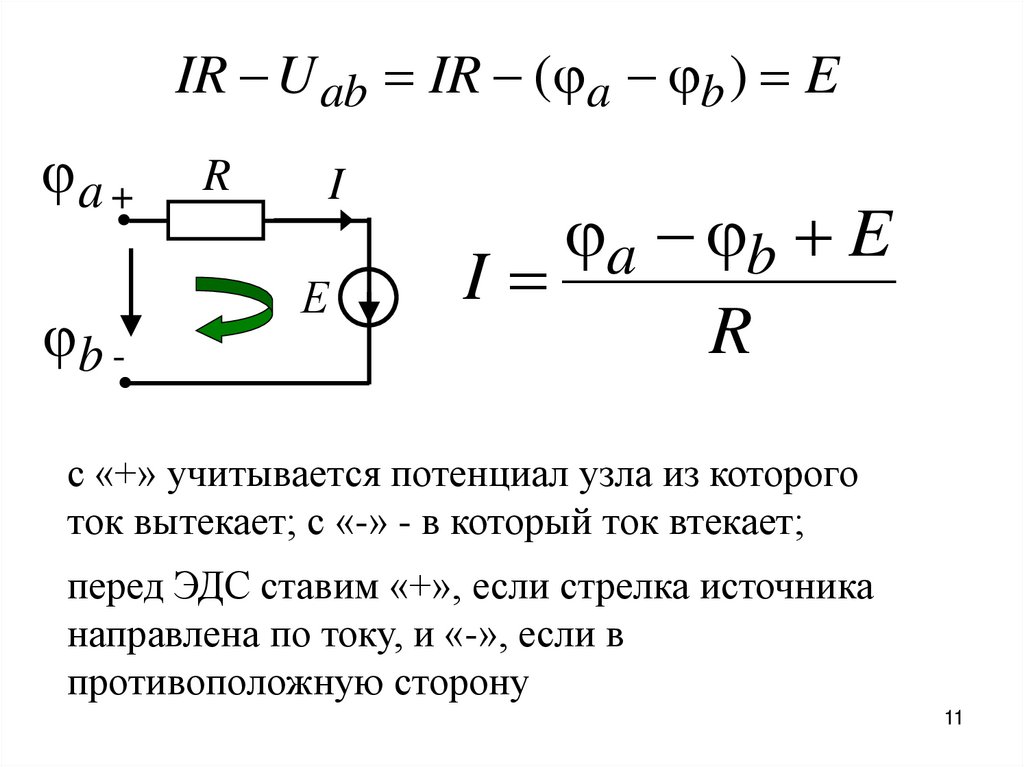
IR U ab IR ( a b ) E
a +
b -
R
I
Е
a b E
I
R
с «+» учитывается потенциал узла из которого
ток вытекает; с «-» - в который ток втекает;
перед ЭДС ставим «+», если стрелка источника
направлена по току, и «-», если в
противоположную сторону
11

12.

1. Метод законов Кирхгофа
Решение системы уравнений, составленных по
законам Кирхгофа, позволяет определить все
токи и напряжения в рассматриваемой
цепи
12

13.

R1
1к
R3
E1
a
I1
R4
I3
I4
N 4
R2
d
I2
2к
M 6
E2
R5
b
I5
c
3к
UJ
J
По 1ЗК : N 1 3
По 2ЗК : M N 1 3
13

14.

R1
1к
R3
E1
a
I1
R4
R2
d
I3
I4
I2
2к
E2
R5
b
I5
c
3к
UJ
J
R1I1 R 3I 3 R 4I 4 E1
I1 I 4 J 0 1к :
b : I 3 I 4 I 5 0 2к : R 2I 2 R 3I 3 R 5I 5 E 2
c:
I 2 I 5 J 0 3к : R 4I 4 R 5I 5 U J
a:
14

15.

В матричной форме
I1 I 2
I3
I4
I5
UJ
J
0
0 1
0
0
1
0
0
0 1
1
1
0
0
1
0 0 1
0 B J
A
E
0
1
R1 0 R 3 R 4 0
E2
0 R 2 R 3 0 R 5 0
0
0
0 R 4 R 5 1
0
I1 I 4 J 0
I3 I4 I5 0
I2 I5 J 0
R1I1 R 3I 3 R 4I 4 E1
R2I 2 R3I 3 R5I5 E2
R 4I 4 R 5I 5 U J
A матрица коэффициентов перед неизвестными
величинами;
B
матрица источников
15

16.

В матричной форме
A I B
Решение системы:
1
I A B
16

17.

Метод контурных токов
Основан на решении уравнений, составленных
по второму закону Кирхгофа и позволяет
уменьшить порядок системы уравнений
Контурный ток – это ток, текущий
в независимом контуре.
Число уравнений равно числу
независимых контуров: M-N+1
17

18.

Общая форма записи
R кк I кк R кmI mm Eкк
R кк суммарное сопротивление к-контура
I кк
контурный ток к-контура
R кm общее сопротивление между к-контуром и m I mm
контуром
соседний контурный ток m-контура
Eкк суммарная ЭДС к-контура
18

19.

Алгоритм составления уравнений
1. Контурный ток рассматриваемого контура
умножается на сумму сопротивлений этого контура.
2. К этому произведению дописываются произведения
всех соседних контурных токов на общие
сопротивления (c “+” если контурные токи обтекают
общее сопротивление в одном направлении).
3. В правой части уравнения записывается
алгебраическая сумма ЭДС контура (с “+”, если
направление ЭДС совпадает с направлением
контурного тока.
19

20.

Важно!!!
Для контура с источником тока
уравнение не составляется, так как контурный ток
будет равен току источника тока, через источник тока
должен проходить только один контурный ток.
20

21.

Порядок расчета
• Обозначаются токи ветвей
• Выбираются контурные токи
• Составляется система уравнений по алгоритму
• Находятся контурные токи
• Через контурные токи находятся реальные токи
схемы
21

22.

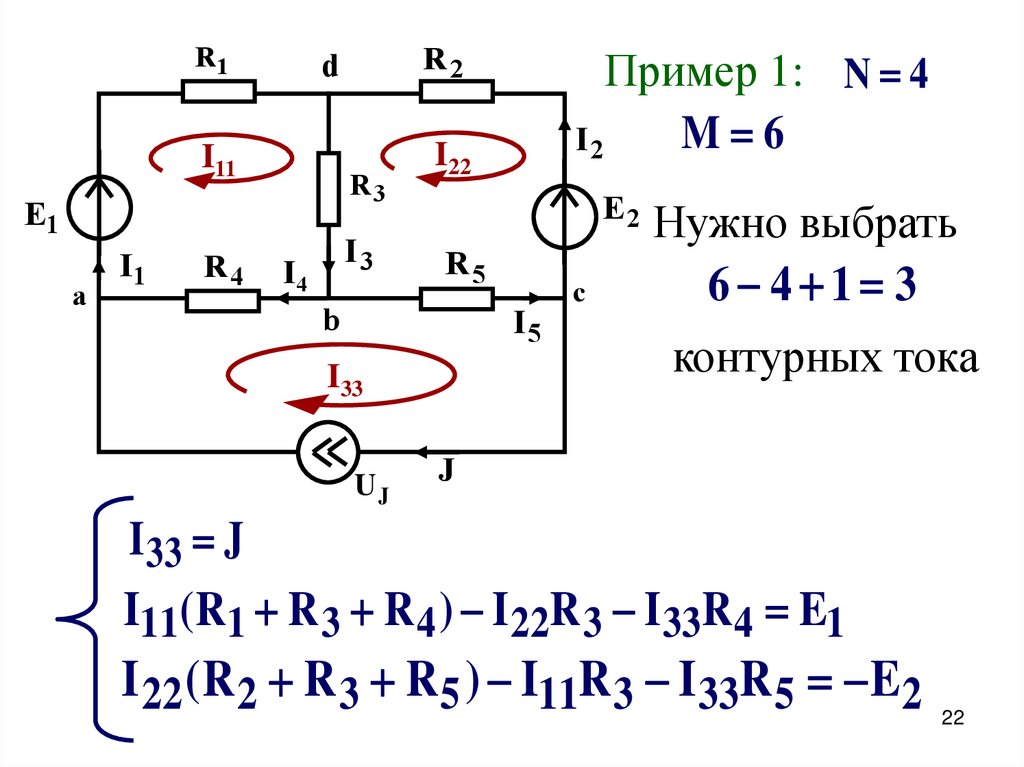
R1
I11
R3
E1
a
I1
R4
R2
d
I3
I4
Пример 1: N 4
M 6
I2
I22
E2
R5
b
I5
I33
UJ
c
Нужно выбрать
6 4 1 3
контурных тока
J
I 33 J
I11( R1 R 3 R 4 ) I 22R 3 I 33R 4 E1
I 22 ( R 2 R 3 R 5 ) I11R 3 I 33R 5 E2
22

23.

R1
I11
R3
E1
a
I1
R4
R2
d
I22
I3
I4
Решаем систему,
I 2 находим контурные
токи, затем находим
E 2 реальные токи
ветвей:
R5
b
I5
I1 I11
I 2 I 22
I33
UJ
c
J
I 4 I11 I 33
I 5 I 22 I 33
I 3 I 22 I11
U J R 4I 4 R 5I 5
23

24.

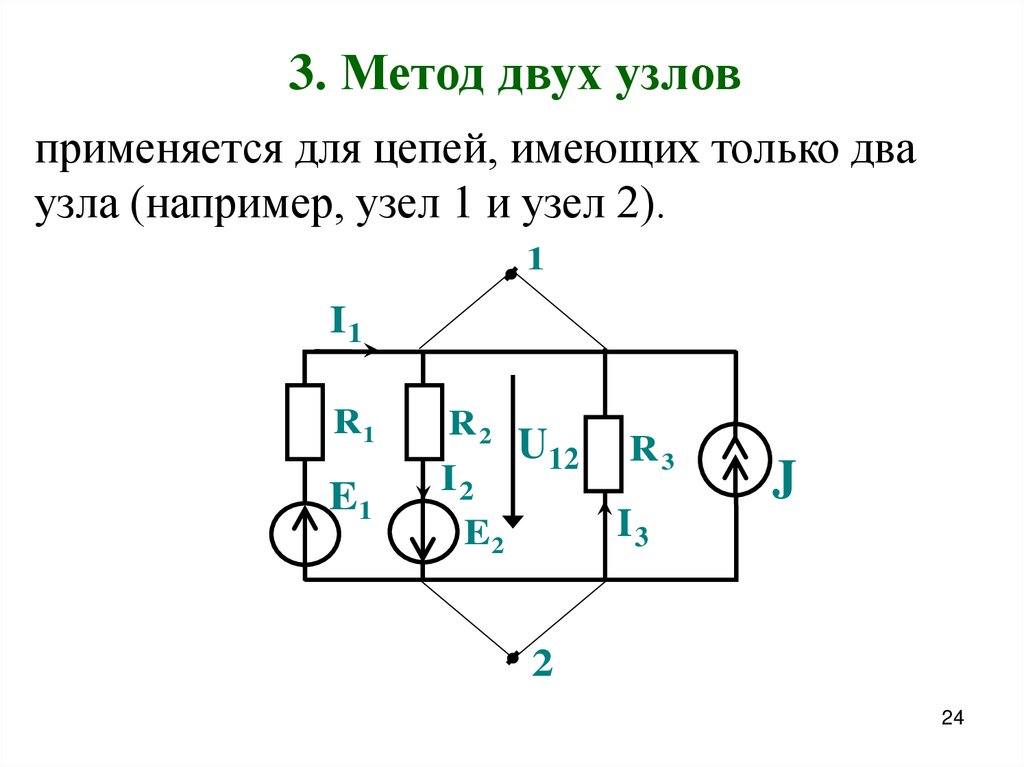
3. Метод двух узлов
применяется для цепей, имеющих только два
узла (например, узел 1 и узел 2).
1
I1
R1
R2
E1
I2
E2
U12
R3
J
I3
2
24

25.

Порядок расчета
1. Вычисляется межузловое напряжение, направленное от узла
1 к узлу 2:
E
n
J
k
R
n
n
k
U12
1
R
m m
En
R – алгебраическая сумма отношений ЭДС ветвей к
n сопротивлениям этих ветвей (с «+», если стрелка ЭДС
n
Jk
k
не совпадает с U12);
– алгебраическая сумма токов источников тока (с «+»,
если его направление не совпадает с U12 );
25

26.

1
R – сумма проводимостей всех ветвей, соединяющих
m
m узлы 1 и 2.
2. Вычисляются токи ветвей по закону Ома:
U12 Ek
Ik
Rk
«+», если направление тока Ik в k-ой ветви совпадает с
направлением U12 и
Ek;
Rk – сопротивление k-ой ветви.
26

27.

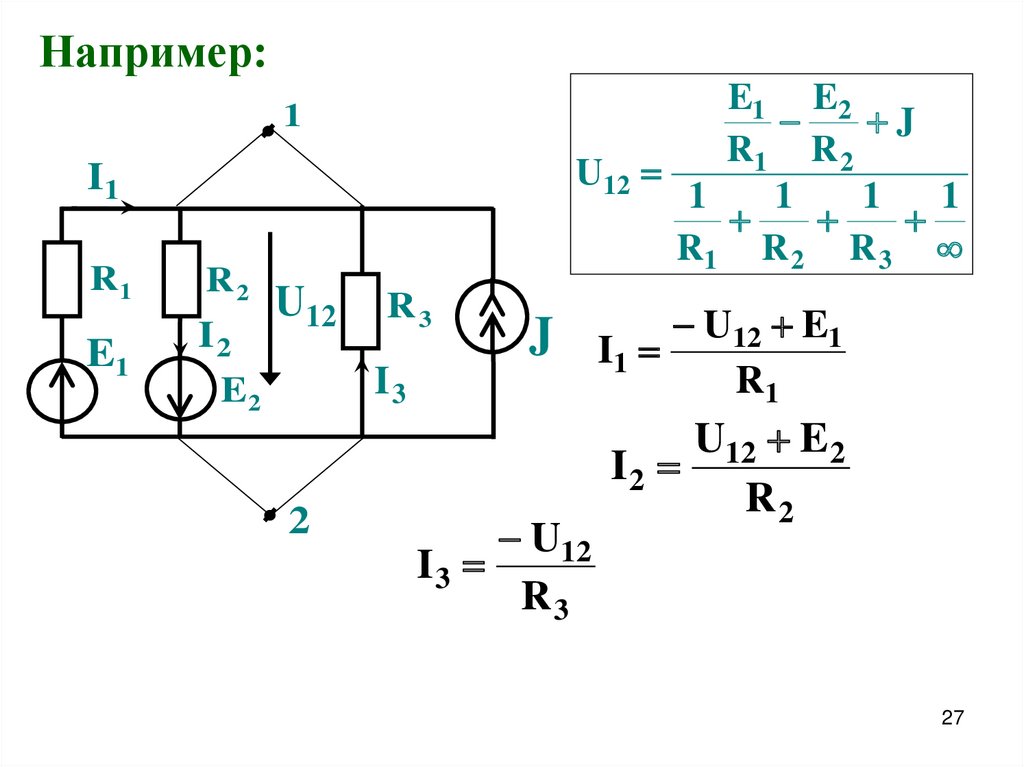
Например:
E1 E2
J
R1 R 2
U12
1
1
1
1
R1 R 2 R 3
1
I1
R1
R2
E1
I2
E2
U12
R3
J
I3
2
U12
I3
R3
U12 E1
I1
R1
U12 E2
I2
R2
27