Законы Кирхгофа. (Лекция 2)

1.

ВУНЦ ВВС «ВВА» (филиал, г. Краснодар)
Кафедра физики и электротехники
Учебная дисциплина
Электротехника и электроника
Тема 1/2
Законы Кирхгофа
Лекция № 2

2.

Учебные вопросы:
1. Первый и второй законы Кирхгофа
2. Последовательное соединение элементов
электрической цепи. Делители напряжения
3. Параллельное соединение элементов электрической
цепи. Делители тока
Литература:
Бухонский М.И., Найдёнов С.В., Тельнов Г.В. Электротехника и электроника.
Аналоговая схемотехника. Часть 1: Учебное пособие.– Краснодар: Филиал
ВУНЦ ВВС «ВВА имени проф. Н.Е.Жуковского и Ю.А.Гагарина» (г. Краснодар),
2011.– с. 26-52.

3.

1. Первый и второй законы Кирхгофа.
В 1845 г. немецким физиком Г. Кирхгофом были
сформулированы
два
закона
разветвленных
электрических цепей, которые имеют огромное значение
для теоретической и практической электротехники.
Законы
Кирхгофа
являются
двумя
основными
постулатами, на которых построена теория цепей.
Первый закон Кирхгофа – закон токов Кирхгофа
(ЗТК) применяется к узлам ЭЦ.
Второй закон Кирхгофа – закон напряжений
Кирхгофа (ЗНК) применяется к контурам ЭЦ .

4.

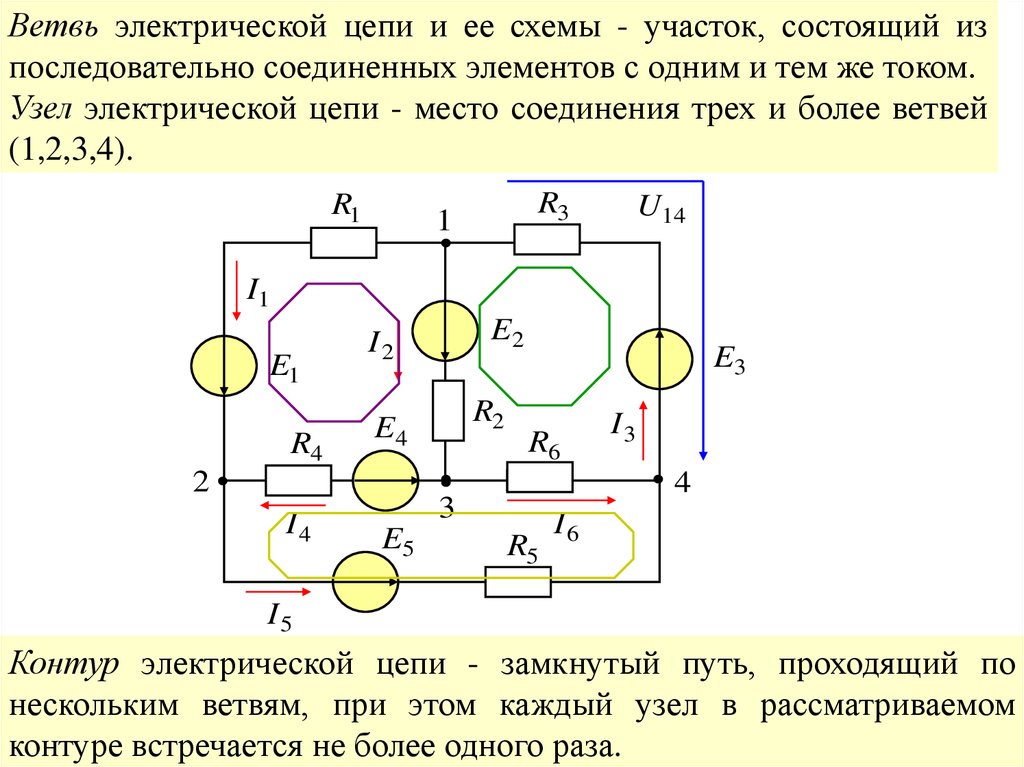
Ветвь электрической цепи и ее схемы - участок, состоящий из
последовательно соединенных элементов с одним и тем же током.
Узел электрической цепи - место соединения трех и более ветвей
(1,2,3,4).
R1
R3
1
U14
I1
E1
R4
R2
E4
2
I4
E2
I2
E3
R6
4
3
E5
I3
R5
I6
I5
Контур электрической цепи - замкнутый путь, проходящий по
нескольким ветвям, при этом каждый узел в рассматриваемом
контуре встречается не более одного раза.

5.

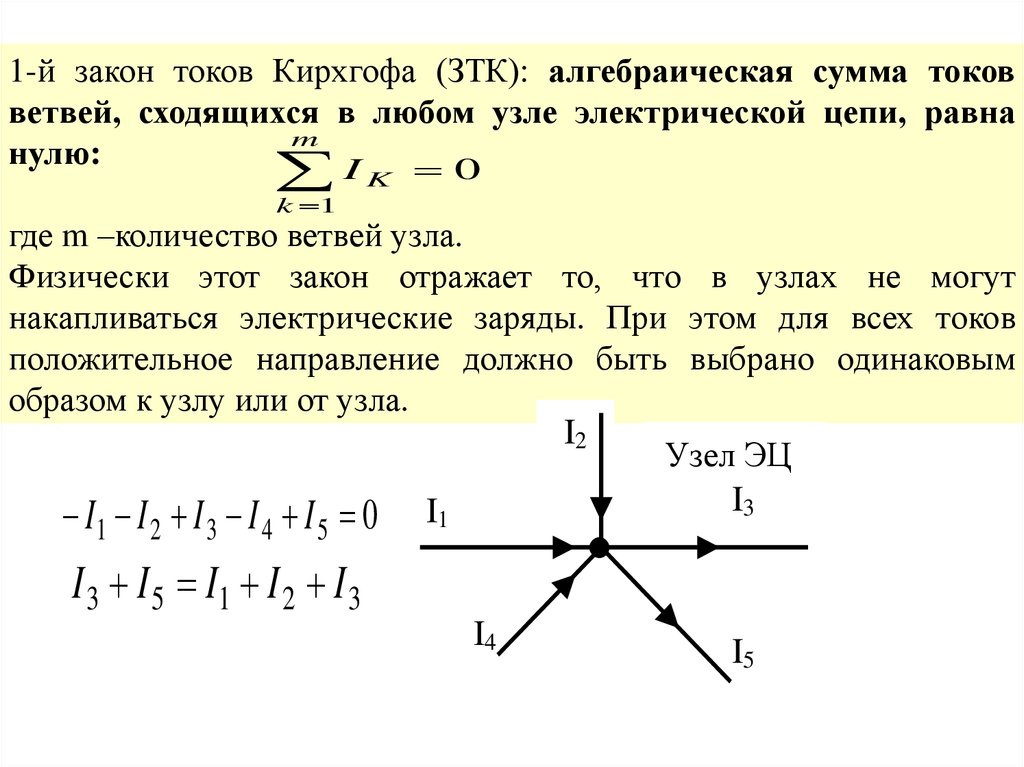
1-й закон токов Кирхгофа (ЗТК): алгебраическая сумма токов
ветвей, сходящихся в любом узле электрической цепи, равна
m
нулю:
I
0
k 1
K
где m –количество ветвей узла.
Физически этот закон отражает то, что в узлах не могут
накапливаться электрические заряды. При этом для всех токов
положительное направление должно быть выбрано одинаковым
образом к узлу или от узла.
I2
Узел ЭЦ
I3
I1
I1 I 2 I 3 I 4 I 5 0
I 3 I 5 I1 I 2 I 3
I4
I5

6.

äëÿ óçëà1 I1 I 2 I 3 0
äëÿ óçëà 2 I 5 I1 I 4 0
äëÿ óçëà3 I 4 I 6 I 2 0
äëÿ óçëà 4 I 3 I 5 I 6 0
Если в электрической схеме имеются источники тока, то они
должны учитываться при составлении уравнений для
соответствующих узлов. Другая формулировка первого закона
Кирхгофа: алгебраическая сумма токов ветвей равна алгебраической
сумме токов, обусловленных источниками тока:
m
p
k 1
n 1
Ik Jn
где р – количество источников тока подсоединенных к
рассматриваемому узлу. Ток , берется со знаком «+», если он
направлен к узлу, из него «–».

7.

2-й закон напряжений Кирхгофа (ЗНК): алгебраическая
сумма напряжений ветвей в любом контуре
электрической цепи равна нулю:
l
U k 0
k 1
для контура 1 3 2 1 E1 I 1 R1 E 2 I 2 R2 E 4 I 4 R4 0
для контура 1 4 3 1 E 2 I 3 R3 E3 I 6 R6 I 2 R2 0
для контура 2 3 4 2 E 4 I 4 R4 I 6 R6 I 5 R5 E5 0
другая формулировка второго закона Кирхгофа: в любом
замкнутом контуре электрической цепи алгебраическая сумма
напряжений на всех элементах контура, равна алгебраической
сумме Э.Д.С., действующих в этом контуре:
m
p
k 1
n 1
I k Rk En

8.

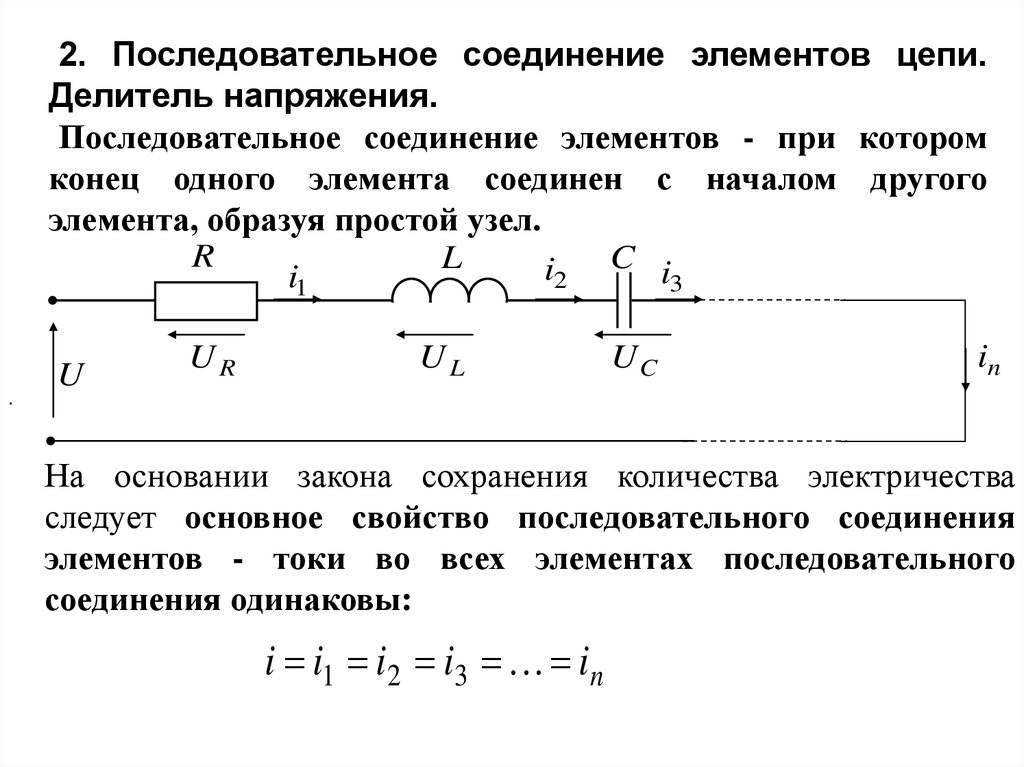
2. Последовательное соединение элементов цепи.
Делитель напряжения.
Последовательное соединение элементов - при котором
конец одного элемента соединен с началом другого
элемента, образуя простой узел.
R
L
i2 C i3
i1
.
U
UR
UL
UC
in
На основании закона сохранения количества электричества
следует основное свойство последовательного соединения
элементов - токи во всех элементах последовательного
соединения одинаковы:
i i1 i 2 i3 i n

9.

Последовательное соединение активных сопротивлений
U
R1
R2
R3
U1
U2
U3
Un
Rn
i
U U1 U 2 U 3 U n 0
или
В соответствии с законом Ома
U U1 U 2 U 3 U n
iRЭ iR1 iR2 iR3 iRn т.к. i одинаков, то
RЭ R1 R2 R3 Rn
Эквивалентное сопротивление последовательно соединенных
активных сопротивлений равно сумме всех активных
сопротивлений данной электрической цепи.
Следствие:
U1 R1
U 2 R2

10. Последовательное соединение индуктивностей.

U
L1
L2
U1
U2
Имеем U K LK
L3
Un
U3
Ln
i
di
.
dt
Тогда:
di
di
di
di
di
LЭ L1 L2 L3 Ln
.
dt
dt
dt
dt
dt
di
Т.к.
dt
одинаков
LЭ L1 L2 L3 Ln
эквивалентная (общая) индуктивность последовательного
соединения индуктивностей равна сумме индуктивностей,
образующих последовательное соединение.

11.

Следствие:
Имеем:
1
iK
U K dt
LK
U1 U 2
L1 L2
или
Тогда:
U1 L1
U 2 L2
.
Вывод: напряжения на последовательно соединенных
индуктивностях распределяются пропорционально величинам
индуктивностей, входящих в последовательное соединение.

12.

Последовательное соединение емкостей
U
C1
C2
C3
U1
U2
U3
Известно, что
Un
Cn
i
UK
1
CK
i dt
1
1
1
1
1
i
dt
i
dt
i
dt
i
dt
i dt
CЭ
C1
C2
C3
Cn
получим
1
1
1
1
1
CЭ C1 C2 C3
Cn
при последовательном соединении емкостей обратная величина
эквивалентной емкости равна сумме обратных величин всех
емкостей, входящих в данное соединение.

13.

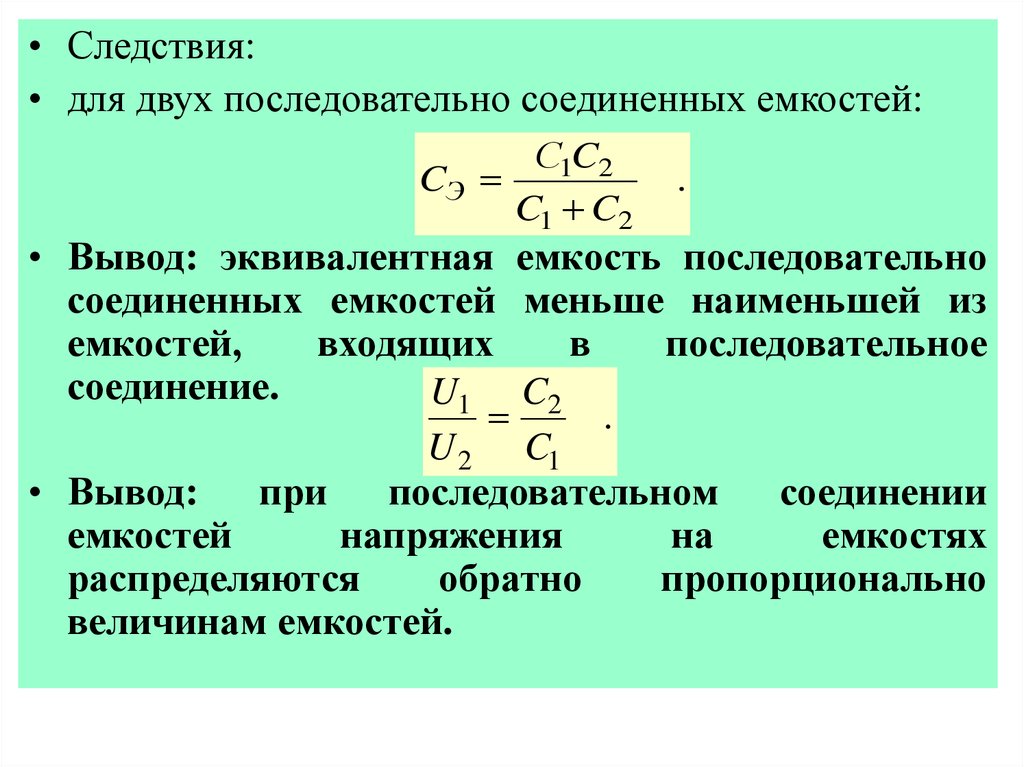
• Следствия:
• для двух последовательно соединенных емкостей:
С1C2
CЭ
C1 C2
.
• Вывод: эквивалентная емкость последовательно
соединенных емкостей меньше наименьшей из
емкостей,
входящих
в
последовательное
соединение.
U1 C2
.
U 2 C1
• Вывод:
при
последовательном
соединении
емкостей
напряжения
на
емкостях
распределяются
обратно
пропорционально
величинам емкостей.

14.

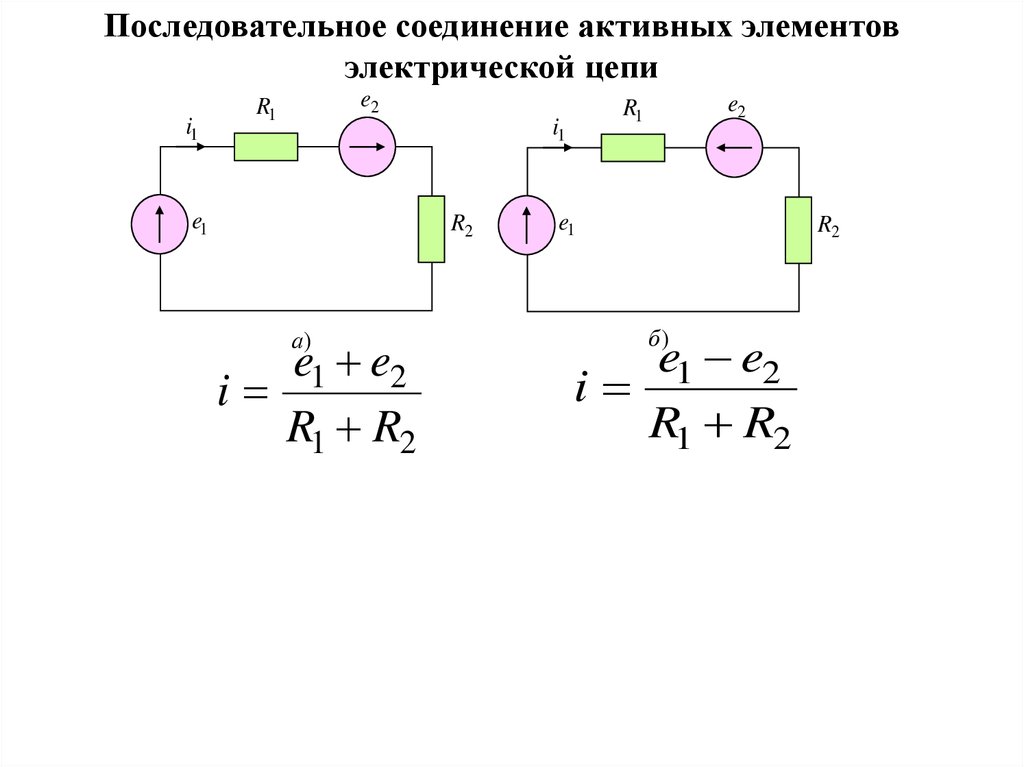
Последовательное соединение активных элементов
электрической цепи
i1
e2
R1
i1
e1
R2
а)
e1 e2
i
R1 R2
e2
R1
e1
R2
б)
e1 e2
i
R1 R2

15.

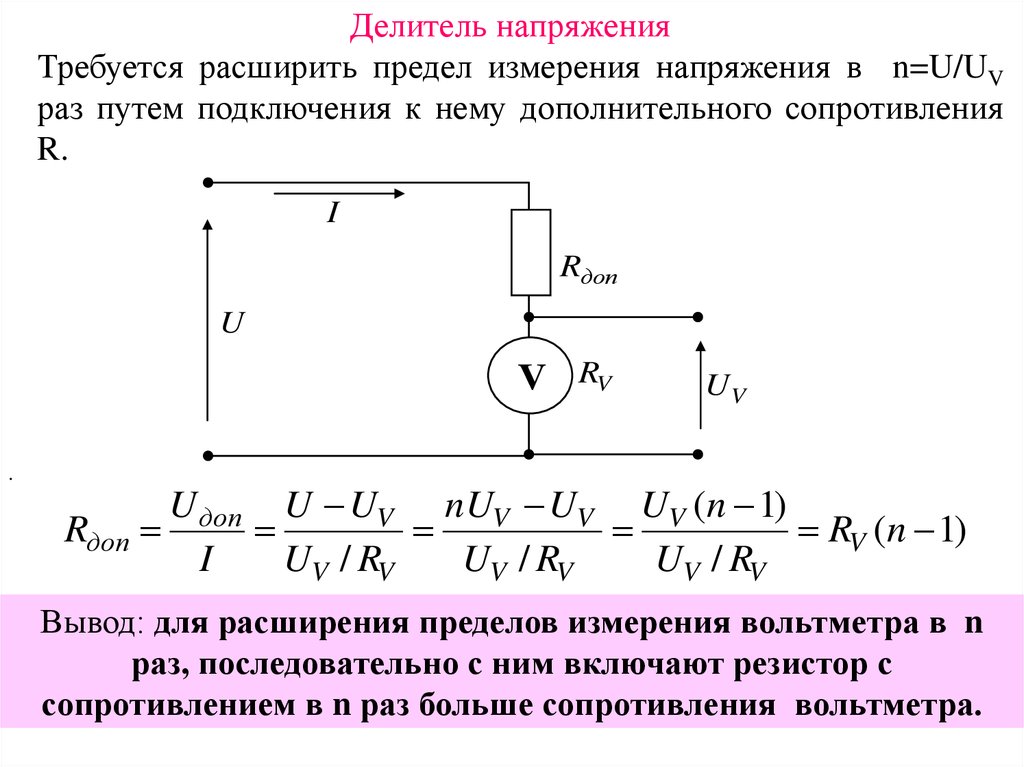
Делитель напряжения
Требуется расширить предел измерения напряжения в n=U/UV
раз путем подключения к нему дополнительного сопротивления
R.
I
Rдоп
U
V RV
.
UV
U доп U UV nUV UV UV (n 1)
Rдоп
RV (n 1)
I
UV / RV
UV / RV
UV / RV
Вывод: для расширения пределов измерения вольтметра в n
раз, последовательно с ним включают резистор с
сопротивлением в n раз больше сопротивления вольтметра.

16.

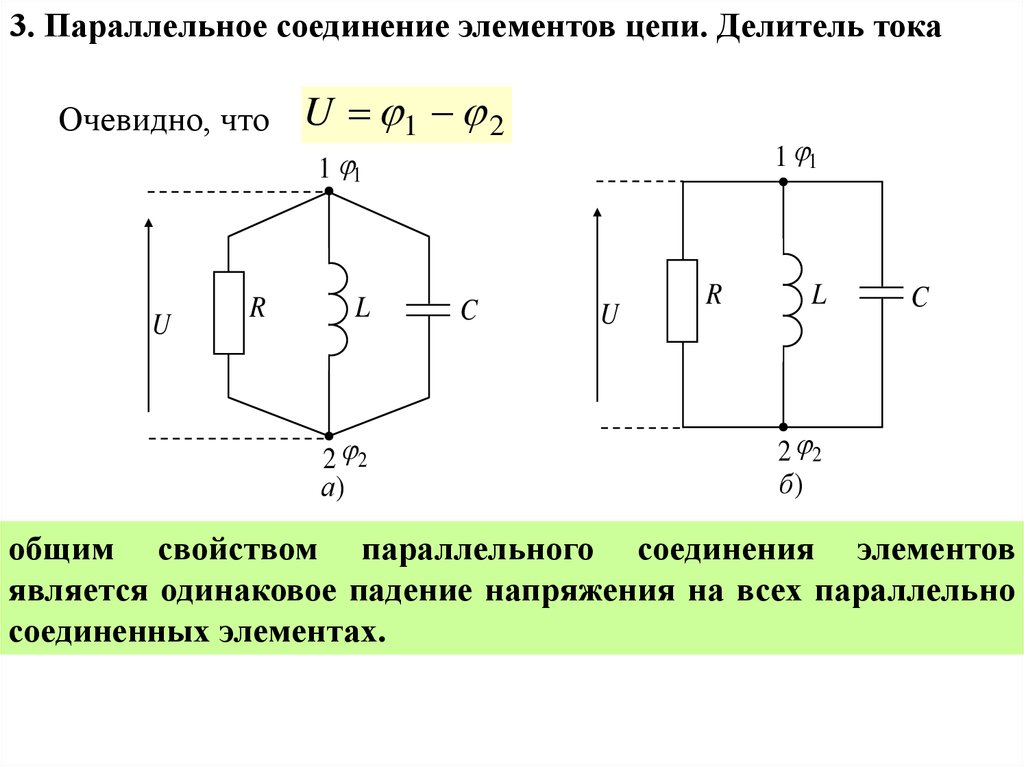
3. Параллельное соединение элементов цепи. Делитель тока
Очевидно, что
U 1 2
1 1
1 1
U
R
L
2 2
а)
C
U
R
L
C
2 2
б)
общим свойством параллельного соединения элементов
является одинаковое падение напряжения на всех параллельно
соединенных элементах.

17.

1 1
i
i1
U
i2
R1
R2
i3
R3
in
Rn
2 2
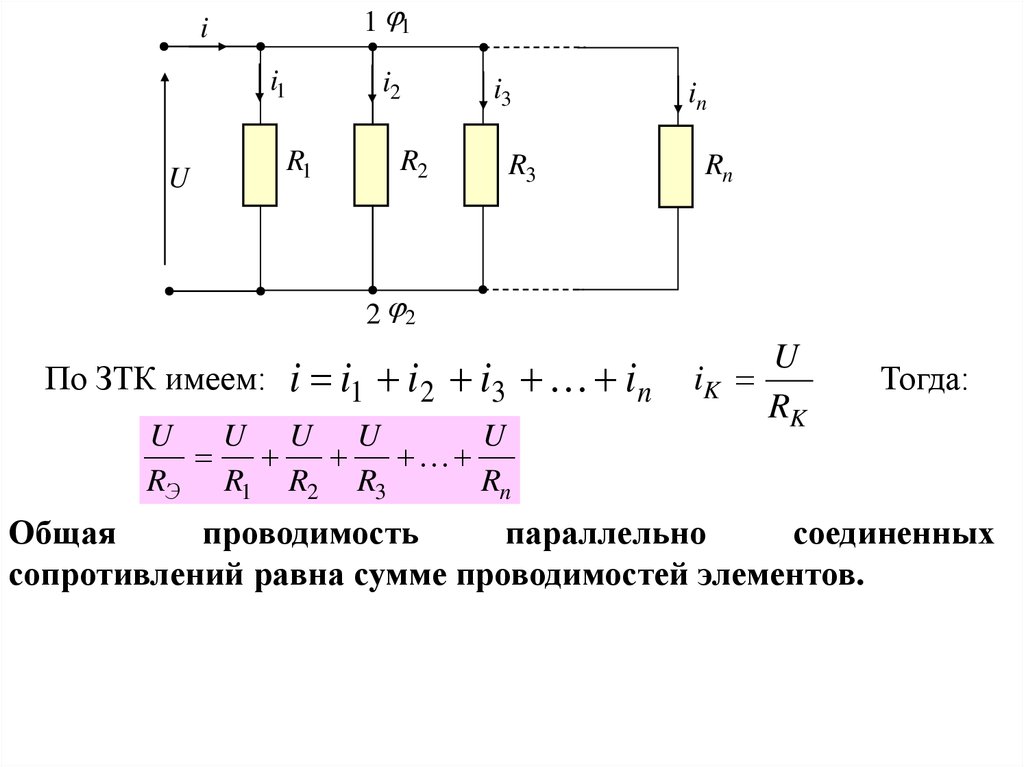
По ЗТК имеем:
i i1 i 2 i3 i n
U
U U U
U
RЭ R1 R2 R3
Rn
U
iK
RK
Тогда:
Общая
проводимость
параллельно
соединенных
сопротивлений равна сумме проводимостей элементов.

18.

Следствия:
при параллельном соединении резисторов
R1 R2
эквивалентное сопротивление меньше
RЭ
R1 R2
наименьшего, входящего в параллельное
соединение.
i1 R2
i 2 R1
токи в параллельных ветвях распределяются
обратно пропорционально сопротивлениям
ветвей.
Полученные выводы аналогичны для соединения
индуктивностей

19.

Параллельное соединение емкостей в электрической цепи.
1 1
i
i1
U
Имеем:
dU
iK CK
dt
C1
i2
i3
C2
in
Cn
C3
2 2
m
I
тогда с учетом ЗТК
dU
dU
dU
dU
dU
С
C1
C2
C3
Cn
dt
dt
dt
dt
dt
k 1
.
k
или
С Э С1 С 2 С 3 С n
эквивалентная (общая) емкость параллельно соединенных
конденсаторов равна сумме их емкостей.
токи в ветвях параллельно соединенных конденсаторов
распределяются пропорционально величинам их емкостей.

20.

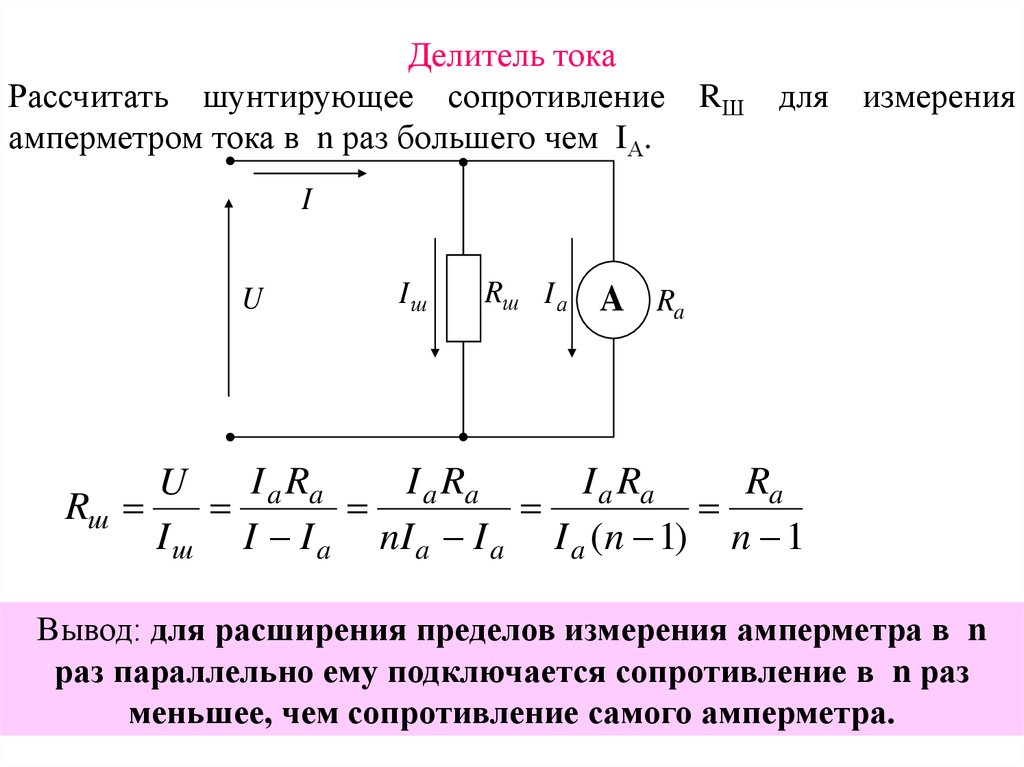
Делитель тока
Рассчитать шунтирующее сопротивление RШ для измерения
амперметром тока в n раз большего чем IА.
I
U
Iш
Rш I а
A Ra
I a Ra
I a Ra
I a Ra
Ra
U
Rш
I ш I I a nI a I a I a (n 1) n 1
Вывод: для расширения пределов измерения амперметра в n
раз параллельно ему подключается сопротивление в n раз
меньшее, чем сопротивление самого амперметра.

21.

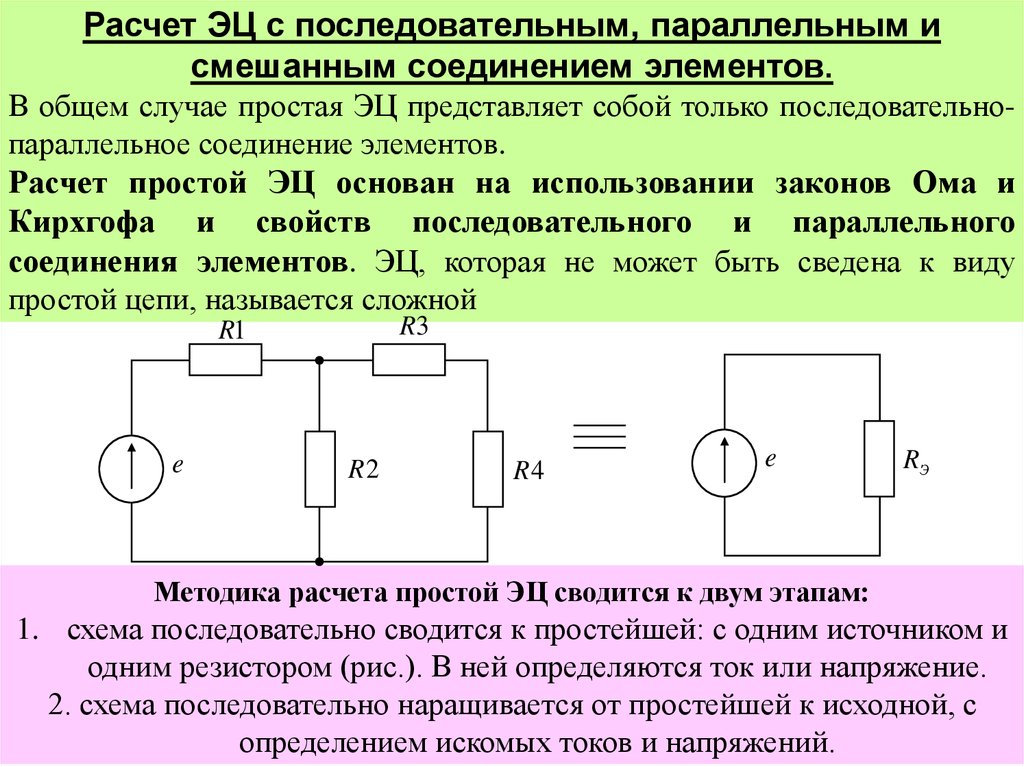
Расчет ЭЦ с последовательным, параллельным и
смешанным соединением элементов.
В общем случае простая ЭЦ представляет собой только последовательнопараллельное соединение элементов.
Расчет простой ЭЦ основан на использовании законов Ома и
Кирхгофа и свойств последовательного и параллельного
соединения элементов. ЭЦ, которая не может быть сведена к виду
простой цепи, называется сложной
R3
R1
e
R2
R4
e
Rэ
Методика расчета простой ЭЦ сводится к двум этапам:
1. схема последовательно сводится к простейшей: с одним источником и
одним резистором (рис.). В ней определяются ток или напряжение.
2. схема последовательно наращивается от простейшей к исходной, с
определением искомых токов и напряжений.

22.

Выберем направление обхода контура по часовой стрелке и запишем
уравнение в соответствии со 2 законом Кирхгофа и с учетом направления тока:
e1 U1 e2 U 2 0
Преобразуем уравнение:
e1 e2 U1 U 2
Получим схему на рис. б. Если принять, что э.д.с. эквивалентного источника
еэ e1 e2
то можно записать:
eэ U1 U 2
В результате цепь сведена к цепи с одним источником э.д.с. (рис., в).
e2
e2
R1
U1
i
R1
U1
i
U2
а)
i
U1
R2
R2
e1
R1
U2
e1
б)
R2
U2
eэ
в)

23.

Пусть дана параллельная резистивная цепь (рис. а). Известна сила тока и
величины сопротивлений и . Необходимо определить напряжение и силу тока,
протекающего через резисторы .
i0
1
i1
R1 U
i
i2
i0
R2
i
U
2
а)
б)
Rэ

24.

Решение:
1. Преобразовать цепь к эквивалентному виду (рис. б) и определить общее
сопротивление цепи:
R1R2
Rэ
R1 R2
Gэ G1 G 2
2. Определить падение напряжения на
U i0 Rэ i0
Rэ
R1R2
i0
U i0 / Gэ
R1 R2
G1 G 2
3. Определим токи в резисторах:
U
R2
i1
i0
R1
R1 R 2
i2
U
R1
i0
R2
R1 R2
i1 UG1 i0
G1
G1 G2
i1 UG2 i0
G2
G1 G2

25.

Пусть дана цепь с параллельно– последовательным соединением резисторов
(рис. 9, а). Известны значение ЭДС источника , величины сопротивлений.
Определить силу тока во всех ветвях схемы, и напряжения на каждом резисторе.
R1
I1
E0
R1
R3
I1
I3,4
I2
R4
R2
E0
I3,4
I2
R2
а)
R1
б)
I1
I1
E0
R2 4
в)
E0
R3,4
RЭ
г)

26.

Решение:
1. В соответствии со свойством последовательного соединения элементов, определим
R3,4 R3 R4
Схема примет вид, показанный на рис. 9 б.
2. В соответствии со свойством параллельного соединения элементов, определим
R2, 4
R2 R3, 4
R2 R3, 4
Схема примет вид, показанный на рис. 9 в.
3. Рассчитываем эквивалентное сопротивление цепи:
RЭ R1 R2 4
4. По закону Ома рассчитываем ток
5. Ток протекает
I1
I1
E0
RЭ
через последовательно соединенные резисторы
следовательно, можно найти падения напряжения на резисторах
U1 I1R1
U 2 I1R2 4
По второму закону Кирхгофа делаем проверку
U 1 U 2 E0
R1и R2 4