Similar presentations:
Законы Кирхгофа
1.
12.
23.
Законы Кирхгофасправедливы для линейных и
нелинейных цепей при
постоянных и переменных
напряжениях и токах
3
4.
45.
Для любого узла цепиалгебраическая сумма токов
равна нулю,
причем со знаком “ + ”
принимаются токи,
входящие в узел
5
6.
i0
k
6
7.
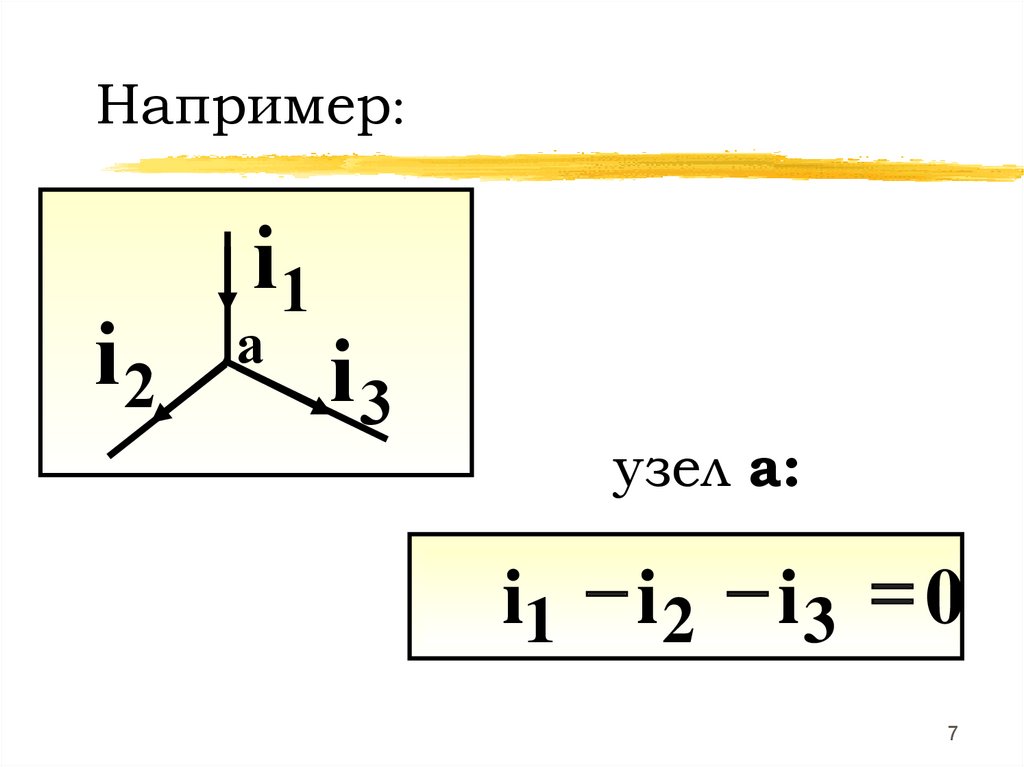
Например:i2
i1
а
i3
узел а:
i1 - i 2 - i 3 0
7
8.
Физически первый законКирхгофа –
это закон непрерывности
электрического тока
8
9.
910.
Для любого контура цепиалгебраическая сумма напряжений
на пассивных элементах и источниках
тока
равна алгебраической сумме
ЭДС
10
11.
Со знаком “+”принимаются те слагаемые,
положительные направления
которых совпадают с
направлением обхода
контура
11
12.
ik Rk uJ k ek12
13.
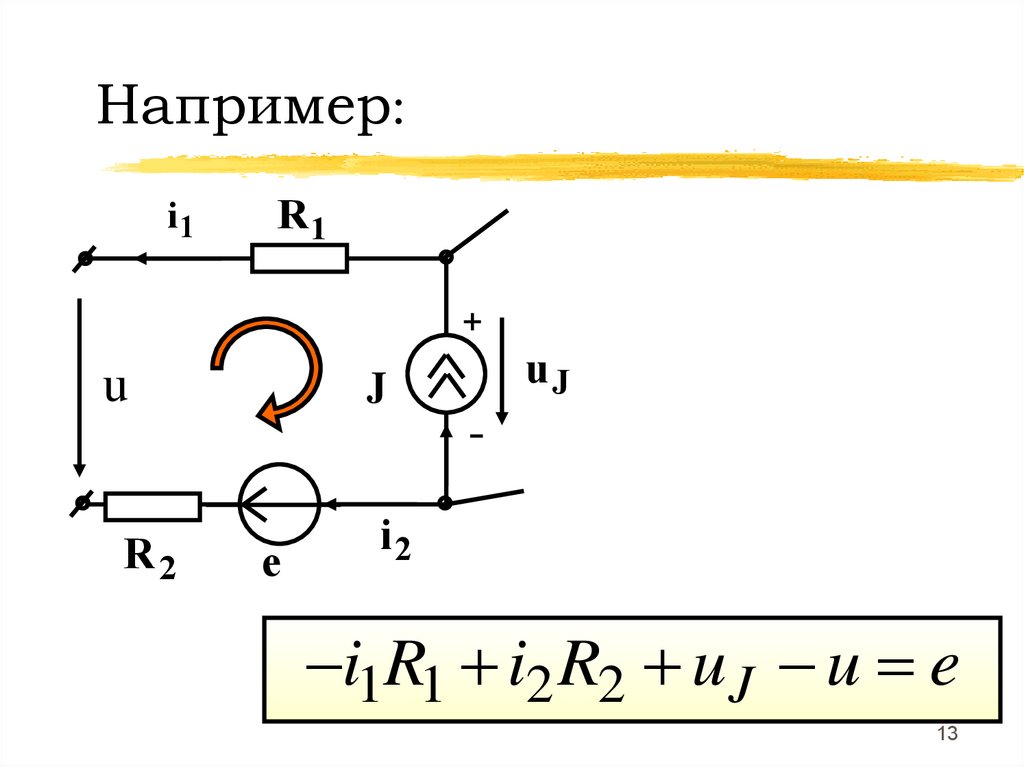
Например:i1
R1
+
u
uJ
J
R2
e
i2
-i1R1 i2 R2 uJ - u e
13
14.
Физически второй законКирхгофа характеризует
равновесие напряжений
в любом контуре цепи
14
15.
1516.
Решение системы уравнений,составленных по законам
Кирхгофа, позволяет
определить все токи и
напряжения в рассматриваемой
цепи
16
17.
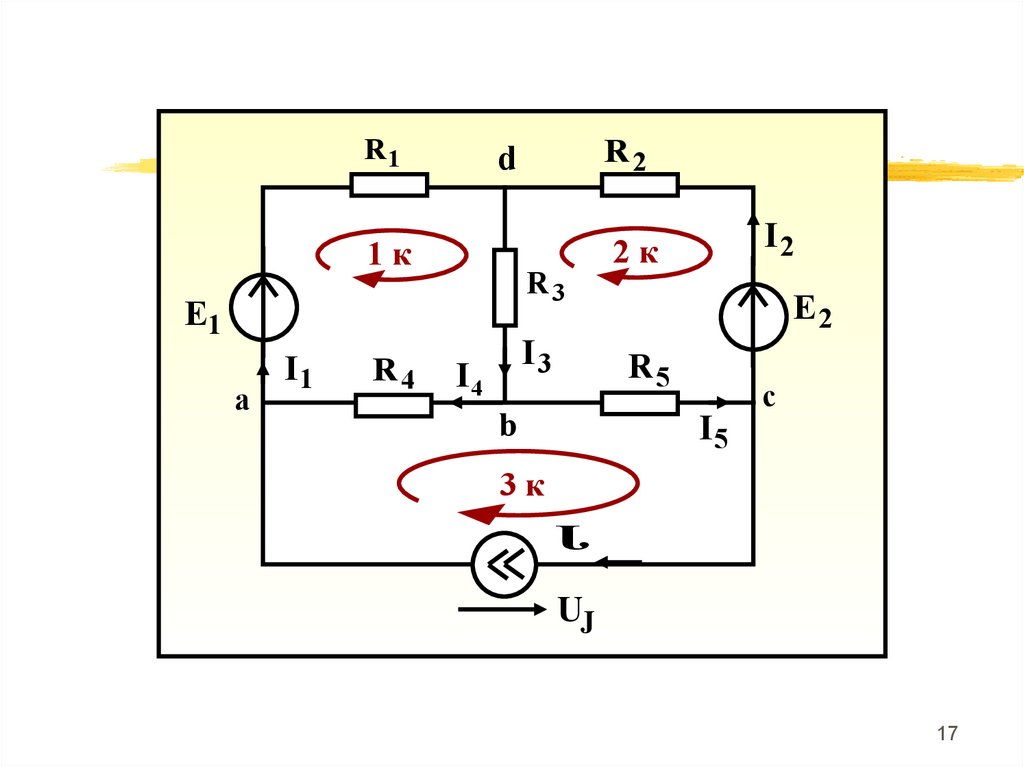
R11к
R3
E1
a
I1
R4
R2
d
I3
I4
I2
2к
E2
R5
b
I5
c
3к
J
UJ
17
18.
nу 4nв 6
n1 n у - 1 3
n 2 nв - n1 3
18
19.
a:I1 - I 4 - J 0
b : - I3 I4 I5 0
c:
I2 - I5 J 0
19
20.
R1I1 R3 I 3 R4 I 4 E12к : - R2 I 2 - R3 I 3 - R5 I 5 - E2
1к :
3к : - R4 I 4 R5 I 5 - U J 0
20
21.
ab
c
1к
2к
3к
I1 I 2 I 3 I 4 I 5
0
0 -1
0
1
0
1
1
0 -1
0 0 -1
1
0
R 0 R R 0
4
3
1
0 - R 2 - R 3 0 - R 5
0 - R4 R5
0
0
UJ
0 I1 J
0
0 I2
0 I 3 - J
0 I 4
E
1
0 I 5 - E 2
- 1 U J 0
21
22.
2223.
Для любого момента временисумма вырабатываемых
мощностей источников равна
сумме потребляемых мощностей
во всех пассивных элементах
рассматриваемой цепи
23
24.
ek i k U J q J q u n i nили
PВ PП
24
25.
Эта теорема является закономсохранения энергии в
электрической цепи и
применяется как баланс
мощностей для проверки
правильности расчетов
25
26.
2627.
Составим баланс мощностейдля резистивной цепи
с постоянными напряжениями
и токами
предыдущего примера
27
28.
Pв Е1I1 Е2I 2 U J J ... Вт2
2
2
2
2
Pп I1 R1 I 2R 2 I 3R 3 I 4 R4 I 5R5
... Вт
28
29.
Pв - Р пр %
100 3%
Pв
29
30.
3031.
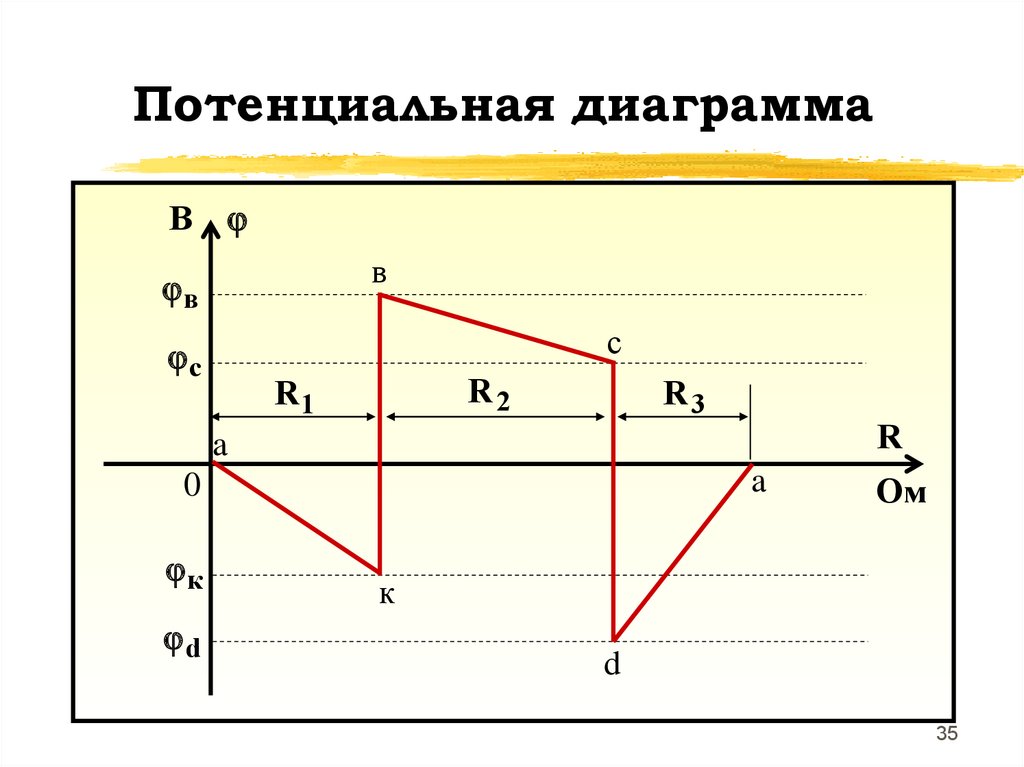
Потенциальная диаграмма это графическое изображениевторого закона Кирхгофа,
которая применяется для
проверки правильности расчетов
в линейных резистивных цепях
31
32.
Потенциальная диаграммастроится для контура без
источников тока, причем
потенциалы точек начала и
конца диаграммы должны
получиться одинаковыми
32
33.
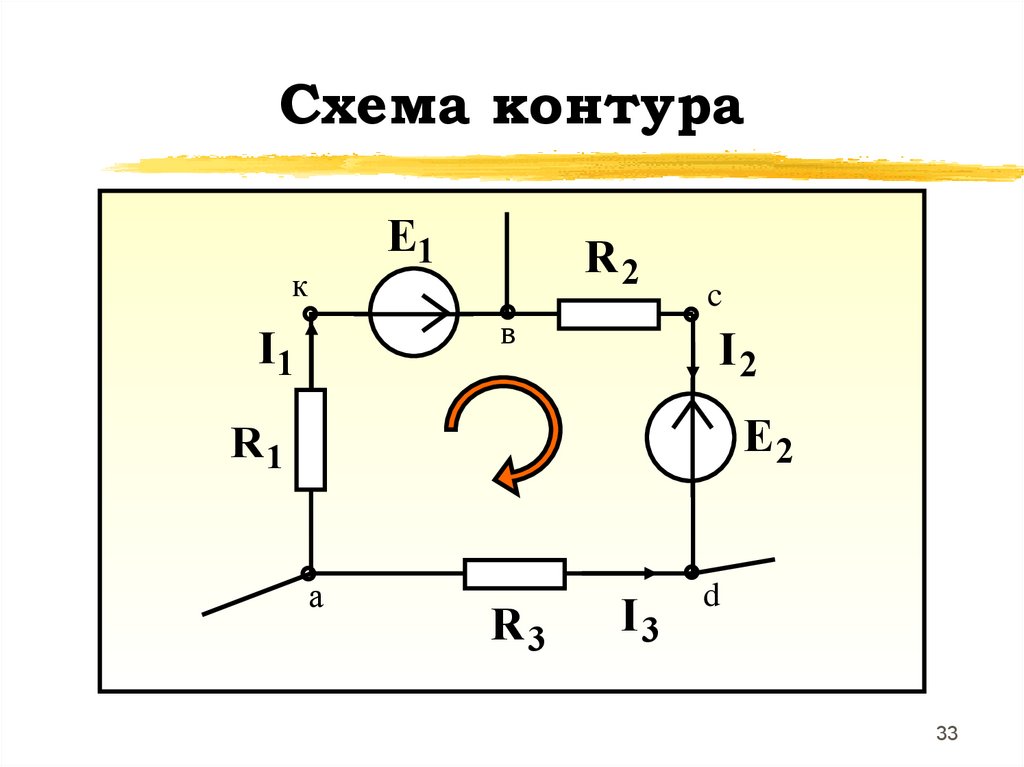
Схема контураE1
к
R2
в
I1
c
I2
E2
R1
а
R3
I3
d
33
34.
Потенциалы точек контура:a 0
к а - I 1R 1
в к Е1
c в - I 2 R 2
d c - E 2
a d I 3 R 3 0
34
35.
Потенциальная диаграммаB
в
в
с
c
R2
R1
R3
R
a
a
0
к
d
Ом
к
d
35
36.
3637.
Теорема компенсации справедливадля линейных и нелинейных
цепей и может быть доказана
при помощи законов Кирхгофа
37
38.
Любой элемент цепи можнозаменить источником ЭДС
или источником тока, причем
ЭДС равна напряжению элемента,
а ток источника равен току
этого элемента
38
39.
+i
a
+
u
а
+
i
e=u
b
u
b
a
+
J=i
u
b
39
40.
Теорему компенсации удобноиспользовать если задано
напряжение u или ток i
на участке цепи
40
41.
4142.
Свойства линейных цепейрассмотрим на примере
резистивных цепей с
постоянными напряжениями
и токами, причем эти свойства
могут быть доказаны при помощи
законов Ома и Кирхгофа
42
43. 1. Принцип наложения
Ik(n )
Ik
43
44.
Ток (напряжение) в любой ветвиможно рассматривать как
алгебраическую сумму
составляющих от действия
каждого источника
в отдельности
44
45.
При этом со знаком “+”пишутся те составляющие,
направления которых совпадает
с направлением результирующих
величин
45
46.
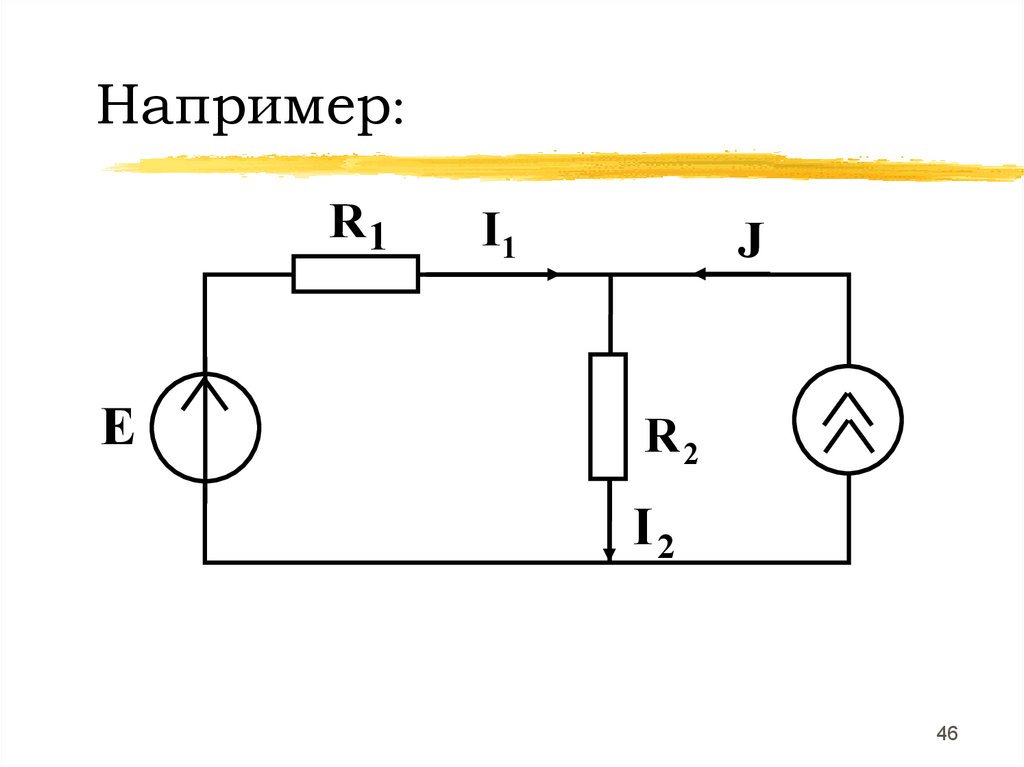
Например:R1
E
I1
J
R2
I2
46
47.
а) подсхема с ЭДС ЕR1
I1(E)
E
R2
I1(E)=E/(R1+R2)
47
48.
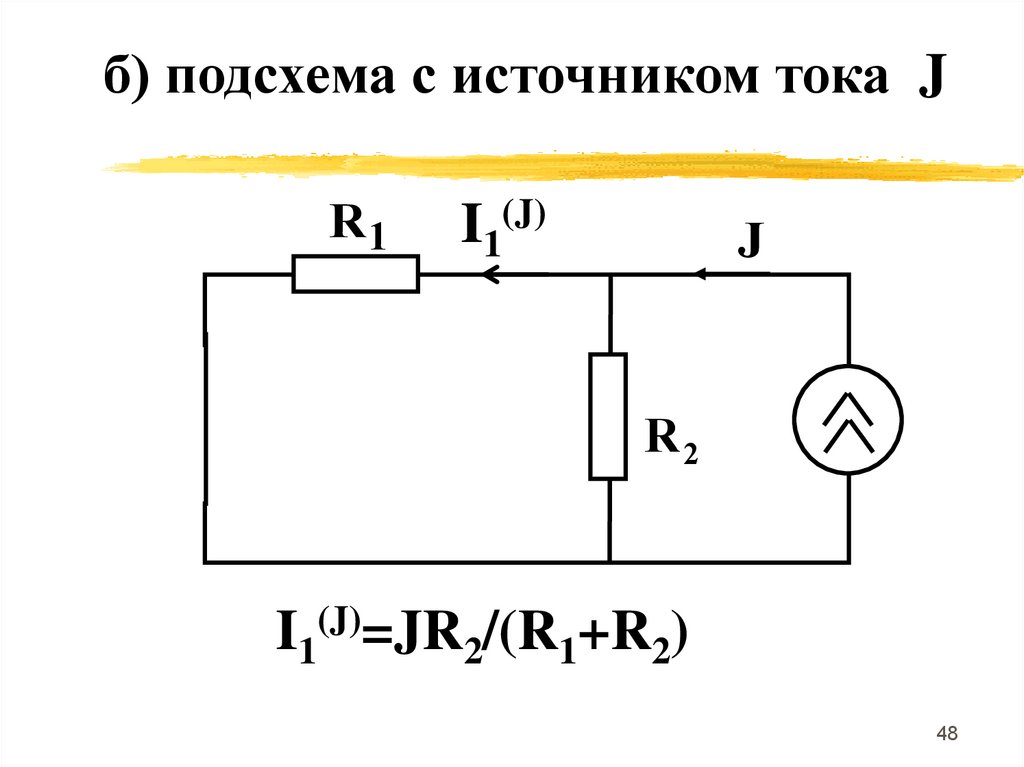
б) подсхема с источником тока JR1
E
I1(J)
J
R2
I1(J)=JR2/(R1+R2)
48
49.
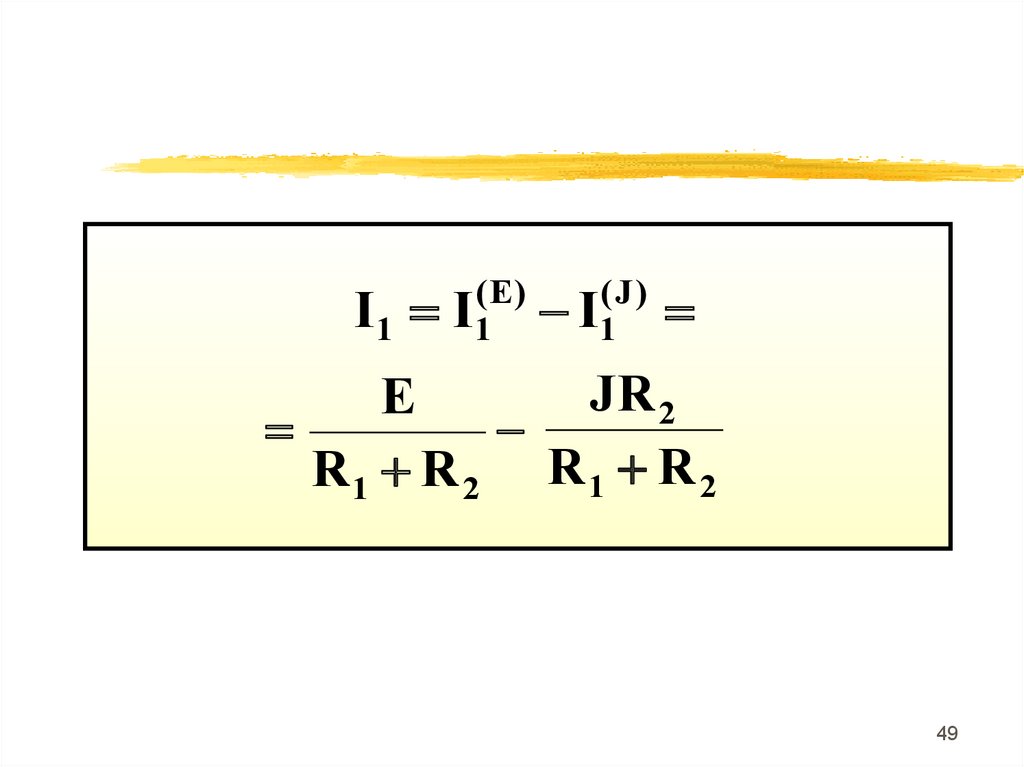
I1( E)
I1
(J)
- I1
JR 2
E
R1 R 2 R 1 R 2
49
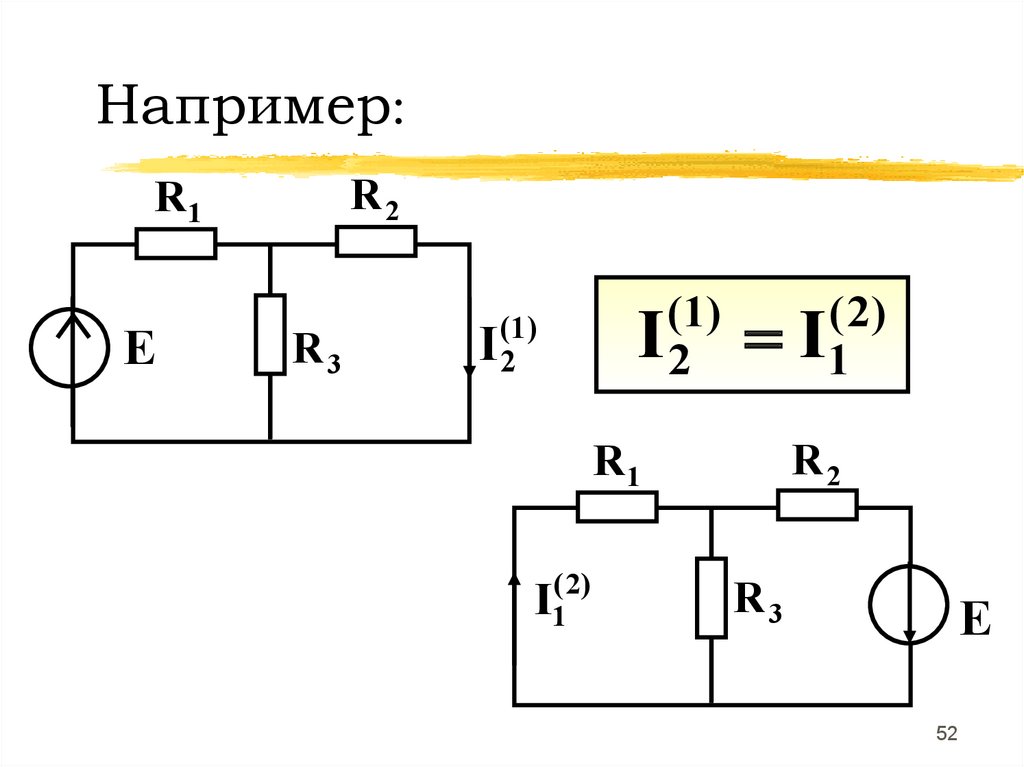
50. 2. Принцип взаимности
(m )In
(n )
Im
50
51.
Перестановка единственногоисточника ЭДС из ветви m
в ветвь n создает в ветви m ток,
равный току в ветви n
до перестановки источника
51
52.
Например:R2
R1
E
R3
(1)
I2
(1)
I2
R2
R1
I1( 2)
( 2)
I1
R3
E
52
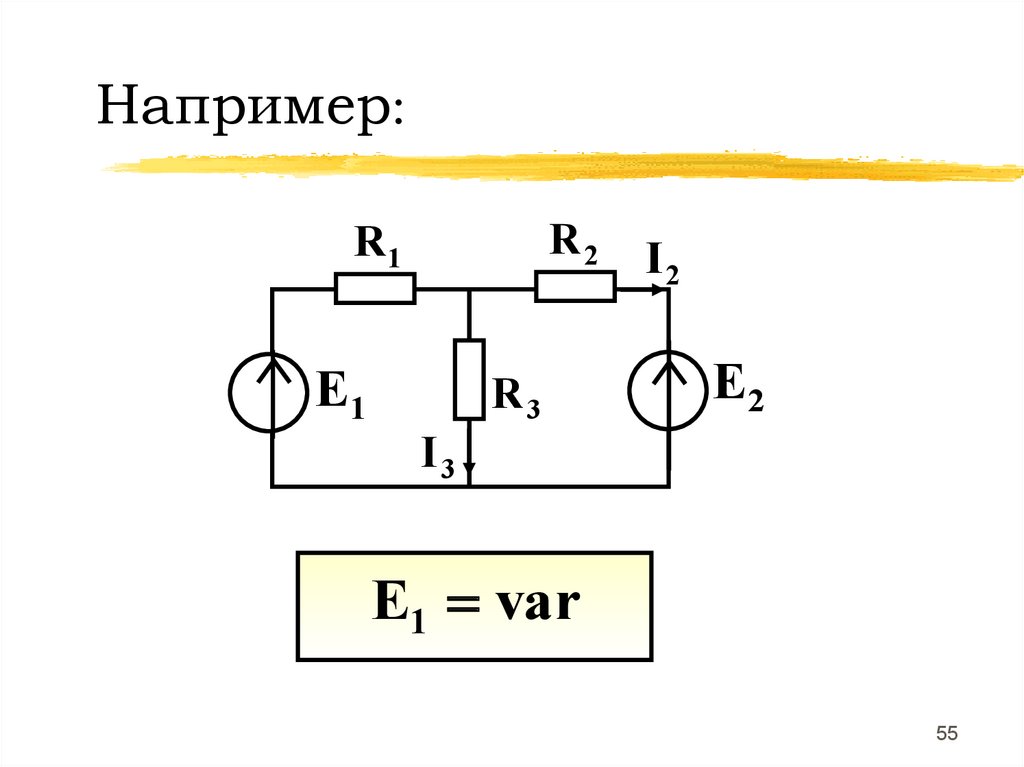
53. 3. Свойство линейности
y=ax+bгде y и x-напряжения или токи,
а, b - постоянные коэффициенты
53
54.
При изменении в цепи одногопараметра (ЭДС, ток источника
тока, сопротивление резистивного
элемента) между
двумя токами (напряжениями)
существует линейная
зависимость
54
55.
Например:R2
R1
E1
R3
I2
E2
I3
E1 var
55
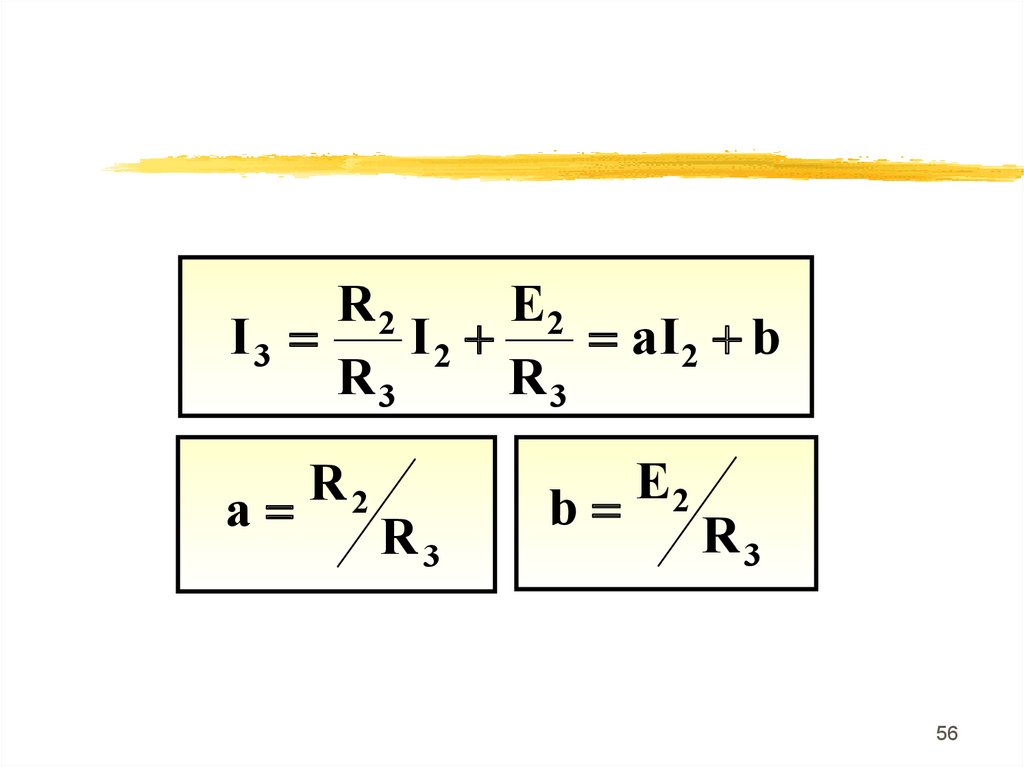
56.
R2E2
I3
I2
aI 2 b
R3
R3
a
R2
R3
b
E2
R3
56
57. 4. Принцип эквивалентного генератора
IК = EГ /(RК +RГ )== JГ /( 1+ RК / RГ )
где EГ = UК(ХХ) , JГ = IК(КЗ) =ЕГ / RГ,
RГ = RЭКВ
57
58.
Ток IK в любой к-ветви можноопределить от действия
ЭДС ЕГ или источника тока
JГ эквивалентного генератора
58
59.
У этого генератора ЭДС EГ равнанапряжению холостого хода UK(XX) ,
когда IK=0, а ток источника
тока JГ равен току короткого
замыкания IK(KЗ), когда UK = 0
59
60.
При этом сопротивление RГгенератора равно
эквивалентному сопротивлению RЭКВ
цепи относительно зажимов
сопротивления RК
60
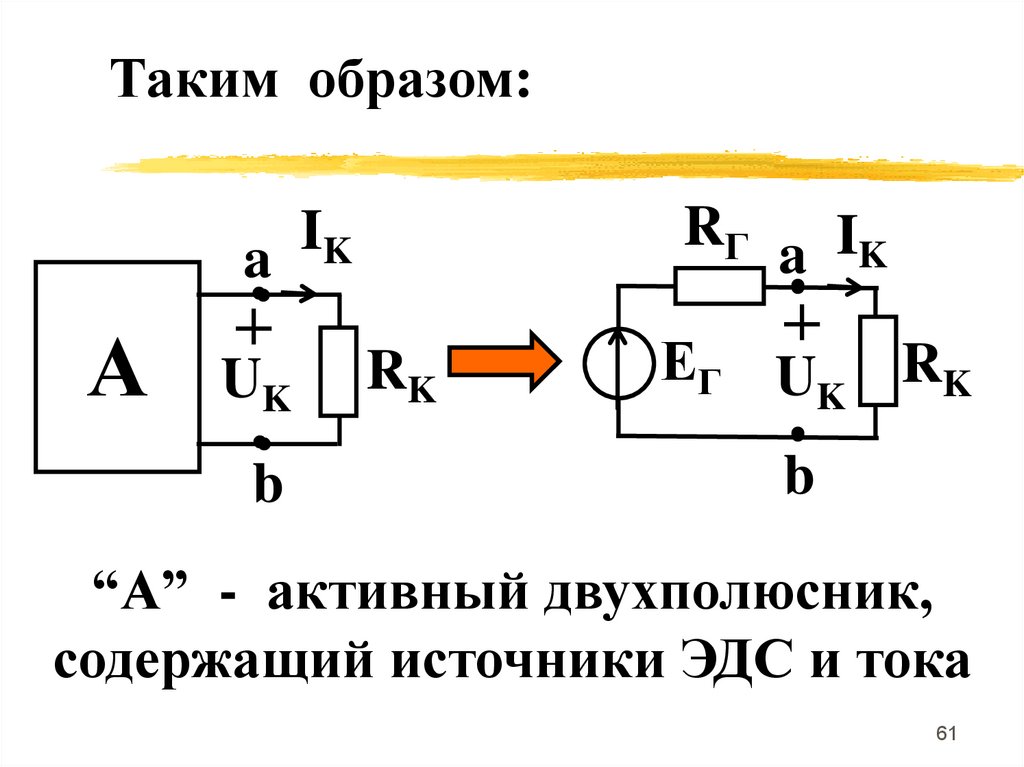
61.
Таким образом:RГ a IK
I
a K
А
UK
b
RK
ЕГ U RK
K
b
“А” - активный двухполюсник,
содержащий источники ЭДС и тока
61
62.
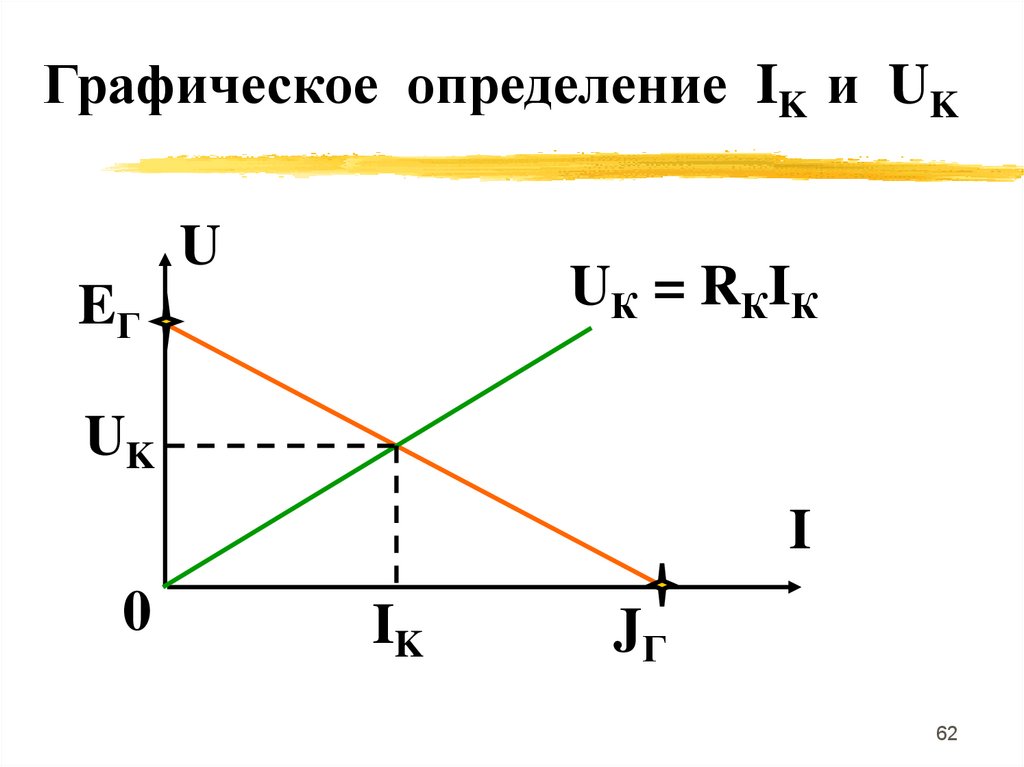
Графическое определение IK и UKU
UК = RКIК
EГ
UK
I
0
IK
JГ
62
63.
Например:R1
I1
J
U1
E
R2
I2
63
64.
Расчетная схема для ЕГ=U1(XX)ЕГ
E
J
R2
64
65.
Расчетная схема для RГ=RЭКВRГ
R2
65
66.
Для тока I1 имеем:EГ = E – R2J
JГ = E / R2 - J
RГ = R2
I1= EГ /(RГ + R1) =
= E /(R1 + R2) – R2J /(R1+ R2)
66










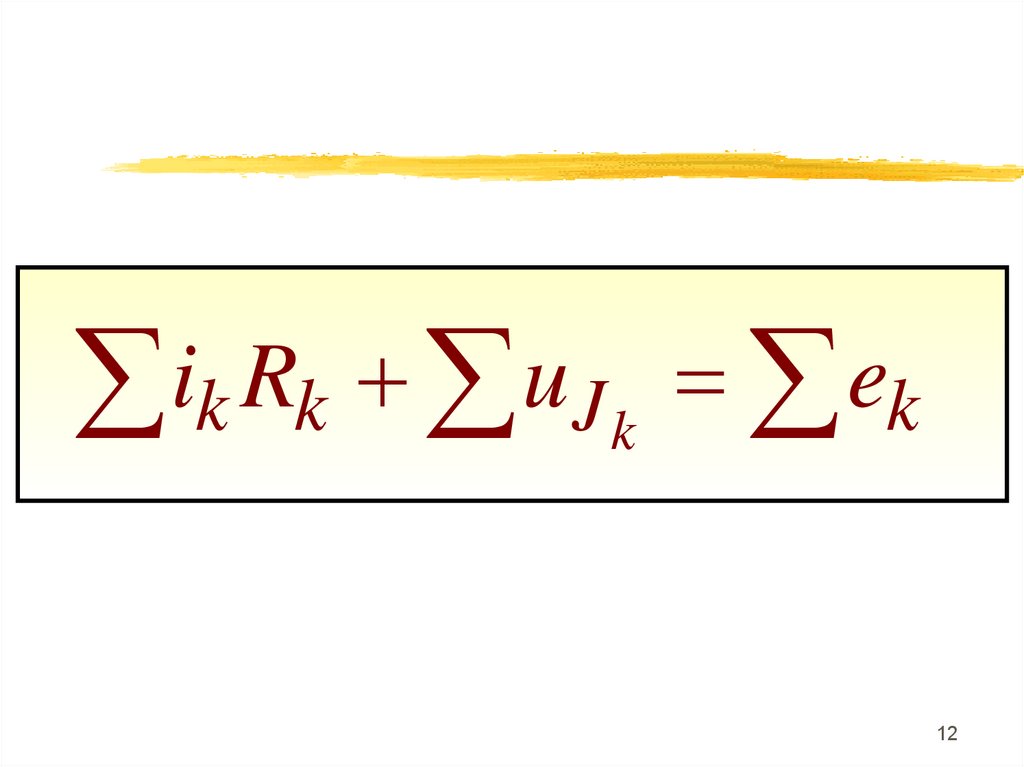





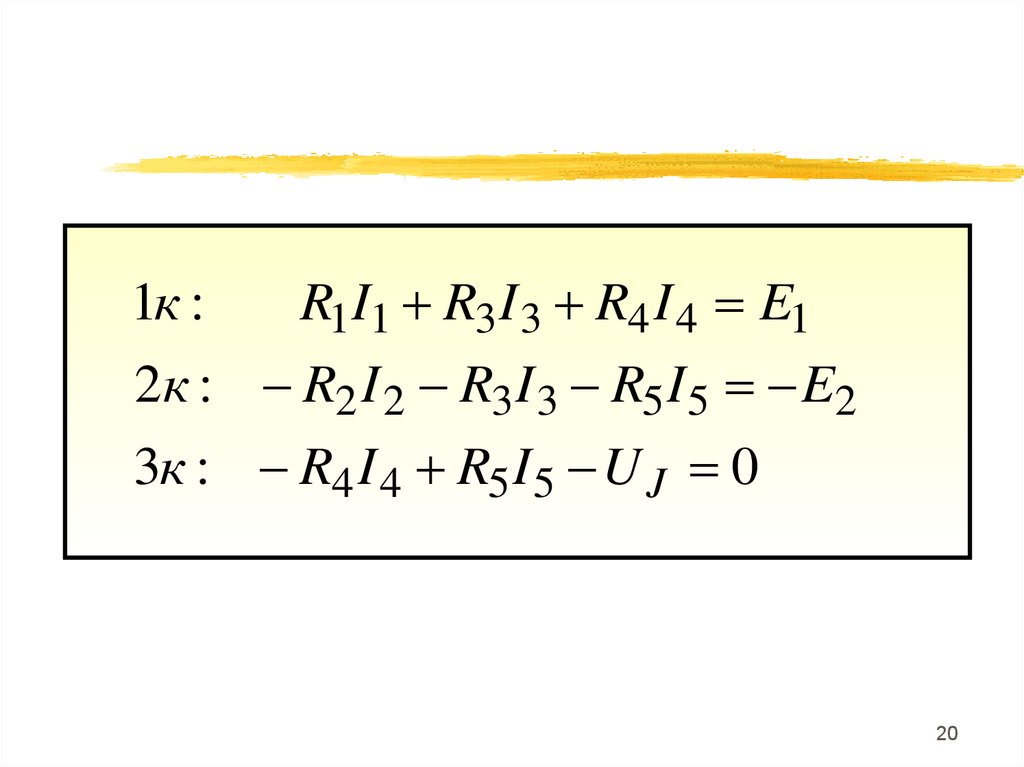



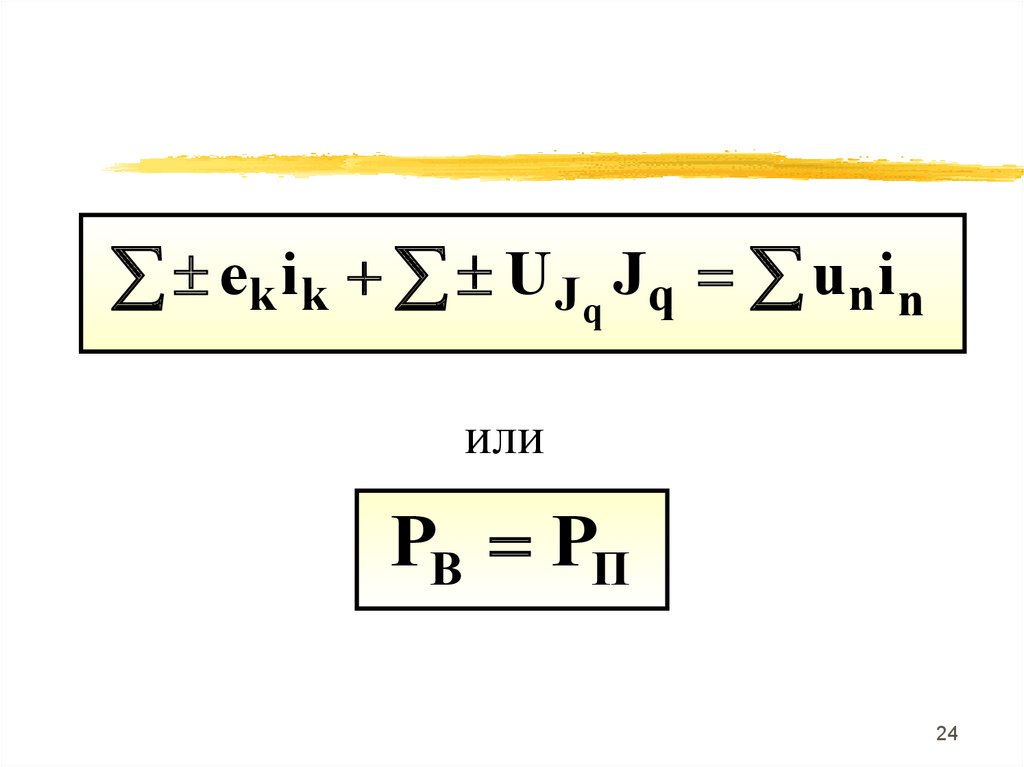




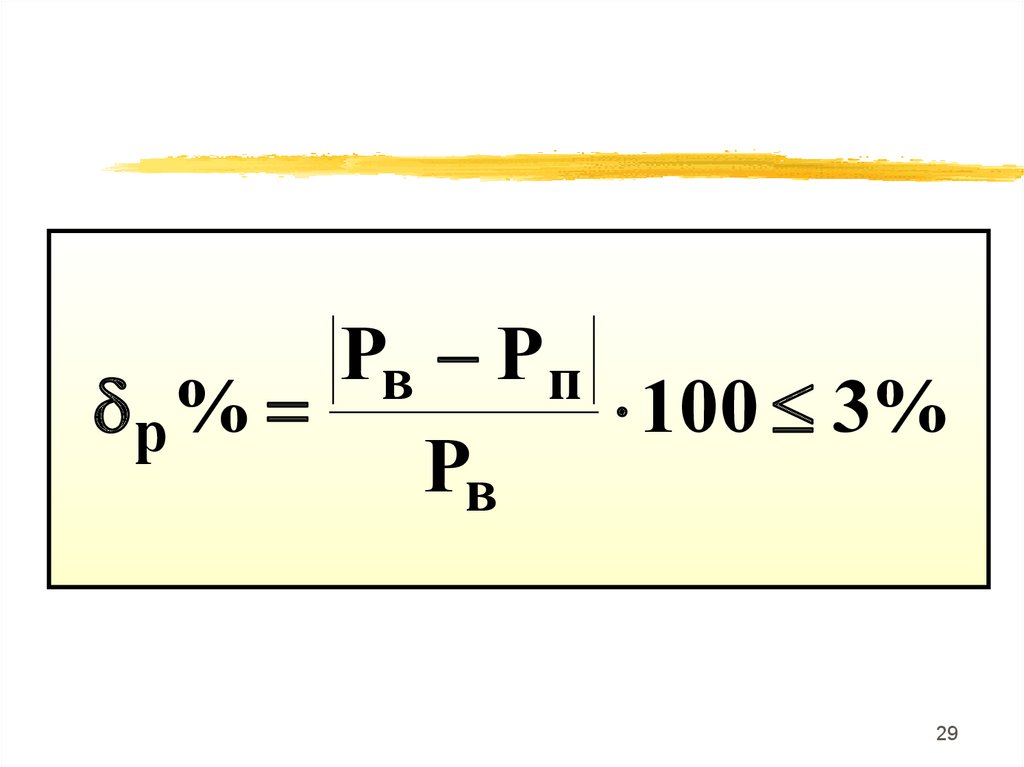


























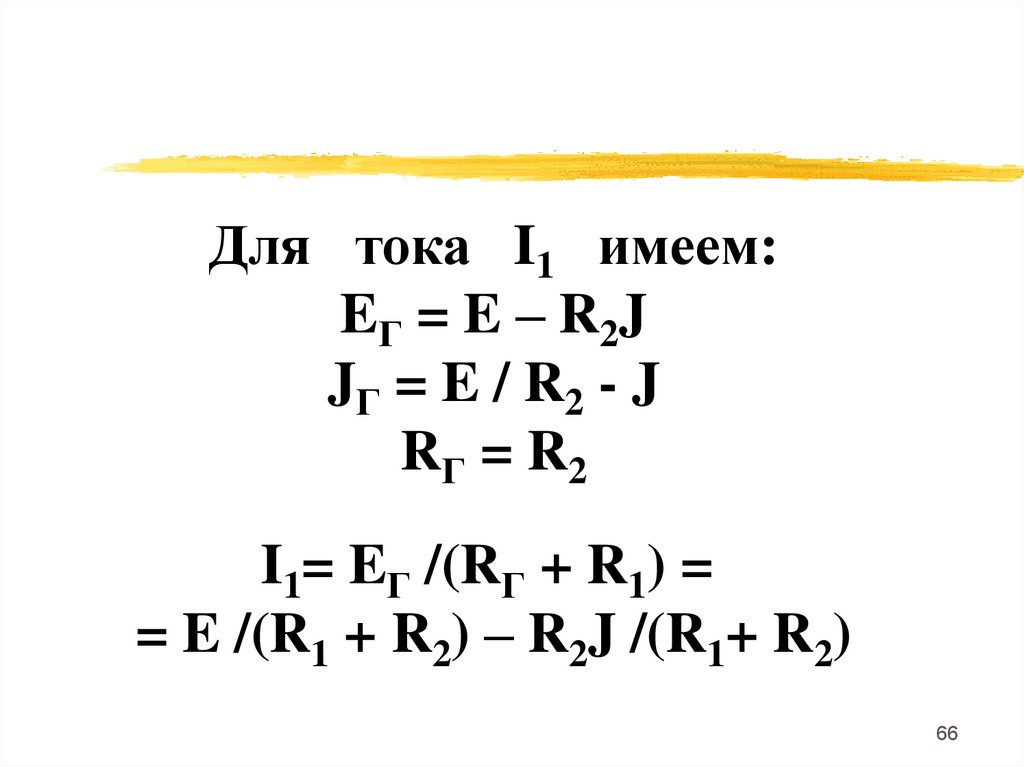
 physics
physics








