Similar presentations:
Принцип и метод суперпозиции (наложения)
1.
Лекция 3Принцип и метод суперпозиции (наложения)
(Частный случай принципа независимости действия сил)
Любой ток разветвленной цепи можно представить, как
алгебраическую ∑ частичных токов, каждый из которых
вызван действием одного источника (при устранении остальных).
Любой интересующий ток можно сделать контурным
R11
R
k 1 21
I k J kk
...
Rn1
R12
... E11
R22
... E22
...
...
...
Rn 2 ... Enn
... R1n
... R2 n
... ...
... Rnn
k1
k 2
kn
E11
E22
... Enn
I k E1ak1 E2 ak 2 E3ak 3 ... I k I k I k ...
2.
NB! Устранить источник, значит оставить на его месте внутреннееcопротивление идеального источника:
ЭДС заменяется на «провод», источник тока на «разрыв».
E
Iк
3.
r1I1
Пример
r2
r3
E1
I2
=
Iк2
I3
I
=
r2
r1
'
1
E1
r3
I
I1
I1''
I
'
2
r3
+
'
3
'
''
I1 I1 ,
E
'
'
I1 I 3
.
r1 r3
r2
r1
I
''
2
Iк2
I 3''
r3
I I
,
r1 r3
''
1
''
2
4.
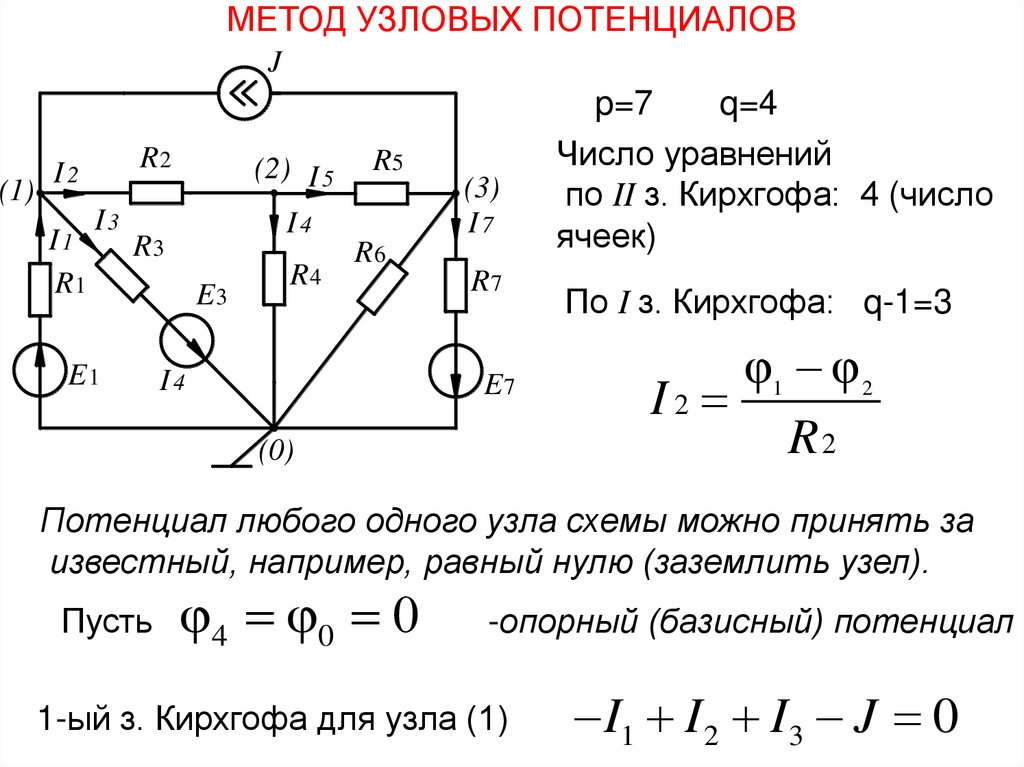
МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВJ
(1)
R2
I2
I1
R1
I3
(2) I 5
I4
R3
E1
E3
R4
R5
(3)
I7
R6
I4
R7
E7
(0)
p=7
q=4
I
Число уравнений
R
по II з. Кирхгофа: 4 (число
ячеек)
По I з. Кирхгофа: q-1=3
φ1 φ 2
I2
R2
Потенциал любого одного узла схемы можно принять за
известный, например, равный нулю (заземлить узел).
Пусть
φ 4 φ0 0
-опорный (базисный) потенциал
1-ый з. Кирхгофа для узла (1)
I1 I 2 I 3 J 0
5.
JСогласно обобщенному з. Ома:
I
(1)
R2
I2
I1
R1
I3
E1
(2) I 5
I4
R3
E3
R4
R5
(3)
I7
R6
I4
R7
E7
(0)
φ0 φ1 R E1
I1
( E1 φ1 )G1
R1
φ1 φ 2
I2
(φ1 φ 2 )G2
R2
φ1 φ0 E3
I3
(φ1 E3 )G3
R3
1-ый з. Кирхгофа для узла (1)
I1 I 2 I 3 J 0
Узловое уравнение для узла (1):
φ1 (G1 G2 G3 ) φ2G2 J E1G1 E3G3
6. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ
Узловые уравнения для 1-го, 2-го и 3-го узлов(1):
φ1 (G1 G2 G3 ) φ2G2 J E1G1 E3G3
φ2 (G2 G4 G5 ) φ1G2 φ3G5 φ0G4 0
(3): φ (G G G ) φ G φ (G G ) J E G
3
5
6
7
2 5
0
6
7
7 7
(2):
J
I
(1)
R2
I2
I1
R1
I3
E1
(2) I 5
I4
R3
E3
R4
I4
R5
R
(3)
I7
R6
R7
E7
(0)
7.
Система уравнений в канонической формеφ1G123 φ 2G2 φ3 0 I У1
φ1G2 φ 2G245 φ3G5 I У2
φ1 0 φ 2G5 φ3G567 I У3
I У1
1 I У2
I У3
G2
G245
G5
0
G5 ;
G567
1
φ1 ;
NB! Симметрия относительно
главной диагонали
G123
G2
0
G123
2 G2
0
2
φ2
;
I У1
I У2
I У3
G2
G245
G5
0
G5 ;
G567
0
G5 ;
G567
3 ...
3
φ3
Токи находят через потенциалы по з.Ома для
активной и пассивной ветвей
8.
Каноническая система уравнений:G11φ1 G12 φ 2 ... G1n φ n I у1
G21φ1 G22 φ 2 ... G2 n φ n I у 2
.....................................
Gn1φ1 Gn 2 φ 2 ... Gnn φ n I уn
Gii
Gij
-собственная
узловая проводимость i-го узла = сумме
проводимостей всех ветвей, сходящихся в этом узле
- общая проводимость между i-тым и j-тым узлами =сумме
проводимостей всех ветвей между этими узлами, всегда со
знаком «-»!
I уn - узловой ток, равен алгебр-ской
∑ произведений эдс на
проводимость своей ветви «+» токи источников тока)
9.
I уn - узловой ток, равен алгебр-ской∑ произведений эдс на
проводимость своей ветви «+» токи источников тока)
Правило знаков:
источник направлен к узлу, знак «+», от узла «-»
Источник напряжения
Источник тока
Ri
E
J
Ri
E
J
EGi
Ri
10.
В матричной форме записи:G y φ y I y
1
φ y Gy I y
Порядок расчета методом узловых потенциалов
1. Заземляется любой узел схемы. Целесообразно
заземлять узел, в котором сходится наибольшее число ветвей.
2. Для остальных узлов составляют уравнения по алгоритму.
3. Решается система и определяются потенциалы всех узлов.
4. С помощью обобщенного з. Ома определяют токи ветвей.
11.
r9r10
r8
E5
r5
r1
b
r4
Пример
q=4
p=8
c
E3
r3
Iк
r2
r7
E6
d
p - (q-1) = 5
a 0,
a
r6
q -1 = 3
d
1 1 1 1
b ( )
r1 r4 r6 r7
1
1 1
1
c d ( ) E6 ,
r4
r6 r7
r6
1 1
1
1
1
1
1
c (
) b d E5
,
r4 r2 r5 r8 r9 r10
r4
r2
r5 r8
1 1 1 1
1 1
1
1
1
d ( ) b ( ) c E6 E3 I к .
r3 r6 r2 r7
r6 r7
r2
r6
r3
12.
r9I8
r8
E5
r5
r1
b
r4
a
I3
E3
r3
r6
I6
E6
Iк
d
d b E6
I6
,
r6
«d»
I5
c
I4
I1
Проверка
a b
I1
,
r1
c d
I2
,
r2
r10
r7
r2
I7
I2
d
d a E3
I3
,
r3
c b
I4
,
r4
a c E5
I5
,
r5 r8
d b
I7
,
r7
I к I3 I 6 I 7 I 2 0
c a
I8
.
r9 r10
13.
Особенности применения метода узловых потенциалов1. Если в цепи имеются источники идеальной эдс, то
заземляют один из узлов, к которому примыкает ветвь с
идеальным источником.
Пример:
6
q=4
I1
(3)
R4
(1)
R5
Число уравнений
по МУП: q-1=3
R1
(2)
Примем φE01=0
R3
R1
E2
E1
тогда φ3 = φ0 + E2=E2
E3
число уравнений сокращается:
(0)
Для узлов (1) и (2):
φ1 (G1 G4 G6 ) φ 2G6 φ3G4 E1G1
φ 2 (G6 G5 G3 ) φ1G6 φ3G5 E3G3
14.
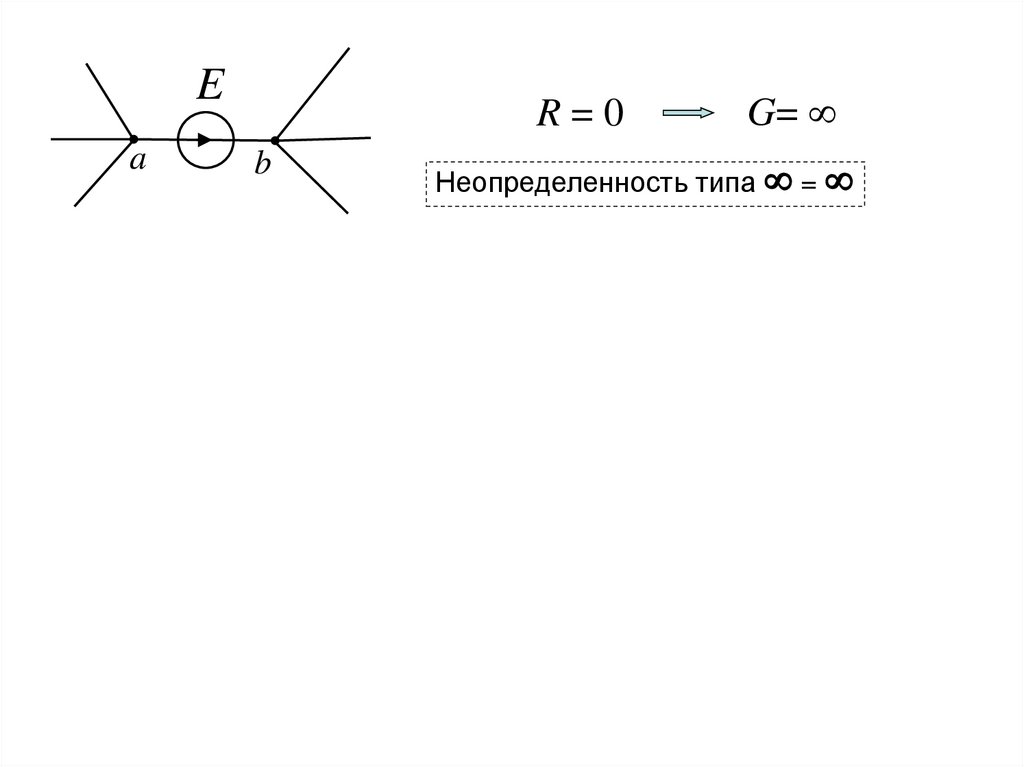
Ea
R=0
b
G=
Неопределенность типа =
15.
φ0 = 0, φ3 = E2,φ1 (G1 G4 G6 ) φ 2G6 E1G1 φ3G4
φ1G6 φ 2 (G6 G5 G3 ) E3G3 φ3G5
По методу узловых потенциалов составляется (q -1)-nист эдс
независимых уравнений
2
φ2
φ1 φ3
φ 0 φ1 E1
I4
I1
R1
R4
1
φ1
φ3 φ 2
I5
R5
I E2 I 5 I 4
R6
R4
(1)
I4
(3)
I5
I2
I1
R5
(2)
I3
R3
R1
E2
E3
E1
(0)
NB!
Ток в ветви с идеальной ЭДС определяют по 1-му з. Кирхгофа
16.
NB! Вместо потенциалов узлов можно записыватьузловые напряжения.
Узловое напряжение – разность между потенциалом
некоторого узла φузла и базисным потенциалом φ0=0:
U10 φ1 φ 0 φ1 ;
U 20 φ 2 φ 0 φ 2 ;
U 30 φ3 φ 0 φ3 ;
Узловое напряжение
в матричной форме –
1
U y Gy I y
Метод узловых потенциалов часто
наз. методом узловых напряжений
17.
2. Случай двух узловφ0 0
φ1 (G1 G2 G4 ) φ 0 (G1 G2 G4 ) E1G1 E2G2 J 3
E1G1 E2G2 J 3
φ1 U10
G1 G2 G4
(1)
J3
R2
R1
E1
R4
E2
U10 φ1
EG J
G
i
i
i
(0)
j
Формула
двух
узлов
В числителе – алгебраическая ∑ токов источников,
в знаменателе – ∑ проводимостей ветвей между
двумя узлами
Правило знаков: источник направлен к узлу ненулевого
потенциала «+», от узла «-»
18.
Пример:(1)
I1
I2
R1
R2
U10
E1
E2
I4
J3
R4
Решение:
1
1
E1 E2 J 3
R2
R1
φ1 U10
1 1 1 1
R1 R2 R4
(φ0 φ1 ) E1 U10 E1
I1
(0)
R1
R1
(φ1 φ0 ) E2 U10 E2
I2
R2
R2
φ0 φ1 U10 4
1 А
I4
R4
4
R4
19.
Эквивалентные преобразования схемЭквивалентные - преобразования, при которых
напряжения и токи в частях схемы, не затронутых
преобразованиями не изменяются
1. Свертывание последовательно-параллельных соединений
а) последовательное соединение сопротивлений:
R1
R2
Rэ
R3
Rэ Ri
б) параллельное соединение сопротивлений:
Gэ Gi ,
где
1
G
R
G1
G2
G3
Gэ
20.
2. Эквивалентная замена источниковнапряжения и тока
Формулы взаимного перехода
Источник тока
Источник напряжения
Ri
J
Ri
E
J
EGi
Ri
E
E J Ri
21.
3. Свертывание параллельных активно- пассивныхI
I
ветвей
Rэ
J3
R2
R1
R4
E1
E2
Eэ
I
I
Eэ
EG J
G
i
i
i
Gэ Gi
i
Правило знаков:
с «+» записываются источники, сонаправленные с Eэ
22.
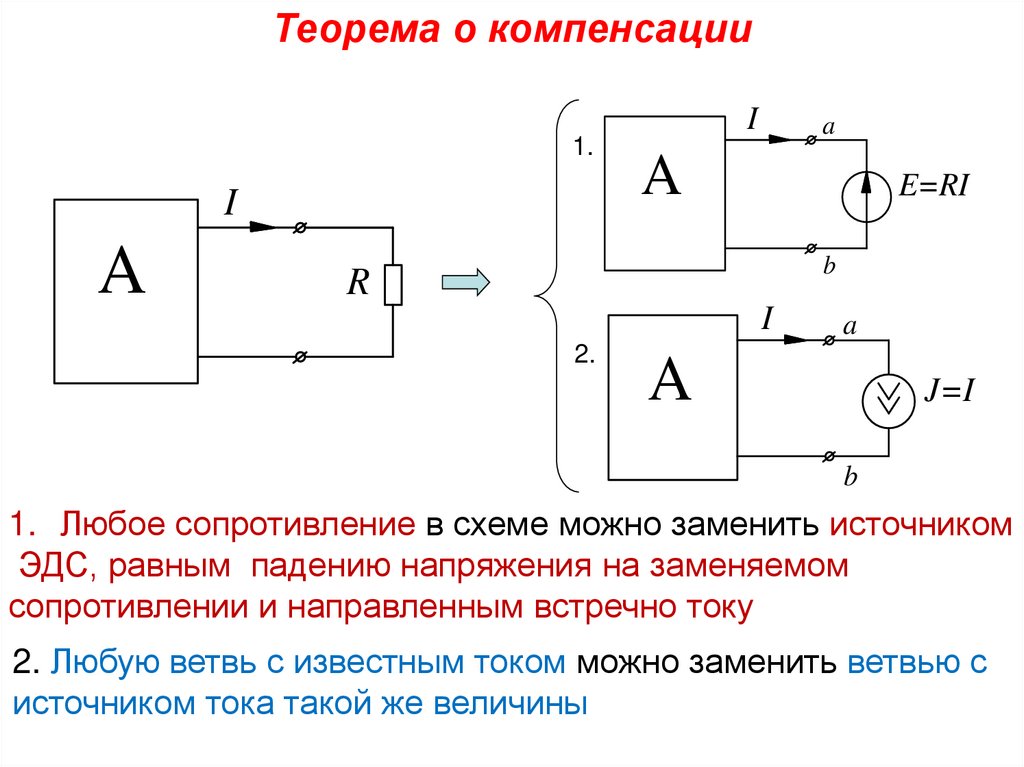
Теорема о компенсацииI
1.
I
A
a
A
E=RI
b
R
I
2.
a
A
J=I
b
1. Любое сопротивление в схеме можно заменить источником
ЭДС, равным падению напряжения на заменяемом
сопротивлении и направленным встречно току
2. Любую ветвь с известным током можно заменить ветвью с
источником тока такой же величины
23.
Метод эквивалентного генератора (МЭГ)Теорема об активном двухполюснике
Любая сложная цепь по отношению к выделенной ветви
м.б. представлена одной ветвью с эквивалентной э.д.с. и
эквивалентным сопротивлением.
Eэкв
I =0
A
R
U хх
b
Rэкв
I =0
a
=
A
R
I =0
a
U хх
b
R=
8
А
=
a
A
E=U хх
b
24.
aA
E 1=U хх
I =?
U ab
a
A
R
A
I` E 1=U хх
U ab
R
R
+
П
a
I`` E 2=U хх
U ab
R
Rэкв
b
I
U ab
b
b
a
E 2=U хх
b
U ab E1 U хх U хх
E2
U хх
0 I I I 0 I
R
R
R Rэкв R Rэкв
25.
РАСЧЕТНЫЕ СХЕМЫ ДЛЯ МЭГ(метода эквивалентного генератора)
a
A
U хх
a
+
П
b
I
Rэкв
E экв
R
Rab
b
Eэкв U хх
Rэкв Rab
Eэкв
U хх
I
R Rэкв
R Rэкв
26. Теорема о компенсации
Порядок расчета по методу эквивалентногоактивного источника (генератора):
1) Размыкается ветвь с искомым током, любым
способом рассчитывается схема и определяется Uхх ,
2) Цепь делается пассивной (источники ЭДС
закоротить, источники тока разомкнуть) и
сворачивается относительно зажимов
рассматриваемой ветви в одно эквивалентное
сопротивление Rэкв,
3) Определяется ток в рассматриваемой ветви
U xx
I
.
Rэкв R
27.
Пример:R1
R2
I3=?
E1
R3
I3
R экв
E2
Eэкв
R3
Eэкв
U xx
I3
Rэкв R3 Rэкв R3
1. Определение
Eэкв =Uхх
Из уравнения по 2 з. Кирхгофа
I1x R1 U xx E1 следует:
U xx E1 I1x R1
E1 E2
где I1x I 2 x
R1 R2
I 1x R 1
E1
R2
U xx
I 2x
E2
28.
2. Определение RэквR1
R2
Rэкв
Eэкв
U xx
I3
Rэкв R3 Rэкв R3
R1R2
R1 R2
29.
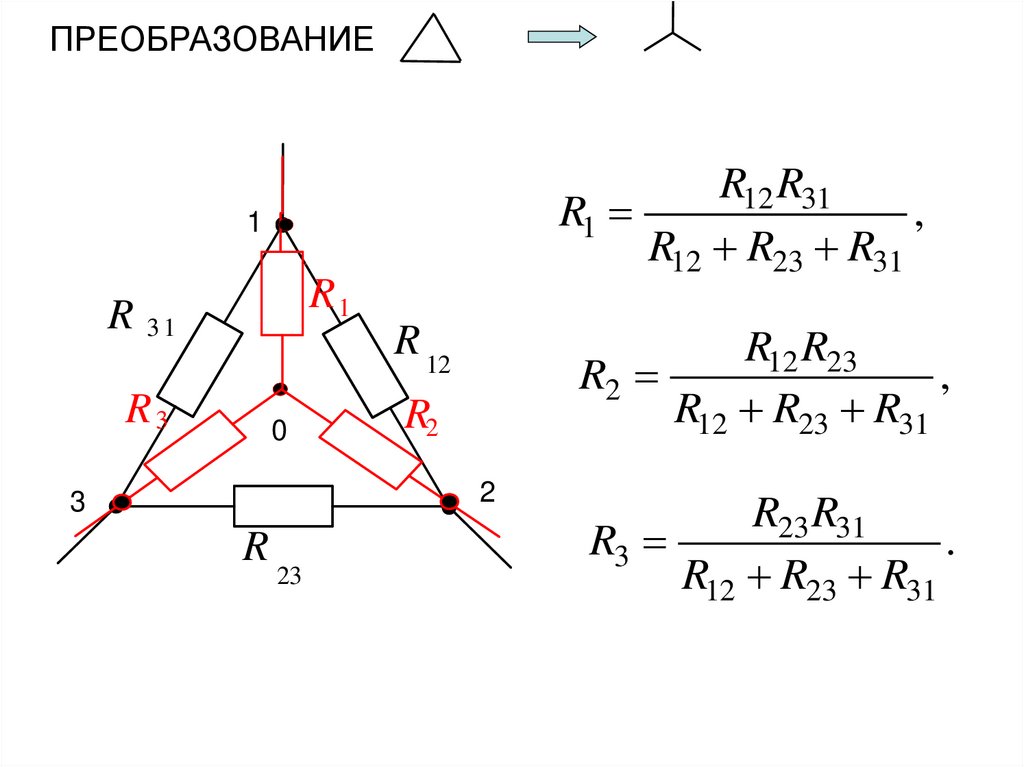
Преобразование электрических цепейПреобразование соединения
и «звезда»
«треугольник»
I1
R 31
R1
R12
R3
2
3
I3
I1
1
1
R23
0
3
I2
R2
2
I2
I3
I1 = I1 ,
I2 = I2 ,
I3 = I3 ,
1 = 1,
2 = 2,
3 = 3.
30.
11
R1
R 31
R12
R3
2
3
0
R2
3
R23
ПРЕОБРАЗОВАНИЕ
R12 R23
R12 R31
,
R1
, R2
R12 R23 R31
R12 R23 R31
R23 R31
R3
.
R12 R23 R31
2
31.
ПРЕОБРАЗОВАНИЕR12 R31
R1
,
R12 R23 R31
1
R
R1
31
R 12
R3
0
R12 R23
R2
,
R12 R23 R31
R2
2
3
R
23
R23 R31
R3
.
R12 R23 R31
32.
11
R1
R3
3
0
R 31
R12
R2
2
2
3
R23
ПРЕОБРАЗОВАНИЕ
R1R2 R R R R2 R3 ,
R12 R1 R2
, 23
2
3
R1
R3
R3 R1
R31 R3 R1
,
R2
33.
ПРЕОБРАЗОВАНИЕ1
R1
R 31
R3
0
3
R 12
R2
2
R
23
R1R2
R12 R1 R2
,
R3
R2 R3
R23 R2 R3
,
R1
R3 R1
R31 R3 R1
,
R2
34.
примерПреобразуем треугольник
сопротивлений R23 , R24 , R 34 в
звезду сопротивлений R2 , R 3 , R4 .
35.
Эквивалентноесопротивление
36.
Рассчитаем токи в ветвяхI = E / Rэкв ,
По формуле делителя тока
I12 = I (R13 + R3 ) / (R12 + R2 + R13 + R3 ),
I13 = I (R12 + R2 ) / (R12 + R2 + R13 + R3 ).
































 physics
physics








