Lektsia_9_Magnitosvyazannye_katushki

1.

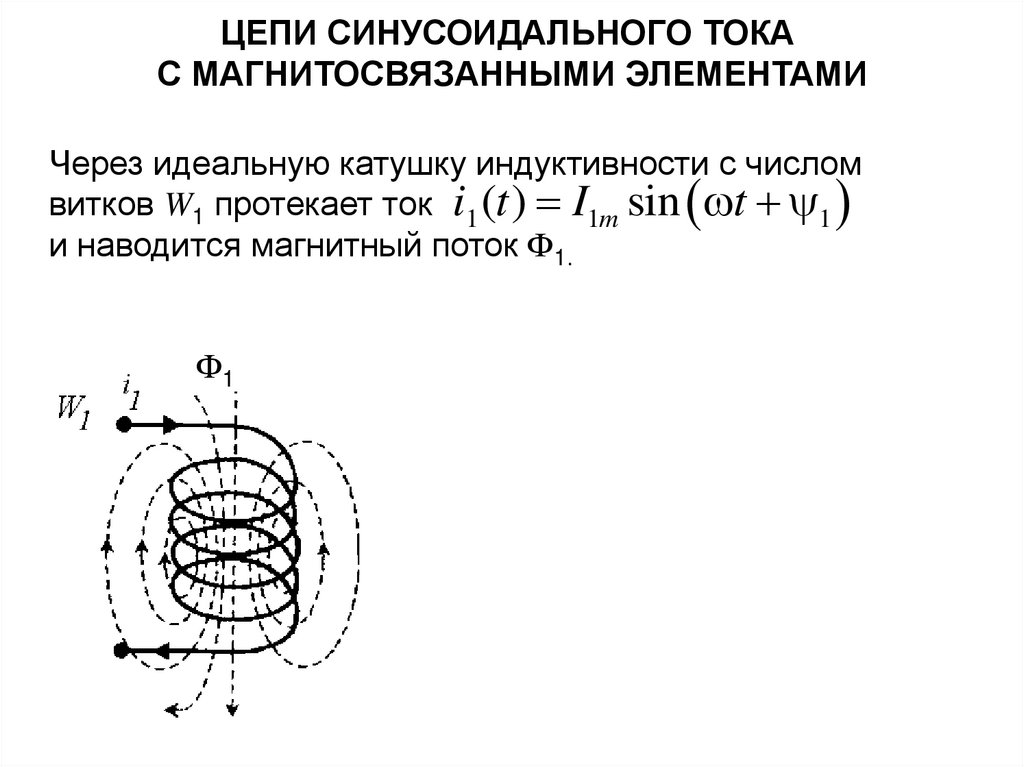
ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
С МАГНИТОСВЯЗАННЫМИ ЭЛЕМЕНТАМИ
Через идеальную катушку индуктивности с числом
витков W1 протекает ток i1 (t ) I1m sin t 1
и наводится магнитный поток Ф1.
Ф1

2.

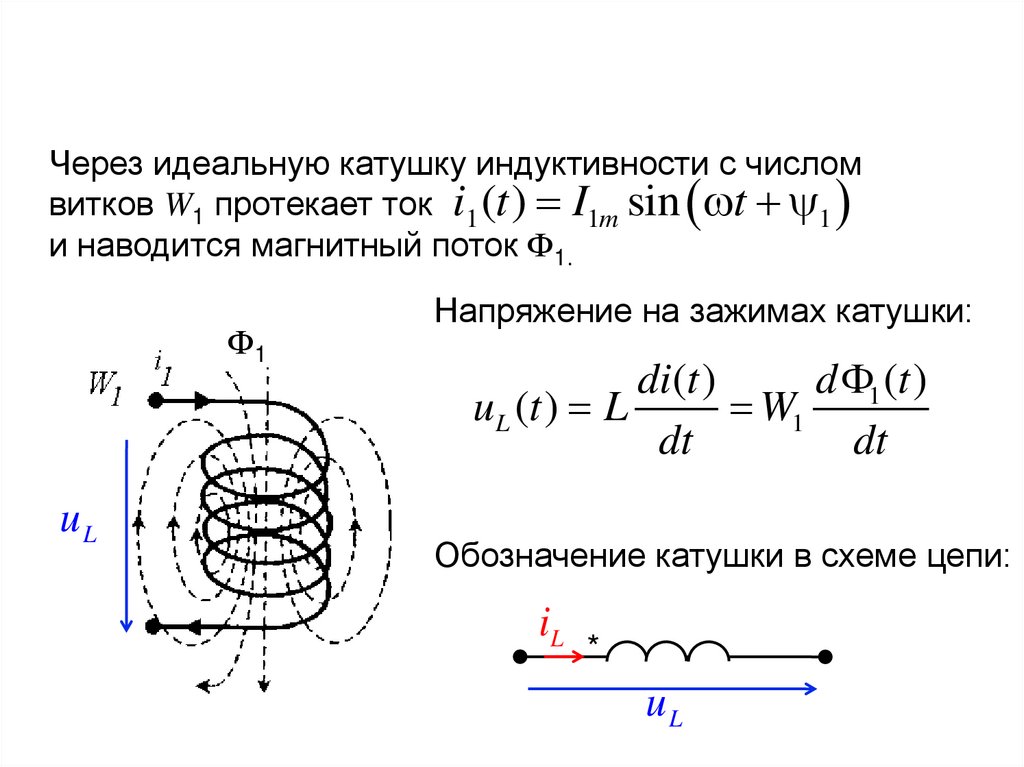
Через идеальную катушку индуктивности с числом
витков W1 протекает ток i1 (t ) I1m sin t 1
и наводится магнитный поток Ф1.
Ф1
uL
Напряжение на зажимах катушки:
d 1 (t )
di (t )
uL (t ) L
W1
dt
dt
Обозначение катушки в схеме цепи:
iL
*
uL

3.

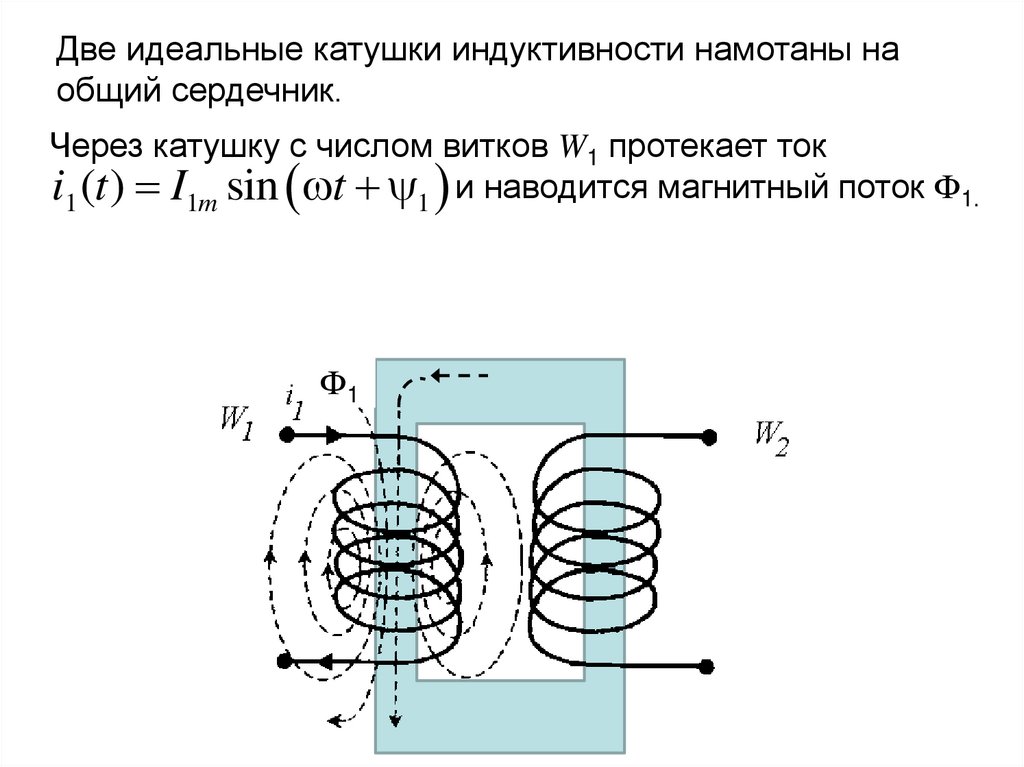
Две идеальные катушки индуктивности намотаны на
общий сердечник.
Через катушку с числом витков W1 протекает ток
i1 (t ) I1m sin t 1 и наводится магнитный поток Ф1.
Ф1

4.

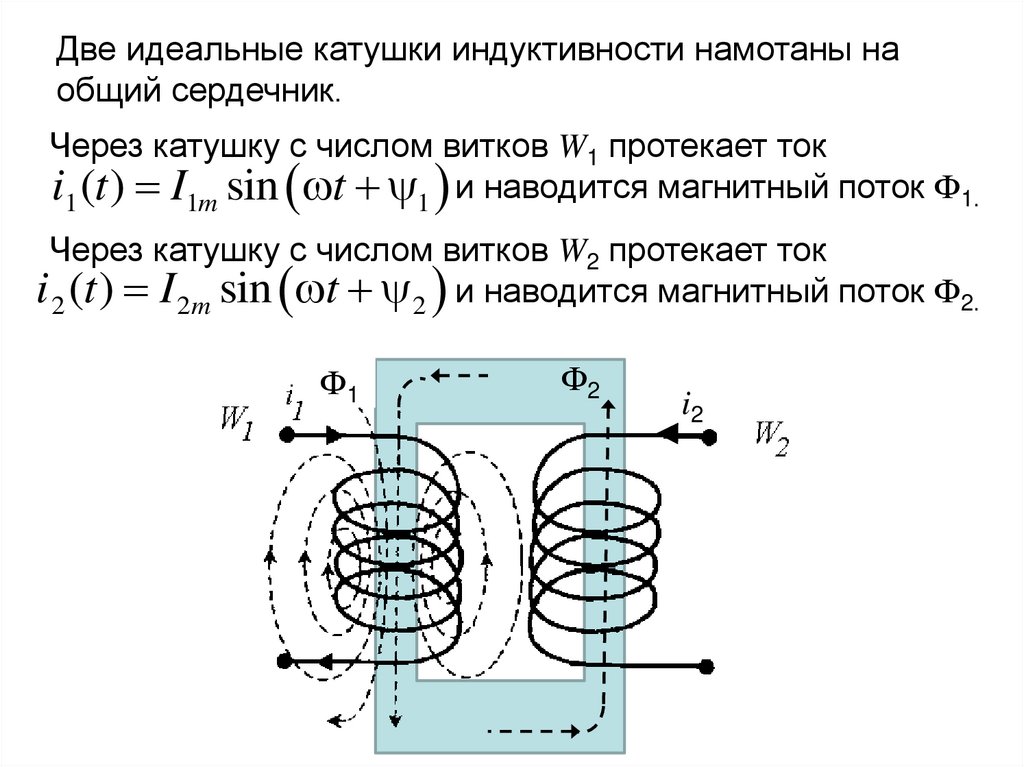
Две идеальные катушки индуктивности намотаны на
общий сердечник.
Через катушку с числом витков W1 протекает ток
i1 (t ) I1m sin t 1 и наводится магнитный поток Ф1.
Через катушку с числом витков W2 протекает ток
i 2 (t ) I 2m sin t 2 и наводится магнитный поток Ф2.
Ф1
Ф2
i2

5.

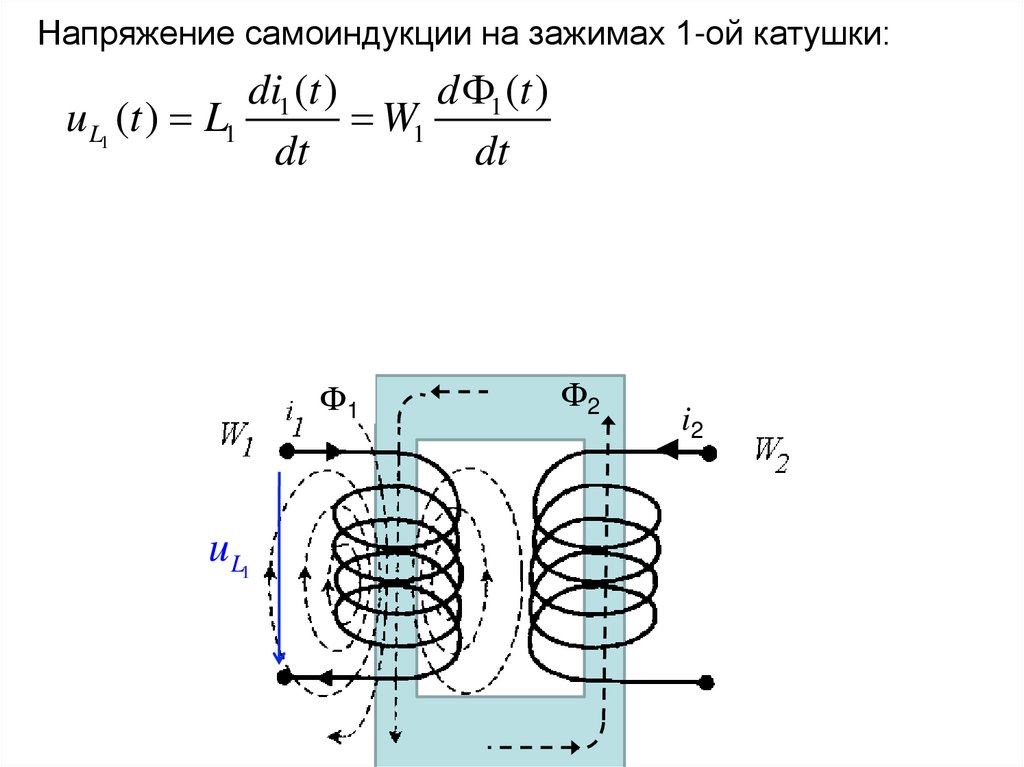
Напряжение самоиндукции на зажимах 1-ой катушки:
di1 (t )
d 1 (t )
uL1 (t ) L1
W1
dt
dt
Ф1
u L1
Ф2
i2

6.

Напряжение самоиндукции на зажимах 1-ой катушки:
di1 (t )
d 1 (t )
uL1 (t ) L1
W1
dt
dt
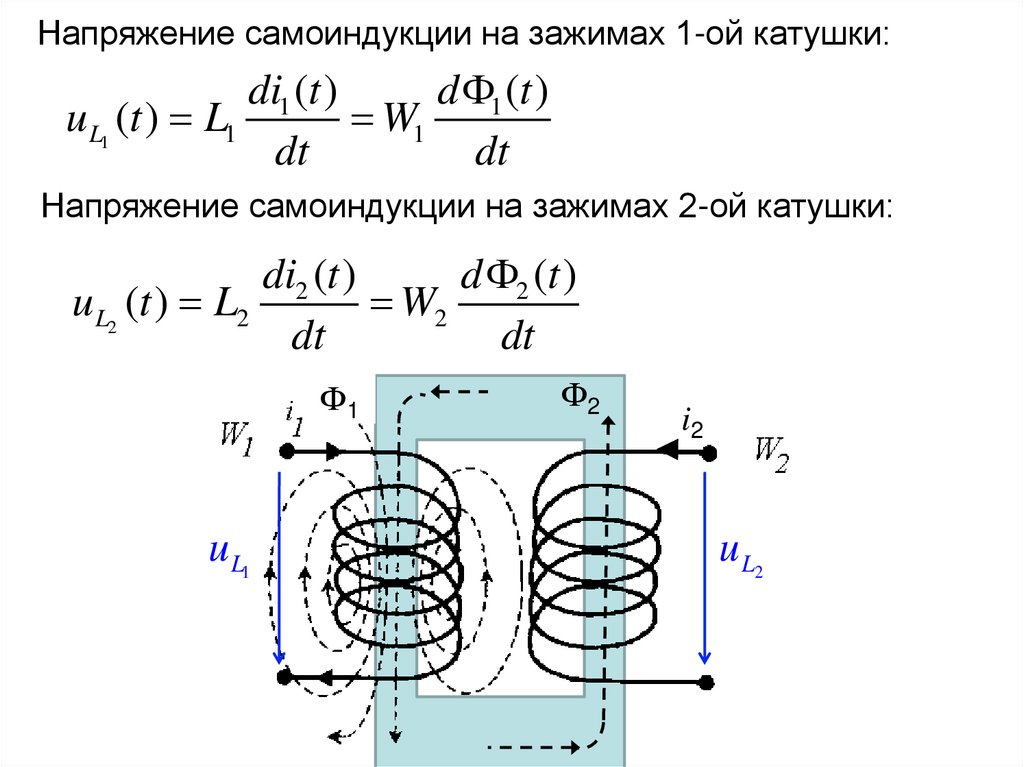
Напряжение самоиндукции на зажимах 2-ой катушки:
di2 (t )
d 2 (t )
uL2 (t ) L2
W2
dt
dt
Ф1
u L1
Ф2
i2
u L2

7.

Часть магнитного потока 1-ой катушки замыкается через 2ую катушку и наводит на ней напряжение взаимоиндукции:
di1 (t )
uM12 (t ) M 12
dt
Ф1
u L1
Ф2
i2
u L2
uM12

8.

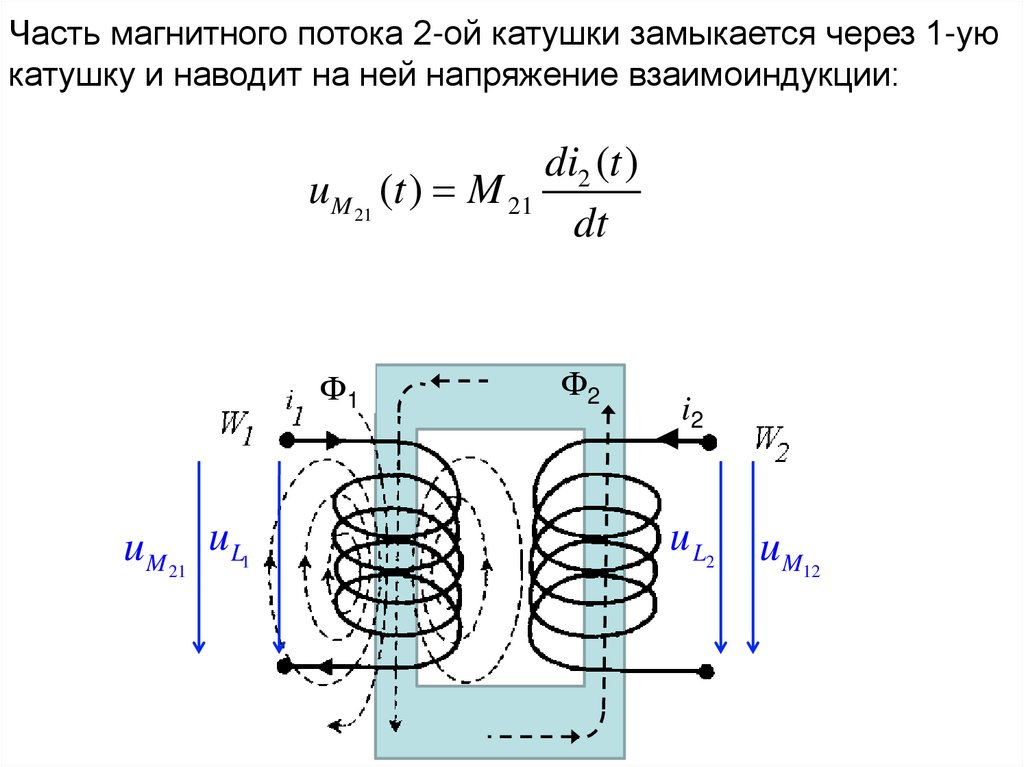
Часть магнитного потока 2-ой катушки замыкается через 1-ую
катушку и наводит на ней напряжение взаимоиндукции:
di2 (t )
uM 21 (t ) M 21
dt
Ф1
uM 21 u L1
Ф2
i2
u L2
uM12

9.

M 21; M12 - взаимоиндуктивность, (Гн)
В линейных средах
M 21 M12 M

10.

Особенности применения символического метода расчета
в цепях с магнитосвязанными элементами.
Изображение напряжений самоиндукции с помощью
комплексных чисел.
i (t )
j I m
t
di1 (t )
u L1 (t ) L1
dt
di2 (t )
u L2 (t ) L2
dt

11.

Особенности применения символического метода расчета
в цепях с магнитосвязанными элементами.
Изображение напряжений самоиндукции с помощью
комплексных чисел.
i (t )
j I m
t
di1 (t )
u L1 (t ) L1
U L1 L1 j I 1
dt
di2 (t )
u L2 (t ) L2
U L2 L2 j I 2
dt

12.

Изображение напряжений взаимоиндукции с помощью
комплексных чисел.
i (t )
j I m
t
di1 (t )
uM12 (t ) M
dt
di2 (t )
uM 21 (t ) M
dt

13.

Изображение напряжений взаимоиндукции с помощью
комплексных чисел.
i (t )
j I m
t
di1 (t )
uM12 (t ) M
dt
di2 (t )
uM 21 (t ) M
dt
U M Mj I 1
12
U M Mj I 2
21

14.

Для того, чтобы учитывать при расчетах способ включения
катушек, обозначают одноименные зажимы катушек.
Одноименными называют такие зажимы катушек,
относительно которых направление намотки одинаково.
начало
намотки
конец
намотки
начало
намотки
конец
намотки

15.

Начало намотки в схеме обычно обозначают *
Конец намотки в схеме обозначают каким-либо
другим значком (например, ▲).
*
одноименные
конец
▲
намотки
начало
намотки
*
конец
▲
намотк
одноименные

16.

Способ включения катушек определяется по тому, как
ориентированы токи относительно одноименных зажимов.
Если токи направлены одинаково относительно
одноименных зажимов, то катушки включены согласно.

17.

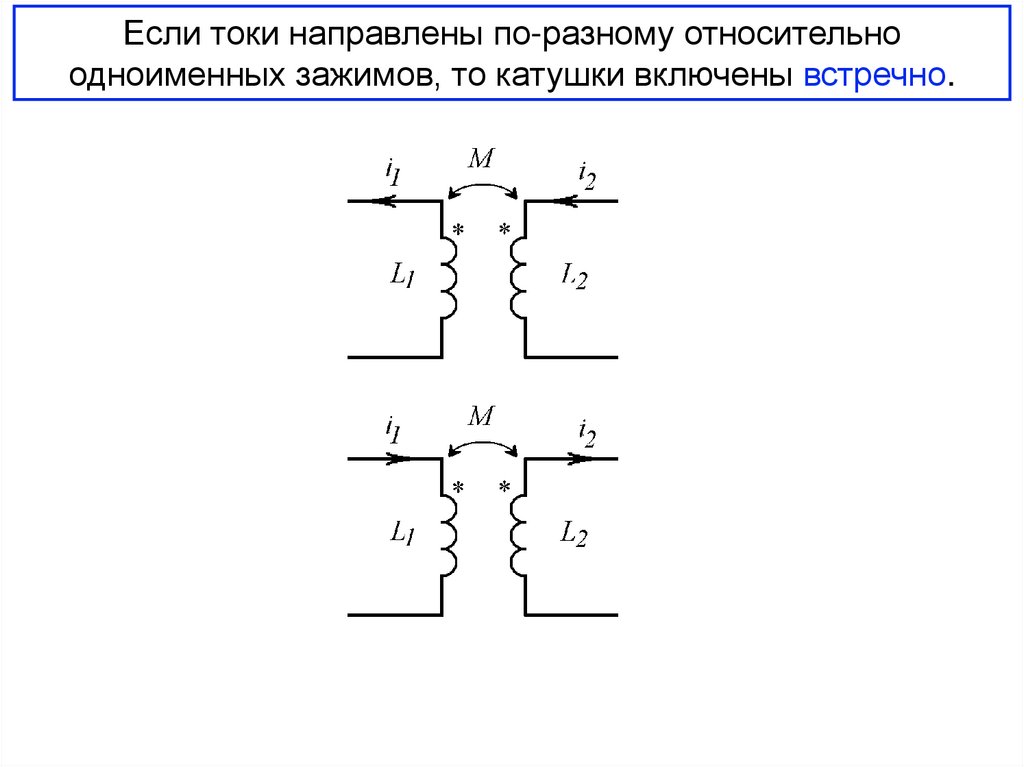
Если токи направлены по-разному относительно
одноименных зажимов, то катушки включены встречно.

18.

Правило знаков.
При согласном включении двух магнитосвязанных катушек
независимо от применяемого метода расчета знаки у ЭДС
само- и взаимоиндукции одинаковы.
При встречном включении знаки будут противоположны.
U1 U L1 U M 21
U 2 U L2 U M12
+ согласное включение
– встречное включение

19.

Расчет индуктивно-связанных цепей производится путем
прямого применения законов Кирхгофа или МКТ.
Все остальные методы расчета, а также методы
преобразования схем неприменимы, если между
катушками существует магнитная связь.

20.

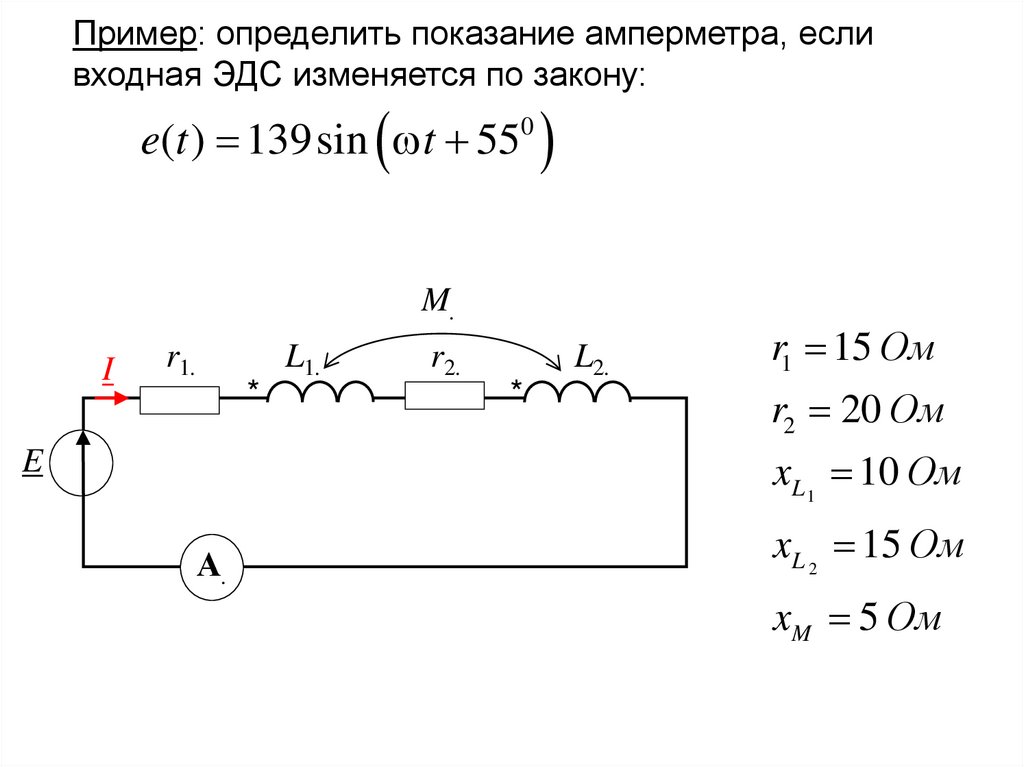
Пример: определить показание амперметра, если
входная ЭДС изменяется по закону:
e(t ) 139sin t 55
0
M.
I
r1.
*
L1.
r2.
*
L2.
r1 15 Ом
r2 20 Ом
xL 1 10 Ом
E
А.
xL 2 15 Ом
xM 5 Ом

21.

Решение:
I
r1.
*
M.
r2.
L1.
*
L2.
E
А.
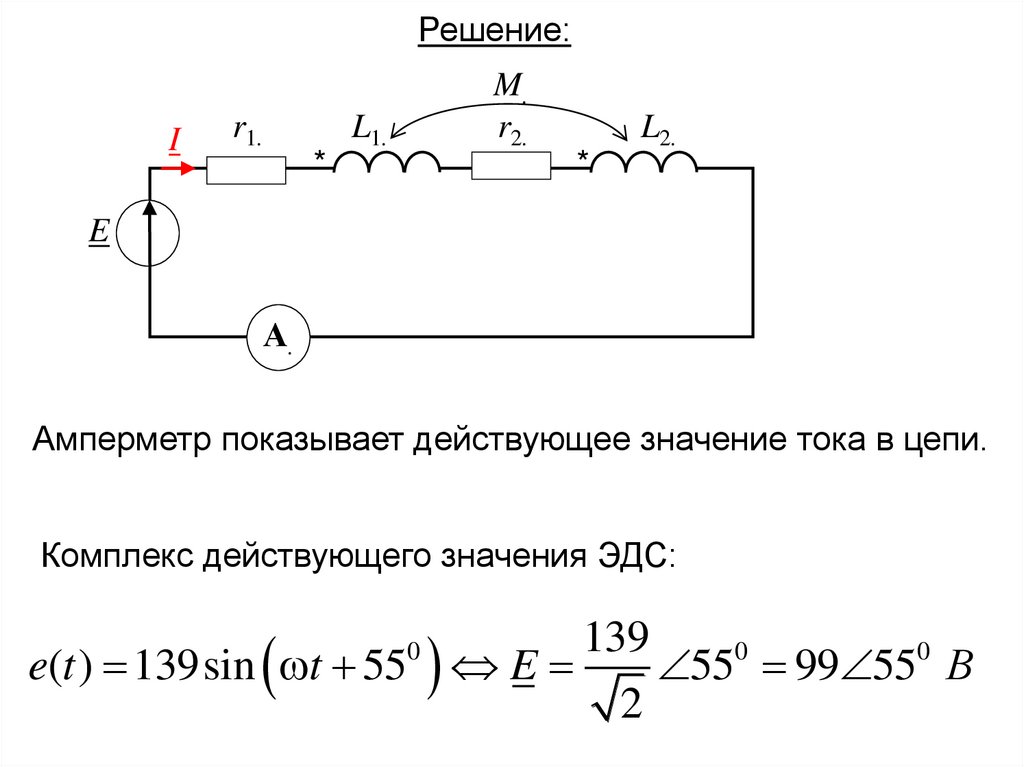
Амперметр показывает действующее значение тока в цепи.
Комплекс действующего значения ЭДС:
139
0
0
e(t ) 139sin t 55 E
55 99 55 В
2
0

22.

Включение магнитосвязанных катушек согласное, поэтому
знаки у напряжений само- и взаимоиндукции одинаковы.
I
E
r1.
*
Ur1.
L1.
UL1.
M.
r2.
Ur2.
*
L2.
UL2.
А.
U L1 ; U L2 - напряжения самоиндукций 1-ой и 2-ой катушек

23.

Включение магнитосвязанных катушек согласное, поэтому
знаки у ЭДС (напряжений) само- и взаимоиндукции
одинаковы.
M.
r1.
L1.
r2.
L2.
I
*
*
UL1.
UL2.
Ur1.
Ur2.
E
U
U
M21.
M12.
А.
U L1 ; U L2 - напряжения самоиндукций 1-ой и 2-ой катушек
U М 21 ;U М12- напряжение взаимоиндукции 1-ой и 2-ой катушек

24.

Запишем уравнение по II закону Кирхгофа в
комплексной форме:
U r1 U L1 U M 21 U r2 U L2 U M12 E

25.

Запишем уравнение по II закону Кирхгофа в
комплексной форме:
U r1 U L1 U M 21 U r2 U L2 U M12 E
Выразим напряжения на элементах по закону Ома в
комплексной форме:
U r1 I r1
U L1 I jxL 1
U r2 I r2
U L2 I jxL 2

26.

Запишем уравнение по II закону Кирхгофа в
комплексной форме:
U r1 U L1 U M 21 U r2 U L2 U M12 E
Выразим напряжения на элементах по закону Ома в
комплексной форме:
U r1 I r1
U L1 I jxL 1
U r2 I r2
U L2 I jxL 2
U M 21 I jxM
U M 21 U M12 U M
U M12 I jxM

27.

I r1 I jxL 1 I r2 I jxL 2 2 I jxM E
E
I
r1 jxL 1 r2 jxL 2 2 jxM
99 55
0
2 10 А
15 j10 20 j15 j10
0
Амперметр покажет значение тока в цепи 2 А.

28.

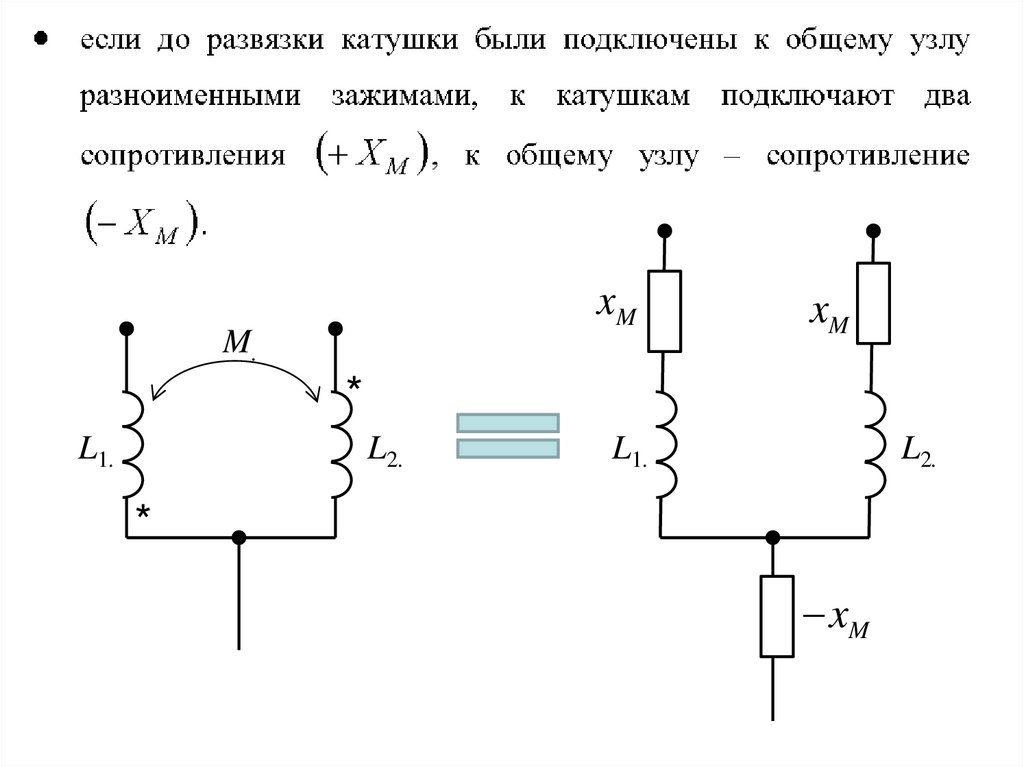
Все ограничения по методам расчета магнитосвязанных
катушек могут быть сняты, если предварительно
выполнена «развязка» индуктивных связей.
Развязка индуктивных связей
Катушки с магнитной связью должны иметь общий узел.
M.
L1.
L2.

29.

xM
M.
L1.
L2.
*
xM
L1.
L2.
*
xM

30.

xM
M.
xM
*
L1.
L2.
L1.
L2.
*
xM

31.

После того, как произведена «развязка» магнитных
связей, магнитные потоки катушек больше не влияют
друг на друга.
Все известные методы расчета цепей синусоидального
тока могут быть применены.

32.

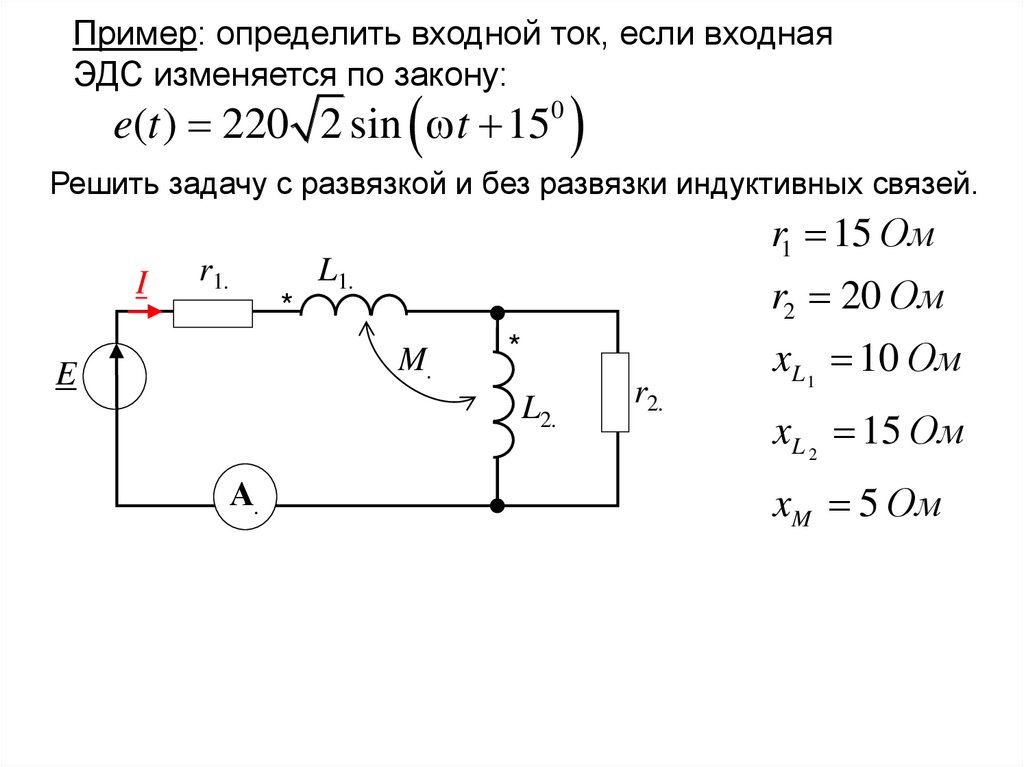
Пример: определить входной ток, если входная
ЭДС изменяется по закону:
e(t ) 220 2 sin t 150
Решить задачу с развязкой и без развязки индуктивных связей.
I
r1.
*
r1 15 Ом
L1.
r2 20 Ом
M.
E
*
L2.
А.
r2.
xL 1 10 Ом
xL 2 15 Ом
xM 5 Ом

33.

Пример: определить входной ток, если входная
ЭДС изменяется по закону:
e(t ) 220 2 sin t 150
Решить задачу с развязкой и без развязки индуктивных связей.
I
E
r1.
*
r1 15 Ом
L1.
r2 20 Ом
M.
*
L2.
r2.
xL 1 10 Ом
xL 2 15 Ом
xM 5 Ом
Комплекс действующего значения ЭДС:
e(t ) 220 2 sin t 150 E 220 150 В

34.

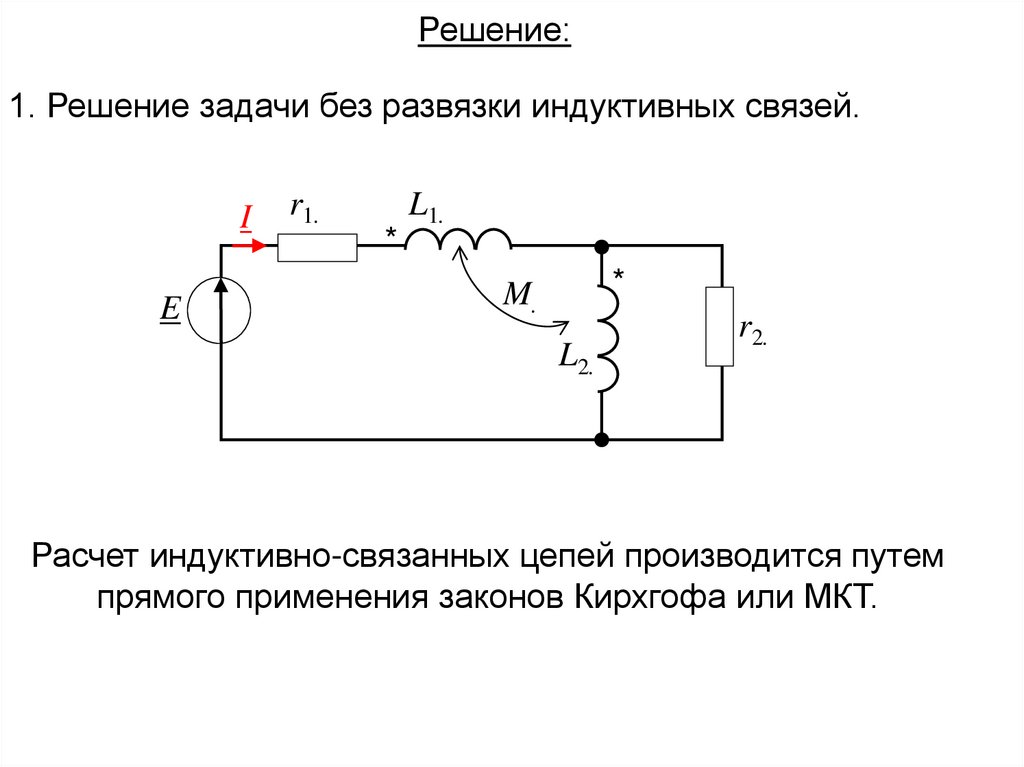
Решение:
1. Решение задачи без развязки индуктивных связей.
I
E
r1.
*
L1.
*
M.
L2.
r2.
Расчет индуктивно-связанных цепей производится путем
прямого применения законов Кирхгофа или МКТ.

35.

Система уравнений по МКТ:
I
r1.
*
L1.
*
M.
E
I11.
L2.
I22.
r2.
I 11 r1 jxL1 jxL 2 2 jxM I 22 jxL 2 jxM E
I 22 r2 jxL 2 jxM I 11 jxL 2 jxM 0
Решая полученную систему уравнений, находим: I I 11

36.

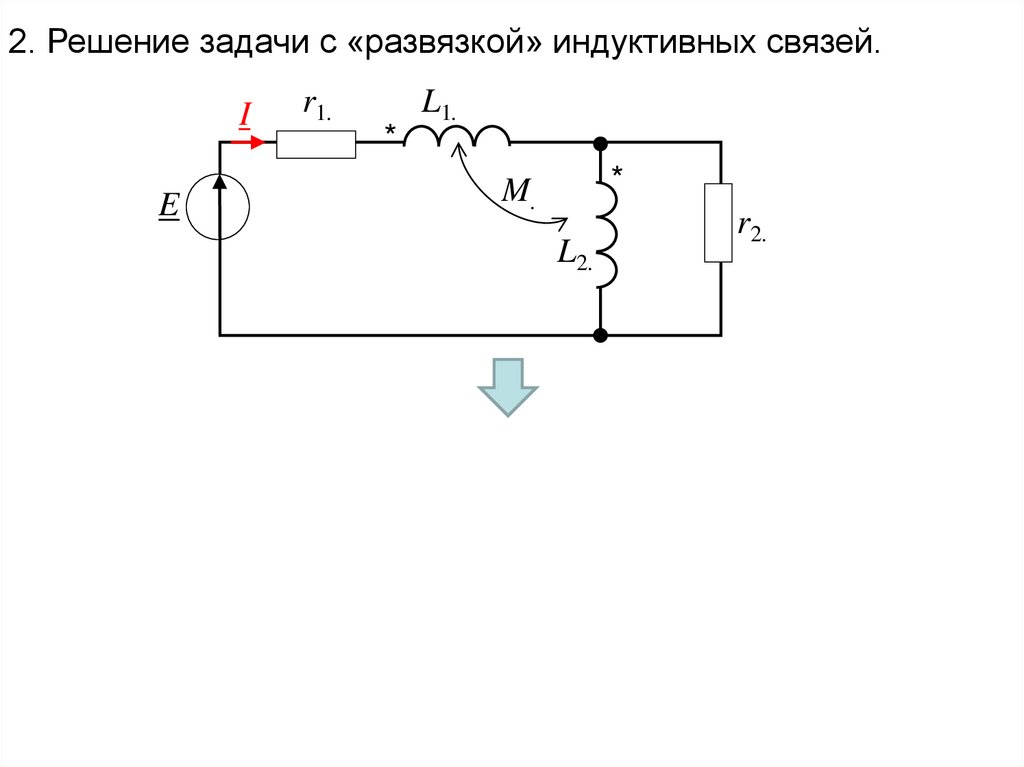
2. Решение задачи с «развязкой» индуктивных связей.
I
E
r1.
*
L1.
*
M.
L2.
r2.

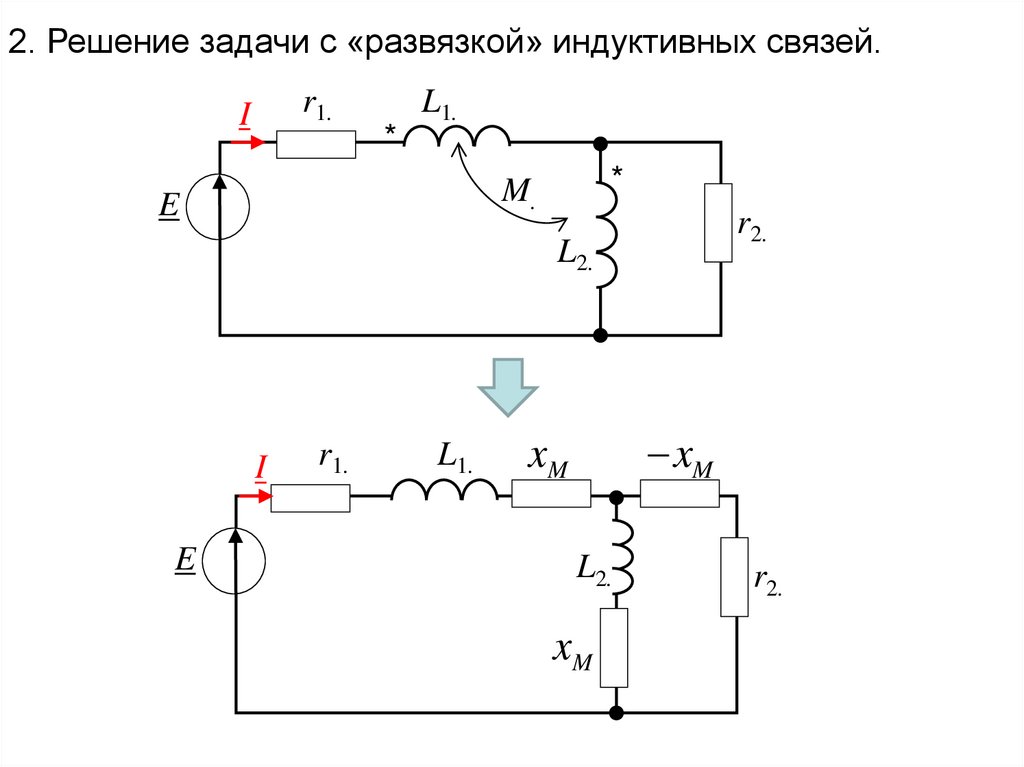
37.

2. Решение задачи с «развязкой» индуктивных связей.
r1.
I
*
L1.
*
M.
E
r2.
L2.
I
E
r1.
L1.
xM
xM
L2.
xM
r2.

38.

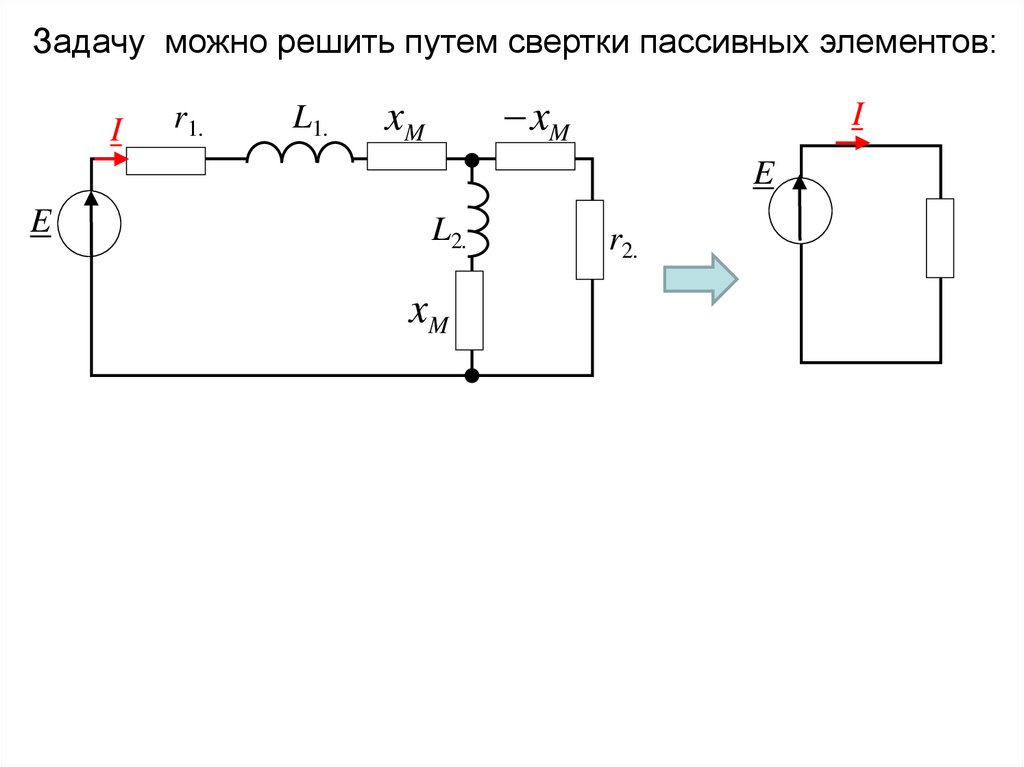
Задачу можно решить путем свертки пассивных элементов:
I
r1.
L1.
xM
xM
I
E
E
L2.
xM
r2.

39.

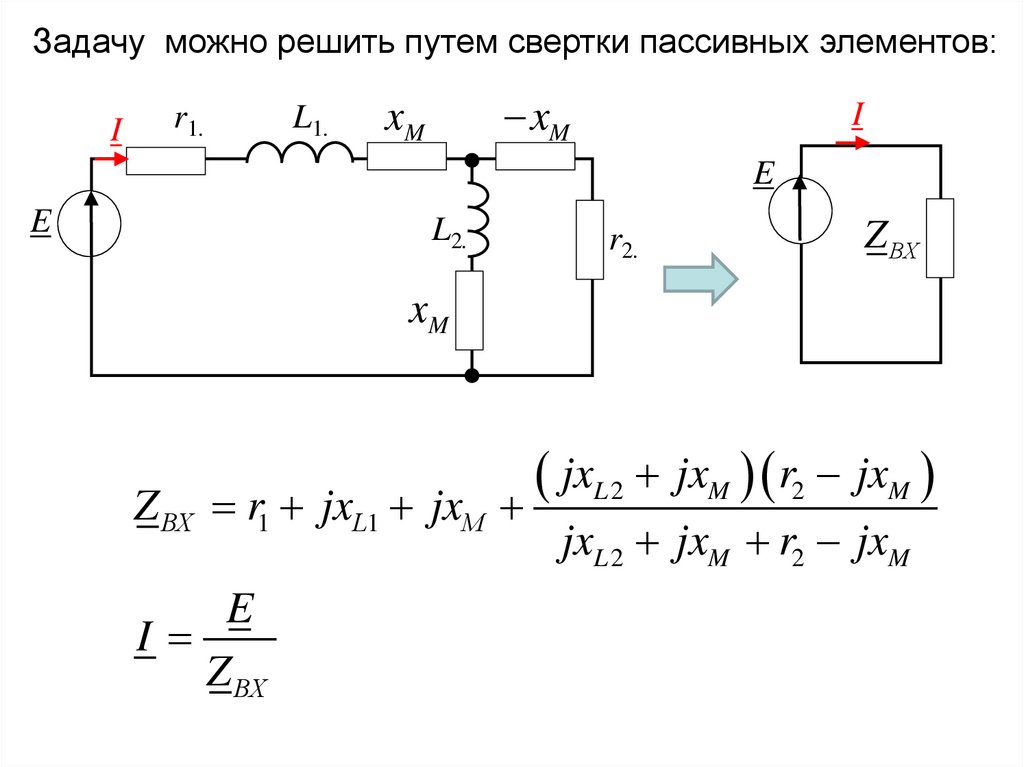
Задачу можно решить путем свертки пассивных элементов:
I
r1.
xM
xM
L1.
I
E
E
L2.
r2.
Z ВХ
xM
Z ВХ
jxL 2 jxM r2 jxM
r jx jx
1
E
I
Z ВХ
L1
M
jxL 2 jxM r2 jxM

40.

i3 (t)
a
r1
r2
e(t)
L
C
b
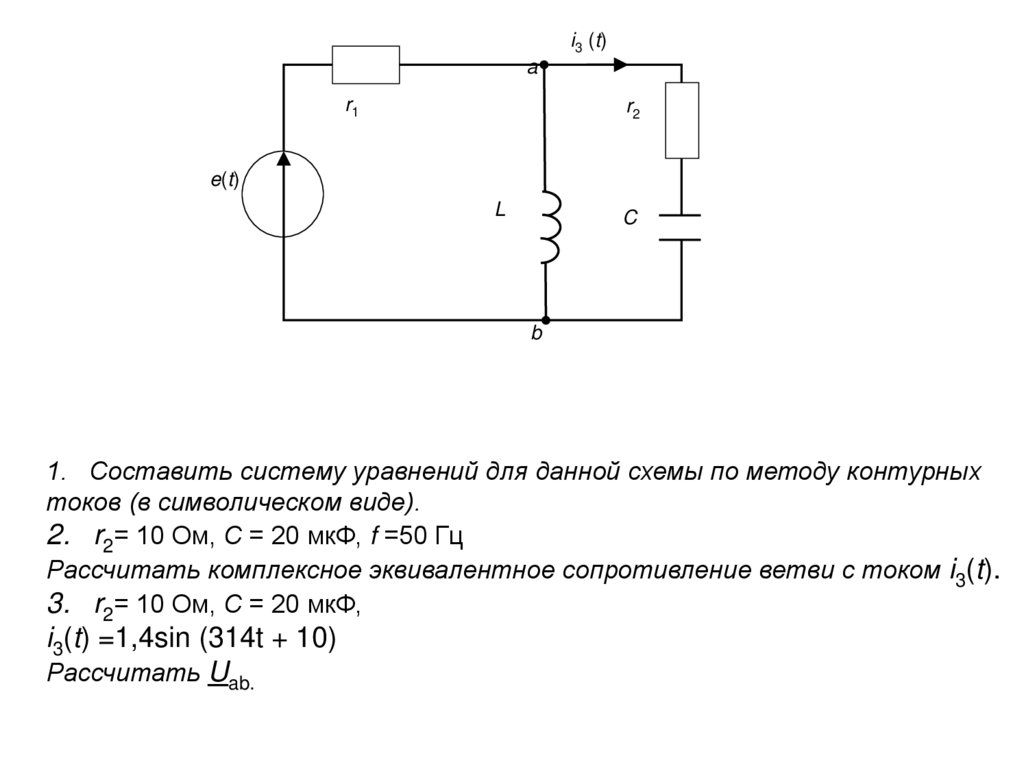
1. Составить систему уравнений для данной схемы по методу контурных
токов (в символическом виде).
2. r2= 10 Ом, С = 20 мкФ, f =50 Гц
Рассчитать комплексное эквивалентное сопротивление ветви с током i3(t).
3. r2= 10 Ом, С = 20 мкФ,
i3(t) =1,4sin (314t + 10)
Рассчитать Uab.