СИСТЕМЫ УПРАВЛЕНИЯ ХТП Лекция №2_Н_Б (1)

1.

Божко В.И., Науменко Э.В.
СИСТЕМЫ УПРАВЛЕНИЯ
ХИМИКО-ТЕХНОЛОГИЧЕСКИМИ
ПРОЦЕССАМИ
ЛЕКЦИЯ 2 (Методы математического описания и
исследования динамики одномерных
управляемых систем, линеаризация
нелинейных ДУ, передаточные функции и
структурные схемы, временные и частотные
характеристики, типовые динамические звенья
и другие типы звеньев)
1

2.

Линейная система n-го порядка с постоянными
параметрами, одной выходной x(t ) и одной входной
g (t ) величинами
описывается
следующим
неоднородным
линейным
дифференциальным
уравнением (ЛДУ) с постоянными коэффициентами
при n начальных условиях ( t0 0 )
(2.1)
(2.2)
В физически реализуемых системах n > m.
В ТАУ принято приводить уравнение системы (звена) к
стандартному виду, в котором выходная величина x(t)
2

3.

должна входить в уравнение с коэффициентом единица:
(2.3)
или в символической записи
, (2.4)
p=d/dt - алгебраизированный оператор
дифференцирования.
В установившемся состоянии, когда x const и g const ,
из (2.3) получаем уравнение статики
x k g .
(2.5)
Уравнение (2.4) в линейных операторах имеет вид
(2.6)
L( p) x(t ) kG( p) g(t ) ,
где
3

4.

–
- линейные операторы.
Соответственно уравнение (2.1) в линейных
операторах запишется в виде
A( p) x(t ) B( p) g (t ) ,
(2.7)
где
- линейные операторы.
Любые формы записи уравнений ДС можно
использовать как для размерных реальных величин,
их отклонений, а также для безразмерных величин и
любых их относительных отклонений.
Однородное дифференциальное уравнение (2.7)
4

5.

A( p) x(t ) 0 ,
характеризует свободное движение системы.
Решение уравнения (2.7) имеет вид
n
x (t ) x c (t ) x в (t ) Ci e i t x в (t ) ,
(2.8)
(2.9)
i
i i j i - корни характеристического уравнения.
Динамика систем – это переходные (неравновесные)
состояния систем, которые определяются уравнениями
динамики (дифференциальными, интегральными и
дифференциально-интегральными уравнениями), или
динамическими характеристиками.
Статические
(равновесные)
состояния
систем
характеризуются постоянством во времени их входных,
5

6.

промежуточных и выходных переменных. Равновесные
состояния нарушаются под действием возмущений.
Поведение системы в установившемся состоянии
определяется уравнением статики, или статическими
характеристиками.
Одним из важных свойств линейных систем является
принцип суперпозиции, или независимости действий
возмущений: реакция системы на сумму входных
воздействий равна сумме реакций на каждое
воздействие в отдельности, т. е. каждая входная
переменная системы создает свою составляющую
выходной переменной независимо от изменения других
входных переменных.
n
x (t ) xi (t )
i 1
6

7.

Принцип суперпозиции позволяет рассматривать
поведение системы отдельно по каждому каналу
прохождения сигнала.
Принцип суперпозиции для нелинейных систем не
применим.
2.2.
Линеаризация
дифференциальных
динамической системы
нелинейных
уравнений
Дифференциальные уравнения ДС и ее подсистем
(элементов, звеньев), составленные в соответствии с
физическими законами их функционирования в
большинстве случаев нелинейные.
7

8.

Простейшим методом изучения нелинейных систем
является линеаризация. Различают следующие методы
линеаризации:
1) касательная – с использованием разложения
нелинейной функции в ряд Тейлора, метод
непосредственной подстановки и графический;
2) метод описывающих функций, или гармонической
линеаризации – линеаризуется нелинейная система не
во временной области, а в частной;
3) статистической линеаризацией – применяется во
временной области: нелинейная система заменяется
эквивалентной линейной моделью в предположении,
что возмущения имеют гауссовское (нормальное)
распределение;
8

9.

,
4) комбинация гармонической и статистической
линеаризации – метод комбинированной, или
совместной, линеаризации.
Рассмотрим
линеаризацию
нелинейной
детерминированной математической модели ДС
методом разложения в ряд Тейлора.
Для простоты изложения предположим, что ДС или ее
звено описывается нелинейным дифференциальным
уравнением n-го порядка с одной выходной x(t ) и
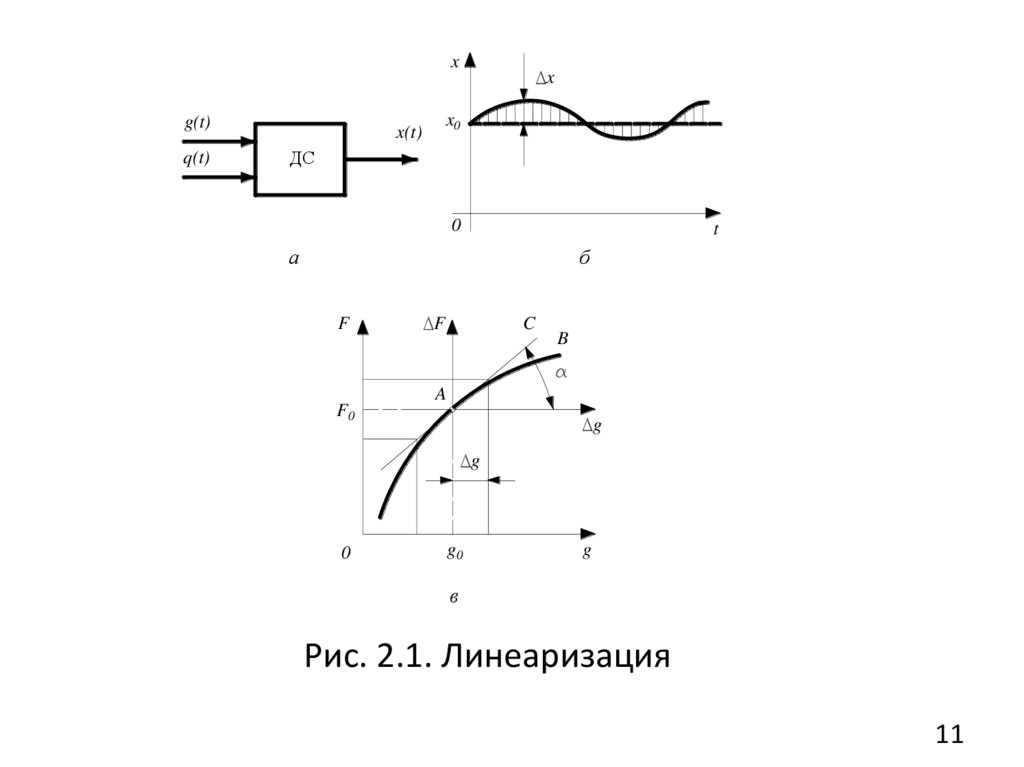
двумя входными g (t ) и q(t ) переменными (рис. 2.1, а).
(2.10)
9

10.

Запишем уравнение (2.10) в виде скалярного уравнения
с векторным аргументом (условная запись)
(2.11)
F x, q g ,
где
Представим переменные, входящие в уравнение (2.10),
в следующем виде:
x x0 x ,
и т. д.
x(i ) x0(i ) x(i ) ,
Здесь нижний индекс «0» – установившееся значение
переменной; символ – отклонение переменной от
установившегося значения.
10

11.

x
g(t)
q(t)
x
x0
x(t)
ДС
0
t
а
б
F
F0
C
F
B
A
g
g
0
g0
g
в
Рис. 2.1. Линеаризация
11

12.

Концепция линеаризации по методу малого отклонения для
САУ, основано на том, что в процессе управления все
управляемые величины мало откланяются от их заданных
значений (рис. 2.1, б), иначе САУ не выполняла бы своей задачи
и не была бы системой управления.
Запишем уравнение ДС или ее подсистемы (2.11) в
установившемся состоянии
(2.12)
F x 0 , q0 g 0 ,
Разложим функцию F x, q ( n kq 2 ) переменных
уравнения (2.11) в ряд Тейлора в окрестности
установившегося режима:
(2.13)
r
d
F x, q – дифференциал r-го порядка функции
где
F x, q ; Rn x, q – остаточный член разложения.
12

13.

,
Далее полагаем
2
Rn x, q 0 , Q x, q 0 .
(2.14)
Из уравнения (2.20) вычтем (2.19) и, учитывая (2.21),
получим уравнение в отклонениях
(2.15)
dF x, q g ,
или в развернутой форме
(2.16)
где g g g0 .
Введем обозначения
0
F
( i ) an i ,
x
0
F
, x an ,
13

14.

0
F
( j ) b( k q j ) ,
q
0
,
F
bk q .
q
С учетом введенных обозначений дифференциальное
уравнение системы примет следующий вид
( - в дальнейшем будем опускать):
(2.17)
или в линейных операторах
A( p) x(t ) B( p)q(t ) (g) .
В случае линеаризации функции
уравнение вида:
(g)
(2.18)
получаем
14

15.

A( p ) x (t ) B1( p )q(t ) B2 ( p ) g (t ) ,
(2.19)
Полученные дифференциальные уравнения (2.17) или
(2.18) и (2.19) являются линейными уравнениями
рассматриваемой
нелинейной
ДС.
Результаты
исследований линеаризованной модели справедливы
только в малом.
Для
линейной
ДС
результаты
исследований
справедливы и в большом.
2.3. Передаточные функции и структурные схемы
2.3.1. Передаточные функции
Уравнение (2.17) можно записать в символической
форме, решив его относительно выходной переменной
15

16.

x(t ) , условно считая оператор дифференцирования
p d / dt алгебраической величиной
Выражения
B ( p)
1
x (t ) 1
q( t )
g .
A( p)
A( p)
(2.20)
1
W2 p
A( p ) ,
(2.21)
B1( p)
W1 p
A( p) ,
называются в ТАУ передаточными функциями.
Более строго передаточная функция определяется
через изображения Лапласа или Карсона-Хевисайда:
L f (t ) F ( s ) f (t )e st dt .
(2.22)
0
16

17.

Если известно изображение F (s) , то соответствующий
ему оригинал f (t ) определяется формулой (обратное
преобразование Лапласа):
q i
1
1
st
F
(
s
)
F
(
s
)
e
ds ,
f (t ) L
2 j q i
(2.23)
где L (L ) 1 – символ операции прямого (обратного)
преобразования Лапласа (используются также символы
f (t ) F ( s) и F ( s) f (t )). Здесь записано
одностороннее преобразование Лапласа, для
двустороннего преобразования вместо нижнего
предела интегрирования «0» необходимо записать « ».
Существует также и преобразование Карсона-Хевисайда.
Между преобразованиями Лапласа F (s)
17

18.

и Карсона-Хевисайда (s ) существует соотношение
( s) sF ( s) .
(2.24)
В табл. 2.1 приведены некоторые основные теоремы
и свойства преобразования Лапласа, которые будут
использоваться при рассмотрении ДС.
Таблица 2.1. Преобразования Лапласа
Наименование
Свойство линейности
Оригинал
f at
Изображение
aF(s)
a1F1( s ) a2 F2 ( s )
a1F1( s ) a2 F2 ( s )
Теорема подобия
f at
1 s
F
a a
Теорема запаздывания
f (t )
e s F (s)
18

19.

Продолжение табл. 2.1
Наименование
Правило
дифференцирования
Оригинал
Изображение
f (1) (t )
sF ( s) f (0)
(n)
s n F ( s) s n 1 f (0)
f
Правило
дифференцирования
при нулевых
начальных условиях.
Правило
интегрирования при
нулевых начальных
условиях
(t )
f ( n ) (t )
t
f ( )d
0
s n F (s )
F ( s)
s
F ( s)
sn
19

20.

Окончание табл. 2.1
Наименование
Оригинал
Изображение
Теорема о конечном
значении
f ( )
lim sF ( s )
Теорема о начальном
значении
f (0)
Единичная импульсная
функция
Единичная ступенчатая
функция
s 0
lim sF ( s )
s
(t )
1
1(t )
1
s
20

21.

Перейдем к определению передаточной функции для ДС
или
какого-либо
ее
звена,
описываемой
дифференциальным уравнением n-го порядка (2.1) при
ненулевых
начальных
условиях.
Применяя
преобразование Лапласа к уравнению (2.1)
и учитывая свойство линейности
дифференцирования оригинала, получим
и
правило
(2.25)
где A0 ( s ) и B0 ( s ) - многочлены, включающие в себя
21

22.

члены с величинами начальных условий
и
переменных x(t ) и g (t ) .
Уравнение (2.25) представляет собой алгебраическое
уравнение n-й степени относительно переменной X (s) ,
которое можно записать в следующем виде:
A( s ) X ( s ) B( s )G ( s ) A0 ( s ) B0 ( s )
(2.26)
где
22

23.

Из уравнения (2.26) следует, что характер
движения системы определяется ее свойствами
A(s) ), внешним воздействием
(многочлен
(многочлены G(s) и B0 ( s ) ) и начальными условиями
A0 ( s ) системы,
которые
при
решении
дифференциального уравнения операционным
методом учитываются с самого начала процесса
решения. Начальные условия также можно считать
возмущающими воздействиями.
При нулевых начальных условиях из уравнения
(2.26) получаем:
23

24.

X ( s)
B( s )
G( s) W ( s)G( s),
A( s)
(2.27)
где A(s ) - характеристический многочлен, а
X ( s ) B( s )
W ( s)
G( s ) A( s )
,
(2.28)
-передаточная функция.
-Нули ( B( s) 0) и полюсы ( A( s) 0 ) – корни уравнений.
Передаточной функцией системы (звена) называется
отношение изображения по Лапласу выходной
величины к изображению по Лапласу входной
величины при нулевых начальных условиях.
Из изложенного выше видно, что дифференциальное
уравнение в операторной форме можно получить из
соответствующего дифференциального уравнения
24

25.

путем замены переменных на принятые обозначения
( f (t ) F ( s) ), оператора дифференцирования р и
аргумента t на комплексную переменную s и с
добавлением многочлена, включающего в себя все
члены с величинами начальных условий для
переменных.
2.3.2. Динамические звенья и структурные схемы
Для исследования различных по природе и конструкции
ДС (ОУ и САУ) с помощью единого математического
аппарата их представляют в виде динамических звеньев,
описываемых определенными дифференциальными
уравнениями. ДС называются подобными, если они
обладают одинаковыми динамическими свойствами.
Поэтому каждая такая система описывается одним или
несколькими одинаковыми звеньями. Динамические
звенья обладают детектирующими свойствами.
25

26.

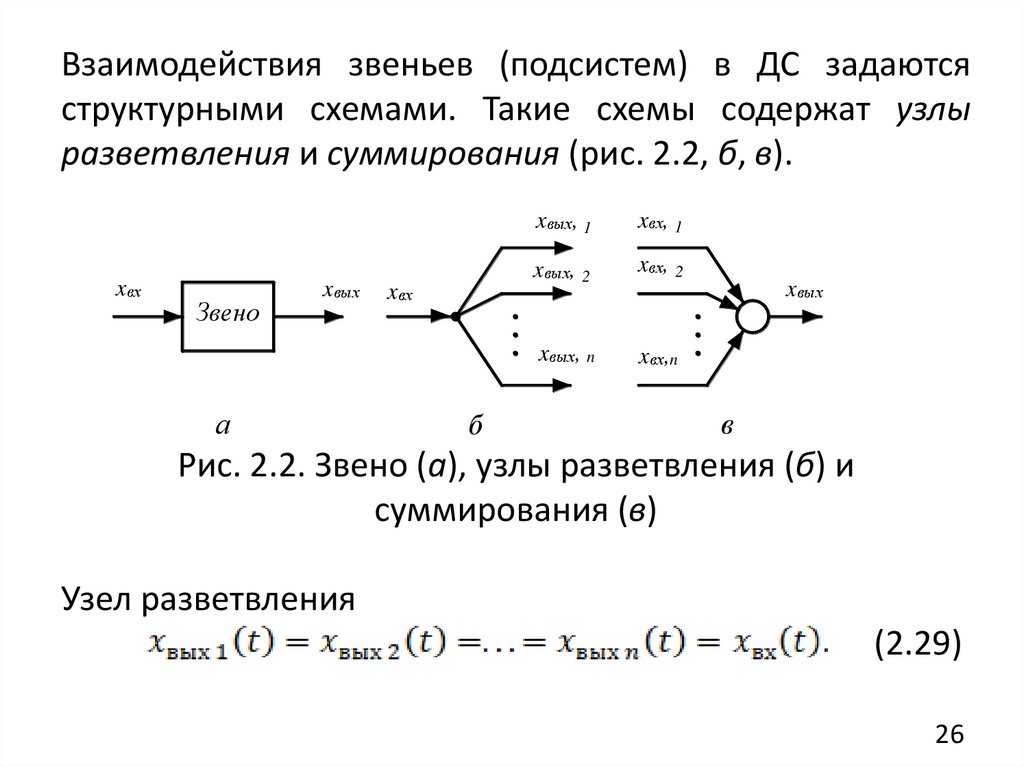
Взаимодействия звеньев (подсистем) в ДС задаются
структурными схемами. Такие схемы содержат узлы
разветвления и суммирования (рис. 2.2, б, в).
xвх
Звено
xвых
а
xвх
б
xвых, 1
xвх, 1
xвых, 2
xвх, 2
xвых, n
xвх,n
xвых
в
Рис. 2.2. Звено (а), узлы разветвления (б) и
суммирования (в)
Узел разветвления
.
(2.29)
26

27.

Суммирующий узел
n
xвых (t ) xвхi (t ) .
i 1
(2.30)
В основу классификации звеньев положены
соответствующие уравнения динамики. Различают
следующие группы динамических звеньев:
позиционные, дифференцирующие, интегрирующие
(астатические) , звено запаздывания.
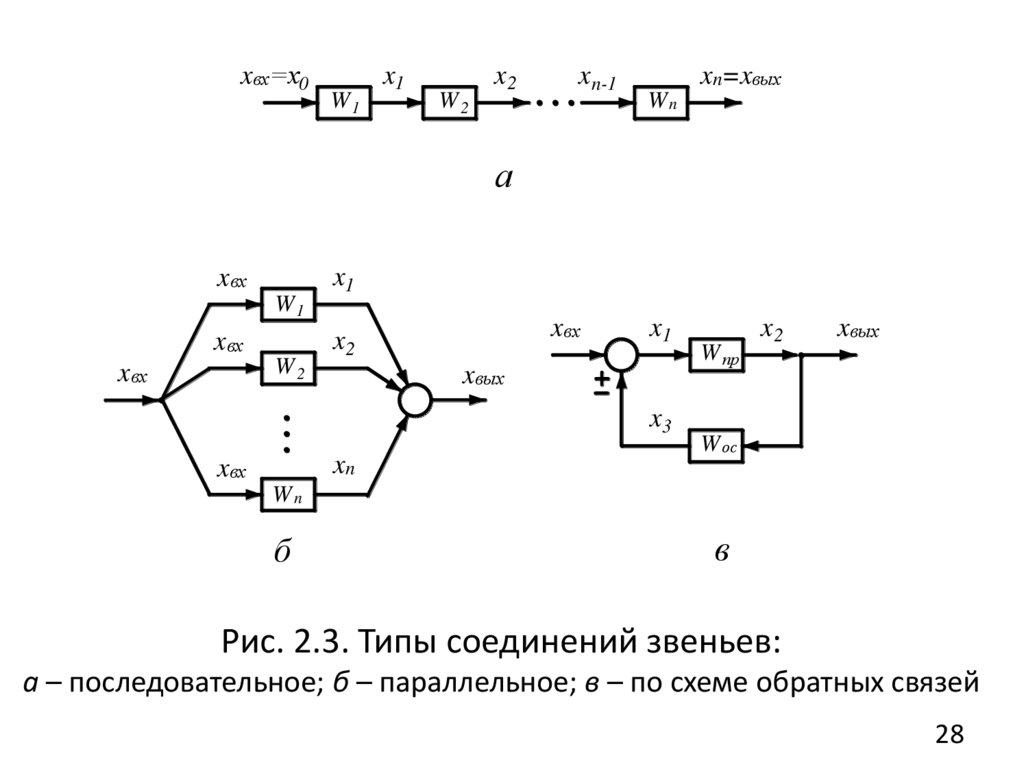
Звенья в ДС могут быть соединены последовательно,
параллельно, по схеме обратной связи и в их различной
комбинации.
Уравнение ДС определяется по уравнениям
динамических звеньев, входящих в систему, и ее
структуре.
27

28.

xвх=х0
W1
x1
W2
x2
xn-1
xn=xвых
Wn
а
xвх
W1
xвх
W2
xвх
x1
xвх
x2
x1
xвых
x3
xn
xвх
W пр
x2
xвых
W ос
Wn
б
в
Рис. 2.3. Типы соединений звеньев:
а – последовательное; б – параллельное; в – по схеме обратных связей
28

29.

1. Результирующая передаточная функция при
последовательном соединении (рис. 2.3, а)
n
W р ( s ) Wi ( s ) .
i 1
2. Результирующая передаточная функция при
параллельном соединении (рис. 2.3, б)
n
W р ( s ) Wi ( s ) .
i 1
3. Результирующая передаточная функция при соединении
по схеме обратных связей (рис. 2.3, в)
29

30.

где Wпр (s ) - передаточная функция канала прямой
Wос (s )
связи;
– передаточная функция канала
обратной связи; знак «–» минус относится к
положительной, а знак «+» плюс – к отрицательной
обратной связи.
Отрицательная обратная связь имеет главное
применение в автоматических системах.
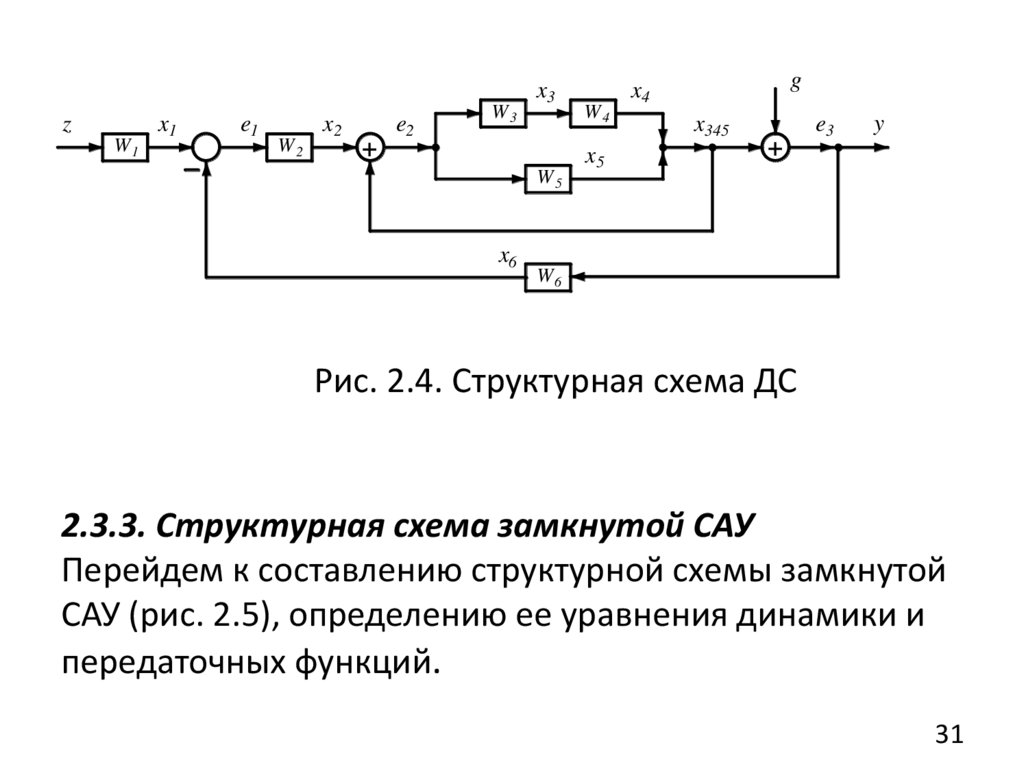
Пользуясь полученными здесь формулами, можно
определить общую передаточную функцию и для более
сложной
системы,
выделяя
в
ее
структуре
рассмотренные выше простейшие соединения и находя
для них результирующие передаточные функции с
последующим их объединением (рис. 2.4).
30

31.

z
W1
x1
e1
W2
x2
+
e2
W3
x3
W5
x6
W4
x5
g
x4
x345
+
e3
y
W6
Рис. 2.4. Структурная схема ДС
2.3.3. Структурная схема замкнутой САУ
Перейдем к составлению структурной схемы замкнутой
САУ (рис. 2.5), определению ее уравнения динамики и
передаточных функций.
31

32.

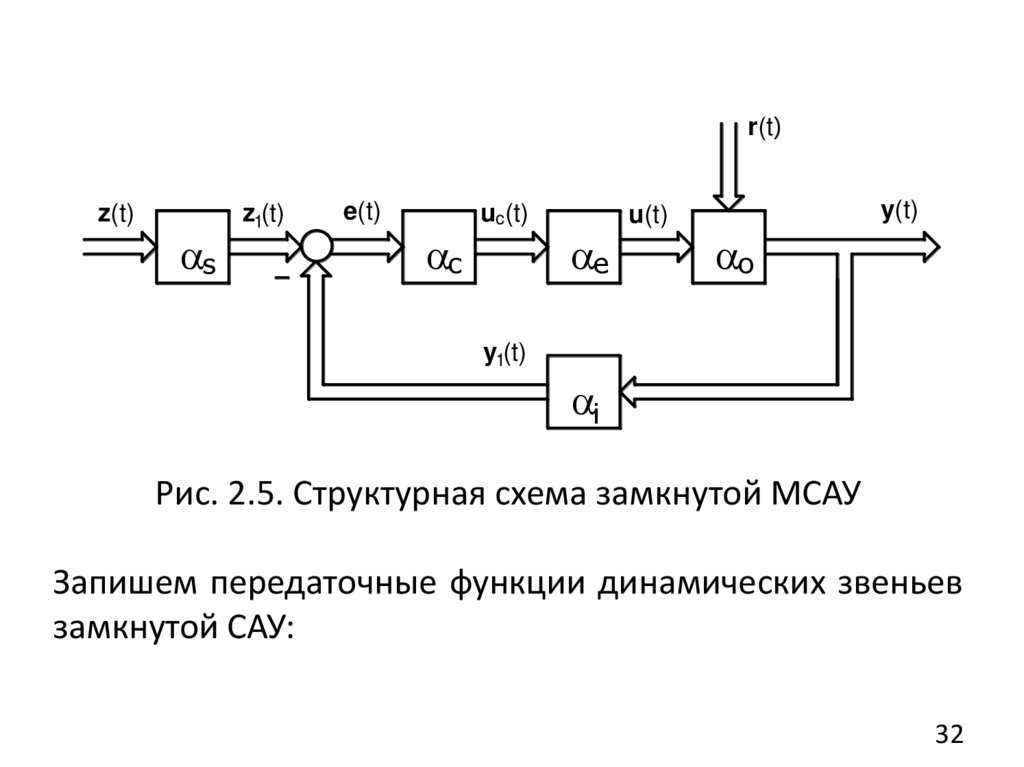
r(t)
z(t)
s
z1(t)
e(t)
uc(t)
c
y(t)
u(t)
e
o
y1(t)
i
Рис. 2.5. Структурная схема замкнутой МСАУ
Запишем передаточные функции динамических звеньев
замкнутой САУ:
32

33.

Wou ( s )
Y ( s)
U ( s)
– передаточная функция
управления по управляющему воздействию;
Wor ( s )
Y ( s)
R( s )
объекта
– передаточная функция объекта
управления по возмущающему воздействию;
Z1 ( s )
Ws ( s )
Z ( s)
–
передаточная
функция
задающей
подсистемы;
Далее для простоты изложения принимаем Ws ( s ) 1 ,
тогда Z1 ( s ) Z ( s ) ;
U ( s)
Wс ( s) c
E ( s)
–
передаточная функция
вычислительной подсистемы (контроллера);
логико33

34.

We ( s )
U ( s)
U c ( s)
– передаточная функция исполнительной
подсистемы;
Y1( s) – передаточная функция цепи обратной
Wi ( s)
Y ( s)
связи (информационно-измерительной подсистемы);
– изображение ошибки между
E ( s ) Z1( s ) Y1( s )
заданным и текущим значениями в замкнутой САУ. Это
уравнение называется уравнением связи.
Структурная схема САУ – передаточные функции
динамических звеньев соединенные в соответствии с их
функциональным
назначением
и
графически
представленные в виде блоков.
34

35.

Уравнение движения САУ записывается на основании
структурной схемы и передаточных функций ее
элементов
Y ( s ) Wou ( s )U ( s ) Wor ( s ) R ( s ),
U ( s ) We ( s )U c ( s ),
U c ( s ) Wс ( s ) E ( s ),
(2.31)
Y1 ( s ) Wi ( s )Y ( s ),
Z1 ( s ) Ws ( s ) Z ( s ),
E ( s ) Z1 ( s ) Y1 ( s ).
Решая систему уравнений (2.31) относительно Y (s) ,
получаем уравнение движения замкнутой САУ в
операторной форме
35

36.

Wп ( s )
Wor ( s )
Y ( s)
Ws ( s ) Z ( s )
R( s ) ,
1 Wп ( s )Wi ( s )
1 Wп ( s )Wi ( s )
(2.32)
где Wп ( s ) Wou ( s )We ( s )Wc ( s )
– эквивалентная
передаточная функция звеньев o , e , c ,
прямой
цепи управления (регулирования). В рассматриваемом
случае звенья (подсистемы) прямой цепи управления
охвачены обратной связью.
Из (2.32) находим передаточные функции замкнутой САУ
по задающему и возмущающему воздействию. Можно
найти передаточные функции по ошибке.
Изложенное выше велось в операторной форме, однако
все рассмотренное справедливо и во временной
области при замене комплексной переменной s на
оператор p. В этом случае выражение (2.32) можно
36

37.

представить в виде уравнения (2.19), решение которого
во временной области можно получить аналитически
или численными методами.
2.4. Временные характеристики
Динамические свойства системы (звена, ОУ, САУ) могут
быть определены по ее временным характеристикам,
которые представляют собой изменение выходного
сигнала во времени при подаче на ее вход типового
апериодического воздействия. В ТАУ используют два
вида временных характеристик:
1) переходная функция (переходная характеристика);
2)
функция
веса
(импульсная
переходная
характеристика).
37

38.

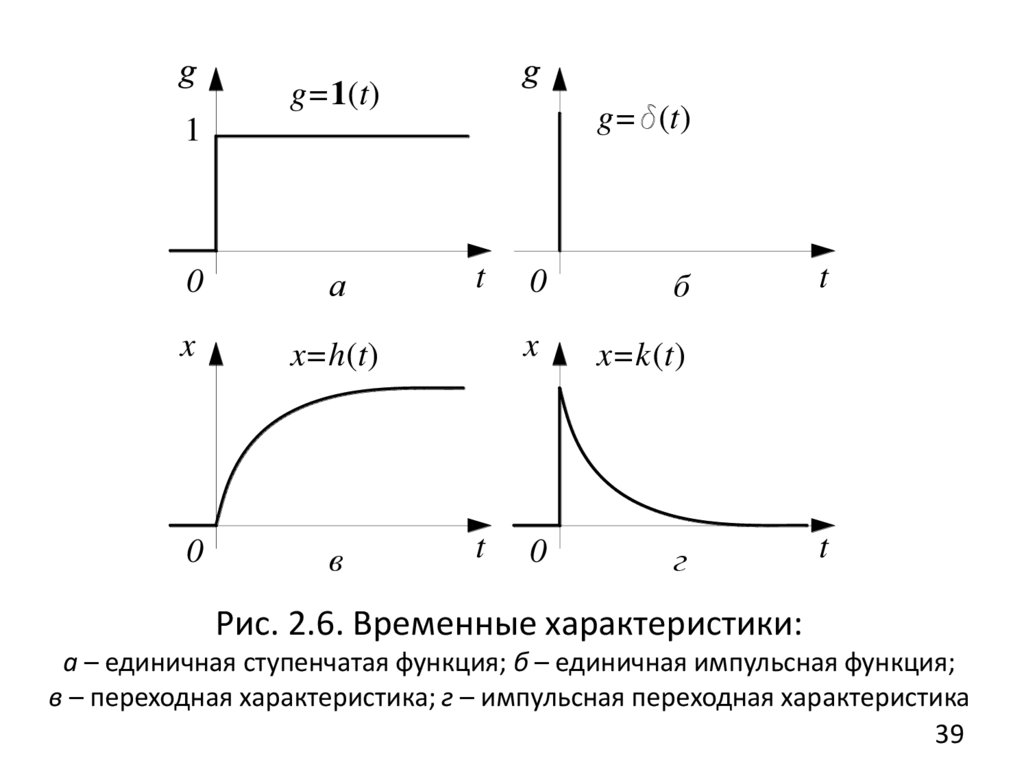
Переходная
функция,
или
переходная
характеристика, h(t ) представляет
собой
переходный процесс на выходе ДС (рис. 2.6, в),
возникающий при подаче на ее вход типового
апериодического воздействия g (t ) в виде единичного
ступенчатого воздействия 1(t ) ( g(t ) 1(t ) , рис. 2.6, а)
при нулевых начальных условиях.
(2.33)
0 при t 0;
1(t )
1 при t 0.
Изображение переходной функции H (s ) можно
определить как
1,
(2.34)
H ( s) W ( s)
s
где W (s) – передаточной функции системы при нулевых
начальных условиях.
38

39.

g=1(t)
g= (t)
1
0
а
x
x=h(t)
0
в
t
t
0
б
x
x=k(t)
0
г
t
t
Рис. 2.6. Временные характеристики:
а – единичная ступенчатая функция; б – единичная импульсная функция;
в – переходная характеристика; г – импульсная переходная характеристика
39

40.

Зная изображение переходной функции H (s) можно
определить переходную функцию h(t ) по формуле
обратного преобразования Лапласа.
При неединичном ступенчатом воздействии g (t ) N 1(t ) ,
где N const , получаем выходную реакцию линейной
системы x(t ) Nh(t ) .
Функция веса, или импульсная переходная
характеристика (ИПХ), k (t ) представляет собой
переходный процесс на выходе ДС (рис. 2.6, г),
возникающий при подаче на ее вход типового
апериодического воздействия g (t ) в виде единичного
импульсного воздействия (дельта-функция Дирака) (t )
(g (t ) (t ) , рис. 2.6, б) при нулевых начальных
условиях. Это входное воздействие аналитически
определяется выражением:
40

41.

при t 0;
(t )
0 при t 0.
(2.35)
Довольно часто в приложениях встречается смещенная
дельта функция
при t ;
(t )
0 при t .
(2.36)
Свойства дельта-функции:
(t )dt (t )dt 1 ,
(2.37)
т. е. площадь от дельта-функции равна единице;
41

42.

(t ) (t )dt (t ) (t )dt ( ) ,
(2.38)
данное соотношение определяет так называемое
«фильтрующее» или «выхватывающее» свойство;
( m)
( m)
m (m)
(
t
)
(
t
)
dt
(
t
)
(
t
)
dt
(
1
)
( ) , (2.39)
– свойство дифференцируемости.
Здесь 0 – произвольное положительное число;
(t ) – обычная функция, обладающая m-й производной;
( m)
(t ) – m-я производная по времени от
дельта-функции. Для несмещенной дельта-функции 0 .
42

43.

:
Соотношения между (t ) и 1(t ) :
d 1(t ) .
(t )
dt
(2.40)
Взаимосвязь между весовой функцией k (t ) и переходной
характеристикой h(t ) :
k (t )
Имеем соотношение:
dh(t )
.
dt
(2.41)
W (s) k (t )e st dt .
(2.42)
0
Функции W (s) и k (t ) полностью эквивалентны друг другу.
43

44.

2.5. Частотные характеристики
Частотные характеристики характеризуют поведение
систем под действием гармонического сигнала
g (t ) Gm cos t ,
(2.43)
- угловая частота этого
где Gm - амплитуда, а
воздействия.
Частотная передаточная функция системы
W ( j ) W ( s) s j A( )e j ( ) , .
(2.44)
44

45.

где
A( ) U 2 ( ) V 2 ( ) ,
( ) arg W ( j ).
Если arg W ( j ) / 2 , то ( ) arctg
V ( )
.
U ( )
Здесь U ( ) и V ( ) – вещественная и мнимая
составляющая частотной передаточной функции.
Выражение (2.44), при изменении частоты ω от 0 до
или же от до , называется амплитудно-фазовой частотной (амплитудно-фазовой) характеристикой (АФЧХ) или (АФХ) системы, также еще
называют диаграммой Найквиста.
45

46.

A( ) W ( j ) - амплитудная частотная функция, а ее
график – амплитудная частотная характеристика
(АЧХ);
( ) arg W ( j ) - фазовая частотная функция, его
график – фазовая частотная характеристика (ФЧХ).
Частотные
характеристики
довольно
широко
используются при анализе и синтезе САУ.
Кроме перечисленных частотных характеристик,
имеются
логарифмические
частотные
характеристики
(ЛЧХ)
–
логарифмические
амплитудные
частотные
характеристики
и
логарифмические фазовые частотные характеристики.
46

47.

Отметим, что все рассмотренные виды динамических
характеристик систем (дифференциальное уравнение,
передаточная функция, весовая функция, амплитуднофазовая частотная функция) связаны между собой
определенными зависимостями. Поэтому все они
эквивалентны друг другу в определении динамических
свойств линейных систем.
47

48.

2.6. Типовые динамические звенья и их
характеристики. Другие типы звеньев
2.6.1. Типовые динамические звенья и их
характеристики
Динамические звенья называют типовыми, если они
описываются
алгебраическими
или
дифференциальными
уравнениями
(передаточной
функцией) не выше 2-го порядка. Типовые звенья имеют
одну входную и одну выходную величину.
Частотные характеристики рассматриваются от 0 до .
2.6.1.1. Позиционные звенья
1. Идеальное усилительное (безынерционное,
пропорциональное) звено
48

49.

Уравнение и передаточная функция звена:
x 2 k1 x1 , W ( s ) k1 .
(2.45)
Переходная и весовая функции (рис. 2.7, а, б):
h (t ) k1 1(t ), k (t ) k1 (t ) .
(2.46)
h(t)
k(t)
h(t)=k1 1(t)
k(t)=k1 (t)
k1
0
а
t
0
б
t
Рис. 2.7. Характеристики идеального усилительного звена:
а – переходная; б – весовая
49

50.

2. Апериодическое (инерционное) звено первого
порядка
Уравнение и передаточная функция звена:
(Tp 1) x2 k1 x1 , W ( s ) k1 .
Ts 1
Переходная и весовая функции (рис. 2.8, а, б):
k1 Tt .
Tt ,
h(t ) k1 1(t ) 1 e k (t ) e
T
(2.47)
(2.48)
Здесь Т – постоянная времени звена, под которой понимают время, в течение которого выходная величина
звена достигла бы своего нового установившегося
значения, если бы она изменялась с постоянной
скоростью, равной скорости ее изменения в начальный
момент времени.
50

51.

h(t)
T
k(t)
k1
k1
T
0.63k1
t
0
T
а
k1
=0
0
>0
8
V( )
45°
=1/T
в
U( )
t
0
A( )
k1
б
( )
0
k1
-90°
2
0
1/T
г
д
Рис. 2.8. Характеристики апериодического звена
первого порядка:
а – переходная; б – весовая; в – амплитудно-фазовая;
г – амплитудно-частотная; д – фазо-частотная
51

52.

Постоянная времени звена T определяет его
динамические свойства. Чем она больше, тем
медленнее протекает переходный процесс в объекте, и
наоборот, т. е. постоянная времени T характеризует
«инерционность» апериодического звена. Рис. 2.8, г.
ср 1 / Т .
Частота среза
Амплитуда – k1 / 2 . То есть апериодическое звено
обладает демпфирующими свойствами.
3. Апериодическое звено второго порядка
Уравнение и передаточная функция звена:
(T22 p 2 T1 p 1) x2 k1 x1 , W ( s )
k1
T22 s 2 T1s 1
,
2.49)
52

53.

причем предполагается, что T1 2T2
1,2
T1 T12 4T22
2T22
и
- корни вещественные.
Апериодическое звено второго порядка можно
представить как последовательное соединение двух
апериодических звеньев первого порядка
k1
W ( s)
.
(T3s 1)(T4 s 1)
Переходная и весовая функции (рис. 2.13, а, б, где
T3T4
T3
T5
ln
):
T3 T4 T4
53

54.

Tt
Tt
T
T
3 e 3
4 e 4
h(t ) k1 1
,
T3 T4
T4 T3
(2.50)
t
t
k1 T3
k (t )
e
e T4 .
T3 T4
h(t)
(2.51)
k(t)
T 3+T 4
k1
0
T4
T5
t
0
t
а
б
Рис. 2.9. Характеристики апериодического звена второго
порядка:
а – переходная; б – весовая
54

55.

2
2
В граничном случае, когда T1 2T2 ( D T1 4T2 0 )
имеем T3 T4
и получаем граничный
апериодический процесс.
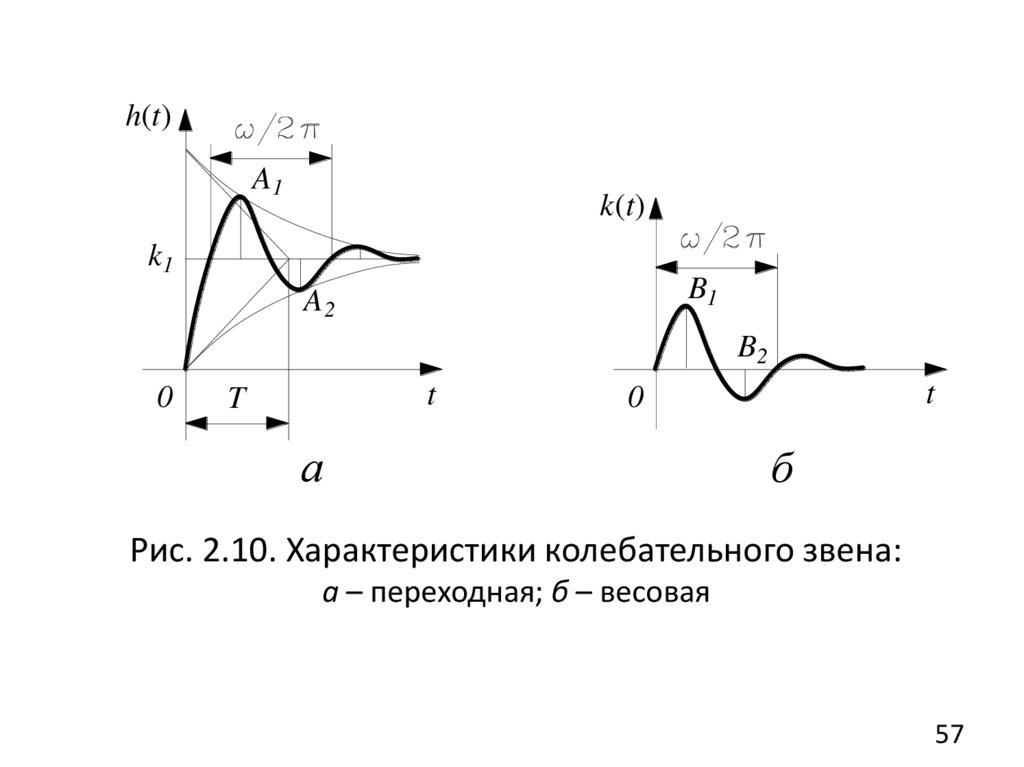
4. Колебательное звено
Звено описывается дифференциальным уравнением
(2.49), причем предполагается T1 2T2 ,
( D T12 4T22 0 ) – корни комплексные.
Уравнение колебательного звена
T 2 p2 2 Tp 1 x2 k1x1 ,
(2.52)
где T T2 , T1 /( 2T2 ) , причем 0 1 ;
(дзета) - коэффициент демпфирования
(параметр затухания).
55

56.

k1
Передаточная функция W ( s ) 2 2
. (2.53)
T s 2 Ts 1
Переходная и весовая функции (рис. 2.10, а, б):
2
2
t
1
1
h(t ) k1 1 e T cos
t
sin
t
,
2
T
T
1
2
t
1
k1
k (t )
e T sin
t.
2
T
T 1
Анализ влияния T1 /( 2T2 ) величины на изменение
амплитуды показывает, что постоянная времени T1
«демпфирует» колебания, а постоянная T2 «раскачивает» их.
56

57.

h(t)
A1
k(t)
k1
B1
A2
B2
0
t
T
t
0
а
б
Рис. 2.10. Характеристики колебательного звена:
а – переходная; б – весовая
57

58.

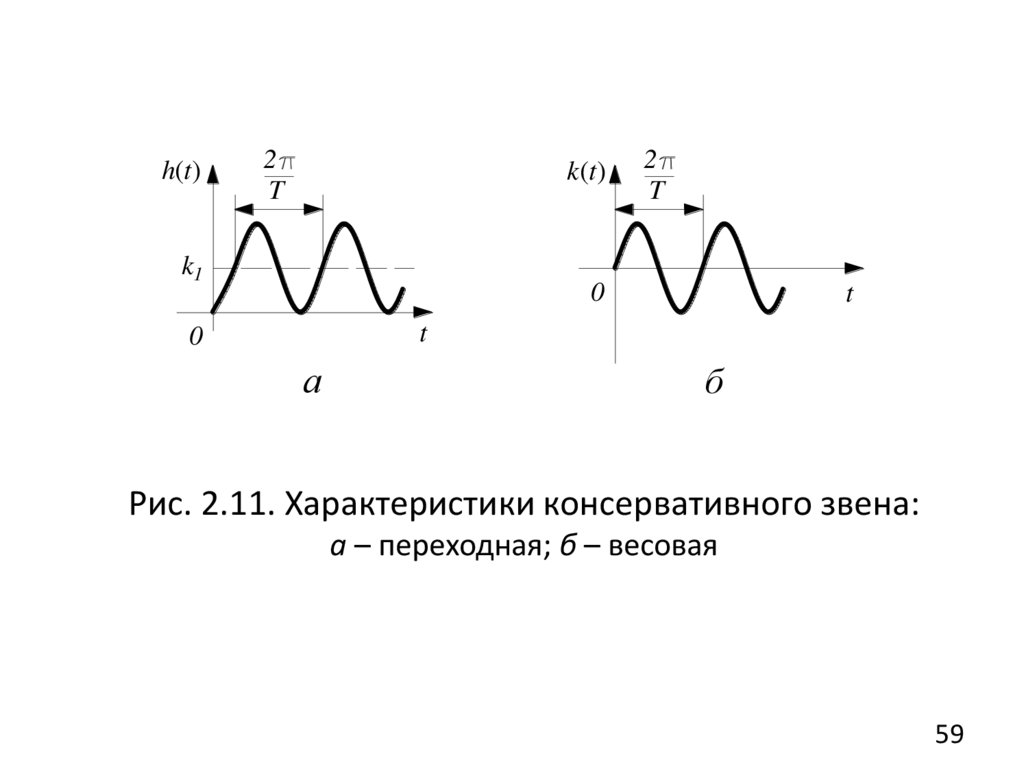
5. Консервативное звено
Консервативное звено является частным случаем
колебательного при 0 .
Уравнение и передаточная функция звена:
(T 2 p 2 1) x2 k1 x1 , W ( s) k1
,
(2.54)
2 2
T s 1
корни 1,2 j / T - гармонические колебания.
Переходная и весовая функции (рис. 2.15, а, б):
h(t ) k1 (1 cos 1t ) , k (t ) k1 1 sin 1t , 1 1 / T .
(2.55)
Переходная и весовая характеристики представляют
собой графики гармонических колебаний.
58

59.

h(t)
2
T
k(t)
k1
2
T
0
t
t
0
а
б
Рис. 2.11. Характеристики консервативного звена:
а – переходная; б – весовая
59

60.

2.6.1.2. Дифференцирующие звенья
1. Идеальное дифференцирующее звено
Уравнение и передаточная функция звена:
W ( s ) k1s .
x2 k1 px1 ,
Переходная и весовая функции (рис. 2.12, а, б):
h(t ) k1 p1(t ) k1 (t ) , k (t ) k1 p (t ) .
h(t)
(2.56)
(2.57)
k(t)
h(t)=k1 (t)
h(t)=k1p (t)
k1
0
t
а
0
t
б
Рис. 2.12. Характеристики идеального дифференцирующего
звена: а – переходная; б – весовая
60

61.

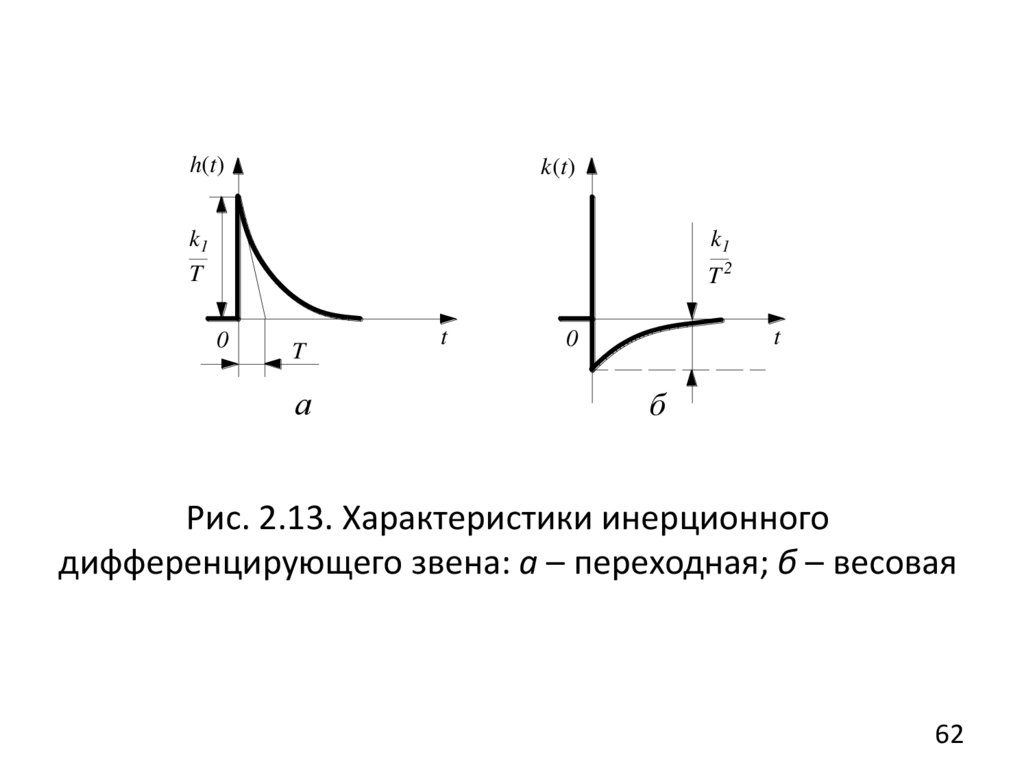
2. Инерционное дифференцирующее звено
(дифференцирующее звено с замедлением, реальное
дифференцирующее звено)
Уравнение и передаточная функция звена:
(Tp 1) x2 k1 px1 , W ( s) k1s s k1 .
Ts 1
Ts 1
(2.58)
Два последовательно включенных звена – идеальное
дифференцирующее и апериодическое первого
порядка.
Переходная и весовая функции (рис. 2.13, а, б):
k1 Tt , k (t ) k1 (t ) k1 e Tt .
h (t ) e
T
T
T2
(2.59)
61

62.

h(t)
k(t)
k1
T
k1
T2
0
T
а
t
t
0
б
Рис. 2.13. Характеристики инерционного
дифференцирующего звена: а – переходная; б – весовая
62

63.

2.6.1.3. Интегрирующие звенья
1. Идеальное интегрирующее звено
Уравнение и передаточная функция звена:
t
k1
x2 k1 x1dt или px2 k1x1 , W ( s )
.
s
0
запись при k1 1 / Tи :
(2.60)
1 t
x2
x1dt ,
Tи 0
где Tи - время интегрирования.
Переходная и весовая функции (рис. 2.14, а, б):
h(t ) k1t ,
k (t ) k1 .
(2.61)
63

64.

h(t)
k1
k(t)
h(t)=k1 t·1(t)
k1
k(t)=k1 ·1(t)
=arctgk1
0
а
t
0
б
t
Рис. 2.14. Характеристики идеального
интегрирующего звена: а – переходная; б – весовая
64

65.

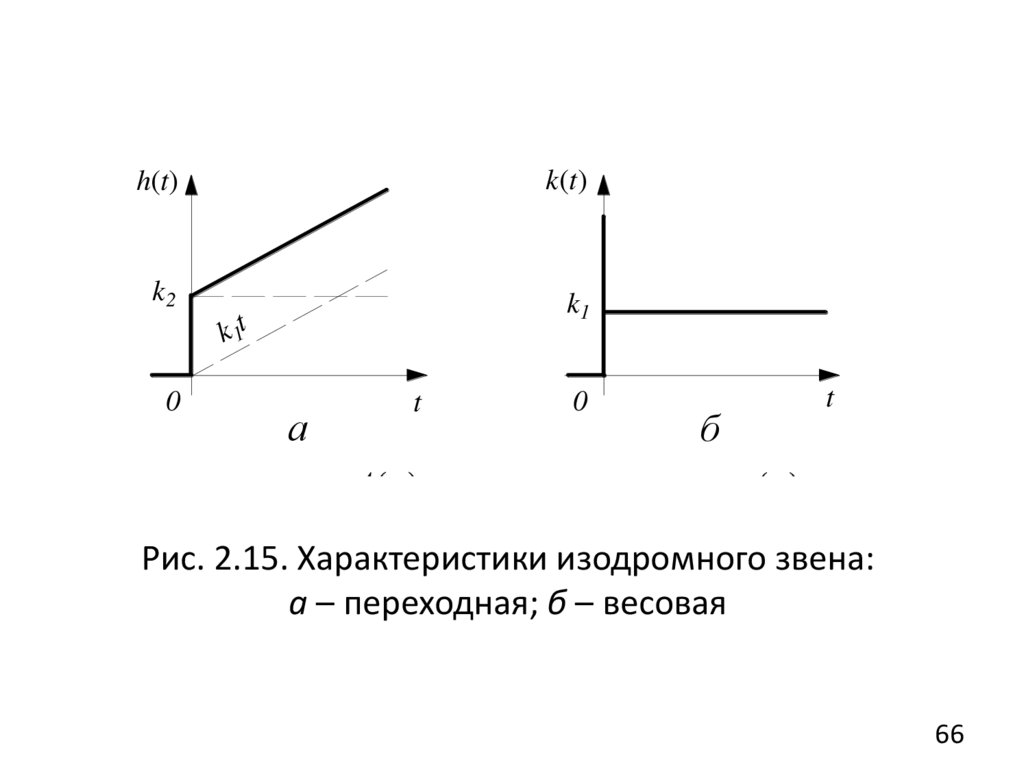
2. Изодромное звено
Уравнение и передаточная функция звена:
px2 ( k1 k2 p ) x1 , W ( s) k1 k k1(1 Ts) ,
s
2
(2.62)
s
где T k2 / k1 - постоянная времени изодромного звена.
Изодромное звено – совокупность двух включенных
параллельно звеньев: идеально интегрирующего и
пропорционального.
Переходная и весовая функции (рис. 2.15, а, б):
h(t ) k1t k2 ,
k (t ) k1 k2 (t ) .
(2.63)
65

66.

k(t)
h(t)
k2
k1
k 1t
0
а
t
0
б
t
Рис. 2.15. Характеристики изодромного звена:
а – переходная; б – весовая
66

67.

2.6.1.4. Звено запаздывания
Уравнение и передаточная функция звена:
0 при t
x2 (t ) x1(t ) или x2 (t )
, W ( s) e s .
x1 при t
(2.64)
Переходная и весовая функции (рис. 2.21, а, б):
h(t ) 1(t ) ,
h(t)
k (t ) (t )
.
k(t)
(t- )
(2.65)
1
t
0
а
0
t
б
Рис. 2.16. Характеристики звена запаздывания:
а – переходная; б – весовая
67

68.

Контрольные вопросы
1. Записать ЛДУ n-го порядка и привести его к стандартной
форме, принятой в ТАУ.
2. Какие типы движений могут возникнуть в ДС, и какими
факторами они определяются?
3. Что такое динамика и статика системы?
4. Что такое принцип суперпозиции, и для каких систем он
применим?
5. Что такое линеаризация, и для каких систем и зачем она
проводится?
6 . Что такое передаточная функция и как она определяется?
7. Чем определяется характер движения ДС?
8. Что такое динамические звенья и что положено в основу их
классификации?
9. Назовите типовые схемы соединений динамических
звеньев и запишите их результирующие передаточные
функции.
68

69.

10. Как и при каких условиях определяются в системе
передаточные
функции
по
управляющему
и
возмущающему воздействиям?
11. Что такое временная характеристика системы, и какие
виды временных характеристик используются для анализа
функционирования ДС?
12. Что такое АФЧХ, АЧХ и ФЧХ и что они характеризуют?
13. Какие звенья относятся к группе позиционных звеньев?
14. Какие звенья относятся к группе дифференцирующих
звеньев?
15. Какие звенья относятся к группе интегрирующих звеньев?
69

70.

БЛАГОДАРЮ ЗА ВНИМАНИЕ.
УСПЕХОВ!
70