Similar presentations:
Теория автоматического управления
1. Теория автоматического управления
Разделы лекционного курса:Основные понятия
Математическое описание систем
Характеристики систем во временной и частотной областях
Устойчивость систем
Оптимальное управление
Лабораторные работы:
Структурные схемы
Переходные характеристики
Частотные характеристики
Устойчивость систем
2. Дисциплина базируется на изучении курсов:
Высшая математикаМатематическое моделирование технологических систем
Основы анализа социальных и технических систем
Основы технологии машиностроения
Оборудование автоматизированных производств
Где применяются знания:
При разработке автоматических систем и их узлов (станки –
автоматы, ЧПУ, пром.роботы и т.п.)
При эксплуатации автоматических систем для устранения или
недопущения нежелательных режимов работы
При общении со специалистами по разработке автоматических
систем (в том числе – при постановке задачи)
При организации управления сложными социальными системами
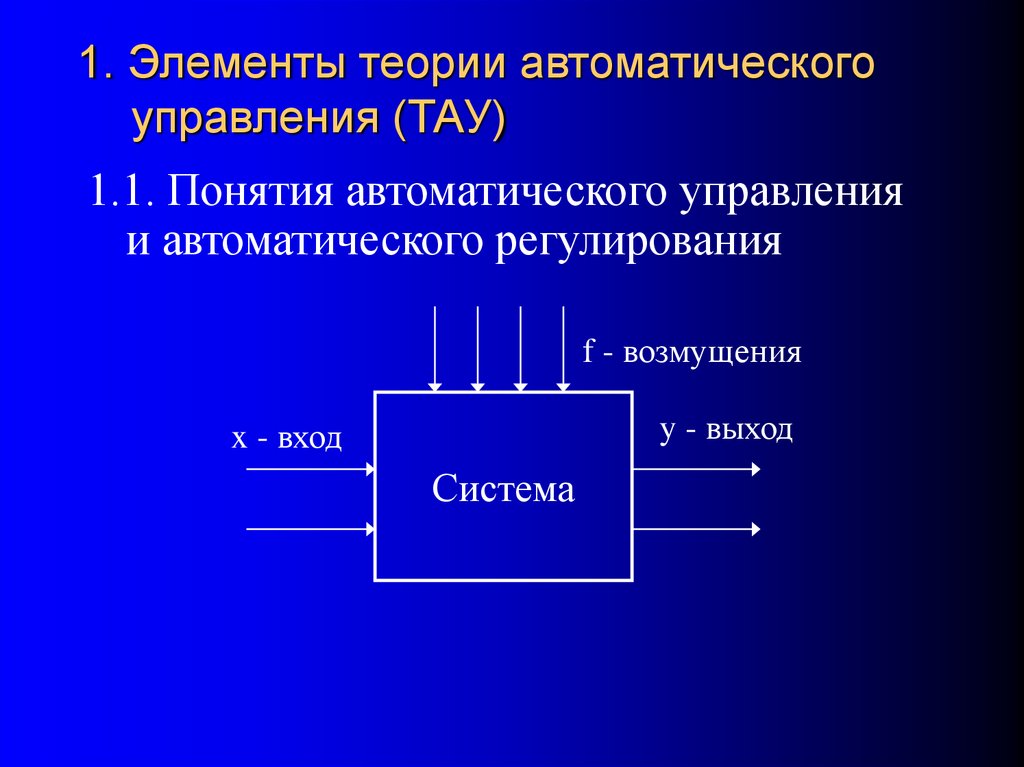
3. 1. Элементы теории автоматического управления (ТАУ)
1.1. Понятия автоматического управленияи автоматического регулирования
f - возмущения
y - выход
x - вход
Система
4. Задача автоматического управления
Найти такое х(t), чтобы достичь цели управления:• min(F1{y(t),x(t)}) при наличии f(t)
• F2{y(tк)} при наличии f(t)
Например:
1. Минимизация отклонений траектории инструмента от
F
заданной:
t
2
min F1 {y ( t) y 0 ( t)} dt
0
2. Получить заданную шероховатость поверхности:
F2 Ra(tк )
5. Задача автоматического регулирования
Разработать техническое устройство, реализующеесистему для решения задачи автоматического управления
Определение Системы Автоматического
Регулирования (САР):
САР называется система, функционирующая для достижения
цели управления без участия человека (автоматически) в условиях воздействия на нее возмущений.
Примеры:
• Бытовой холодильник
• Станок с ЧПУ
• Система стабилизации скорости вращения двигателя
• Система стабилизации получения заданного размера детали
……………….
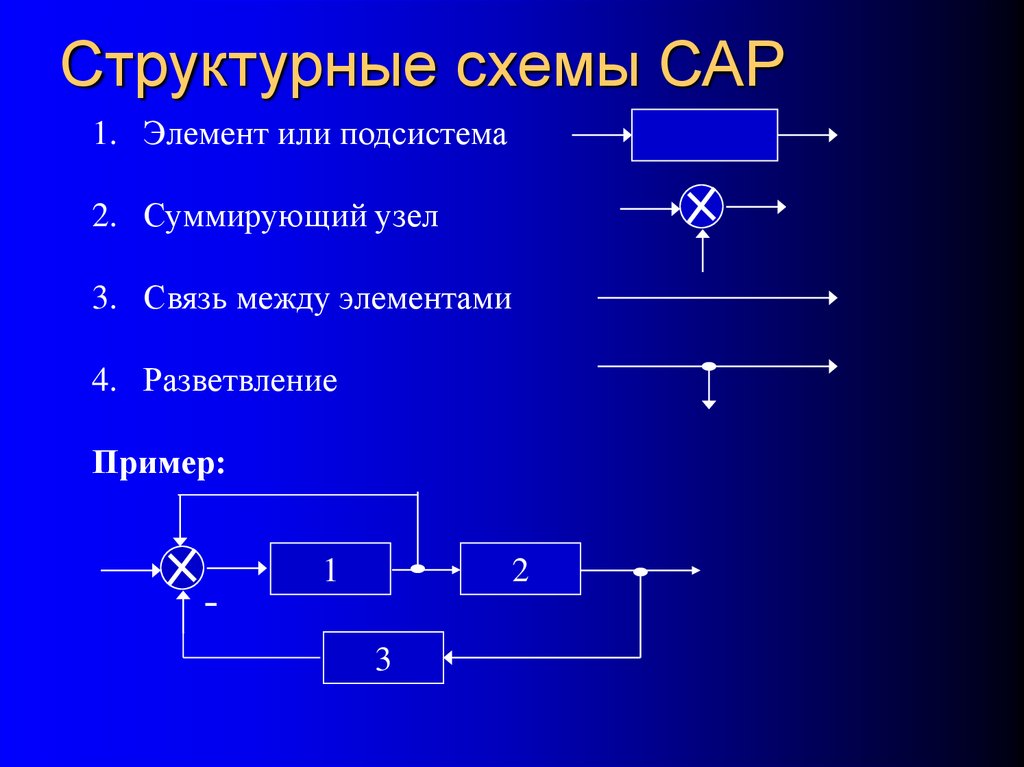
6. Структурные схемы САР
1. Элемент или подсистема2. Суммирующий узел
3. Связь между элементами
4. Разветвление
Пример:
-
1
2
3
7. 1.2. Состав и структура САР
Состав:1. Объект регулирования
2. Датчик
3. Автоматический регулятор
Структура:
Определяется соединением составных частей САР, которые
зависят от принципов регулирования
1.
2.
3.
4.
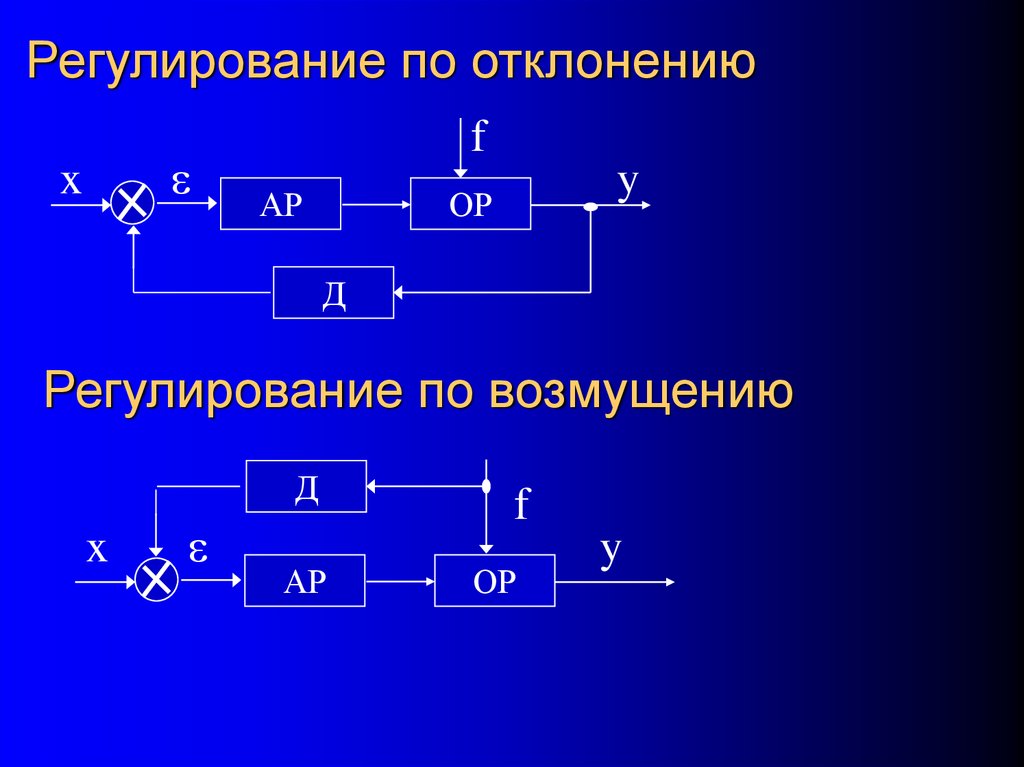
Регулирование по отклонению
Регулирование по возмущению
Комбинированные системы
Системы программного управления
8. Регулирование по отклонению
xf
АР
y
ОР
Д
Регулирование по возмущению
Д
x
АР
f
ОР
y
9. 1.3. Классификация САР
1. Работающие по замкнутому циклу• Системы стабилизации
• Следящие системы
2. Работающие по разомкнутому циклу
• Системы компенсации (по возмущению)
• Системы программного управления
3. Комбинированные системы
4. Самонастраивающиеся (адаптивные) САР – параметры
системы могут изменяться при изменении внешних
условий (процесс обучения)
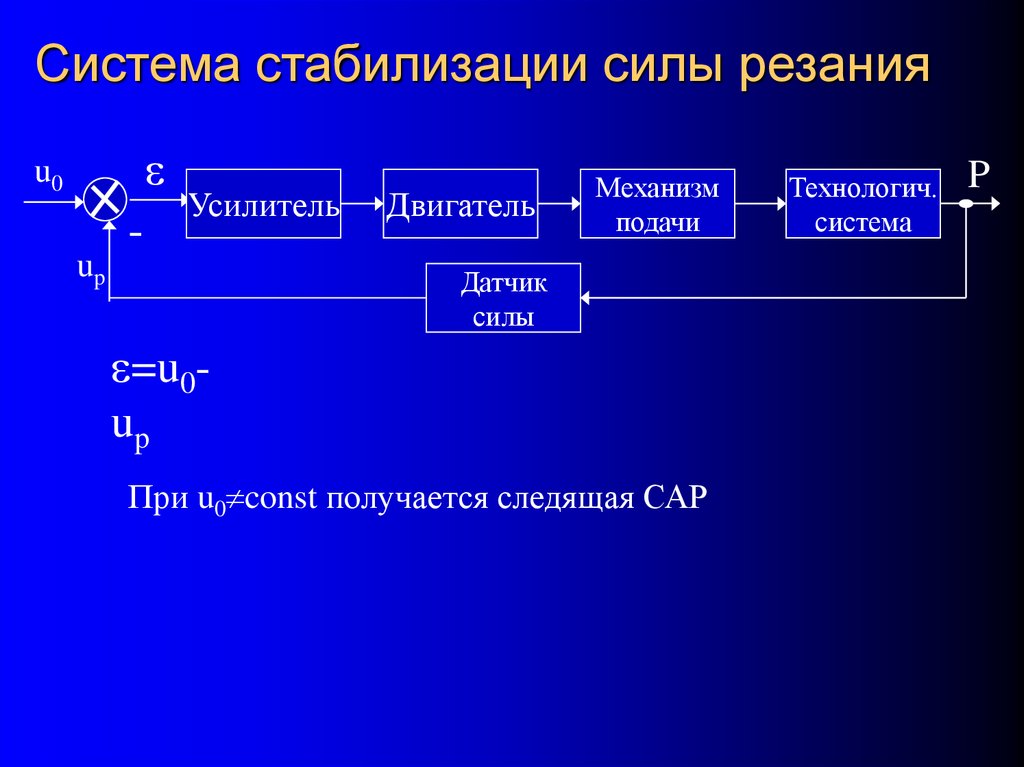
10. Система стабилизации силы резания
u0up
-
Усилитель
Двигатель
Механизм
подачи
Датчик
силы
=u0up
При u0 const получается следящая САР
Технологич.
система
P
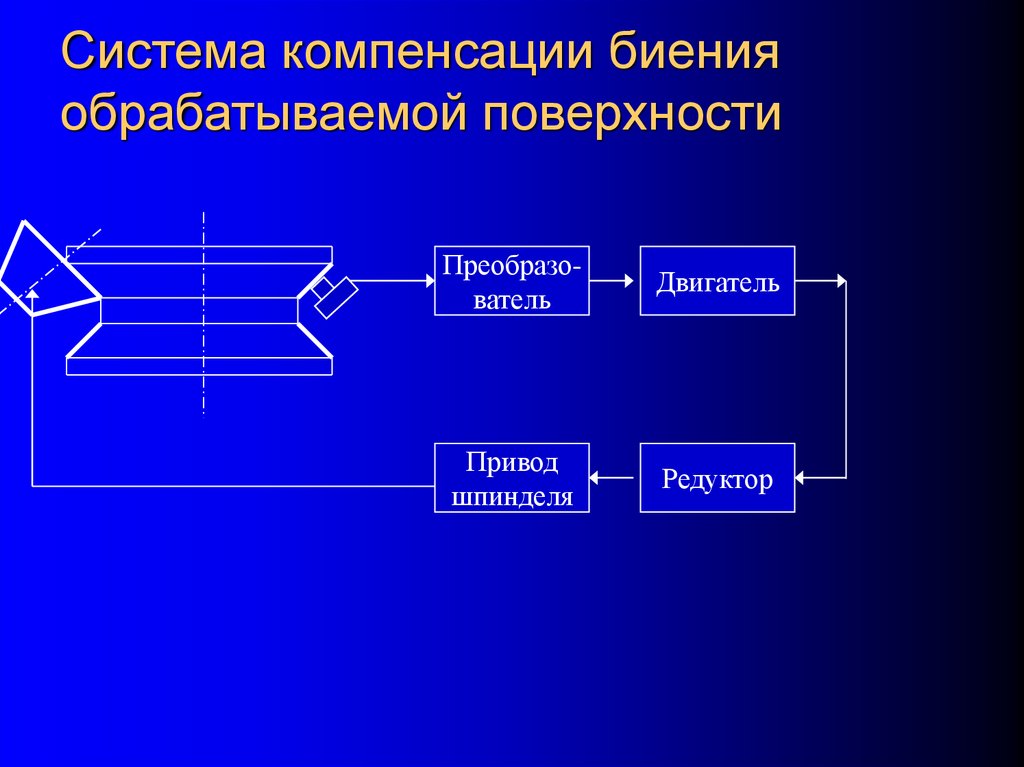
11. Система компенсации биения обрабатываемой поверхности
ПреобразовательДвигатель
Привод
шпинделя
Редуктор
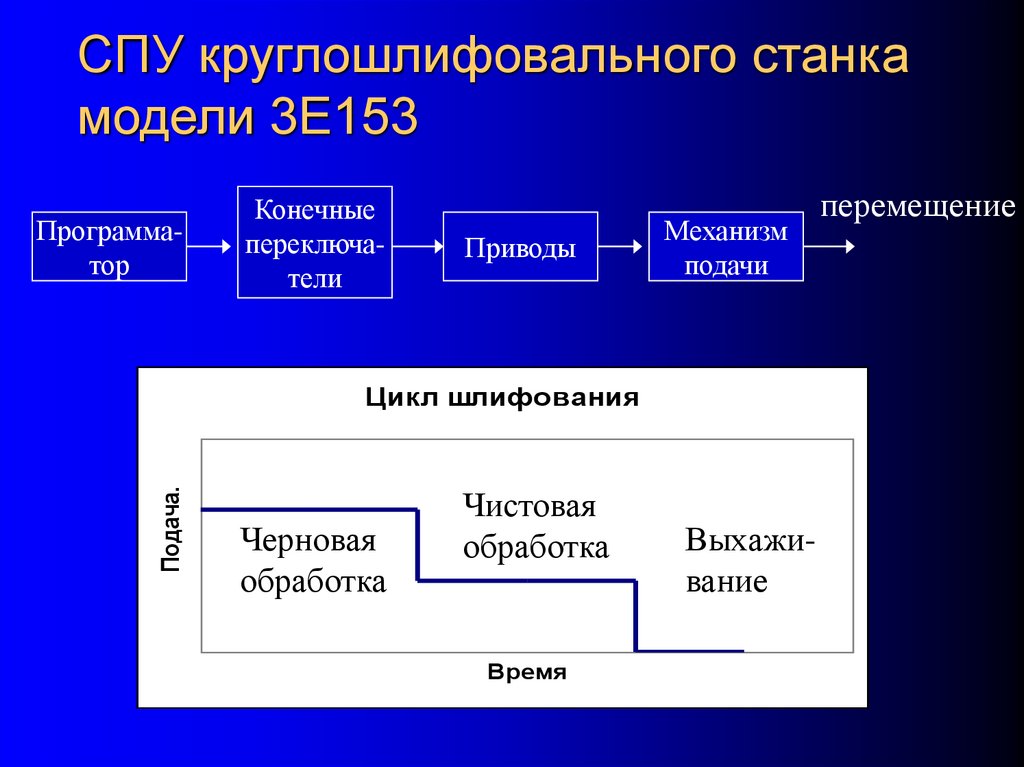
12. СПУ круглошлифовального станка модели 3Е153
ПрограмматорКонечные
переключатели
Приводы
Механизм
подачи
Подача.
Цикл шлифования
Черновая
обработка
Чистовая
обработка
Время
Выхаживание
перемещение
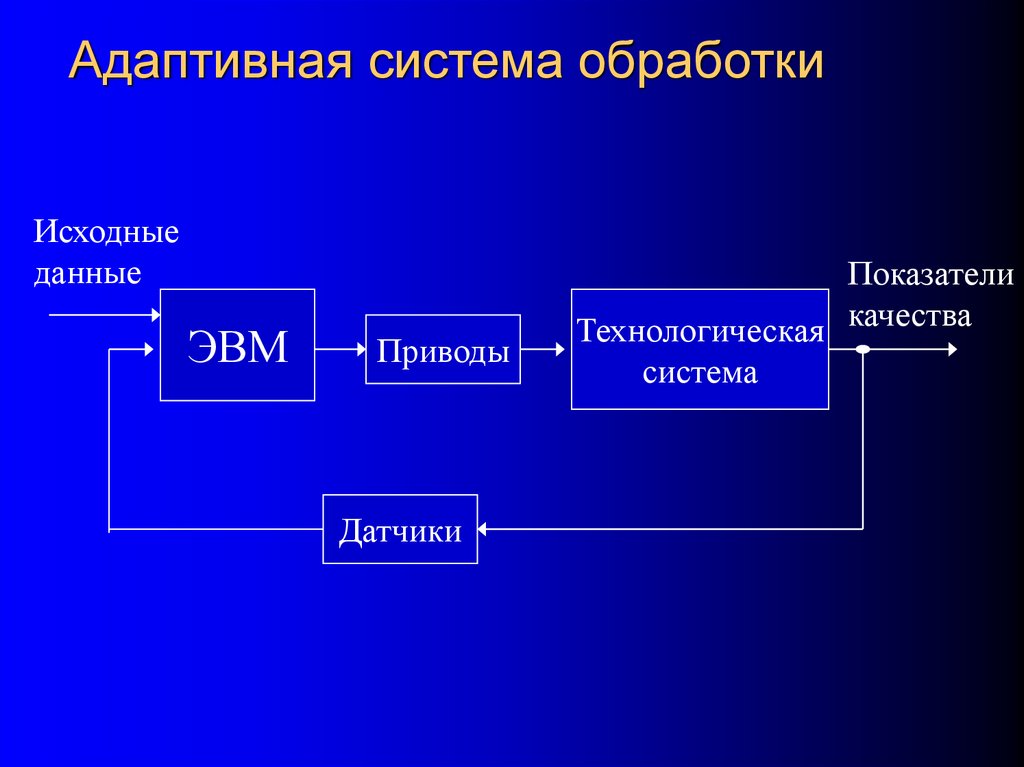
13. Адаптивная система обработки
Исходныеданные
ЭВМ
Приводы
Датчики
Показатели
Технологическая качества
система
14. 1.4. Математическое описание САР
Любую непрерывную систему можно описатьуравнением:
F(x(k), x(k-1),…,x’,x, y(n), y(n-1),…,y’,y) = 0
Если зависимость F линейна, то она принимает вид:
any(n)+…+a1y’+a0y = bkx(k)+…+b1x’+b0x
Это выражение – линейное дифференциальное
уравнение с постоянными коэффициентами.
15. Передаточная функция линейной системы
Система описывается дифференциальным уравнением:any(n)+…+a1y’+a0y = bkx(k)+…+b1x’+b0x
Формально заменим символ дифференцирования
символом s:
d
di
dt
s;
i
s
dti
(ansn+an-1sn-1+…+a1s+a0)y = (bksk+…+b1s+b0)x
Обозначим
b k s k ... b1s b 0
y ( s)
W ( s)
x ( s)
a n s n ... a1s a 0
Это выражение называется
передаточной функцией линейной системы
16. Передаточная функция линейной системы
Определение: Передаточной функцией линейной системыназывается отношение лапласова изображения
выходной величины системы к лапласову
изображению входной величины, полученные
при нулевых начальных условиях.
Пример:
Cy F( t)
m
y Gy
ms
2
)
Gs C y ( s) F( s)
y ( s)
1
W ( s)
2
F( s )
ms Gs C
Передаточная функция это другая форма записи дифференциального уравнения, более удобная для некоторых приложений.
17. Коэффициент передачи системы
Если входной сигнал x(t)=const=x0, то с течением временивыходной сигнал устанавливается: y(t)=const=y0.
Отношение k=y0/x0 называется коэффициентом передачи
системы (коэффициентом усиления).
1. Т.к. для установившегося режима и входной сигнал х, и
выходной сигнал у постоянны, то все их производные
равны нулю. Тогда дифференциальное уравнение
превращается в: a0y0=b0x0;
k=y0/x0 = b0/a0.
2. Коэффициент передачи получается из передаточной
функции при s=0:
W(0) = k = b0/a0.
18. Коэффициент передачи системы
Коэффициент передачи характеризует статические свойствасистемы, т.е. ее свойства при очень медленном изменении
входного сигнала:
yст k xст
y
tg = k
x
19. 1.5. Преобразование структурных схем
Задано математическое описание (передаточные функции)звеньев (составных элементов) САР и структура системы.
Необходимо найти передаточную функцию всей системы.
1. Последовательное соединение звеньев:
с
x
x1
x2
W1
W2
W3
x1 (s)
W1
; x1 W1 x
x ( s)
x 2 ( s)
W2
; x 2 W2 x1 W1 W2 x
x1 (s)
y
x
W0
W3
y ( s)
; y W3 x 2 W1 W2 W3 x
x 2 ( s)
y ( s)
W0
W1 W2 W3
x ( s)
20. Преобразование структурных схем
2. Параллельное согласное соединение звеньев:x1
W1
x2
y
x3
y x1 x 2 x 3
x
W2
W3
y
x
W0
xi
Wi ; x i Wi x
x
y ( W1 W2 W3 ) x
y
W0 W1 W2 W3
x
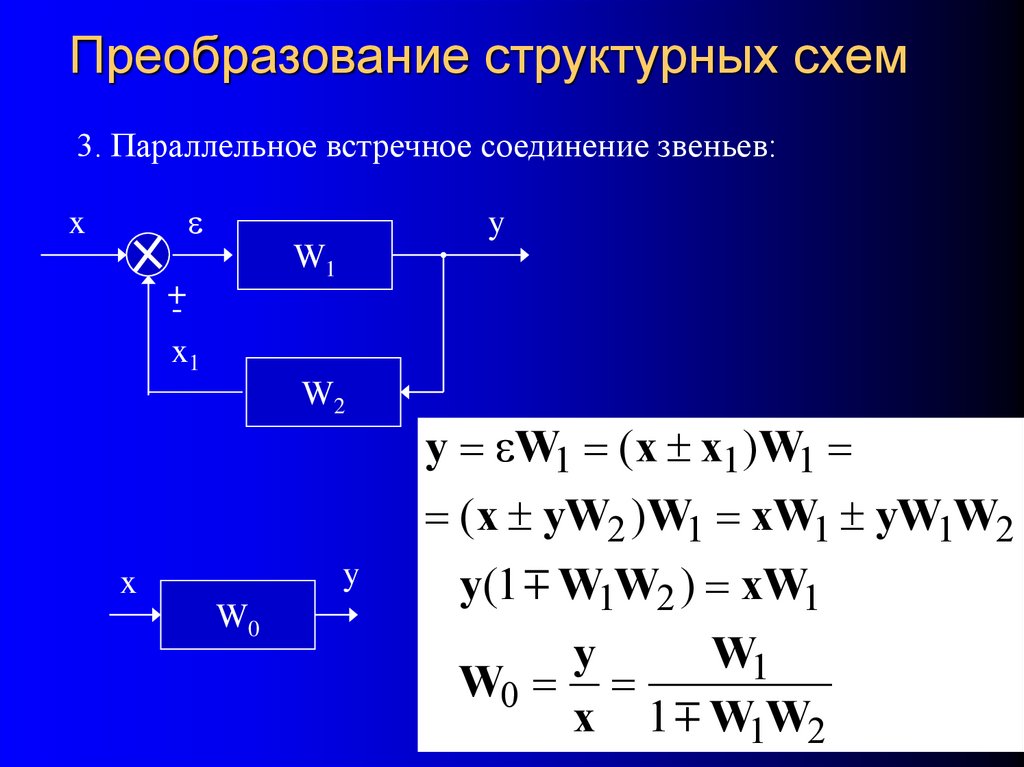
21. Преобразование структурных схем
3. Параллельное встречное соединение звеньев:x
y
W1
+x1
W2
y W1 ( x x1 ) W1
( x yW2 ) W1 xW1 yW1W2
y
x
W0
y (1 W1W2 ) xW1
y
W1
W0
x 1 W1W2
22. Преобразование структурных схем Примеры:
1.2.
1
a bs
1
s
1
a bs
1
s
-
1
a bs
3.
-
1
s
W0
1
as bs 2
1
1 s a bs
W0
2
a bs s as bs
(1 b)s a
as bs 2
1
s
a
bs
W0
1
1 a ( b 1)s
a bs s
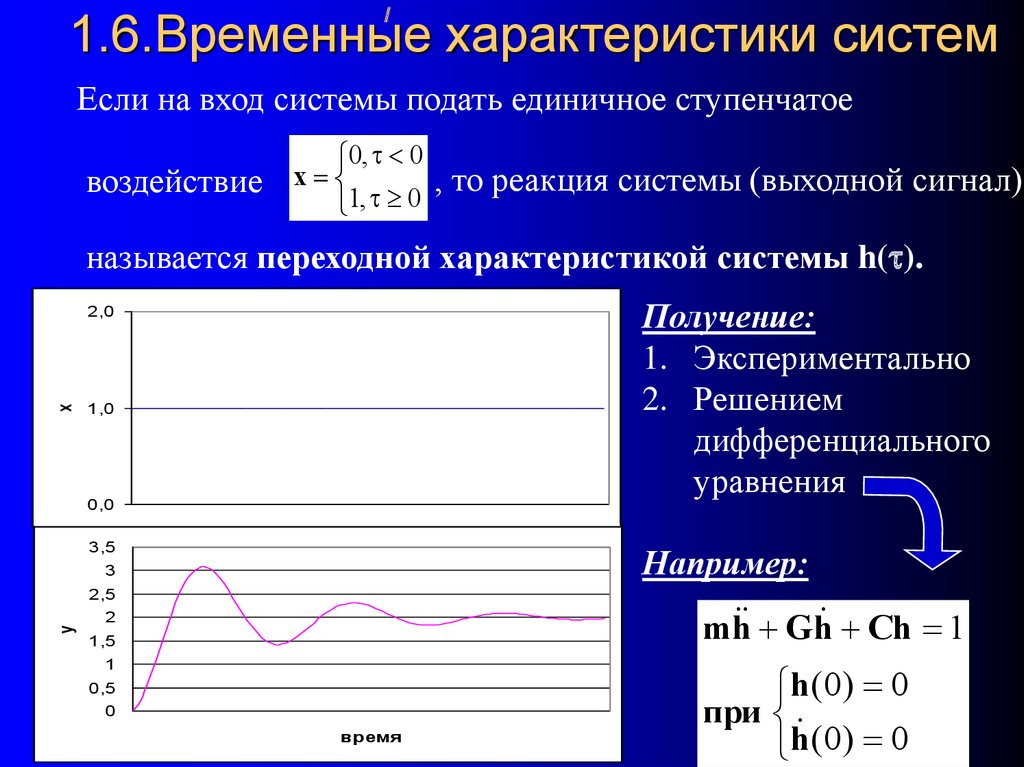
23. 1.6.Временные характеристики систем
/1.6.Временные характеристики систем
Если на вход системы подать единичное ступенчатое
воздействие
0, t 0
x
1, t 0
, то реакция системы (выходной сигнал)
называется переходной характеристикой системы h(t).
Получение:
1. Экспериментально
2. Решением
дифференциального
уравнения
x
2,0
1,0
0,0
3,5
Например:
3
y
2,5
Gh Ch 1
mh
2
1,5
1
0,5
0
время
h ( 0) 0
при
h
( 0) 0
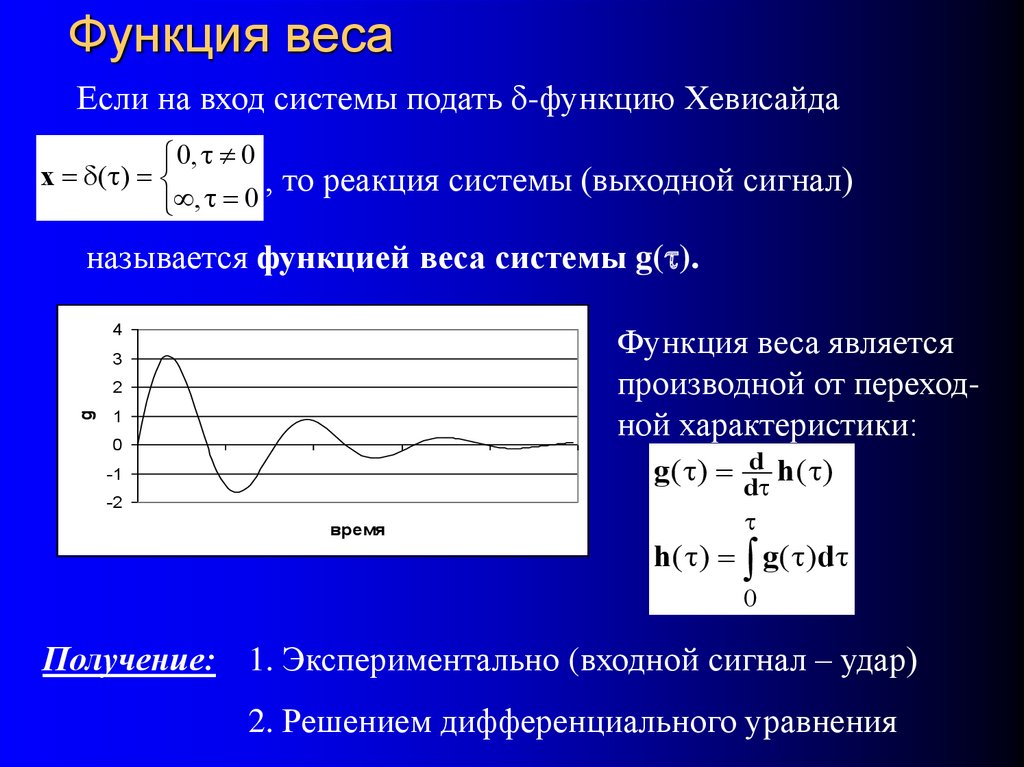
24. Функция веса
Если на вход системы подать -функцию Хевисайда0, t 0
x ( t)
,
,
t
0
то реакция системы (выходной сигнал)
называется функцией веса системы g(t).
4
Функция веса является
производной от переходной характеристики:
3
g
2
1
0
g ( t) ddt h( t)
-1
-2
время
t
h( t) g ( t)dt
0
Получение: 1. Экспериментально (входной сигнал – удар)
2. Решением дифференциального уравнения
25. Временные характеристики систем
/Временные характеристики систем
Временные характеристики h(t) и g(t) наиболее полно отражают
динамические свойства системы (изменение ее параметров во
времени). Они показывают как система реагирует на ступенчатый
(резко изменяющийся) входной сигнал и как затем она
устанавливается у постоянного значения (успокаивается). Именно
по этим характеристикам можно определить насколько САР
быстро и точно реагирует на входной сигнал.
Для сравнения динамических свойств систем кривые h (t) и g(t)
использовать неудобно. Для этого на этих кривых выделяют
специальные параметры качества. Обычно параметры качества
определяют по переходной характеристике. По этим параметрам
можно сравнить быстродействие , чувствительность САР и т.п.
26. Параметры качества на переходной характеристике
1. Коэффициент передачи (усиления) k.2. Перерегулирование - в абсолютных значениях или в
процентах от k.
3. Время переходного процесса tп.
4. Колебательность N – количество полных колебаний за время tп
h
±5% от k
k
tп
27. Пример расчета переходной характеристики
m y Gy Cy 1. Частное решение : y k 1C
Однородное уравнение : m y Gy Cy 0.
G G 2 4mC
Характерис тическое уравнение : mr Gr C 0; r
2m
2
1. При G 2 4mC ; r1 и r2 - действительные числа и решение ДУ имеет вид : y k С1e r1t С 2 e r2 t
k С1 С 2 0
y С1r1e r1t С 2r2 e r2 t . Из нач.условий :
С1r1 С 2r2 0
2. При G 2 4mC r12 b j и решение ДУ имеет вид : y k e bt (С1 sin t C 2 cos t)
k С2 0
y e bt [b(C1 sin t C 2 cos t) (C1 cos t C 2 sin t)]. Из нач.условий :
bС 2 С1 0
y e bt [( bC1 C 2 ) sin t ( bC 2 C1 ) cos t]
ОКОНЧАТЕЛЬ НО :
k С1e r1t С 2 e r2 t при G 2 4mC ;
h( t )
k e bt (С1 sin t C 2 cos t) при G 2 4mC ;
С1r1e r1t С 2r2 e r2 t при G 2 4mC ;
g( t) bt
e [( bC1 C 2 ) sin t ( bC 2 C1 ) cos t] при G 2 4mC;
28. 1.7.Частотные характеристики систем
Если на вход системы подать гармонический сигнал x = a sin t,то на выходе системы по истечении времени переходного
процесса установится также гармонический сигнал той же
частоты, но другой амплитуды и фазы: y = b sin ( t+ ).
При этом b = b( ) и = ( ). Эти зависимости и определяют
частотные свойства системы.
Частотные характеристики:
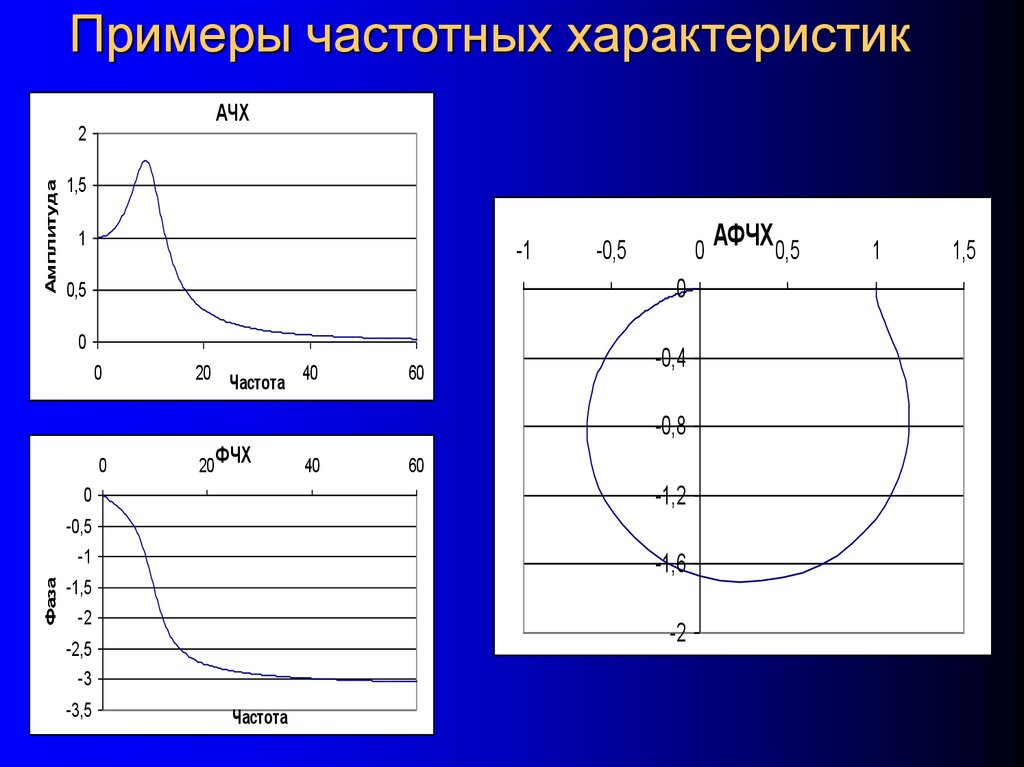
1. Амплитудно-частотная характеристика (АЧХ): A( ) =b ( )/a
(при a=1 A( ) =b ( )).
2. Фазо-частотная характеристика (ФЧХ): = ( ).
3. Амплитудно-фазовая частотная характеристика (АФЧХ):
показывает связь амплитуды A( ) и фазы ( ) в полярных
координатах.
29. Примеры частотных характеристик
АЧХАмплитуда
2
1,5
1
-1
-0,5
0
0
0,5
0
0
20 Частота 40
60
-0,4
-0,8
Фаза
0
20ФЧХ
40
60
0
-1,2
-0,5
-1
-1,6
-1,5
-2
-2
-2,5
-3
-3,5
Частота
АФЧХ 0,5
1
1,5
30. Получение частотных характеристик
Из передаточной функции системыЗаменим в передаточной функции W(s) s на j , где j2 = -1:
W( j ) U( ) jV ( ) - АФЧХ.
Построим на комплексной плоскости годограф – графическое
представление АФЧХ.
V( )
U( )
( )
A( )
Из геометрических построений:
A ( )
U 2 ( ) V 2 ( )
sin( )
cos( )
V ( )
A ( )
U( )
A ( )
31. Получение частотных характеристик
Пример:1
1
1 j
W ( s)
; W( j )
;
s 1
j 1 (1 j )(1 j )
1 j
1
W ( j )
j U( ) jV ( );
2
2
2
1
1
1
2
2
A ( ) U V
0
…
1
…
U
1
…
0.5
…
0
V
0
…
-0.5
…
0
1 2
2
1
1
1 2
;
=1
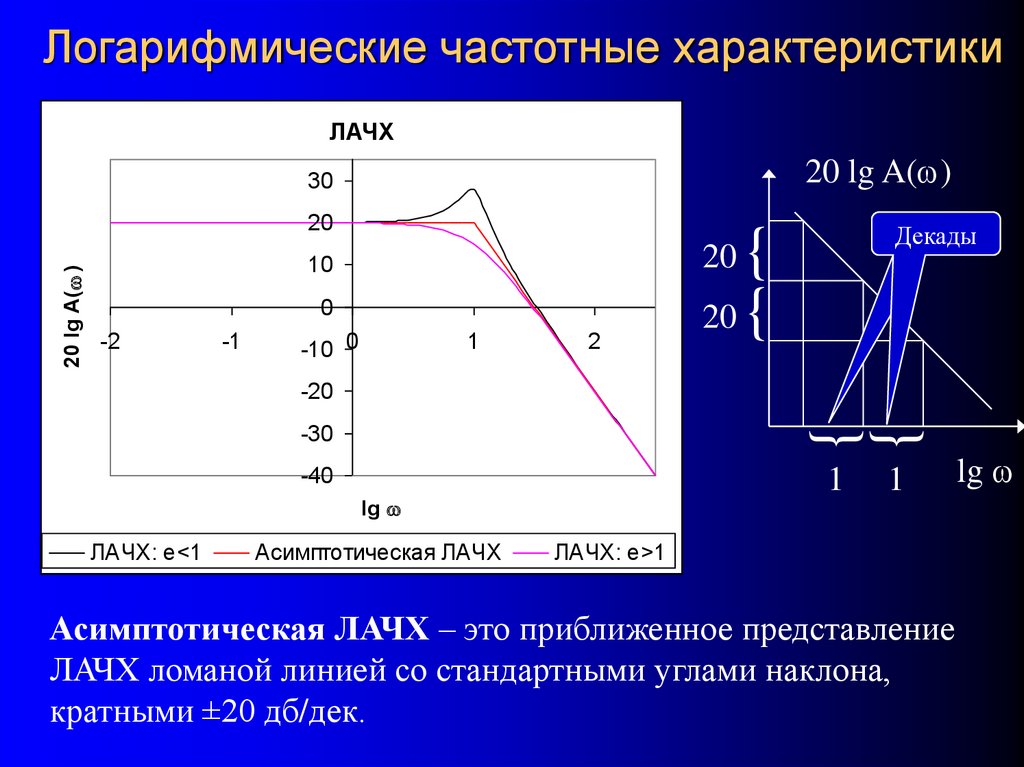
32. Логарифмические частотные характеристики
Позволяют более подробно рассмотреть начало и окончаниечастотной характеристики за счет логарифмического масштаба по
осям.
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ):
20 lg A( )
0.01
0.1
1
10
100
-2
-1
0
1
2
lg
lg
Логарифмическая фазо-частотная характеристика:
( )
lg
33. Логарифмические частотные характеристики
ЛАЧХ20 lg A( )
30
20 lg A( )
20
0
-1
{
20 {
20
10
-2
Декады
Декада
-10 0
1
2
-20
{
{
-30
-40
1
lg
ЛАЧХ: e<1
Асимптотическая ЛАЧХ
1
ЛАЧХ: e>1
Асимптотическая ЛАЧХ – это приближенное представление
ЛАЧХ ломаной линией со стандартными углами наклона,
кратными ±20 дб/дек.
lg
34. 1.8. Типовые звенья САР 1. Усилительное звено
Уравнение: y = k x; Передаточная функция: W(s) = k.Примеры: рычаг, редуктор, широкополосный усилитель и т.п.
Fx
ux
Fy
Усилитель
h
uy
A
k
k
t
L
20 lg k
lg
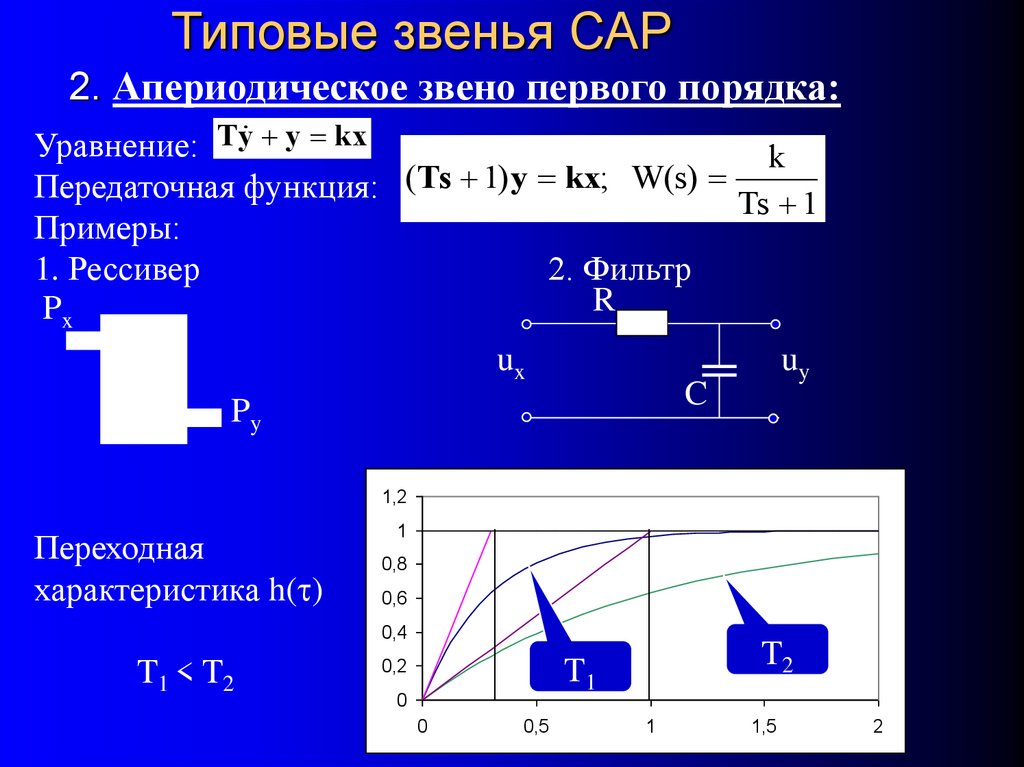
35. Типовые звенья САР 2. Апериодическое звено первого порядка:
Уравнение: Ty y kxk
Передаточная функция: (Ts 1) y kx; W(s) Ts 1
Примеры:
1. Рессивер
2. Фильтр
R
Px
ux
uy
C
P
y
1,2
Переходная
характеристика h(t)
1
0,8
0,6
0,4
T1 < T2
0,2
T2
T1
0
0
0,5
1
1,5
2
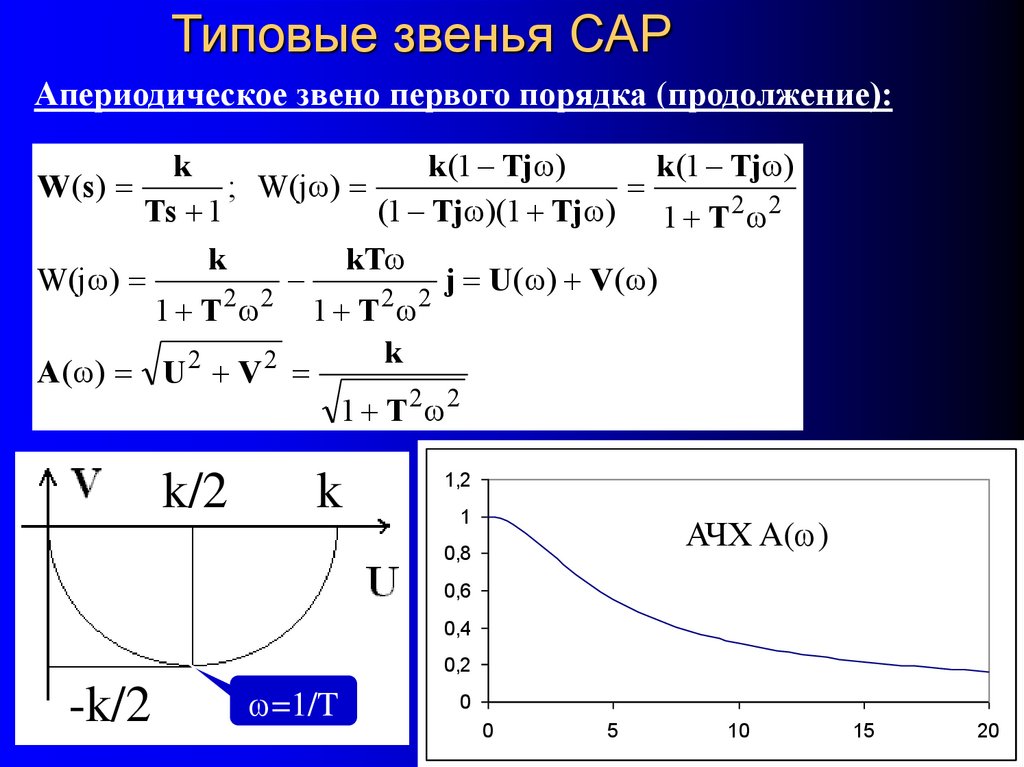
36. Типовые звенья САР
Апериодическое звено первого порядка (продолжение):k
k (1 Tj )
k (1 Tj )
; W(j )
Ts 1
(1 Tj )(1 Tj ) 1 T 2 2
k
kT
W(j )
j U( ) V( )
2 2
2 2
1 T
1 T
k
2
2
A ( ) U V
1 T 2 2
W ( s)
k/2
k
1,2
1
АЧХ A( )
0,8
0,6
0,4
0,2
-k/2
=1/T
0
0
5
10
15
20
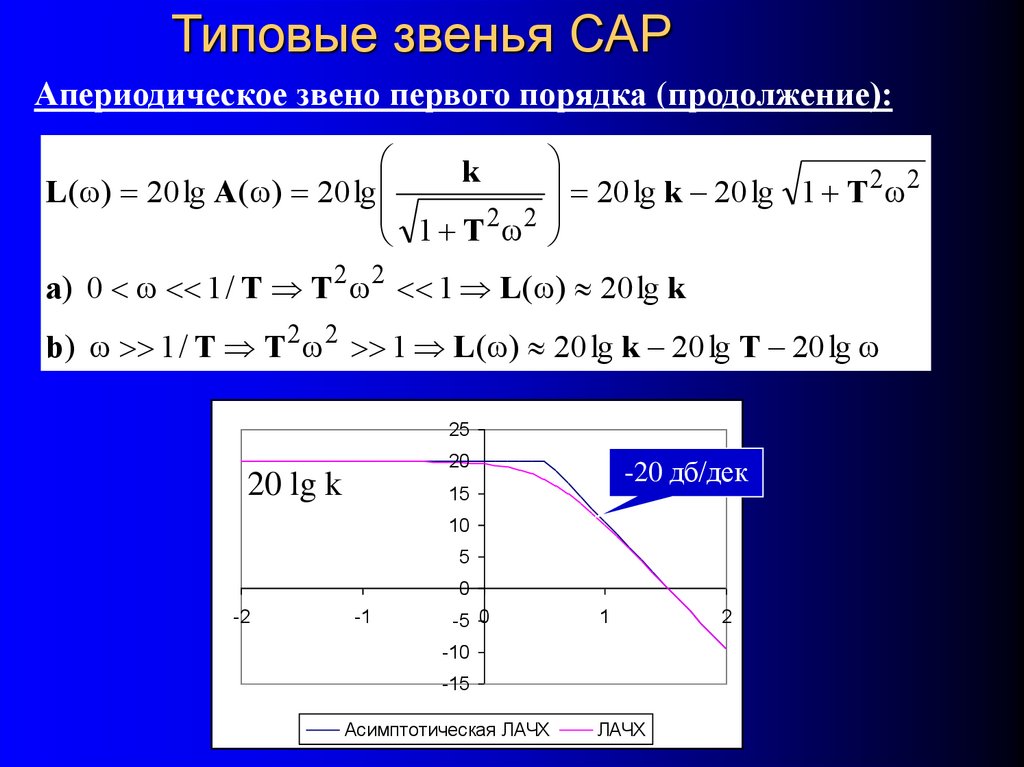
37. Типовые звенья САР
Апериодическое звено первого порядка (продолжение):k
L( ) 20 lg A( ) 20 lg
2 2
1
T
20 lg k 20 lg 1 T 2 2
a) 0 1 / T T 2 2 1 L( ) 20 lg k
b) 1 / T T 2 2 1 L( ) 20 lg k 20 lg T 20 lg
25
20
20 lg k
-20 дб/дек
15
10
5
0
-2
-1
-5 0
1
-10
-15
Асимптотическая ЛАЧХ
ЛАЧХ
2
38. Типовые звенья САР 3. Интегрирующее звено:
Ft
Пример:
Уравнение: y kx; y k xdt
0
Передаточная функция: sy kx; W(s)
Переходная характеристика h(t) = kt
k
s
y
h
tg = k
t
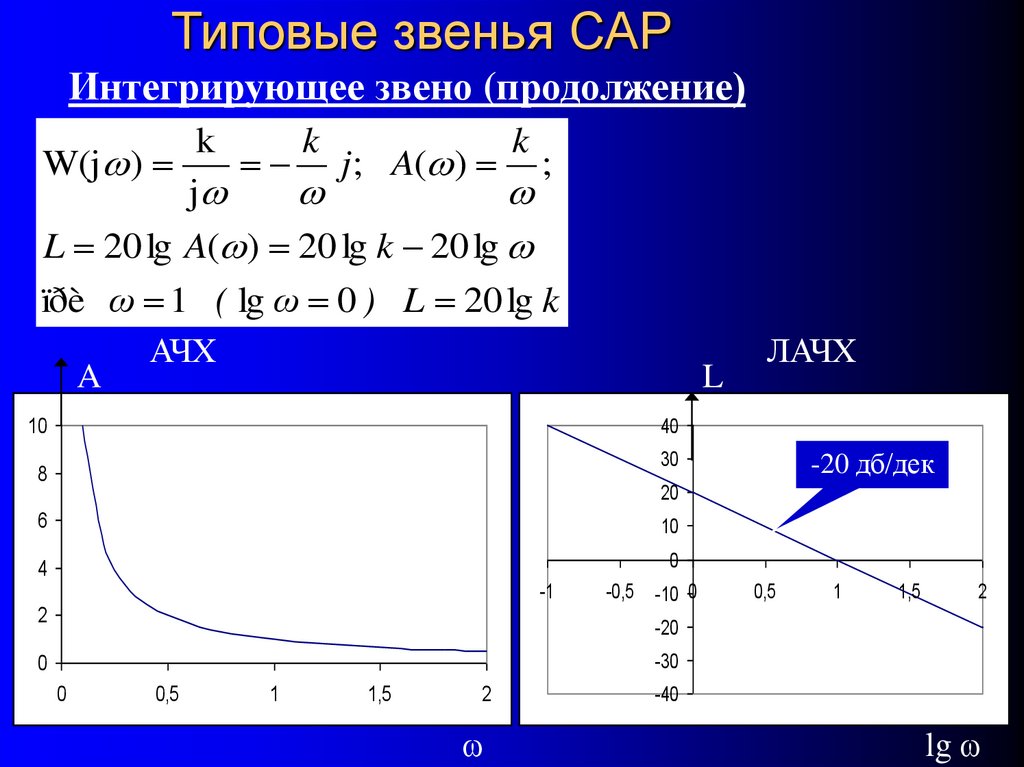
39. Типовые звенья САР Интегрирующее звено (продолжение)
kk
k
W(j )
j; A( ) ;
j
L 20 lg A( ) 20 lg k 20 lg
ïðè ω 1 ( lg ω 0 ) L 20 lg k
A
АЧХ
L
10
ЛАЧХ
40
30
8
-20 дб/дек
20
6
10
4
0
-1
2
-0,5 -10 0
0,5
1
1,5
2
-20
-30
0
0
0,5
1
1,5
2
-40
lg
40. Типовые звенья САР 4. Звенья второго порядка:
Пример:Уравнение: T 2 y 2eTy y kx;
k
Передаточная функция: W(s) 2 2
T s 2eTs 1
1. При 0<e <1 – колебательное звено (корни характеристического уравнения комплексные)
2. При e 1 – апериодическое звено второго порядка
(корни характеристического уравнения
действительные)
Переходная характеристика:
3,5
3
3,5
Колебательное
3
2,5
2,5
h
2
h
1,5
1
0,5
0
2
1,5
1
Апериодическое
время
0,5
0
время
K
G
M
F
y
41. Типовые звенья САР Звенья второго порядка (продолжение):
АЧХАмплитуда
2
1,5
A( )
Колебательное
0,5
0
0
20 Частота 40
60
(1 T 2 2 ) 2 4T 2 e 2 2
АЧХ
2
Резонансная
частота
1,5
1
0,5
0
0
20 Частота 40
При e 0 рез 1
A ( рез )
Апериодическое
Амплитуда
k
1 2e 2
рез
;
T
1
60
Пример:
K
G
T
M
k
2e 1 e 2
F
При 0<e<1 – колебательное звено, но
max на АЧХ имеется только при
e2<0,5
(0<e<0,707).
y
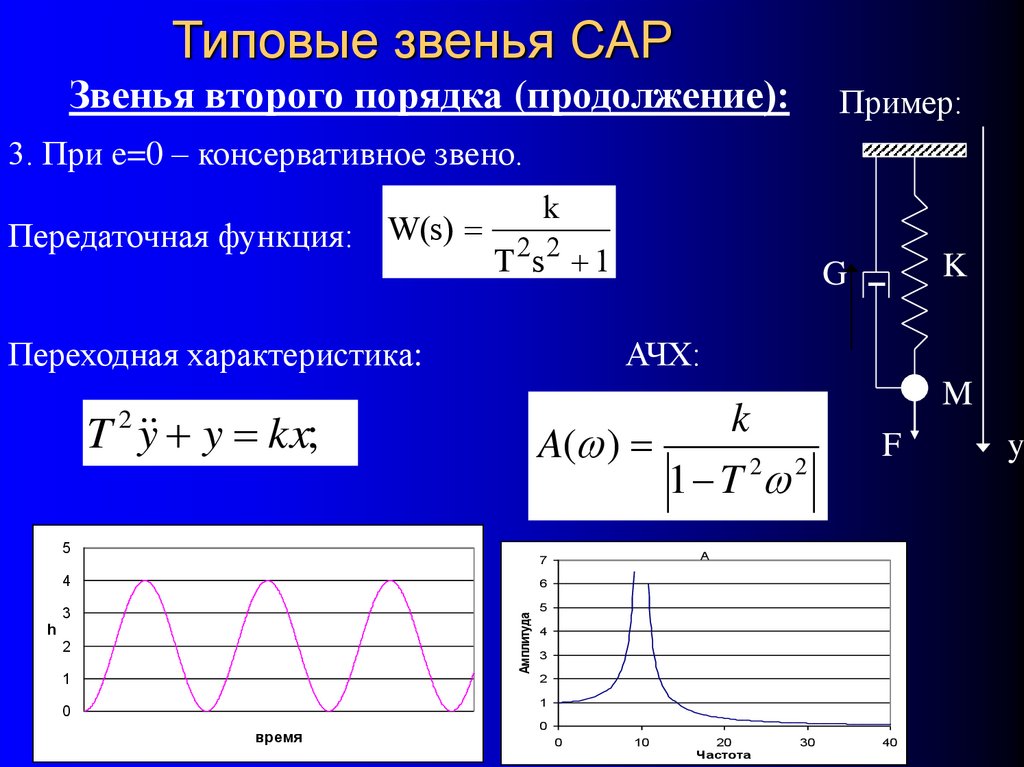
42. Типовые звенья САР Звенья второго порядка (продолжение):
Пример:3. При e=0 – консервативное звено.
k
Передаточная функция: W(s) 2 2
T s 1
Переходная характеристика:
АЧХ:
k
A( )
1 T 2 2
T 2 y y kx;
5
4
6
3
5
2
1
M
F
A
7
Амплитуда
h
K
G
4
3
2
1
0
время
0
0
10
20
Частота
30
40
y
43. Типовые звенья САР Звенья второго порядка (продолжение):
Типовые звенья САРПример:
Звенья второго порядка (продолжение):
k
20 lg k 20 lg 1 T 2 2
L( ) 20 lg A( ) 20 lg
1 T 2 2
a) 0 1 / T T 2 2 1 L( ) 20 lg k
K
G
b) 1 / T T 2 2 1 L( ) 20 lg k 40 lg T 40 lg
ЛАЧХ
F
20 lg A( )
30
20 lg k
-40 дб/дек
20
10
0
-2
-1
-10 0
1
2
-20
-30
-40
lg
ЛАЧХ: e<1
M
Асимптотическая ЛАЧХ
ЛАЧХ: e>1
y
44. Типовые звенья САР Звенья второго порядка (продолжение):
Типовые звенья САРПример:
Звенья второго порядка (продолжение):
Апериодическое звено второго порядка можно
представить как два последовательно соединенных
апериодических звена первого порядка:
k
k1
k2
W(s) 2 2
T s 2eTs 1 T1s 1 T2 s 1
k k1 k 2
K
G
M
F
T 2 T1 T2
2eT T1 T2
ЛАЧХ последовательно соединенных апериодических звеньев
первого порядка более точно отображают ЛАЧХ апериодического
звена второго порядка.
y
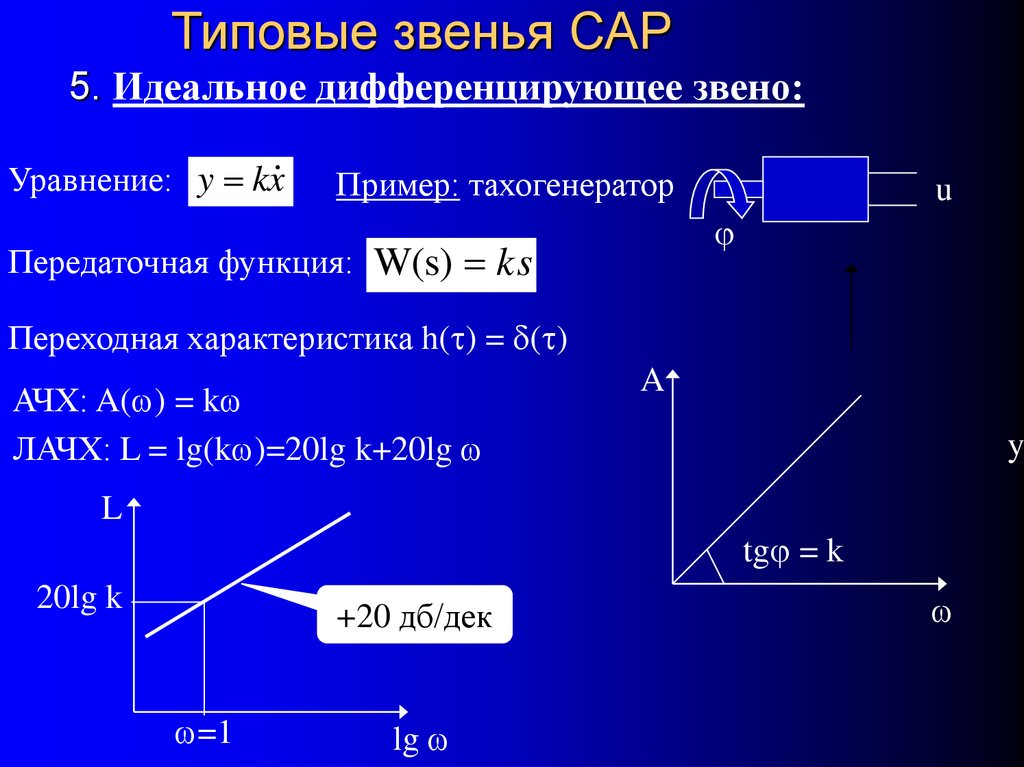
45. Типовые звенья САР 5. Идеальное дифференцирующее звено:
Уравнение: y kxПример: тахогенератор
u
Передаточная функция: W(s) ks
Переходная характеристика h(t) = (t)
АЧХ: A( ) = k
ЛАЧХ: L = lg(k )=20lg k+20lg
A
y
L
tg = k
20lg k
+20 дб/дек
=1
lg
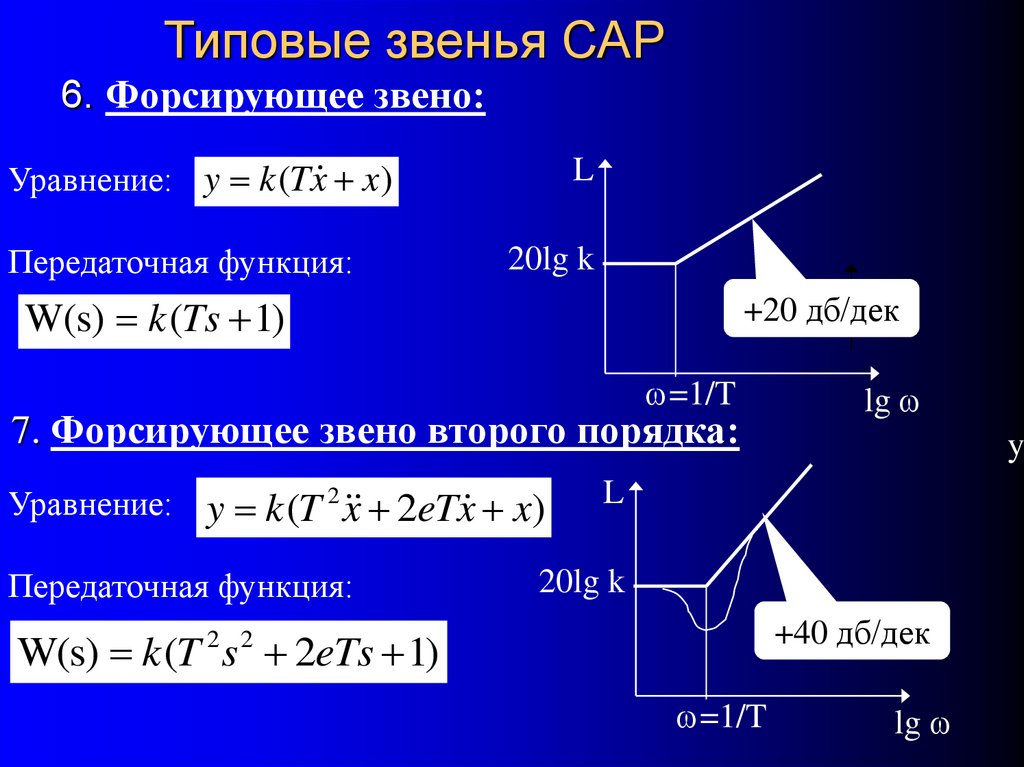
46. Типовые звенья САР 6. Форсирующее звено:
Уравнение: y k (Tx x)Передаточная функция:
L
20lg k
+20 дб/дек
W(s) k (Ts 1)
=1/T
7. Форсирующее звено второго порядка:
Уравнение: y k (T 2 x 2eTx x)
Передаточная функция:
lg
y
L
20lg k
+40 дб/дек
W(s) k (T s 2eTs 1)
2 2
=1/T
lg
47. Типовые звенья САР Сводная таблица:
Типовые звенья САРНазвание
Усилительное
Апериодическое 1-го
порядка
Интегрирующее
Колебательное
Уравнение
y kx
Ty y kx
y kx
T 2 y 2eTy y kx
0 e 1
Дифференцирующее
Форсирующее
Форсирующее 2го порядка
y kx
y k (Tx x)
Сводная таблица:
Передат. функция
W k
W
k
Ts 1
k
W
s
k
W 2 2
T s 2eTs 1
ЛАЧХ
20 lg k
20 lg k
=1/T
20 lg k
=1
-20 дб/дек
20 lg k =1/T
W ks
20 lg k
=1
W k (Ts 1)
20 lg k
=1/T
2 2
y k (T 2 x 2eTx x) W k (T s 2eTs 1)
20 lg k
=1/T
-20 дб/дек
-40 дб/дек
+20 дб/дек
+20 дб/дек
+40 дб/дек
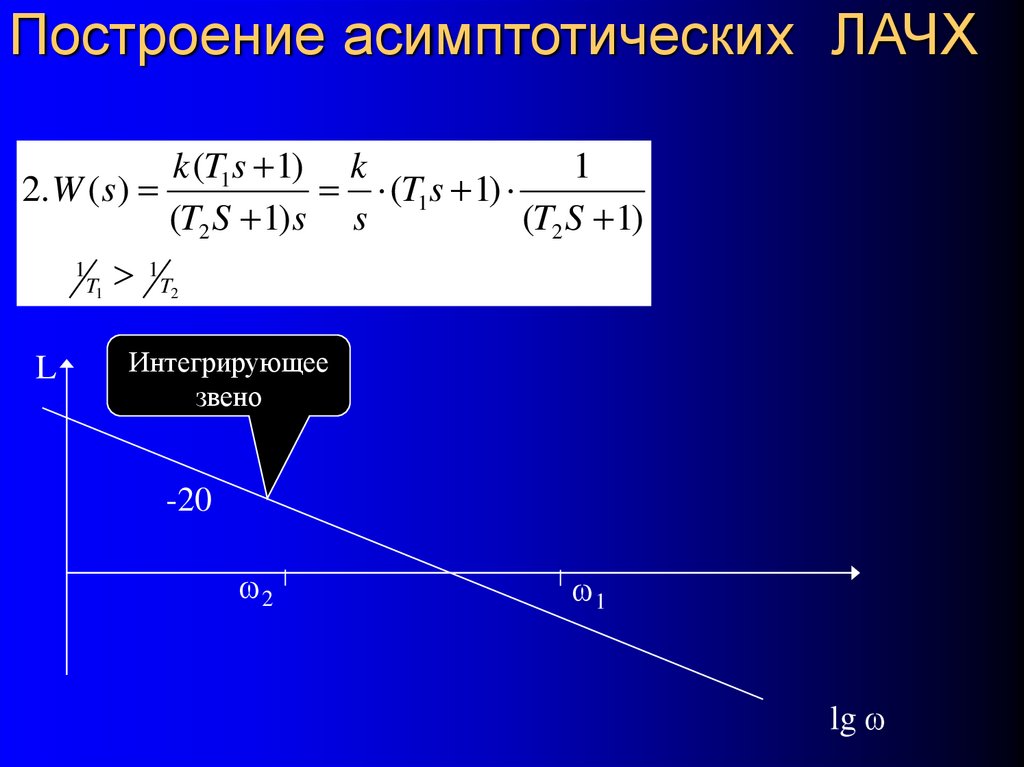
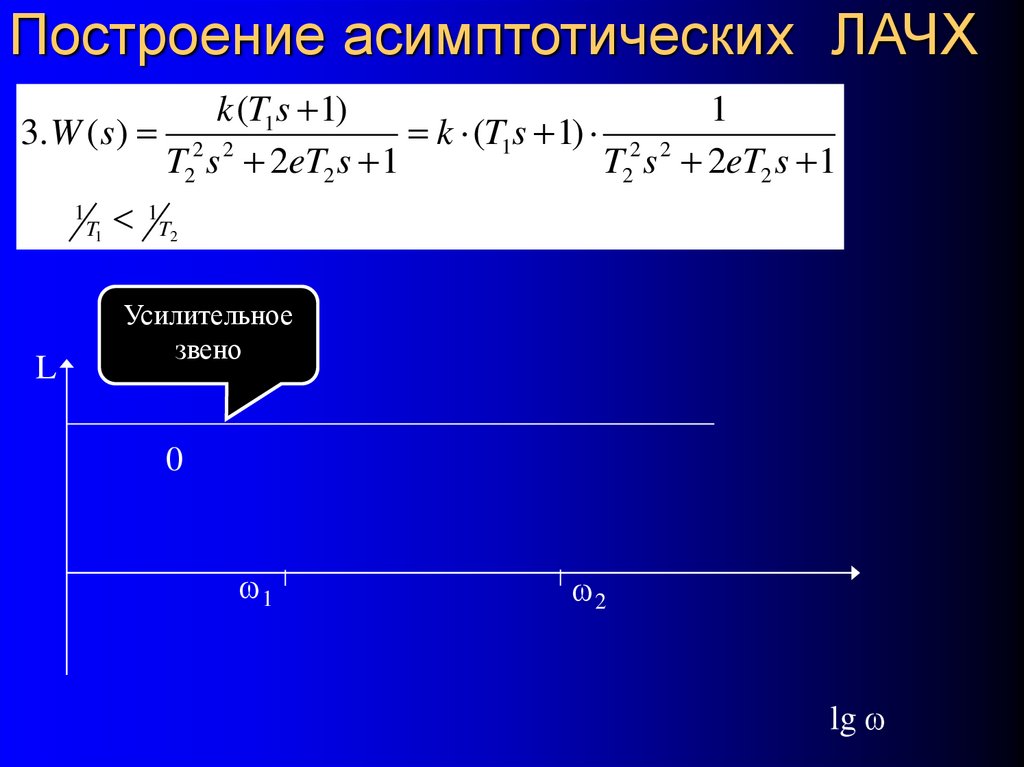
48. 1.9. Построение асимптотических ЛАЧХ
k (T1s 1) k1
1. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
T1
1
T2
L
-20 дб/дек
1= 1/T1
Интегрирующее
звено
2=1/T2
lg
49. 1.9. Построение асимптотических ЛАЧХ
k (T1s 1) k1
1. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
T1
1
T2
L
-20 дб/дек
Интегрирующее
звено
Форсирующее
звено
+20 дб/дек
1= 1/T1
2=1/T2
lg
50. 1.9. Построение асимптотических ЛАЧХ
k (T1s 1) k1
1. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
T1
1
T2
L
-20 дб/дек
Интегрирующее
звено
+20 дб/дек
1= 1/T1
2=1/T2
Форсирующее
звено
Апериодическое
звено 1 порядка
-20
lg
51. 1.9. Построение асимптотических ЛАЧХ
k (T1s 1) k1
1. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
T1
1
T2
Суммарная
ЛАЧХ
L
-20
0
-20
1= 1/T1
2=1/T2
lg
52. Построение асимптотических ЛАЧХ
k (T1s 1) k1
2. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
L
T1
1
T2
Интегрирующее
звено
-20
2
1
lg
53. Построение асимптотических ЛАЧХ
k (T1s 1) k1
2. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
L
T1
1
Форсирующее
звено
T2
Интегрирующее
звено
+20
-20
2
1
lg
54. Построение асимптотических ЛАЧХ
k (T1s 1) k1
2. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
L
T1
1
Форсирующее
звено
T2
Интегрирующее
звено
Апериодическое
звено 1 порядка
+20
-20
2
1
-20
lg
55. Построение асимптотических ЛАЧХ
k (T1s 1) k1
2. W ( s)
(T1s 1)
(T2 S 1) s s
(T2 S 1)
1
T1
1
T2
Суммарная
ЛАЧХ
L
+20
-20
2
1
-20
-40
-20
lg
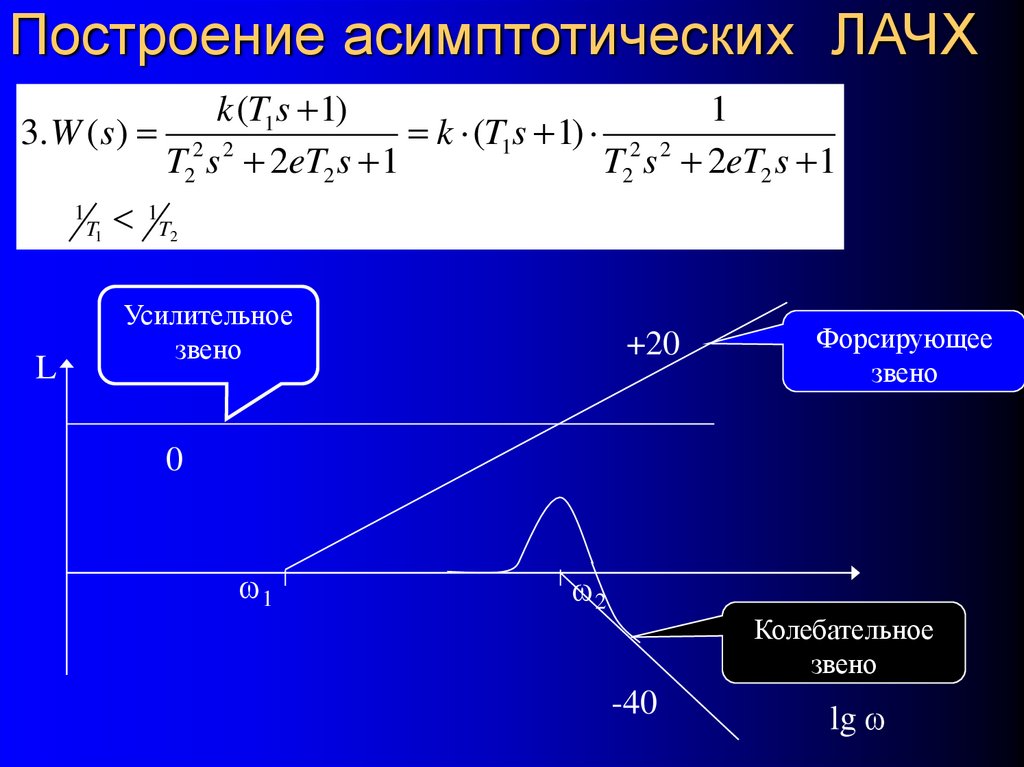
56. Построение асимптотических ЛАЧХ
k (T1s 1)1
3. W ( s) 2 2
k (T1s 1) 2 2
T2 s 2eT2 s 1
T2 s 2eT2 s 1
1
L
T1
1
T2
Усилительное
звено
0
1
2
lg
57. Построение асимптотических ЛАЧХ
k (T1s 1)1
3. W ( s) 2 2
k (T1s 1) 2 2
T2 s 2eT2 s 1
T2 s 2eT2 s 1
1
L
T1
1
T2
Усилительное
звено
+20
Форсирующее
звено
0
1
2
lg
58. Построение асимптотических ЛАЧХ
k (T1s 1)1
3. W ( s) 2 2
k (T1s 1) 2 2
T2 s 2eT2 s 1
T2 s 2eT2 s 1
1
L
T1
1
T2
Усилительное
звено
+20
Форсирующее
звено
0
1
2
Колебательное
звено
-40
lg
59. Построение асимптотических ЛАЧХ
k (T1s 1)1
3. W ( s) 2 2
k (T1s 1) 2 2
T2 s 2eT2 s 1
T2 s 2eT2 s 1
1
L
T1
1
T2
Суммарная
ЛАЧХ
-20
+20
0
+20
1
2
-40
lg
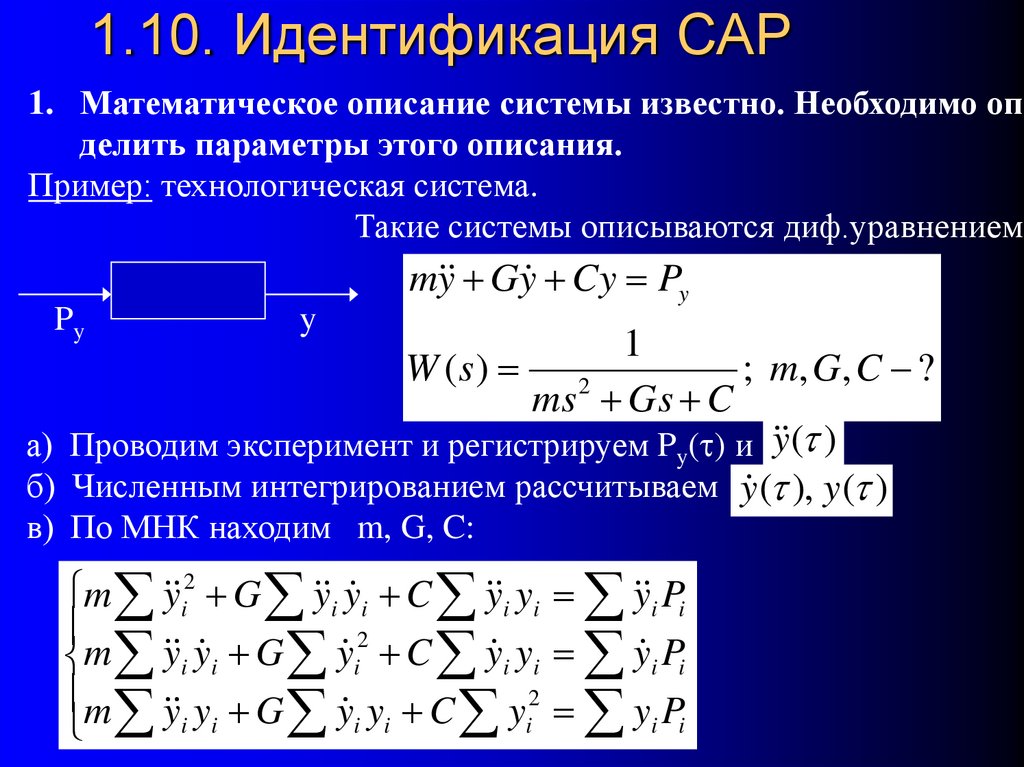
60. 1.10. Идентификация САР
1. Математическое описание системы известно. Необходимо опрделить параметры этого описания.
Пример: технологическая система.
Такие системы описываются диф.уравнением:
m y Gy Cy Py
Py
y
1
W (s) 2
; m, G, C ?
ms Gs C
а) Проводим эксперимент и регистрируем Py(t) и y (t )
б) Численным интегрированием рассчитываем y (t ), y (t )
в) По МНК находим m, G, C:
m y i2 G y i y i C y i yi y i Pi
2
m
y
y
G
y
i i
i C y i yi y i Pi
m y y G y y C y 2
i i i yi Pi
i i
61. Идентификация САР
2. Определение вида W(s) по ЛАЧХ:а) Строим экспериментальную ЛАЧХ
б) Проводим асимптотическую ЛАЧХ (ломаную линию с углами
наклона ±20 дб/дек)
в) Определяем частоты сопряжения и резонансные частоты
i=1/Ti.
г) Восстанавливаем W(s) по виду асимптотической ЛАЧХ
д) Уточняем коэффициенты передаточной функции по МНК
L
k
1
0
W (s)
2 2
(T3 s 1)
T1s 1 T2 s 2eT2 s 1
-20
-60
3
1
2
-40
lg
62. Идентификация САР
Проблемы построения W(s):1. Сложность подачи гармонического сигнала на вход системы
2. Неоднозначность восстановления W(s) по ЛАЧХ
Принцип суперпозиции:
Если на вход линейной системы подать сумму сигналов, то на
ее выходе получается также сумма реакций системы на каждый
из входных сигналов:
x(t ) x1 (t ) x2 (t ) y(t ) y1 (t ) y2 (t )
ãäå y1 ïîëó÷àåòñÿ ïðè x1
y2 ïîëó÷àåòñÿ ïðè x2
ИТАК: на вход системы подаем:
На выходе получаем:
x(t ) bi sin it
y (t ) ai sin( it i )
Ai
ai
bi
À×Õ
63. Идентификация САР
Экспресс-методика идентификации операции ТП:1. Создаем заготовку в виде шлицевого валика. Профиль заготовки описывается рядом Фурье – коэффициенты известны.
2. Устанавливаем заготовку на станке и срезаем шлицы. В
соответствии с принципами технологического наследования профиль заготовки также описывается рядом Фурье.
3. Устанавливаем заготовку в кругломер, записываем профиль
и рассчитываем коэффициенты Фурье.
4. По отношению коэффициентов строим АЧХ и ЛАЧХ и
восстанавливаем по ним вид W(s).
5. Уточняем коэффициенты передаточной функции по МНК.
6. Полученное выражение для W(s) позволяет прогнозировать
результаты обработки на исследуемой операции.
64. 1.11. Статические и астатические САР
ux
yp
АР
f
ОР
y
=u-x
Д
y(s)
Îáîçíà÷èì
Wf
ÎÐ ïî âîçìóùåíèþ
u 0 - ÏÔ
f (s)
y y f yc fW f y pWOP fW f WAPWOP
fW f uWAPWOP xWAPWOP fW f uWAPWOP yW Ä WAPWOP
y
Wf
1 W Ä WAPWOP
WAPWOP
f
u
1 W Ä WAPWOP
ПФ САР по возмущению
ПФ САР по управлению
65. Статические и астатические САР
ux
y
yp
АР
f
ОР
y
=u-x
Д
Wf
1 W Ä WAPWOP
WAPWOP
f
u
1 W Ä WAPWOP
A( s ) ak s k ... a0
Ïóñòü WOP , W Ä , W f
, a0 , b0 0
n
B( s ) bn s ... b0
1. WAP
yñòàò
a0 AP
A( s )
; K AP
B( s)
b0 AP
Kf
1 K Ä K AP K OP
K AP K OP
f
u
1 K Ä K AP K OP
При увеличении КАР можно сколь угодно уменьшить влияние f.
66. Статические и астатические САР
ux
y
yp
АР
f
ОР
y
=u-x
Д
Wf
1 W Ä WAPWOP
f
WAPWOP
u
1 W Ä WAPWOP
A( s ) ak s k ... a0
Ïóñòü WOP , W Ä , W f
, a0 , b0 0
n
B( s ) bn s ... b0
A( s )
2. WAP
; K AP
sB ( s )
1
yñòàò 0 f
u
KÄ
В статике влияние f отсутствует.
67. Статические и астатические САР
ux
АР
yp
f
ОР
y
=u-x
Д
1. Астатические системы – системы не имеющие статической
ошибки: в состав АР входит интегрирующее звено. В статике
(возмущение f и все сигналы в САР находятся на постоянном
уровне) влияние возмущения на выходной сигнал отсутствует.
2. Системы, имеющие статическую ошибку (статические
системы): возмущение оказывает влияние на выходной
сигнал, но это влияние можно уменьшить за счет увеличения
коэффициента передачи АР.
ПРИМЕЧАНИЕ: Рассматривается только установившийся
режим работы системы (статический). В динамическом
режиме при изменении f в астатических системах ошибка
может быть даже больше, чем в статических.
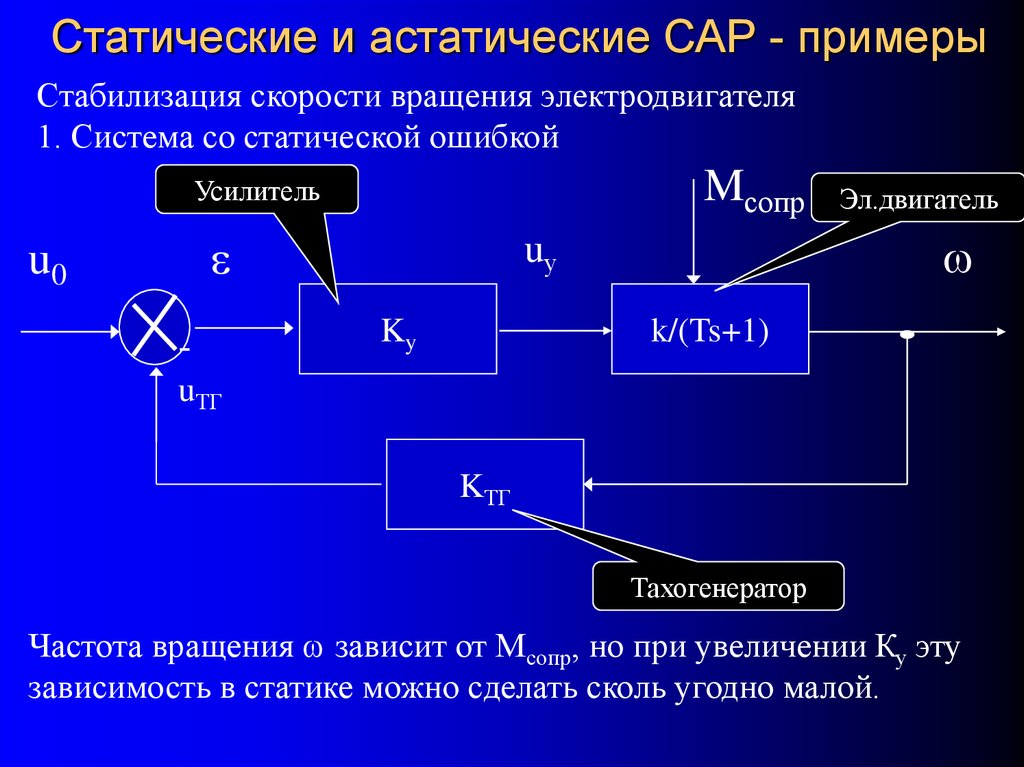
68. Статические и астатические САР - примеры
Стабилизация скорости вращения электродвигателя1. Система со статической ошибкой
Mсопр
Усилитель
u0
-
uу
Ky
Эл.двигатель
k/(Ts+1)
uТГ
KТГ
Тахогенератор
Частота вращения зависит от Мсопр, но при увеличении Ку эту
зависимость в статике можно сделать сколь угодно малой.
69. Статические и астатические САР - примеры
2. Астатическая системаУсилитель
u0
-
uТГ
uу
Ky
Потенциометр
Электропривод
L
kП
uп
Mсопр
k2/(T2s+1)
KТГ
Тахогенератор
Эл.двигатель
Частота вращения не зависит от Мсопр при Мсопр= const.
При изменении Мсопр в связи с повышенной инерционностью
системы влияние Мсопр на может быть значительным .
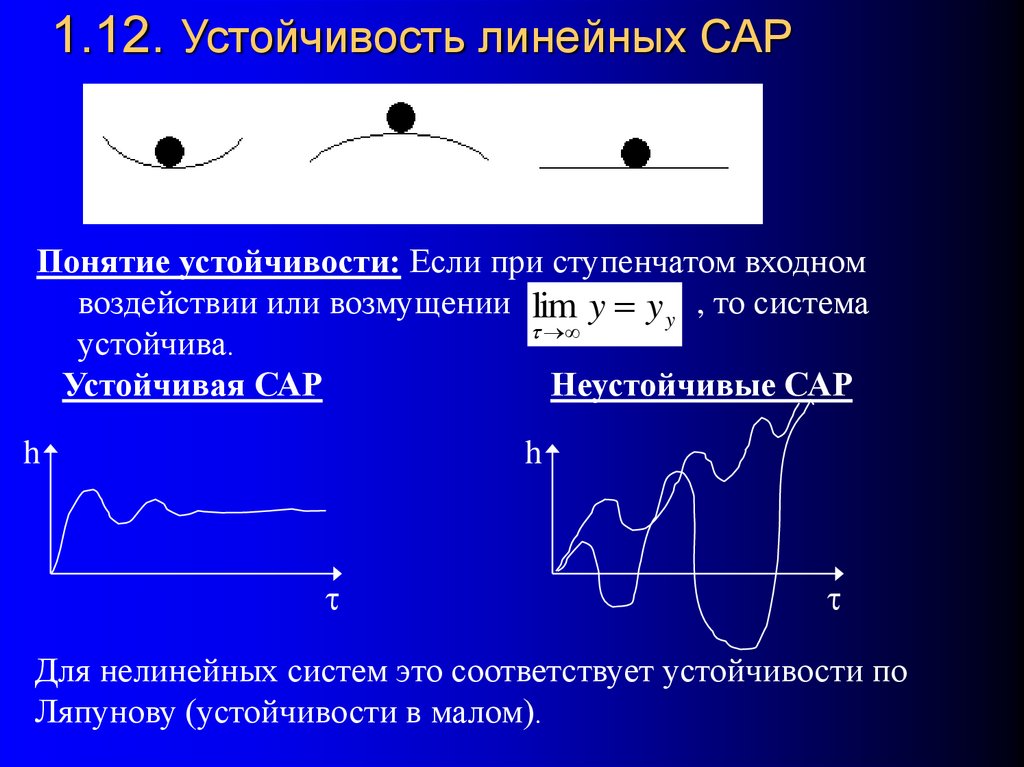
70. 1.12. Устойчивость линейных САР
Понятие устойчивости: Если при ступенчатом входномвоздействии или возмущении lim y y y , то система
t
устойчива.
Устойчивая САР
Неустойчивые САР
h
h
t
t
Для нелинейных систем это соответствует устойчивости по
Ляпунову (устойчивости в малом).
71. Устойчивость линейных САР
Необходимое и достаточное условие устойчивости:Система описывается передаточной функцией:
an s n ... a0
W ( s)
bk s k ... b0
Для устойчивости системы необходимо и достаточно, чтобы
корни знаменателя ПФ (bksk+…+b0) имели отрицательные
вещественные части.
Действительно, устойчивость системы определяется решением
однородного уравнения, которое зависит от решения характеристического уравнения bksk+…+b0=0.
1. Действительный корень si: yi(t)=Ciexp(sit); при si>0 lim y
t
2. Пара комплексных корней si= i± j:
yi (t ) e it (Ci sin it Di cos it ); i 0 lim yi
y (t ) yi (t )
i
t
72. Устойчивость линейных САР
Необходимое и достаточное условие устойчивости:Примеры:
2
1)
2
W (s)
2s 2s 1
s1, 2 0,5 0,5 j
2
Im
; 2 s 2 s 1 0;
Re
Т.к. действительная часть корня (-0,5) отрицательна – система
устойчива.
2)
3s 2
4 16 4
2
W ( s) 2
; s 4 s 1 0; s1, 2
2 3
s 4s 1
2
s1 2 3 0,268 0; s2 2 3 3,732 0
Т.к. оба корня отрицательны – система устойчива.
3) W ( s)
2
2
;
4
s
1 0; s1, 2 j 1/ 4 0,5 j
2
4s 1
Действительная часть корня равна 0 – система находится на
границе устойчивости.
73. Устойчивость линейных САР
Необходимое условие устойчивости:(не является достаточным)
Для устойчивости системы необходимо, чтобы все
коэффициенты знаменателя передаточной функции
(характеристического уравнения) имели одинаковые знаки.
Если хоть один из коэффициентов имеет знак, отличный от
остальных коэффициентов – система неустойчива. Если все знаки
одинаковые – ничего неизвестно.
74. Устойчивость линейных САР
Критерий Рауса-Гурвица (необходимый и достаточный):Знаменатель передаточной функции: Q(s)=b0sn+b1sn-1+…+bn
Матрица коэффициентов:
b1
b
3
b5
b7
...
0
b0
0
0
0
0
0
0
...
b2
b1
b0
0
0
0
0
...
b4
b3
b2
b1
b0
0
0
...
b6
b5
b4
b3
b2
b1
b0
...
... ... ... ... ... ... ... ...
0
0
0
0
0
0
0
...
0
0
0
0
...
bn
Размерность n*n
Для устойчивости системы необходимо и достаточно, чтобы
все угловые определители матрицы были положительны и
выполнялось необходимое условие устойчивости.
75. Устойчивость линейных САР
Критерий Рауса-ГурвицаПримеры:
2s 1
1) W ( s)
;
4s 3 3s 2 2s 1
2)
Система неустойчива по необходимому
условию.
3 4 0
2s 1
W (s) 3
; 1 2 3
2
4 s 3s 2 s 1
0 0 1
a) 3 0
b)
3 4
1 2
6 4 2 0
3 4 0
c) 1 2 3 2 0
0 0 1
Система устойчива.
76. Устойчивость линейных САР
Критерий Рауса-ГурвицаСведение к более простым условиям:
1) Система 1-го порядка: b0s+b1=0 → b1>0; b0>0
2) 2-го порядка: b0
s2+b
1s+b2=0→
3) 3-го порядка: b0
s3+b
1
b1 b0
0
2s+b3=0
s2+b
b2
→
→ b0>0; b1>0; b2>0
bi 0, i 0...3
b1b2 b0b3
4) 4-го порядка: b0s4+b1s3+b2s2+b3s+b4=0 →
bi 0, i 0...4
2
b
(
b
b
b
b
)
b
b
4 1
3 1 2 0 3
5) 5-го порядка: b0s5+b1s4+b2s3+b3s2+b4s+b5=0
bi 0, i 0...5
b1b2 b0b3
(b b b b )(b b b b ) (b b b b ) 2
1 4
0 5
1 2 0 3 3 4 2 5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
77. Устойчивость линейных САР
Частотный критерий Михайлова:Знаменатель передаточной функции: Q(s). Заменим s на j :
Q(j ) = U( )+jV( ). Годограф этого выражения называется
годографом Михайлова.
САР n-го порядка устойчива, если годограф Михайлова
начинается при =0 на положительной действительной
полуоси (V(0)=0, U(0)>0) и с увеличением от 0 до проходит
в положительном направлении последовательно n квадрантов
нигде не обращаясь в 0.
НЕУСТОЙЧИВЫЕ
V
V
n=2
U
n=3
n=4
U
78. Устойчивость линейных САР
Частотный критерий Найквиста:Замкнутая система
W1
W2
W3
Разомкнутая система, соответствующая замкнутой
W1
W2
W3
Если разомкнутая САР устойчива или находится на границе
устойчивости, то соответствующая ей замкнутая САР
устойчива, если АФЧХ разомкнутой системы не охватывает
точку с координатами (-1; 0j). И наоборот.
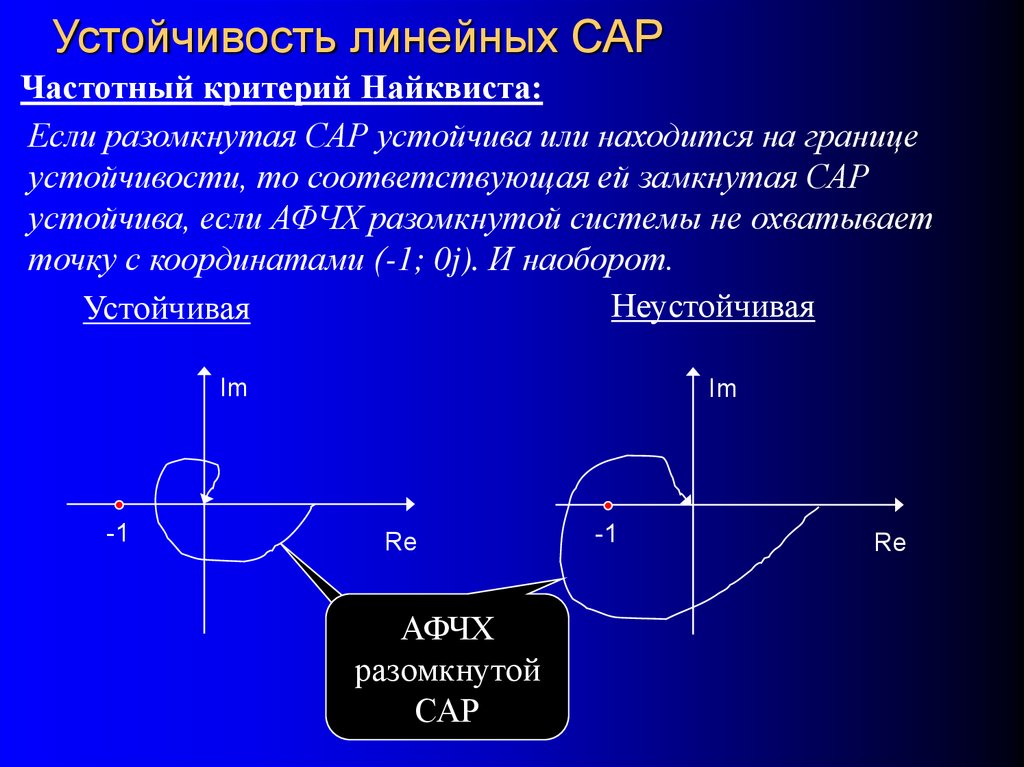
79. Устойчивость линейных САР
Частотный критерий Найквиста:Если разомкнутая САР устойчива или находится на границе
устойчивости, то соответствующая ей замкнутая САР
устойчива, если АФЧХ разомкнутой системы не охватывает
точку с координатами (-1; 0j). И наоборот.
Неустойчивая
Устойчивая
Im
-1
Im
Re
АФЧХ
разомкнутой
АФЧХ
САР
-1
Re
80. Устойчивость линейных САР
Сравнительные характеристики критериев устойчивости:1. Необходимое и достаточное условие устойчивости (по корням
знаменателя передаточной функции) носит вспомогательный
характер (основа для вывода других критериев)
2. Необходимое условие устойчивости (по коэффициентам
знаменателя передаточной функции) дополняет другие
критерии и позволяет отсеять явно неустойчивые системы.
3. Критерий Рауса-Гурвица используется для систем
сравнительно невысокого порядка – обычно до 10-го. Для
более высоких порядков условия устойчивости становятся
слишком сложными.
4. Частотные критерии (Михайлова и Найквиста) обычно
используются для систем высокого порядка, т.к. сложность
критериев мало растет с увеличением порядка системы.
5. Критерии Михайлова и Найквиста обладают примерно
одинаковой сложностью, но критерий Найквиста используется
только для замкнутых САР.
81. 1.13. Запас устойчивости САР
1. Рассмотрим снова систему стабилизации скорости вращенияэлектродвигателя:
Передаточная функция
u0
-
uТГ
АФЧХ -
uу
Ky
KТГ
Mсопр
k/(Ts+1)
разомкнутой системы
Wp
k y kkÒÃ
Ts 1
Замкнутая система всегда устойчива
(по критерию Найквиста).
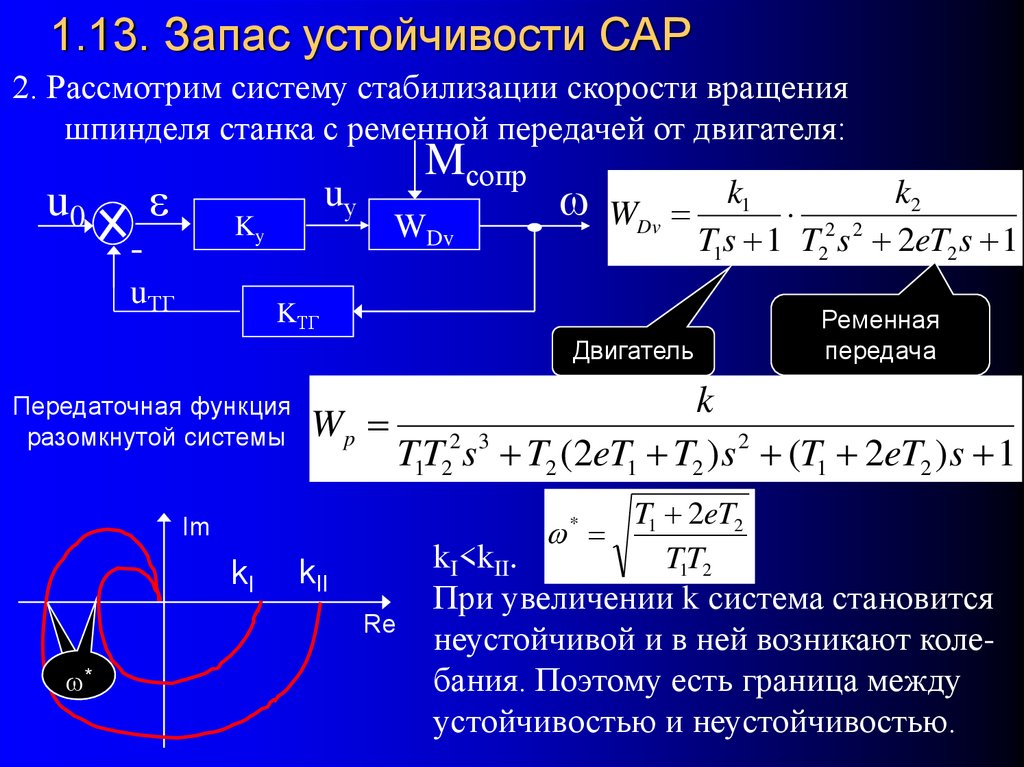
82. 1.13. Запас устойчивости САР
2. Рассмотрим систему стабилизации скорости вращенияшпинделя станка с ременной передачей от двигателя:
u0
uу
Ky
uТГ
Mсопр
WDv
k1
k2
WDv
2 2
T1s 1 T2 s 2eT2 s 1
KТГ
Двигатель
Передаточная функция
разомкнутой системы
k
Wp
T1T22 s 3 T2 (2eT1 T2 ) s 2 (T1 2eT2 ) s 1
T1 2eT2
kI<kII.
T1T2
*
Im
kI
kII
Re
*
Ременная
передача
При увеличении k система становится
неустойчивой и в ней возникают колебания. Поэтому есть граница между
устойчивостью и неустойчивостью.
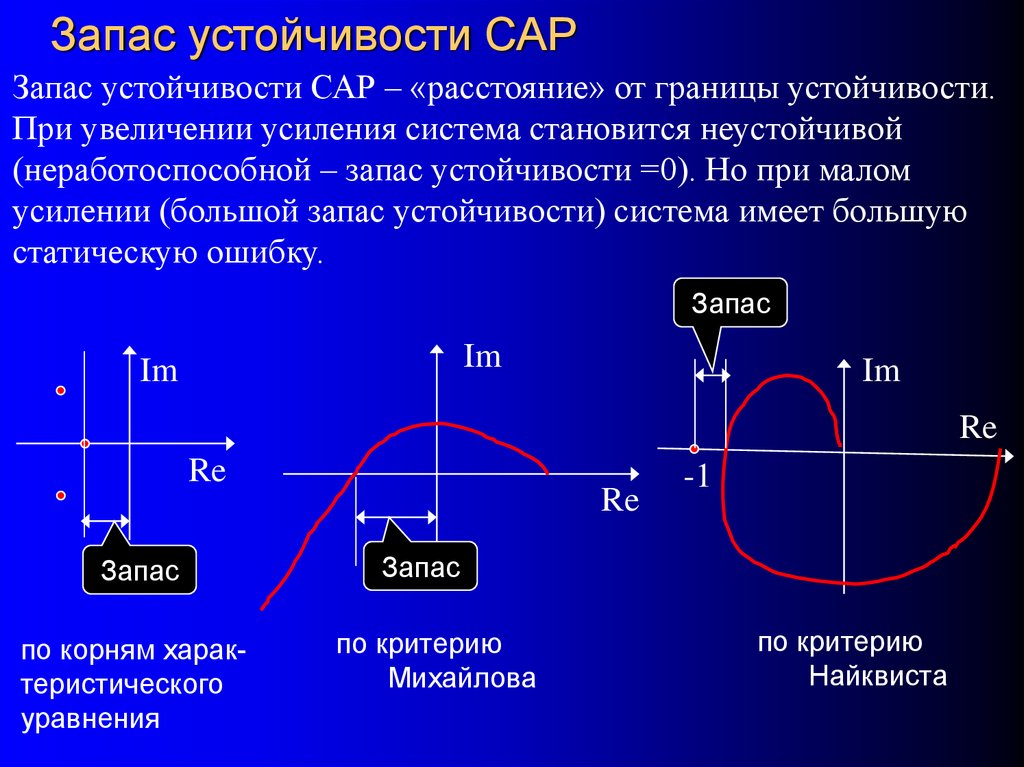
83. Запас устойчивости САР
Запас устойчивости САР – «расстояние» от границы устойчивости.При увеличении усиления система становится неустойчивой
(неработоспособной – запас устойчивости =0). Но при малом
усилении (большой запас устойчивости) система имеет большую
статическую ошибку.
Запас
Im
Im
Im
Re
Re
Запас
по корням характеристического
уравнения
Re
-1
Запас
по критерию
Михайлова
по критерию
Найквиста
84. D-разбиение
Это оценка запаса устойчивости одновременно по двум параметрам.Обозначим знаменатель передаточной функции Q(s).
Q(j )=U( )+jV( ). Граница устойчивости по критерию Михайлова:
U ( ) 0 Пусть Q(s)=Q(s,A,B).
U ( , A, B) 0
Q( j ) 0
V ( ) 0 Тогда граница устойчивости:
V ( , A, B) 0
Это параметрически-заданная кривая называется D-разбиение.
Пример: Q(s)=as3+2s2+s+k; Q(j )= -j 3a - 2 2+j +k=
=k-2 2+j( -a 3) = 0
10
2
k
2
U ( ) k 2 0
1 2
3
a
V
(
)
a
0
2
9
8
7
6
a 5
0
1
2
…
k
0
2
8
…
2
a
1
0.25
…
0
0
4
3
1
0
2
4
k
6
8
10
85. 1.14. Законы регулирования
Автоматическийрегулятор
y
1. Пропорциональный закон (П-регулятор): y=k ; W(s)=k.
Обладает хорошими динамическими свойствами. Система с
П-регулятором имеет статическую ошибку.
Пример: усилитель.
t
2. Интегральный закон (И-регулятор): y k dt y k W (s)
0
Обладает пониженными динамическими свойствами. Система
с И-регулятором не имеет статической ошибки (астатическая
САР.
Пример: двигатель+заслонка.
k
s
86. 1.14. Законы регулирования
Автоматическийрегулятор
y
3. Пропорционально-интегральный закон (ПИ-регулятор):
1t
k (Ts 1)
1
y k ( dt) y k W ( s)
T0
T
Ts
Обладает хорошими динамическими свойствами. Система с
ПИ-регулятором не имеет статической ошибки (астатическая
САР).
4. Пропорционально-дифференциальный закон (ПД-регулятор):
y k ( T ) W (s) k (Ts 1)
Обладает очень хорошими динамическими свойствами, но
САР имеет статическую ошибку.
87. 1.14. Законы регулирования
Автоматическийрегулятор
y
5. Пропорционально-интегрально-дифференциальный закон
(ПИД-регулятор):
1
1
y k ( dt T2 ) y k T2
T1 0
T1
t
k (T1T2 s 2 T1s 1)
W (s)
T1s
Обладает очень хорошими динамическими свойствами.
Система с ПИД-регулятором не имеет статической ошибки
(астатическая САР).
88. 2. Датчики САР
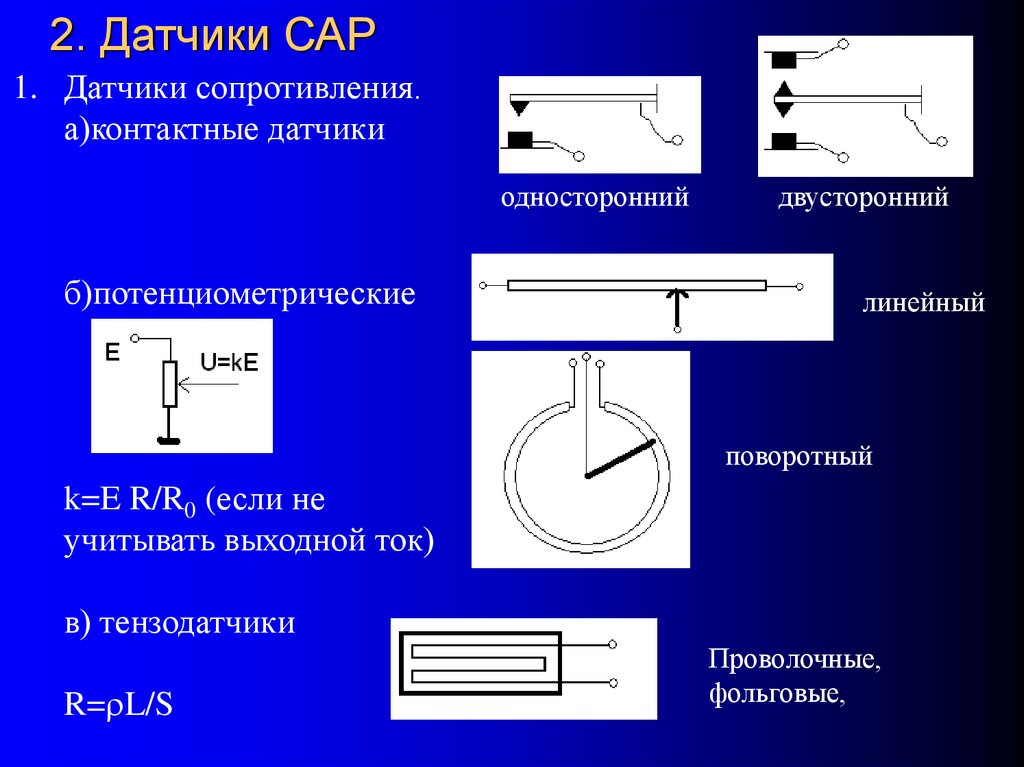
1. Датчики сопротивления.а)контактные датчики
односторонний
б)потенциометрические
двусторонний
линейный
поворотный
k=E R/R0 (если не
учитывать выходной ток)
в) тензодатчики
R= L/S
Проволочные,
фольговые,
89. Датчики САР
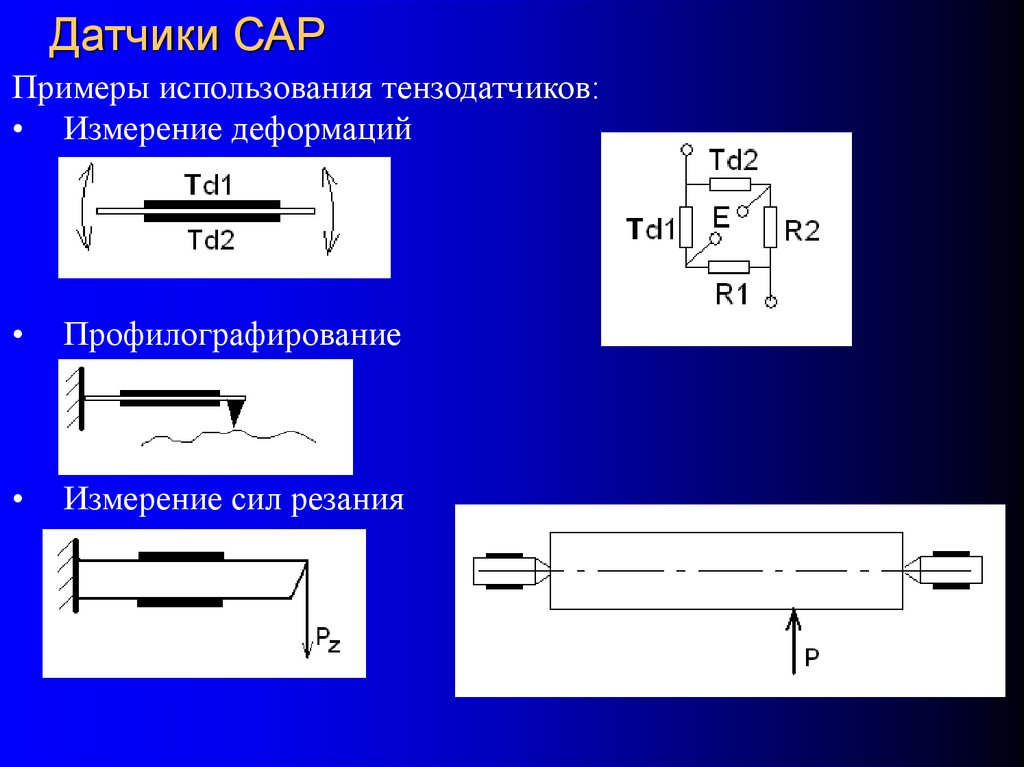
Примеры использования тензодатчиков:• Измерение деформаций
Профилографирование
Измерение сил резания
90. 2. Датчики САР
1. Датчики сопротивления.г) термосопротивления. Применяются для измерения
медленно изменяющейся температуры: R = R0(1+ T).
полупроводниковые термисторы – нелинейная зависимость от
температуры (0…100 ºС), но высокая чувствительность.
проволочные – никелевая или платиновая проволока –
зависимость от температуры почти линейная (до 800 ºС), но
чувствительность низкая.
Применяются для регулирования температуры при нагревании (печи, термошкафы) или охлаждении (вентиляции).
д) фотосопротивления. Применяются для измерения
медленно изменяющейся освещенности. Имеют нелинейную характеристику и значительную инерционность.
Кроме того, фотосопротивления чувствительны к
температуре.
91. 2. Датчики САР
Использование фотосопротивлений:Измерение светового потока (пирометры)
Определение степени прозрачности объекта
Определение состояния поверхности
Определение количество и размера
объектов
92. 2. Датчики САР
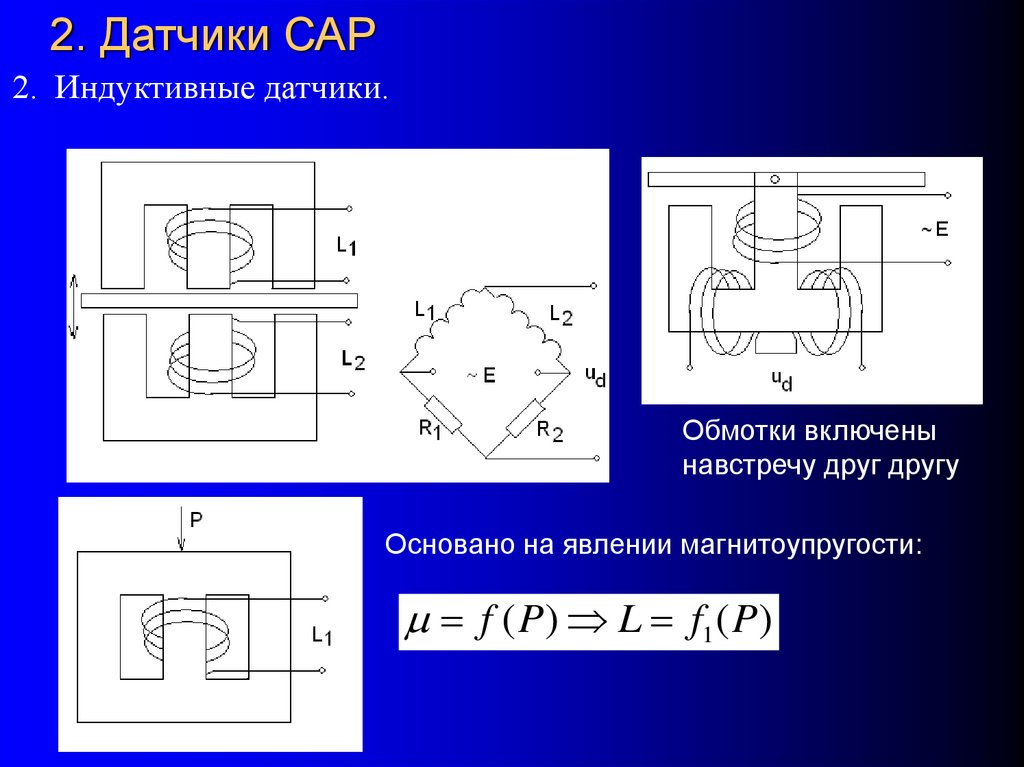
2. Индуктивные датчики.Обмотки включены
навстречу друг другу
Основано на явлении магнитоупругости:
f ( P) L f1 ( P)
93. 2. Датчики САР
3. Емкостные датчики.Измерение износа шлифовального круга и относительных колебаний
•Замена контактного датчика емкостным
•Измерение перемещений
94. 2. Датчики САР
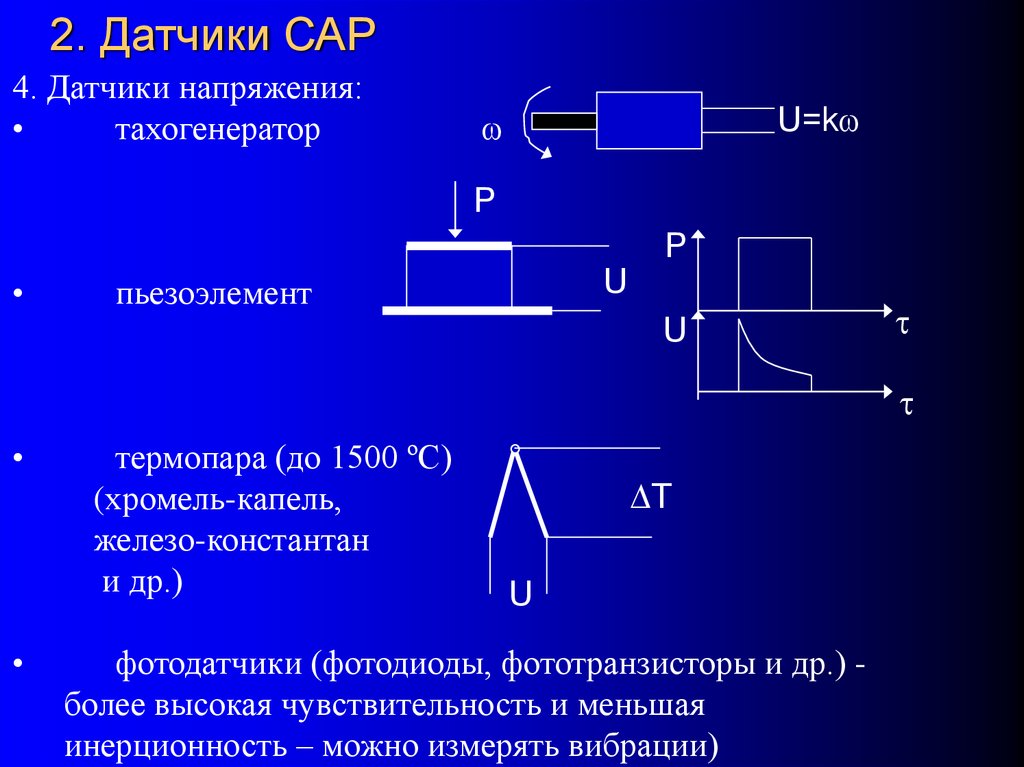
4. Датчики напряжения:тахогенератор
U=k
P
P
U
пьезоэлемент
U
t
t
термопара (до 1500 ºС)
(хромель-капель,
железо-константан
и др.)
T
U
фотодатчики (фотодиоды, фототранзисторы и др.) более высокая чувствительность и меньшая
инерционность – можно измерять вибрации)
95. 2. Датчики САР
4. Датчики напряжения:сельсины (измерение углов поворота)
Силовая схема – для передачи крутящего момента
Трансформаторная схема – для измерения углов поворота
96. 2. Датчики САР
5. Датчики оборудования с ЧПУ:линейный магнитный зубчатый датчик
Зубья одного сердечника смещены относительно другого на
0,5 шага
U
L
шаг
Точность – до 10 мкм
97. 2. Датчики САР
5. Датчики оборудования с ЧПУ:фотоэлектрический импульсный датчик
Зубчатая передача
Осветитель
Фотоприемник
Осветитель
Диск
U
L
Точность – до 5 мкм
98. 2. Датчики САР
5. Датчики оборудования с ЧПУ:• фотоэлектрический датчик c дифракционными решетками
U
L
Точность – до 0,5 мкм
99. 2. Датчики САР
5. Датчики оборудования с ЧПУ:• вращающиеся трансформаторы
Статор
U c K E sin
U k K E cos
Ротор
100. 2. Датчики САР
5. Датчики оборудования с ЧПУ:• индуктосины
Обмотки AB и CD смещены
на ¼ шага.
Обмоток может быть больше
двух.
При подаче на обмотки AB и BC напряжений, смещенных по фазе на 90°, на обмотке EF индуцируется напряжение, фаза которого зависит от положения, а амплитуда постоянна. Точность – до 1 мкм.
101. 2. Датчики САР
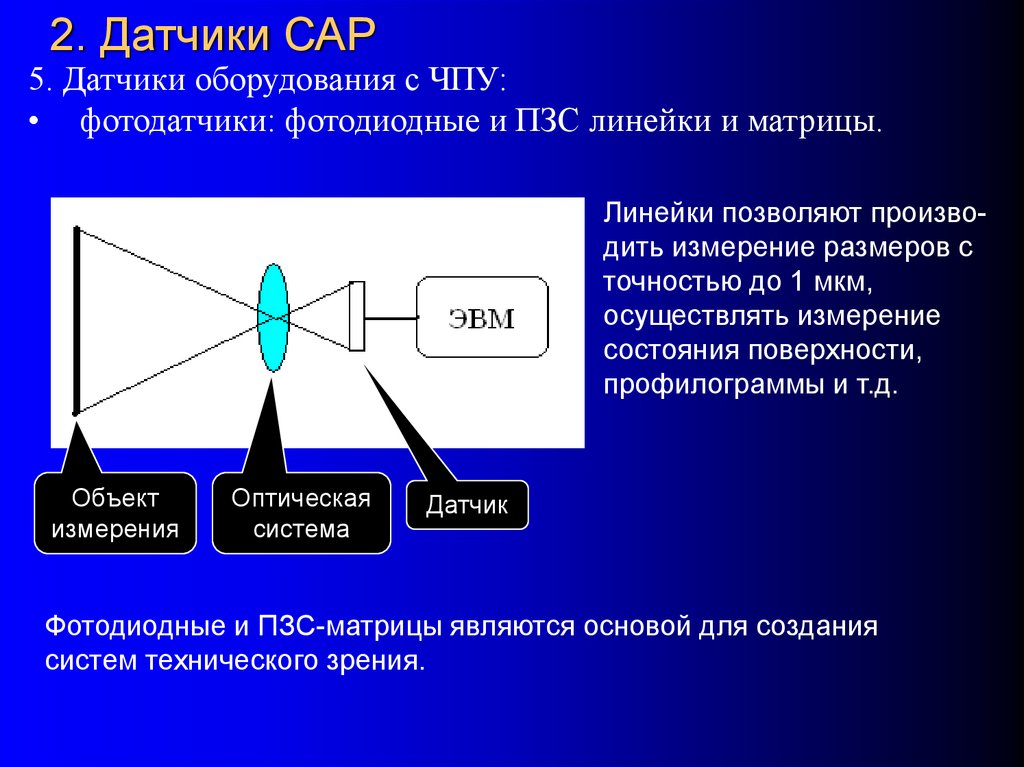
5. Датчики оборудования с ЧПУ:• фотодатчики: фотодиодные и ПЗС линейки и матрицы.
Линейки позволяют производить измерение размеров с
точностью до 1 мкм,
осуществлять измерение
состояния поверхности,
профилограммы и т.д.
Объект
измерения
Оптическая
система
Датчик
Фотодиодные и ПЗС-матрицы являются основой для создания
систем технического зрения.
102. Усилительные элементы
№ Усилитель Чувствительность Мощность Быстро-действие
1
Реле
средняя
средняя
низкое
2
Электронный
высокая
низкая
высокое
3
Магнитный
средняя
средняя
среднее
4
Электромашинный
низкая
высокая
низкое
103. Моделирование САР
1. ЭЦВМ – для моделирования используются численные методырешения дифференциальных уравнений (метод Эйлера, РунгеКутта и др.)
Преимущества:
Универсальность
Удобное оформление результатов (красивость)
Проблемы:
Точность и время решения зависят от шага интегрирования
Сложности представления решения в графическом виде
Высокая цена
2. АВМ – моделирование на основе использования электронной
схемы.
Преимущества:
Высокое быстродействие (теоретически )
Низкая цена
Простота изучения и программирования
Удобство сопряжения с графическими устройствами
Недостатки
Специализированность
Более низкая точность
104. Моделирование САР
Блоки АВМ:1. Сумматор
R0
R2
R1
U U1
U 2 1U 1 2U 2)
R0
R0
U1
R1
U2
R2
2. Интегросумматор
С
t
U1
R1
U2
R2
t
1
1
U
U1
U 2 dt 1U 1 2U 2)dt
R2C
0 R1C
0
105. Моделирование САР
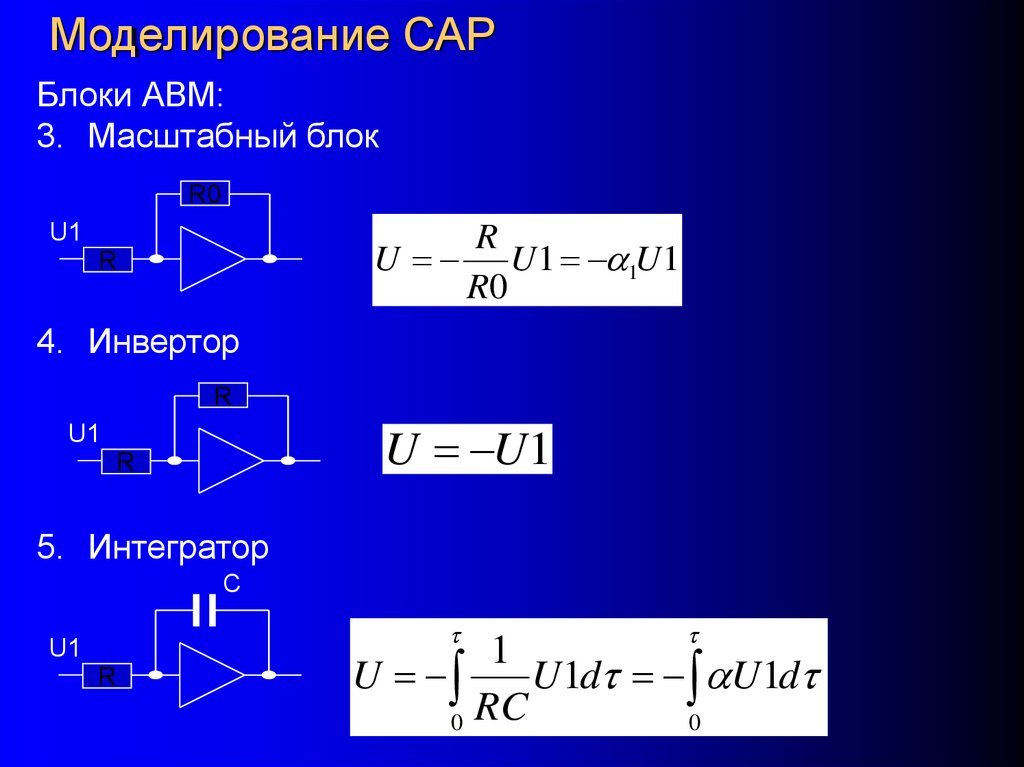
Блоки АВМ:3. Масштабный блок
R0
U1
R
U U1 1U1
R0
R
4. Инвертор
R
U U1
U1
R
5. Интегратор
С
t
U1
R
t
1
U
U1dt U1dt
0 RC
0
106. Моделирование САР
Решение линейных дифференциальных уравнений:a y by cy x(t ); y (0) y0 ; y (0) y1
1. Выражаем старшую производную:
y 1a x(t ) ba y ac y
2. Составляем схему
y
y
1
y
1
107. Моделирование САР
Решение линейных дифференциальных уравнений:a y by cy x(t ); y (0) y0 ; y (0) y1
1. Выражаем старшую производную:
y 1a x(t ) ba y ac y
2. Составляем схему
y
y
y
x(t)
1/a
c/a
b/a
y
y
1
108. Моделирование САР
Решение линейных дифференциальных уравнений:a y by cy x(t ); y (0) y0 ; y (0) y1
1. Выражаем старшую производную:
y 1a x(t ) ba y ac y
Последовательность
действий:
2. Составляем схему
y
x(t)
1/a
y
1
1.
2.
c/a
b/a
3.
y
1
Соединяем последовательно n интеграторов
На входе первого
интегратора создаем
схему, соответствующую
преобразованному ДУ
Соединяем входы этой
схемы с соответствующими выходами интеграторов, при необходимости
включая инверторы










































































 physics
physics








