Similar presentations:
Принципы построения автоматических систем
1.
ПРИНЦИПЫ ПОСТРОЕНИЯ АВТОМАТИЧЕСКИХ СИСТЕМЛюбой реальный технический процесс можно разбить на ряд простых
процессов – единичных цепей воздействия
1
3
2
Рис. 1.1. Элементы простого процесса
Единичная цепь воздействия состоит из источника технического воздействия
– 1, приемника технического воздействия – 2, линии передачи технического
воздействия – 3.
Любой технический процесс характеризуются:
1) продолжительностью протекания;
2) качественными показателями, т.е. активными силами, приложенными к
цепи;
3) количественными показателями, т.е. физическими величинами,
определяющими интенсивность протекающего процесса.
Совокупность качественных и количественных показателей называется
режимом процесса.
2.
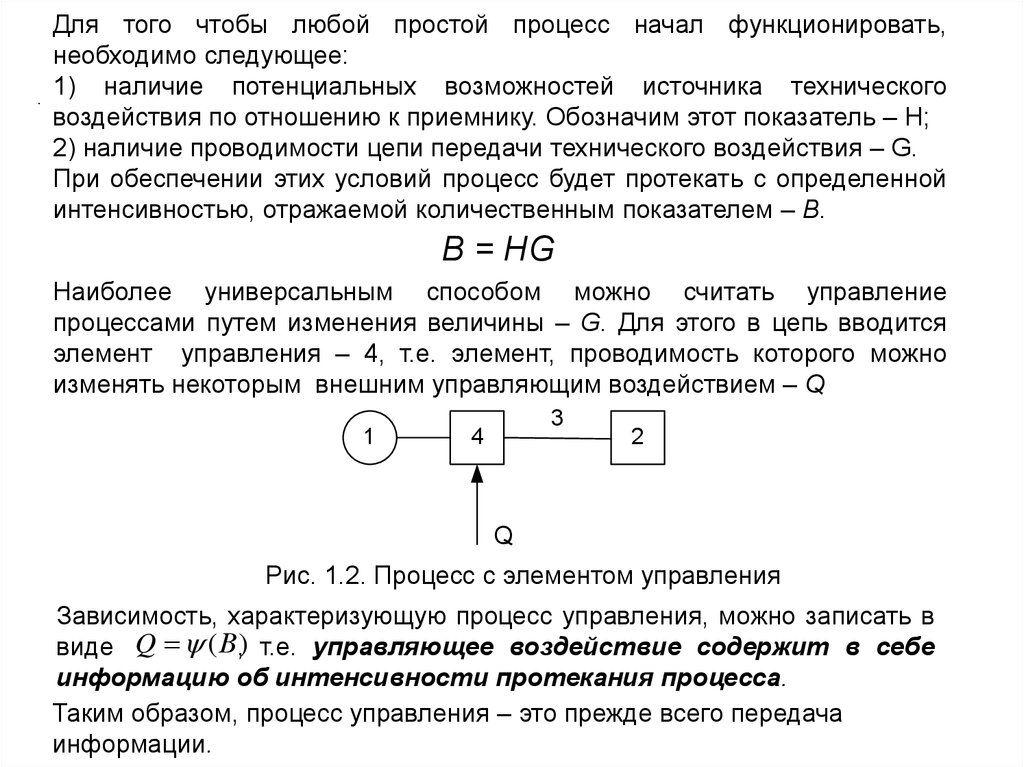
.Для того чтобы любой простой процесс начал функционировать,
необходимо следующее:
1) наличие потенциальных возможностей источника технического
воздействия по отношению к приемнику. Обозначим этот показатель – Н;
2) наличие проводимости цепи передачи технического воздействия – G.
При обеспечении этих условий процесс будет протекать с определенной
интенсивностью, отражаемой количественным показателем – В.
B = HG
Наиболее универсальным способом можно считать управление
процессами путем изменения величины – G. Для этого в цепь вводится
элемент управления – 4, т.е. элемент, проводимость которого можно
изменять некоторым внешним управляющим воздействием – Q
1
4
3
2
Q
Рис. 1.2. Процесс с элементом управления
Зависимость, характеризующую процесс управления, можно записать в
виде Q (В,) т.е. управляющее воздействие содержит в себе
информацию об интенсивности протекания процесса.
Таким образом, процесс управления – это прежде всего передача
информации.
3.
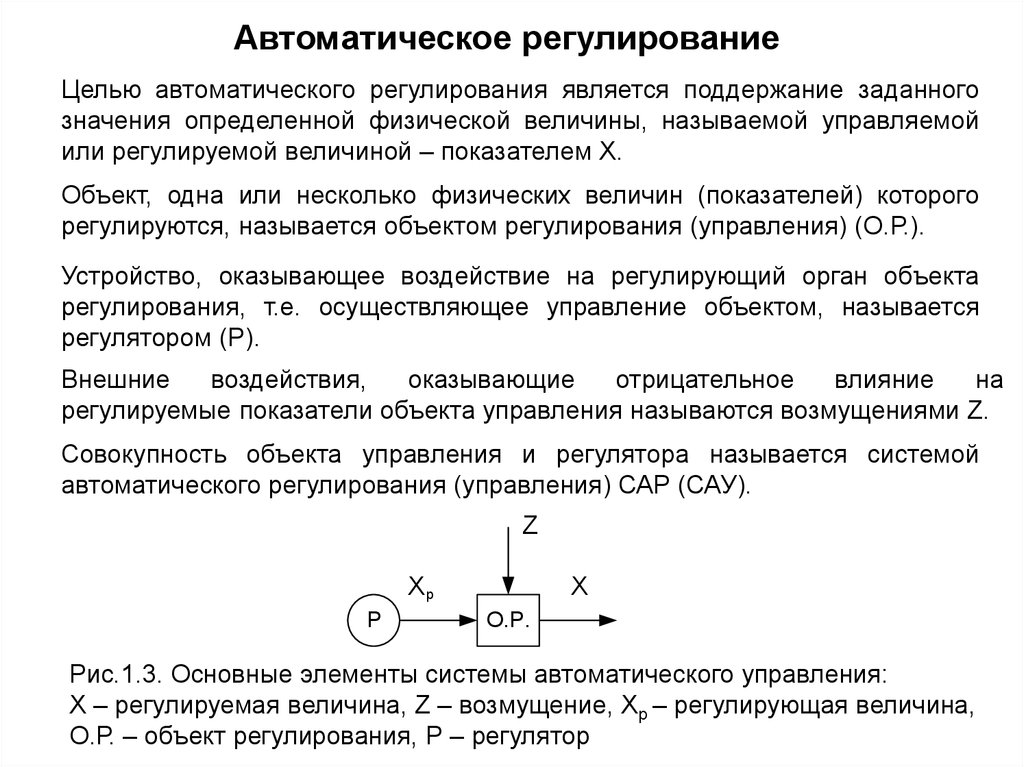
Автоматическое регулированиеЦелью автоматического регулирования является поддержание заданного
значения определенной физической величины, называемой управляемой
или регулируемой величиной – показателем Х.
Объект, одна или несколько физических величин (показателей) которого
регулируются, называется объектом регулирования (управления) (О.Р.).
Устройство, оказывающее воздействие на регулирующий орган объекта
регулирования, т.е. осуществляющее управление объектом, называется
регулятором (Р).
Внешние
воздействия,
оказывающие
отрицательное
влияние
на
регулируемые показатели объекта управления называются возмущениями Z.
Совокупность объекта управления и регулятора называется системой
автоматического регулирования (управления) САР (САУ).
Z
Xp
P
X
O.P.
Рис.1.3. Основные элементы системы автоматического управления:
Х – регулируемая величина, Z – возмущение, Хр – регулирующая величина,
О.Р. – объект регулирования, Р – регулятор
4.
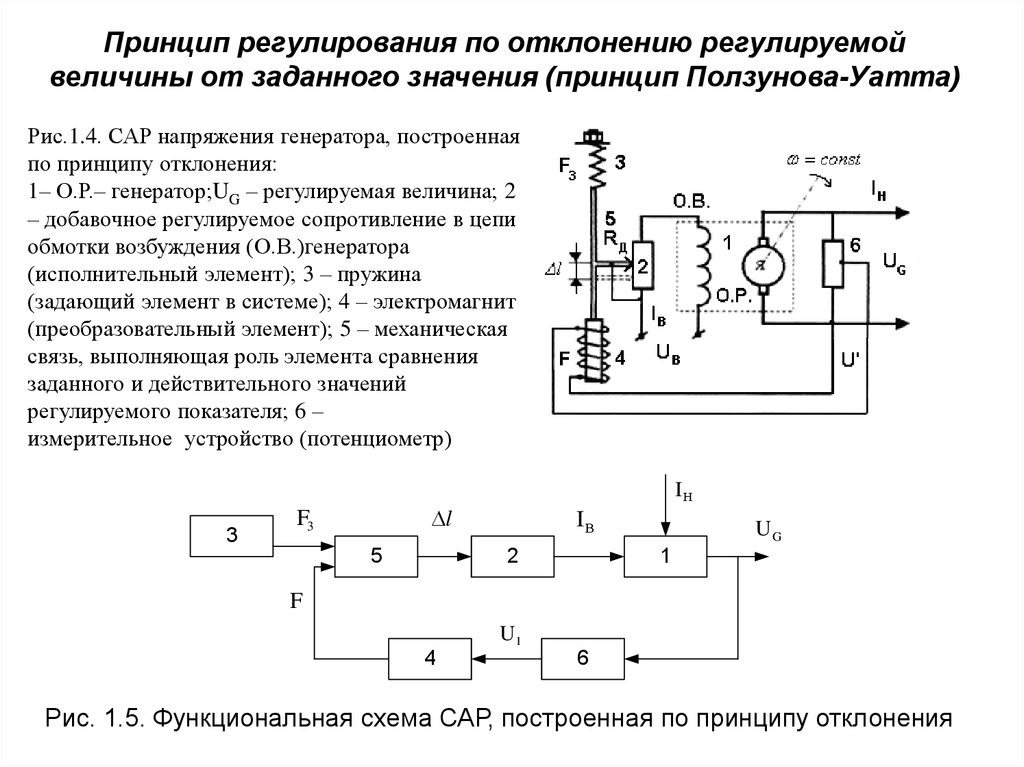
Принцип регулирования по отклонению регулируемойвеличины от заданного значения (принцип Ползунова-Уатта)
Рис.1.4. САР напряжения генератора, построенная
по принципу отклонения:
1– О.Р.– генератор;UG – регулируемая величина; 2
– добавочное регулируемое сопротивление в цепи
обмотки возбуждения (О.В.)генератора
(исполнительный элемент); 3 – пружина
(задающий элемент в системе); 4 – электромагнит
(преобразовательный элемент); 5 – механическая
связь, выполняющая роль элемента сравнения
заданного и действительного значений
регулируемого показателя; 6 –
измерительное устройство (потенциометр)
3
IН
l
F3
5
IВ
2
UG
1
F
U1
4
6
Рис. 1.5. Функциональная схема САР, построенная по принципу отклонения
5.
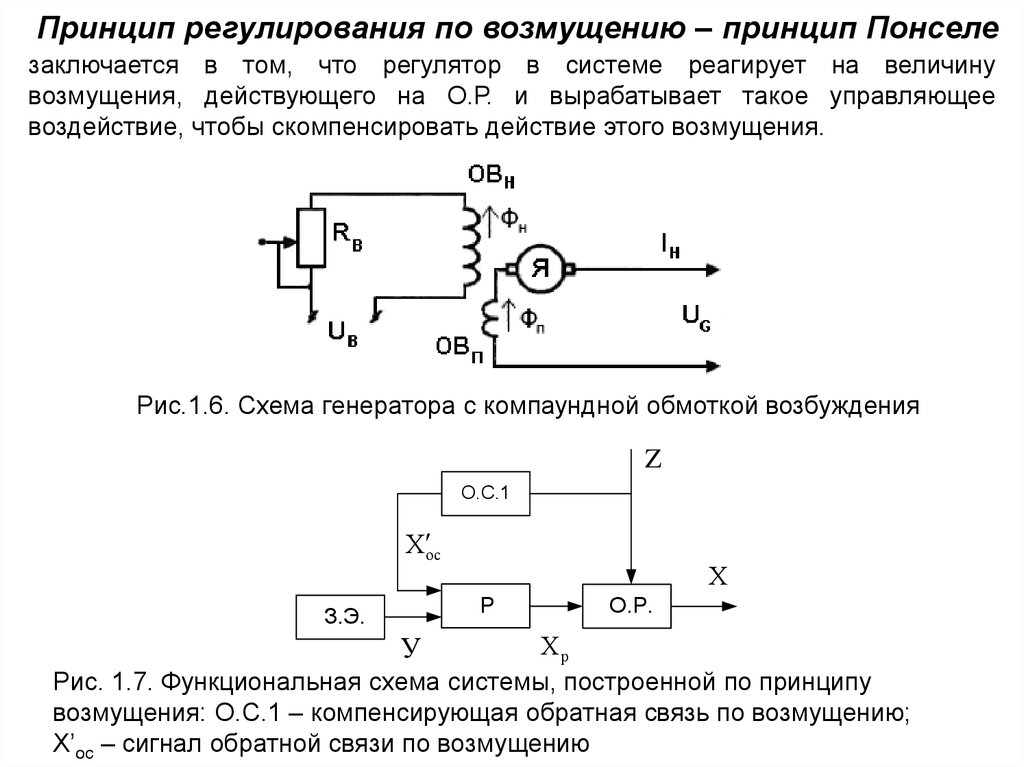
Принцип регулирования по возмущению – принцип Понселезаключается в том, что регулятор в системе реагирует на величину
возмущения, действующего на О.Р. и вырабатывает такое управляющее
воздействие, чтобы скомпенсировать действие этого возмущения.
Рис.1.6. Схема генератора с компаундной обмоткой возбуждения
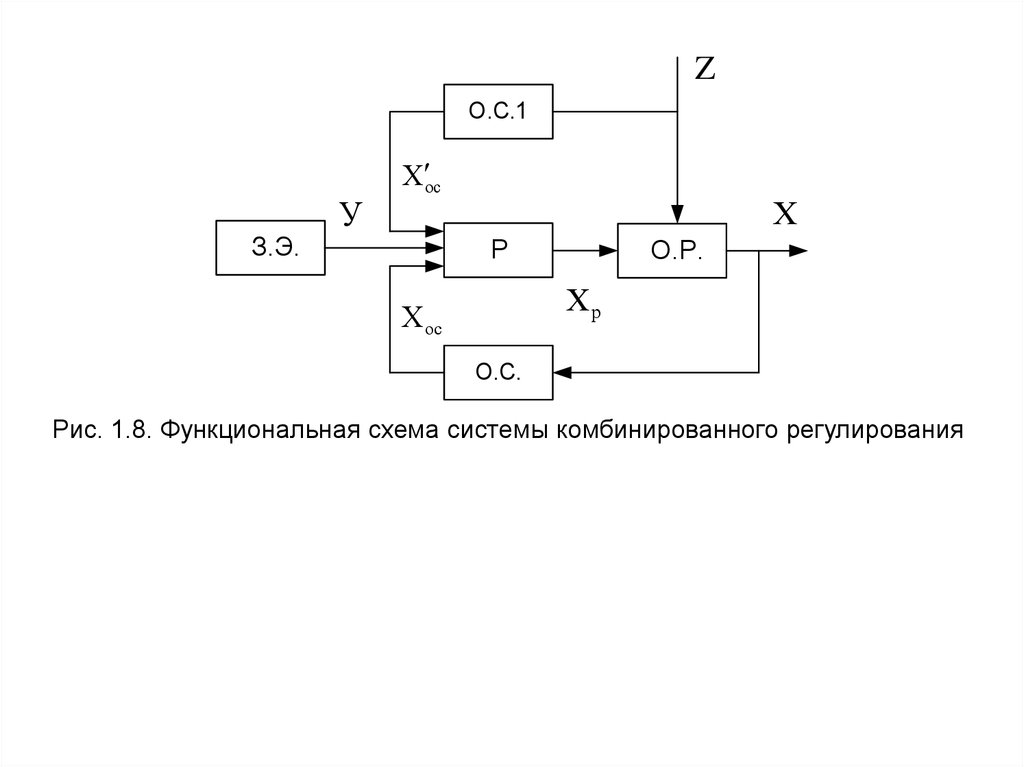
Z
О.С.1
Х ос
Х
Р
З.Э.
О.Р.
Хр
Рис. 1.7. Функциональная схема системы, построенной по принципу
возмущения: О.С.1 – компенсирующая обратная связь по возмущению;
Х’ос – сигнал обратной связи по возмущению
У
6.
ZО.С.1
З.Э.
У
Х ос
Х
Р
О.Р.
Хр
Х ос
О.С.
Рис. 1.8. Функциональная схема системы комбинированного регулирования
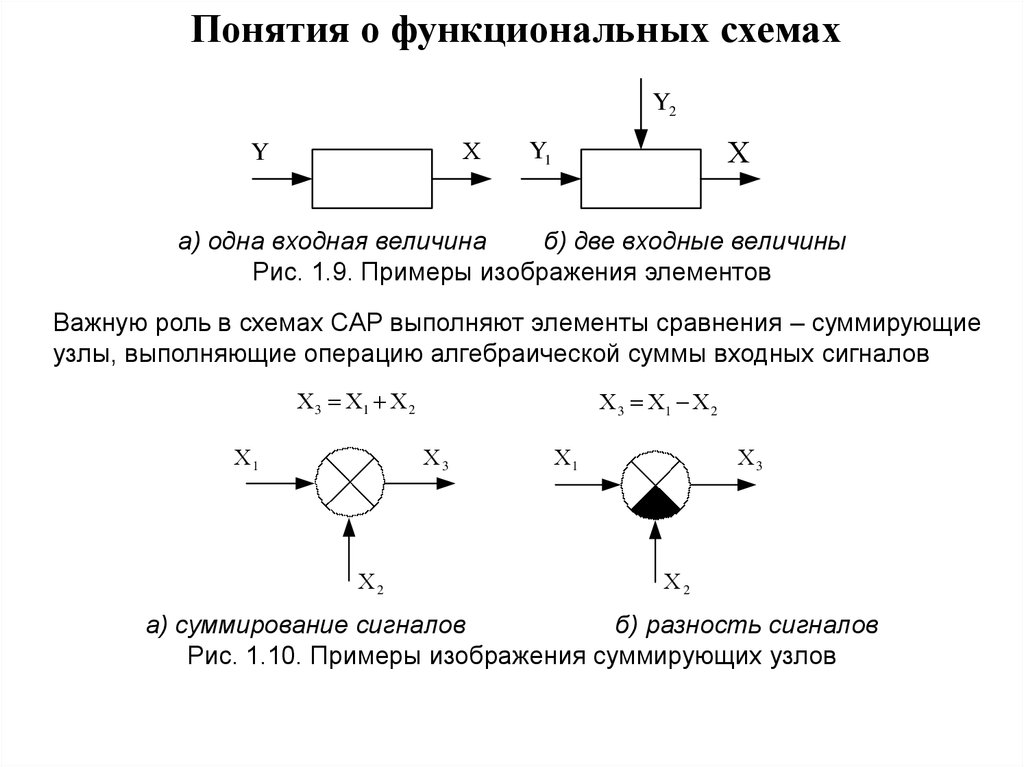
7.
Понятия о функциональных схемахY2
Х
Y
Х
Y1
а) одна входная величина
б) две входные величины
Рис. 1.9. Примеры изображения элементов
Важную роль в схемах САР выполняют элементы сравнения – суммирующие
узлы, выполняющие операцию алгебраической суммы входных сигналов
Х 3 Х1 Х 2
Х 3 Х1 Х 2
Х3
Х1
Х2
Х1
Х3
Х2
а) суммирование сигналов
б) разность сигналов
Рис. 1.10. Примеры изображения суммирующих узлов
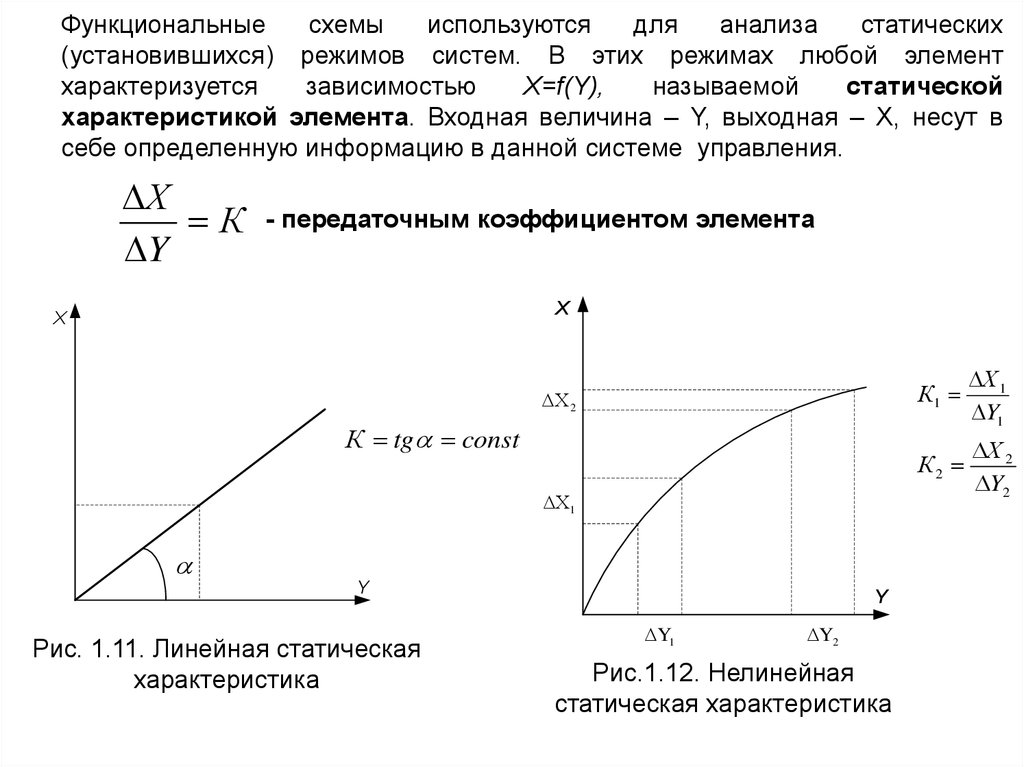
8.
Функциональныесхемы
используются
для
анализа
статических
(установившихся) режимов систем. В этих режимах любой элемент
характеризуется
зависимостью
Х=f(Y),
называемой
статической
характеристикой элемента. Входная величина – Y, выходная – X, несут в
себе определенную информацию в данной системе управления.
Х
К
Y
- передаточным коэффициентом элемента
X
X
Х 2
К tg const
Х1
Y
Рис. 1.11. Линейная статическая
характеристика
Y
Y1
Y2
Рис.1.12. Нелинейная
статическая характеристика
К1
Х 1
Y1
К2
Х 2
Y2
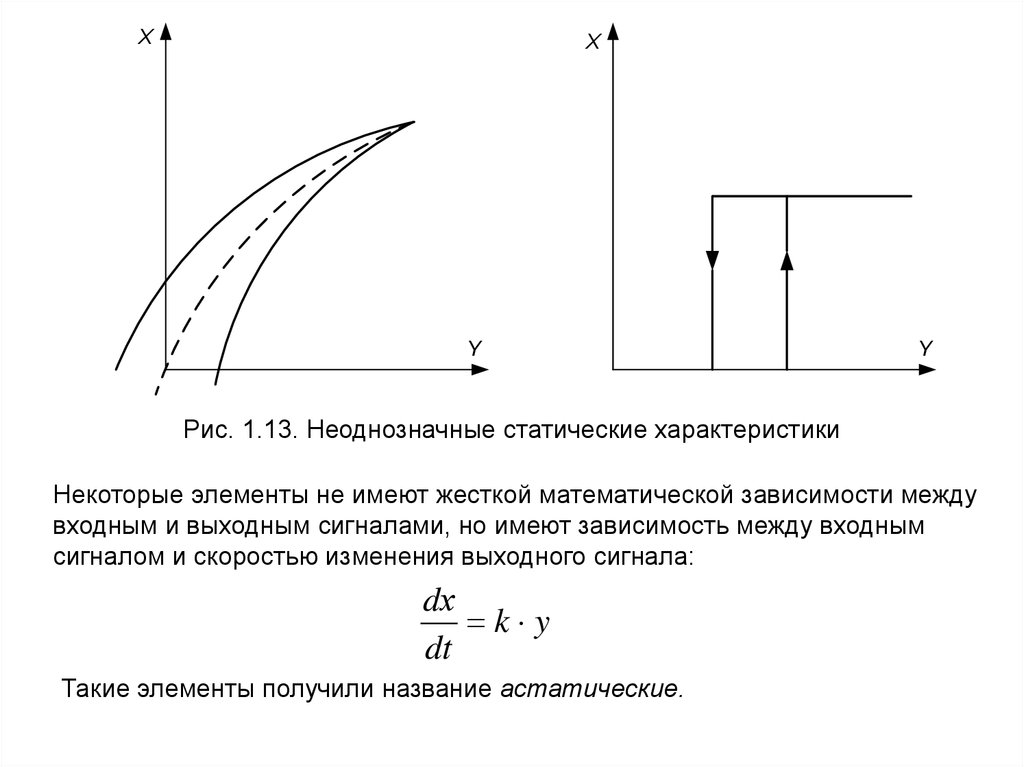
9.
XX
Y
Y
Рис. 1.13. Неоднозначные статические характеристики
Некоторые элементы не имеют жесткой математической зависимости между
входным и выходным сигналами, но имеют зависимость между входным
сигналом и скоростью изменения выходного сигнала:
dх
k y
dt
Такие элементы получили название астатические.
10.
Для линейных элементов соотношение между входным и выходнымсигналами записывается выражением х k y ,
которое
называется
уравнением
элемента
в
установившемся
(статическом) режиме.
Поскольку любой элемент – это устройство, связанное с передачей
информации, то для него присущи понятия погрешности и зоны
нечувствительности по аналогии с измерительной техникой:
Х Х вых1 Х вых2
Х
100%
Х в ых1
Х
Х в ых max
100%
11.
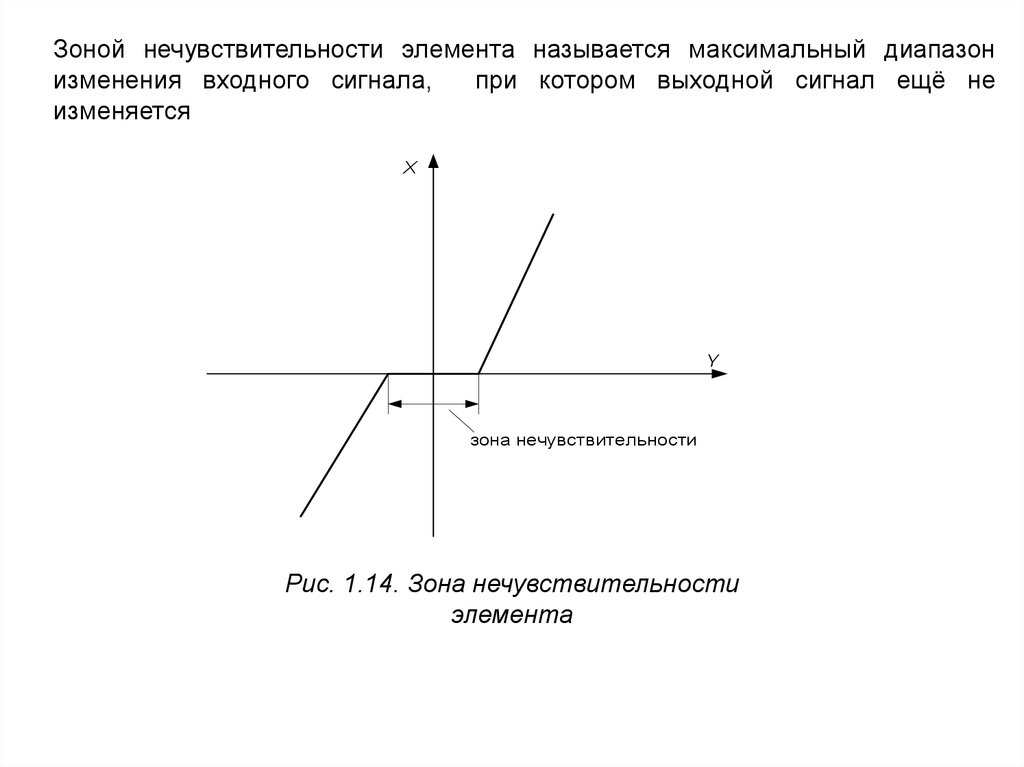
Зоной нечувствительности элемента называется максимальный диапазонизменения входного сигнала,
при котором выходной сигнал ещё не
изменяется
X
Y
зона нечувствительности
Рис. 1.14. Зона нечувствительности
элемента
12.
В схемах элементы могут соединяться между собой различным образом.Однако самые сложные схемы содержат три основных вида соединений
элементов:
1. Последовательное соединение
Y
К1
Х1
К2
Х2
К3
Х
Записывая для каждого элемента уравнения статики, получим
Х1 = К1 × Y;
Х2 = К2 × Х1;
Х = К3 × Х2.
Исключая промежуточные неизвестные, можно записать соотношение
между входным и выходным сигналами системы:
Х = К1 × К2 × К3 × Y.
Таким образом, обобщённый передаточный коэффициент для n
последовательно соединенных элементов можно определить как
произведение n передаточных коэффициентов отдельных элементов.
n
К Кi
i 1
13.
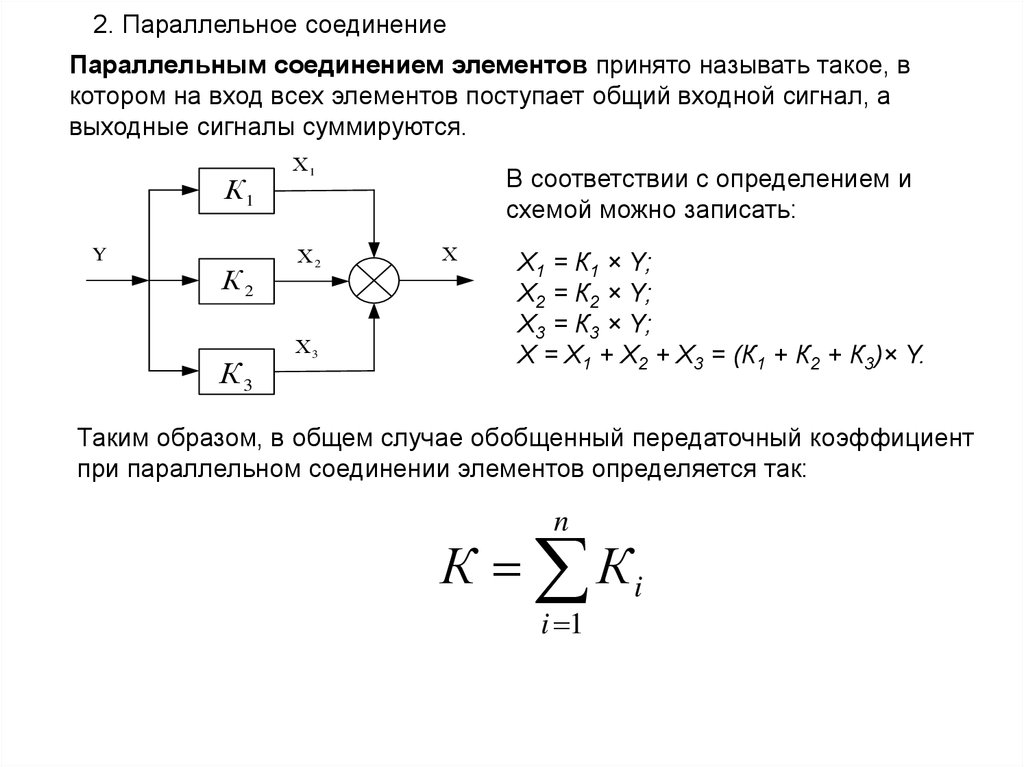
2. Параллельное соединениеПараллельным соединением элементов принято называть такое, в
котором на вход всех элементов поступает общий входной сигнал, а
выходные сигналы суммируются.
К1
Y
К2
К3
Х1
Х2
Х3
В соответствии с определением и
схемой можно записать:
Х
Х1 = К1 × Y;
Х2 = К2 × Y;
Х3 = К3 × Y;
Х = Х1 + Х2 + Х3 = (К1 + К2 + К3)× Y.
Таким образом, в общем случае обобщенный передаточный коэффициент
при параллельном соединении элементов определяется так:
n
К Кi
i 1
14.
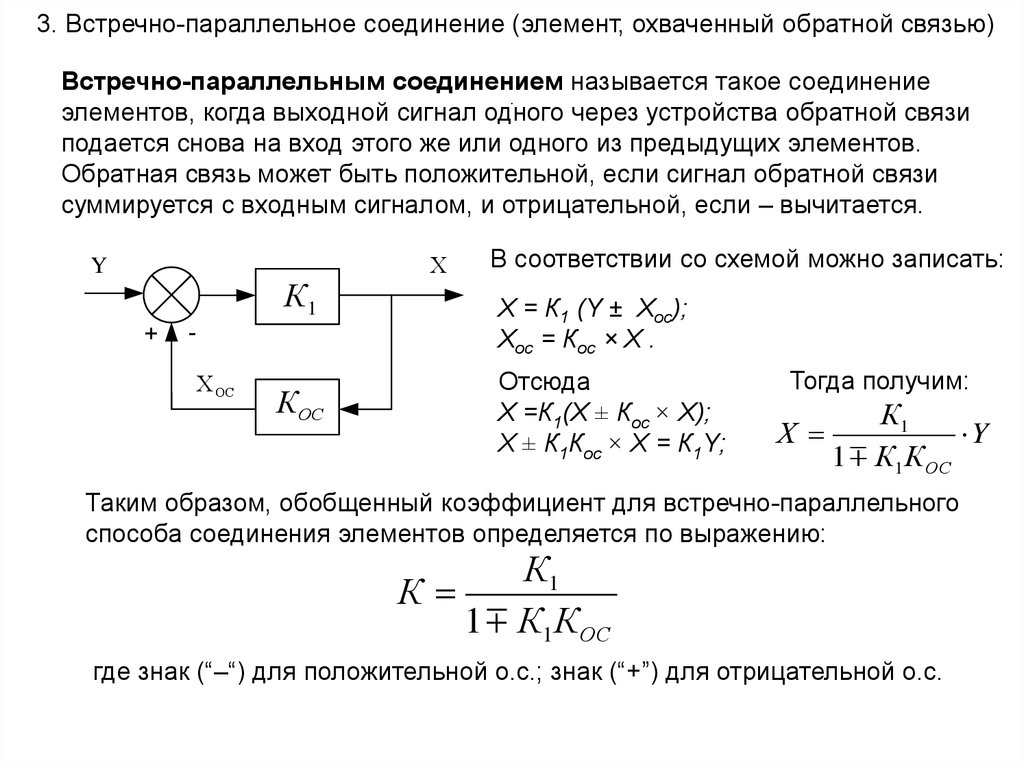
3. Встречно-параллельное соединение (элемент, охваченный обратной связью)Встречно-параллельным соединением называется такое соединение
.
элементов, когда выходной сигнал одного через устройства обратной связи
подается снова на вход этого же или одного из предыдущих элементов.
Обратная связь может быть положительной, если сигнал обратной связи
суммируется с входным сигналом, и отрицательной, если – вычитается.
Y
К1
+
Х ОС
К ОС
Х
В соответствии со схемой можно записать:
Х = К1 (Y ± Хос);
Хос = Кос × Х .
Отсюда
Х =К1(Х ± Кос × Х);
Х ± К1Кос × Х = К1Y;
Тогда получим:
Х
К1
Y
1 К1К ОС
Таким образом, обобщенный коэффициент для встречно-параллельного
способа соединения элементов определяется по выражению:
К1
К
1 К1К ОС
где знак (“–“) для положительной о.с.; знак (“+”) для отрицательной о.с.
15.
СТАТИКА ЛИНЕЙНЫХ СИСТЕМ НЕПРЕРЫВНОГО ДЕЙСТВИЯРазличают два основных состояния систем:
-статическое (установившийся режим);
- динамическое (режим переходного процесса).
Установившееся состояние системы принято характеризовать
следующими признаками:
- регулируемый параметр Х достиг установившегося значения, которое
равно заданному или отличается от него на определенную величину, которая
получила название статической ошибки Х= Хзад – Х
- регулирующий орган неподвижен, находится в состоянии равновесия, т.е.
Хр = const.
Цель статического расчёта:
1. Определение статической ошибки в системе, если заданы параметры
системы (передаточные коэффициенты элементов) и величина максимально
возможных возмущений.
2. Определение тех или иных параметров системы по заданной точности
(статической ошибке) при заданном возмущении и известных остальных
параметрах элементов.
16.
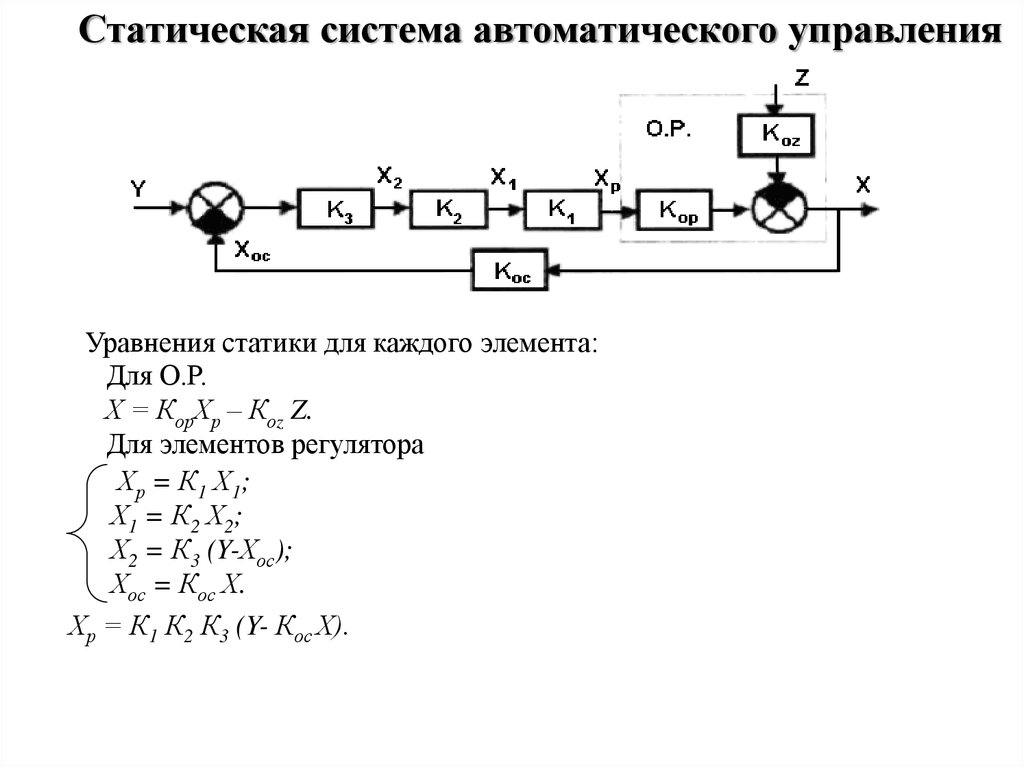
Статическая система автоматического управленияУравнения статики для каждого элемента:
Для О.Р.
Х = КорХр – Коz Z.
Для элементов регулятора
Хр = К1 Х1;
Х1 = К2 Х2;
Х2 = К3 (Y-Хос);
Хос = Кос Х.
Хр = К1 К2 К3 (Y- Кос Х).
17.
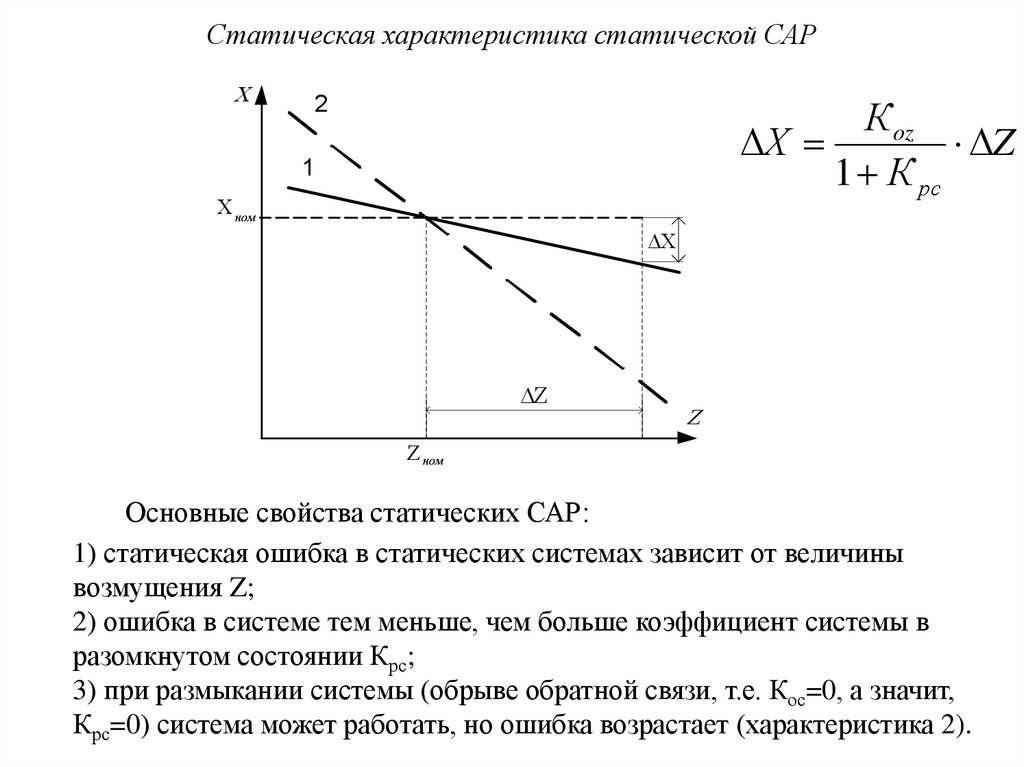
Статическая характеристика статической САРКoz
Х
Z
1 К рс
2
1
ном
ном
Основные свойства статических САР:
1) статическая ошибка в статических системах зависит от величины
возмущения Z;
2) ошибка в системе тем меньше, чем больше коэффициент системы в
разомкнутом состоянии Крс;
3) при размыкании системы (обрыве обратной связи, т.е. Кос=0, а значит,
Крс=0) система может работать, но ошибка возрастает (характеристика 2).
18.
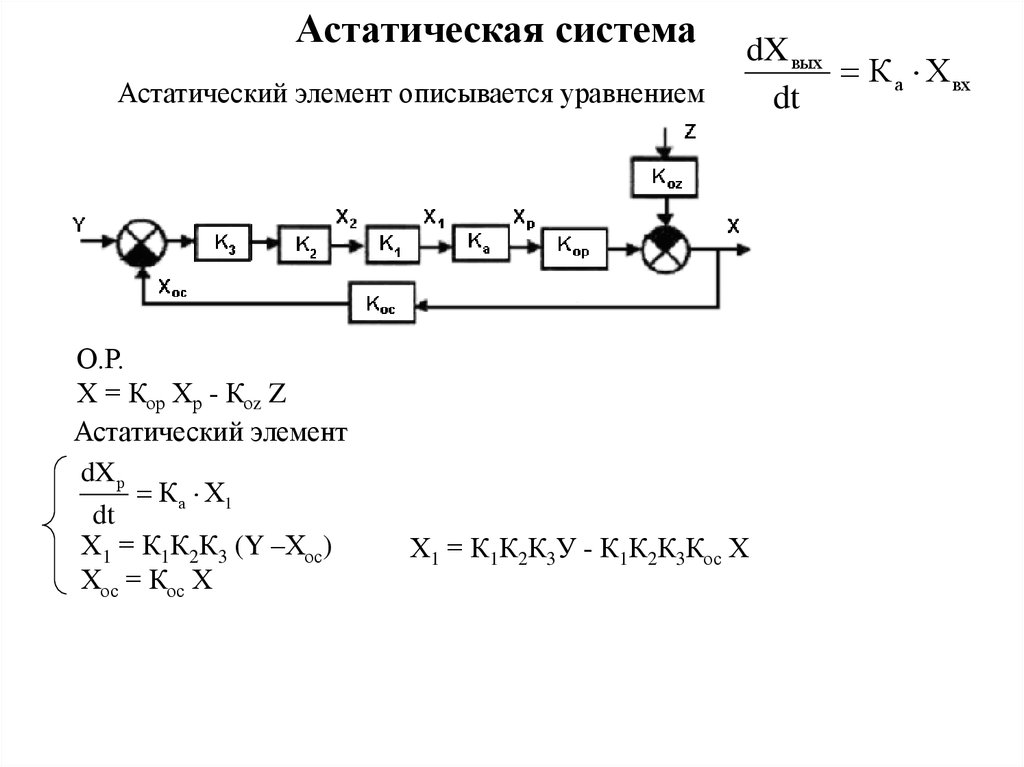
Астатическая системаАстатический элемент описывается уравнением
О.Р.
Х = Кор Хр - Коz Z
Астатический элемент
dXр
Ка Х1
dt
Х1 = К1К2К3 (Y –Хос)
Хос = Кос Х
dX вых
К а Х вх
dt
Х1 = К1К2К3У - К1К2К3Кос Х
19.
Статическая характеристика астатической системыX
Х
К1К 2 К 3К ос
зад
Z
Свойства астатических систем:
20.
Динамика линейных системВ общем виде уравнение системы автоматического управления
n-го порядка после линеаризации:
dn x
d n 1x
dm y
d m 1y
а 0 n a1 n 1 a n x b0 m b1 m 1 b m y
dt R
dt R 1
dt
dt
d z
d z
c0 R c1 R 1 c R z,
dt
dt
Для линейных системах:
dn x
d n 1x
dm y
d m 1y
а 0 n a1 n 1 a n x b0 m b1 m 1 b m y
dt
dt
dt
dt
21.
Применение операторных методов в теорииавтоматического управления
прямое преобразование Лапласа
Х(р) х ( t ) e ptdt
0
dx
L
P X(p) x (0)
dt
d2x
dx
L 2 P 2 X(p) Р x (0)
dt
dt 0
При нулевых начальных условиях
dk x
L k P k X ( p)
dt
Уравнение линейной системы автоматического управления в
операторном виде
а 0рn X(p) a1pn 1 Х(р) a n Х(р) b0рm У(р)
b1рm 1 У(р) bm У(р)
22.
Понятие о передаточной функции и комплексномпередаточном коэффициенте
Передаточной функцией в форме преобразования Лапласа принято
называть отношение изображения по Лапласу выходного сигнала к
изображению входного при нулевых начальных условиях:
X ( p)
W ( p)
У ( р)
Для уравнения обобщённой САР можно записать
Х(р) (а 0 р n a1p n 1 a n ) У(р) (b0 р m b1р m 1 b m )
X(p) b0 р m b1р m 1 b m
W ( p)
У(р) а 0 р n a1p n 1 a n
23.
Преобразование Фурье отличается от преобразования Лапласа тем, что вкачестве комплексного переменного используется комплекс частоты, т.е. р=jɷ.
Уравнение обобщённой САР в форме преобразования Фурье
а 0 ( j )n X( j ) a1 ( j )n 1 Х( j ) a n Х( j )
b0 ( j )m У( j ) b1 ( j )m 1 У( j ) bm У( j )
комплексный передаточный коэффициент
X( j ) b0 ( j ) m b1 ( j ) m 1 b m
W( j )
У( j ) а 0 ( j ) n a1 ( j ) n 1 a n
24.
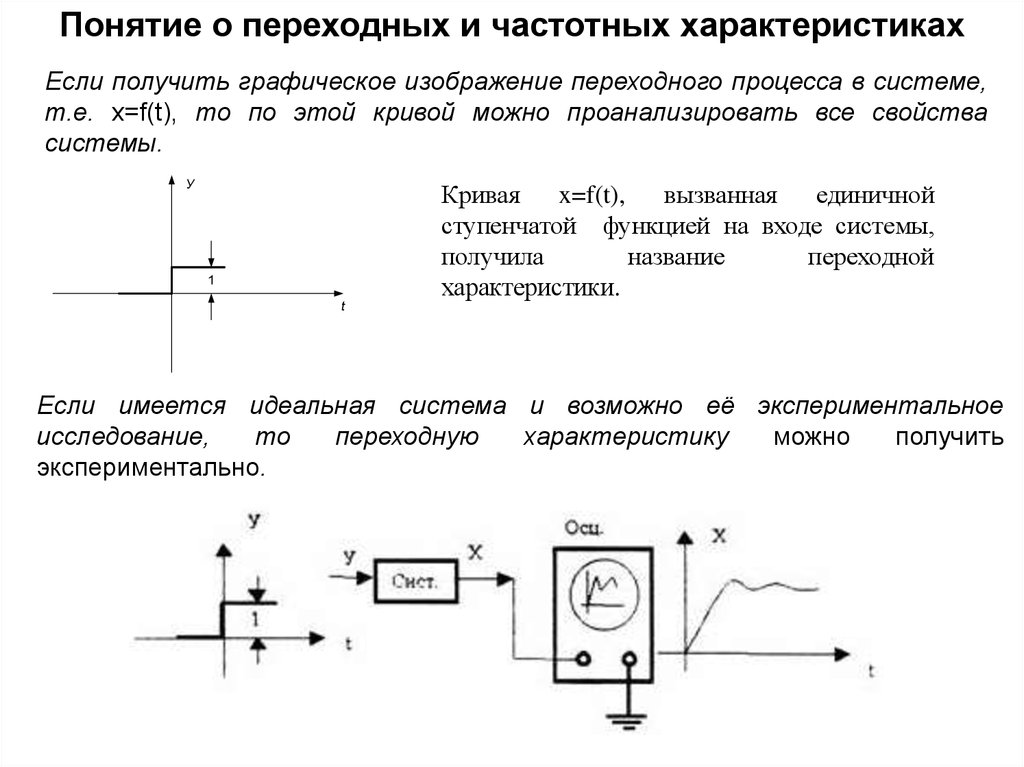
Понятие о переходных и частотных характеристикахЕсли получить графическое изображение переходного процесса в системе,
т.е. x=f(t), то по этой кривой можно проанализировать все свойства
системы.
У
Кривая
x=f(t),
вызванная
единичной
ступенчатой функцией на входе системы,
получила
название
переходной
характеристики.
1
t
Если имеется идеальная система и возможно её экспериментальное
исследование,
то
переходную
характеристику
можно
получить
экспериментально.
25.
Физический смысл частотных характеристик – это различные аспектыреакции системы на синусоидальные входные сигналы различной частоты.
Аналитически все основные частотные характеристики получаются из
выражения для комплексного передаточного коэффициента W(jɷ)
W( j ) U( ) jV ( ) R ( )е
j ( )
U(ɷ) – вещественная частотная характеристика (в.ч.х.);
V(ɷ) – мнимая частотная характеристика (м.ч.х.);
R ( ) U 2 ( ) V 2 ( ) – амплитудно-частотная характеристика (а.ч.х.);
V( )
– фазово-частотная характеристика (ф.ч.х.).
( ) arctg
U( )
Любое комплексное число – это вектор, который можно изобразить в комплексной
плоскости. При изменении частоты от 0 до ∞ вектор W(jɷ) будет описывать
кривую, которая получила название амплитудно-фазовой характеристики:
26.
В практике построения частотных характеристик частота может меняться в оченьшироких пределах, поэтому линейные шкалы частот не всегда удобны. В связи с этим
получили широкое применение логарифмические частотные характеристики.
Таким образом, из одного и того же выражения для комплексного передаточного
коэффициента W(jɷ) получается семь основных частотных характеристик:
1. вещественная частотная характеристика (в.ч.х.);
2. мнимая частотная характеристика (м.ч.х.);
3. амплитудно-частотная характеристика (а.ч.х.);
4. фазово-частотная характеристика (ф.ч.х);
5. амплитудно-фазовая характеристика (а.ф.х.);
6. логарифмическая амплитудно-частотная характеристика (ЛАЧХ);
7. логарифмическая фазово-частотная характеристика (ЛФЧХ).
27.
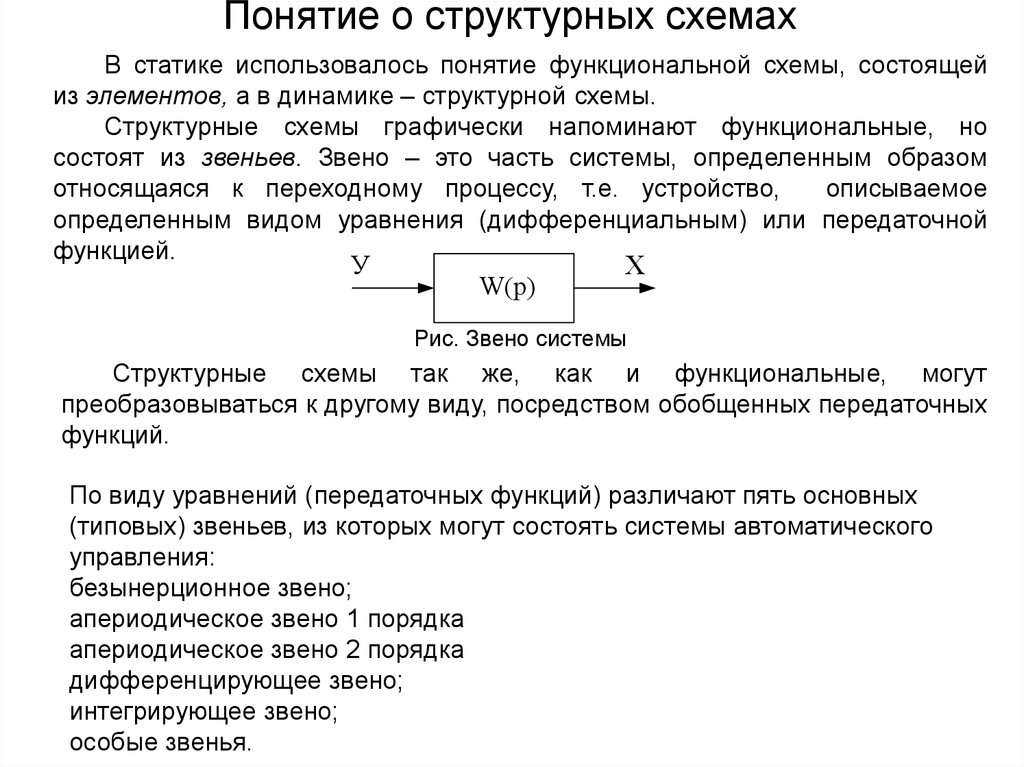
Понятие о структурных схемахВ статике использовалось понятие функциональной схемы, состоящей
из элементов, а в динамике – структурной схемы.
Структурные схемы графически напоминают функциональные, но
состоят из звеньев. Звено – это часть системы, определенным образом
относящаяся к переходному процессу, т.е. устройство,
описываемое
определенным видом уравнения (дифференциальным) или передаточной
функцией.
У
W(р)
Рис. Звено системы
Структурные схемы так же, как и функциональные, могут
преобразовываться к другому виду, посредством обобщенных передаточных
функций.
По виду уравнений (передаточных функций) различают пять основных
(типовых) звеньев, из которых могут состоять системы автоматического
управления:
безынерционное звено;
апериодическое звено 1 порядка
апериодическое звено 2 порядка
дифференцирующее звено;
интегрирующее звено;
особые звенья.
28.
Типовые звенья, их переходные и частотные характеристикиБезынерционное звено
У
х = к· у.
Для того чтобы получить частотные
характеристики, необходимо записать
уравнение в операторной форме:
1
t
Х(р) = к·У(р);
Х
Передаточная функция:
k у
t
Рис. Переходная характеристика
безынерционного звена
Х ( р)
k
У ( р)
Комплексный передаточный W ( j ) Х ( j ) k
коэффициент:
У ( j )
R
W ( р)
Частотные характеристики:
W ( j ) k j 0 Rе j
k
а) амплитудно-частотная
б) фазово-частотная
R k 2 02 – а.ч.х.
0
arctg 0 – ф.ч.х..
k
29.
jVR k
U
Рис. Амплитудно-фазовая частотная характеристика безынерционного звена
Рис. Логарифмическая амплитудно-частотная характеристика безынерционного звена
30.
Апериодическое звено 1 порядкаt
х k у 1 е Т
dx
Т
х k у
dt
Уравнение в операторной форме:
Y
Передаточная функция:
Х ( р)
k
W ( р)
У ( р) Т Р 1
1
t
Комплексный передаточный коэффициент:
X
Т
k у
t
Переходная характеристика
Х ( j )
k
W ( j )
У ( j ) j T 1
31.
Апериодическое звено 1 порядкакомплексный передаточный коэффициент:
k (1 j T )
k
k T
W ( j )
j
2 2
(1 j T )(1 j T ) 1 Т
1 2Т 2
U ( )
в.ч.х
k
1 2Т 2
м.ч.х
V( )
k T
1 2Т 2
а.ч.х
ф.ч.х
k 2 k 2 2Т 2
k
R U V
(1 2Т 2 )2
1 2Т 2
2
2
k
V
artg ( Т ) arctg ( Т )
U
R
jV
а.ч.х.
k
2
k
1
Т
45
90
arctg
R
U
ф.ч.х.
Амплитудно-фазовая характеристика
32.
Апериодическое звено 1 порядкаЛогарифмическую
амплитудно-частотную
построить из выражения:
20 lg R 20 lg
k
1 2Т 2
характеристику
можно
20 lg k 20 lg 1 2Т 2
Эту характеристику обычно строят не по точкам, а упрощенно. Для этого
задаются следующими условиями:
Особенность 2-го участка такова, что величина наклона независимо
от параметров данного звена будет одинаковой. Для определения наклона
характеристики вычислим изменение амплитуды характеристики на
участке при изменении частоты в 10 раз (на одну декаду):
33.
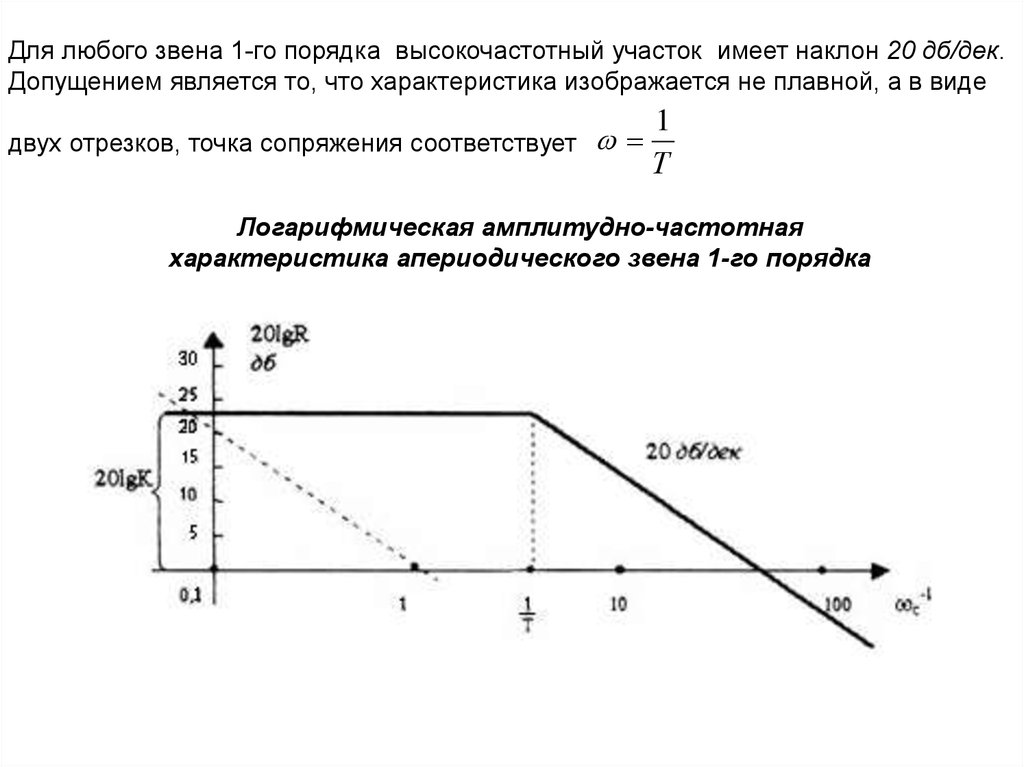
Для любого звена 1-го порядка высокочастотный участок имеет наклон 20 дб/дек.Допущением является то, что характеристика изображается не плавной, а в виде
двух отрезков, точка сопряжения соответствует
1
Т
Логарифмическая амплитудно-частотная
характеристика апериодического звена 1-го порядка
34.
Интегрирующее звеноУравнение интегрирующего звена
dx
Ка у
dt
t
или
х К а у dt
где Ка – постоянный коэффициент
0
t
При у=1:
х К а 1 dt К а t
0
т.е. линейно нарастающая зависимость под углом α=arctg(Ка )
Переходная характеристика интегрирующего звена
Х
t
35.
Интегрирующее звеноДля получения частотных характеристик необходимо записать уравнение
интегрирующего звена в операторной форме:
Комплексный передаточный коэффициент:
Передаточная функция:
W ( р)
АЧХ:
Ка
Ка
W ( j )
0 j
j
Х ( р) К а
У ( р)
Р
R 0
2
К а2
2
Ка
ФЧХ: arctg
0
Ка
arctg 90
Частотные характеристики интегрирующего звена
R
jV
а.ч.х.
U
-45
ф.ч.х.
-90
а.ф.х.
36.
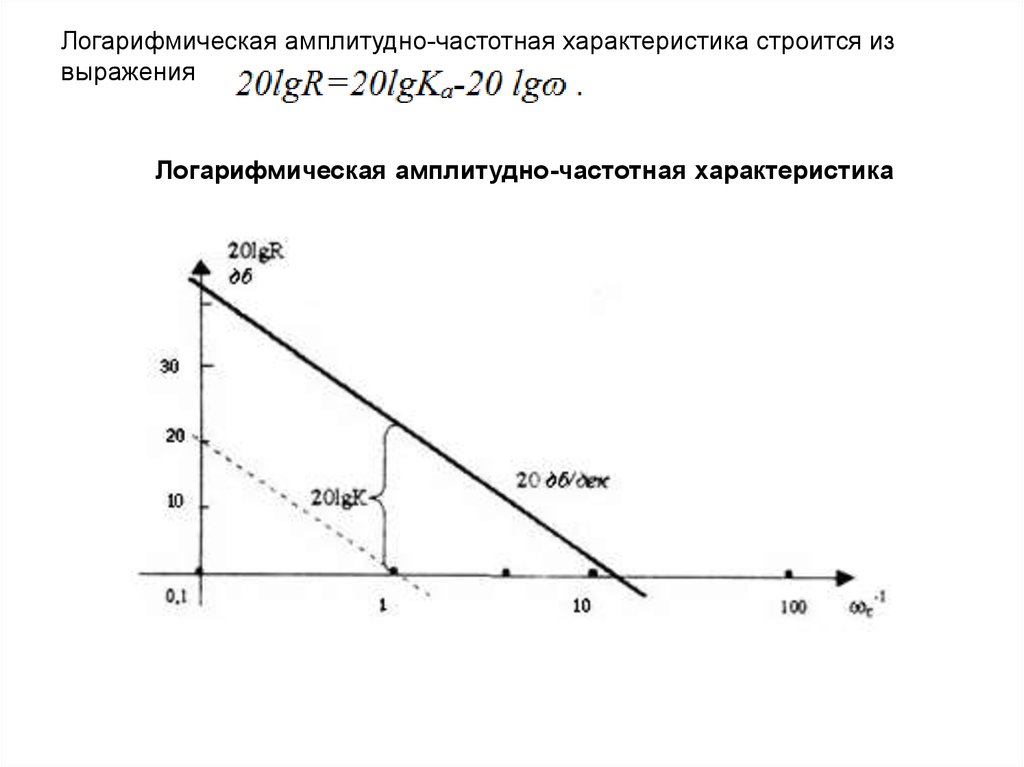
Логарифмическая амплитудно-частотная характеристика строится извыражения
Логарифмическая амплитудно-частотная характеристика
37. Дифференцирующие звенья
Три вида дифференцирующих звеньев со следующими уравнениями:1) идеальное дифференцирующее звено
dу
х Кд
dt
2) реальное дифференцирующее звено
Т
dx
dу
х Кд
dt
dt
3) реальное дифференцирующее звено со статизмом
dx
dу
Т х Кд К у
dt
dt
где Кд – коэффициент пропорциональности; К – передаточный коэффициент;
Т – постоянная времени
38.
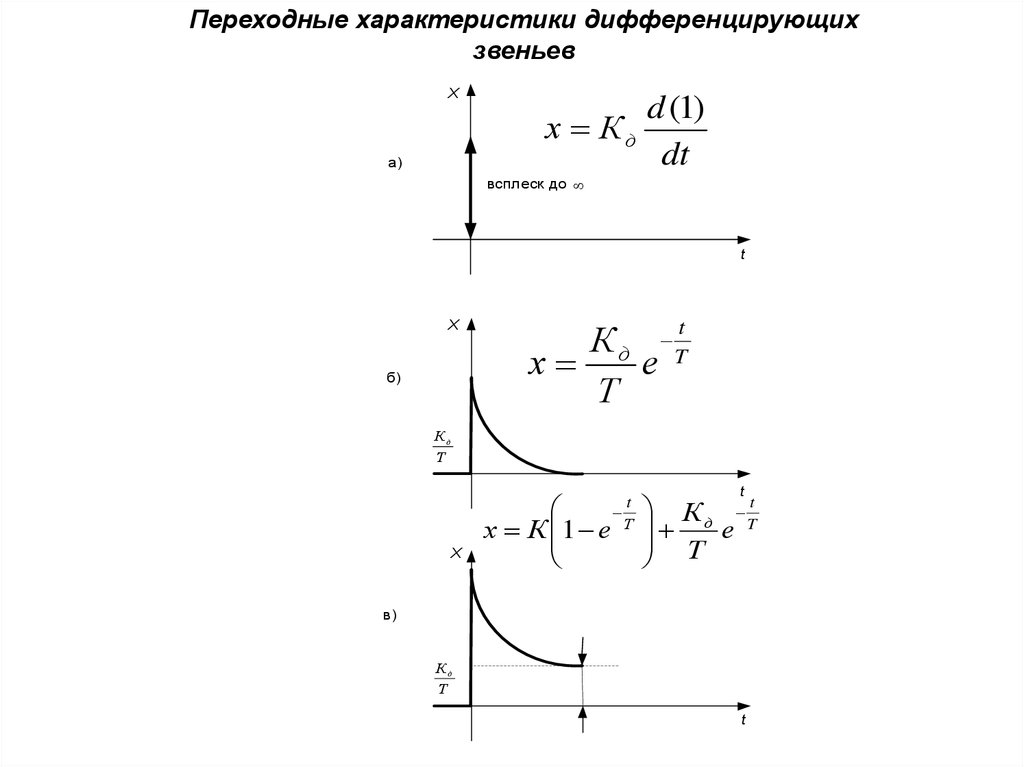
Переходные характеристики дифференцирующихзвеньев
X
а)
d (1)
х Кд
dt
всплеск до
t
X
б)
К д Tt
х
е
Т
Кд
Т
X
х К 1 е
t
Т
Кд
Т е
t
в)
Кд
Т
t
t
T
39.
Частотные характеристики идеального дифференцирующего звенаУравнение идеального дифференцирующего звена в операторной
форме:
Передаточная функция:
W ( р)
Комплексный передаточный коэффициент:
Х ( р)
Кд Р
У ( р)
W ( j ) jКд 0 jКд
ФЧХ:
АЧХ:
arctg
R 0 К Кд
2
2
д
2
V
arctg 90о
U
R
jV
ф.ч.х.
а.ч.х.
90
arctgК д
а.ф.х.
45
U
40.
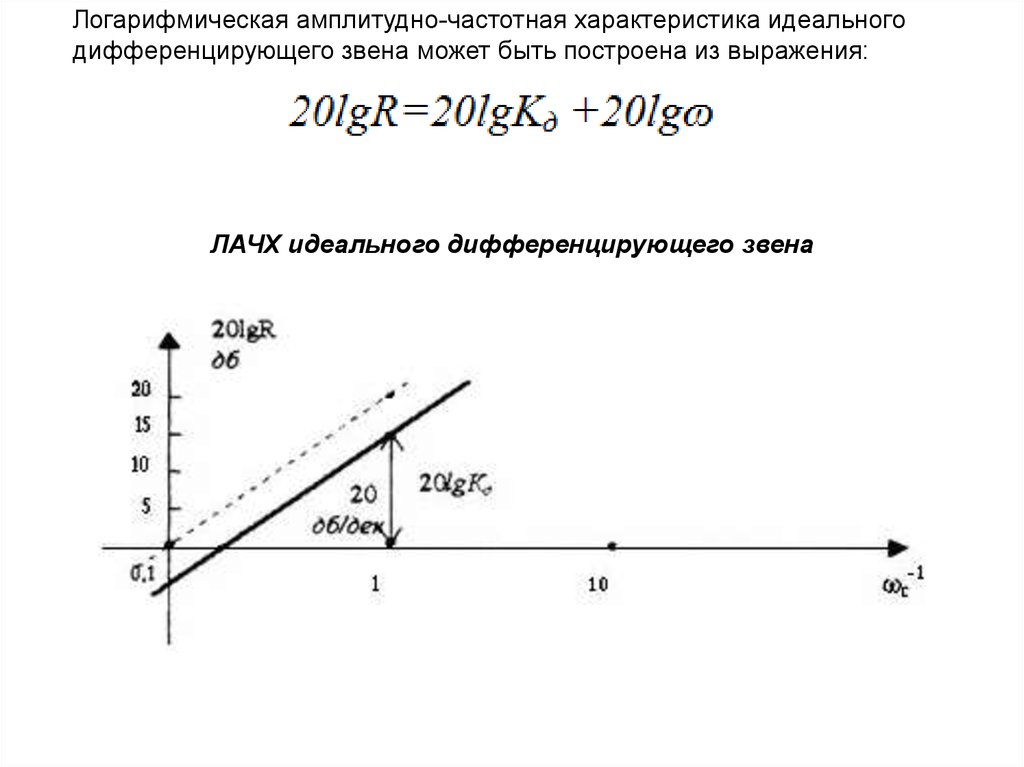
Логарифмическая амплитудно-частотная характеристика идеальногодифференцирующего звена может быть построена из выражения:
ЛАЧХ идеального дифференцирующего звена
41.
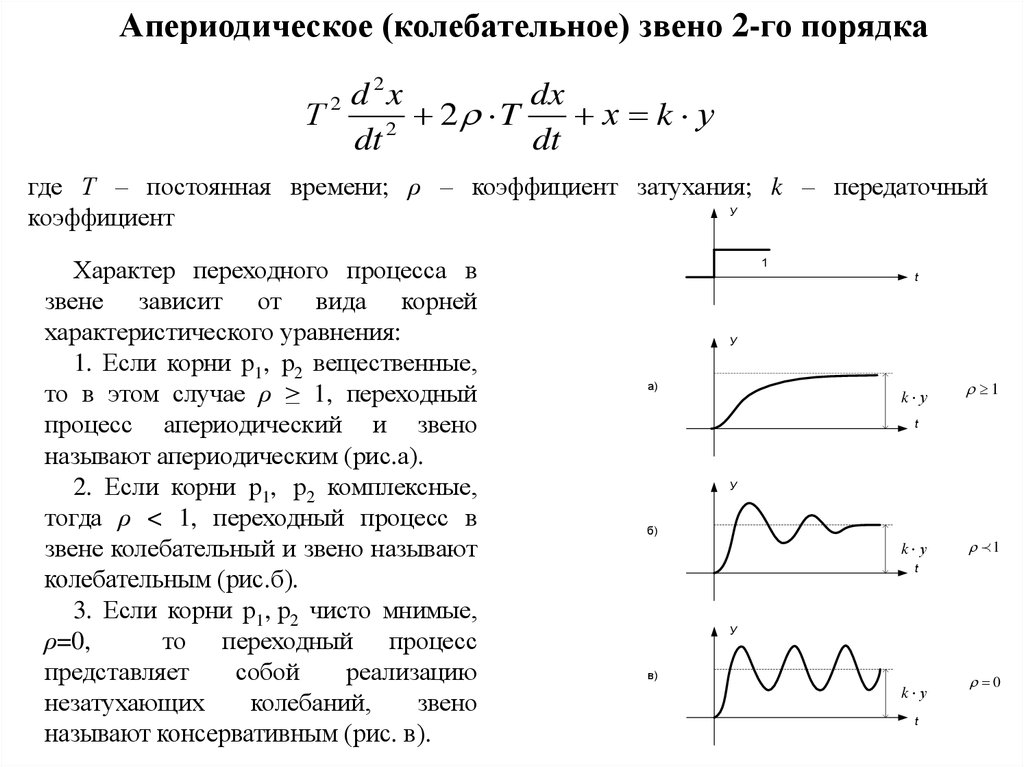
Апериодическое (колебательное) звено 2-го порядкаd 2x
dx
Т
2 T
х k у
2
dt
dt
2
где Т – постоянная времени; ρ – коэффициент затухания; k – передаточный
У
коэффициент
Характер переходного процесса в
звене зависит от вида корней
характеристического уравнения:
1. Если корни р1, р2 вещественные,
то в этом случае ρ ≥ 1, переходный
процесс апериодический и звено
называют апериодическим (рис.а).
2. Если корни р1, р2 комплексные,
тогда ρ < 1, переходный процесс в
звене колебательный и звено называют
колебательным (рис.б).
3. Если корни р1, р2 чисто мнимые,
ρ=0,
то переходный процесс
представляет
собой
реализацию
незатухающих
колебаний,
звено
называют консервативным (рис. в).
1
t
У
а)
k у
1
t
У
б)
k у
1
t
У
в)
k у
t
0
42.
Для построения частотных характеристик уравнение звена необходимо записать воператорной форме
2 2
Т Р Х ( р) 2 T Р Х ( р) Х ( р) k У ( р)
Передаточная функция:
Комплексный передаточный коэффициент:
k
W ( j )
T 2 2 j 2 T 1
k
W ( p) 2 2
T P 2 TP 1
Умножим и разделим W(jɷ) на выражение, сопряженное знаменателю:
k (1 T 2 2 ) j 2 T
W ( j )
2 2
2 2
(1 T ) j 2 T (1 T ) j 2 T
k (1 T 2 2 )
2k T
j
2 2 2
2 2 2
(1 T ) 4 T
(1 T 2 2 ) 2 4 2T 2 2
43.
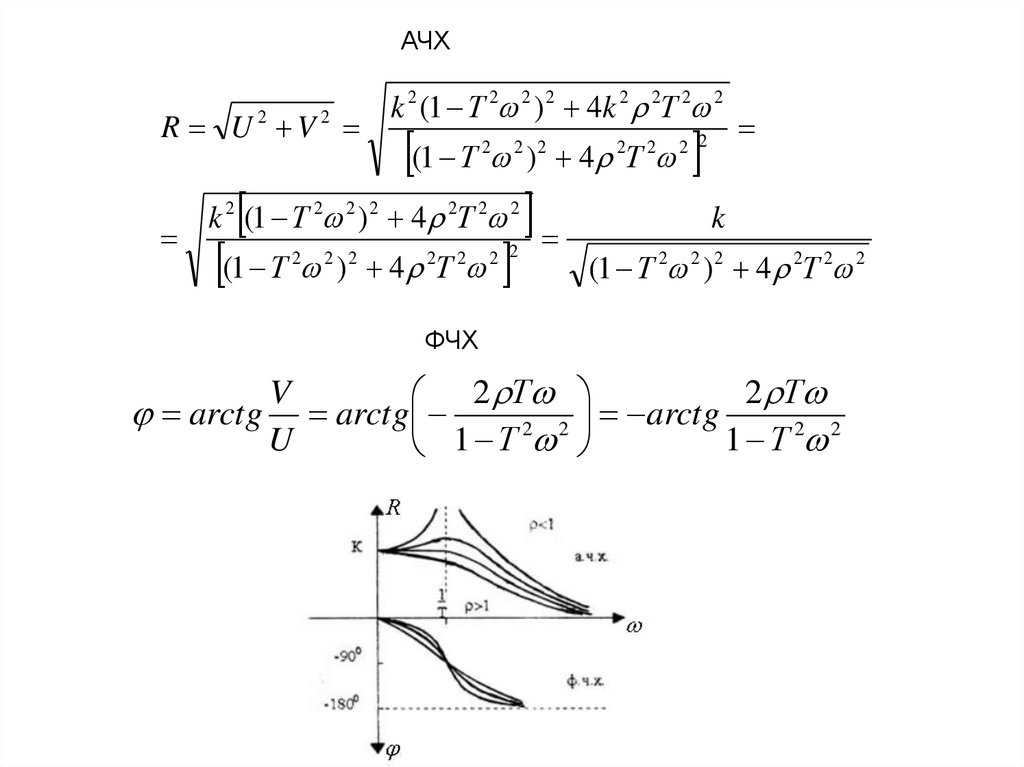
АЧХR U V
2
2
k 2 (1 Т 2 2 ) 2 4k 2 2Т 2 2
(1 Т ) 4 Т
k (1 Т ) 4 Т
k
(1 Т ) 4 Т (1 Т ) 4 Т
2
2
2
2 2
2 2
2
2
2
2
2 2
2
2
2 2
2
2 2
2
2
2 2
2
2
ФЧХ
V
2 Т
2 Т
arctg arctg
arctg
2 2
U
1 Т 2 2
1 Т
2
44.
Амплитудно-фазовые характеристики звена 2-го порядка, т.е. кривые, описываемыевектором W(jɷ) в комплексной плоскости при изменении частоты от 0 до ∞.
jV
R k
ф.ч.х.
U
1
1
ЛАЧХ звена 2-го порядка получается на основании выражения:
20 lg R 20 lg k 20 lg (1 Т 2 2 ) 2 4 2Т 2 2
В упрощённом (асимптотическом) варианте эту характеристику можно построить
состоящей из двух отрезков (аналогично звену 1-го порядка).
45.
Частотные характеристики системРис.1. Разомкнутая система
Передаточная функция этой системы: Комплексный передаточный коэффициент:
W ( р) W1 ( р) W2 ( р) W3 ( р) W4 ( р)
W ( j ) W1 ( j ) W2 ( j ) W3 ( j ) W4 ( j )
или
R ре
j р
R1е j 1 R 2е j 2 R 3е j 3 R 4е j 4 R1R 2R 3R 4е j( 1 2 3 4 )
ЛАЧХ строится по выражению:
46.
Поскольку ЛАЧХ обычно строятся упрощённо, суммарную ЛАЧХ разомкнутойсистемы можно построить непосредственно по передаточной функции.
Например, дана передаточная функция для четырех последовательно
соединённых звеньев 1-го порядка:
В этом случае необходимо определить 20lgКр, что является амплитуда
низкочастотного горизонтального участка ЛАЧХ. Затем необходимо рассчитать
частоты сопряжений
Каждая
последующая
частота
сопряжений
характеристики, увеличивая её наклон на 20 дб/дек.
обеспечивает
излом
47.
Устойчивость линейных системСистема автоматического регулирования или любая другая система считаются
устойчивыми, если, будучи выведенной из состояния равновесия, а затем
предоставленной самой себе, возвращается в прежнее или занимает новое
состояние равновесия.
Система автоматического регулирования считается устойчивой, если переходный
процесс в ней затухающий; неустойчивой – если переходный процесс в ней
расходящийся.
Устойчивость линейных систем зависит только от параметров самих систем и не
зависит от величины возмущающих и других внешних воздействий.
Пусть система описывается дифференциальным уравнением n-го порядка:
d nx
d n 1 x
dmy
d m 1 y
а0 n a1 n 1 an x b0 m b1 m 1 bm y
dt
dt
dt
dt
Решение этого дифференциального уравнения состоит из свободной и вынужденной
составляющих: х(t) = хсв(t) + хвын(t)
48.
Для того чтобы проанализировать систему на устойчивость, достаточнополучить хсв, т.е. решить уравнение без правой части:
d nx
d n 1 x
а0 n a1 n 1 an x 0
dt
dt
Из математики известно, что свободная составляющая может быть найдена
в следующем виде:
Р3 t
Рn t
Р1t
Р2 t
св
1
2
3
n
х се
с е
с е
с е
Область устойчивой
работы
САУ будет устойчива, т.е. переходный
процесс в ней будет сходящимся, если среди
корней
характеристического
уравнения
системы не окажется ни одного с
положительной вещественной частью.
j
Р2
Р1
Р3
49.
Алгебраические критерии устойчивостиФормулировка критерия Гурвица:
Для того чтобы все корни характеристического уравнения системы имели
отрицательную вещественную часть, т.е. система была устойчива, необходимо и
достаточно, чтобы при а0 > 0 главный определитель характеристического
многочлена и его диагональные миноры были больше 0.
Пусть имеется характеристическое уравнение:
а0 р n a1 р n 1 an 0
Главный определитель имеет n-строк и n-столбцов. По главной диагонали
записываются коэффициенты от а1 до аn . Выше коэффициентов, записанных по
главной диагонали, записываются коэффициенты на порядок выше, ниже –
коэффициенты на порядок ниже.
Выше аn записываются 0, ниже коэффициента а0 также записываются 0.
Диагональные миноры получаются последовательным вычеркиванием последнего
столбца и последней строки, начиная с главного определителя.
50.
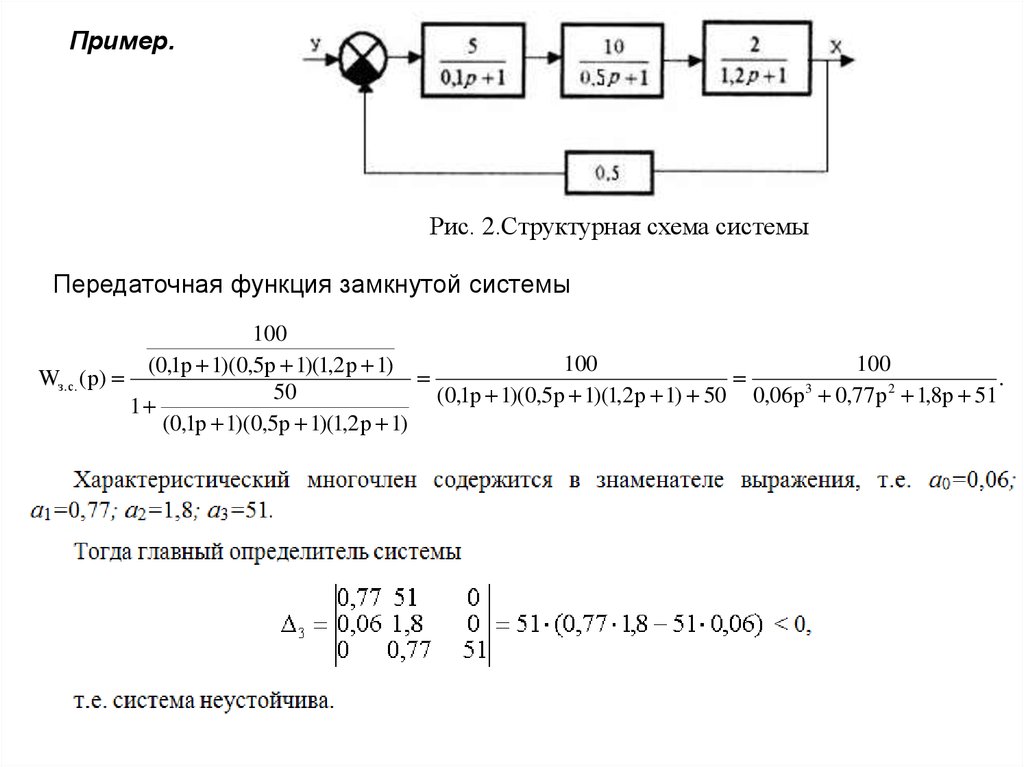
Пример.Рис. 2.Структурная схема системы
Передаточная функция замкнутой системы
100
100
100
(0,1р 1)(0,5р 1)(1,2р 1)
Wз.с. (р)
.
3
2
50
(
0
,
1
р
1
)(
0
,
5
р
1
)(
1
,
2
р
1
)
50
0
,
06
р
0
,
77
р
1
,
8
р
51
1
(0,1р 1)(0,5р 1)(1,2р 1)
51. Геометрические критерии устойчивости
Критерий МихайловаПусть имеется передаточная функция замкнутой системы:
X(p) b 0 р m b1р m 1 b m
W ( p)
У(р) а 0 р n a1p n 1 a n
Подставив в выражение для передаточной функции р=jw, получим выражение для
комплексного передаточного коэффициента:
b 0 ( j ) m b1 ( j ) m 1 b m
W( j )
а 0 ( j ) n a1 ( j ) n 1 a n
Знаменатель комплексного передаточного коэффициента (характеристический
многочлен в комплексной форме записи) есть некое комплексное число, т.е.
некоторый вектор. Это выражение получило название вектора Михайлова:
F ( j ) а0 ( j ) n a1 ( j ) n 1 an
52.
а) для устойчивой системыб) для неустойчивой системы
53.
Критерий НайквистаДля того чтобы замкнутая САР была устойчива, необходимо и достаточно,
чтобы а.ф.х. этой системы в разомкнутом состоянии не охватывала точку в
комплексной плоскости с координатами [-1;j0].
кривая 1 – замкнутая система устойчива;
кривая 2 – замкнутая система неустойчива .
При этом предполагается, что разомкнутая система заведомо устойчива.
54.
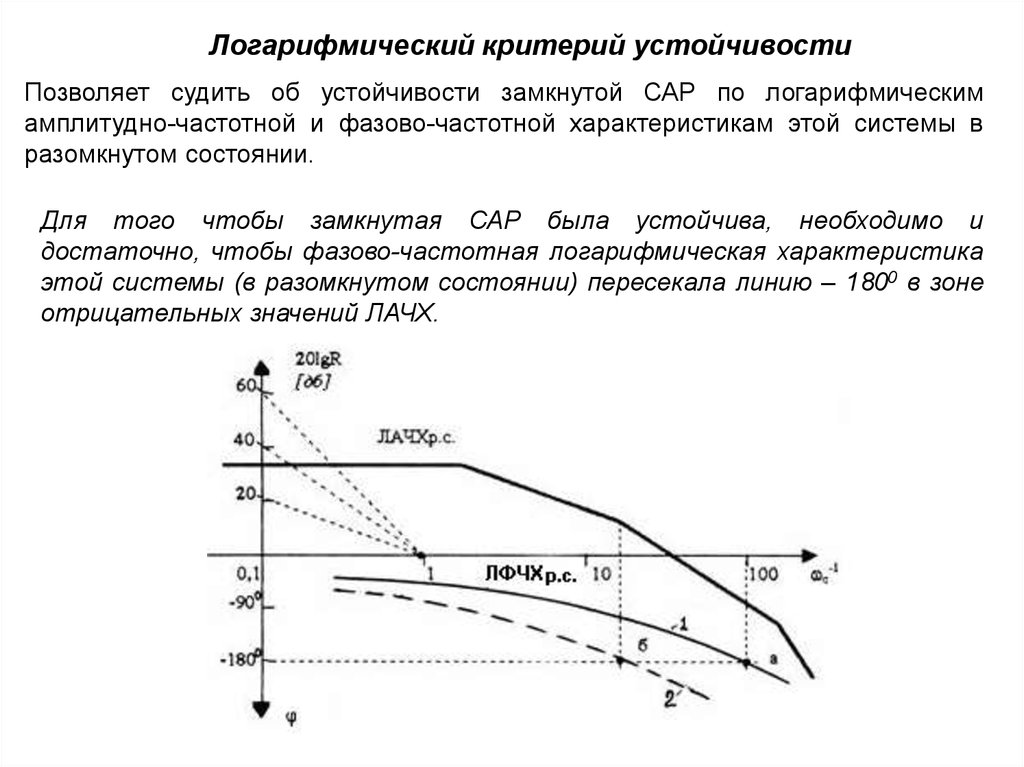
Логарифмический критерий устойчивостиПозволяет судить об устойчивости замкнутой САР по логарифмическим
амплитудно-частотной и фазово-частотной характеристикам этой системы в
разомкнутом состоянии.
Для того чтобы замкнутая САР была устойчива, необходимо и
достаточно, чтобы фазово-частотная логарифмическая характеристика
этой системы (в разомкнутом состоянии) пересекала линию – 1800 в зоне
отрицательных значений ЛАЧХ.
55.
Построение областей устойчивости в пространствепараметров систем (областей D-разбиения)
Если изменяется какой-либо один вещественный параметр, то задача
заключается в отыскании граничных значений этого параметра на некой
числовой оси:
Если изменяются два вещественных или один комплексный параметр –
задача состоит в отыскании некоторой области в прямоугольной системе
координат, ограниченной кривой.
В общем случае в системе может изменяться S параметров, поэтому можно
говорить о нахождении некой области устойчивости системы в S-мерном
пространстве. Гиперповерхность, ограничивающая эту область, будет
границей устойчивости в области параметров.
Области параметров, соответствующие равному количеству корней
характеристического уравнения с отрицательной (положительной)
вещественной частью, получили название областей D-разбиения.
56.
Построение областей D-разбиения в пространствеодного (комплексного) параметра
Пусть имеется некоторый параметр t = ± А ± jВ .
В характеристическом уравнении системы этот
параметр содержится в коэффициентах. При
изменении этого параметра будут изменяться те
коэффициенты, которые его содержат. Будут
изменяться коэффициенты – будут изменяться
корни характеристического уравнения системы,
т.е. как-то перемещаться по комплексной
плоскости корней:
57.
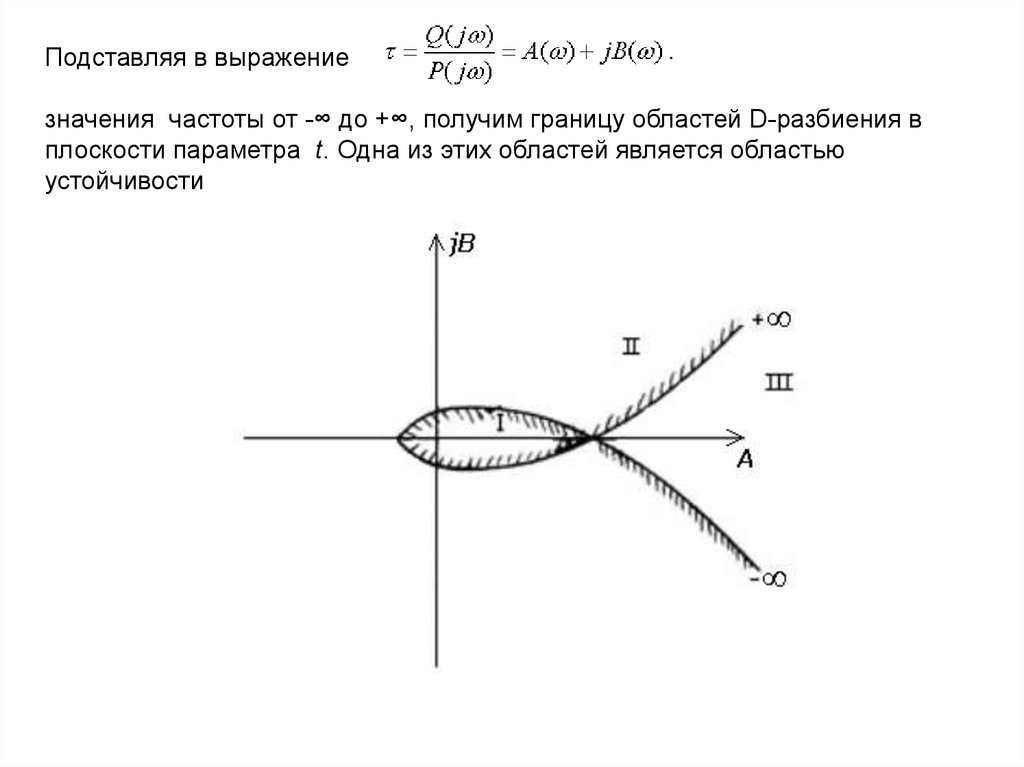
Подставляя в выражениезначения частоты от -∞ до +∞, получим границу областей D-разбиения в
плоскости параметра t. Одна из этих областей является областью
устойчивости
58.
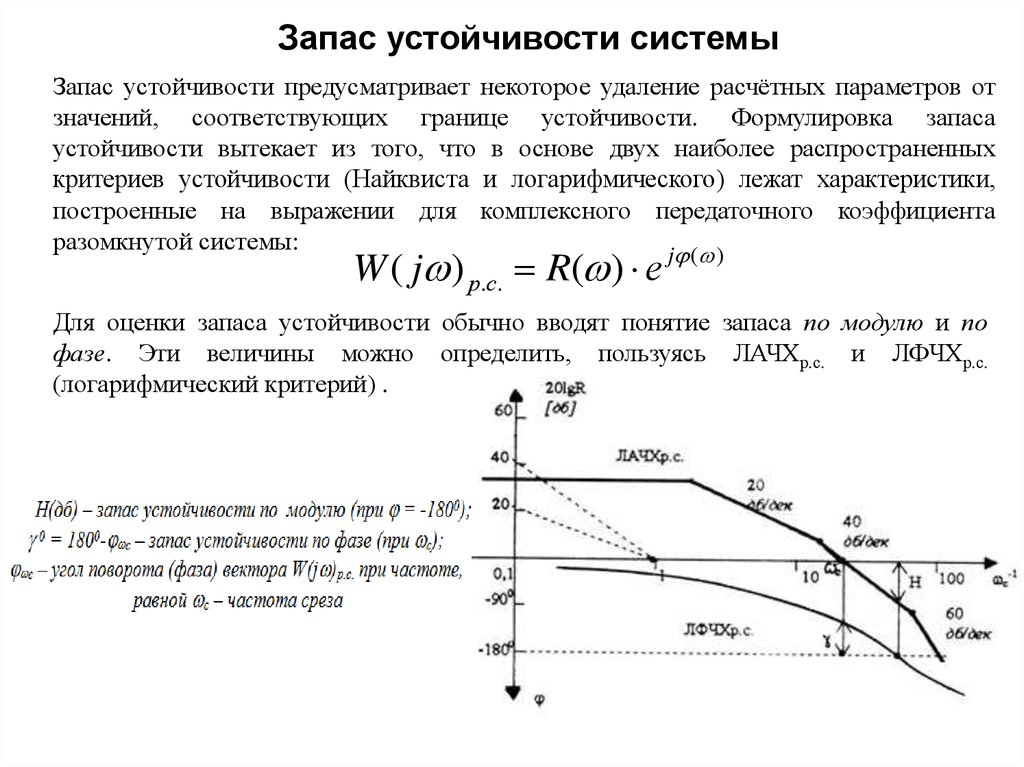
Запас устойчивости системыЗапас устойчивости предусматривает некоторое удаление расчётных параметров от
значений, соответствующих границе устойчивости. Формулировка запаса
устойчивости вытекает из того, что в основе двух наиболее распространенных
критериев устойчивости (Найквиста и логарифмического) лежат характеристики,
построенные на выражении для комплексного передаточного коэффициента
разомкнутой системы:
W ( j ) р.с. R( ) е j ( )
Для оценки запаса устойчивости обычно вводят понятие запаса по модулю и по
фазе. Эти величины можно определить, пользуясь ЛАЧХр.с. и ЛФЧХр.с.
(логарифмический критерий) .
59.
Качество переходного процесса в системах и методыего исследования
Качество процесса оценивается следующими основными показателями:
1. Устойчивость и запас устойчивости
- показатели, характеризующие работоспособность системы.
2. Колебательность
При переходном процессе регулируемая величина может до достижения
нового установившегося значения с определённой точностью совершать
большее или меньшее число колебаний. Колебания в системе – явление
нежелательное, т.к. это приводит к дополнительному износу деталей,
отклонению выходного сигнала от установившегося значения. Поэтому
стремятся так выполнить САР, чтобы колебательность свести к минимуму.
Колебательность процесса соответствует наличию комплексных корней в
характеристическом уравнении системы. Аналитически колебательность
оценивается показателем
0
0
где – мнимая часть комплексного корня (р = +j );
– вещественная часть комплексного корня.
- колебания незатухающие
0
- колебаний нет, процесс апериодический
60.
3. Быстродействие системыБыстродействие характеризует скорость реагирования САР на внешние
воздействия. Для оценки быстродействия используется величина времени
переходного процесса, т.е. времени, за которое выходной сигнал с
определенной заданной точностью достигает своего установившегося
значения.
61.
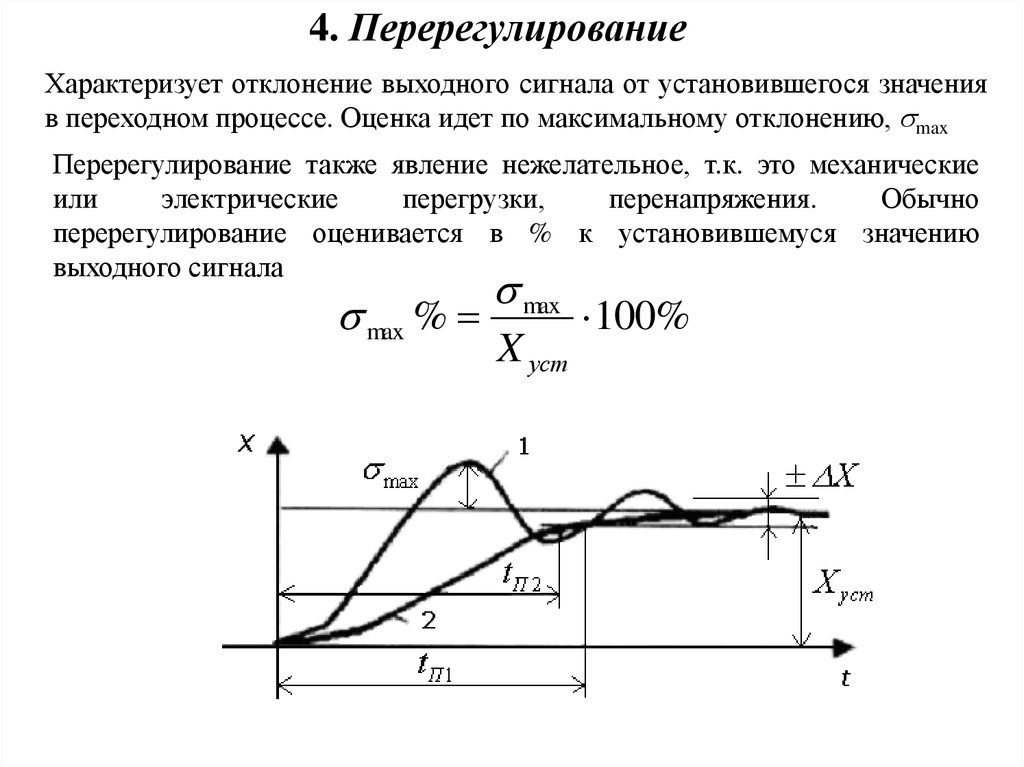
4. ПеререгулированиеХарактеризует отклонение выходного сигнала от установившегося значения
в переходном процессе. Оценка идет по максимальному отклонению, smax
Перерегулирование также явление нежелательное, т.к. это механические
или
электрические
перегрузки,
перенапряжения.
Обычно
перерегулирование оценивается в % к установившемуся значению
выходного сигнала
s max %
s max
X уст
100%
62.
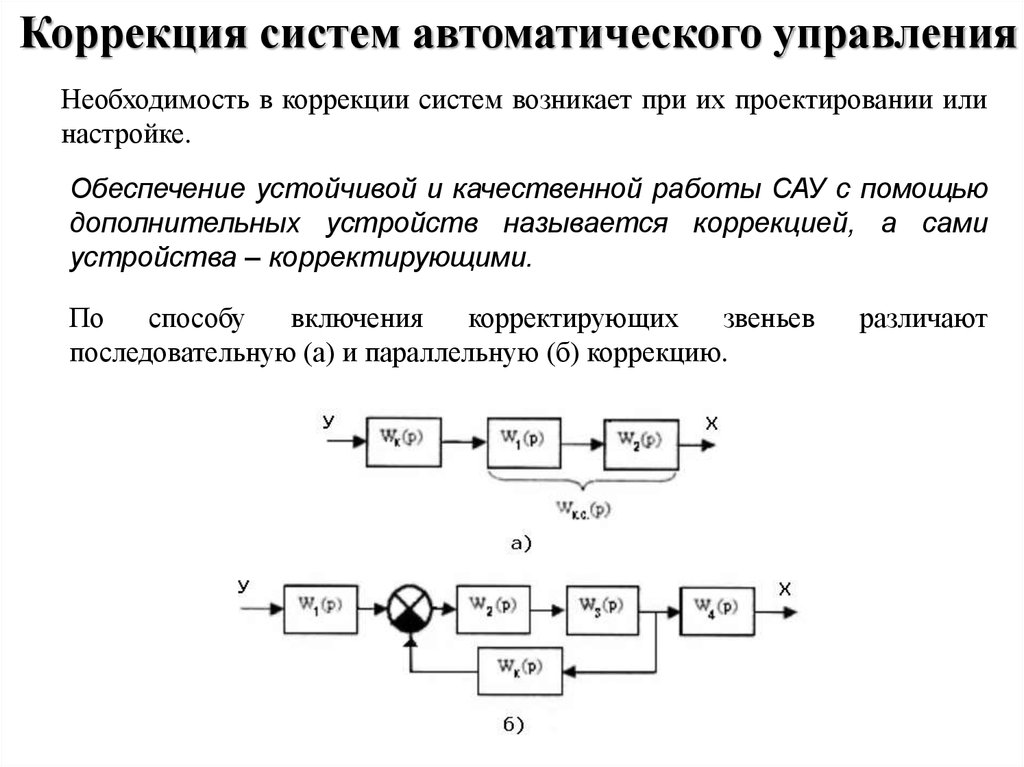
Коррекция систем автоматического управленияНеобходимость в коррекции систем возникает при их проектировании или
настройке.
Обеспечение устойчивой и качественной работы САУ с помощью
дополнительных устройств называется коррекцией, а сами
устройства – корректирующими.
По
способу
включения
корректирующих
звеньев
последовательную (а) и параллельную (б) коррекцию.
различают
63.
.Задача синтеза корректирующего звена по заданным показателям
качества решается в следующей последовательности:
1) по заданным показателям качества (smax, tn, Н, g ) ищут либо
передаточную функцию, либо частотную характеристику, либо
уравнение системы, удовлетворяющей исходным требованиям
(желаемой системы);
2) по передаточной функции (характеристике, уравнению) желаемой
системы, сравнивая её с передаточной функцией (характеристикой,
уравнением) исходной системы, находят передаточную функцию
(характеристику, уравнение) дополнительного, корректирующего
звена;
3) по передаточной функции (характеристике, уравнению)
корректирующего звена определяют его вид и рассчитывают его
параметры.
64.
Синтез последовательного корректирующего звенаметодом ЛАЧХ
Передаточная функция скорректированной
(желаемой)
системы
в
разомкнутом
состоянии будет иметь вид:
Wж ( р) Wк ( р) Wн.с. ( р)
Где передаточная функция исходной (нескорректированной) системы:
Wн.с. ( р) W1 ( p) W2 ( p)
Перейдя к комплексной форме записи, получим
или
Wж ( j ) Wк ( j ) Wн.с. ( j )
Rж е j ж Rк е j к Rн.с.е j н .с . Rк Rн.с.е j ( к н .с . )
Перейдя к ЛАЧХ, запишем
65.
Синтез последовательного корректирующего звена можно осуществить вследующей последовательности:
66.
67.
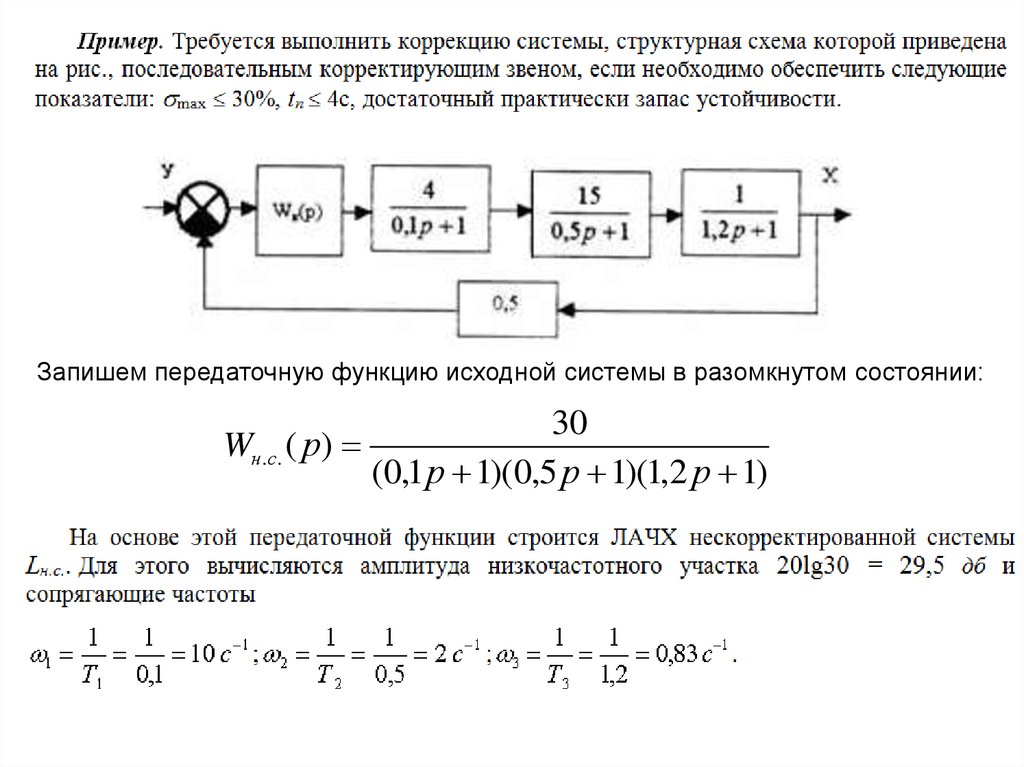
Запишем передаточную функцию исходной системы в разомкнутом состоянии:30
Wн.с. ( р)
(0,1 р 1)(0,5 р 1)(1,2 р 1)
68.
По характеристике Lк запишемпередаточную функцию
Wк ( р )
1 (Т 3 р 1)(Т 2 р 1)
1
1
р
1
р
1







































 physics
physics








