Similar presentations:
Автоматизация производственных процессов. Теория автоматического управления
1. Кудряшев Сергей Борисович
Канд. техн. наук доценткаф. «Автоматизация
производственных процессов»
2. Введение
• Теория управления - наука, изучающая законы управления,принципы управления, принципы построения систем
управления, а также методы анализа и синтеза систем
управления.
• Автоматика – это отрасль науки и техники, охватывающая
теорию и практику автоматического управления.
• Система – это целенаправленное множество
взаимосвязанных элементов любой природы.
• Состояние системы - минимальный набор переменных
величин, способных однозначно определить положение
системы в данный момент времени.
3.
• Управление – это такая организация того или иного процесса,которая обеспечивает достижение поставленных целей.
Необходимыми условиями управления являются наличие объекта
управления и цели управления. Задача управления заключается в
формировании требуемого для достижения цели закона управления.
Кроме того, управление можно рассматривать как целенаправленное
воздействие на объект управления, в результате которого последний
переходит в требуемое состояние.
• Объект управления – это часть окружающего нас мира, на которую
можно воздействовать с определенной целью.
В технике под объектом управления подразумевается техническое
устройство или технологический процесс, некоторые физические
величины которого подлежат стабилизации или целенаправленным
изменениям.
В зависимости от участия человека в процессе управления последнее
подразделяется на ручное, автоматическое и автоматизированное.
4. Водяные часы Ктесибиоса
5. Центробежный регулятор Уатта (1769 г.)
6.
7. Поплавковый регулятор уровня воды
8. Перспективы развития роботов и систем управления
9. Принципы управления
• Принцип разомкнутогоуправления;
• Принцип замкнутого цикла
(обратной связи);
• Комбинированный;
• Принцип адаптации.
10. Принцип разомкнутого управления
ОУ – объект управления;ЗУ – задающее устройство;
R – регулятор.
Координаты (переменные) системы:
g(t) – задающее воздействие;
y(t) – управляемая (регулируемая) величина;
f(t) – возмущающее воздействие;
u(t) – управляющее воздействие.
11. Принцип замкнутого цикла (обратной связи)
ОУ – объект управления;ЗУ – задающее устройство;
ИПУ - измерительнопреобразовательное устройство;
СУ - сравнивающее устройство;
R – регулятор.
Координаты (переменные) системы:
g(t) – задающее воздействие;
y(t) – управляемая (регулируемая)
величина;
f(t) – возмущающее воздействие;
x(t) - рассогласование (ошибка);
u(t) – управляющее воздействие.
12.
13. Комбинированный принцип
• КЦЗ – компенсирующая цепь по задающему воздействию,позволяет скомпенсировать ошибку работы системы от
задающего воздействия.
• КЦВ – компенсирующая цепь по возмущающему
воздействию, позволяет скомпенсировать негативное влияние
возмущающего воздействия на работу системы.
14. Принцип адаптации
Адаптивные системы разделяются на:• экстремальные,
• самонастраивающиеся;
• самоорганизующиеся.
15. Функциональная схема экстремальной системы
УАПЭ - устройство автоматического поиска экстремума, котороеанализирует параметр объекта управления , определяющий его
режим работы, и воздействует на задающее устройство с целью
изменения задающего воздействия g(t) для обеспечения
наивыгоднейшего режима работы объекта управления.
16. Классификация систем управления
1. По принципу действия:а) разомкнутые системы;
б) замкнутые системы;
в) комбинированные системы;
г) адаптивные системы
2. По виду задающего воздействия g(t):
а) системы стабилизации, если g(t)=const;
б) системы программного управления, если g(t) – предварительно
заданная функция времени;
в) следящие системы, если g(t) – случайная величина.
3. По математическому описанию:
а) линейные системы;
б) нелинейные системы.
17.
4. По характеру передачи сигналов:а) непрерывные системы, такие, у которых все координаты или
переменные являются непрерывными функциями времени;
б) дискретные системы - это системы, в составе которых имеется хотя бы
один квантователь сигналов по времени. Включают: релейные,
импульсные и цифровые.
5. По реакции системы на входное воздействие:
а) детерминированные системы - это системы, отвечающие на один и тот
же входной сигнал всегда одним и тем же вполне определенным выходным
сигналом;
б) стохастические системы - это системы, у которых реакция на входное
воздействие представляет собой случайный выходной сигнал в
соответствии с некоторым распределением вероятностей;
в) стационарные системы - это системы, реакция которых не зависит от
момента времени подачи входного воздействия;
г) нестационарные системы - системы, реакция которых зависит от
момента приложения входного воздействия.
18.
6. По виду используемой энергии:а) электрические системы, обладают удобством и легкостью обработки и
передачи информации;
б) пневматические системы, используют энергию сжатого газа и
обеспечивают высокое быстродействие;
в) гидравлические системы, используют энергию жидкости и
обеспечивают высокую мощность;
г) электропневматические системы;
д) электрогидравлические системы.
7. По числу управляемых величин.
а) одномерные системы, имеют одну управляемую величину;
б) многомерные или многосвязные системы - это системы, имеющие
много входов и выходов.
8. По точности в статическом режиме.
Статически и астатические
19. Функциональная схема типовой автоматической системы
20. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕМЕНТОВ И СИСТЕМ УПРАВЛЕНИЯ
Поведение координат системы во времени называетсядинамикой системы.
Математическое описание элемента устанавливает связь
во времени между его текущими значениями выходных y(t) и
входных x(t) величин.
Динамика элемента, то есть поведение его координат во
времени, описывается дифференциальными уравнениями.
При времени, стремящемся к бесконечности t ,
текущие координаты y(t) и x(t) принимают постоянные
установившиеся значения и наступает статика элемента, которая
описывается алгебраическими уравнениями.
В статике входные и выходные величины элемента
постоянные: x( )=x0=const; y( )=y0=const. Эти постоянные
величины
называются
установившимися.
А
процесс,
соответствующий
статике,
называется
установившимся
процессом.
21.
ЛинеаризацияБольшинство реальных элементов имеют нелинейные
характеристики и описываются нелинейными ДУ. Многие нелинейные
элементы можно линеаризовать, то есть заменить нелинейные уравнения
элемента приближенными линейными.
В основе линеаризации
лежит предположение, что в
исследуемом динамическом
процессе переменные
системы изменяются таким
образом, что их отклонения
от установившихся значений
остаются все время
достаточно малыми
величинами.
22.
где:Текущее значение координат y и x
y(t) = y0 + y(t);
x(t) = x0 + x(t);
y0, x0 – установившиеся значение,
y, x – отклонения от установившихся значений.
(1)
В рабочей точке ( x0, y0),заменим участок кривой касательной
y = yн + kx ,
(2)
где: yн - постоянная величина,
k – коэффициент, определяемый наклоном касательной к кривой в
рабочей точке (x0, y0).
Для исключения из уравнения величины yн перенесем начало
координат в рабочую точку. Тогда получим линейное уравнение, связывающее
между собой отклонения переменных величин от своих установившихся
значений, вида
y(t) = k x(t)
Ограничение метода. Данным методом могут быть линеаризованы
уравнения элементов, статические характеристики которых в окрестности
точки установившегося режима гладкие, то есть их производные непрерывны
и однозначны.
23. Формы записи линеаризованных уравнений
an yn
a n 1 y
n 1
a1 y
1
a0 y
bm u m b m 1 u m 1 b1u 1 b0 u
(3)
c r v r c r 1 v r 1 c1v 1 c0 v
Это вход-выходное дифференциальное уравнение, в котором u,v является
входами, а y(t) – выходом, a, b, c – коэффициенты, могут быть нулевыми.
При исследовании линейных систем широко применяются так называемые
операторные методы. Из операторных методов наиболее известны:
1) Преобразование Лапласа:
X p L x t x t e p t dt
0
2) Преобразование Фурье:
X j x t e j t dt
24.
Применяем преобразование Лапласа с учетом нулевых начальных условий.(a n p n a n 1 p n 1 a1 p a0 ) Y ( p )
(bm p b m 1 p
m
m 1
b1 p b0 ) U ( p )
(4.1)
(cr p r c r 1 p r 1 c1 p c0 ) V ( p )
n
m
r
( ai p i ) Y ( p) ( bi p i ) U ( p) ( ci p i ) V ( p)
i 0
i 0
A(p)
i 0
B(p)
(4.2)
C(p)
A( p)Y ( p) B( p)U ( p) C ( p)V ( p)
при нулевом возмущающем воздействии:
A( p)Y ( p) B( p)U ( p)
Y ( p)
B( p)
W ( p)
U ( p)
A( p )
- передаточная
функция
Передаточной функцией объекта или системы называется отношение
изображения по Лапласу выходной переменной к входной при нулевых
начальных условиях.
25.
Свойства передаточной функции динамического звена.1) Передаточная функция линейного звена является дробно-рациональной, т.е.
отношением полиномов к комплексной переменной Р (или S).
2) Для физической реализуемости (реальные объекты и системы) порядок полинома в
числителе не должен превышать порядок полинома в знаменателе.
3) Передаточная функция объекта по каналам для одной и той же выходной переменной
имеет в знаменателе один и тот же полином, который называется характеристическим,
т.к. его структура и параметры определены фундаментальными свойствами объекта.
Свойства полиномов числителя и знаменателя передаточной функции:
A( p) a n p n a n 1 p n 1 ..... a1 p a0 a n ( p p1 )( p p 2 ).....( p p n )
p1 0
p3, 4 j
p2 b
A( p) a4 p( p b)( p 2 2 p 2 2 )
A( p) a n p
v
ks
i 1
j 1
( p pi ) ( p 2 2 i p j j )
- количество нулевых корней в полиноме
2
2
- количество вещественных корней
ks - количество пар комплексно - сопряженных корней
26.
Произвольная форма записиW ( p)
bm p m b( m 1) p m 1 ..... b1 p b0
an p n a( n 1) p n 1 ..... a1 p a0
Каноническая форма записи
m
m 1
b0 bm p b( m 1) p ..... b1 p 1
WK ( p)
p
*
*
*
a0
an p n a( n 1) p n 1 ..... a1 p 1
*
a
ai i
a0
*
b0
k
a0
b
bi i
b0
- коэффициент передачи
(усиления при к>0)
- количество нулевых корней в знаменателе
- количество нулевых корней в числителе
*
*
*
Последовательно-структурированная форма записи
v1
WК
ПС
( p ) kp
ks1
(Ti p 1) (T j p 2 2 T j p 1)
i 1
j 1
v2
ks 2
(T p 1) (T
i
i 1
2
2
j
p 2 2 T j p 1)
j 1
Ti , j- постоянные времени элементарных звеньев
- Коэффициент демпфирования
1
Ti
( pi )
Tj
1
j2 j2
j
j2 j2
характеризует порядок астатизма сложного динамического звена; если 0, то звено является
v -статическим,
если больше 0, то звено обладает астатизмом.
27.
Элементарная передаточная функция – передаточная функция, представленная дробью,содержащей не более одного элементарного полинома в числителе и знаменателе.
Приведенная форма записи:
p m b( m 1) p m 1 ..... b1 p b0
*
*
*
bm
W ПР ( p)
p
*
*
*
an
p n a ( n 1) p n 1 ..... a1 p a 0
bm
k ПР
an
bi
bi
bm
*
ai
ai
an
*
Такая форма записи используется для перехода в матрично-векторную форму.
Условие реализуемости передаточной функции: m n
28. Типовые входные воздействия
Характеристика звена - это его реакция на определенное входное воздействие.В качестве входных воздействий, на которые ищется реакция звена, приняты
воздействия, описываемые элементарными математическими функциями, то
есть такими, на которые можно разложить любые произвольные функции.
В теории автоматического управления в качестве типовых входных
воздействий используются:
1) дельта-функция (t);
2) единичная ступенчатая функция 1(t);
3) гармоническая функция X0sin( t).
29.
-функцией называется функция, равная нулю всюду, кроме начала координат,но притом так, что интеграл от нее по любому интервалу, содержащему нуль,
равен единице, т.е.
0 при t 0, Кроме того,
(t) =
(t)dt =1
при
t
=
0.
при любом >0.
Весовая функция w(t) представляет собой реакцию на выходе звена при
подаче на его вход -функции.
30.
Единичная ступенчатая функция удовлетворяет следующему условию0 при t 0,
1(t) =
1 при t 0.
Переходная функция является реакцией на выходе звена при единичном скачке
на его входе.
31.
Частотнымихарактеристиками
называются
формулы
и
графики,
характеризующие реакцию звена на гармоническое входное воздействие в
установившемся режиме, т.е. вынужденные синусоидальные колебания звена.
Если на вход линейного звена подать гармоническое воздействие
x(t)=X0sin( t),
где
X0 - амплитуда,
- угловая частота, имеющая размерность [рад/с] или [c-1 ],
то, на выходе звена в установившемся режиме будет также гармоническая
функция той же частоты, но, в общем случае, другой амплитуды Y0 и сдвинутая
по фазе относительно входной величины на угол
y(t)=Y0sin( t+ ).
Связь между выходной гармоникой и входной устанавливается с помощью
частотной передаточной функции звена W(j ).
32.
Частотная передаточная функция W(j ), как видно, представляет собойкомплексное число, которое можно записать как в полярной, так и декартовой
системах координат:
j ( )
= U( ) + jV( ),
W(j ) = A( ) e
где А( ) - модуль или амплитуда частотной передаточной функции,
представляющий собой отношение амплитуды выходной величины к
амплитуде входной, т.е. коэффициент передачи звена k
- аргумент или фаза частотной передаточной функции, показывает
фазовый сдвиг выходной гармоники по отношению к входной на частоте
= arg W(j );
U( ) - вещественная составляющая частотной передаточной функции
U( ) = Re W(j );
V( ) - мнимая составляющая частотной передаточной функции
V( ) = Im W(j ).
2
2
A( ) = U ( ) V ( )
( ) = arctg
V( )
U( )
33. Частотные характеристики
Амплитудно-фазовая частотная характеристика (АФЧХ). Строится накомплексной плоскости и представляет собой геометрическое место конца
вектора, соответствующего частотной передаточной функции W(j ) при
изменении от 0 до .
34.
Амплитудная частотная характеристика (АЧХ). Показывает, какпропускает звено сигнал различной частоты. АЧХ представляет собой
коэффициент изменения амплитуды гармонических колебаний при
прохождении через звено.
где р - резонансная частота, т.е. частота, на которой амплитудная частотная
характеристика достигает максимума,
с - частота среза, частота, на которой амплитудная частотная характеристика,
уменьшаясь, принимает значение, равное единице, и при дальнейшем повышении частоты
остается меньше единицы;
п - частота пропускания, частота, на которой амплитудная частотная характеристика,
уменьшаясь, принимает значение, равное 0,707, и при дальнейшем повышении частоты не
увеличивается;
п=2 п - полоса пропускания, диапазон частот гармонических колебаний,
пропускаемых звеном без заметного ослабления.
35.
Фазовая частотная характеристика (ФЧХ). Показывает фазовые сдвиги,вносимые звеном на различных частотах.
Вещественная частотная характеристика (ВЧХ).
Мнимая частотная характеристика (МЧХ)
36.
Логарифмические частотные характеристики (ЛЧХ).L( ) = 20 lg A( ) = 20 lg W(j )
= argW(j )
37.
Типовыединамические звенья
38.
Пропорциональное (безинерционное) звеноОписывается алгебраическим уравнением y(t) = k·x(t).
Передаточная функция:
W(p) = k.
Амплитудно-фазовая частотная характеристика:
W(j ) = k, A( ) = k, ( ) = 0.
, град
L, дБ
ЛАЧХ
ЛФЧХ
20 lg k
, дк
, дк
39.
Интегрирующее звеноW ( p)
k
T p
U ( ) 0; V ( )
L( ) 20 lg
k
jk
Tj T
k
A( )
; ( ) arctg ( )
T
2
W ( j )
k
;
T
k
T
При увеличении частоты на декаду оцениваем наклон ЛАЧХ:
L(10 ) 20 lg
Наклон ЛАЧХ: 20
ЛАЧХ
k
1
k
k
20 lg 20 lg
20 20 lg
10 T
10
T
T
дБ
дк
ЛФЧХ
L, дБ
φ
20 lg k/T
0
Переходной процесс
0
ω, дк
2
H
ω, дк
0
t, с
40.
Дифференцирующее звеноW ( p) kTp W ( j ) jkT
U ( ) 0; V ( ) kT ; A( ) kT ; ( ) arctg ( )
L( ) 20 lg( kTp)
2
При увеличении частоты на декаду оцениваем наклон ЛАЧХ:
L(10 ) 20 lg 10kT 20 20 lg kT
Наклон ЛАЧХ: 20
дБ
дк
ЛАЧХ
ЛФЧХ
L, дБ
Переходной процесс
φ
H
20 lg kT
2
0
ω, дк
0
ω, дк
0
t, с
41.
Апериодическое звеноk
k
k (1 j T )
k jk T
W ( j )
Tp 1
Tj 1 (1 j T )(1 j T ) 1 2T 2
k
k T
U ( )
; V ( )
; ( ) arctg ( T )
2 2
2 2
1 T
1 T
1
при С
( ) 450 ; С сопрягающа я частота
T
при C W ( j ) k
W ( p)
при C W ( j )
k
j T
ЛАЧХ
ЛФЧХ
L, дБ
H
φ
ωС
20 lg k
20
Реально
0
Переходной процесс
ωС
дБ
дк
0
ω, дк
H(уст)
ω, дк
4
2
0
t, с
42.
Пропорционально-дифференцирующее звеноW ( p) k (Tp 1) W ( j ) kTj k
U ( ) k ; V ( ) kT ; ( ) arctg ( T )
ЛАЧХ
ЛФЧХ
L, дБ
20 lg k
0
20
ωС
2
дБ
дк
Переходной процесс
H
φ
4
ω, дк
0
ωС
ω, дк
0
t, с
43.
Колебательное звеноk
W ( p) 2 2
T p 2 Tp 1
два комплексно сопряженных корня
ЛАЧХ
2
1
L, дБ
20 lg k
0
Переходной процесс
H
φ
ωС
дБ
40
дк
ωС
ЛФЧХ
1 2
ω, дк
0
1
H(уст)
2
ω, дк
2
0
t, с
44.
Пропорционально-дифференцирующее 2-го порядкаW ( p) k (T p 2 Tp 1)
2
ЛАЧХ
ЛФЧХ
L, дБ
дБ
40
дк
20 lg k
0
ωС
2
ω, дк
Переходной процесс
H
φ
2
0
ωС
ω, дк
0
t, с
45.
Правила преобразованияструктурных схема
46.
Виды соединений звеньевВ системах управления
соединений звеньев:
выделяют
три
- последовательное
- параллельное
- с обратной связью (положительной или
отрицательной).
вида
47.
Последовательноех
у1
W1(p)
у2
W2(p)
WЭ(p)
у
х
W3(p)
WЭ(p)
Обозначим промежуточные выходы
W1 ( p)
WЭ ( p)
у1 ( р)
у ( р)
у ( р)
, W2 ( p) 2
, W3 ( p)
,
х( р )
у1 ( р)
у2 ( р)
у ( р)
W1 ( p) W2 ( p) W3 ( p)
х( р)
где n - число последовательно включенных звеньев
у
n
W ( p )
i
i 1
48.
Параллельноеу1
WЭ(p)
у2
у
W1(p)
х
х
у
WЭ(p)
W2(p)
у3
у( р) у1 ( р) у2 ( р) у3 ( р)
W3(p)
у3 ( р )
у1 ( р )
у2 ( р)
W1 ( p )
, W2 ( p )
, W3 ( p )
y( р)
у ( р)
у ( р)
у ( р ) у1 ( р ) у 2 ( р ) у3 ( р )
WЭ ( p )
х( р)
х( р)
n
W1 ( p ) W2 ( p ) W3 ( p )
W ( p)
i
i 1
где n – число параллельно включенных звеньев
49.
Обратная связьх
у
е
х
W1(p)
у1
у
WЭ(p)
у3
W2(p)
WЭ(p)
где знак “+” относится к положительной, а знак “-” - к отрицательной обратной
связи.
у ( р)
у ( р)
W1 ( p )
, W2 ( p ) 1
, е( p ) х ( р ) у ( р )
е( р )
у ( р)
W ( р ) e( p )
у ( р)
WЭ ( p )
1
х( р)
e( р ) y1 ( p )
W1 ( p )
W1 ( p )
WЭ ( p )
у1 ( р )
1 W1 ( p ) W2 ( p )
1
e( р )
где знак “+” соответствует ООС, знак “ ” - ПОС.
50.
ПримерW1
W34
W4
W2
W34 W3 W4
W3
W5
W234 W2 (W3 W4 )
W234
W1
W2
W34
W5
WЭ
W1
W2345
W234
W5
W2 (W3 W4 )
W2345
1 W2 W5 (W3 W4 )
W2 (W3 W4 )
WÝ W1
1 W2 W5 (W3 W4 )
51.
Основные правила эквивалентныхпреобразований структурных схем
- перенос сумматора через звено
- перенос точки съёма через звено
- перенос сумматора через сумматор
- перенос точки съёма через точку съёма
52.
Сумматор через звено1.
х1
уА
х1
уВ
W
W
х2
А
yB x1 W x2 A
y A ( x1 x2 ) W x1 W x2 W
y A yB
2.
х2
х1
уА
при
A W
х1
уВ
W
W
х2
А
х2
y A x1 W x2
y ( x1 x2 A) W x1 W x2 A W
1
y A y B ïðè A
W
53.
Точка съема через звенох
W
1.
у
х
W
у
у
А
х
х
y x W
х
2.
1
x y
W
у
W
х
W
х
А
у
y x W
1
A
W
у
x y
1
W
A W
у
54.
Сумматор через сумматор(точка съема через точку съема)
Если два сумматора стоят рядом, то можно без
преобразований из менять местами
Аналогично для точек съема стоящих рядом
55.
ПримерW3
W1
W2
W4
W3
W1
W2
W2
W4
W124
W23
W24
WЭ
W124
W23 W2 W3
W24 W2 W4
W24
W1
W23
Переносим точку
съема через звено W2
назад
и добавляем звено,
через которое
осуществляем
перенос
W23
W1
W124
1 W2 W4 W1
WЭ
W1 (W2 W3 )
1 W2 W4 W1
56.
Построение логарифмическихчастотных характеристик
(ЛЧХ) сложных
динамических звеньев
57.
Построение логарифмических частотных характеристик (ЛЧХ) сложныхдинамических звеньев.
Исходными данными для построения этих характеристик является передаточная функция
объекта или системы, преобразуемая к канонической последовательно-структурированной форме
записи.
m
ПС
K
i
i 1
W
( p ) kp
W ( p)
Построение ЛАЧХ сложного динамического звена.
При этом процедура графического сложения необязательна и неэффективна с
временной точки зрения, т.к. возможно последовательное построение графика асимптотической
характеристики путем поворота асимптот в сопрягающих частотах при движении по оси частот
слева направо.
Построение ЛФЧХ сложного динамического звена.
Строится ЛФЧХ элементарных динамических звеньев, входящих в сложное по
отдельности. После этого они суммируются и формируют ЛФЧХ сложного звена.
58.
При построении ЛАЧХ важно:1) Правильно строить низкочастотную асимптоту;
2) При построении двигаться строго слева направо.
Правило построения низкочастотной асимптоты:
20 * lg( kp ) 20 * lg( k ) ( )20 * lg( p)
Таким образом на оси частот откладывается точка соответствующая нулю, на оси
ординат откладывается 20*lg(k) и через эту точку проводится линия с наклоном 20( ).
Правило построения среднечастотной асимптоты:
Определяется сопрягающие частоты всех элементарных звеньев входящих в сложное;
они располагаются на оси частот в порядке возрастания, через эти частоты проводятся ординаты
пунктиром. Построенная низкочастотная асимптота проводится до точки пересечения с первой
ординатой – это будет первая точка поворота ЛАЧХ. Далее определяется звено, которое
соответствует этой частоте и в соответствии с его характеристиками изменяется наклон ЛАЧХ
сложного звена; она продолжается до точки пересечения со следующей ординатой.
59.
Правило построения высокочастотной асимптоты:Последняя построенная асимптота продолжается до бесконечности.
Пример.
б)
40(5 p 1)
W ( p)
;
2
(4 p 3 p 1)(0.2 p 1)
1) k=40;
0; 0
20 lg( 40) 32;
20( ) 0 дб / дк
( p) 5 p 1;
1 1
C 1 0 .2
T 5
lg( 0.2) 0.7
2)а) W
1
в)
1
W2 ( p )
4 p2 3p 1
T 4 2
1
C 2 0 .5
2
lg( 0.5) 0.3
(КЗ)
2 T 3; 4 3 0.75
1
W3 ( p)
(АЗ)
0.2 p 1
1
C 3
5
0 .2
lg( 5) 0.7
60.
61.
Устойчивость систем.Критерии устойчивости.
62.
Исследование замкнутых одноконтурныхсистем автоматического управления.
WЗС
ZY
WPWOY
1 WPWOY
WPC ( p) WPWOY
L( p )
S ( p)
S ( p ) L( p )
H ( p)
S ( p)
WЗС
ZE
1
1 W PWOY
H ( p ) 1 WPWOY
- характеристическая функция.
где S(p) - характеристический полином
разомкнутой системы.
WЗС
ZY
L( p ) / S ( p )
L( p )
L( p )
S ( p ) L( p )
1
S ( p)
N(p)
В характеристической функции в числителе стоит характеристический
полином замкнутой системы, а в знаменателе характеристический
полином разомкнутой системы.
63.
Понятие устойчивости.Методы оценки устойчивости объектов и систем.
Корневой критерий (Ляпунова)
Для корневой устойчивости линейной
системы необходимо и достаточно, чтобы
все корни характеристического полинома
ее передаточной функции имели
отрицательные вещественные части.
1 – устойчивые корни
2 – нулевой корень
3 – нейтральные корни
4 – неустойчивые корни
64.
Качественная оценка характеристического полинома.Необходимое условие устойчивости всех корней характеристического полинома:
1) Все корни характеристического полинома должны быть одного знака;
2) Характеристический полином должен быть полным, т.е. содержать все
нулевые коэффициенты, т.е. для каждого а i 0 i 0, n
Эти же условия для полинома второго порядка являются и
достаточными, а для полиномов более высокого порядка они только
необходимые.
Все методы оценки устойчивости делятся на 2 основных класса:
а) Алгебраические (с помощью алгебраических вычислений)
б) Частотные (используя частотные характеристики)
Алгебраические критерии: Раусса
Гурвица
65.
Критерий ГурвицаВ 1895 году новый критерий изобрел немецкий математик Гурвиц.
N ( p ) a0 p n a1 p n 1 ..... an 1 p an
Для оценки устойчивости также используется характеристический полином.
На его основе составлен главный определитель Гурвица
a1 a3 0 0
n
a 0 a 2 ... ...
0 a1 ... 0
0 a0 ... an
Для проверки правильности
составления определителя,
анализируется главная
диагональ, где должны
стоять все коэффициенты
характеристического
полинома от а1 до аn
66.
Критерий устойчивости Михайлова:Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова
начинался на положительной вещественной оси из точки аn и последовательно против
часовой стрелки проходил такое количество квадрантов, какова степень
характеристического полинома.
Пример: устойчивые
67.
Пример: неустойчивыеПример: на границе устойчивости
68.
Модифицированный критерий Михайлова.Обычно применяется при
математических пакетов.
построении
M ( j )
и
анализе
годографа
Михайлова
в
N ( j )
N ( j ) 1
В данном критерии фазовый сдвиг вносимый корнями сохраняется и проходит такое
же количество квадрантов как в обычном критерии, а изменяется только модуль,
который нормируется в соответствии с коэффициентом стоящим в знаменателе.
69.
Критерий Найквиста: Для оценки устойчивости используют АФЧХразомкнутой системы.
L( p )
WPC ( p )
S ( p)
S ( p)
L( p) S ( p )
H ( p) 1 WPC ( p )
0
S ( p)
- характеристический полином разомкнутой системы
L ( p ) S ( p ) - характеристический полином замкнутой системы
n PC n ЗС
70.
Графическая трактовка критерия Найквиста.1) Разомкнутая система является устойчивой
Для устойчивости
замкнутой системы
необходимо и остаточно,
чтобы годограф АФЧХ не
охватывал точку с
координатами (-1, j0). Для этого
применяется эмпирическое
правило правой штриховки: на
годограф АФЧХ наносится
штриховка справа по мере
увеличения частоты, если
точка (-1 , j0) попадает в
область штриховки, значит
годограф охватывает ее.
71.
2)Разомкнутая
система
обладает
астатизмом
первого порядка
q 1
3) Разомкнутая система обладает
астатизмом произвольного
порядка (допустим третьего)
q 3
1 – устойчива
2 – неустойчива
72.
Понятие запасов устойчивости замкнутой системы.Критерий Найквиста имеет некоторое преимущество над другими,
анализируя АФЧХ разомкнутой системы можно оценить количественно
близость устойчивости системы к границе неустойчивости и наоборот. Она
определяется с помощью специальных запасов устойчивости.
m
- запас по амплитуде
или по модулю
- запас по фазе
73.
Трактовка критерия Найквиста с использованием ЛЧХ.Применение рассмотренных ранее аналитической и графической трактовки
критерия Найквиста приводит к более наглядной оценки устойчивости и
запасов устойчивости.
Для
устойчивости
замкнутой
системы необходимо и достаточно
чтобы ЛАЧХ разомкнутой системы
пересекала раньше ось 0, чем
ЛФЧХ ось
L
F
- запас по амплитуде (по
модулю) (в дб.)
- запас по фазе, в град. (рад.)
74.
В инженерной практике, в процессе проектирования реальных системуправления были выработаны эмпирические оценки и значения запасов
устойчивости, обеспечивающих не только устойчивость системы, а и
удовлетворительное качество переходных процессов в них протекающих.
Связь между качеством системы и значением запасов – не жесткая, но
величина запасов зависит от порядка разомкнутой системы и степени ее
астатизма. Чем больше порядок астатизма и размерность разомкнутой
системы, тем выше запас устойчивости.
Статические системы управления
Степень ХП
F
(град)
( 0)
L
(дб)
n 3
35-45
7-10
3 n 6
45-60
10-15
n 6
>60
>15
75.
Астатические первого порядкаСтепень ХП
F
(град)
( 1)
L
(дб)
n 3
45-60
10-15
3 n 6
60-90
15-20
n 6
>90
>20
Астатические второго порядка
Степень ХП
F
(град)
( 2)
L
(дб)
n 3
60-90
15-20
3 n 6
90-120
20-25
n 6
>120
>25
76.
Оценка качества управления в линейных САУ.Основные понятия и определения.
Под качеством управления в динамической системе понимают совокупность
показаний как качественного, так и количественного типа, которые характеризует
основные свойства системы как в установившемся состоянии, так и в процессе
реализации функции управления. Эти показатели также позволяют произвести
оценку соответствия результатов управления целям и требованиям управляемой
технологии.
К качественным показателям относят такие оценки как:
- быстродействие;
- колебательность;
- астатизм …
Для оценки качества систем управления используют понятие как критерий
качества. Под ним понимается математическое выражение или техническую
систему, позволяющую вычислить количественную оценку качества управления
по результатам исследований системы или ее математической модели.
77.
Методы оценки качества и видыиспытываемых воздействий для оценки.
В теории управления применяют два основных
подхода для оценки качества:
- Прямая оценка качества (осуществляется по
переходному процессу);
-Косвенная оценка качества (осуществляется по
другим характеристикам, например, частотным или
корневым).
78.
Оценка качества системы управления по виду переходного процесса.Вид переходного процесса зависит не только от динамических и
статических свойств исследования системы, но и от вида входных воздействий, для
которых этот процесс получен.
1) Переходной процесс с
перерегулированием, где
- величина перерегулирования.
hMAX hУСТ
100%
hУСТ
В реальных системах
35%
2) Апериодический переходной процесс
Δдоп – допустимая трубка регулирования (по
сути – допустимое отклонение переходного
hУСТ
процесса от
Δдоп = 1% - 10%
Самые распространенные – 3% и 15%
tH
t MAX
- время нарастания переходного процесса;
- время достижения первого максимума;
tp1, 2
- время регулирования
переходного процесса
79.
A1 A3A1
- (показатель колебательности)
80.
Косвенный метод оценки качестваМатематической основой косвенного метода оценки является связь между
частотными характеристиками системы и качеством переходного процесса.
Установлено, что если на систему действует единичное задающее воздействие и
начальные условия являются нулевыми, то реакцию системы, которая
представляет собой переходную характеристику, в этом случае можно
определить как
2
sin t
y(t) = h(t) =
d
P( )
0
где P( ) - вещественная частотная характеристика замкнутой системы;
81.
1.18 P max P(0)100%
P(0)
tp
( 2..4)
ср
82.
Корневые оценки качестваКритерии основываются на исследовании расположения корней характеристического
уравнения замкнутой системы для оценки быстродействия системы используется понятие
степени устойчивости, являющейся простейшей корневой оценкой качества.
Под степенью устойчивости
понимается абсолютное значение вещественной части
ближайшего к мнимой оси корня.
Если ближайшим является вещественный корень, то такая степень устойчивости
называется апериодической, так как ей соответствует апериодическая составляющая
переходного процесса.
Время ее затухания характеризует общую длительность переходного процесса, так как
все члены решения, соответствующие остальным корням, затухают быстрее.
tp 3/ .
Если ближайшем к мнимой оси окажется пара комплексных корней, то ей соответствует
колебательная составляющая переходного процесса, при этом оценка длительности
переходного процесса остается прежней.
Такая степень устойчивости называется колебательной.
83.
Для оценки запаса устойчивости системы введено понятие колебательности переходногопроцесса.
Колебательность
где и вещественная и мнимая части корней характеристического уравнения.
Именно эта величина характеризует
быстроту затухания колебаний за
каждый период T=2 / . Чем выше
колебательность, тем слабее
затухание колебаний в переходном
процессе.
84.
Суммарное требование определенных значений степени устойчивости иколебательности приводит к области, изображенной на рисунке, внутри которой
должны располагаться все корни характеристического уравнения замкнутой системы.
Далее необходимо иметь в виду, что для определения качества переходного процесса
при единичном скачке задающего воздействия существенны не только корни
характеристического уравнения, т.е. полюса, но также и нули передаточной функции
замкнутой системы.
где з и з заданные значения
степени
устойчивости
и
колебательности
85.
Оценка точности работы систем.Коэффициенты ошибок.
Одно из основных требований, которым должна удовлетворять система управления,
заключается в обеспечении необходимой точности воспроизведения задающего
воздействия в установившемся режиме. Для оценки точности системы определяется
установившаяся ошибка
E ( p) = Wg ( p) G( p) =
1
G( p)
1+ W( p)
Где Wg - передаточная функция замкнутой системы по каналу ошибки,
G(p) – изображение задающего воздействия.
Разложив выражение в ряд по возрастающей степени комплексной величины p
c2 2
E ( p) c0 c1 p
p ... G( p)
2!
C0, C1 – коэффициенты ошибок
86.
d i W (p)1
g
c
i i!
i
dp
p = 0
Коэффициенты c0, c1 и c2
называются соответственно
коэффициентами ошибки по
положению, скорости и
ускорения.
Перейдя к оригиналу, выразим установившуюся ошибку через
коэффициенты ошибок, задающее воздействие и его
производные:
dg(t)
2
d g(t)
E(t) = c0g(t) + c1
c2
...
2
dt
dt
Статическая система: с0≠0, с1≠0, с2≠0.
Астатическая 1 порядка: с0=0, с1≠0, с2≠0.
Астатическая 2 порядка: с0=0, с1=0, с2≠0.
Астатическая 3 порядка: с0=0, с1=0, с2=0.
87.
Построение областей устойчивости САУв плоскости их параметров.
Для построения областей устойчивости применяется метод
предложенный Неймарком и названным - метод D – разбиения.
Исходными данными для построения областей
характеристический полином замкнутой системы.
N ( p , k , T Д ) N ( j , k , T Д )
Re[ N ( ,{ })] Im[ N ( ,{ })] 0
Re[ N ( , { })] 0
{ }
Im[ N ( ,{ })] 0
–
это
88.
Однопараметрическое D-разбиение.Исходными данными являются характеристический полином
замкнутой системы, в котором присутствует один варьируемый
параметр.
N ( p, ) S ( p) Q( p) 0
S ( j ) Q( j ) 0
S ( j )
Re ( ) j Im ( )
Q( j )
Для определения области устойчивости САУ
на параметрическую кривую необходимо
нанести штриховку слева по мере увеличения
частоты (по аналогии с корневой плоскостью).
89.
Примечание: для построения параметрического годографа необязательно изменятьот 0 до ,
до . Достаточно рассмотреть
частоту от
при этом оставшаяся часть будет зеркальным отражением построенного участка
вещественной оси. Так как варьируемый параметр является вещественным числом, то из
полученной области устойчивости выделяется только отрезок вещественной оси,
лежащей в области устойчивости.
Двухпараметрическое D-разбиение
Исходные данные: характеристический полином замкнутой системы, в который
входят два варьируемых параметра.
N ( p, , ) K ( p) L( p) M ( p) 0 K1( ) L1( ) M 1( )
p j
K 2 ( ) L2 ( ) M 2 ( )
K ( j ) K1( ) jK 2 ( )
M1( ) L1( )
K1( ) L1( )
L( j ) L ( ) jL ( )
1
;
1
2
M 2 ( ) L2 ( )
K 2 ( ) L2 ( )
M ( j ) M ( ) jM ( )
1
2
K1( ) M 1( )
1 2
;
K ( j ) L( j ) M ( j ) 0 2
K 2 ( ) M 2 ( )
90.
Так как M2 L2 и K2 являются нечетными функциями, то и , и 21
также нечетные функции, а функции и будут четными. При построении
параметрических кривых необходимо соблюдать следующее: по оси абсцисс
располагается параметр , а по оси ординат - .
Рассмотрим три возможных случая решения систем уравнений.
1)
2)
Уравнения совместны и
имеют общее решение
Уравнения несовместны и не
имеют общее решение
91.
3)K ( k ) L( k ) M ( k ) 0
-
- уравнение особой прямой
В большинстве практических случаев особые
прямые получаются при
и
.
0
Правила штриховки параметрических кривых и особых прямых.
до
от
1. (Для параметрической кривой) При возрастании
D-разбиения заштриховывается слева, если
0 , и справа, если
функции
и
четные, то при
0 и 0
граница
0.
кривые совпадают. Таким образом,
кривая D-разбиения обходится дважды и поэтому она всегда заштриховывается
двойной штриховкой.
Так как
92.
2. (Для особых прямых) Штриховка особых прямых, как правило, одинарная ии производится так, чтобы в точке сопряжения особой прямой и параметрической
кривой заштрихованные стороны кривой и прямой были направлены друг к другу.
После нанесения штриховки определяется область, претендующая на область устойчивост
Области, претендующие на
устойчивость – I и II. Область II после
проверки будет действительно являться
областью устойчивости.
При переходе через линию двойной
штриховки их заштрихованной области
в незаштрихованную два устойчивых
корня становятся неустойчивыми.
При переходе через линию одинарной
штриховки аналогично, неустойчивым
становится первый корень.
93.
Регуляторы.Законы регулирования.
94.
Автоматический регулятор – устройство, усиливающее ипреобразующее сигнал отклонения регулируемой величины и
целенаправленно воздействующий на объект управления.
ξ
ξ = g(t) – y(t)
Регуляторы подразделяются
1) по виду регулируемой величины:
давление, температуры, переходного уровня и т.д.
2) по виду источника:
- прямого действия – не требуется дополнительной энергии (сливной бочок)
- непрямого действия – требует дополнительной энергии (электрические,
гидравлические, пневматические др.)
95.
Типовые законы регулированияСуществует 5 типовых регуляторов. Среди этих регуляторов есть простые и сложные.
1) П – пропорциональный регулятор, W(p)=k (является простым, т.к. один
параметр настройки - k). Является статическим регулятором.
1
2) И – интегрирующий регулятор
W ( p)
TИ p
Так же является простым, но в отличие от первого он является астатическим.
3) ПИ – пропорционально-интегрирующий регулятор
W ( p) k
Является сложным и астатическим.
4) ПД – пропорционально-дифференцирующий регулятор
W ( p)
P
k TД p
T T Д
Tp 1
T 0
1
TИ p
TИ p
W И ( p) k T Д p
- является сложным и статическим.
5) ПИД – пропорционально-интегрально-дифференцирующий регулятор
W ( p) k T Д p
1
- является сложным и астатическим
96.
1) П – пропорциональный регуляторW ( p) k
Достоинства: Простота регулятора
Недостатки: Если объект
статический, то П – регулятор не
повысит порядок астатизма.
Является достаточно эффективным для астатических объектов.
97.
2) И – интегрирующий регулятор(применяется для статических систем)
Достоинства: Позволяет повысить порядок
астатизма и прост в настройке;
Недостатки: Применительно к данному объекту:
т.к. уменьшилась частота среза, то увеличилось
время протекания переходных процессов в
системе.
W ( p)
1
TИ p
98.
3) ПИ – пропорционально-интегрирующий регуляторW ( p) k
1
TИ p
kTИ p 1
TИ p
.
Достоинства: Позволяет повысить порядок
астатизма, при одновременном уменьшении
времени затухания переходных процессов в
системе по сравнению с И – регулятором.
Недостатки: Cложность настройки,
т.к. имеет два параметра
Применяется для статических систем
распространенным в инженерной практике.
и
является
самым
99.
4) ПД – пропорционально-дифференцирующий регуляторW И ( p) k T Д p
Достоинства:
Расширяет возможности
по обеспечению инженерных запасов
устойчивости, для данного объекта
уменьшает время переходного процесса.
Применяется
обычно
астатических объектов.
для
Недостатки: - Не повышает порядок
астатизма и имеет 2 параметра
настройки.
100.
5) ПИД – пропорционально-интегрально-дифференцирующий регуляторW ( p) k T Д p
1
TИ p
TИ T Д p 2 kTИ p 1
TИ p
101.
Корректирующиеустройства
102.
Корректирующие устройстваОсновная задача корректирующих устройств состоит в
улучшении точности системы и качества переходных процессов.
Однако наряду с этим путем дополнительного введения в
систему корректирующих устройств решается более общая
задача - обеспечение устойчивости системы, если она была
неустойчивой, а затем и желаемого качества процесса
управления.
Различают три вида основных корректирующих
устройств.
1.Последовательные корректирующие устройства.
2.Параллельные корректирующие устройства
3.Обратные связи
103.
1. Последовательные КУМетод нашел широкое применение, особенно при коррекции систем, в
которых используется электрический сигнал в виде напряжения
постоянного тока, величина которого функционально связана с сигналом
рассогласования. Однако, последовательные корректирующие устройства
не ослабляют влияния изменений параметров элементом системы на ее
показатели качества. Поэтому последовательные корректирующие
устройства рекомендуется применять в системах, в которых элементы
имеют достаточно стабильные параметры.
104.
2. Параллельные КУКоррекция
систем
управления
с
помощью
параллельного
корректирующего устройства эффективна, когда требуется формировать
сложные законы управления с введением производных и интегралов от
сигнала ошибки. Примером этому могут служить рассмотренные ранее
типовые регуляторы.
105.
3. Обратные связиВводятся в цепь регулятора и охватывают какие-либо его звенья. Могут быть
положительными (ПОС) и отрицательными (ООС), кроме того - жесткими и
гибкими.
Основными
видами
корректирующих
обратных
связей
являются:
k
ос
а) жесткая обратная связь WОС(p) = kОС;
б) инерционная жесткая обратная связь WОС(p) = T s+ 1
ос
в) гибкая обратная связь WОС(p) = kОС p;
г) инерционная гибкая обратная связь WОС(p) =
k
s
ос
T s+ 1
ос
106.
Синтез последовательного КУАлгоритм синтеза
Строится ЛАЧХ исходной системы;
Строится желаемая ЛАЧХ;
Получим ЛАЧХ КУ вычитая их
желаемой характеристики исходную.
107.
При построении желаемой ЛАЧХ выделяют три частотные области:1. низких частот (НЧ); 2. средних частот (СЧ); 3. высоких частот
(ВЧ)
Низкочастотная часть желаемой ЛАЧХ формируется из
условия обеспечения требуемой точности работы системы
управления в установившемся режиме, то есть из условия
того, что установившаяся ошибка системы не должна
превышать заданное значение.
Среднечастотный
участок
желаемой ЛАХ строится из условия
обеспечения основных показателей
качества переходного процесса перерегулирования
и
времени
регулирования. Это достигается тем,
что он имеет наклон 20 дб/дек и
пересекает ось частот на частоте
среза с, которая определяется по
номограмме
В.В.Солодовникова,
исходя
из
заданных
значений
величины перерегулирования и
времени регулирования tр.
срж
1
1 К
tp
108.
Протяженность среднечастотного участка определяется номограммой,устанавливающей связь между показателями качества и запасами
устойчивости. Так, например, для обеспечения =25% требуется запас
устойчивости по модулю Lh=20 дб и по фазе =580. Среднечастотный участок
проводится с наклоном 20 дб/дек влево и вправо от частоты среза с до
достижения модулей, равных Lh и Lh. После этого участки средних и низких
частот сопрягаются прямой с наклоном 40 или 60 дб/дек, как удобнее.
109.
110.
Анализ систем впространстве состояний
111.
Современная теория управления основана на описании систем впространстве состояний. С математической точки зрения анализ систем в
пространстве состояний означает использование методов матричного исчисления
и векторного анализа.
Понятие состояния является определяющим в современной теории
управления.
Под состоянием системы понимается минимально-необходимый набор
переменных величин системы x1,x2,...,xn, способных однозначно и единственным
образом определить положение системы в любой момент времени t.
Совокупность переменных величин x1,x2,...,xn образует n-мерное
пространство состояний Rn. Вектор с компонентами x1,x2,...,xn называется
вектором состояния.
Рассмотрим систему с m
входами (u1,u2,...,um), r выходами
(y1,y2,..., yr) и n переменными
координатами (x1,x2,...,xn).
112.
Линейную систему управления можно описать с помощью системыдифференциальных уравнений вида
x1 a11 x1 a12 x 2 ... a1n xn b11 u1 b12 u2 ... b1m um
x 2 a21 x1 a22 x 2 ... a2 n xn b21 u1 b22 u2 ... b2 m um
.........
x n an1 x1 an 2 x 2 ... ann xn bn1 u1 bn 2 u2 ... bnm um
Кроме того, для описания выходной переменной используем уравнение
y1 c11 x1 c12 x2 ... c1n xn d11 u1 d12 u2 ... d1m um
y2 c21 x1 c22 x2 ... c2 n xn d 21 u1 d 22 u2 ... d 2 m um
......
yr cr1 x1 cr 2 x2 ... crn xn d r1 u1 d r 2 u2 ... d rm um
Рассматриваемая система может быть определена следующей векторноматричной формой
X = AX+ BU
Y = CX+ DU
113.
где X - вектор состояния системы, Y - вектор выходных управляемых величин, U вектор внешних воздействий (задающих и возмущающих),A,B,C,D – матрицы, а именно:x
x 1
X = 2
...
x n
y
y 1
Y = 2
...
y
r
u
u1
U= 2
...
u
m
b
... b
b
11
12
1m
b
b
... b
21
22
2m
B=
...
... ... ...
b
b
...
b
n1 n2
nm n x m
d
... d
d
11
12
1m
d
d
... d
21
22
2m
D=
...
... ... ...
d
d
...
d
r1
r2
rm r x m
a
... a
a
11
12
1n
a
a
... a
21
22
2n
A=
...
... ... ...
a
a
...
a
n1 n2
nn n x n
c
c
11
12
c
c
21
22
C=
...
...
c r1 c r2
,
,
... c
1n
... c
2n
... ...
... c
rn r x n
A – системная матрица,
В – матрица управления,
С – матрица выхода по состоянию
(наблюдения),
D – матрица выхода по управлению (связи).
114. Синтез последовательного КУ
Структурная схема систему управления впространстве состояний
115. При построении желаемой ЛАЧХ выделяют три частотные области: 1. низких частот (НЧ); 2. средних частот (СЧ); 3. высоких частот
Построение МВ ММ по структурной схеме.Алгоритм построения:
1)
Исходная математическая модель, представленная в графической
форме преобразуется к структуре, содержащей только элементарные
звенья нулевого или первого порядков (ПЗ или ИЗ).
2)
На выходах динамических звеньев первого порядка назначаются
переменные состояния xi выходы звеньев нулевого порядка
не обозначаются (они входят в МВ ММ в качестве коэффициентов).
3)
Формируются сигналы на входах динамических звеньев, согласно
полученной на первых этапах структуре, при этом участвуют
как назначенные переменные состояния, так и сумматоры и звенья
нулевого порядка.
4)
Составляется система операторных алгебраических уравнений, после
применения обратного преобразования Лапласа она преобразуется
в систему дифференциальных уравнений в форме Коши, по которой
строится МВ ММ.
116.
ПримерДана структурная схема объекта управления
Необходимо построить МВ ММ
117.
px1 10(U 15 x2 )px 0,1x 2 x
2
2
1
px3 2 x2
y 5 x1 x3
0
A 2
0
x Ax Bu
y Cx
- 150
- 0,1
2
0
0
0
10
B 0
0
C 5 0 1
118.
Построение вход-выходных моделей поматрично-векторным
px( p) Ax( p) Bu ( p)
Y ( p ) Cx( p) Du ( p )
x Ax Bu
y Cx Du
1
( pE A) x ( p ) Bu ( p )
характеристическая матрица
det( pE A) N ( p )
характеристический полином
1
x( p ) ( pE A) Bu ( p )
ux
WПМ ( p ) n m
Передаточная матрица (ПМ) по состоянию
119.
Y ( p ) Cx( p ) Du ( p )2
ux
Y ( p ) C[WПМ
( p)u ( p )] Du ( p )
Y ( p ) [CW
( p ) D]u ( p )
ux
ПМ
uy
WПМ
( p) p m
Передаточная матрица по выходу
Передаточная матрица – это матрица, в ячейках которой стоят
передаточные функции по соответствующим каналам
Пример
1
x1
p
5
x2
p
10
U1
p 1
1
U
p 2 2
1
5
U1 X 2
W
( p)
W
( p)
p
p
10
1
U2 X1
U2 X 2
W
( p)
W
( p)
p 1
p 2
U1 X 1
120.
Свойства системы в пространствесостояний
К фундаментальным свойствам системы в ПС можно
отнести: управляемость и наблюдаемость.
Управляемость и наблюдаемость, так же как и
устойчивость, относятся к числу важнейших
характеристик динамических систем.
Если устойчивость характеризует свойство системы
возвращаться после возмущения в положение
равновесия, то управляемость характеризует
возможность изменения состояния системы с помощью
входных сигналов, а наблюдаемость возможность
определения состояния системы по наблюдениям за ее
выходными сигналами.
121.
Система называется управляемой, если для любого начальногосостояния X(0) Rn существует управление U(t), переводящее ее за
конечное время T в нулевое состояние X(T)=0.
Для оценки управляемости использую матрицу управляемости
Q у B AB A B ... A B
2
n -1
Необходимым и достаточным условием управляемости системы
является невырожденность матрицы управляемости.
Система управляема, если ранг матрицы управляемости равен
размерности системы n. Если ранг меньше n система частично
управляема, равен 0 – неуправляема полностью.
122.
Система называется наблюдаемой, если по наблюдениям за выходнымсигналом Y(t) в течение конечного времени T можно определить ее
начальное состояние X(0).
Для оценки управляемости использую матрицу наблюдаемости
Необходимым и достаточным
условием наблюдаемости системы
является невырожденность матрицы
наблюдаемости.
C
CA
Qн CA
2
......
CA
n 1
Система наблюдаема, если ранг
матрицы наблюдаемости равен
размерности системы n. Если ранг
матрицы меньше n система частично
наблюдаема, равен 0 – ненаблюдаема
полностью.
123.
Пример. Оценить принципиальные возможности системы автоматическогоуправления, заданной матрицами:
0 1 1
A = 1 0 1
1 1 0
1
B = 0
0
C = 0 0 1
Решение. Характеристический определитель матрицы A
p
pE A = 1
1 1
p
1 1
p3 3 p 2 0
1 0 2
Qу = 0 1 1
0 1 1
0 1 1
Qн = 0 1 1
1 0 2
1 p ( p 2 1) p 1 1 p p 3 3 p 2
p
Система неустойчива.
Матрица управляемости
, det Qу=1 1=0, следовательно, система неуправляема.
Матрица наблюдаемости
, det Qн=1 1=0, следовательно, система ненаблюдаема.
124.
Основные формы представления МВ ММи способы перехода к ним
Для исследования динамических систем в пространстве состояний в
теории управления используется семь основных форм:
1) Основная нормальная форма (ОН)
AOH
0
1
0
...
0
0
0
0
0
1
...
0
......................................... BOH ...
0
0 ...
1
...
0
1
a 0 a1 a 2 ... a n 1
C OH 1 0 ... 0
N ( p ) p n a n 1 p n 1 a n 2 p n 2 ... a1 p a 0
В ОН форме управляемой матрица В имеет стандартную форму, а С
может быть произвольной.
В ОН форме наблюдаемой матрица С должна быть стандартной, а В
может быть произвольной.
Для перехода к ОН форме используют преобразования на основе
матриц управляемости или наблюдаемости.
125.
2) Транспонированная ОН (ТОН)AТОН
a0
0 0 0 ...
1
1 0 0 ...
0
a
1
.................................... BTOH ...
0
0
0
...
a
n 2
...
0 0 0 ... a n 1
0
CTOH 0 0 ... 1
Для перехода к данной форме, обычно используют специальные
преобразования:
а)
TOH
Р1
CAn 1 an 1CAn 2 ... a1C
..........
..........
..........
..........
....
CA2 an 1CA an 2C
CA a n -1C
C
Исходный базис должен быть в ОН – форме.
б)
Р2
ТОН
Qу
1
, где
Qу
- матрица управляемости
126.
3) Дополнительная нормальная формаA ДОП
a n 1 1 0 ... 0
a
0
1
...
0
n
2
............................
a1 0 0 ... 1
a 0 0 0 ... 0
В ДОП ВОН
С ДОП С ОН
4) Обратная нормальная форма
AОБР
an 1 an 2 ... a0
1
0 ... 0
...................................
0
0 . .. 0
0 . .. 0
0
ВОБР ВТОН
С ОБР СТОН
Для перехода к ней применяют преобразования на основе матриц управляемости
или наблюдаемости.
5) Каноническая диагональная форма (КД)
AКД
где
1 0 ... 0
0 ... 0
2
....................
0
0
...
0
0 0 ... n
BКД
1
1
...
...
1
b1
b2
....
....
bn
C КД b1 b2 ... bn
i - собственные числа матрицы А
1
1
...
1
127.
Для перехода к данной форме записи используют специальныепреобразования с помощью матрицы Вандермонда:
1
1 ... 1
1
2 3 ... n
1
W 12
22 32 ... 2n
.......................................
n 1 n 1 n 1 ... n 1
2
3
n
1
PКД W 1
Для перехода к диагональной форме записи необходимо сначала
преобразовать к ОН форме.
6) Жарданово - каноническая форма
AЖК
A1 0 ... 0
0 A ... 0
2
......................
0
0
...
0
0 0 ... A n
В ЖК В КД С ЖК С КД ,где
7) Треугольная форма
AТР
1 a 12 ... a 1,n
0 2 ... a 2,n
.................... ...........
0 0 ... a n -1,n -1
n
0 0 ...
ВТР В КД СТР С КД
Ai - клетки Жордана
Из данных 7 форм, наибольшее
распространение получили три:
а) ОН
б) ТОН
в) КД
128. Свойства системы в пространстве состояний
Понятие базиса в пространстве состоянийСистема всегда записана относительно некоторых конкретных базовых
векторов , которые называются базисом (векторы при этом должны быть
линейно независимыми решениями между собой).
Форма записи матрично-векторных моделей не является единственной
для каждых конкретных A,B,C, конкретные A,B,C соответствуют некоторому
конкретному базису в пространстве состояний. Любое n-мерное линейное
пространство имеет множество различных базисов.
x Ax Bu
y Cx Du
Для перехода к новому базису существует некоторое преобразование,
которое обозначается: x * Px.
Это преобразование должно удовлетворять следующим условиям: - p –
квадратная матрица и невырожденная [ rang ( p ) 0 ].
x Р 1 x *
A* РAР 1
Р 1 x * AР 1 x* Bu
y CР 1 x* Du
B * РB
C * Р 1C
x * РAР 1 x* BРР
y CР 1 x * Du
D* D
129.
Общие закономерности преобразования МВ ММк произвольно выбранному базису
Поиск необходимого преобразования P может быть различным в
зависимости от того, какова исходная предпосылка преобразования.
1) Преобразование на основе управляемости.
Необходимо, чтобы объект был полностью управляемым.
Qу [ B | AB | A2 B | ... | A N 1 B]
Qу * [ B* | A* B * | ( A* ) 2 B * | ... | ( A* ) N 1 B* ]
*
Q у [ РB | РAР 1 РB | ... | ( РAР 1 ) N 1 РB]
*
Q у PQу P Q у *Q у 1
После определения преобразования обязательно необходимо сделать его
проверку. Если преобразование из исходного базиса в новый не дает
положительного результата, то преобразовать объект исходного базиса в
заданный невозможно.
2) Преобразование на основе свойств наблюдаемости
Для его построения необходимо, чтобы объект был полностью наблюдаемым.
QH [C T | AT C T | ... | ( AT ) n 1 C T ]
Q * H [(C * )T | ( A* )T (C * )T | ... | (( A* )T ) n 1 (C * )T ]
P (Q * H ) 1 Q H
T
T
130.
Наблюдатели (идентификаторы) состояния линейныхдинамических объектов и систем
Динамический наблюдатель состояния (ДНС) – техническое устройство,
позволяющее с использованием доступных измерению вход-выходных
переменных объекта, получать текущую оценку состояния объекта с
некоторой, достаточной степенью точности.
x н Aн x н BнU FнY
Схема наблюдателя:
131.
В теории управления применяется 2 типа наблюдателей состояний:1) Наблюдатель состояния Калмана (так называемый полный наблюдатель).
2) Наблюдатель состояния Луенбергера (так называемый редуцированный
наблюдатель).
Наиболее распространенным в инженерной практике является ДНС
Калмана.
Условия асимптотической оценки наблюдателя состояния:
1) B H B
2) A H a FH C
( FH - вектор обратных связей наблюдателя, формирующий его динамические
свойства).
Модель наблюдателя (Калмана):
x н Ax н BU FH (Y Y н )
132.
Для обеспечения асимптотического затухания ошибки наблюдениянеобходимо, чтобы имела устойчивый спектр корней и чтобы характер
затухания удовлетворял условиям асимптотической ошибки необходимо
H
выполнение условия:
min Re( p ) max Re( p )
i
i
Из второго условия можно определить вектор обратных связей наблюдателя:
FH C A AH
1) AOH
1
0
0
0
0
1
- a 0 a1 a 2
0
1
0
H
AOH
0
0
1
- aH aH aH
1
2
0
f1
FH f 2
C [1 0 0]
f 3
C OH [1 0 0]
н
COH
[1 0 0]
Вывод: Основная
нормальная форма записи
является непригодной для
формирования вектора
обратных связей ДНС, т.к.
невозможно определить все
его ( F ) коэффициенты.
Н
f1 0 0
0
0
0
FH C f 2 0 0 AOH A0HH H
H
H
(
a
a
)
(
a
a
)
(
a
a
)
0
1
1
2
2
0
f 3 0 0
133.
2)AТОН
H
TOH
A
0 0
1 0
0 1
0 0
1 0
0 1
a0
a1 CTOH 0 0 1
a 2
Н
a0
Н
a1
Н
a 2
H
CTOH
0 0 1
0 0 a 0H a 0
0 0 f 1
H
H
FH C 0 0 f 2 AТOH ATOH 0 0 a1 a1
0 0 a H a
0 0 f 3
2
2
f i a iH 1 a i 1
a iH
(i 1, n)
- коэффициент характеристического полинома наблюдателя.
134.
Преимуществом использования ДНС при построении САУ посравнению с классическими вход - выходными методами
является то, что появляется возможность для формирования
закона управления не только непосредственно изменяемых Y и
входных воздействий U, но и всех наблюдаемых переменных
состояния, оценивающих реальные переменные с точностью
определенной выбранными параметрами асимптотической
оценки.
Достоинство асимптотического ДНС Калмана состоит в его
универсальности и в высокой эффективности наблюдаемых
переменных состояния, т.е. независимо от причин отклонения
действительных значений этих переменных, наблюдаемые
переменные сводятся к ним со скоростью, определяемой
выбранными значениями собственных чисел наблюдателя.
135.
Недостатком является его большая сложность при высокойразмерности объекта, т.к. он является полным. Во многих
реальных случаях выходная переменная Y совпадает с одной из
переменных состояния, тогда оценка соответствующей
переменной оказывается лишней, кроме того практически всегда
базис объекта можно преобразовать так, чтобы указанное
условие соблюдалось, более того в многомерных объектах базис
можно построить таким образом, чтобы выходные переменные
совпадали с таким же количеством переменных состояния, тогда
появляется возможность создать редуцированный или усеченный
наблюдатель с общей экономией, соответствующий общему
количеству выходных переменных Y.
136.
Пример.1
0
0
A 0
0
1
- 0,03 0,43 1,4
p1 0.1
ATOH
0
В 0
1
p 2 0.3
0 0 - 0.03
TOH
TOH
P1 A( P1 ) 1 1 0 - 0.43
0 1 - 1.4
1
BTOH 0
0
Выберем корни наблюдателя:
С 1 0 0
p 3 1
1
pTOH
0.43 1.4 1
1.4 1 0
1
0 0
CTOH 0 0 1
p1, 2,3 2
137.
N H ( p) ( p 2) 3 p 3 6 p 2 12 p 8H
ATOH
0 0 8
1 0 12
0 1 6
f1 8 0.03 7.97
f 2 12 0.43 11.57
f 3 6 1.4 4.6
a 0 0.03
a 0H 8
a1 0.43
a 1H 12
a 2 1 .4
a H2 6
7.97
FH 11.57
4.6
x H AxH BU FH (Y Y )
H
BTOH
1
0
0
138.
139.
Нелинейные системы140.
Нелинейной системой называется такая система, в состав которой входитхотя бы одно звено, описываемое нелинейным уравнением. Такое звено называется нелинейным звеном или нелинейным элементом.
Путем эквивалентного преобразования структурных схем и нелинейных
звеньев большое число нелинейных систем можно представить в виде
замкнутого контура с последовательным включением нелинейного элемента
(НЭ) и линейной части (ЛЧ), как показано на рисунке
Нелинейные звенья классифицируются по различным признакам.
Наибольшее распространение получила классификация по статическим и
динамическим характеристикам, так как в системах чаще всего нелинейности
приходится учитывать в виде характеристик. Эти характеристики могут быть как
однозначными, так и двузначными
(петлевыми), симметричными и
несимметричными относительно начала координат.
141.
Гладкие криволинейные характеристики: а - гистерезисная; б, в - усилительныеКусочно-линейные
характеристики:
а - с насыщением;
б - с зоной нечувствительности;
в - с насыщением и зоной
нечувствительности; г - люфт
142.
Релейные характеристики:а - идеальная; б - с зоной нечувствительности; в - гистерезисная
143.
Особенности нелинейных систем.Поведение нелинейных систем, при наличии существенных нелинейностей,
значительно отличается от поведения их линейных моделей.
1. Выходная величина нелинейной системы непропорциональна
входному воздействию; форма реакции системы зависит от величины входного
воздействия.
2. Характер процессов в нелинейной системе зависит от величины
начального отклонения, вызванного возмущением. В связи с этим для
нелинейных систем существуют понятия об устойчивости “в малом”, “в
большом”, “в целом”.
Система устойчива “в малом”, если она устойчива при малых
(бесконечно малых) начальных отклонениях. Система устойчива “в большом”,
если она устойчива при больших (конечных по величине) начальных
отклонениях. Система устойчива “в целом”, если она устойчива при любых
больших (неограниченных по величине) начальных отклонениях.
3. Для нелинейных систем характерен режим незатухающих
периодических колебаний с постоянной амплитудой и частотой
(автоколебаний), возникающий в системах при отсутствии периодических
внешних воздействий.
4. При затухающих колебаниях переходного процесса в нелинейных
системах происходит изменение периода колебаний.
144.
Прямой метод ЛяпуноваПри использовании прямого метода Ляпунова (второй методой
Ляпунова), исследуемая система описывается
дифференциальными уравнениями первого порядка, полагая, что
они записаны для переходного процесса в отклонениях всех
переменных xi (i = 1, 2, ... , n) от их значений в установившемся
процессе при новых постоянных значениях возмущающего f = f0
и задающего g = g0 воздействий.
dxi
Fi (x1, x 2 ,..., x n )
dt
где Fi
- нелинейные
удовлетворяющие условию
функции
(1)
произвольного
F1 = F2 = ... = Fn = 0 при x1 = x2 = ... = xn = 0
вида,
145.
Теорема Ляпунова об устойчивости нелинейных системЕсли при заданных в форме (1) уравнениях системы n-го
порядка можно подобрать такую знакоопределенную функцию
Ляпунова V(x1, x2, ..., xn ), чтобы ее производная по времени
W(x1, x2, ..., xn ), тоже была знакоопределенной (или
знакопостоянной), но имела знак, противоположный знаку V, то
данная система устойчива; при знакоопределенной функции W
будет иметь место асимптотическая устойчивость.
Теорема Ляпунова о неустойчивости нелинейных систем
Если при заданных в форме (1) уравнениях системы n-го
порядка производная по времени W(x1, x2, ..., xn) от какойнибудь функции Ляпунова V(x1, x2, ..., xn) окажется
знакоопределенной, причем сама функция V в какой-нибудь
области, примыкающей к началу координат, будет иметь знак,
одинаковый со знаком производной W, то данная система
неустойчива.
146.
Замечания к теореме Ляпунова об устойчивости.1. При заданных в форме (1) уравнениях системы выбор
функции V неоднозначен, поэтому данная теорема Ляпунова
обеспечивает получение достаточных условий устойчивости,
которые не всегда будут и необходимыми, т.е. при выполнении
условий теоремы система наверняка будет устойчивой, но эти
условия могут не охватывать всей области устойчивости
системы по параметрам.
2. Понятие устойчивости по Ляпунову допускает, что при
знакоопределенной функции V производная от нее по времени W
была не обязательно знакоопределенной или знакопостоянной, а
могла быть и тождественно равна нулю. В результате система
хотя и не будет асимптотически приближаться к
установившемуся состоянию, но все же будет все время в
достаточной близости от него.
147.
Функция V называется знакоопределенной в некоторойобласти, если она во всех точках этой области в окрестности
начала координат сохраняет один и тот же знак и нигде не
обращается в нуль, кроме начала координат.
Функция V называется знакопостоянной, если она сохраняет
один и тот же знак, но может обращаться в нуль не только в
начале координат, но и в других точках данной области.
Функция V называется знакопеременной, если она в данной
области вокруг начала координат может иметь разные знаки.
148.
Пример. Исследовать устойчивость системы, заданной уравнеdx1
dt
(x1
dx 2
x 2 )(1 ax12 bx 22 )
dt
(x 2 x1 )(1 ax12 bx 22 )
где а, b - положительные постоянные числа.
Р е ш е н и е. Выбираем положительно-определенную функцию
;
Ляпунова
V = x12 + x22 .
Находим производную от функции Ляпунова по времени
W
dV
dt
2 x
dx
1
1
dt
2 x
dx
2
2
dt
W= 2 x1 (x1 x2 )(1 ax12 bx22) 2 x2 (x2 + x1 )(1 ax12 bx22) =
= 2(1 ax12 bx22)( x12 + x22) .
Тогда W < 0 при (1 ax12 bx22 ) > 0 или ax12 + bx22 < 1.
Это достаточное условие устойчивости исследуемой нелинейной
системы.
149.
Частотный метод ПоповаЧастотный метод Попова решает задачу об абсолютной
устойчивости системы с одной однозначной нелинейностью и
имеющая не более 2 нулевых корней характеристического
полинома линейной части (ЛЧ).
150.
Нелинейность yн = F(x) имеет любое очертание, не выходящееза пределы заданного угла arctg k, т.е. при любом x
0 F(x) kx
yн
x
НЭ
yн
yн F( x )
arctg k
x
Нелинейная система называется абсолютно устойчивой, если
она устойчива при любых начальных отклонениях и любой
форме нелинейной характеристики, удовлетворяющей условиям
0
F( )
k; F(0) 0,
где k - заданное число.
151.
Теорема ПоповаДля установления абсолютной устойчивости нелинейной
системы достаточно подобрать такое конечное действительное
число q, при котором для всех частот 0
Re[(1+ j q)WЛЧ(j )] + > 0,
где
k - предельное значение коэффициента передачи
нелинейного элемента;
WЛЧ (j ) - амплитудно-фазовая частотная характеристика
линейной части системы.
Все полюсы передаточной функции линейной части
системы должны быть с отрицательными вещественными
частями или же кроме них имеется еще не более двух нулевых.
При наличии одного нулевого полюса требуется еще,
чтобы
Im WЛЧ (j ) при 0,
а при двух нулевых полюсах
Re WЛЧ(j ) при 0, а Im WЛЧ(j ) < 0 при малых .
152.
Другая формулировка той же теоремы, дающая удобнуюграфическую интерпретацию, связана с введением
видоизмененной частотной характеристики линейной части
системы W*(j ), которая определяется следующим образом
U * (j ) Re W * (j ) Re W (j ),
лч
*
*
V
(j
)
Im
W
(j ) T0 Im Wлч (j ),
Графическая интерпретация теоремы Попова:
Для установления абсолютной устойчивости нелинейной
системы достаточно подобрать такую прямую на комплексной
плоскости W*(j ), проходящую через точку (-1/k, j0), чтобы вся
кривая W*(j ) лежала справа от этой прямой.
153.
Графическая интерпретация теоремы В.М. Попова:а - абсолютно устойчивая система; б - система не имеет
абсолютной устойчивости
154.
Для определения абсолютной устойчивости нелинейнойсистемы по методу В.М. Попова необходимо построить
видоизмененную частотную характеристику линейной части
системы W*(j ), определить предельное значение коэффициента
передачи k нелинейного элемента из условия 0 F(x) k
и через точку ( 1/k) на вещественной оси комплексной плоскости
провести некоторую прямую так, чтобы характеристика W*(j )
лежала справа от этой прямой.
Если такую прямую провести нельзя, то это значит, что
абсолютная устойчивость для данной системы невозможна.
155.
Пример. Определить предельное значение коэффициентапередачи k нелинейного элемента из условия обеспечения
абсолютной устойчивости нелинейной системы, передаточная
функция линейной части которой
10
Р е ш е н и е. По передаточной функции
линейной части системы находим ее
частотную передаточную функцию
Wлч (j )
*
W (j )
10
j (j 1)
10
2 1
j
10
2 1
j
10
( 2
10
2
Wлч (s)
1
Исследуемая нелинейная система
абсолютно устойчива при k > 0.
1)
s(s 1)
.
156.
Метод гармонической линеаризацииМетод гармонической линеаризации базируется на
замене нелинейного элемента системы линейным звеном,
параметры которого определяются при гармоническом
входном воздействии из условия равенства амплитуд
первых гармоник на выходе нелинейного элемента и
эквивалентного ему линейного звена.
Данный метод может быть использован в том случае,
когда линейная часть системы является низкочастотным
фильтром, т.е. отфильтровывает все возникающие на выходе
нелинейного элемента гармонические составляющие, кроме
первой гармоники.
157.
Коэффициенты гармонической линеаризацииВ основе метода гармонической линеаризации нелинейностей
(рисунок), описываемых уравнением
yн = F(x), лежит
предположение, что на вход нелинейного элемента подается
гармоническое воздействие с частотой и амплитудой a, а из
всего спектра выходного сигнала выделяется только первая
гармоника yн1 = aн1 sin( t + н1) при этом высшие гармоники
отбрасываются и устанавливается связь между первой гармоникой
выходного сигнала и входным гармоническим воздействием
нелинейного элемента.
x
2 π/ω
a
yн
x
t
yн
aн1
yн
t
н1
158.
В случае нечувствительности нелинейной системы к высшимгармоникам нелинейный элемент может быть в первом
приближении заменен некоторым элементом с эквивалентным
коэффициентом передачи, который определяет первую гармонику
периодических колебаний на выходе в зависимости от частоты и
амплитуды синусоидальных колебаний на входе.
Для нелинейных элементов с характеристикой yн = F(x) в
результате разложения периодической функции F(x) в ряд Фурье
при синусоидальных колебаниях на входе x = a sin t получим
выражение для первой гармоники сигнала на выходе
yн1 = b1F sin t + a1F cos t
где b1F, a1F - коэффициенты разложения в ряд Фурье, которые
определяются по формулам:
a 1F
1
2
0 F(a sin t ) cos t d t. b
1F
1
2
0 F(a sin t ) sin t d t,
159.
Так как x = a sin t, то px = a cos t (где p = d/dt).Поэтому связь между первой гармоникой периодических
колебаний на выходе нелинейного элемента и синусоидальными
колебаниями на его входе можно записать в виде
y
н1
( q q
p
)x
где q = b1F/a, q = a1F/a.
Уравнение
называется
уравнением
гармонической
линеаризации, а коэффициенты q и q - коэффициентами
гармонической линеаризации.
160.
Таким образом, нелинейный элемент при воздействиигармонического сигнала с точностью до высших гармоник
описывается уравнением гармонической линеаризации, которое
является линейным.
Коэффициенты q и q изменяются при изменении
амплитуды a и частоты колебаний на входе. Именно в этом
заключается
принципиальное
отличие
гармонической
линеаризации от обычной, коэффициенты которой не зависят
от входного сигнала, а определяются только видом
характеристики нелинейного элемента.
161.
Проведя преобразование Лапласа при нулевых начальныхусловиях с последующей заменой оператора p на j , получим
эквивалентный комплексный коэффициент передачи нелинейного
элемента
WЭ(j , a) = q + jq = AЭ( , a) e j э( , a)
где модуль и аргумент эквивалентного комплексного
коэффициента передачи связаны с коэффициентами
гармонической линеаризации выражениями
AЭ( , a) =
[q( a, )]2 [q ( a, )]2 ;
Э( , a) = arctg[q (a, )/q(a, )].
162.
Исследование симметричных периодических режимов внелинейных системах.
При исследовании нелинейных систем на основе метода
гармонической линеаризации в первую очередь решают вопрос о
существовании и устойчивости периодических режимов. Если
периодический режим устойчив, то в системе существуют
автоколебания с частотой 0 и амплитудой a0.
Частотный метод. В соответствии с критерием устойчивости
Найквиста незатухающие колебания в линейной системе возникают
в том случае, когда амплитудно-фазовая характеристика
разомкнутой системы проходит через точку с координатами [ 1, j0].
Данное условие является также условием существования
автоколебаний в гармонически линеаризованный нелинейной
системе, т.е.
Wн(j , a) = 1
Wн(j , a) = Wлч(j ) WЭ(j , a)=-1
Wлч(j ) =-1/ WЭ(j , a)
163.
Решение уравнения относительно частоты и амплитудыавтоколебаний можно получить графически как точку пересечения
годографа частотной характеристики линейной части системы
Wлч(j ) и годографа обратной характеристики нелинейной части
1/WЭ(j ). Если эти годографы не пересекаются, то режим
автоколебаний в исследуемой системе не существует.
Im
5
=0 Re
1
4
( 0,
4
1
WЭ (a )
5
2
3
3
1
2 WЛЧ(j )
164.
Для устойчивости автоколебательного режима с частотой 0и амплитудой a0 требуется, чтобы точка на годографе нелинейной
части, соответствующая увеличенной амплитуде a0+ a по
сравнению со значением в точке пересечения годографов, не
охватывалась годографом частотной характеристики линейной
части системы и охватывалась точка, соответствующая
уменьшенной амплитуде a0 a.
На рисунке дан пример расположения годографов для
случая, когда в нелинейной системе существуют устойчивые
автоколебания, так как a3 < a0 < a4 .
165.
Методы фазового пространстваФазовым пространством называется пространство, по осям
координат которого отложены переменные, характеризующие
состояние системы.
Точка, характеризующая состояние системы, называется
изображающей точкой.
При движении системы изображающая точка описывает в
фазовом пространстве некоторую кривую, называемую фазовой
траекторией. Каждому определенному переходному процессу в
фазовом пространстве соответствует определенная фазовая
траектория.
Начальное положение изображающей точки определяется
начальными условиями. В установившемся равновесном состоянии
системы все производные рассматриваемой переменной равны нулю;
соответствующие этому точки фазового пространства находятся в
покое и называются особыми точками. Совокупность фазовых
траекторий для всевозможных начальных отклонений называется
фазовым портретом системы.
Имея фазовый портрет системы, определяют по нему особые
точки и траектории, исследуют устойчивость системы и оценивают
качество процесса управления.
166.
Метод фазовой плоскости используется для исследованиясистем второго порядка и заключается в построении фазовых
портретов на плоскости. Для этого из уравнений состояния
исключается время и определяются уравнения фазовых кривых.
Для изображения процессов на фазовой плоскости нелинейное
уравнение, описывающее систему, заменяют эквивалентными
уравнениями первого порядка вида
dy
dt f (x, y);
dx
y,
dt
где x, y - координата системы и ее первая
производная;
f(x, y) - нелинейная функция.
Разделив
первое
из
уравнений
на
второе,
получим
дифференциальное уравнение, из которого исключено время t:
dy f (x, y)
dx
y
dy
x
= a1 a 2 .
dx
y
167.
yx
Im
t
Re
1. a1=0, a2>0
x
особая точка центр
x
Im
y
Re
2. a12>4a2, a1>0, a2>0
x
t
особая точка устойчивый узел
Im
3. a2<0
x
y
Re
x
t
особая точка неустойчивый фокус
168.
yx
Im
x
t
Re
4. a12<4a2, a1<0, a2>0
особая точка седло
5. a12<4a2, a1>0, a2>0
y
Im
Re
x
x
t
особая точка устойчивый фокус
x
Im
6. a1
2>4a
2,
a1<0, a2>0
Re
y
t
x
особая точка неустойчивый узел
169.
170.
171.
172.
173.
174.
175.
176.
Дискретные системыуправления
177.
Дискретные системы - системы, в состав которых, помимотиповых динамических звеньев, входят одно или несколько
звеньев, производящих квантование непрерывного сигнала в
дискретный.
К дискретным системам относятся импульсные, релейные
и цифровые.
В импульсных системах производится квантование сигнала
по времени, в релейных - по уровню, в цифровых - по времени и по
уровню.
Импульсная система состоит из импульсных элементов
(одного или нескольких) и непрерывных частей, содержащих
типовые динамическое звенья. Импульсные элементы,
производящие квантование (прерывание) сигнала по времени,
позволяют получать весьма большие коэффициенты усиления по
мощности. Кроме того, при импульсном режиме уменьшается
расход потребляемой энергии системы.
Примерами импульсных систем могут служить системы
радио и оптической локации, системы с частотными датчиками и
др.
178.
Релейные системы автоматического управления можноотнести, как и импульсные, к системам прерывистого действия, но
их существенное отличие от импульсных состоит в том, что
релейные системы по своему принципу являются нелинейными
системами.
В релейных системах моменты времени, в которые
происходит замыкание и размыкание системы, заранее
неизвестны; они определяются внутренними свойствами самой
системы. Этим обусловливаются основные особенности динамики
процессов регулирования в релейных системах.
Благодаря простоте реализации и приемлемому качеству
работы релейные системы получили широкое распространение в
бытовой технике, например, системы регулирования температуры в
холодильниках или нагрева электрического утюга и др.
179.
К цифровым системам относятся системы автоматическогоуправления , в замкнутый контур которых включается цифровое
вычислительное устройство, что позволяет реализовать сложные
алгоритмы управления.
Включение цифрового вычислительного устройства в контур
системы управления сопряжено с преобразованием непрерывных
величин в дискретные на входе и с обратным преобразованием на
выходе.
При достаточно высокой тактовой частоте работы
вычислительного устройства во многих случаях можно производить
расчет цифровой системы в целом как непрерывной, а достаточно
большое числе разрядов (8 16) преобразователей непрерывной
величины в дискретную и дискретной в непрерывную позволяет во
многих
случаях
пренебрегать
нелинейностью
операции
квантования сигнала по уровню. В общем случае цифровая
система автоматического управления является нелинейной
дискретной системой.
Примерами цифровых систем служат системы, содержащие
в своем составе компьютеры, разнообразные микропроцессорные
системы управления и т.д.
180.
Математическое исследование дискретных системсущественно упрощается в том случае, когда все величины
рассматриваются в дискретные равноотстоящие моменты времени.
Решетчатая функция времени x[nT], или в сокращенной
записи x[n] - это математическая функция, значения которой
определены в дискретные равноотстоящие друг от друга моменты
времени t = nT, где n - целое положительное число 0, 1, 2 ..., а Т период дискретности.
Z-пребразованием решетчатой функции x[nT] называется
функция комплексного аргумента z, определяемая выражением
-n
X(z) = Z x[nT] x[nT] z
n=0
Преобразование, в котором z = epT, называется - “дискретное
преобразование Лапласа”.
181.
Устойчивость дискретных системКак и для непрерывных систем, устойчивость дискретных
систем является необходимым условием их работоспособности.
Линейная дискретная система называется устойчивой, если
переходная составляющая процесса регулирования yп[n, ] затухает
с течением времени.
Для устойчивости дискретной системы необходимо и
достаточно, чтобы все корни характеристического полинома
замкнутой системы (полюса передаточной функции замкнутой
дискретной системы) удовлетворяли условию zi < 1; i = 1, 2, ..,
m.
Если хотя бы один корень zi > 1, система будет
неустойчивой. Значением какого-либо корня zi = 1 при всех
остальных zi < 1 определяется граница устойчивости дискретной
системы.
182.
Графически область устойчивости дискретной системы наплоскости z корней характеристического уравнения изображается
единичным кругом.
183.
Передаточные функции разомкнутых импульсных системРазомкнутая линейная импульсная система может быть
схематически представлена в виде последовательного соединения
импульсного элемента (ИЭ) и непрерывной части (НЧ) ).
Импульсный элемент преобразует задающее воздействие g(t) в
последовательность
импульсов
x*,
амплитуда
которых
пропорциональна входному непрерывному сигналу. Импульсная
последовательность после прохождения через непрерывную часть
вследствие сглаживающих свойств последней превращается в
непрерывную величину на выходе y(t).
184. Дискретные системы управления
При исследовании импульсной системы ее структуру приводят к расчетной схемепутем замены ИЭ последовательным соединением простейшего импульсного
(ПИЭ) и формирующего элементов (ФЭ). Простейший импульсный элемент
преобразует непрерывный сигнал в мгновенные импульсы в виде -функций,
модулированные по площади, а формирующий элемент формирует импульс
заданной формы из -функций, соответствующей форме выходного импульса
реального импульсного элемента.
В большинстве случаев импульсный элемент
формирует прямоугольные или близкие к
прямоугольным
импульсы
длительности
Tимп = Т, то есть импульсная функция
формирующего элемента имеет вид
W
ФЭ
(s) = L w
ФЭ
(t)
1 e
- Ts
s
.
185.
Частотные характеристики импульсных системЧастотные характеристики импульсных систем определяются
аналогично обыкновенным линейным системам.
Выражения для частотных характеристик импульсных систем
получаются из их передаточных функций путем замены оператора z на ej T.
Так как частота входит в показатель степени числа e, то частотные
характеристики являются периодическими функциями частоты, период
изменения которых равен T. Следовательно, нельзя различить
составляющие, частоты которых кратны частоте квантования импульсного
элемента 0 = 2 /Т.
На практике применяются частотные характеристики относительно
абсолютной псевдочастоты . Переход к псевдочастоте основан на переходе
от z-преобразования к w-преобразованию с помощью подстановки
z=
1+ w
1 w
c последующей заменой комплексной переменной w на
абсолютную псевдочастоту w = j T/2.
При этом реальная частота и псевдочастота
связаны соотношением
2 T
tg
.
T
2
186.
Описание дискретных систем в пространстве состоянийСовременная теория дискретных систем, так же как и
непрерывных, базируется на описании их в пространстве состояний
X(n+ 1) = Ф X(n) + Г U(n);
Y(n) = CX(n) + DU(n),
T
Ap
AT
Ф e , Г e
Bdp
0
Матрицы Ф и Г определяется разложением матричной
экспоненты в ряд
Ф
i 0
Г BT
АТ i ,
i!
при i 1 Ф E AT
187.
Точность импульсных системДля импульсных систем, как и для непрерывных, введены
определения статической ошибки, астатизма, коэффициентов
ошибок, ошибки при гармоническом воздействии.
В замкнутой импульсной системе ошибка x, задающее воздействие
g и возмущающее воздействие f связаны следующей зависимостью
относительно z-изображений
X(z, ) = Xg(z, ) + Xf(z, )
Выражение содержит z-изображения двух составляющих ошибки:
Xg(z, ) - от задающего и Xf(z, ) - от возмущающего воздействий.
188.
Коэффициенты ошибок. Если задающее воздействие g(t) имеетпроизвольный вид, предельное значение ошибки вычисляется по
формуле
c
c
(k)
x[n]= c g[n] c g [n] 2 g [n] ... k g [n],
0
1
k!
2!
Коэффициенты ошибок находят по дискретной передаточной
функции замкнутой импульсной системы по ошибке
c i!
i
di
dz i
Ф (z)
xg
z 1
,
189.
Коррекция импульсных системВведение в систему корректирующих устройств
необходимо, чтобы в результате этого система
удовлетворяла заданным требованиям по точности и по
качеству процесса управления, в том числе переходных
процессов.
Исходя из требований составляются желаемые
характеристики импульсной системы. Чтобы их реально
получить, в систему вводятся корректирующие устройства.
Для коррекции импульсных систем имеется большее
разнообразие технических средств, чем у непрерывных
систем, так как кроме непрерывных корректирующих
устройств можно вводить импульсные и цифровые.
190.
Непрерывная коррекция. В случае непрерывнойкоррекции изменяют характеристики непрерывной части
импульсной системы путем введения либо последовательных
или параллельных корректирующих устройств, либо местной
отрицательной или положительной обратной связи, в
результате чего формируется передаточная функция
скорректированной системы.
При расчете непрерывных корректирующих цепей
целесообразно перейти от желаемой характеристики
импульсной системы к желаемой характеристике ее
непрерывной части. После нахождения желаемых
характеристик непрерывной части задача синтеза решается
так же, как она решалась для обыкновенных линейных
систем автоматического управления
191.
Импульсная коррекция осуществляется включением в контурсистемы импульсного фильтра, который преобразует входной
сигнал x в последовательность импульсов u. Импульсы на
выходе фильтра образуются путем амплитудно-импульсной
модуляции входного воздействия с необходимыми для коррекции
системы преобразованиями
k
u[n] w [n i]x[i],
i 0
k
где wk[n] - импульсная функция непрерывной части импульсного
фильтра.
Наиболее просто импульсные корректирующие устройства
реализуются с помощью импульсных RC-цепей.
Различают
три
структуры
импульсных
RC-цепей:
последовательную, с обратной связью и с каскадным
соединением импульсных цепей первых двух структур.
192.
Цифровые корректирующие фильтры реализуются с помощьюцифрового вычислителя. В этом случае входной сигнал фильтра x
преобразуется в АЦП, и далее решение разностного уравнения на
цифровом вычислителе u выводится в непрерывную часть
импульсной системы через ЦАП.
Широкое распространение получили цифровые системы, в
которых функцию вычислительного устройства выполняют
микропроцессоры и компьютеры.
Синтез цифровых систем сводится к выбору цифрового
корректирующего фильтра, последовательное включение которого с
непрерывной частью системы, обычно включающей в себя объект
управления, регулирующий орган, исполнительный механизм,
усилитель мощности и датчик, позволяет получить систему с
желаемыми характеристиками. Часто в качестве таких
характеристик используют аналоговые эквиваленты: импульсные
функции, переходные функции и частотные характеристики, что
обосновано при достаточно высокой тактовой частоте работы
цифрового вычислителя и большой разрядности преобразователей.
193.
194.
195.
196.
Используя последовательную коррекцию, выполнить синтез замкнутойсистемы, имеющей заданные показатели качества (перерегулирование и
время регулирования).
Передаточная функция исходного объекта имеет вид:
k
W ( p) v
p (T1 p 1)(T 2 p 1)(T 3 p 1)
1. Оценить устойчивость исходной замкнутой системы.
2. Определить перерегулирование и время регулирования.
3. Построить ЛАЧХ и ЛФЧХ исходной разомкнутой системы.
4. Увеличить требования к качеству и реализовать их с помощью
последовательной коррекции.
197.
Чувствительностьсистем автоматического
управления
198.
Чувствительность систем автоматического управления - этостепень влияния разброса параметров и их изменений в процессе работы
на статические и динамические свойства системы управления (точность,
показатели качества, на частотные свойства и др.).
Параметры системы управления (коэффициенты передачи и
постоянные времени) определяются физическими параметрами
составляющих ее элементов (резисторов, конденсаторов, катушек
индуктивностей и т.п.), которые имеют технологический разброс и
подвержены эксплуатационным изменениям с течением времени.
Задача оценки работы системы при изменении параметров
составляющих ее элементов решается путем количественной оценки
чувствительности системы.
Для этого требуется описать систему
управления уравнениями в нормальной форме, т.е.
dx
i a x + a x + ... + a x + f
i1 1 i 2 2
in n i
dt
(1)
где n - порядок системы;
xi - координаты состояния системы;
fi - внешние воздействия, прикладываемое к системе;
aik - коэффициенты уравнения, определяемые величинами физических
параметров составляющих систему элементов.
199.
Изменяющиеся со временем параметры элементов системы в процессеэксплуатации и от разброса при изготовлении обозначим через j (j=1, 2, ... , m).
Тогда уравнение системы (1) можно записать в виде
dx
i (x ,x , ... ,x , , , ... , ,f )
n 1 2
m i
i 1 2
dt
(2)
Решение уравнений (2) определяет координаты системы: x1(t), x2(t), ... ,
xn(t), образующие исходное движение системы.
Пусть параметры j изменяются на малые величины j , тогда имеем
~
1
1
1
~
m
m
m
Рассматривая малые изменения параметров j (j=1, 2, ... , m), получим новые
уравнения
d~x
;
i (~
x1, ~x2, ... , ~xn , 1 + 1, 2 + 2 , ... , m + m , fi )
i
dt
(3)
200.
Процесс в той же системе, но с измененными параметрами, определяемыйрешением уравнений (3), т.е.
~
x (t), ~
x (t), ... , ~
x (t)
1
2
n
называется варьированным движением.
Возникшее различие в протекании процессов в системе за счет изменения
параметров
x (t) = x (t) - ~
x (t)
i
i
i
называется дополнительным движением.
При малых отклонениях j эта разность может быть определена следующим
образом:
xi (t) =
x
i
1
1
x
Обозначим
i
u (t) =
ij
j
x
i ...
2
2
x
i
m
m
(4)
Тогда дополнительное движение будет
x (t) = u u ... u
i
i1
1
i2
2
im
m
при i=1, 2, ... , n.
201.
Величины u ij (t), представляют собой функции чувствительности i-ой
координаты системы по j-ому параметру.
Для оценки степени влияния разброса и изменения параметров на
координаты системы необходимо определить функции чувствительности
по каждой координате от каждого изменяющегося параметра.
В рассматриваемом случае xi(t) являются координатами состояния
системы. Вообще же аналогичные характеристики чувствительности
вводятся так же для различных показателей качества системы. Тогда в
формуле (4) вместо xi будет стоять соответствующий показатель качества,
Функции чувствительности для частотных характеристик будут функциями
не времени, а частоты.
Если показатели качества выражаются не функциями, а числами, то uij
называются коэффициентами чувствительности.
Если в качестве изменяющихся параметров
j выбрать внешние
воздействия, то можно получить функции чувствительности системы по
отношению к внешним воздействиям.



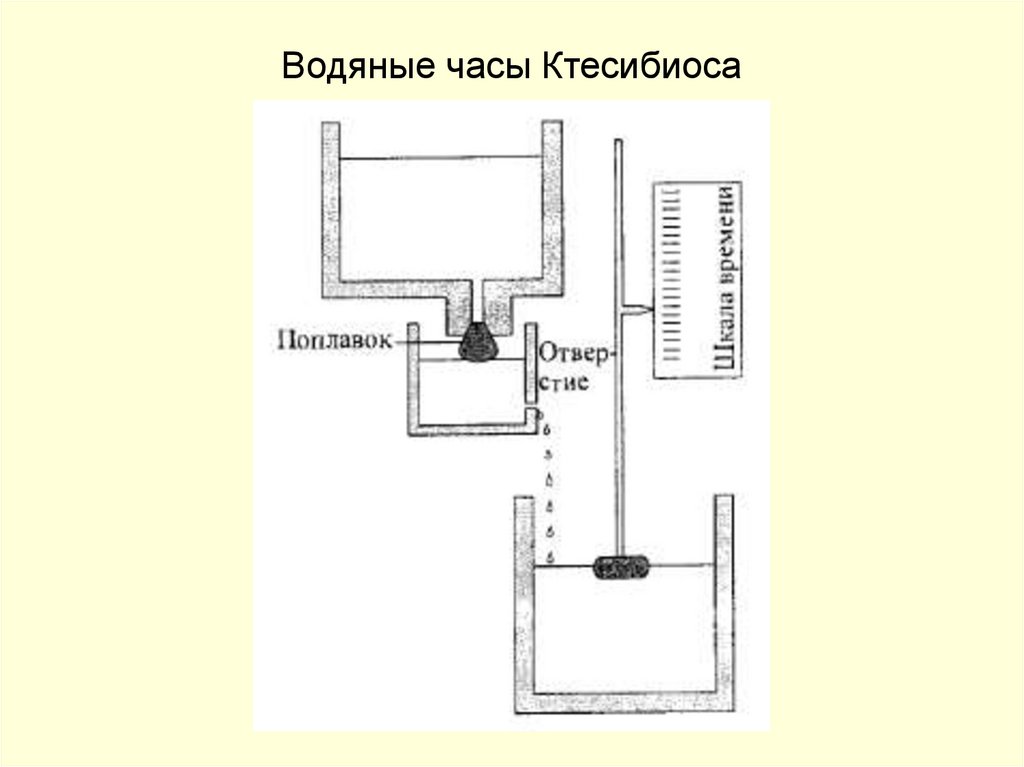
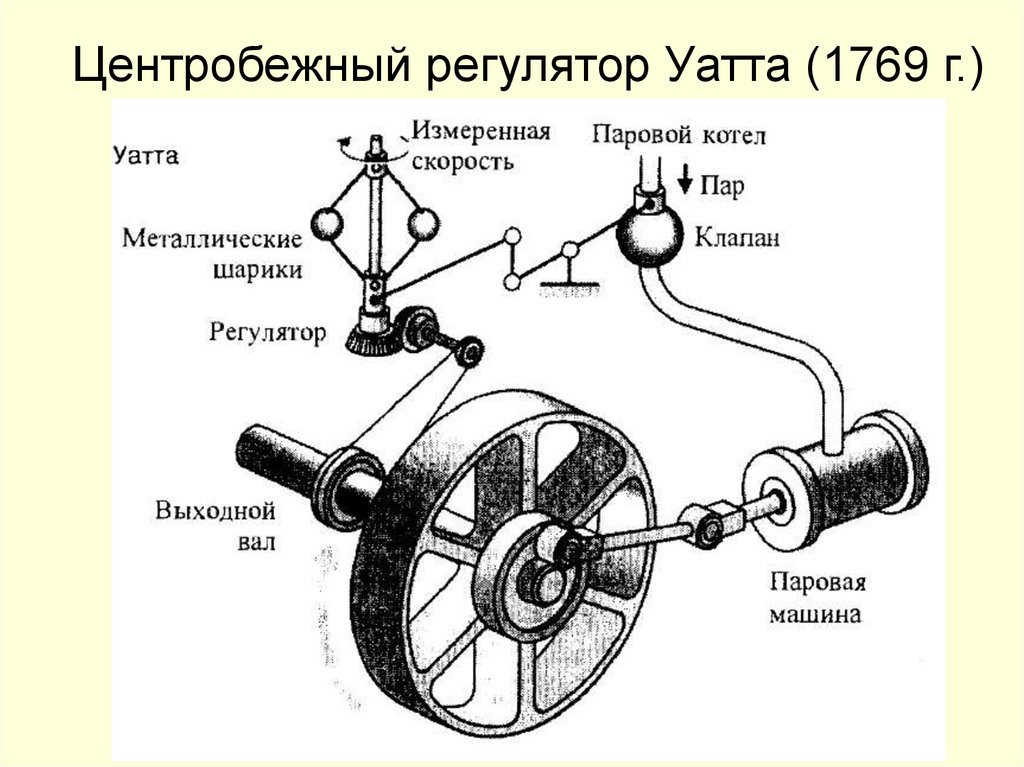
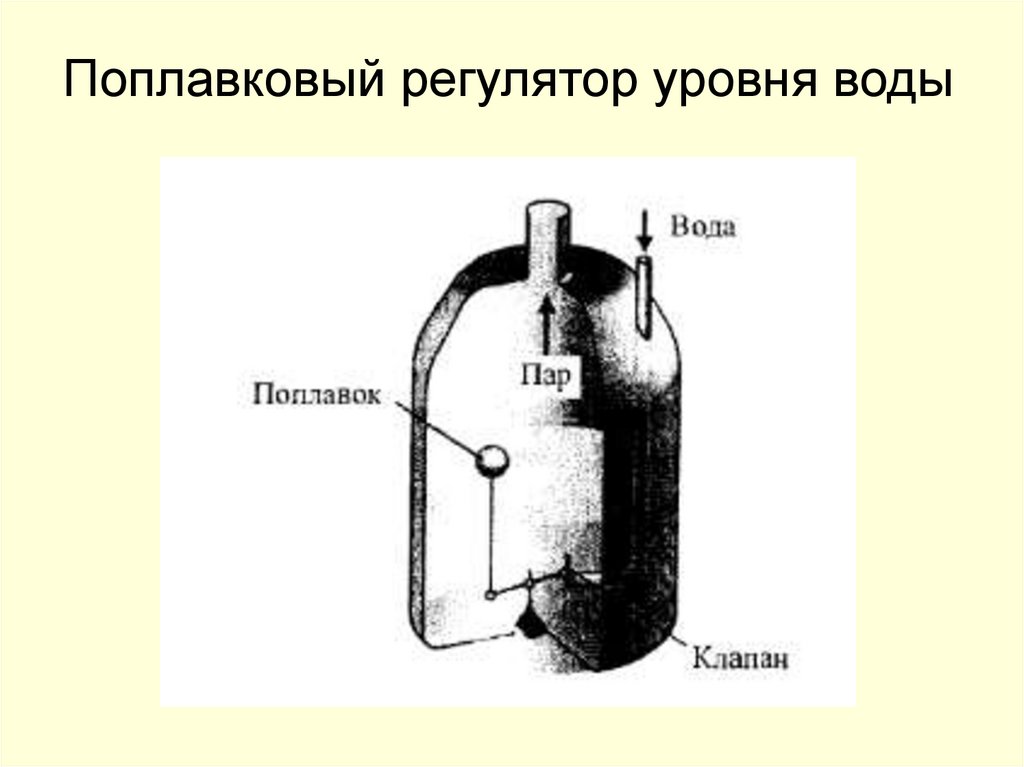
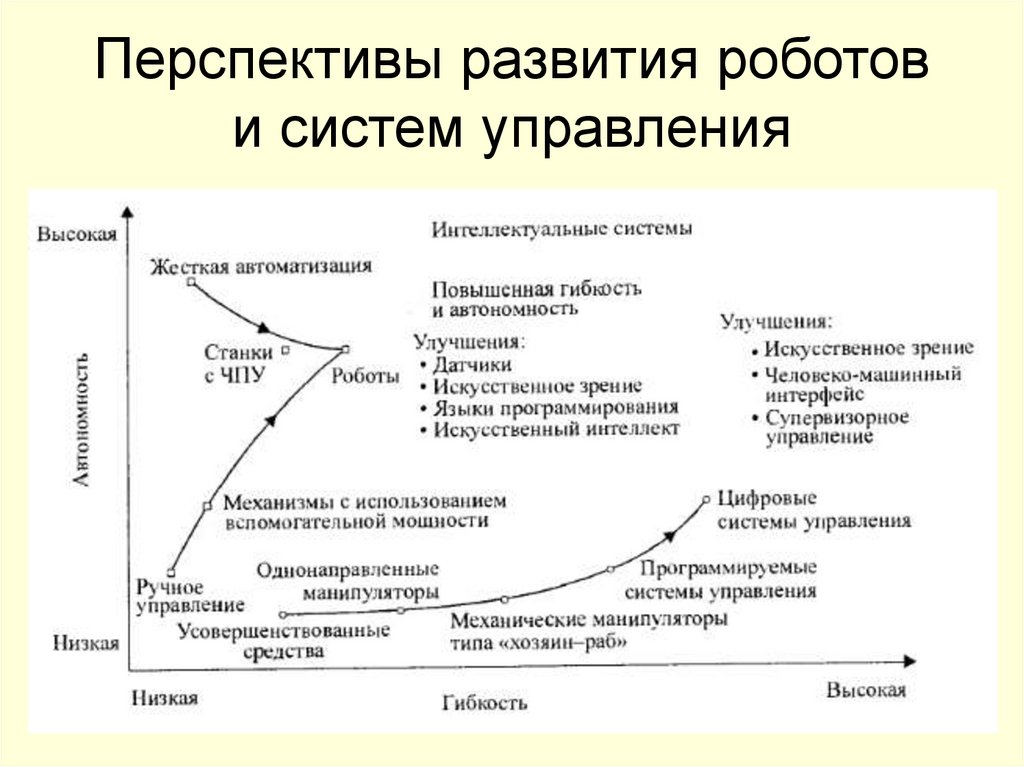

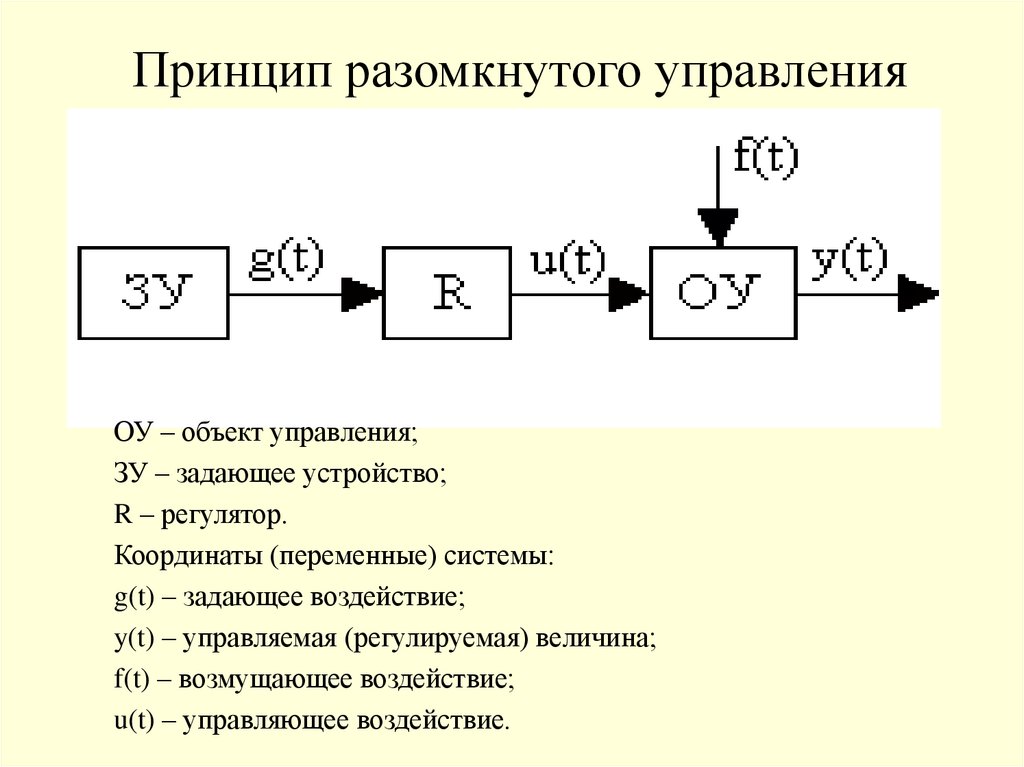
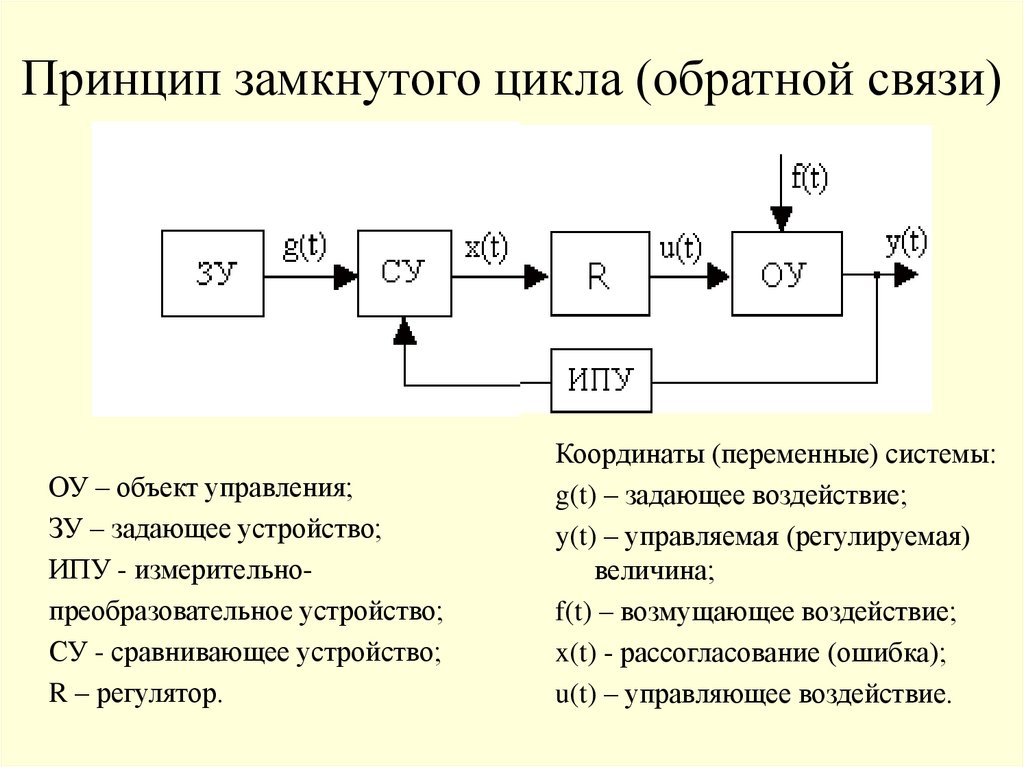
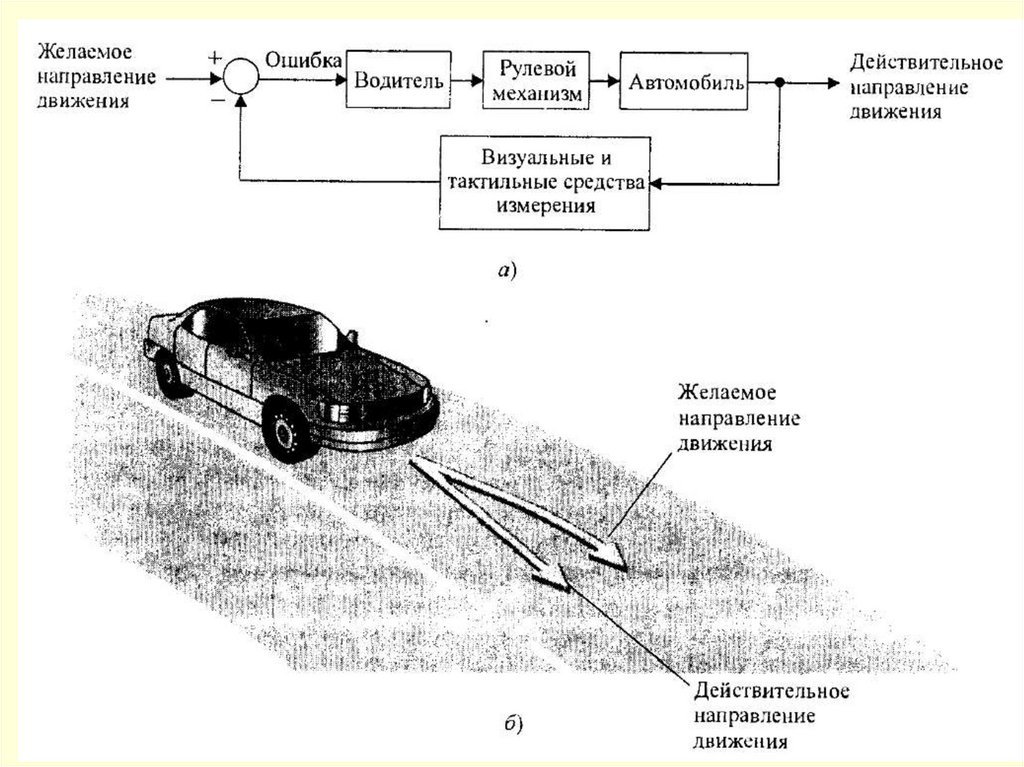
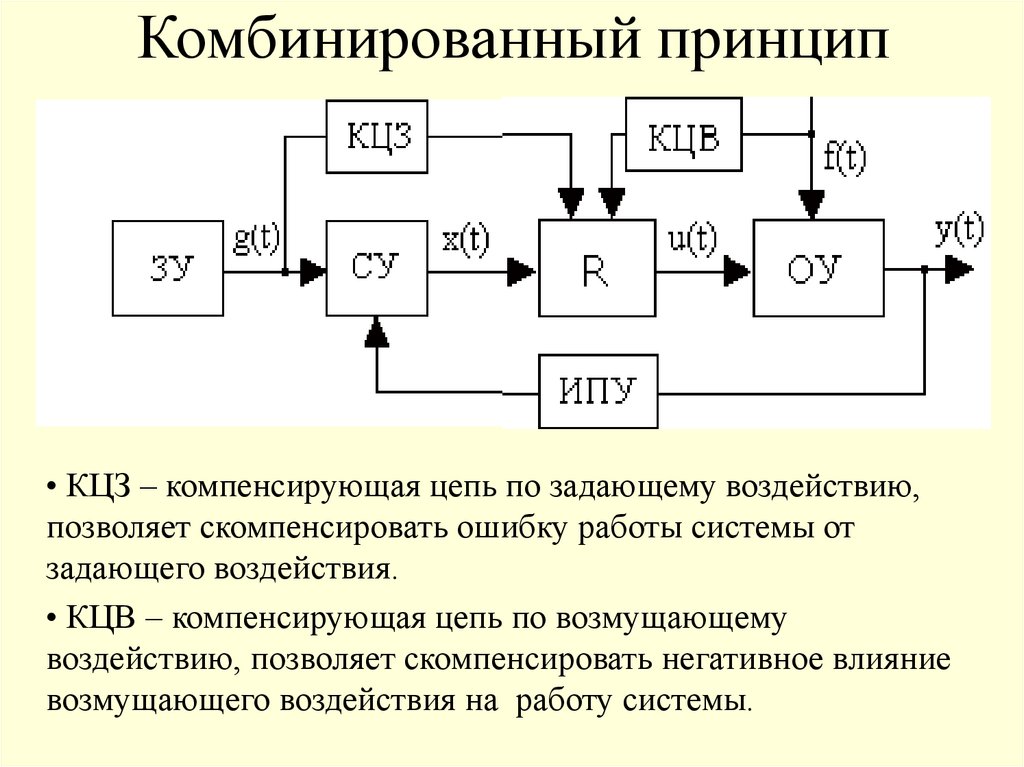

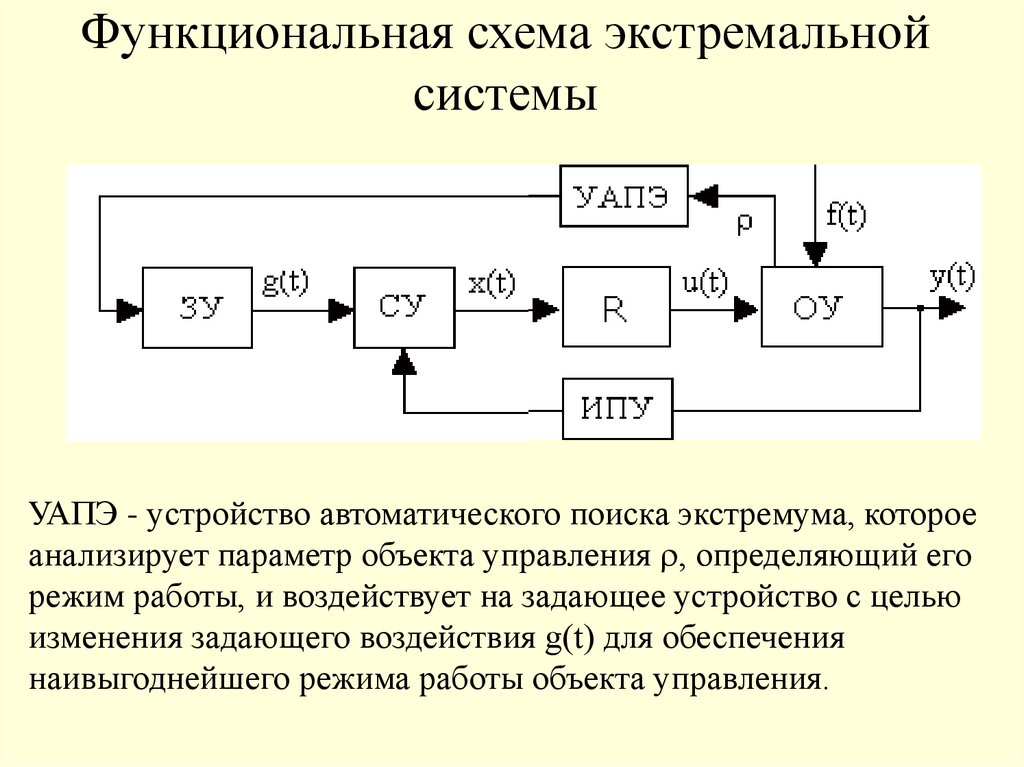



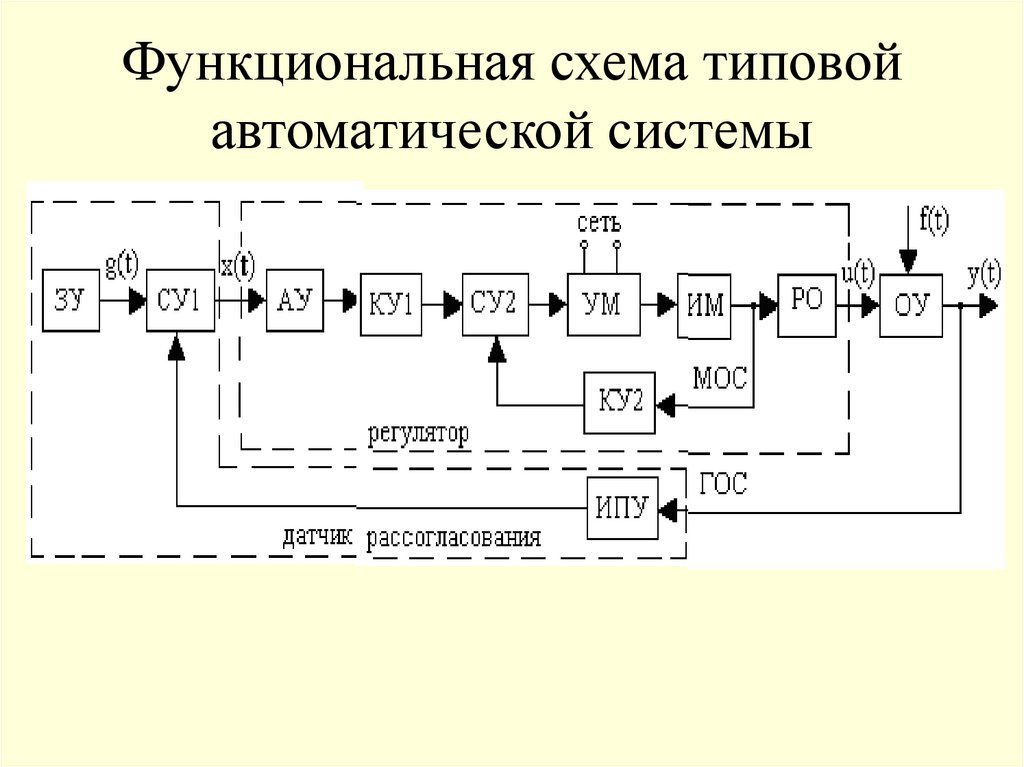

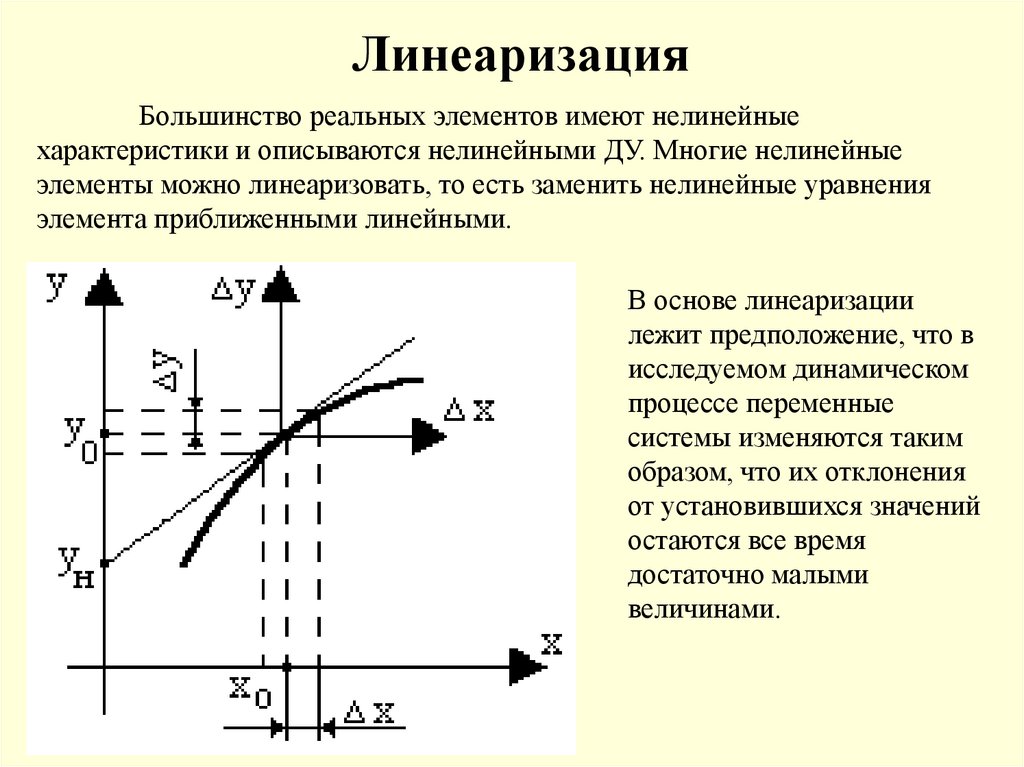







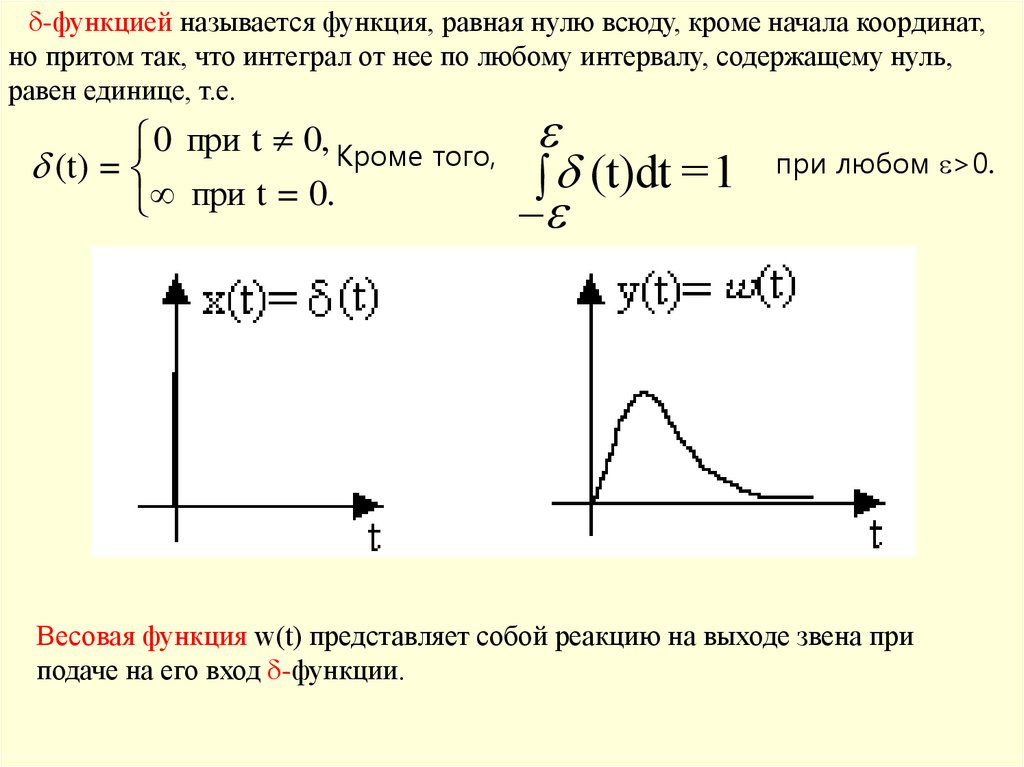
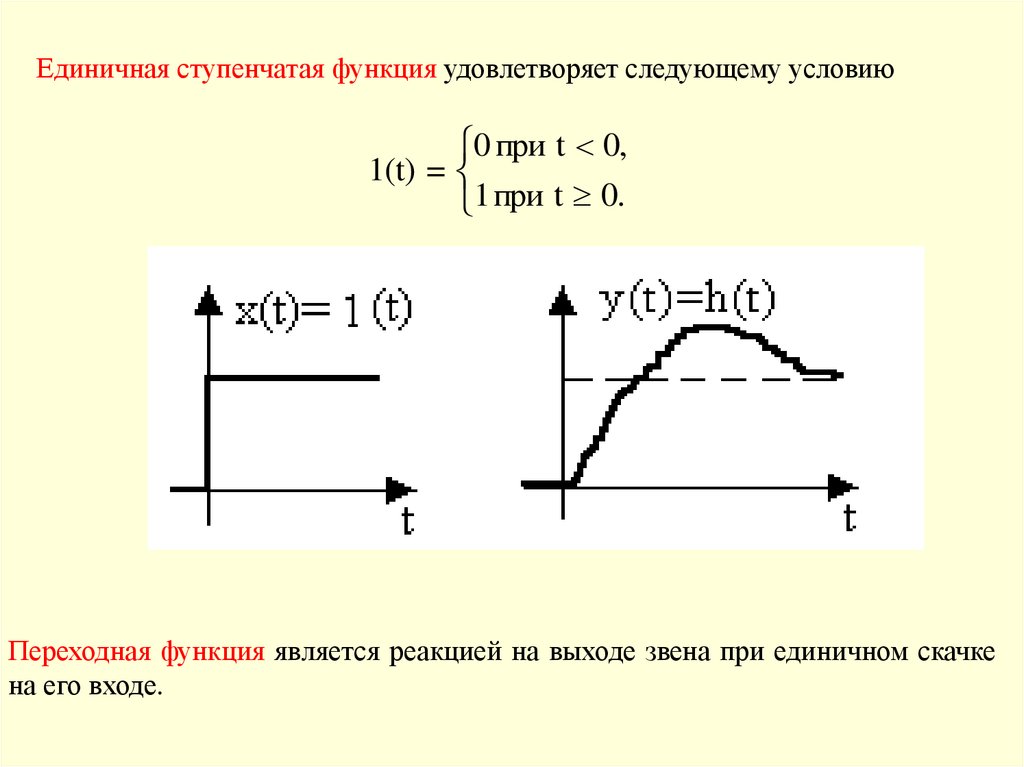


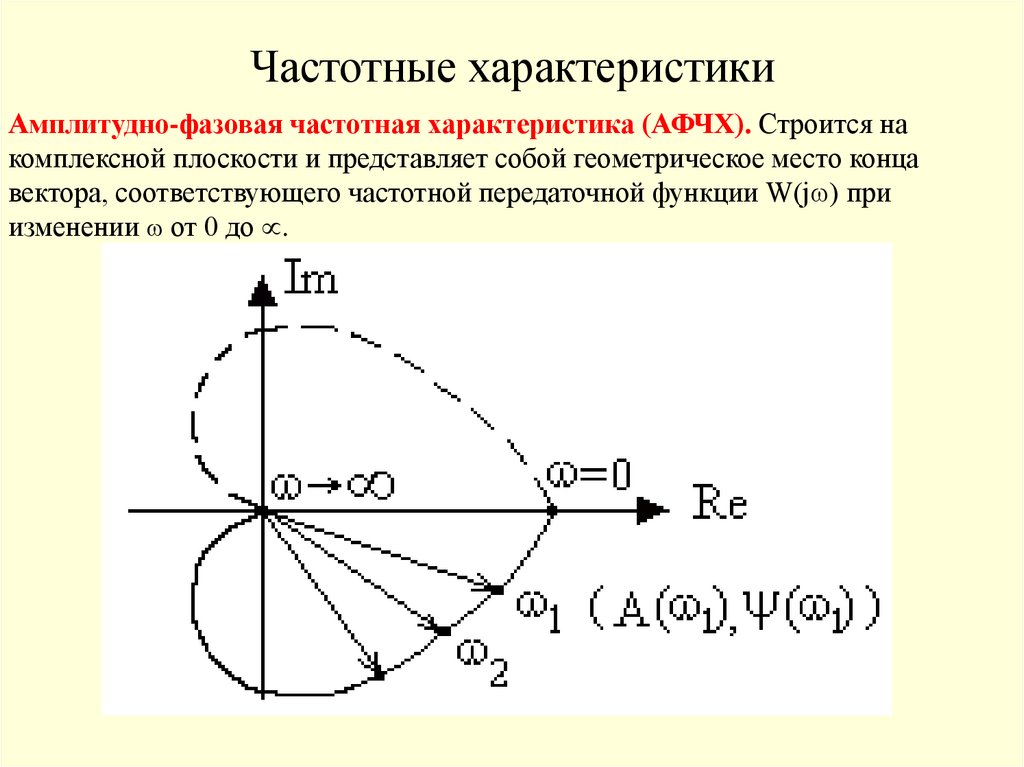
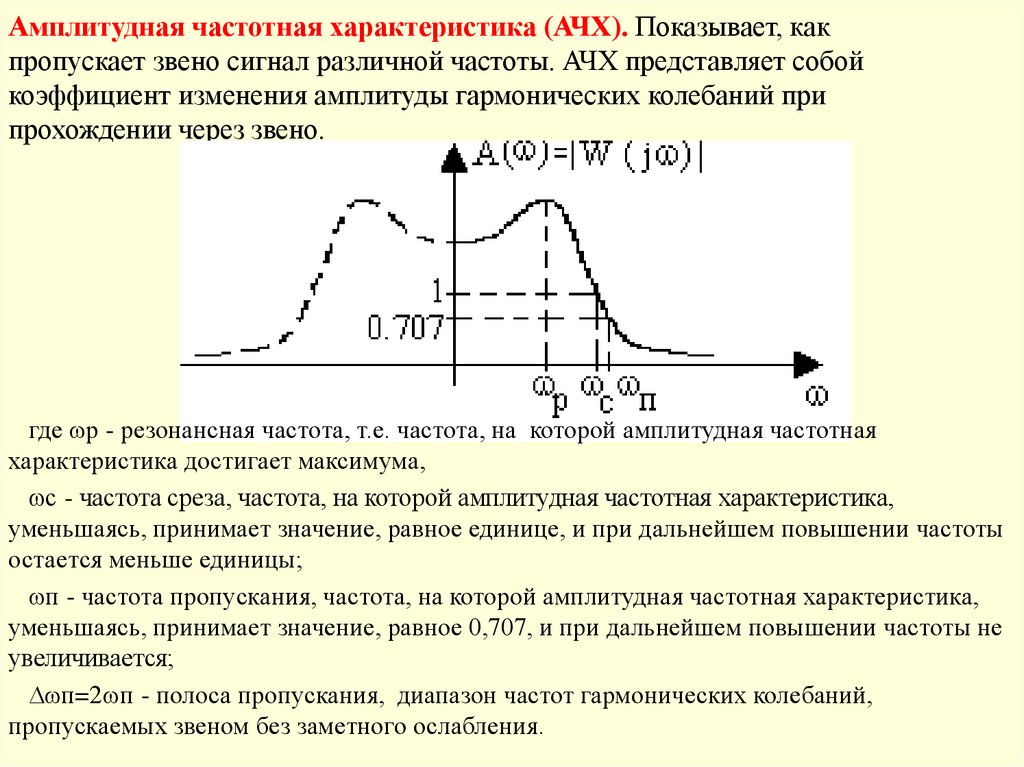
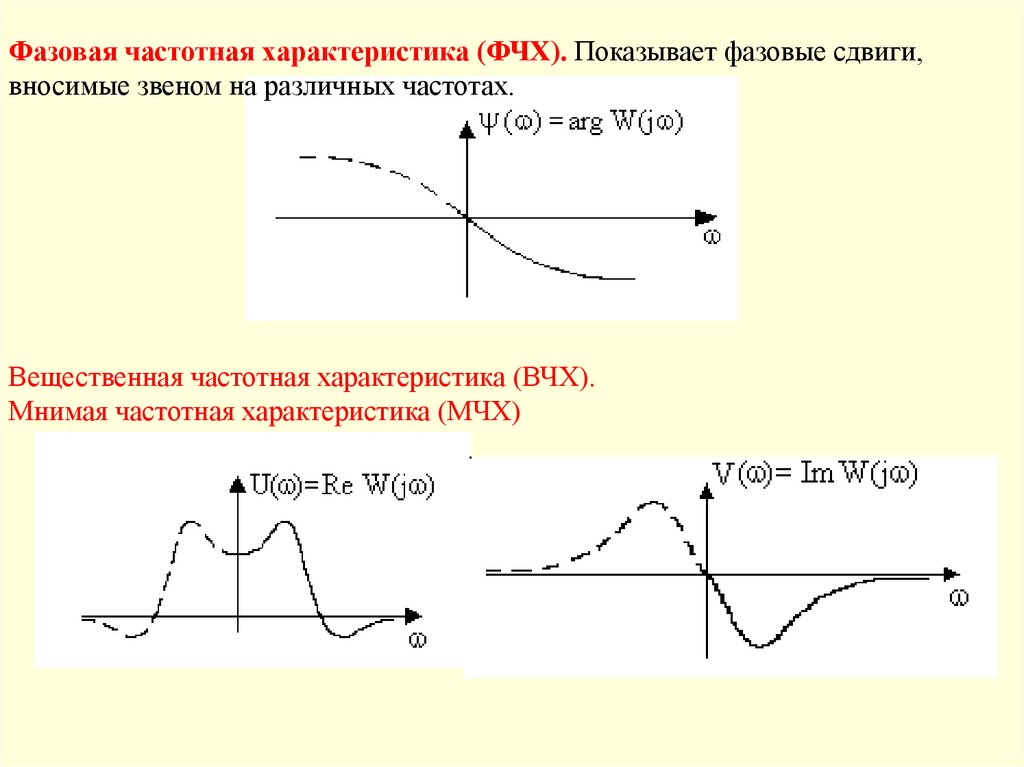
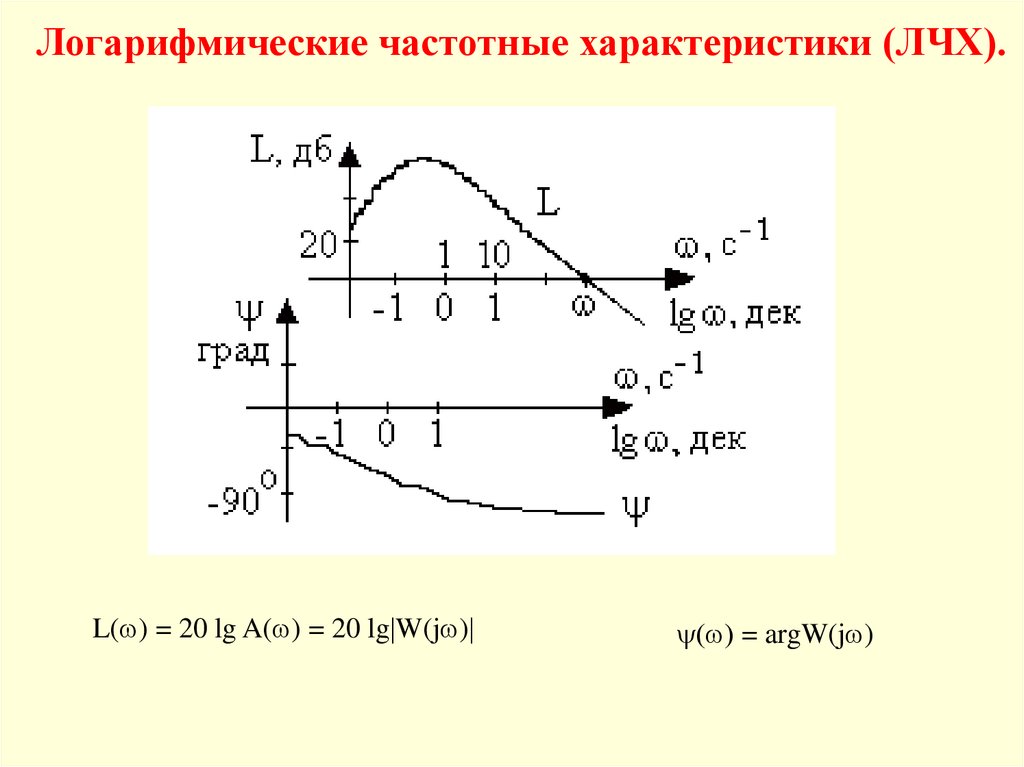



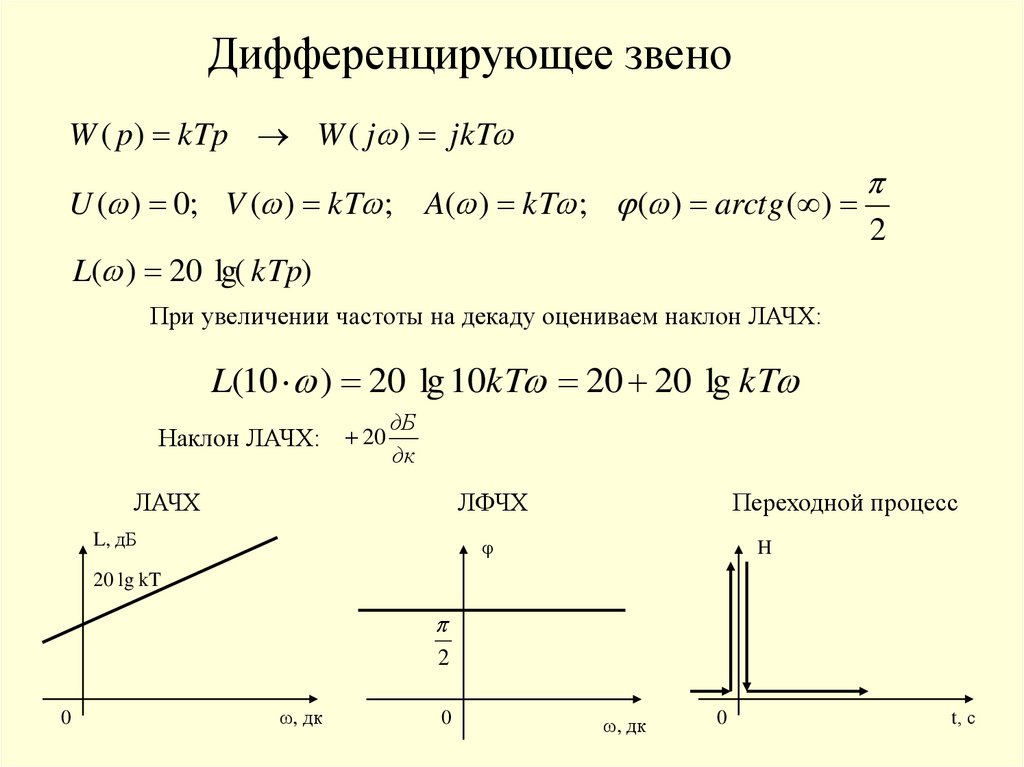
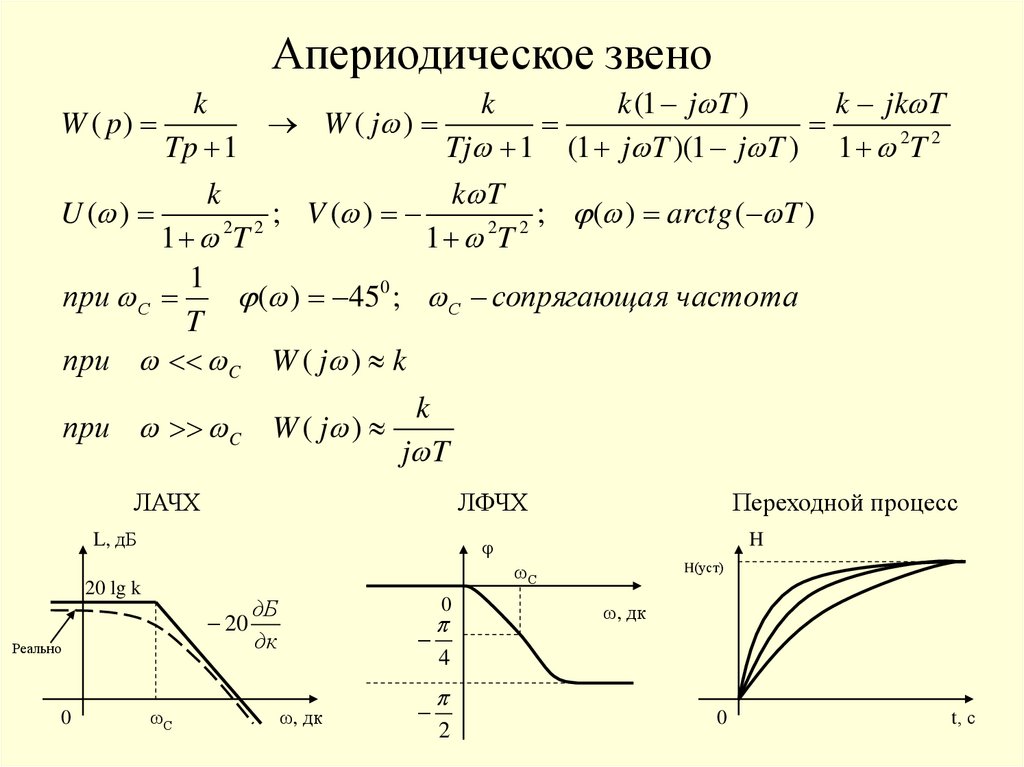
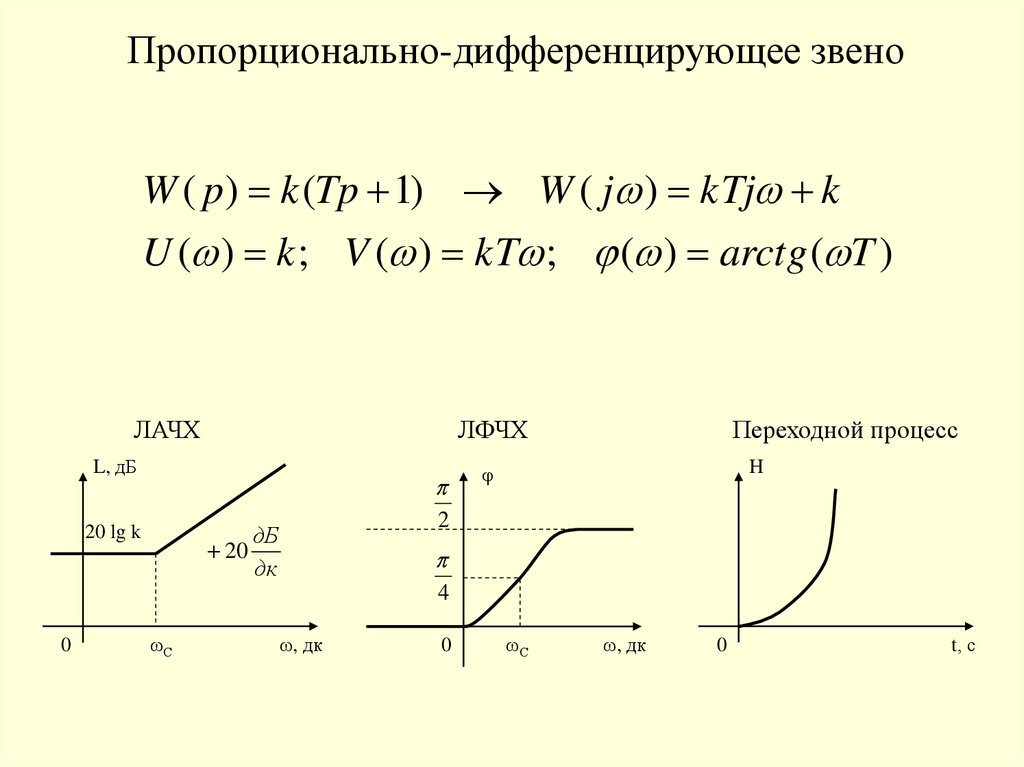
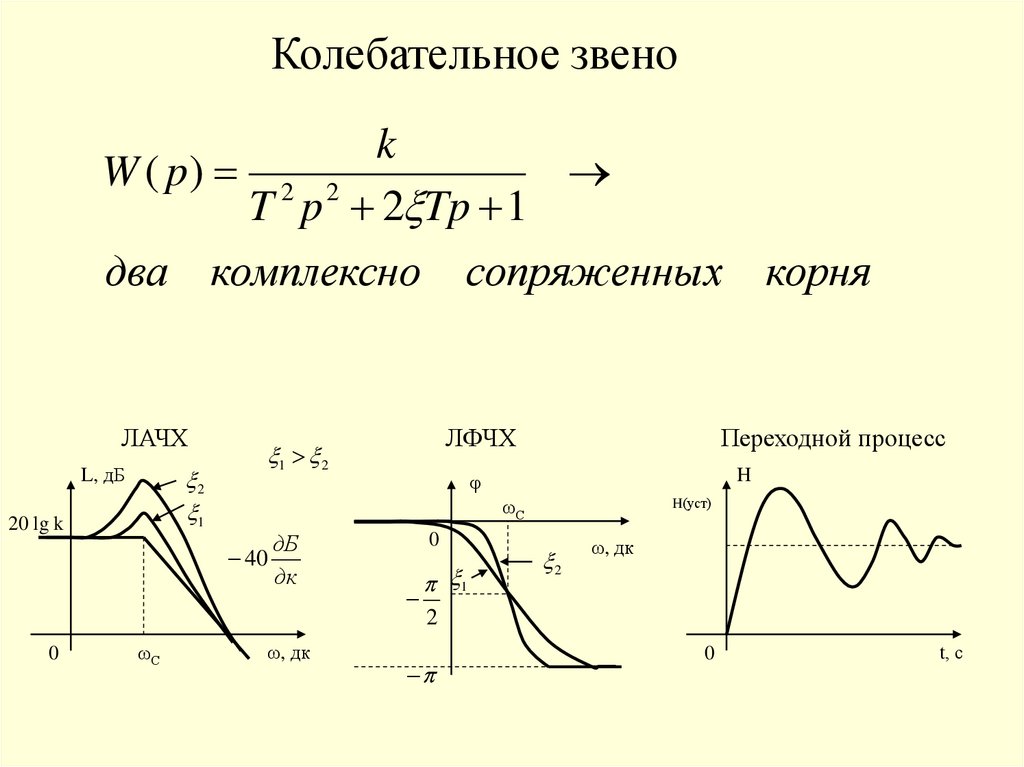
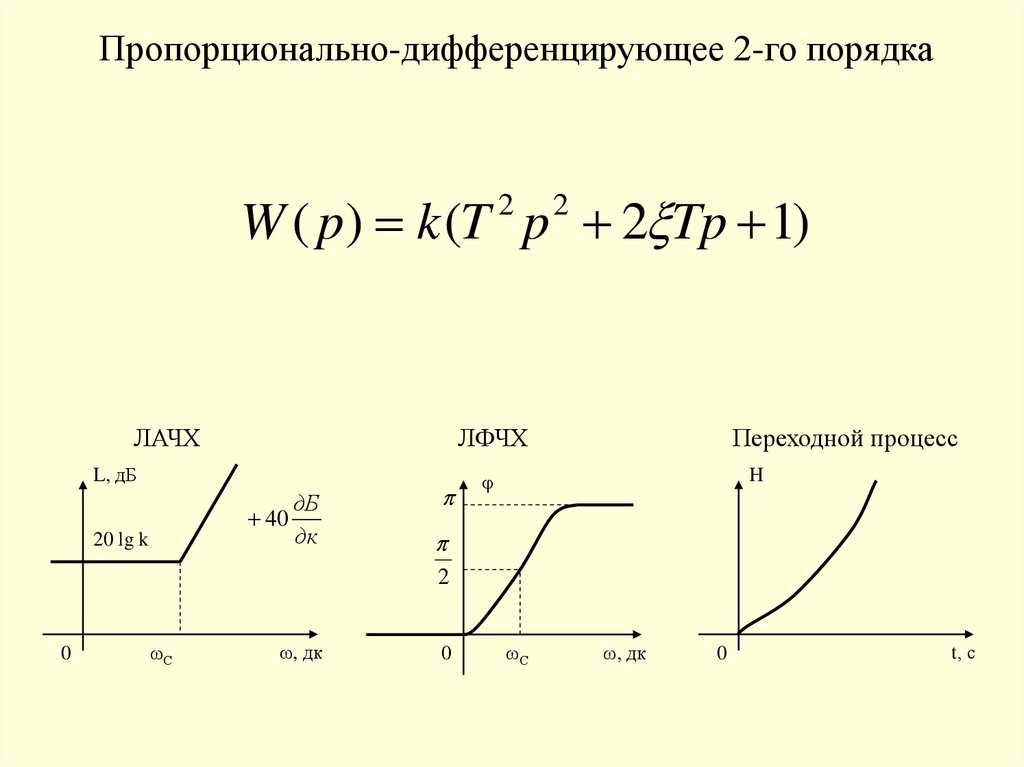


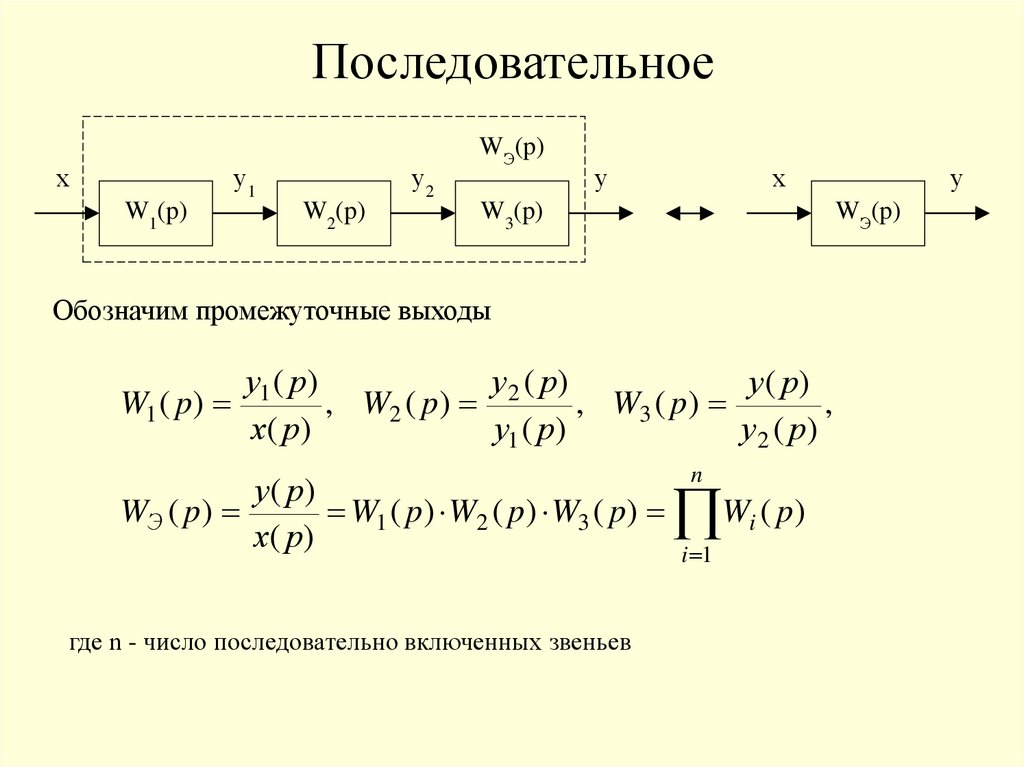
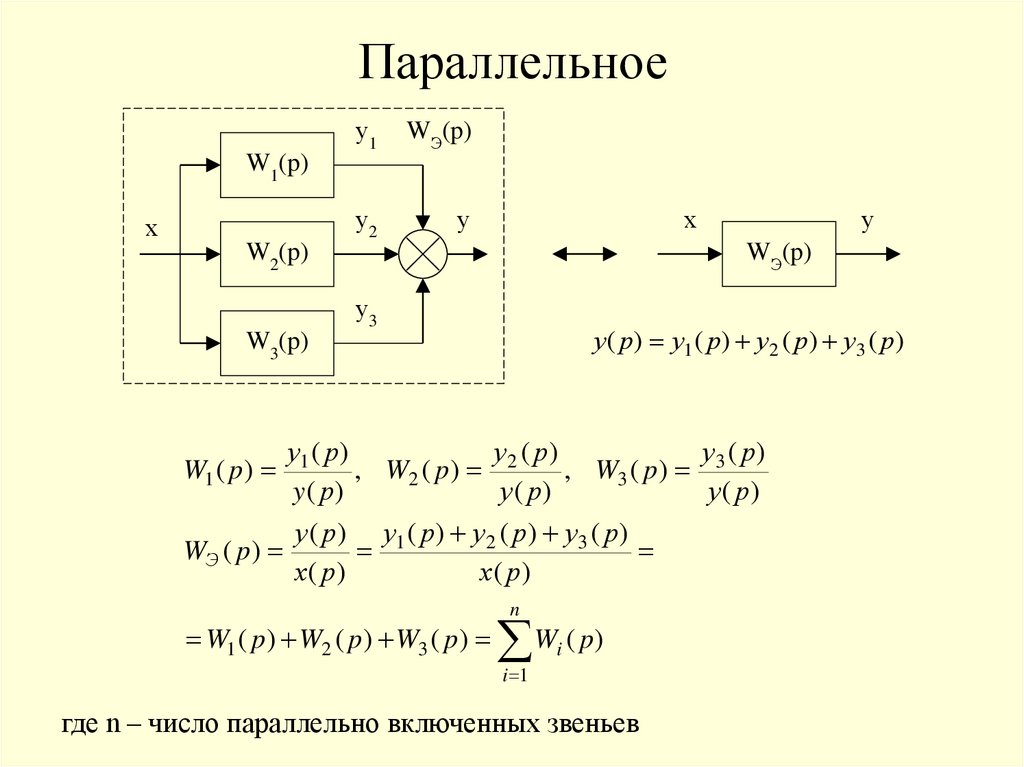
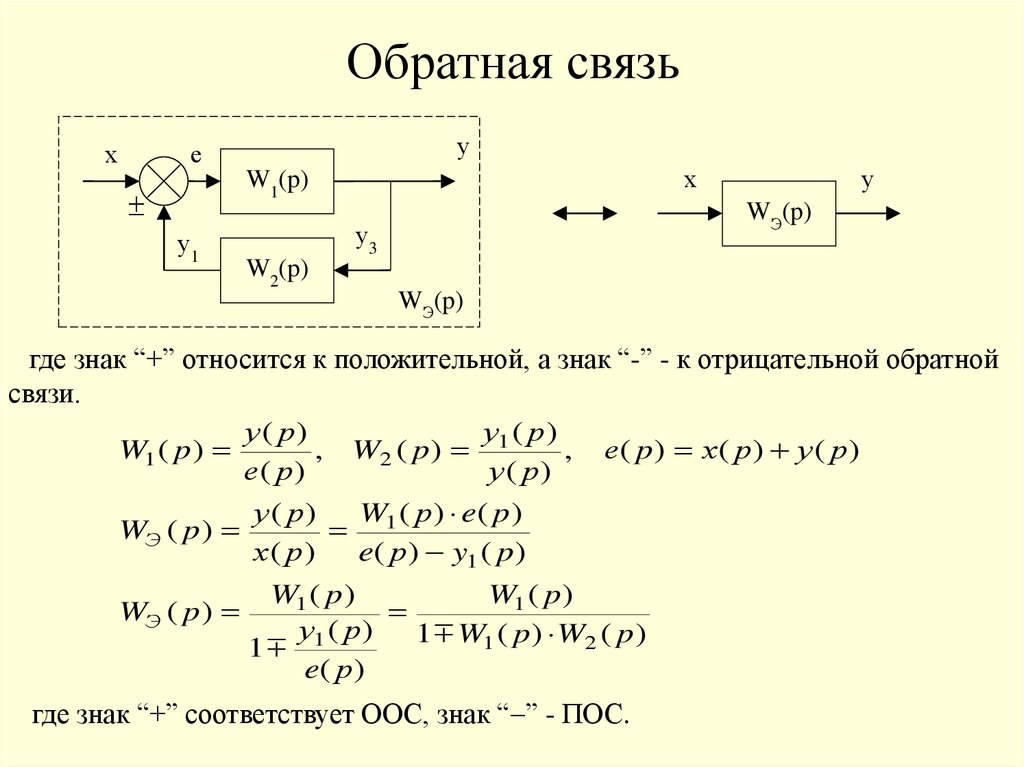
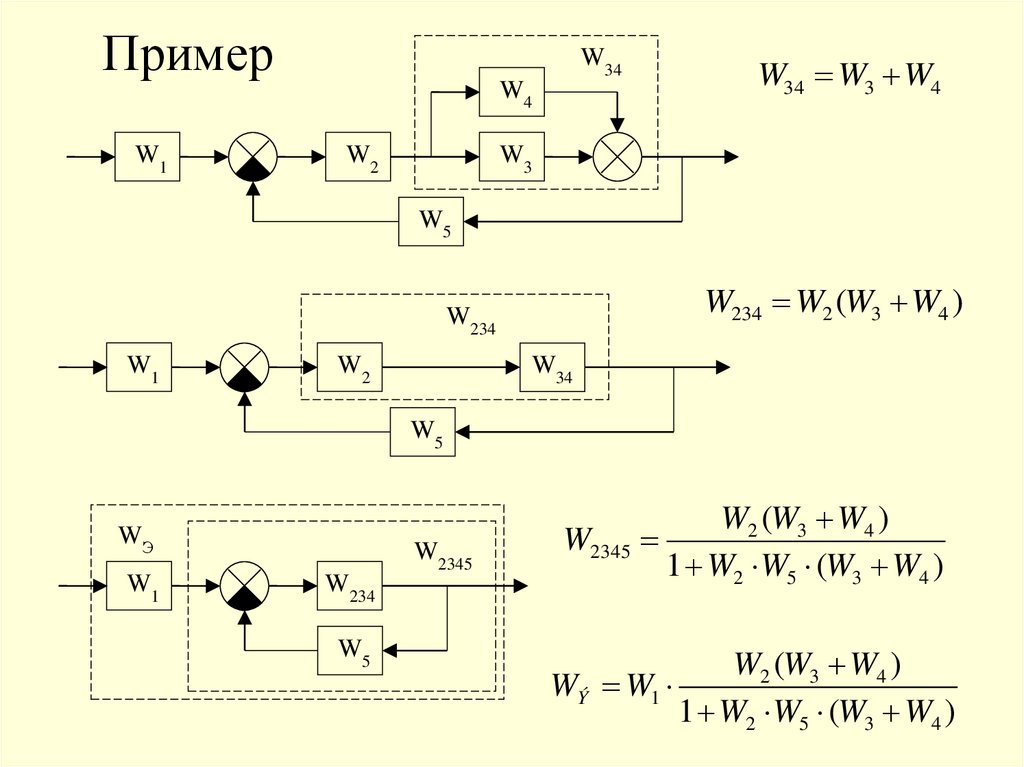

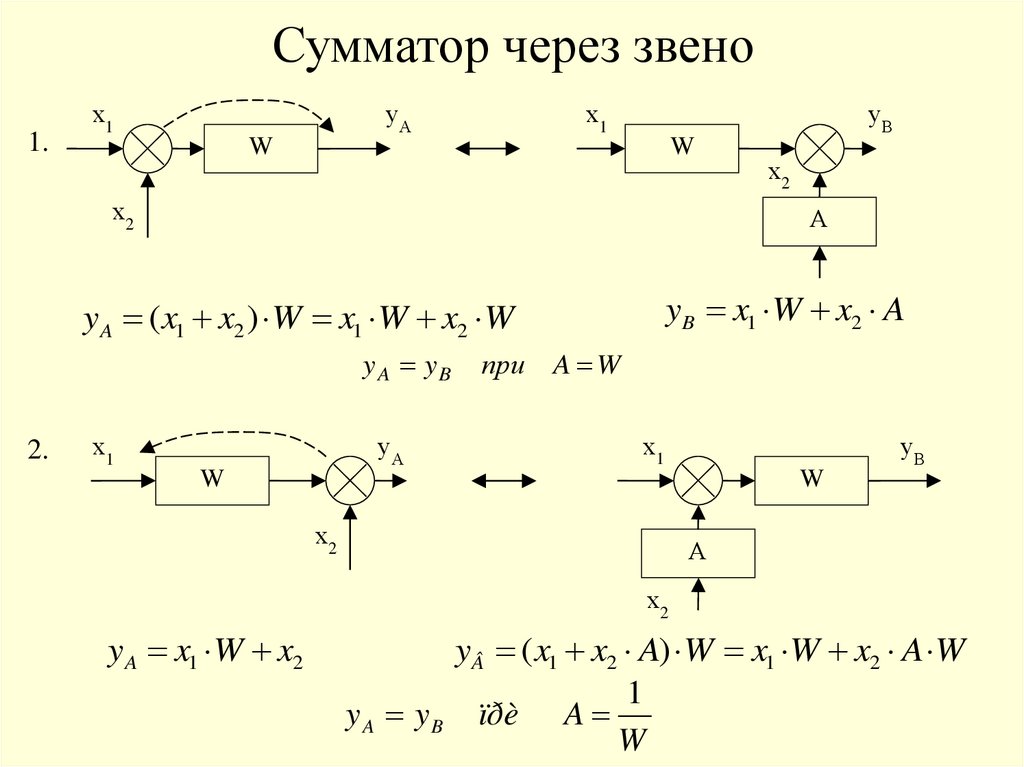
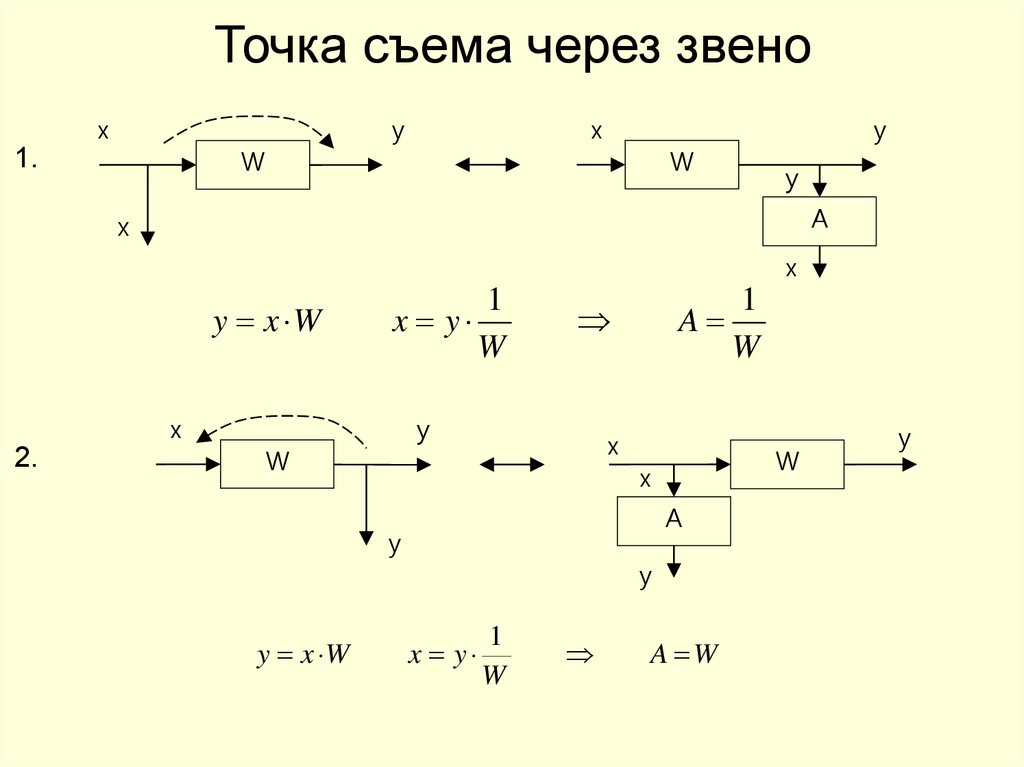
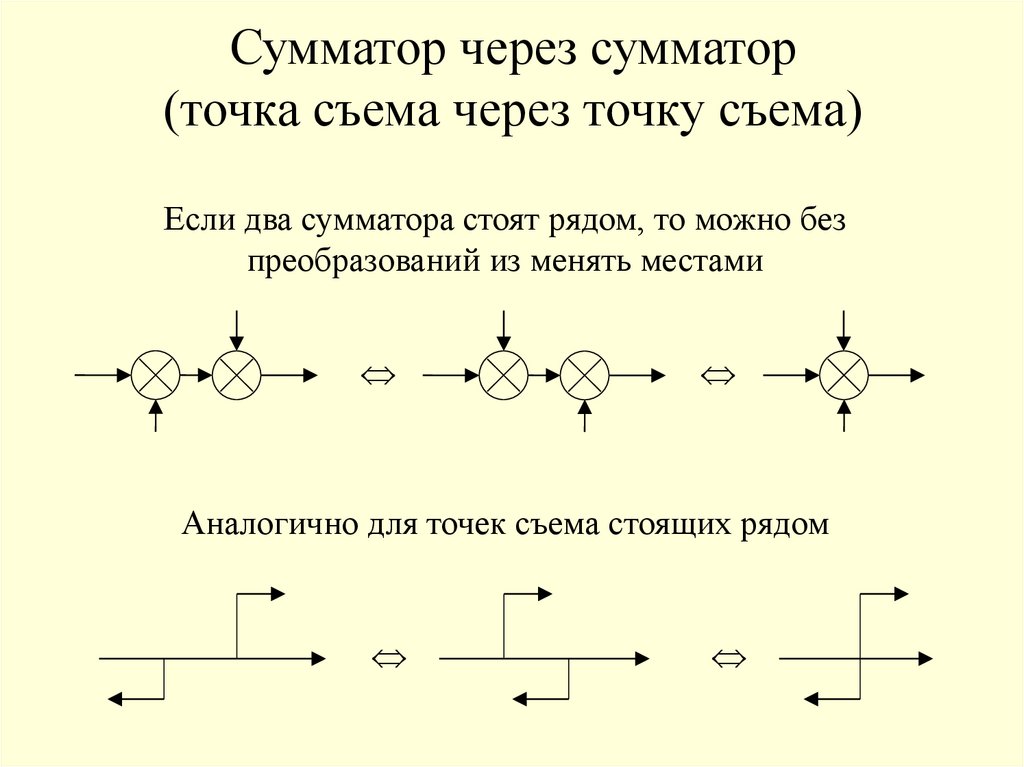
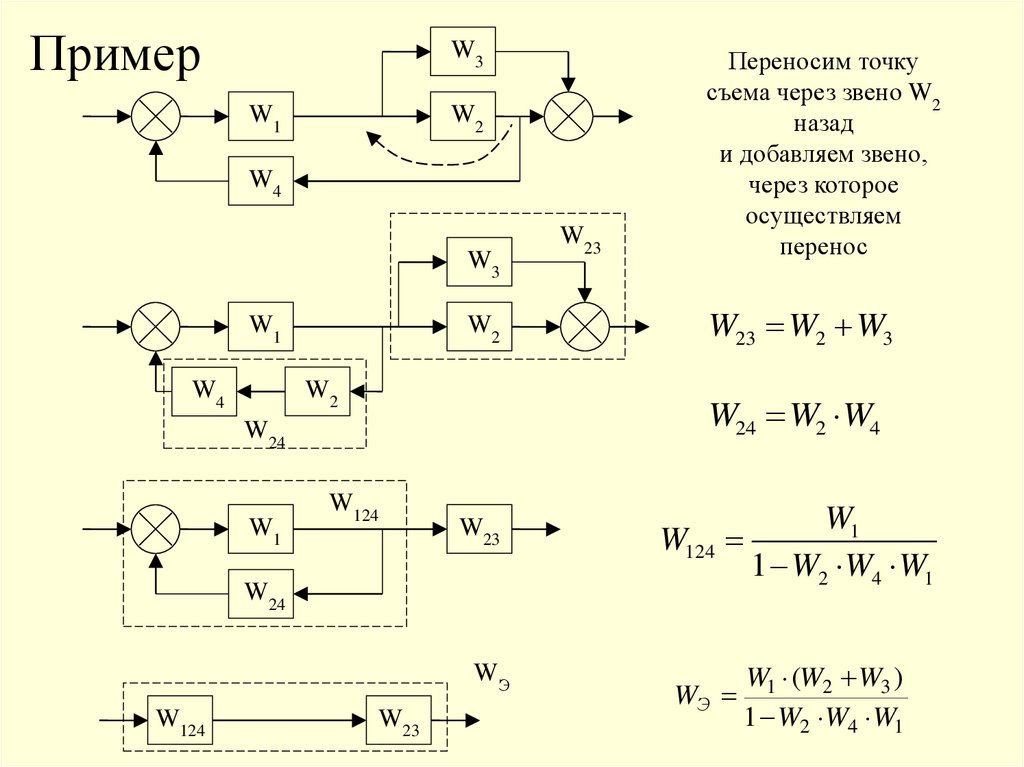





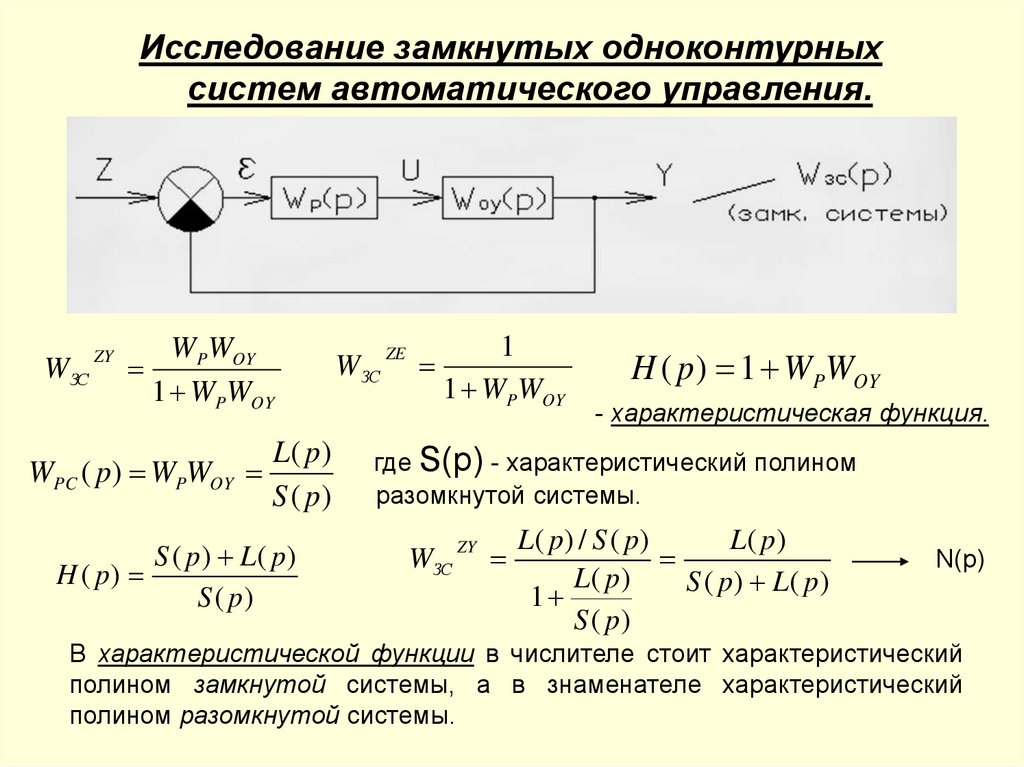
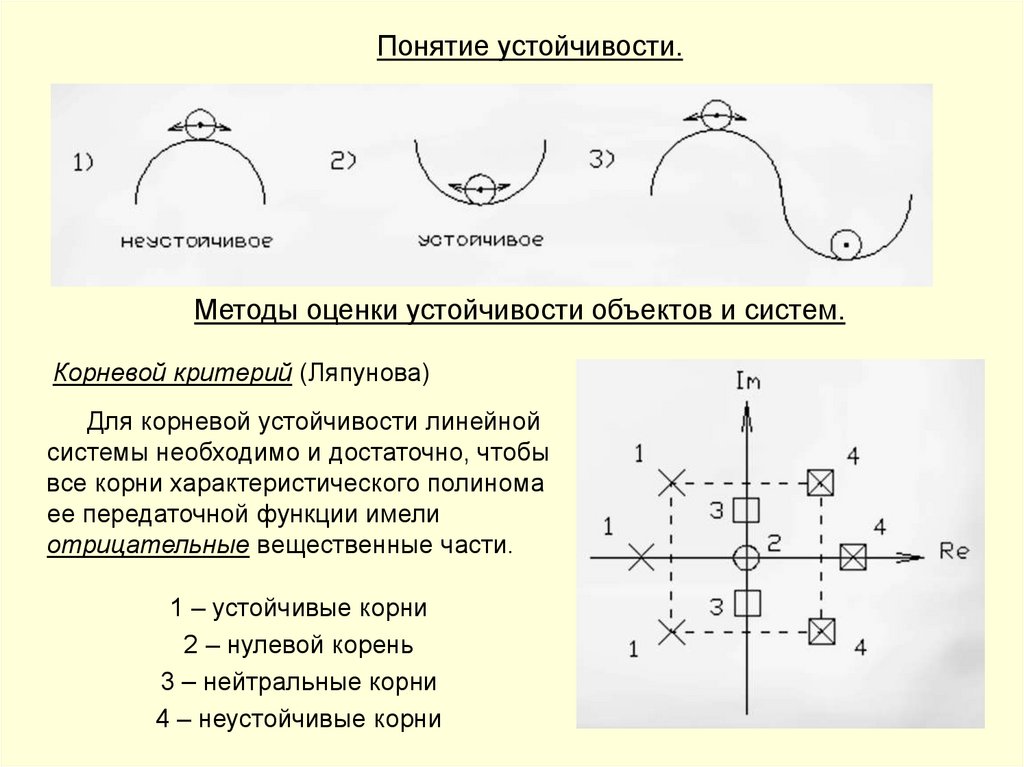


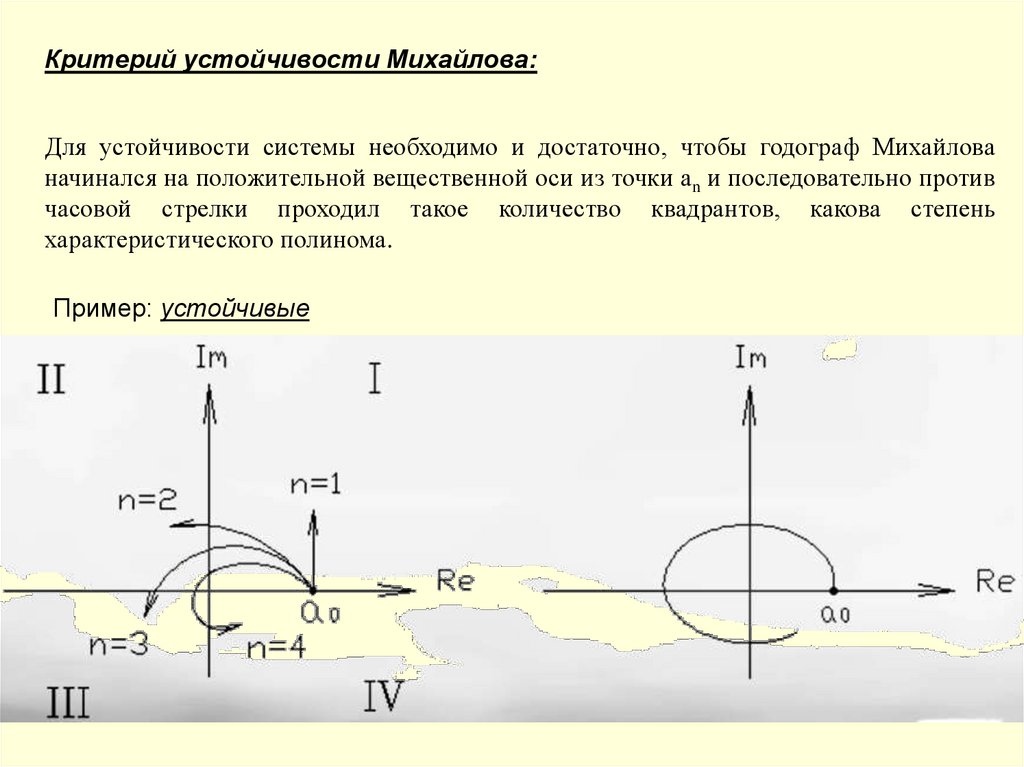
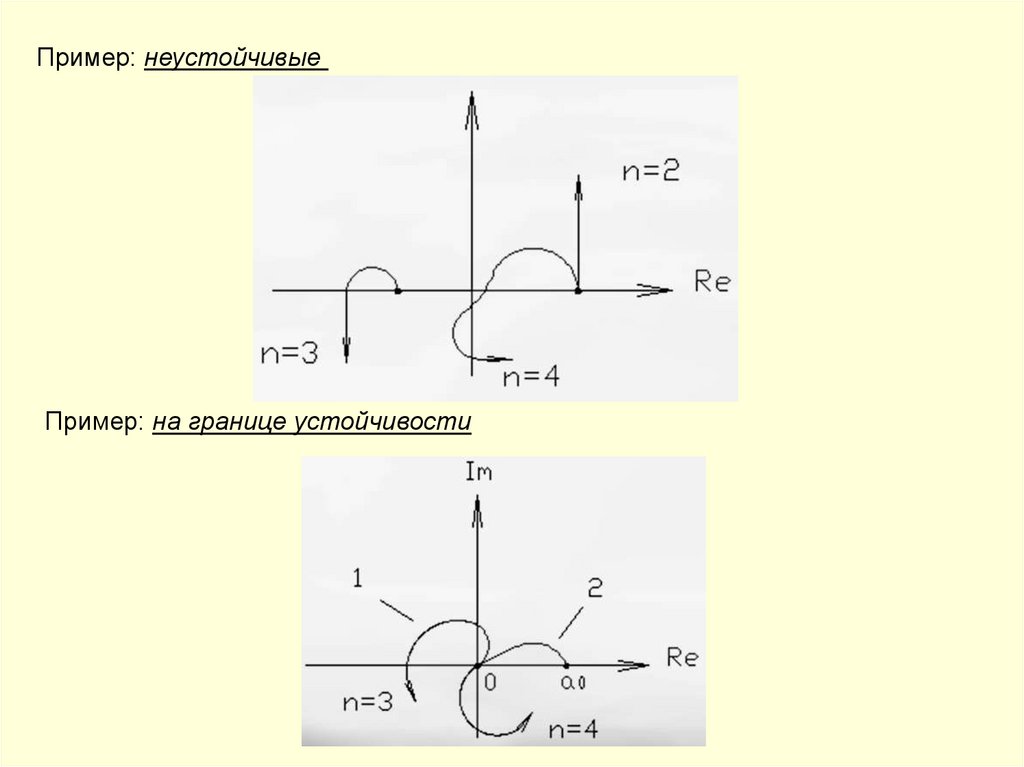


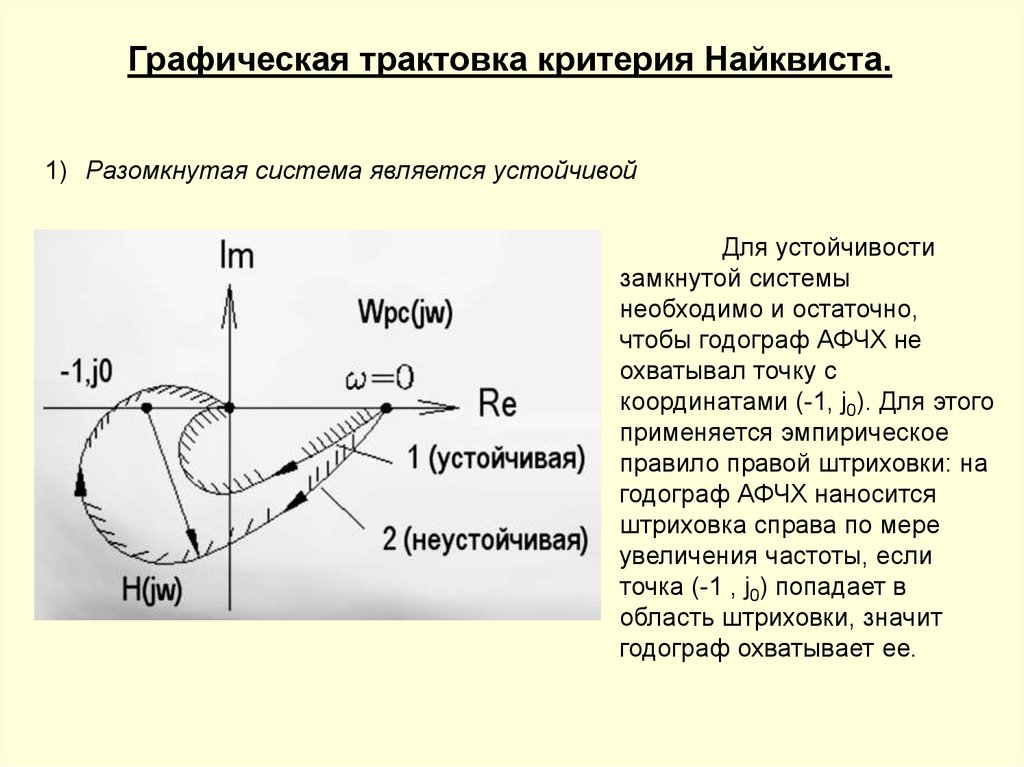
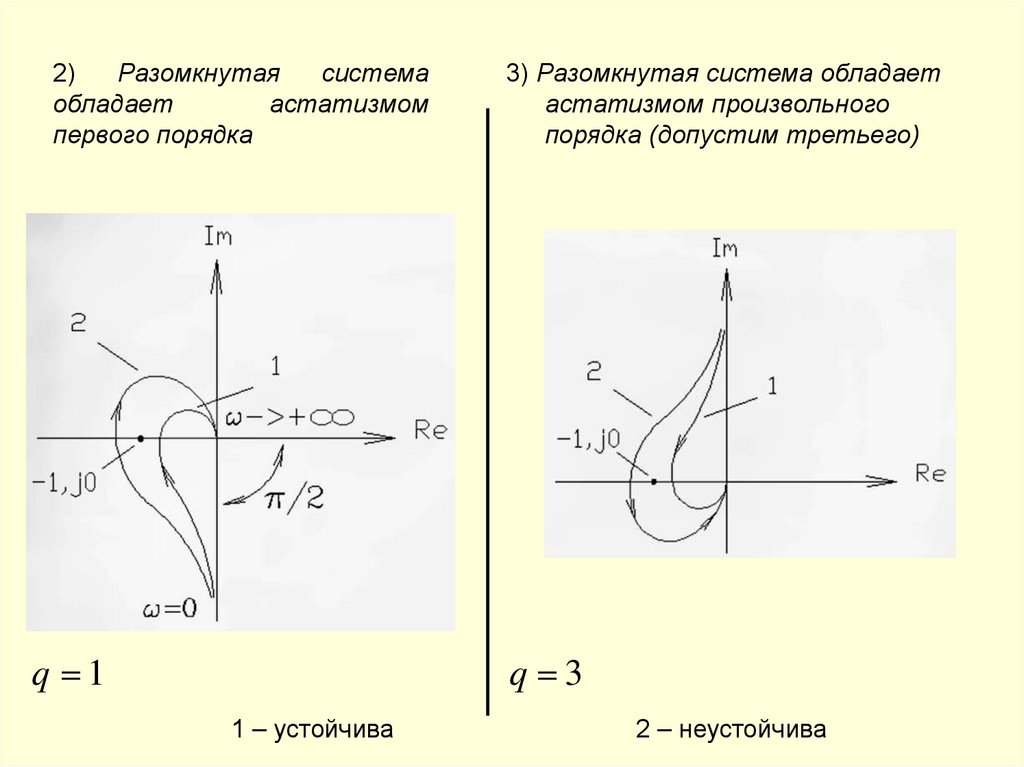






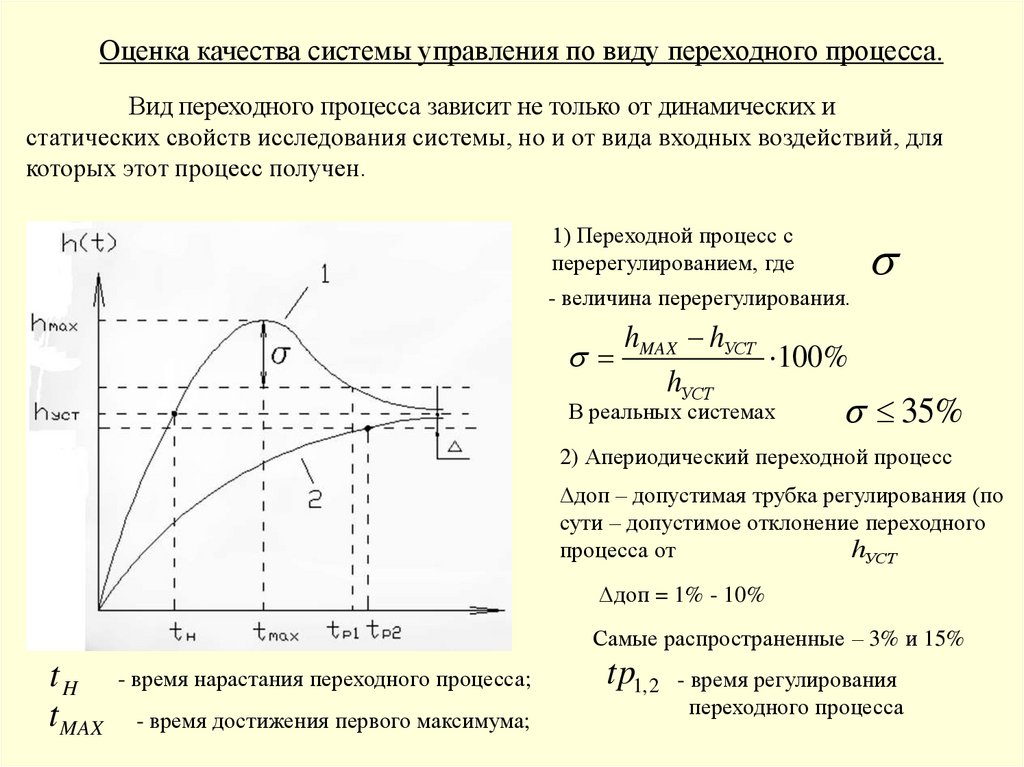
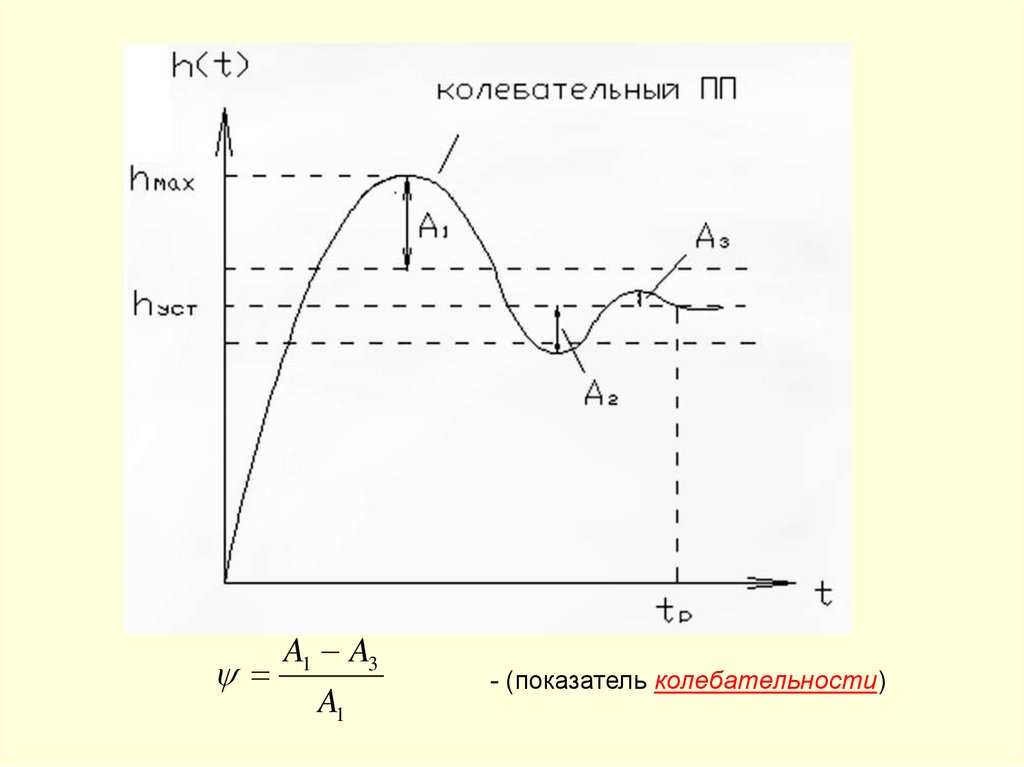

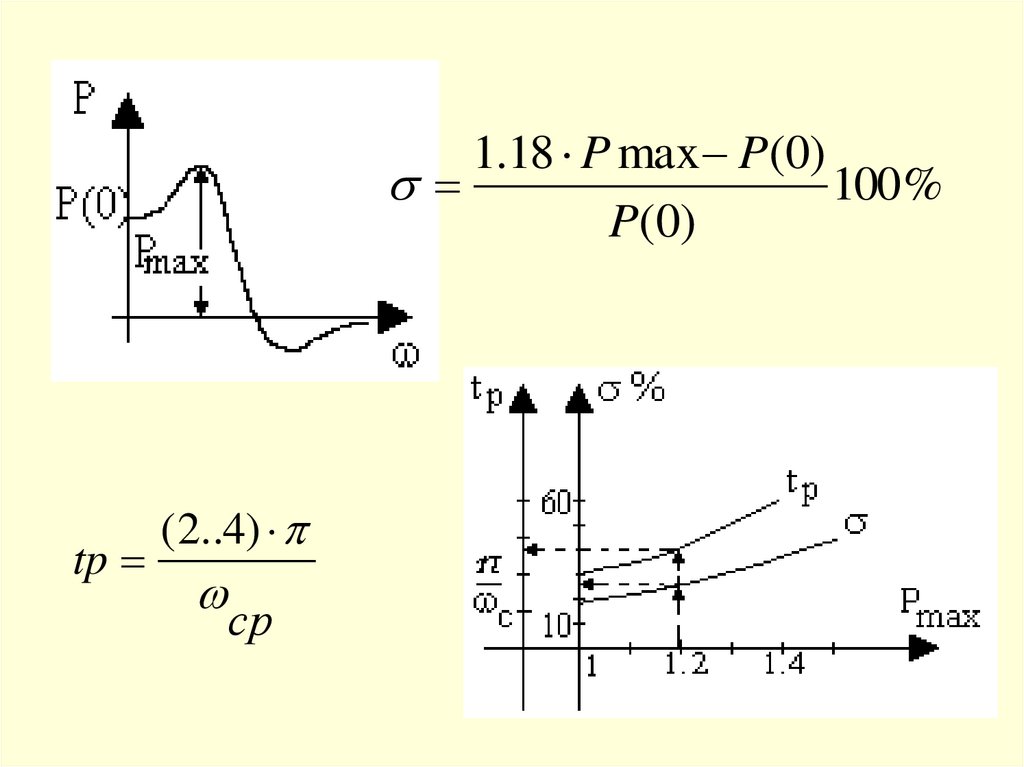

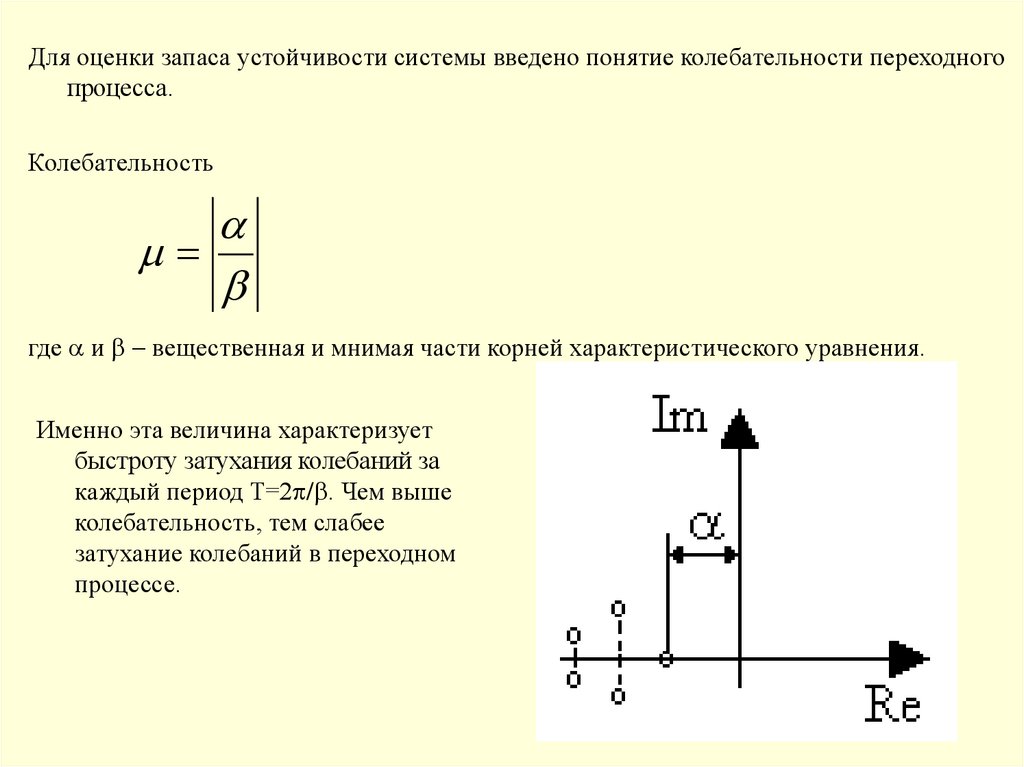
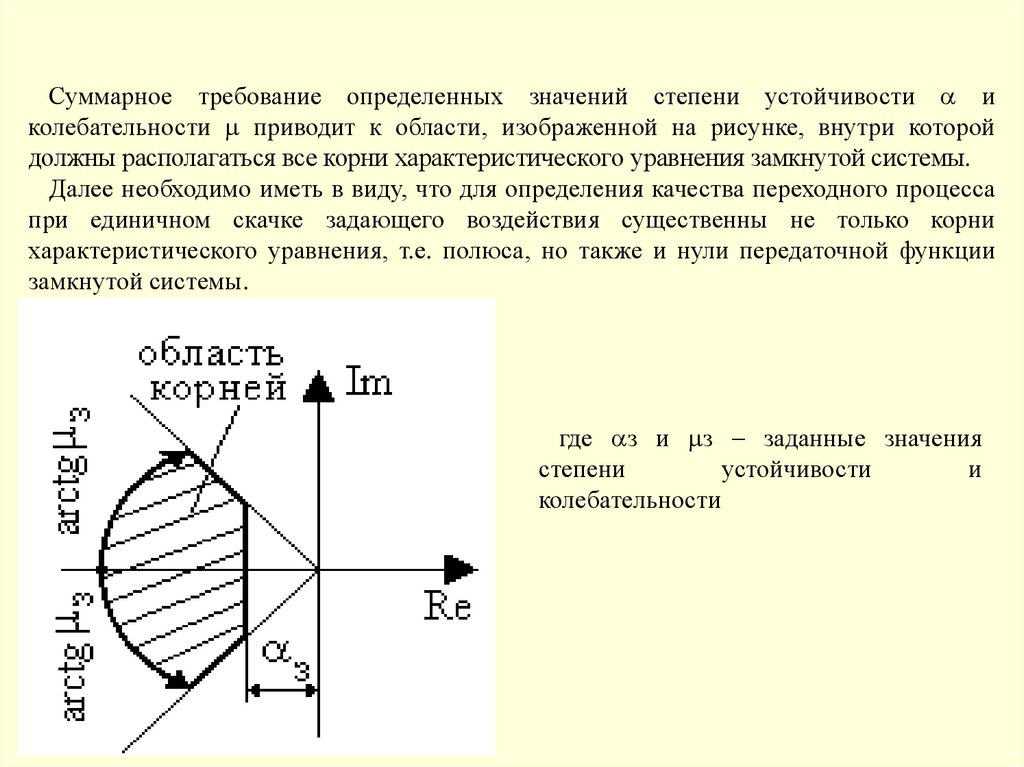


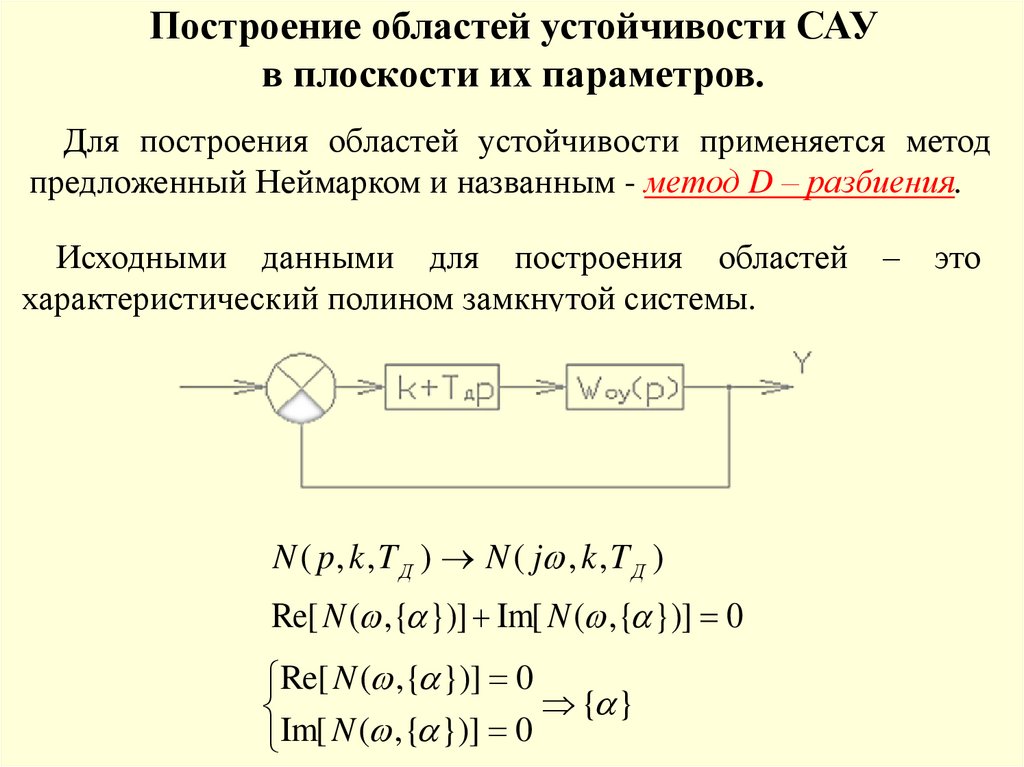






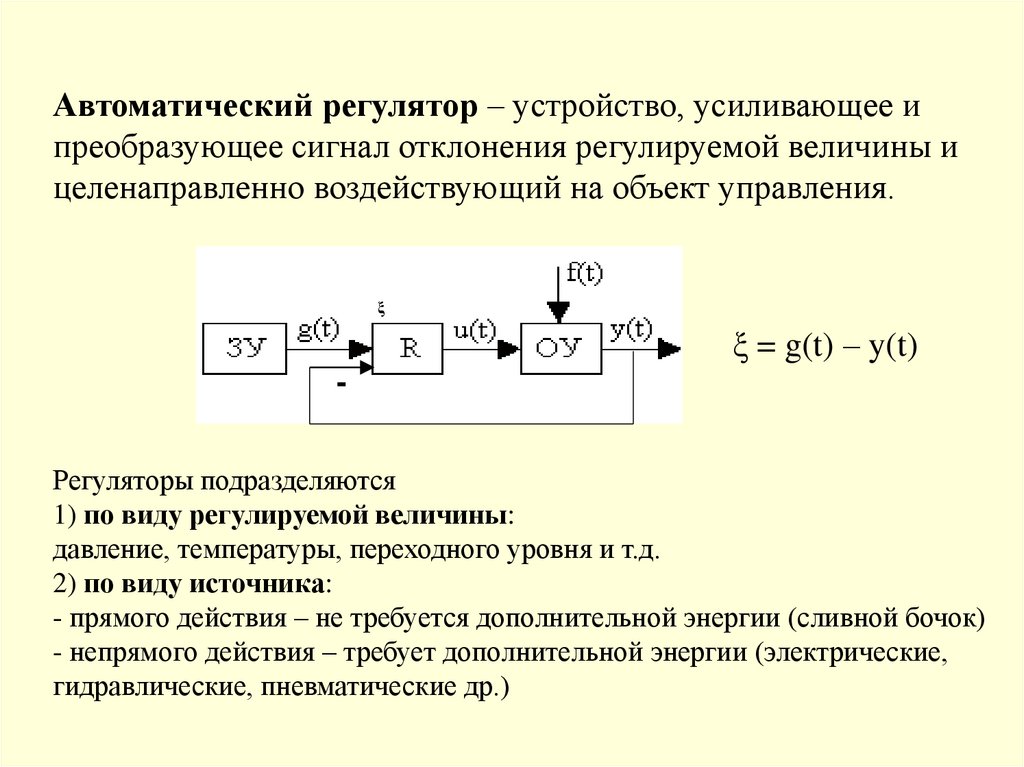

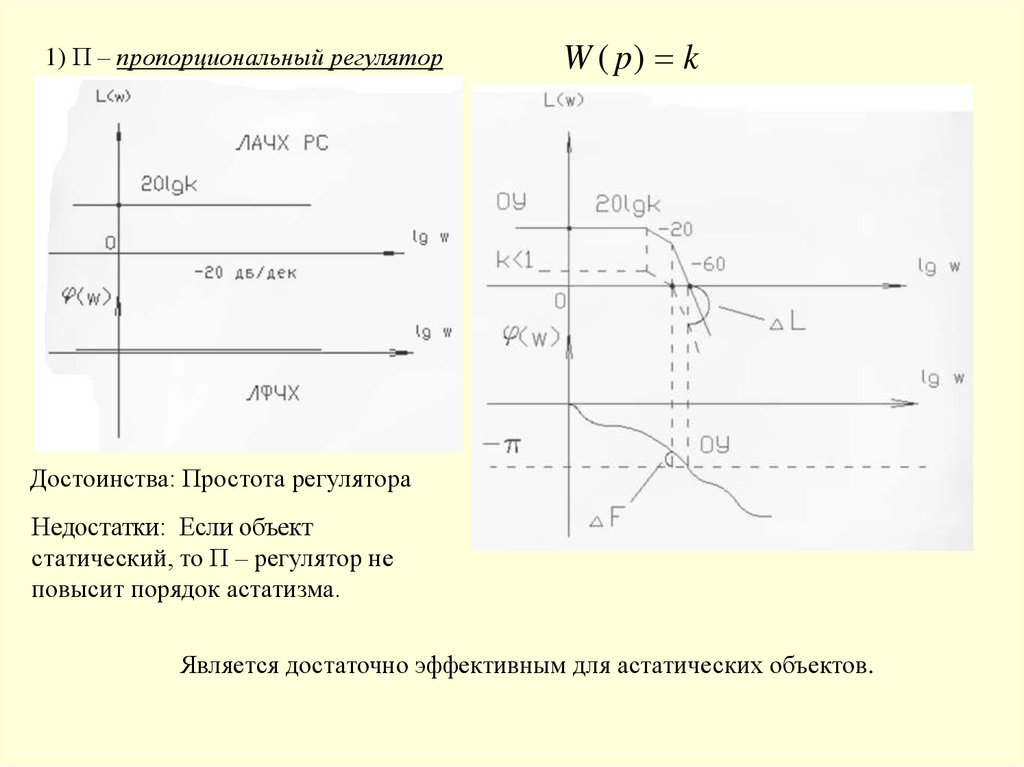
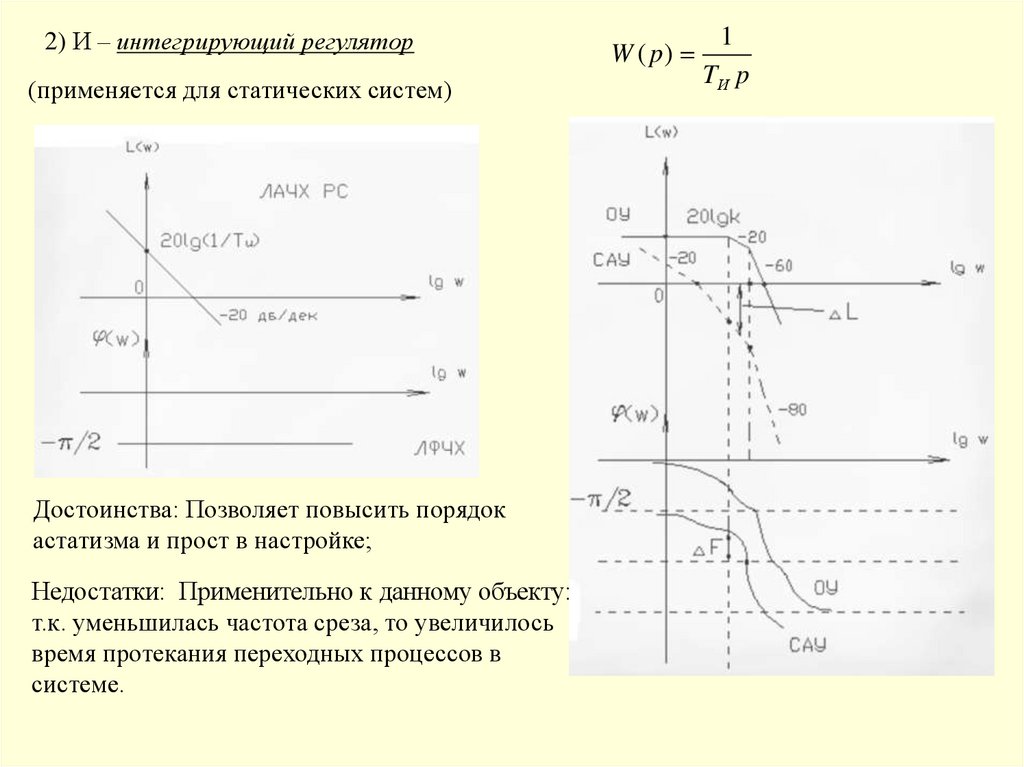
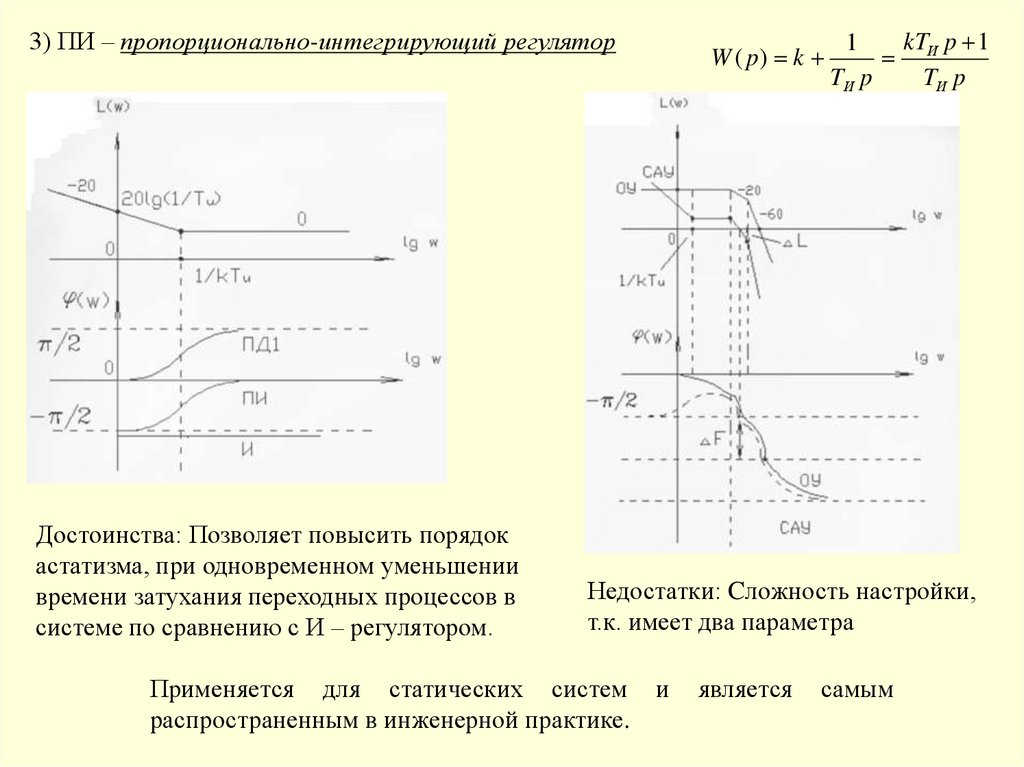
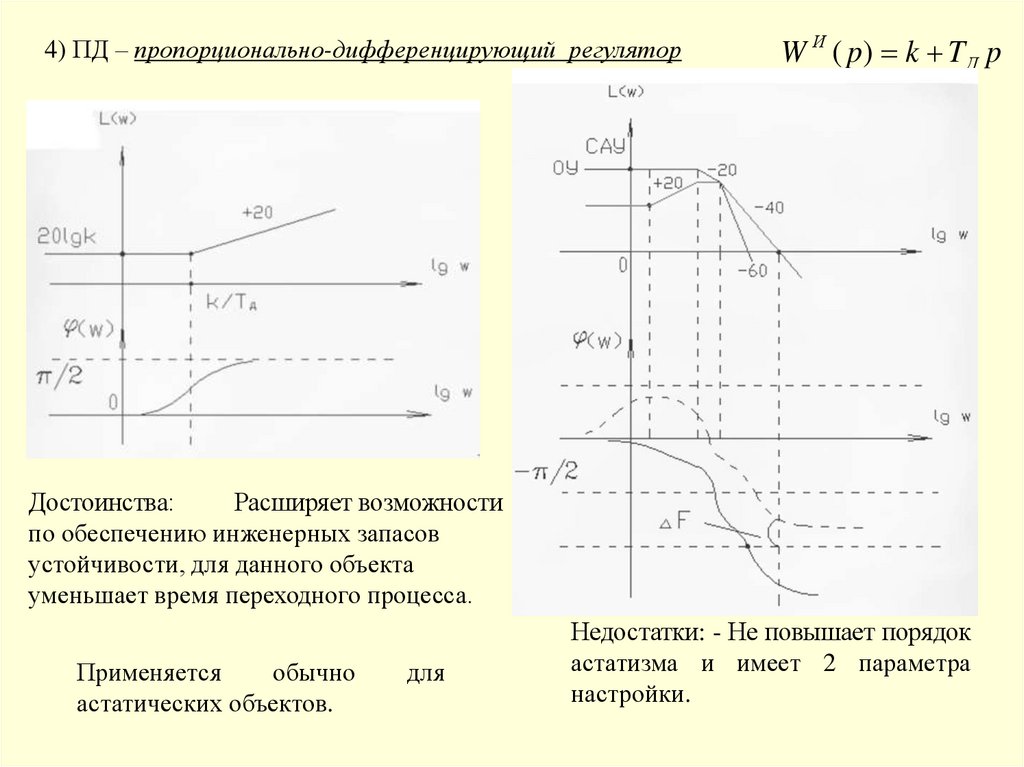
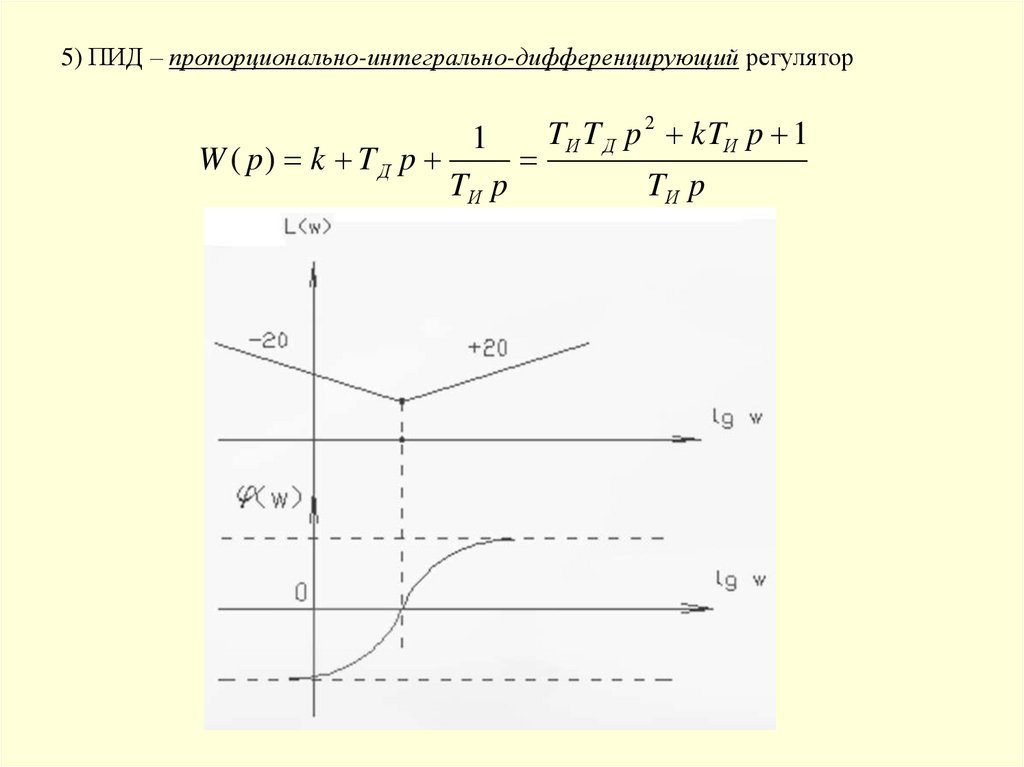


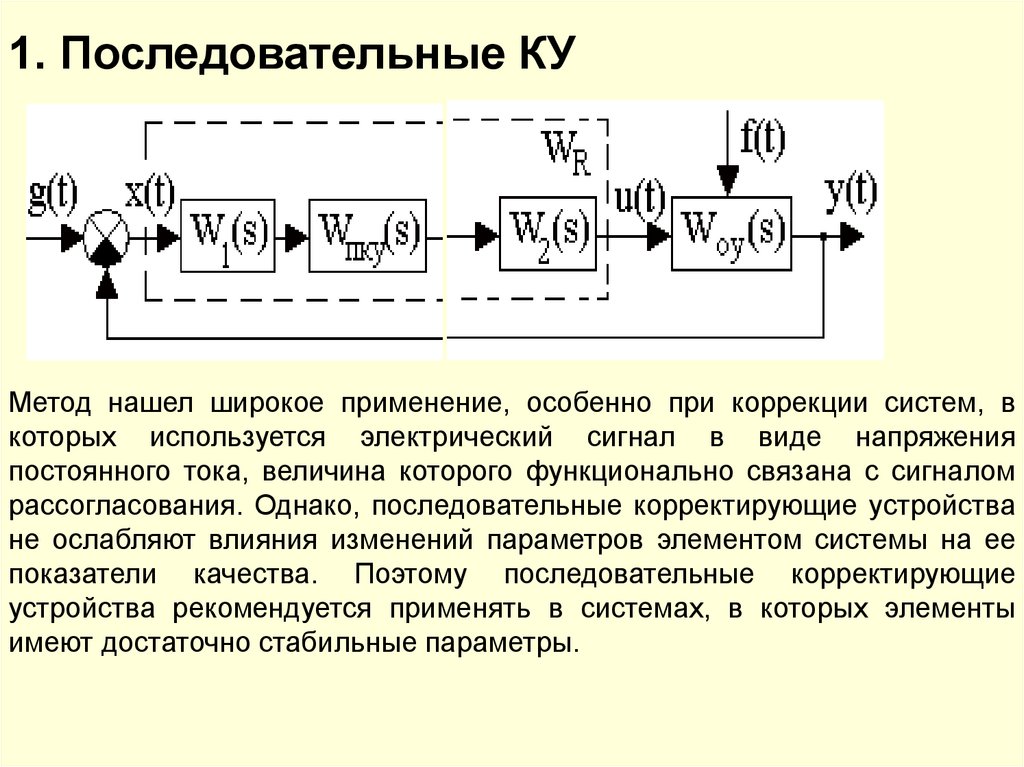
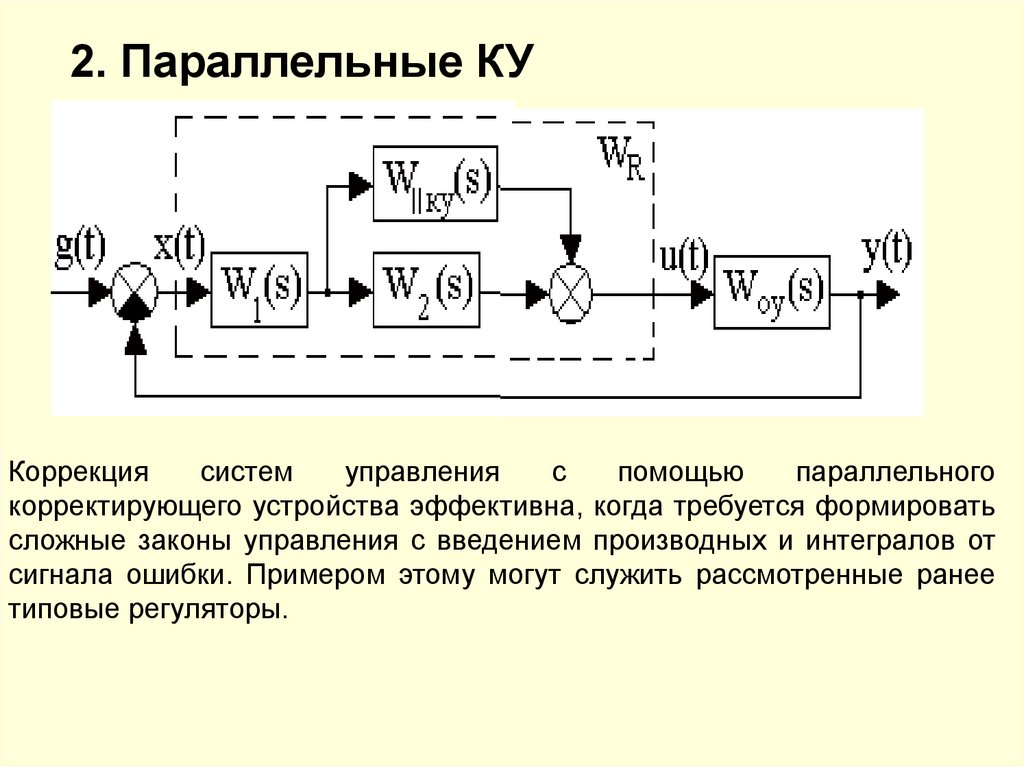
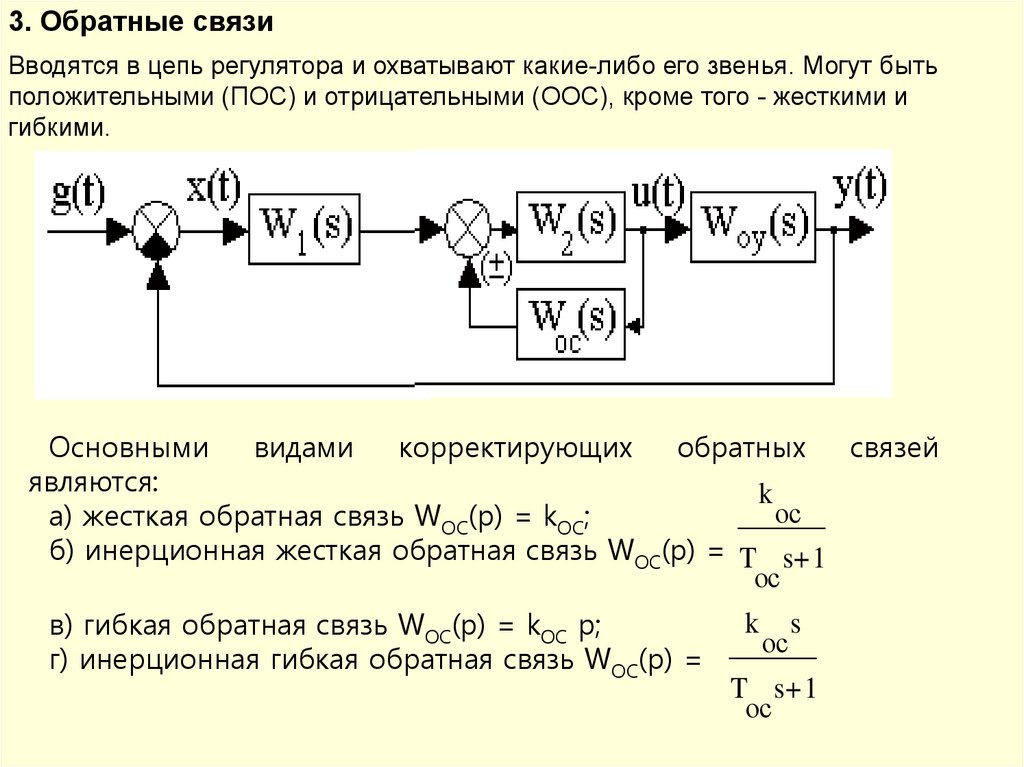

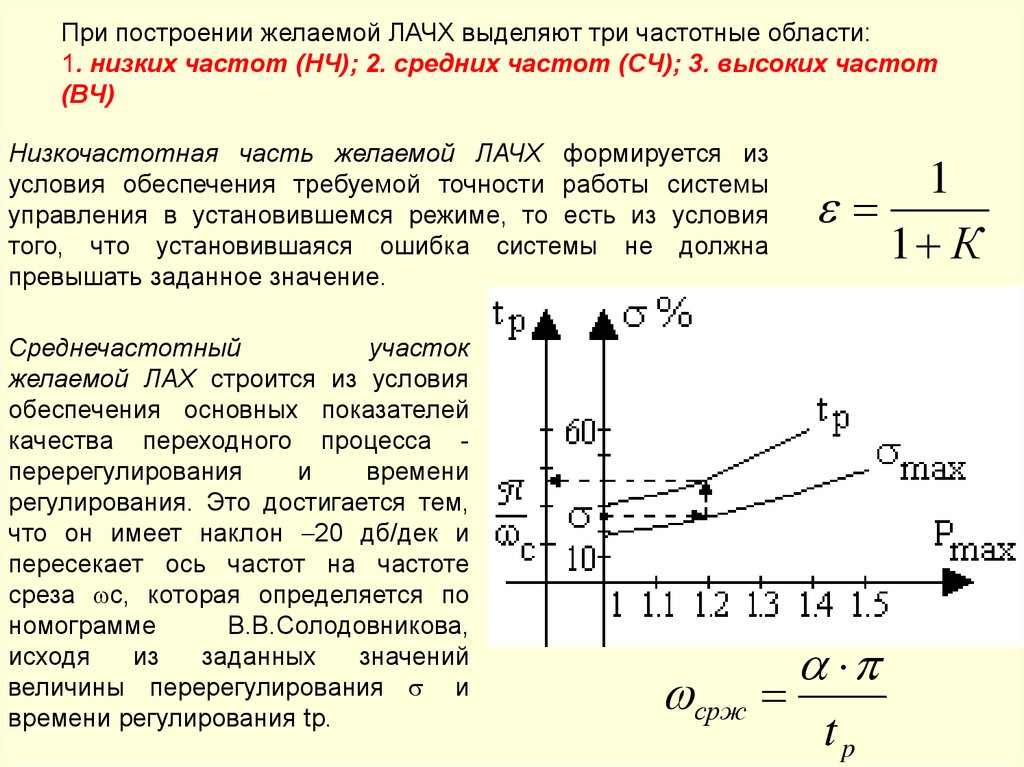
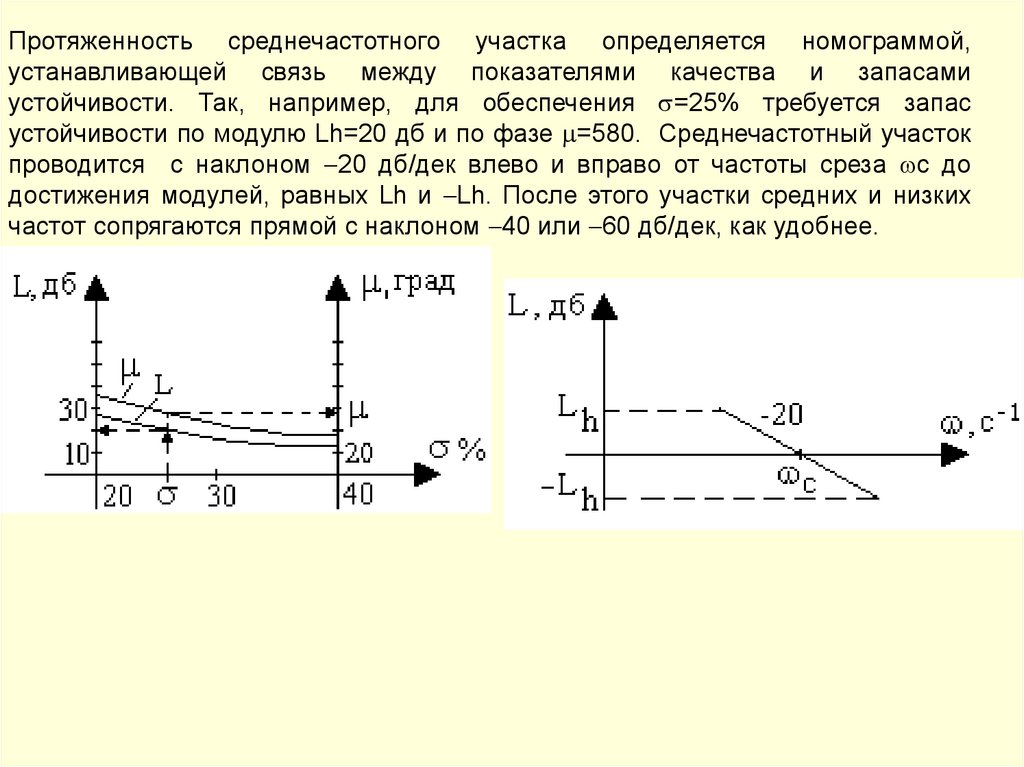
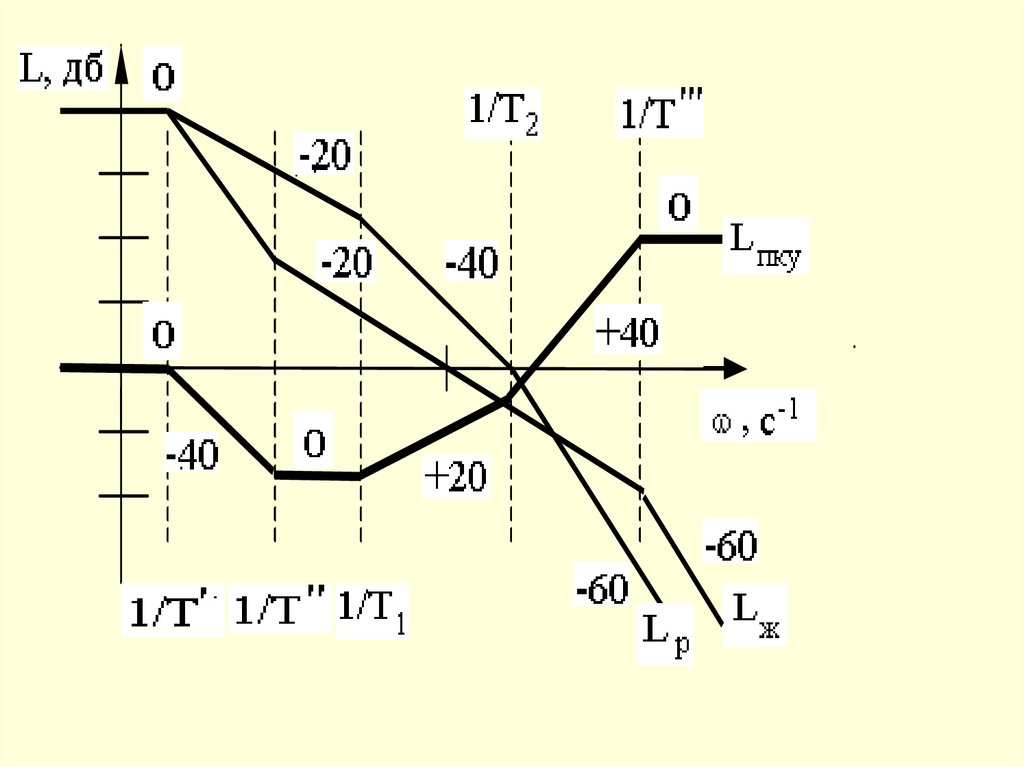

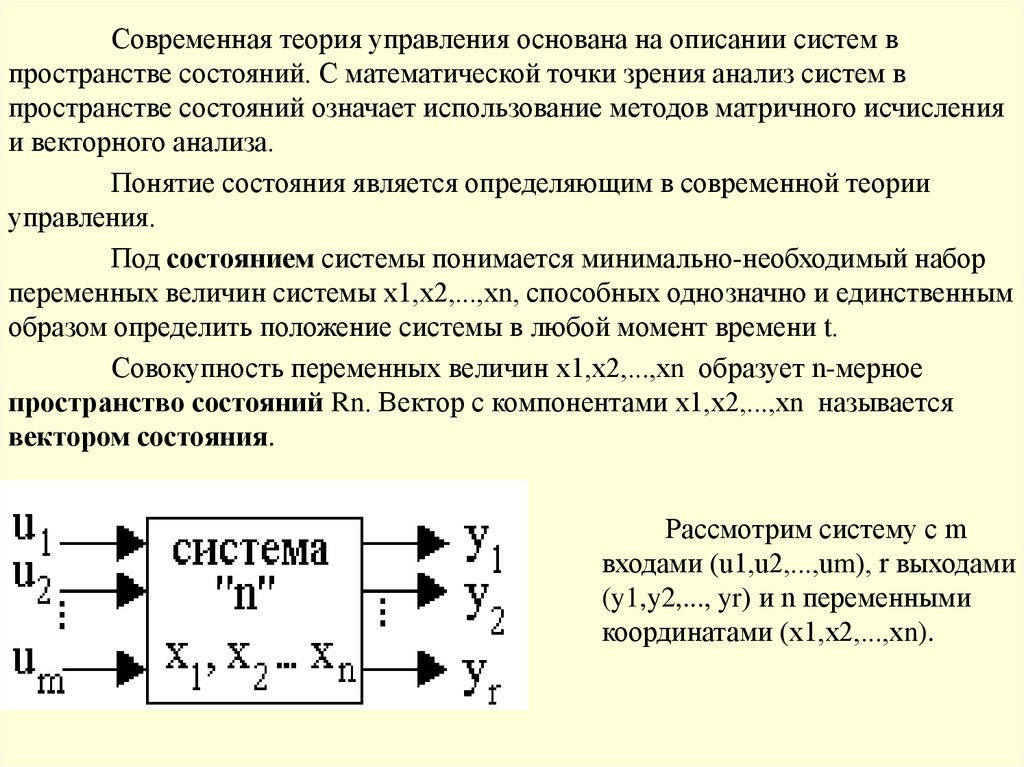


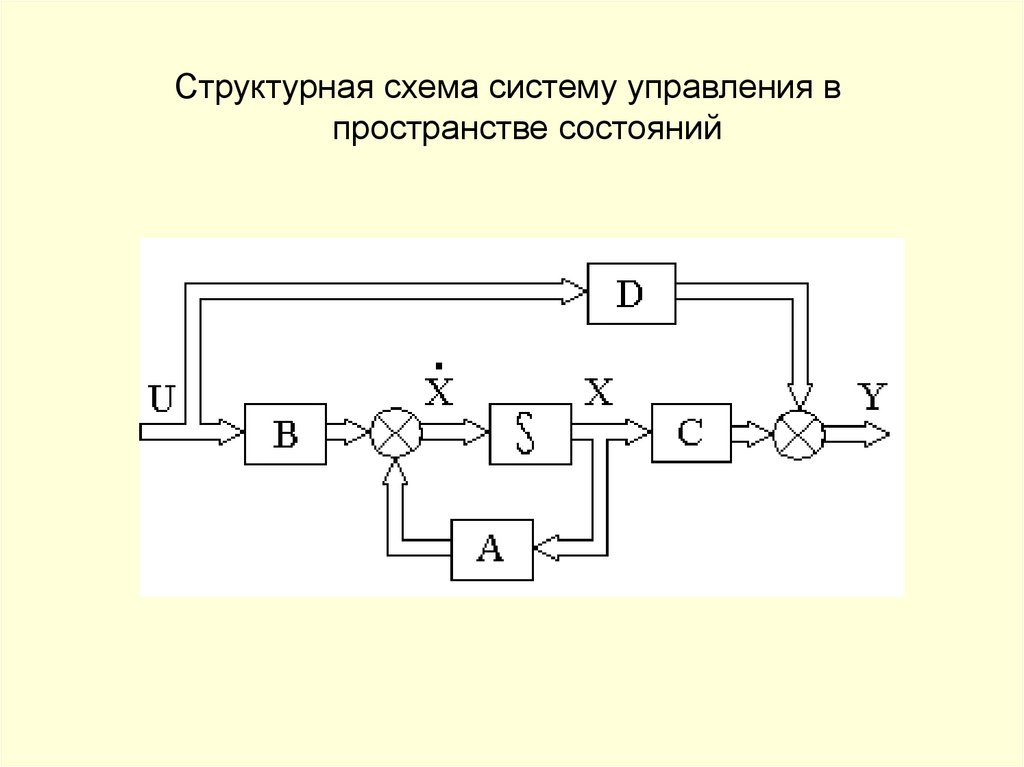

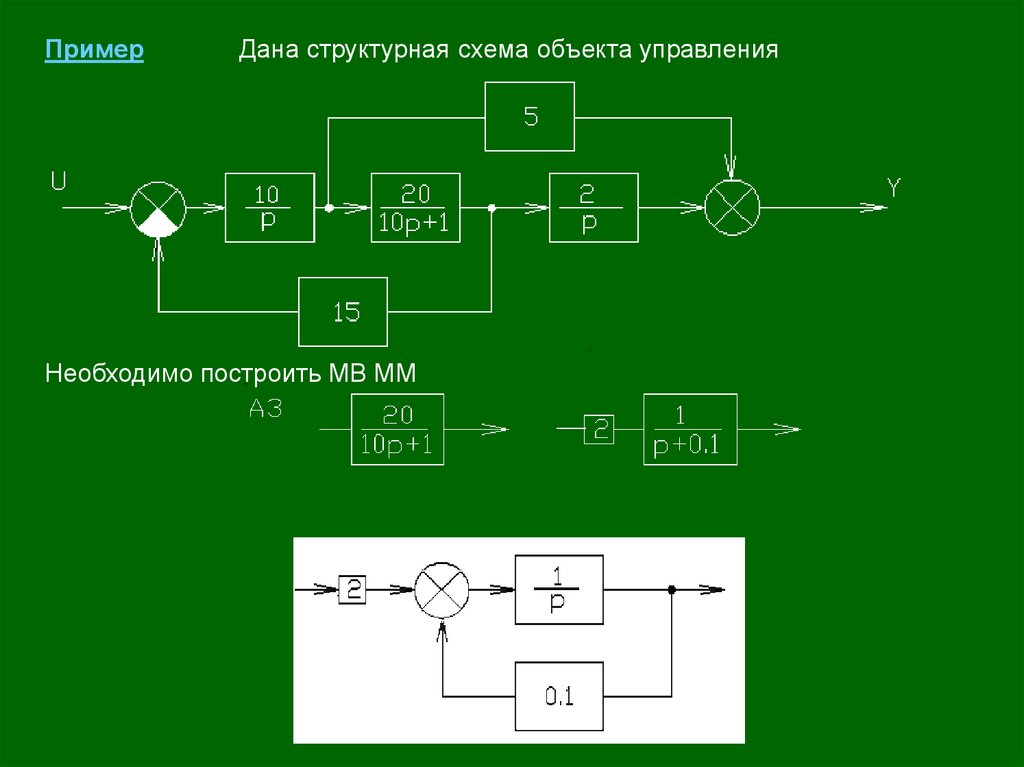
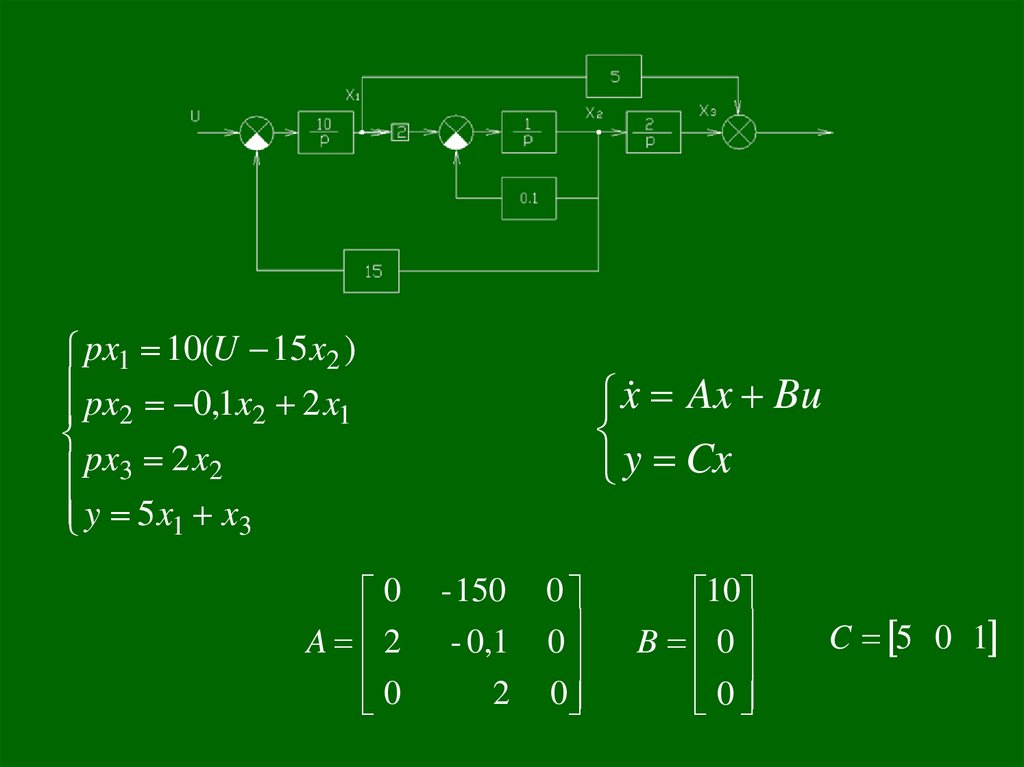







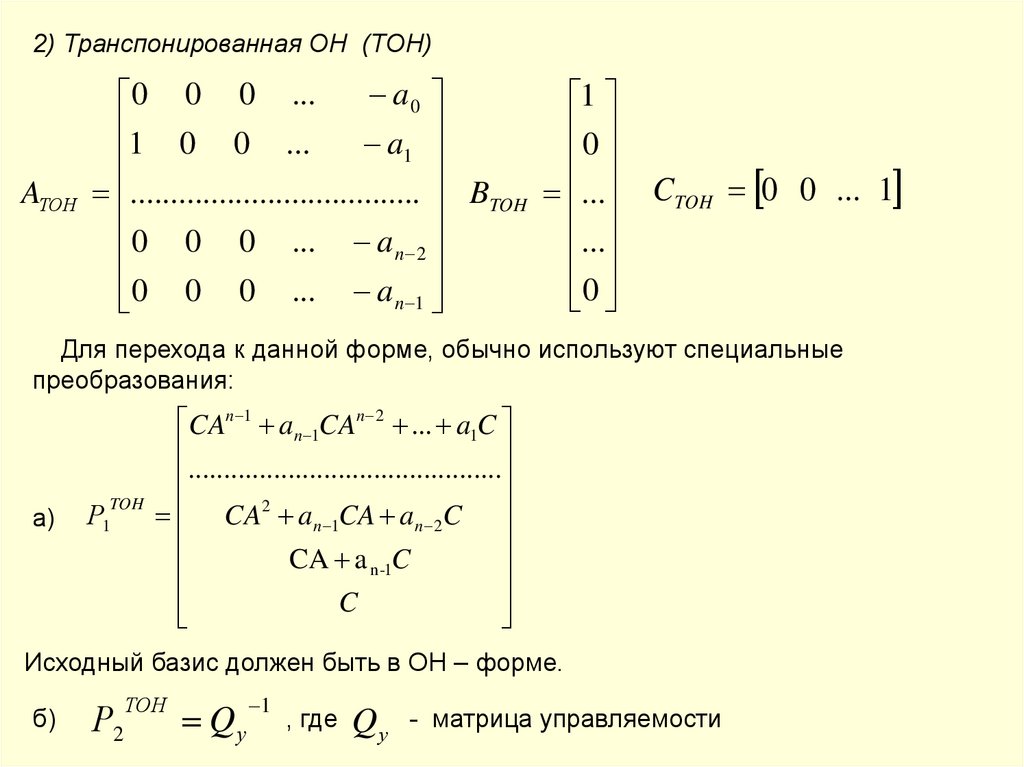




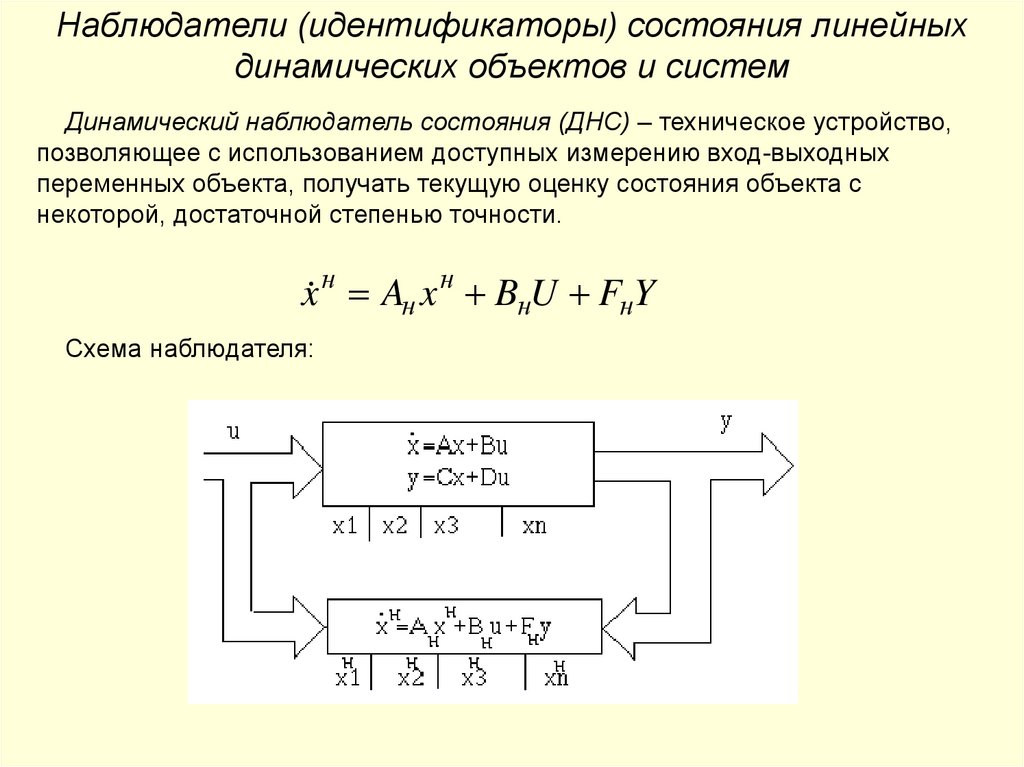
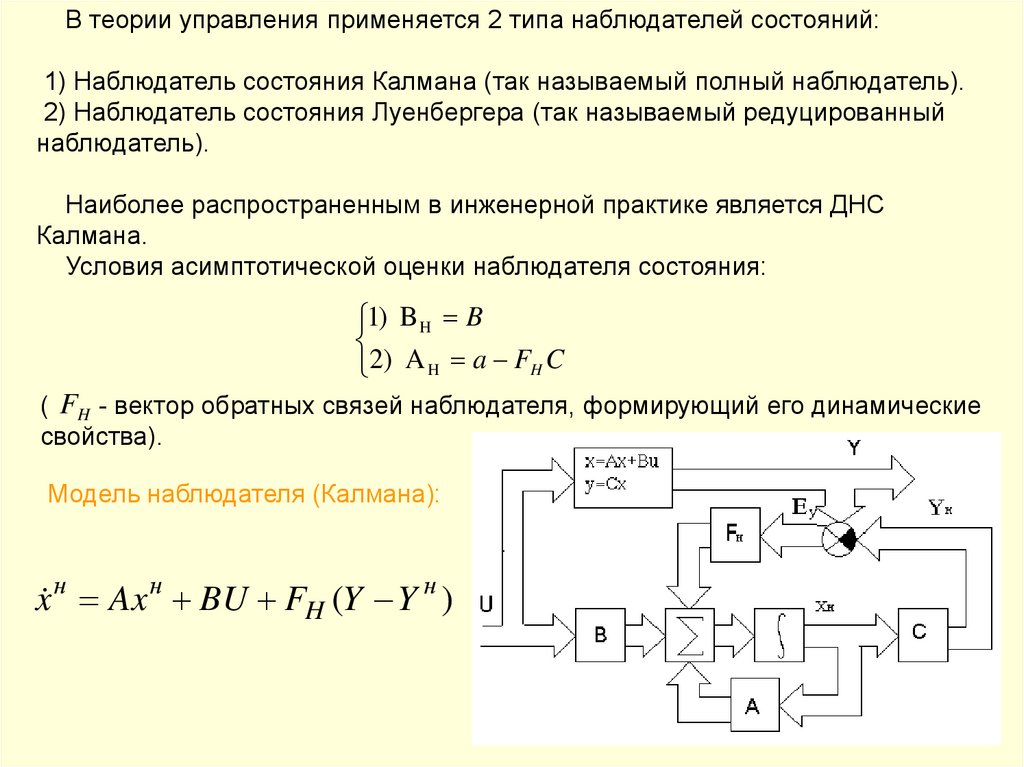





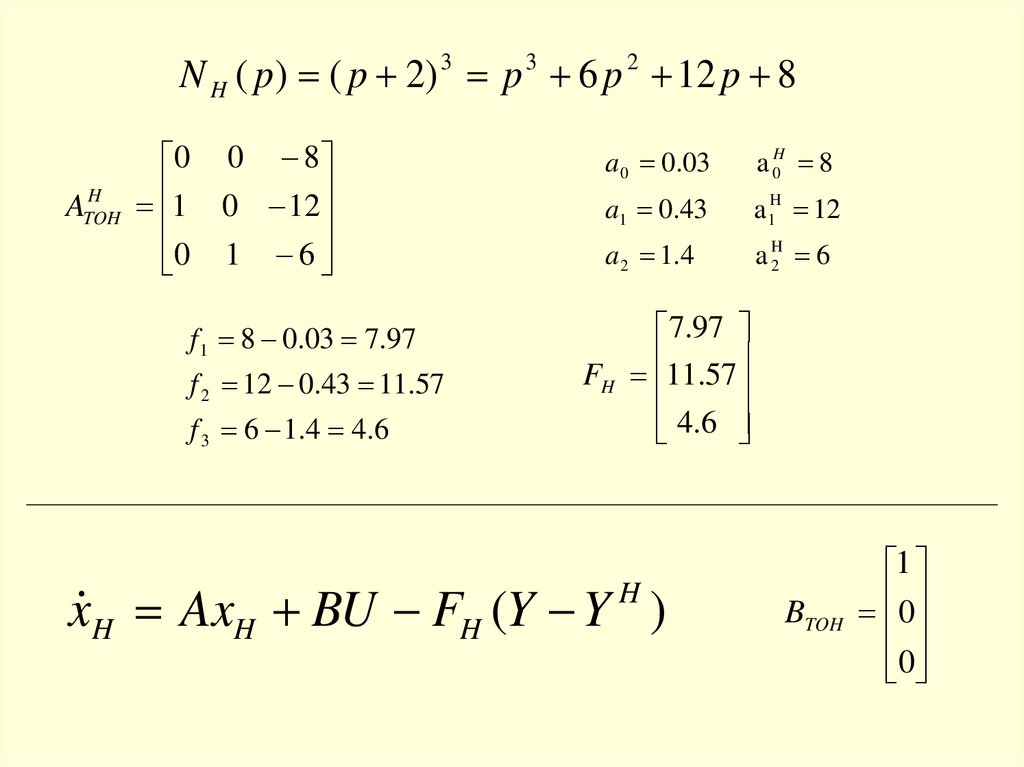
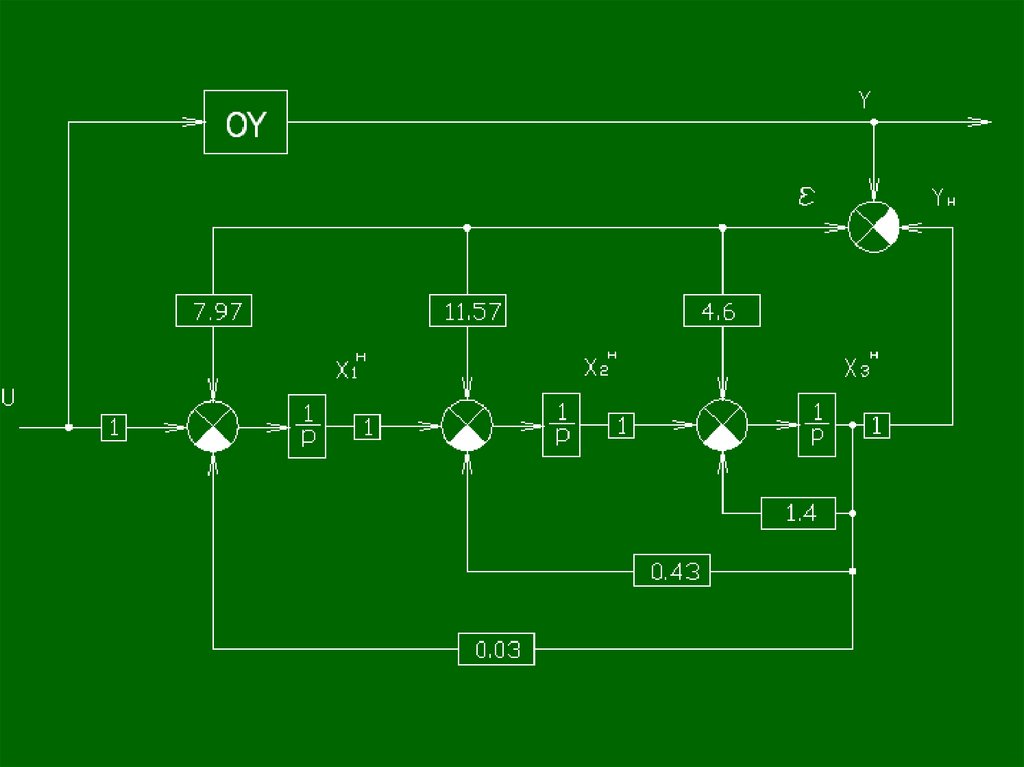

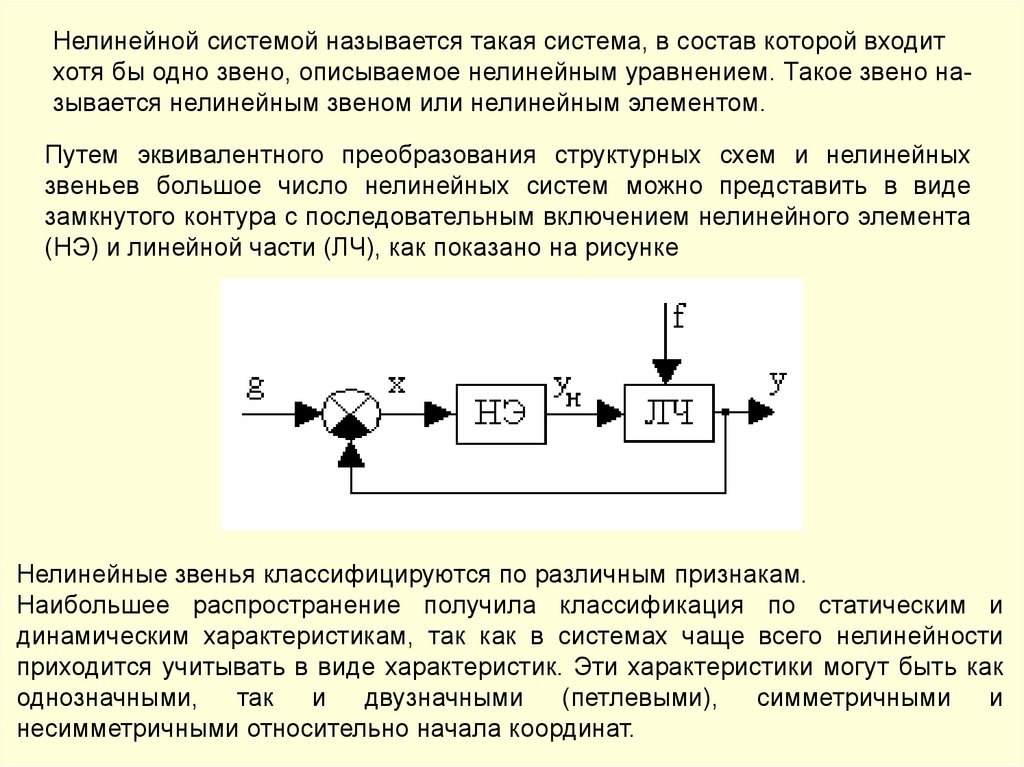
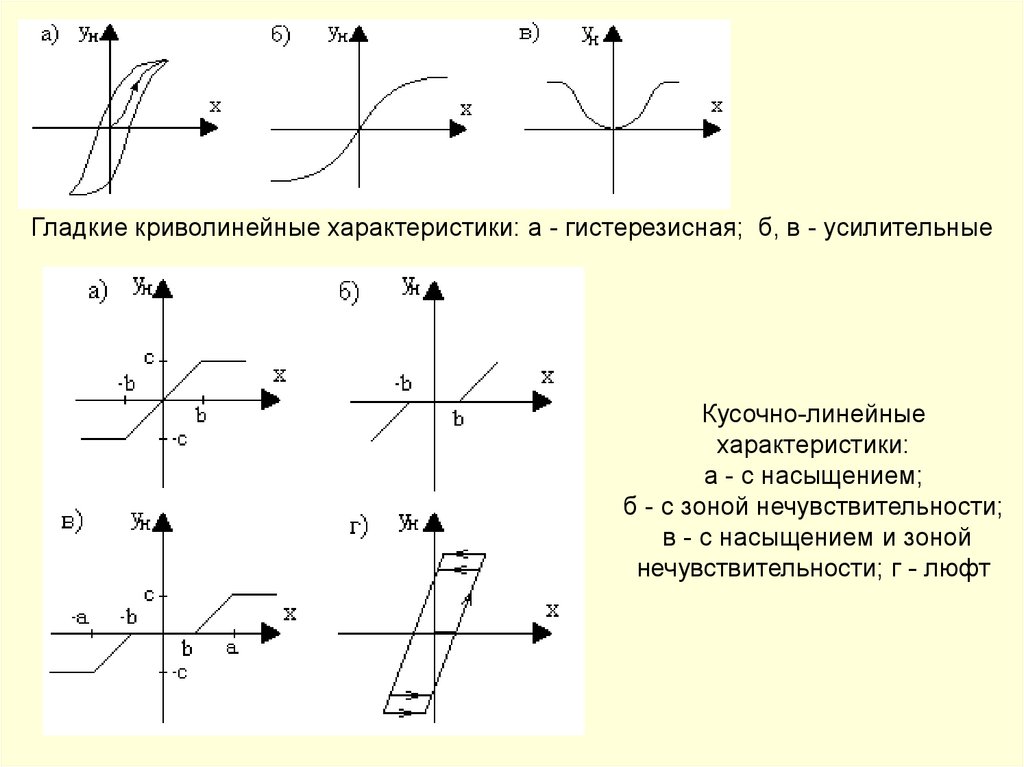
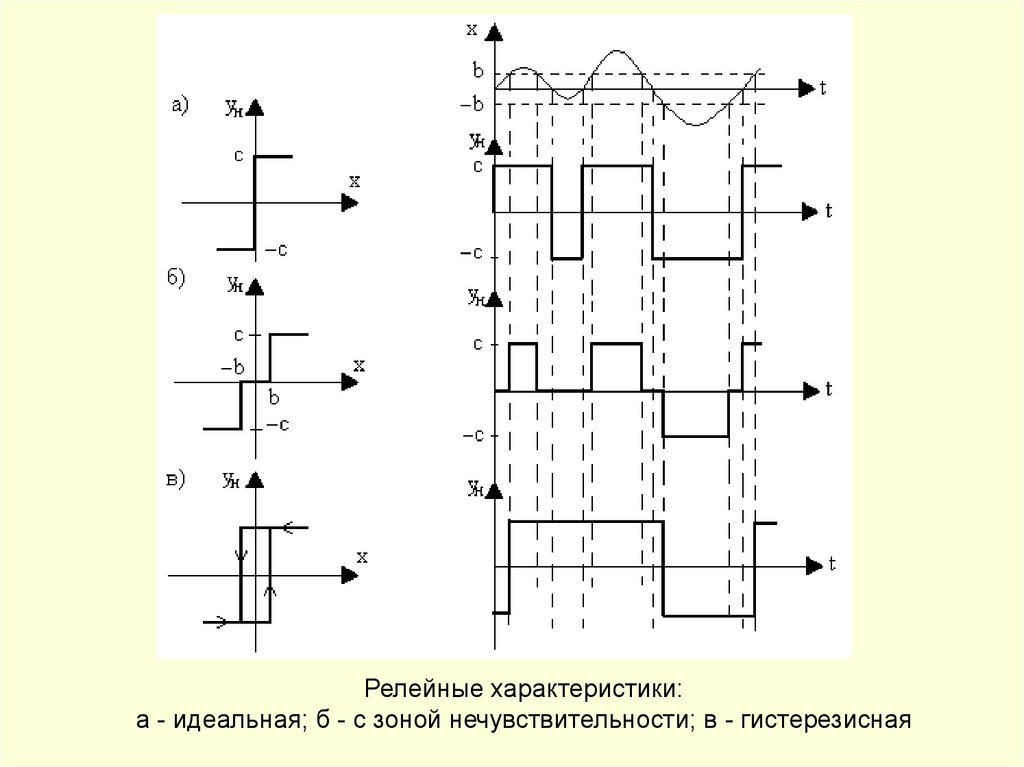






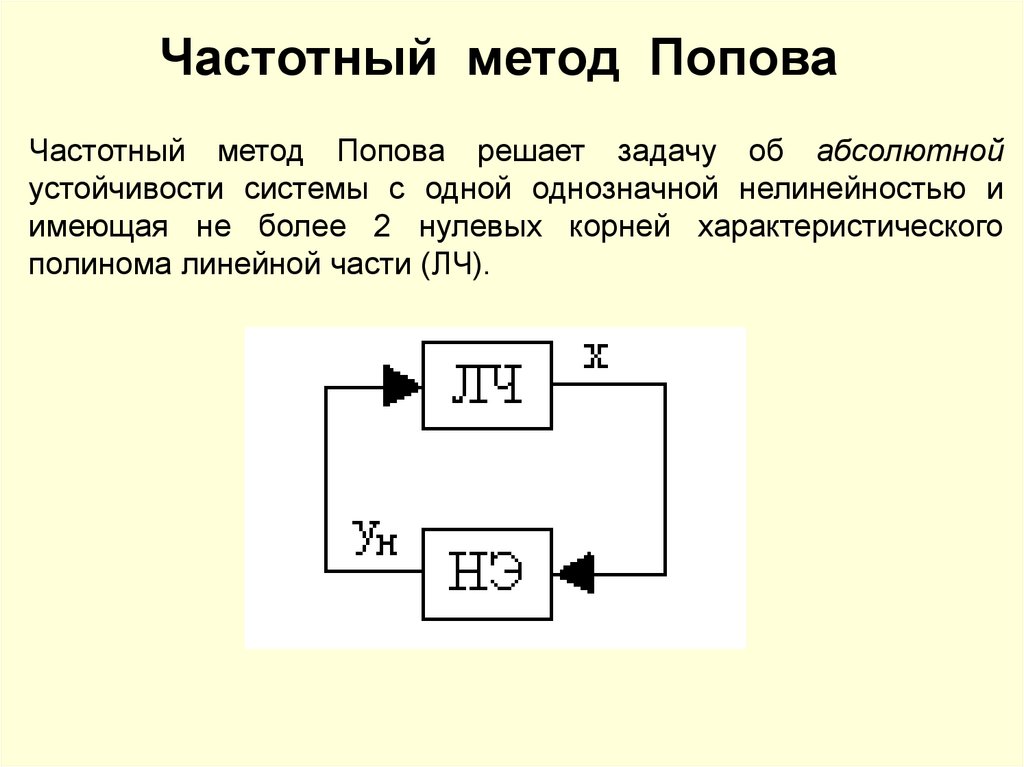
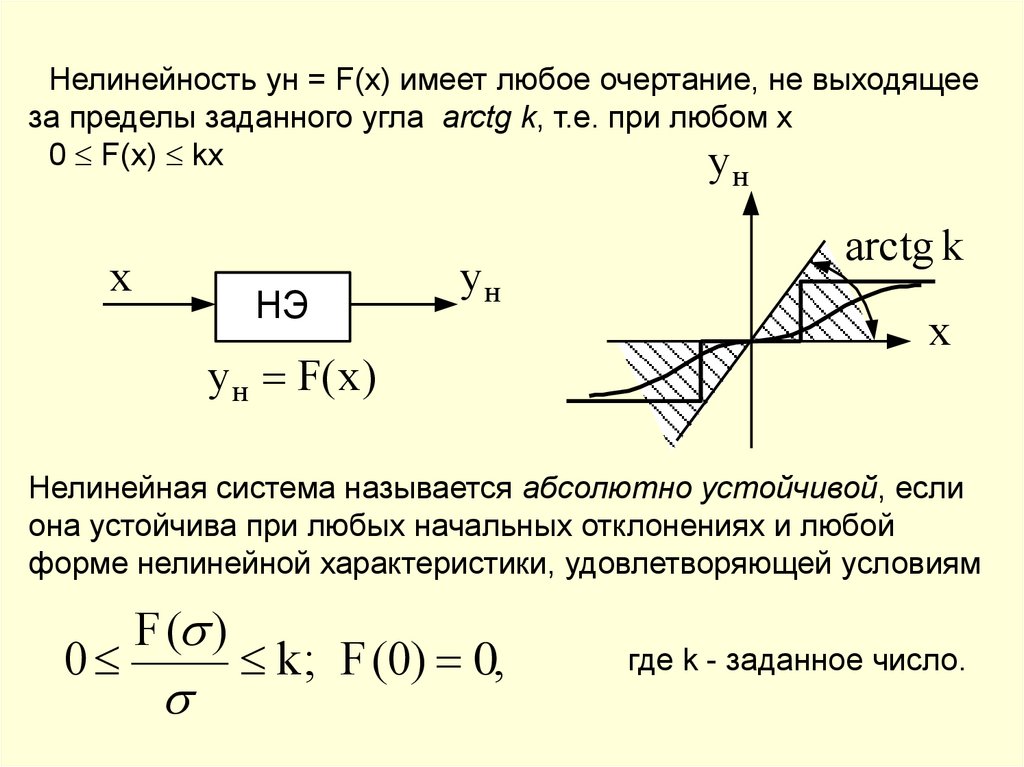


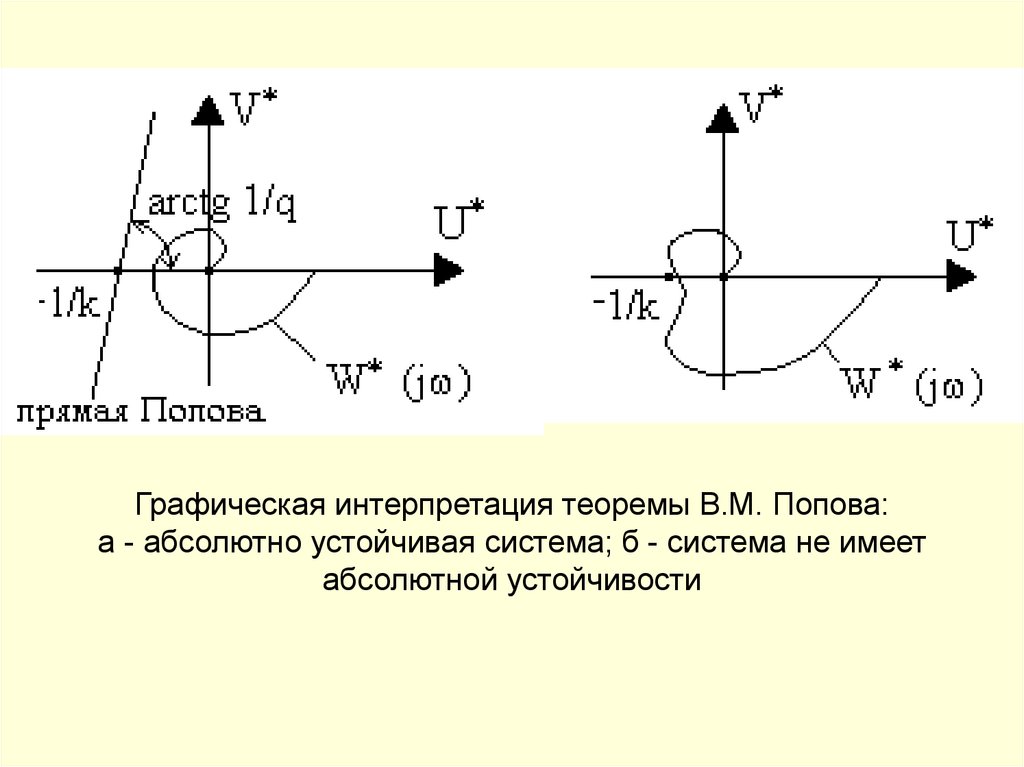



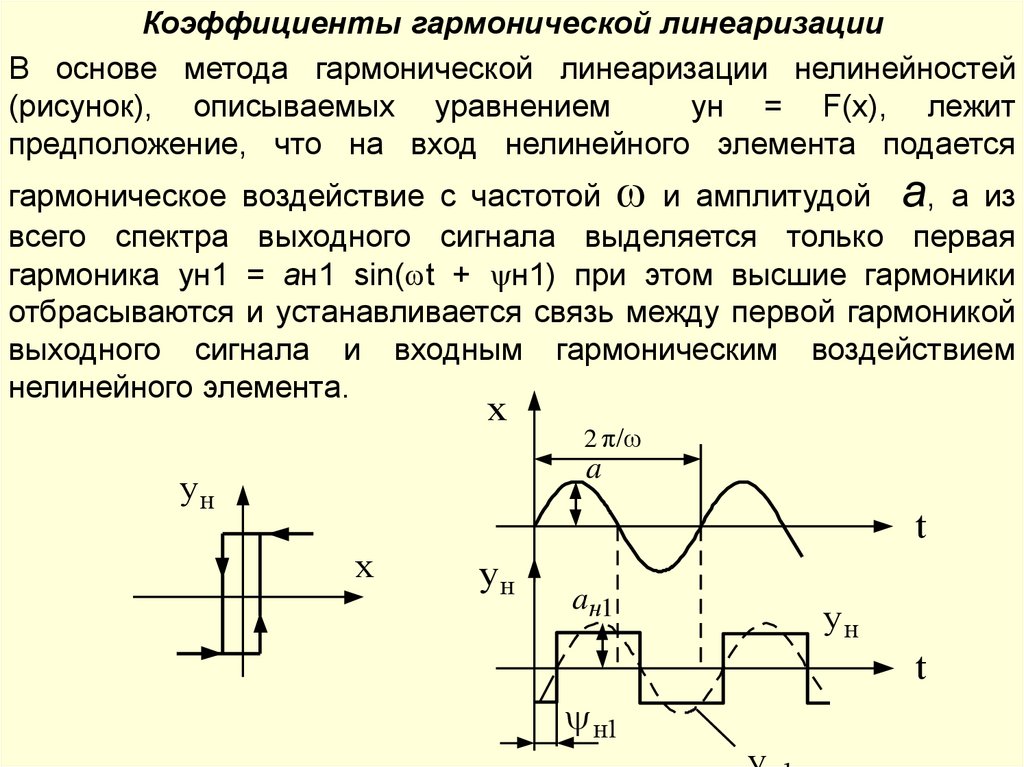





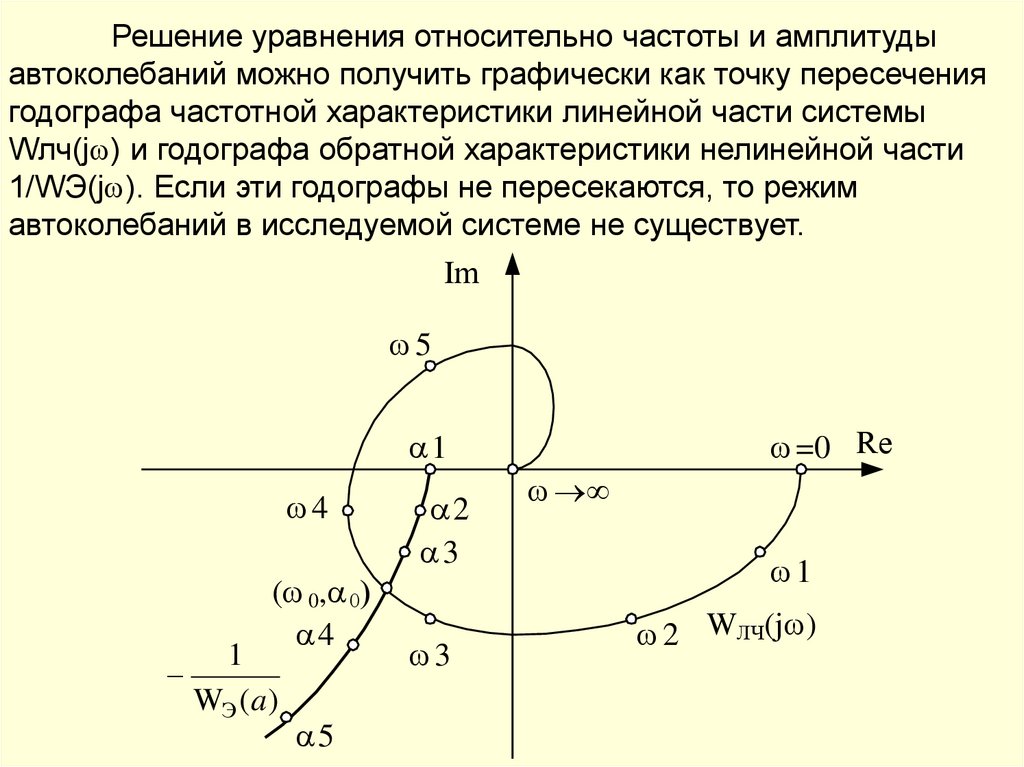



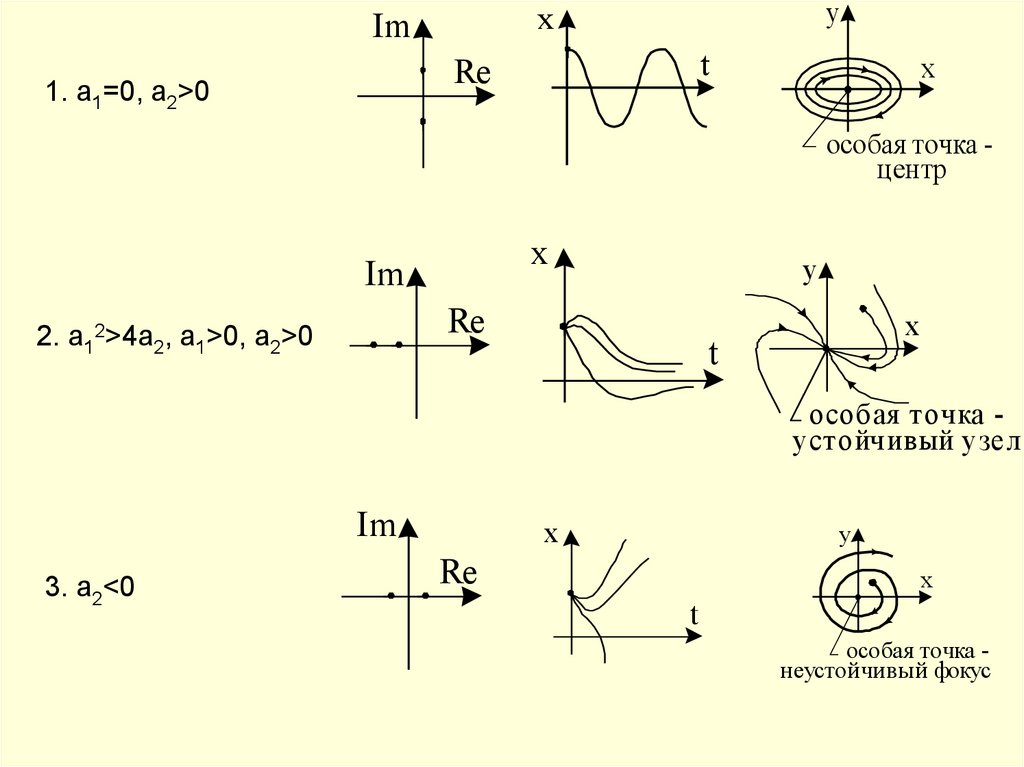
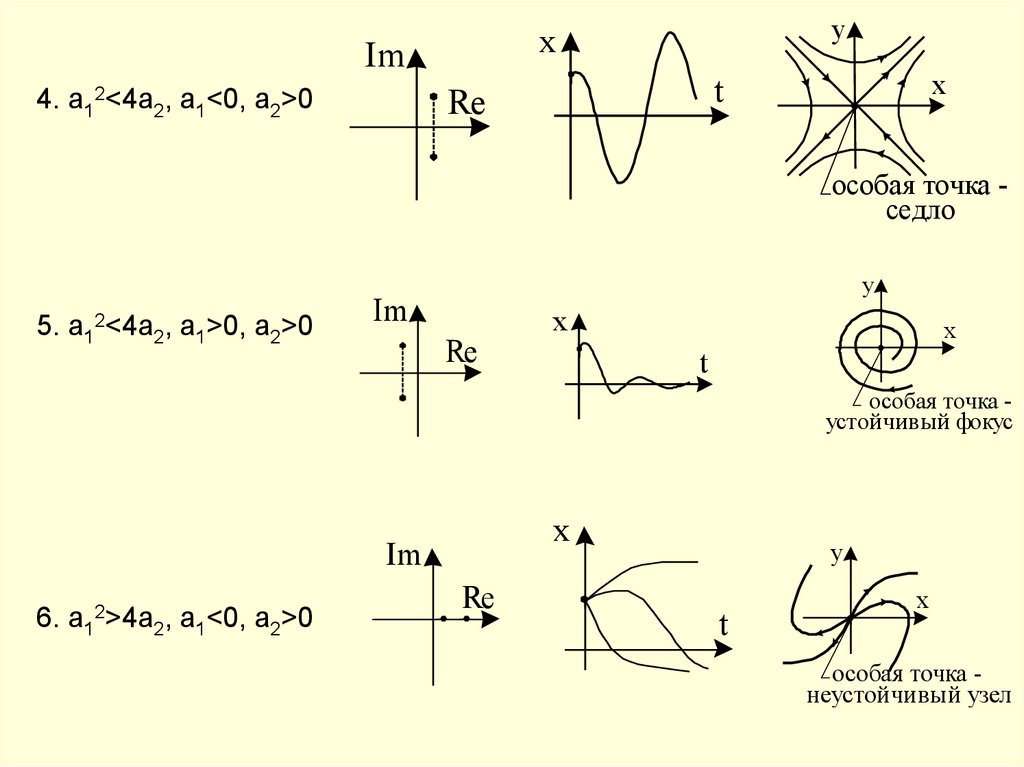













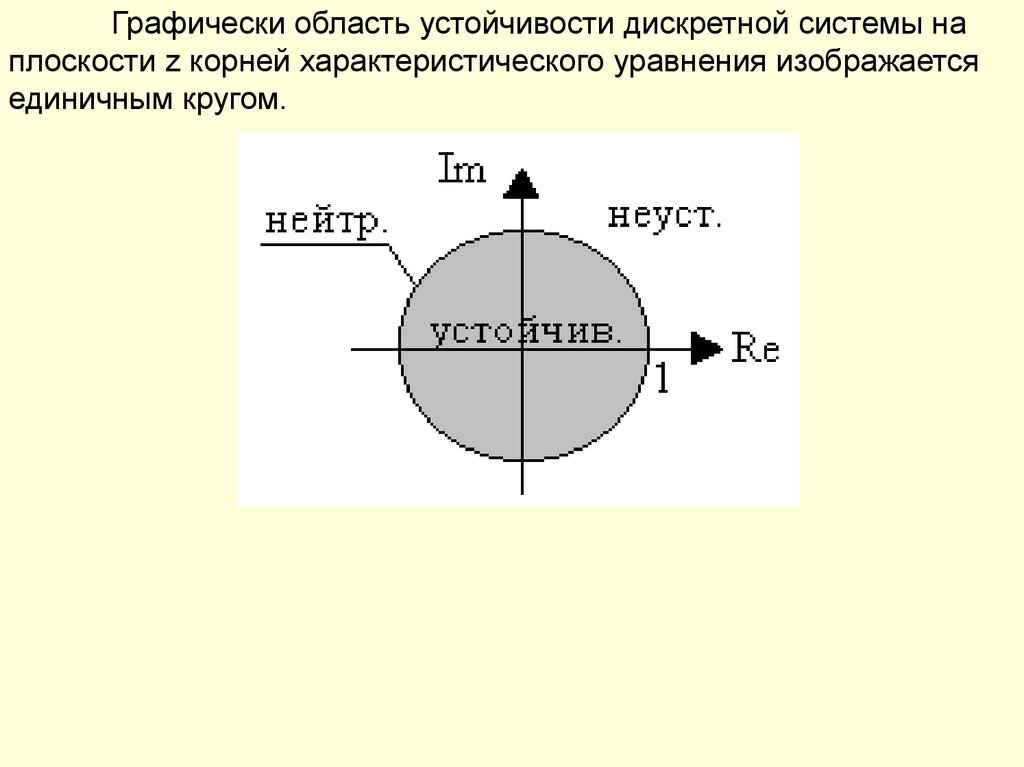
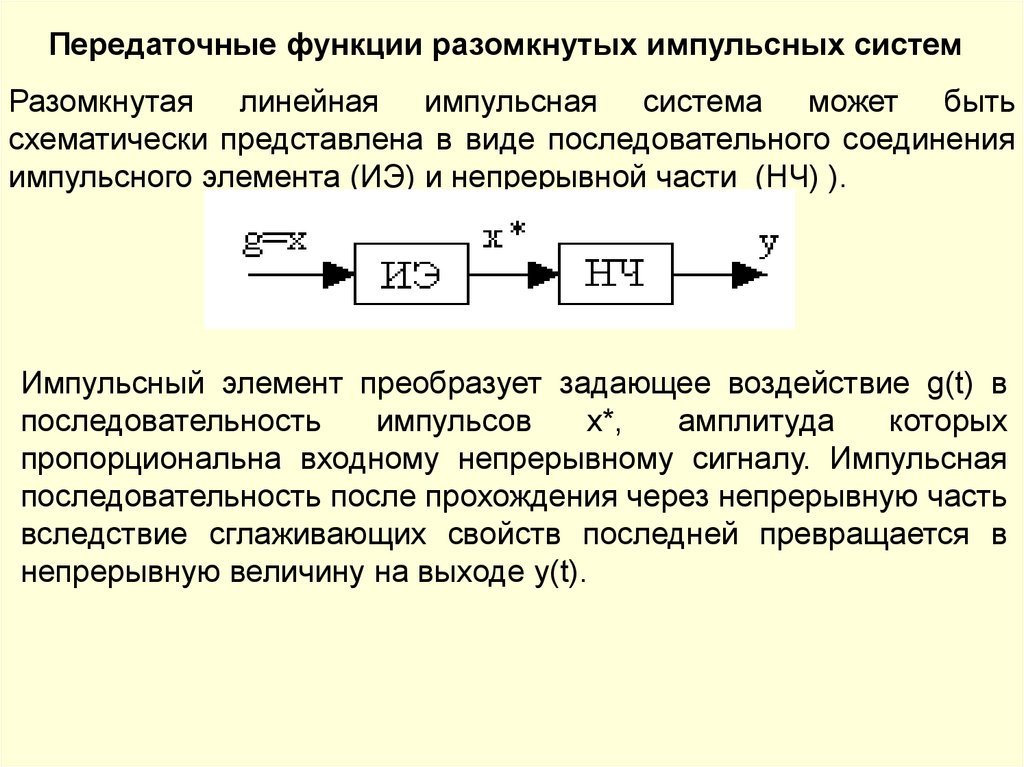
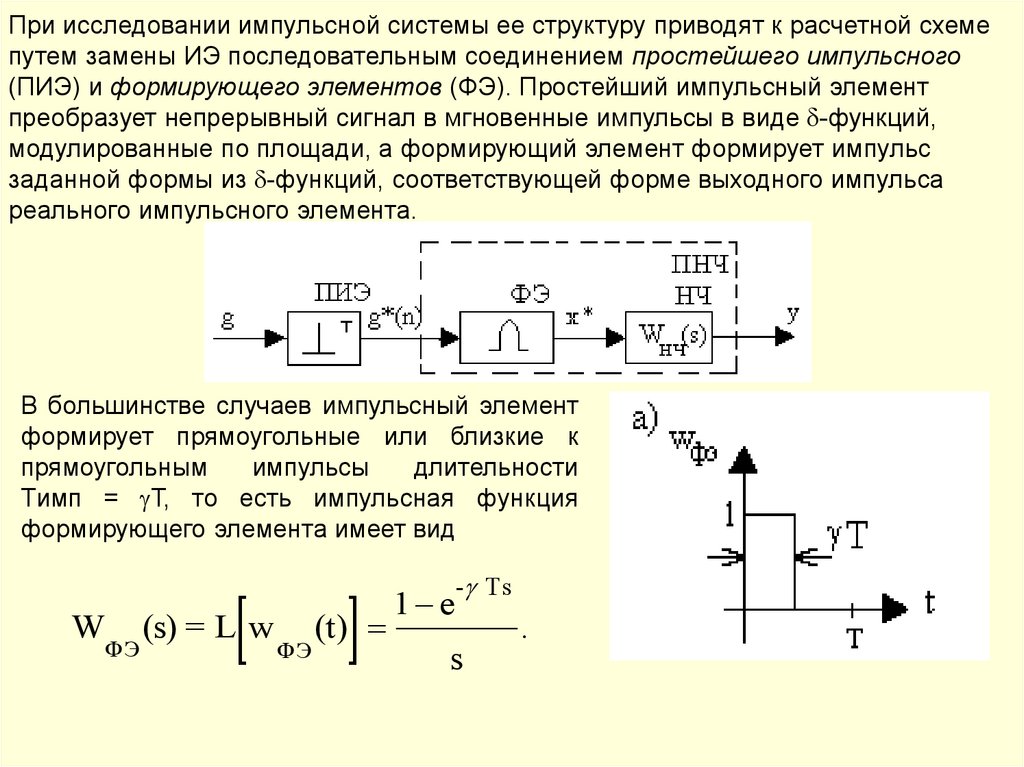


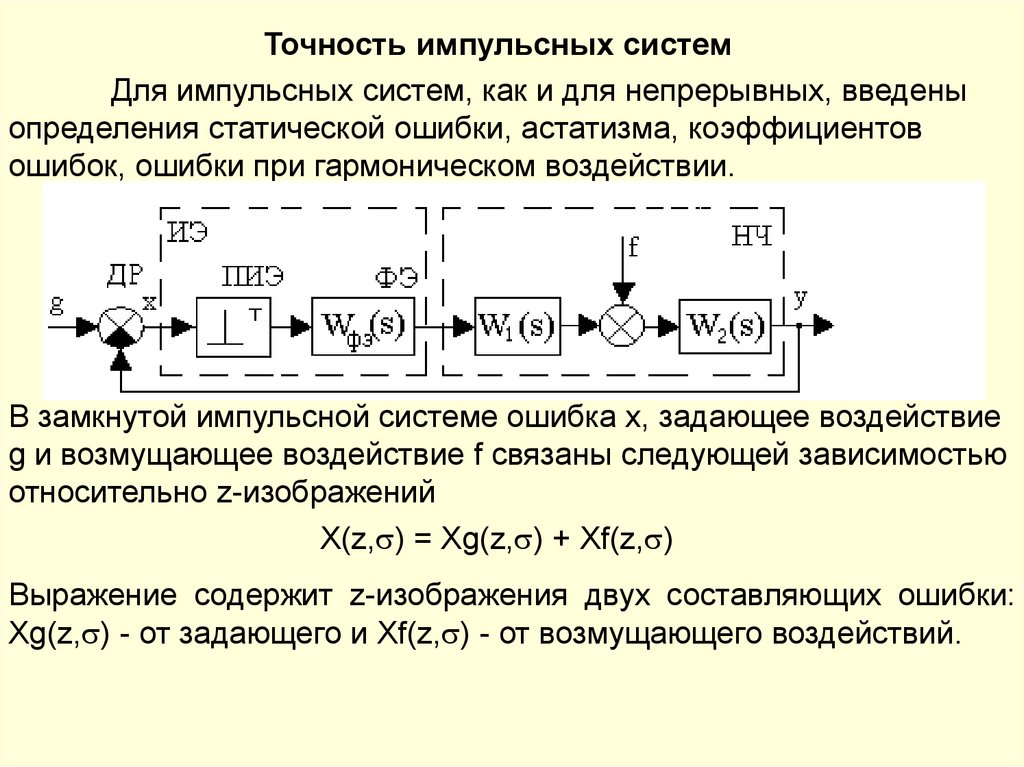














 physics
physics electronics
electronics








