Similar presentations:
Основы теории управления. Типовые динамические звенья и их характеристики
1. Основы теории управления
Типовые динамические звенья иих характеристики
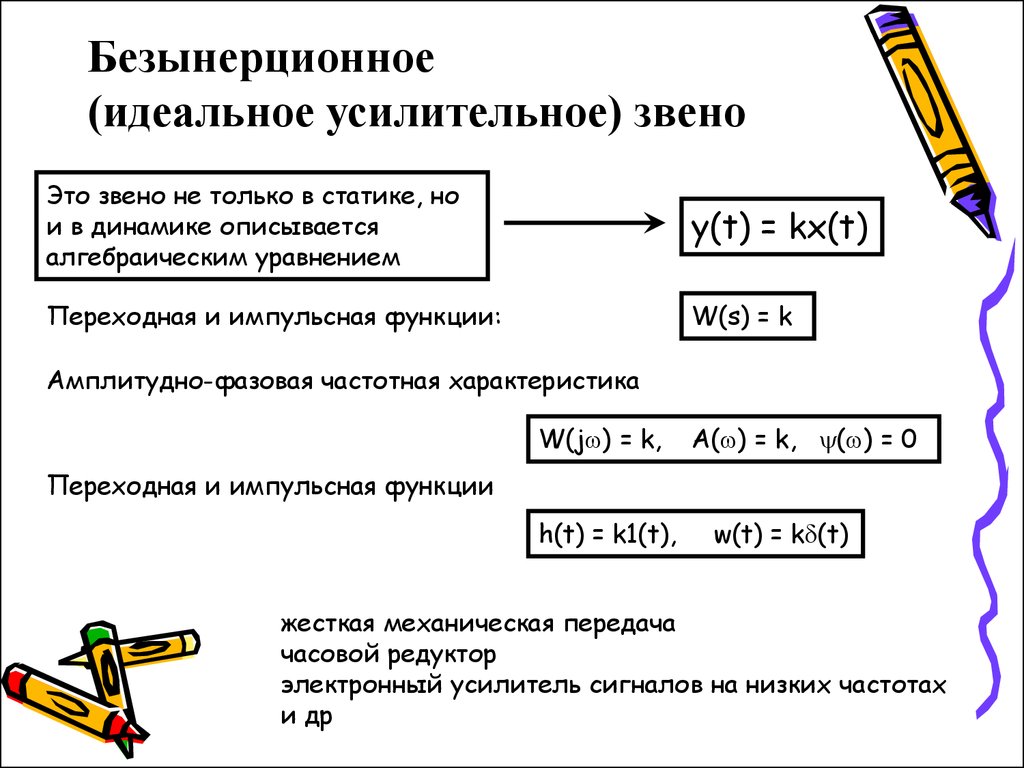
2. Безынерционное (идеальное усилительное) звено
Это звено не только в статике, нои в динамике описывается
алгебраическим уравнением
y(t) = kx(t)
Переходная и импульсная функции:
W(s) = k
Амплитудно-фазовая частотная характеристика
W(j ) = k,
A( ) = k, ( ) = 0
Переходная и импульсная функции
h(t) = k1(t),
w(t) = k (t)
жесткая механическая передача
часовой редуктор
электронный усилитель сигналов на низких частотах
и др
3. Апериодическое (инерционное) звено первого порядка
Уравнение и передаточная функция звена:1
W(s) =
(Tp+1)y(t) = x(t)
Ts+ 1
T - постоянная времени, характеризует степень
Амплитудно-фазовая частотная характеристика
инерционности звена, т.е. длительность
переходного процесса
W(j ) =
1
A( ) =
2 2
T
Tj + 1
Переходная и импульсная функции
h(t ) 1 e
1
t
T
( ) = - arctgT
1
t
1 T
w( t ) e
T
апериодическое звено первого порядка является фильтром
низких частот.
RC цепочка, нагревательный элемент
4. Апериодическое (инерционное) звено второго порядка
При 2Т2 Т1 корнивещественные,
T 2 p 2 T p + 1 y(t) = x(t)
1
2
( T3p+1)(T4p+1) y(t) = x(t)
T3, T4
T
1
2
T2
1
4
T2
новые постоянные времени
2
Передаточная функция звена
W(s) =
1
(T s + 1)(T s + 1)
3
4
1
1
(T s + 1) (T s + 1)
3
4
двойная RC цепочка, электродвигатель постоянного тока
5. Колебательное звено
T 2 p 2 T p + 1 y(t) = x(t)1
2
При Т1 2Т2 корни
комплексные,
(T2p2+2 Tp+1) y(t) = x(t)
Т - постоянная времени,
определяющая угловую частоту
свободных колебаний =1/Т
передаточная функция
W(s) =
1
Амплитудно-фазовая частотная характеристика
2 2
T s 2 Ts + 1
A( ) =
- параметр затухания,
лежащий в пределах 0< <1
W(j ) =
1
2
2
T (j ) 2 Tj + 1
Временные характеристики представляют
1
собой затухающие
периодические процессы
2
2 2
2 2 2
(1 - T ) 4 T
( )= - arctg
2 T
2 2
1 T
электрический колебательный контур,
электродвигатель постоянного тока,
маятник
6. Консервативное звено
частный случай колебательного при =0представляет собой идеализированный случай, когда можно
пренебречь влиянием рассеяния энергии в звене
Амплитудно-фазовая характеристика
совпадает с вещественной осью.
При 0 1/T характеристика совпадает с
положительной полуосью,
При 1/T - с отрицательной полуосью.
Временные характеристики соответствуют
незатухающим колебаниям с угловой
частотой 1/T
7. Интегрирующие звенья
dyx
dt
t
y = x(t)dt
0
8. Идеальное интегрирующее звено
W(s) =py(t) = x(t)
Амплитудно-фазовая частотная характеристика
W ( j ) - j
1
, A( )
1
1
s
, ( ) 90
0
Переходная и импульсная функции
h(t) = t,
w(t) = 1(t)
операционный усилитель в режиме интегрирования,
гидравлический двигатель,
емкость
9. Дифференцирующие звенья
ydx
dt
10. Идеальное дифференцирующее звено
y(t) = px(t), W(s) = sАмплитудно-фазовая частотная характеристика
W(j ) = j , A( ) = , ( ) = +90
Переходная и импульсная функции
h(t) = (t),
w(t) =
d
dt
операционный усилитель в режиме дифференцирования
11. Форсирующее (дифференцирующее) звено первого порядка
y(t) = ( p+1) x(t) , W(s) = s+1- постоянная времени дифференцирования
Амплитудно-фазовая частотная характеристика
W(j ) = (j + 1), A( )=
2 2
1+
= arctg
Переходная и импульсная функции
d
h(t ) 1(t ), w(t )
(t )
dt
12. Форсирующее (дифференцирующее) звено второго порядка
y(t) = ( 2p2+2 p+1)x(t), W(s) = 2s2+2 s+1Амплитудно-фазовая частотная характеристика
W(j ) =
(1- 2 2)
+ j2
A( )=
( )=arctg
2 2 2
2 2 2
(1 - ) + 4
2
2 2
1
Переходная и импульсная функции
2
d
d
d
2
2
h(t )
2 (t ) 1(t ), w(t )
2
(t )
2
dt
dt
dt
13. Комбинации типовых звеньев
Дифференцирующее звено с замедлениемидеальное
дифференцирующее
звено
+
апериодическое
звено
первого порядка
Уравнение и передаточная функция звена
(Tp+1) y(t) = px(t) W(s) =
p(Tp+1) y(t) = x(t)
W(s) =
s
Ts + 1
1
s(Ts + 1)
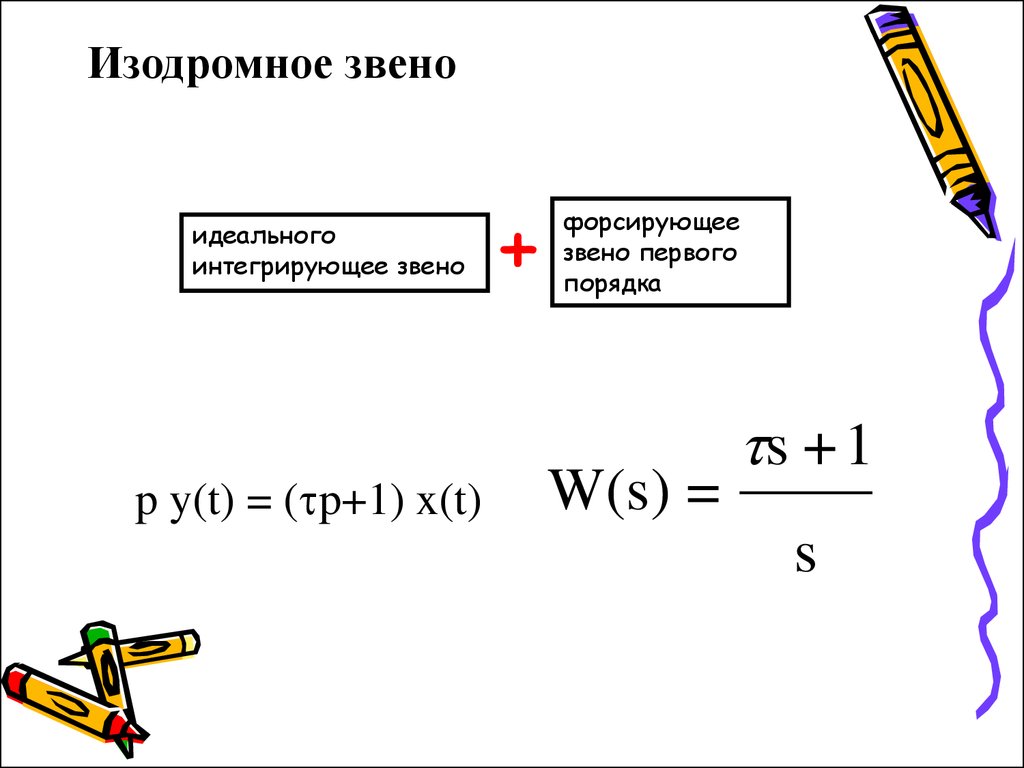
14. Изодромное звено
идеальногоинтегрирующее звено
p y(t) = ( p+1) x(t)
+
форсирующее
звено первого
порядка
W(s) =
s + 1
s
15. Интегро-дифференцирующее звено
форсирующее звенопервого порядка
+
апериодическое
звено первого
порядка
Уравнение и передаточная функция звена
(Tp+1)y(t) = ( p+1) x(t)
W(s) =
s+ 1
Ts+ 1
16. Неминимально-фазовые звенья
звенья, которые, в отличие от обычных типовыхзвеньев, при равенстве амплитудных частотных
характеристик имеют большие по абсолютному
значению фазовые сдвиги
Звено с чистым запаздыванием
выходная величина повторяет входную
с некоторой задержкой во времени
y(t) = x(t- ),
( s)
s
W(s) = e
1 s+
2!
2
( s)
3!
3
...
- время чистого запаздывания
Амплитудно-фазовая частотная характеристика:
- j А( ) = 1, = [рад]= - 180
W(j ) = e
[угл.град]
Переходная и весовая функции
h(t) = 1(t- ),
w(t) = (t- )
линия связи, трубопровод,
транспортер, конвейер
17. Звено с положительным полюсом
1W(s) =
Ts - 1
Здесь имеется положительный полюс (корень
знаменателя) s1=1/T. В полюсе передаточная
функция стремится к бесконечности (W(s) )
Амплитудно-фазовая частотная характеристика
W(j ) =
1
Tj 1
A( ) =
1
2 2
T
1
= + arctg T
18. Звено с положительным нулем
W(s) = (1- s)Здесь имеется положительный нуль (корень числителя) s1=1/ .
В нуле передаточная функция равна нулю (W(s)=0).
Амплитудно-фазовая частотная характеристика
W(j ) = (1 - j ) A( )=
2 2
1+
= - arctg





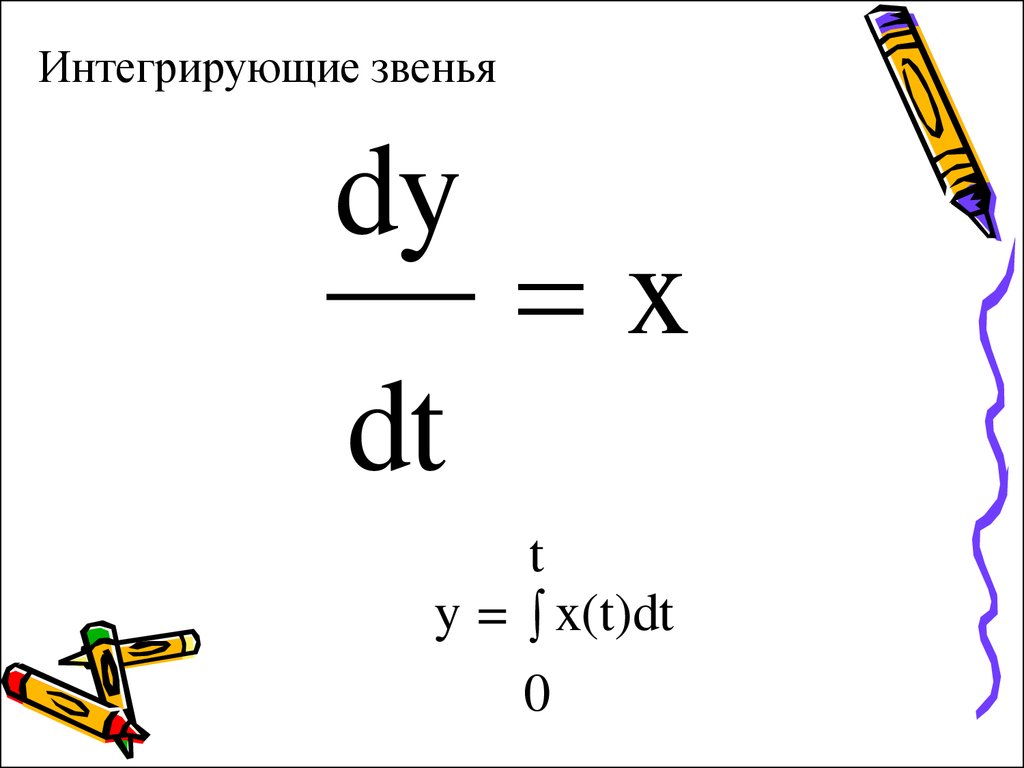

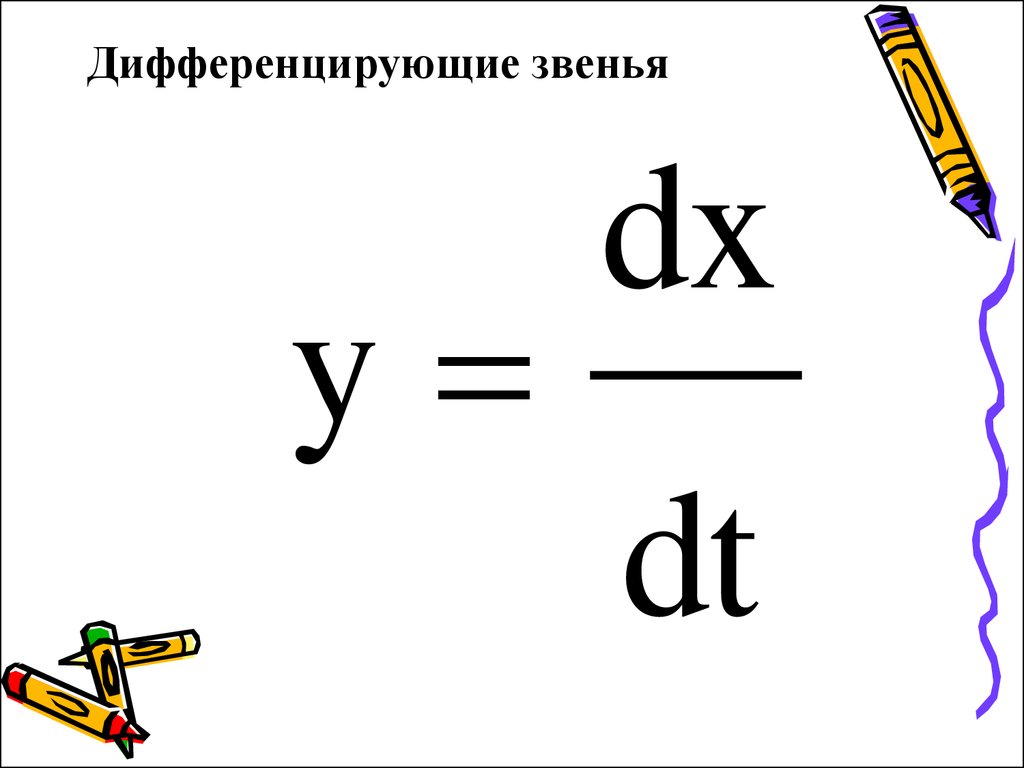








 management
management








