Similar presentations:
Основы автоматического управления. Введение. Основные понятия и определения
1.
Министерство образования и науки Российской Федерациифедеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ВОЕНМЕХ» им. Д.Ф. УСТИНОВА
Кафедра Н1
Мехатроника и робототехника
К.т.н., доцент Савельев Б.Н.
Иллюстративный материал
курса лекций
Часть первая
Санкт – Петербург
2015 г.
2.
ВведениеОсновные понятия и определения
1. Техническая система - устройство, которое обладает совокупностью следующих основных признаков:
- является законченным видом технической продукции;
- состоит из взаимодействующих элементов, узлов, агрегатов, подсистем;
- самостоятельно выполняет определенные функции;
- взаимодействует с внешней средой и другими техническими объектами.
2. Управление - процесс целесообразного воздействия на объект управления, обеспечивающий его
желаемое (заданное) поведение, режим работы или выходные переменные.
3. Регулирование - частный случай процесса управления, целью которого является воспроизведение
системой поступающих на нее извне заданий (задающих воздействий).
4. Автоматизация - процесс исключения человека из технологического процесса или из отдельных
его операций (выполнение операций без непосредственного участия человека).
5. Система автоматического управления (САУ)
САУ каким-либо объектом называется техническая система, включающая в себя этот объект
управления(ОУ) и присоединяемую к нему автоматическую аппаратуру, обеспечивающую
заданный режим работы или выходные переменные объекта в соответствии с командами
задающего устройства, являющегося частью этой автоматической аппаратуры.
6. Автоматическая управляющая система -автоматическая аппаратура САУ.
7. Система автоматического регулирования (САР)
САР – техническая система, в которой задаваемый от внешнего задающего устройства режим
работы ОУ или его регулируемая переменная воспроизводится и поддерживается с помощью
присоединяемых к ОУ автоматически действующих устройств.
8. Автоматический регулятор - автоматические устройства САР,
3.
Обобщенные схемы САУ и САРV
U
АУС
АЗУ
ОУ
Авт. рег
Условные обозначения:
Y
Y - регулируемые переменные ОУ;
- возмущающие воздействия на ОУ;
V
U - управляющие воздействия на ОУ;
Рис.1 Обобщенная схема САУ
V
ЗУ
Авт. рег
U
ОУ
Рис.2 Обобщенная схема САР
ОУ – объект управления;
АУС – автоматическая управляющая
система;
Авт. Рег. – автоматический регулятор;
АЗУ – автоматическое задающее
устройство;
Y
- управляющие воздействия на САР;
ЗУ – внешнее задающее устройство.
4.
Обобщенные функциональные схемы САРРис.3 САР непрямого действия.
Авт. рег
ЗУ
УИ
РО
U
Рис.4 САР прямого действия.
V
ОУ
Y
Условные обозначения:
ИУ – исполнительное устройство;
УПУ – усилительнопреобразовательное устройство;
УУ – устройство управления;
УИ – устройства измерений;
УПОИ – устройства предварительной
обработки информации;
РО – регулирующий орган,
5. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРЯМОГО ДЕЙСТВИЯ
РЕГУЛЯТОР ПОЛЗУНОВАРЕГУЛЯТОР УАТТА
ВОДА
ПАР
ОН
Паровая
турбина
Объект
нагрузки
Масса
Регулирующий
орган
Центробежный
механизм
ДАТЧИК УРОВНЯ
Регулирующий
орган
ПАР
ТОПКА
Рис. 6
Рис. 5
6.
САР температуры охлаждающей жидкости в двигателеАккумуляторная
батарея
Датчик
Двигатель
вентилятора
Задатчик
0
tC
Термо
Р
а
д
и
а
т
о
р
стат
ДВ
Регулир.
объект
Рис.7
7.
ФУНКЦИОНАЛЬНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО МОМЕНТНОГО ПРИВОДАпри косвенном измерении момента и компенсации противо ЭДС
3 220 v
Г
ИD
ОЯг
Mf Г Г
ПD
E ЯГ
M пд
M ТР Г M Г
IЯ
UЯ
УУ
U Мо
КК
U
ЭУ
BГ
BAD
I BГ
ОВг
MД
DМ
DС
Рис.8
РЕД
I BД
O
MUo
ОУ
MТР Д
Ф BД
U BД
д
E ЯД
КОд
КОг R ш
Ф BГ
U Мз
ОЯд
Mfo
ОВд
Mfд i Р Р
MРo
8.
Обобщенная функциональная схема электрогидравлического следящего приводаР1
ПД
М ПД
Н М Ин
ГН
ИД
ГЗ
ПК
ок
МУ
ЗУ
с
с
УМ
ок
ПК
ЦУ
ЦАП
ЭУ
ДУД
А
д
а
п
т
е
р
ЗГУ
РПП с
ДОС
СЦ
Р2
СИГП
ГН ПП
ПД П
ДД2
ВАД
с
МПБ
эмп
с
УУ
МП
ПК
Ф
ДД1
ТО
ГП
ОУ
БП
ДС
ДП
ДВВ
Энергетическая часть
Информационная часть
Рис.9
9.
САР, работающие по разомкнутому циклу (разомкнутые системы)V
ЗУ
Авт. рег
U
Y
ОУ
Рис. 10 Управление по задающему воздействию
V
ЗУ
const
Авт. рег
U
Y
ОУ
Рис. 11 Управление по возмущающему воздействию
САР, работающие по замкнутому циклу
(замкнутые системы)
V
Авт. рег
ЗУ
U
ОУ
Y
ОС
Рис. 12 Управление по отклонению
САР комбинированного управления
V
ЗУ
Авт. рег
U
ОУ
Y
ОС
Рис. 13 Управление по отклонению и возмущению
10.
Статические характеристики звеньев непрерывного действияРис.14 Пропорциональная
Рис.15 Кусочно - линейная
Рис.17 Зона нечувствительности
Рис.16 Насыщение
И тому подобные
11.
Статические характеристики звеньев дискретного действияРис.18 Статические характеристики звеньев релейного действия
t
t
Рис.19 Статические характеристики звеньев импульсного действия
12. Классификация приводов по схеме построения силовой части
Индивидуальный однодвигательныйпривод
Групповой привод
УУ
УУ
УМ
ИП
ИД
ИД
МП
МП
ОУ
Рис.20
ИП
УМ
ОУ2
ОУ1
1
ОУ3
2
Рис.21
3
13.
Индивидуальный многодвигательныйпривод
Дифференциальный привод
УУ
УУ
УМ
ИП
ИД
МП
ОУ
Рис.22
УМ
УМ
ИД
ИД
ИП
УМ
ИД
МД
ОУ
Рис.23
14.
Многокоординатный привод(система приводов)
У У2
У У1
У М1
ИП
У М2
ИД1
ИД2
МП1
МП2
ОУ
Рис.24
2
1
15.
Обобщенная функциональная схема САПИП
ВАД
УИ
Эл-ты вспомогат.
подсистем
ЗУ
U
му
УУ
ЭУ
ВАД
УИ
УПУ
Информационная часть САП
Рис.25
ИД
МП
ОУ
О
Энергетическая часть САП
Условные обозначения:
ИД – исполнительный двигатель;
УПУ – усилительно-преобразовательное устройство;
ЭУ – электронный усилитель;
УУ – устройство управления;
ОУ – объект управления;
МП – механическая передача;
УИ – устройства измерений;
ВАД– вторичная аппаратура датчиков;
16.
Теория линейных САУ непрерывного действияМатематическое описание линейных систем автоматического управления
Цель и задачи
Целью рассмотрения САУ и САР, как правило, является решение одной из двух основных задач
- задачи анализа системы;
- задачи синтеза системы.
Первая задача возникает тогда, когда имеется система и необходимо исследовать ее
свойства и качество,
Вторая задача -, когда задаются требования к качеству системы, и необходимо построить
(создать) САУ, соответствующую этим требованиям.
При решении этих задач используются различные методы анализа и синтеза САУ и САР.
Методы исследований САУ и САР:
- экспериментальные.
- опытно-теоретические методы;
-теоретические методы;
При их реализации используются:
- натурные и полигонные испытания образцов систем в составе технических комплексов;
- стендовые (лабораторные и заводские) испытания натурных образцов систем и их узлов;
- испытания с применением различного вида моделей (воздействий и свойств узлов системы);
- математическое моделирование систем (математические модельные эксперименты).
Моделирование включает в себя два этапа:
1. Построение модели оригинала (реального образца);
2. Использование модели при решении задач анализа и синтеза систем или других задач.
Модель
Под моделью понимается овеществленный, программный, символьный или мысленный объект,
отображающий в определенном отношении оригинал, замещающий его при решении каких-либо
задач и позволяющий получить новую информацию о замещаемом объекте.
17.
Виды моделейПостроение моделей базируется на теории подобия и ее различных аспектах.
В зависимости от используемого вида подобия и различают виды моделей:
- Геометрическое подобие используется при построении геометрически подобных
моделей (макетов), адекватных оригиналу в отношении размеров, форм, габаритов, при
абстрагировании от других свойств и характеристик оригинала;
- Функциональное подобие (изофункционализм) используется при построении
функциональных моделей адекватных оригиналу в отношении лишь некоторых функций,
но имеющих другую физическую природу, состав, структуру и т.д.;
- Физическое подобие позволяет строить физические модели адекватные оригиналу
в отношении физических свойств и процессов, т.е.модели той же физической природы, что и
оригинал;
- математическое подобие (изоморфизм) позволяет строить математические модели,
адекватные оригиналу в отношении математического описания свойств и процессов оригинала;
Математической моделью системы (или ее звена) называют
представленное в той или иной форме математическое описание системы
(звена),адекватно отражающее ее статические и динамические свойства в
определенном диапазоне режимов функционирования.
18.
Линеаризация звеньев САУРассмотрим для примера звено с двумя входными воздействиями Х1 и Х2 и одной выходной
величиной Y, динамическое уравнение которого имеет вид нелинейного дифференциального
уравнения:
1
( х1, х 1, х 1,... х2, х 2, х 2,... y, у , у ...) 0
(1)
х
y
х2 х1, х2
Будам считать, что динамический процесс в системе протекает в окрестности некоторой точки
установившегося статического
режима, в которой переменные звена имеют постоянные
о
о
о
значения
Эту точку называют точкой линеаризации.
1
2
о
о
о
(2)
Уравнение звена в этом режиме:
х ;х ; у .
( х1 , 0, 0,... х2, 0, 0,... у ,0,0...) 0,
а переменные в динамическом режиме можно представить:
о
х1 t х1 х1 t ;
о
t
х2
х2 х2 t ;
о
у t у у t ;
х 1 t х 1 t ;
х 2 t х 2 t ;
у t у t ;
х 1 t х 1 t ;
х 2 t х 2 t ;
у t у t и т.д.
При линеаризации производные рассматриваются как самостоятельные переменные.
Пути линеаризации
х х у 0
1. Если
близка к линейной в окрестности точки линеаризации, то ее
1, 2,
можно просто заменить линейной зависимостью, и ограничить диапазон изменения
воздействий.
х х у 0
2. Если
не линейна в окрестности точки линеаризации, но непрерывно
1, 2,
дифференцируема, ее можно разложить в ряд Тейлора в этой точке.
х х у 0
3. Если
существенно не линейна, т.е. не является непрерывно
1, 2,
дифференцируемой, а содержит разрывы, неоднозначности и т.п. используют гармоническую
линеаризацию, т.е. при эквивалентном гармоническом воздействии выходную переменную
раскладывают в ряд Фурье. Из него и определяют коэффициенты линеаризации.
19.
Основным является второй путь. Рассмотрим его подробнееУравнение звена в результате разложения в ряд Тейлора примет вид:
( х1о , 0, 0,... хо2, 0, 0,... уо ,0,0...) х1 t х 1 t ... х2 t х 2 t ...
х1 0
х 1 0
х2 0
х 2 0
... у (t ) у t у t ... (члены высшего порядка малости) 0 (3)
у 0
у 0
у 0
- значение частной производной при подстановке в нее значений переменных и их
производных в точке линеаризации. х1
х1 0
Пренебрегая членами высшего порядка малости и вычитая из уравнения (3) уравнение
установившегося режима (2),получим линеаризованное дифференциальное уравнение звена в
отклонениях или в вариациях:
х1 t х 1 t ..... х2 t х 2 t ...
х1 0
х 1 0
х2 0
х 2 0
... у t у t у t ... 0
у 0
у 0
у 0
(4)
Комментарий:
- Линеаризованное уравнение звена является приближенным, т.к. не учитывает малые высшего
порядка.
- Переменными в уравнении являются отклонения от значений в точке линеаризации.
- Уравнение справедливо при малых отклонениях от значений в точке линеаризации.
20.
Графическая интерпретация линеаризацииу у
у
о
Коэффициенты линеаризации
1
х1
2
х2
о
х1
о
х2
х1
tg 1
х1 0
tg 2
х 2 0
В статических установившихся режимах
у tg 1 x1 tg 2 x2
х2
Рис.26
21.
Аналитические формы представления математического описания звеньев и систем1. Уравнение движения
2
d y
m 1
n 1
d
x1 ...
d
x
y
1
y
y
d
d
d
a
y
n 1
am
.... b2
b1
bn 1
bn
m
n 1
2
d t n 1
n
d
t
dt
dt
dt
dt
r
d x2
x2
2
d
d
x
(5)
1
...
a02 x2
a12
a0 x1 a r 2
.... a 2 d 2x1 a1
r
dt
dt
dt
dt
n
m
(k )
( j)
y (i )
х
2 0
х1 0 ( j 1 m); а k 2
0
(k 1 r );
; (i 1 n); а j
bi
y 0
y 0
y 0
d
p , уравнение (5) записывают в виде:
Вводя обозначение
dt
(bn p n bn 1 p n 1 ... b1 p 1) y t (a m p m ... a1 p a01) x1 t (a r 2 p r ... a 02) x 2 t (6)
или
где:
Bn p y t а01 Am
X1
p x1 t а02 Ar p x2 t
(7)
X2
i
1
2
n 1
n
p
1
1
.....
p
p
p
p
p
b
b
b
b
b
Вn
i
1
2
n 1
n
n
i 1
m
Am
X1
p 1 a j x p j 1 a1x p1 a2 x1 p2 ..... am 1x pm 1 am x pm
j 1
r
1
k 1
2
1
1
1
k
1
2
r 1
r
Ar x p 1 ak x p 1 a1x p a2 x p ..... ar 1x p ar x p
2
2
2
2
2
- полиномы от р
22.
аКоэффициенты bi , a j , ak полиномов Bn p , Am x1 p , Ar x2 p имеют размерность времени в
степени i, j , k , соответственно, а коэффициенты 01 и а02 - размерность отношения
размерностей у t к х1 t и у t к х 2 t , поэтому часто вводят обозначения:
k
j
bi Тii ; a j Т j ; a k Т k ; a01 К х ; a02 К х
1
2
Ti ; T j ; Tk
- называют постоянными времени звена ;
Кх ; Кх
- называют коэффициентами передачи звена по соответствующему входу.
1
2
Коэффициенты передачи – это соотношение между выходной и входной переменными звена в
статических режимах работы при нулевых отклонениях других воздействий от их значений в
точке линеаризации:
у
Кх
х
1 0
х 2 рi p k 0
у
Кх
хi 2 0j
х1 р p 0
2
1
С учетом этих обозначений уравнение (7) может быть представлено в виде:
(Tnn pn Tnn 11 pn 1 ... T1 p 1) y Kx (Tmm x1 p ... T1x p 1) x1 K x (Trr x2 p ... 1) x2
m
r
1
1
(8)
2
Уравнения (6), (7) и (8) будем называть уравнением движения звена в операторной форме.
Считая условно оператор дифференцирования
представим уравнение (8) в виде:
d
p
dt
алгебраической величиной,
m
r
m
r
K x 1 T1x p ... Tm x p
K x 1 ... Tr x p
y t
х1 t
x2 t
2
n
2
n n
1 T1 p T2 p ..... Tn p
1 T1 p T2 p ..... Tn p
1
1
1
2
2
(9)
23.
2. Передаточные функции звенаВыражения
1
и
m
m
K x 1 T1x p ... Tm x p
K x Am x p
Wx p
2 2
n n
1 T1 p T2 p ..... Tn p
Bn p
1
1
1
1 ... T
1
p
Kx
K x Ar x p
p
Wx
1 T1 p T22 p2 ..... Tnn pn
Bn p
2
2
r
r x2
r
2
(10)
1
2
(11)
называются передаточными функциями звена соответственно по входу x1 t и
При введении этих понятий уравнение движения звена может быть представлено через
передаточные функции в виде:
x 2 t
y t W x p x1 t W x p x2 t
1
(12)
2
В ТАУ под передаточными функциями, строго говоря, понимается иное, а форма записи (12)
используется для компактной записи дифференциального уравнения движения звена. Будем
называть выражения (10) и (11) операторными передаточными функциями звена.
Введем более строгое определение понятия передаточной функции.
Представим уравнение (7) в виде:
(13)
Bn p y t K x Am p x1 t K x Ar p x2 t
1
X1
2
X2
Перейдем в выражении (13) от переменных во времени к их изображениям по Лапласу
x1 t x1 s x1 t e st dt
0
x2 t x2 s x2 t e st dt - изображения по Лапласу переменных
x1 t , x 2 t и у t ;
0
- комплексная переменная
y t y s y t e st dt
преобразования Лапласа.
0
s c j
24.
Обратный переход к оригиналу можно осуществить, используя обратное преобразование Лапласа1 c j
st
x t
x s e ds, справедливое при нулевых начальных условиях.
j 2 c j
Важным свойством преобразования является следующее:
d x t
1 c j
st
dt
p x t
j 2
sx s e ds
c j
k
p x t sk x s
p x t sx s ,
x t x s ,
(14)
или, если
то
а
(Здесь использована символическая форма, обозначающая, что переменная от s является
изображением по Лапласу переменной от t)
С учетом этого свойства уравнение (13) после перехода к изображениям переменных по Лапласу
можно представить в виде:
Bn s y s K x Am s x1 s K x Ar s x2 s
K A s
K x A x s
y s x x
x1 s
x 2 s
B
s
B
s
Обозначим:
1
1
1
X1
2
2
X2
или
2
y s
y s
K x A x s
K x A x s
W x s
s
W
x
и
B s
B s
x1 s x2 s 0
x2 s x1 s 0
W x s , W x s - и называют передаточными функциями звена по входам х1 и х2.
1
1
2
1
1
2
2
(15)
(16)
(17)
2
Передаточная функция – отношение изображений по Лапласу выходной и входной
переменных звена при нулевых начальных условиях и отсутствии других воздействий ( или их
отклонений от значений в точке линеаризации)
y s W x s x1 s W x2 s x2 s
1
- описание свойств звена с помощью
(18)
его передаточных функций
25.
Преобразование Лапласа применимо к функциям удовлетворяющим условиям:1. Функция равна нулю
x t 0 при t 0 ,
с 0 , при котором x t e ct dt
0
Величина «С» (вещественная часть s с j ) называется абсциссой абсолютной сходимости.
2. Существует
Эти условия выполняются для большинства функций, описывающих процессы в САУ, более того
абсцисса абсолютной сходимости для них часто равна нулю
, т.е
, что
позволяет применять к ним и преобразование Фурье:
(с 0)
s j
x t x j x t e j t dt ,
x t
1
j t
d
x j e
2
- частота
(19)
(20)
Используя изображения по Фурье входной и выходной переменных звена введем понятие
частотной передаточной функции звена.
Частотной передаточная функция называется отношение изображений по Фурье выходной
и входной переменных звена при нулевых начальных условиях и отсутствии других
воздействий ( или их отклонений от значений в точке линеаризации)
y j
W x j и y j W x j
x1 j x2 0
x2 j x1 0
K x A x j
K x A x j
y j
x 2 j
x1 j
B j
B j
1
1
1
2
2
2
- частотные передаточные функции
звена по соответствующему входу.
-уравнение движения в
изображениях по Фурье
(21)
описание свойств звена с помощью
(22)
y j W x j x1 j W x 2 j x2 j -частотных
передаточных функций
1
26.
Графо-аналитические формы математического описания звеньев и системСтруктурные схемы
Передаточные функции используются при построении математической модели в виде
динамических структурных схем.
Структурной схемой в ТАУ называют математическую модель оригинала представленную в
виде совокупности элементов с указанием их передаточных функций или выполняемых
математических операций и связей между ними.
Так как уравнения движения звена в операторной форме и для изображений переменных по
Лапласу или Фурье, а также его передаточные функции совпадают с точностью до обозначений,
структурные схемы можно строить как во временной области, так и в области изображений. При
этом вид структурных схем будет идентичен.
Например, математическая модель звена в форме уравнения движения вида (12), уравнения
для изображений по Лапласу (12) или уравнения для изображений по Фурье (22) может быть
представлена в форме структурных схем вида Рис. 27 а),b) и c),соответственно.
x1 t
Wx p
1
x 2 t
Wx p
+
у t
x1 s
W x s
1
x 2 s
W x s
2
2
b)
а)
+
у s
x1 j
W x j
1
x 2 j W
x2
j
+
у j
c)
Рис.27
Одному звену можно поставить в соответствие несколько различных по виду, эквивалентных
структурных схем.
27.
Пример эквивалентных структурных схемПусть звено описывается дифференциальным уравнением в операторной форме вида:
2 2
(T2 p T1 p 1) у (t ) K x1(1 T x1 p) х1 (t ) K x2 (1 T x2 p) х2 (t )
Соответствующие ему структурные схемы приведены на Рис.28, Рис.29 и Рис.30:
х1 (t )
х1 (t ) K x1 (1 T x p)
1
2 2
T2 p T1 p 1
х2 (t ) K x (1 T x p)
2
2
T2
2
p T1 p 1
2
K x1 (1 T x1 p)
у (t )
х2 (t )
K x2 (1 T x2 p)
Рис.29
Рис.28
х1 (t )
х2 (t )
у (t )
1
2 2
T2 p T1 p 1
K x1
K x2
1
T x1 p
1
T x2 p
Рис.30
у (t )
1
2 2
T2 p T1 p 1
28.
Графические формы представления математического описания звеньев и системВременные характеристики
1.Переходная функция (переходная характеристика)
Переходной функцией (переходной характеристикой) называется переходной процесс (изменение во времени)
выходной переменной звена, вызванный подачей на его вход скачкообразного воздействия единичной величины
Такое воздействие называется единичной ступенчатой функцией и обозначается X(t) = 1(t).
1(t)
Переходная характеристика обозначается
Функции
1 t и h t
0
1
h t , т.е.
при
t 0
при
t 0
y t h t при x t 1 t
(23)
могут быть представлены в графической форме:
y (t ) h(t )
x(t)
y уст
1
0.95 у уст
t
Рис.32
Tп t
Рис.31
Звенья с различными динамическими свойствами будут иметь разные реакции на скачкообразное воздействие.
Реакции пропорциональных звеньев с различными динамическими свойствами приведены на Рис. 32
По виду реакции можно судить о динамических свойствах звена, т.е. реакция содержит информацию об этих
свойствах и может служить их моделью.
Теоретически процессы смогут стремиться к установившемуся значению бесконечно долго.
В ТАУ принято считать, что процесс закончен, если / y t у
/ 0,05 у
при всех t T
Tп
Tп
- называется временем переходного процесса.
уст
уст
П
29.
2.Весовая функция (импульсная переходная характеристика)Весовая функция представляет собой реакцию звена (изменение во времени выходной переменной)
при подачи на его вход единичной импульсной функции (дельта функции).
Под дельта функцией понимается импульс бесконечно малой продолжительности и бесконечно большой
амплитуды с площадью равной 1. Дельта функцию обозначают
.
Аналитически это выражается так:
(t)
(t )
w(t ).
Весовую функцию будем обозначать
Графически
(t)
и
( t ) dt 1
0 при t 0
при t 0
Иными словами
(24)
y (t ) w(t )
при
х(t) (t )
w ( t ) представляются следующим образом:
х(t)
y (t ) w(t )
t
t
Рис.33
Легко заметить, что
Рис.34
d
( t ) 1 ( t ); 1(t ) (t )dt ,
dt
Действительно, импульс шириной
d
h ( t ); h ( t ) w ( t ) dt
и установить w ( t )
dt
и амплитудой N можно представить в виде двух скачков N 1 ( t ) и - N1(t ).
Тогда реакцию звена можно выразить через переходные характеристики
Помножив и поделив на
0 и увеличивая
y(t) w ( t ) lim
0
N так, чтобы
N 1
N (h(t) - h(t - ))
y(t) N h(t) - h(t - )
, в пределе получим:
dh(t)
dt
30. Связь переходных характеристик с передаточной функцией звена
По определению передаточная функция звена или системы равна отношению изображений по Лапласувыходной и входной переменных при нулевых начальных условиях, следовательно при подаче на вход звена
дельта функции она будет равна отношению изображений по Лапласу весовой функции и дельта функции, т.е.
где:
y(s) w( s )
W(s)
w( s ) w(t ) e stdt
x(s) ( s )
0
st
w ( s ) w ( t ) e dt изображение по Лапласу весовой функции w ( t ) ,
(25)
(26)
0
st
( s ) ( t ) e dt 1
изображение по Лапласу дельта функции
( t ) ,равно 1.
0
Таким образом весовая функция связана с передаточной функцией звена преобразованием Лапласа.
Используя обратное преобразование, получим:
c j
st
1
(27)
w(t )
Так как
где
w t
j2
W(s) e
ds
c- j
d
h t и w( s ) sh( s ) W s
dt
h( s ) w(t ) e stdt изображение по Лапласу переходной функции h ( t ) , получим :
0
h(s)
st
W(s)
sh ( s ) s h ( t ) e dt , или
1( s )
0
c j
W(s) st
1
h(t )
ds
j2 c- j s e
Т.е. переходная характеристика связана с передаточной функцией звена преобразованием Карсона.
Воздействия вида 1(t) и
(t)
называются типовыми воздействиями
(28)
(29)
31. Реакция звена или системы при не типовых воздействиях
Переходные функции (характеристики),как и другие виды мат. моделей звена, позволяют получитьреакцию звена при воздействиях произвольного вида и нулевых начальных условиях, т.е. когда входное
воздействие может быть представлено X(t)1(t).
Произвольную функцию времени Х(t)1(t) можно представить в виде суммы ступенчатых воздействий
величиной
Хк , подаваемых через промежутки времени , или в виде суммы импульсов высотой Xi
и длительностью .
Х(t)
Х(t)
Хк
Хi
t
Рис.35
t
Рис.36
Переходный процесс y(t) на выходе звена в этом случае может быть определен как предел суммы реакций
звена на ступенчатые воздействия величиной X pX ( ) при 0 , или как предел
суммы реакций на импульсы величиной X( ) и длительностью
при 0 .
Пределом суммы при 0 является интеграл, который носит название интеграла Дюамеля-Карсона
t
y(t) h(t)X(0) h(t - ) px( )d
(30)
0
t
y(t) w(t - )x( )d
0
Последнее выражение называется также интегралом свертки
(31)
32. Частотные характеристики звеньев и САР
Частотная передаточная функцияОсновной частотной характеристикой динамических звеньев или САР является их частотная передаточная
функция, под которой понимают отношение изображений по Фурье выходной и входной переменных при
нулевых начальных условиях и отсутствии других воздействий. Рассмотрим существо этого понятия. Пусть
есть звено или САР с одним входом и одним выходом, динамика которого описывается линейным уравнением:
B(p) y(t) k A(p) x(t),
где: X(t) и Y(t) – входное воздействие и выходная переменная звена или САР;
K – коэффициент передачи звена или САР;
A(p) 1 a p
m
i
i 1
n
B(p) 1 b p
j 1
i
j
- полиномы от Р (
p
d
dt
) степени m и n.
j
Схема такого звена или САР может быть представлена в виде:
x(t)
W(p)
y(t) k A(p)
W(p)
x(t) B(p)
y(t)
Подадим на вход звена гармоническое воздействие:
x(t) Xm Cos t ,
где: Хm – амплитуда воздействия;
2
T
- угловая частота;
Т – период.
На выходе звена в установившемся режиме будут вынужденные колебания переменной той же частоты,
но другой амплитуды и фазы, т.е.:
y(t) ym Cos ( t ),
где:
ym –амплитуда выходной переменной;
- сдвиг по фазе относительно Х(t).
33. Используя формулы Эйлера, представим Х(t) и y(t) в другом виде:
x(t) Xm (e j t e j t ) x(t) x(t)2(32)
ym j ( t ) j ( t )
y(t) (e
e
) y(t) y(t)
2
Такое представление косинуса соответствует изображению его
Im
(33)
t
t
на комплексной плоскости в виде двух векторов вращающихся с
частотой
в разные стороны.
В линейном звене можно рассматривать прохождение каждой
составляющей входного воздействия отдельно, а т. к. они
отличаются лишь знаком в показателе степени и соотношения
между y(t)+ и x(t)+,а также y(t) и x(t) одинаковы, будем
рассматривать лишь одну и использовать символическую запись
x(t) xm e
j t ;
Cos t
y(t) ym e j( t )
Рис.37
Не трудно получить выражения для производных от х(t) и y(t):
pk x(t) (j )k xm e j t ;
Подставляя выражения для x(t),
Re
pk y(t) (j )k ym e j ( t )
y(t) и их производных в уравнение движения звена, получим:
B(j ) ym e j ( t ) kА( j ) x m e j t ,
из которого
y(t) ym j kA(j ) W(j ) - частотная передаточная функция звена или САР.
x(t) x m e B(j )
y(j )
Она совпадает по виду с передаточной функцией
x(j ), y(j ) -
W(j )
x(j )
,
где
изображения по Фурье воздействия и выходной переменной, которая применяется в
более общем случае, при воздействиях произвольного вида, а не только гармонических.
(34)
34.
Частотная передаточная функция отображает свойства звена и показывает как изменяются амплитуда ифаза при прохождении гармонического воздействия через него. При фиксированной частоте входного
воздействия W( j ) представляет собой комплексное число, которое может быть представлено:
W(j ) M( ) e j ( ) U( ) jV( ), где :
M( ) W(j )
ym
xm
- модуль частотной передаточной функции, равен отношению
амплитуд выходной и входной переменных;
( ) argW(j )
- аргумент частотной передаточной функции, равный сдвигу фаз
гармоник на выходе и входе звена;
k
( )
( ) VA ( ) VB( )
U( ) U A U2 B
2
U B( ) VB( )
k
( )
( ) VA ( ) U B( )
V( ) - U A V2 B
2
U B( ) VB( )
m
U A ( ) 1 a 2i ( j ) ;
2i
i 1
n
U B ( ) 1 b 2i ( j )
i 1
2i
- действительная часть частотной передаточной функции,
- мнимая часть частотной передаточной функции,
2i-1
1m
- действительная и мнимая части
(
)
(
j
)
VA
j i 1 а 2i-1
полинома A(j )
; VB( )
2i-1
1 n
- действительная и мнимая части
(
j
)
b
j i 1 2i-1
полинома B(j )
Связывающие соотношения:
M( ) U
2
2
(35)
( ) V ( );
( ) arctg
V( )
;
U( )
U( ) M( )Cos ( ); V( ) M( )Sin ( ).
(36)
(37)
35. Частотные характеристики
При различных частотах входного воздействия будут различными модуль, фаза, действительная и мнимаясоставляющие частотной передаточной функции звена, т.е. они являются функциями частоты. Следовательно
они могут быть построены графически.
Зависимость M(
) от частоты называют «амплитудно-частотной характеристикой»(АЧХ)
Зависимость
от частоты называют «фазовой частотной характеристикой»(ФЧХ)
Зависимость U(
) от частоты называют «действительной частотной характеристикой» (ДЧХ)
Зависимость V( ) от частоты называют «мнимой частотной характеристикой» (МЧХ)
Примерный вид этих характеристик для инерционных звеньев:
( )
M( )
U( )
Рис.38
АЧХ
Рис.40 ДЧХ
( )
90
R
V( )
0
180
0
Рис.39 ФЧХ
Рис. 41 МЧХ
АЧХ показывает, какой коэффициент передачи (усиления) звена будет на каждой частоте, а ФЧХ- каким будет
сдвиг фазы.
АЧХ может быть монотонной или иметь максимум. При наличии max звено имеет собственную частоту, которая
называется резонансной.
ФЧХ у инерционных звеньев отрицательна, т.к. выходные колебания отстают по фазе от колебаний на входе.
36. АМПЛИТУДНО-ФАЗОВАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА
Наряду с рассмотренными частотными характеристиками в ТАУ широко используется и объединяющая иххарактеристика, которая называется амплитудно-фазовой частотной характеристикой (АФЧХ).
Амплитудно-фазовая частотная характеристика имеет аналитическое выражение в виде частотной
передаточной функции
kA(j )
W(j )
U ( ) jV( ) M( ) e j ( )
B ( j )
(38)
АФЧХ строится на комплексной плоскости и представляет годограф вектора частотной передаточной функции
при изменении частоты от 0 до
.
В соответствии с представлением частотной передаточной функции через действительную и мнимую
составляющие или через модуль и фазу АФЧХ может быть построена с использованием прямоугольной или
полярной систем координат. По оси абсцисс откладывают действительную часть
ReW(j ) , а по оси
ординат – мнимую часть ImW(j ) частотной передаточной функции, или откладывают угол (фазу
(
и модуль M( ) W(j )
))
ImW(j )
0
0
4
Примерный вид АФЧХ позиционных звеньев и
систем приведен на Рис.42.
При
сдвиг по фазе у таких звеньев и
систем
,т.е. характеристика начинается на
оси абсцисс, а модуль равен К.
Фаза откладывается от оси абсцисс против часовой
стрелки. При этом следует помнить, что для
инерционных звеньев, у которых сигнал на выходе
запаздывает по отношению сигнала на входе, фаза
будет иметь отрицательное значение. В этом
случае она должна откладываться по часовой
стрелке.
С ростом частоты фаза будет возрастать, а
амплитуда выходного сигнала уменьшаться
стремясь к 0 при
,т.е. инерционные
звенья обладают свойствами фильтра.
M( )
V( )
3
Рис. 42
U( ) 0
( ) К ReW(j )
2
АФЧХ
1
37. СВЯЗЬ ЧАСТОТНЫХ И ВРЕМЕННЫХ ХАРАКТЕРИСТИК
Частотные характеристики имеют более широкое применение и используются не только для случаевгармонических воздействий.
Если входное воздействие Х(t) периодическая функция времени, то ее можно разложить в ряд Фурье и
представить в виде суммы гармоник или, используя формулы Эйлера, в виде суммы сопряженных векторов
вращающихся на комплексной плоскости
X(t) XKCos( K x1t xk ) x k (e j ( k 1t xk ) e j ( k 1t xk ))
k 0
k 0 2
k 0
k
(c xk e jk 1t c-xk e jk 1t ) , c xk e jk 1t
где: Хк – амплитуда;
k k 1
- угловая частота k-ой гармоники;
1
(39)
2
-основная частота, Т – период.
T
гармоники на комплексной
xk
модуль сопряженных векторов К-ой
c xk e j xk - комплексный
плоскости, содержащий информации о модуле векторов и их начальной фазе.
2
Если входное воздействие функция произвольного вида Х(t)1(t) (непериодическая), то, используя
преобразования Фурье, ее можно представить в виде бесконечной суммы бесконечно малых по величине
гармоник или сопряженных векторов вращающихся на комплексной плоскости с различными частотами
.
Эта сумма выражается обратным преобразованием Фурье
где
1
j t
x(t )
X(j ) e d ,
2 -
X ( j ) x ( t ) e
j t
dt изображение
(40)
Х(t) по Фурье.
0
Это следует из сути преобразований Фурье, как предельного случая разложения периодической
функции в ряд при периоде Т и основной частоте d 0
d
X(j )
c ( j ) - комплексный модуль вектора К-той гармоники (содержит информацию о
2
величине и начальной фазе) .
c ( j )
2
X(j )
c ( j )
- относительный комплексный модуль К-ой гармоники.
d
f1
38. Использование преобразований Фурье
1 Для линейных звеньев и систем прохождение каждой гармонической составляющей входного воздействияможно рассматривать отдельно. Она будет вызывать в выходной переменной составляющую той же
частоты, но другой амплитуды и фазы. Сумма составляющих на выходе звена и представляет собой
выходную переменную y(t). Для периодического сигнала
c yk x
yk j ( k t )
k j ( k t xk )
jk
t
y1
y(t) yKCos( K y1t yk )
yk c e y1
е
e
yk
(41)
k 0
2
2
k
k cxk
k
2
где: yк – амплитуда; k k 1 - угловая частота k-ой гармоники; 1
-основная частота, Т – период.
yk j - комплексный модуль сопряженных векторов К-ой Tгармоники y(t) на комплексной
c yk e yk плоскости, содержащий информацию о модуле векторов и их начальной фазе.
2
Для сигнала произвольного вида y(t)1(t),
j t
1
y(t )
где:
2
Y(j ) e
-
Y ( j ) y ( t ) e
0
W(j )
1
d
2
j t
Y(j )
X(j )
dt изображение
W(j )X(j ) e
j t
d ,
(42)
-
y(t) по Фурье
частотная передаточная функция
2 Суммирование ведется от
до
,отрицательная частота это вращение сопряженного
вектора на комплексной плоскости в противоположную сторону. Это обеспечивает возвращение от
символической формы представления гармоники Cos t 0 , 5 j t к полной, соответствующей формуле
Эйлера. С учетом этого и АФЧХ может быть достроена для частот от
до 0 .
j t
3 Изображение по Фурье весовой функции ( j ) ( t )
dt 1 ,следовательно
0
w( j )
j t
e
W(j )
w ( j ) w ( t ) e
( j )
0
w(t )
1
j t
W(j ) e d ,
2 -
e
dt ,
т.е. частотная передаточная функция связана с
весовой функцией преобразованием Фурье
39.
Логарифмические частотные характеристикиПрименительно к САУ и их звеньям амплитудную и фазовую частотные характеристики удобно
строить в логарифмических масштабах координат.
Построенные с использованием логарифмических масштабов эти характеристики называются:
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) ;
Логарифмическая фазовая частотная характеристика (ЛФЧХ) .
При построении ЛАЧХ используется величина L( ) 20 lg M( ) 20lg W( j ) .
Ее единицей измерения является децибел, т.е. 0,1 бела. (1бел – десятичный логарифм,
соответствующий усилению мощности в 10 раз, 2 бела – в 100 раз и т.д.).
Сигналы на входе и выходе звеньев САР обычно представлены одной из составляющих
2
мощности (напряжение или ток, момент или скорость, давление или расход и т.д.),
U
2
а мощность пропорциональна квадрату их амплитуды или значения (например, N эл r I
),
y
y
r
Поэтому
lg Nвых 2 lg вых бел 20 lg вых децибел
Nвх
xвх
xвх
Величина L( ) 20 lg M( ) 20lg W( j ) .откладывается по оси ординат, а по оси абсцисс –
частота
в логарифмическом масштабе.
Ось абсцисс проходит через (.) 0дб, что
L ( )
соответствует модулю звена равному1, а ось
ординат привязывают к какой – либо частоте,
так чтобы ЛАЧХ в основном была справа.
40дб
При построении ЛФЧХ используют такую же
ось частот, а по оси ординат откладывают
аргумент W( j ) (сдвиг по фазе
)в
градусах, причем отрицательный сдвиг по
фазе откладывают вверх.
20дб
0
0.01
180о
0
0.1
1
10
Рис.43
100
1000
1/с
Если ЛАЧХ и ЛФЧХ строят
о
вместе, то 180 совмещают с
осью 0 дб
40.
Примеры построения ЛАЧХ или ЛФЧХПостроим характеристики некоторых идеализированных звеньев на плоскости логарифмических
частотных характеристик.
1 Пусть звено имеет W(s) K.
Его частотная передаточная функция
W( j ) K.
W( j ) M( ) K, а аргумент
L( ) 20 lg M( ) 20 lg K,
Модуль частотной передаточной функции
K W( j ) K .
2 Пусть W(s) .
j
K s
W( j ) M( ) , L( ) 20 lg K - 20lg ,
L ( )
40дб
20 lg K
arctg
20дб
1К
0.01
K
0
180о
0.1
1
К
10
ср
100
1000
о
90
0.01
0.
0
90о
K W( j ) K .
3 Пусть W(s) 2 .
2
(
j
)
s
K L( ) 20 lg K - 40lg ,
M( ) 2 ,
1/с
0
arctg
4
0.1
1
10
100
1000
0
90o
1/с
o
180
2
W(s) Ks. W( j ) Kj .
W( j ) M( ) K ,
L( ) 20 lg K 20lg ,
Пусть
arctg
Рис.44
K
90o
0
41.
1.2 Позиционное (пропорциональное, статическое, апериодическое) звено первого порядкаЗвенья этого типа в установившемся статическом режиме дают на выходе сигнал пропорциональный входному
воздействию, однако в динамике пропорциональность нарушается из-за инерционных свойств звена.
Звенья этого типа описываются дифференциальными уравнениями вида:
b1dy(t) y(t) ( Tp 1)y(t) kx(t)
dt
W(s)
Передаточная функция таких звеньев имеет вид:
(43)
K
Ts 1
(44)
1.2.1 Временные характеристики позиционного звена первого порядка.
- переходная характеристика
Аналитическим выражением переходной характеристики является решение дифференциального уравнения звена,
n
которое ищется в виде:
it
y(t) y ч ( t ) y об ( t ) ( y уст C i e
где:
),
(45)
i 1
yч(t ) y уст - частное решение, соответствует установившемуся
значению y(t) y( ),
y об (t ) - общее решение,
i - корень характеристического уравнения вида В( )= 0 порядка n, соответствующего В(Р)=0,
Сi
- постоянные интегрирования, определяются из начальных условий.
Для дифференциального уравнения первого порядка при Х(t)=1(t)
где:
-t
T
y(t) h(t) k(1 e ) 1 ( t ),
(46)
= -1/Т - корень характеристического уравнения Тs+1=0 звена, K - установившееся значение
Графическое изображение переходной характеристики звена первого порядка представлено на Рис.45
h(t)
y( )
y уст
По переходной функции h(t), полученной
экспериментально, можно определить К и Т
звена. При времени t = T
(1)
(2)
0.632К
1
К
Т1 Т 2
Рис.45
t
h(t) K(1 e ) 0 , 632 K
К у уст у ( )
(47)
42. -весовая функция или импульсная переходная функция
dАналитическое выражение весовой функции может быть получено из выражения для h(t),т.к. w ( t ) h ( t )
dt
Для пропорционального звена первого порядка
K Tt
w ( t ) e 1( t )
T
(48)
Графически она представляет собой экспоненту, начинающуюся на оси ординат в точке К/Т и
асимптотически стремящуюся к 0. Внешний вид весовой функции позиционного звена первого порядка
показан на Рис.46
w (t)
По весовой функции w(t), полученной экспериментально,
тоже можно определить К и Т звена. При времени t = T
K
T
K TT
K
w ( t ) e 0 , 368
T
T
h(t)
0.368
K
T
Откладывая 0,368К/Т на характеристике
получить Т. Величина К определяется как
Т1 Т 2
t
(49)
w ( t ) , легко
К Tw(0)
Рис.46
Теоретически переходный процесс в звене длится бесконечно долго, т.к. h(t) К, а w ( t ) 0 ,
асимптотически. На практике считают, что переходный процесс закончен при п 3 Т. y( t 3 T ) К.
Найденные значения К и Т позволяют записать передаточную функцию пропорционального звена
первого порядка
K
t
W(s)
Ts 1
или его уравнение движения
( Tp 1)y(t) kx(t)
Характеристики звеньев этого типа носят монотонный характер, поэтому их также называют
апериодическими звеньями первого порядка.
43. 1.2.2 Частотные характеристики апериодического звена первого порядка
Частотные характеристики строятся по выражению частотной передаточной функции звенаW(j )
j ( )
K
U ( ) jV ( ) M ( ) e
, где
Tj 1
U ( )
K
- действительная часть частотной ПФ,
T 1
KT
V ( ) 2 2
T 1
M ( )
2
2
- мнимая часть частотной ПФ,
K
T
2
( ) arctg
2
1
- модуль частотной ПФ,
V( )
arctgT - аргумент частотной ПФ.
U( )
АФЧХ такого звена имеет вид
ImW(j )
K
2
( )
4
U( )
0
K
ReW(j )
M( )
V( )
K
2
3
1
2 T
Рис.47
1
(50)
44. Логарифмические характеристики позиционных звеньев первого порядка
Аналитическим выражением ЛАЧХ позиционных звеньев первого порядка являетсяL ( ) 20 lg M ( ) 20 lg
K
2
T
20 lg K 20 lg ( T
2
2 1
2
1
1 ) 2
(51)
ЛАХ может быть построена по точкам L ( i ) , вычисленным для различных значений частот
i или
приближенно - в виде ломаных прямых (асимптот). Приближенная ЛАХ называется асимптотической.
Для ЛАХ звеньев этого типа могут быть найдены 2-е асимптоты, к которым стремится характеристика на
1
1
двух диапазонах частот, а именно: при
,
и
,
.
Т
T
Аналитическое выражение первой асимптоты L1 ( ) получается из выражения для L ( ) при
1
2 2
2 2
, когда
и T
1, что позволяет T пренебречь по сравнению с 1
0
0
T
L1 ( ) 20 lg K 20 lg1 20 lg K
(52)
Аналитическое выражение второй асимптоты L 2 ( ) получается из выражения для
1 и 2 2 1, что позволяет пренебречь 1 по сравнению с T 2 2
когда
T
T
L ( )при
L 2 ( ) 20 lg K 20 lg T
(53)
На плоскости логарифмических характеристик первая асимптота проходит параллельно оси частот на
1
уровне 20 lg K , а вторая асимптота – под наклоном -20дб/дек через точку { L ( ) 20 lg K ; = }
Т
Асимптоты пересекаются в указанной
1
L ( )
1
точке. Частота =
называется
Т
T
сопрягающей.
40дб
Действительная ЛАХ (красная линия)
проходит ниже асимптотической,
L 1 ( ) 20 lg K
0дб/дек
стремясь к ней при 0 и
3.03дб
1
Максимальное отличие на =
20дб
Т
составляет
L ( ) L 1(
1
1
) L ( )
T
T
К
2
1/с
20lg 2 3.03 дб
M ас( )
2
Что соответствует
M( )
20lg K 20lg
0.01
1
0.1
Рис.48
сопр10
100
)
L 2 ( 1000
45. Логарифмическая фазовая характеристика пропорционального звена первого порядка
ЛФЧХ строится по выражению( ) arctg
V( )
V ( )
V ( )
arctg ч
arctg З
arctgT
U( )
(
)
(
)
Uч
UЗ
(55)
При изменении частоты от 0 до
, аргумент частотной передаточной функции изменяет свои значения от 0
0
0
0
0 , а при
до 90, т.е. при
ЛФХ асимптотически стремится
- к значению 90 .
При частоте сопряжения
( 1 ) arctg 1
сопр
1
Т
Т
4
45 0
Если нужны дополнительные точки, можно использовать значения аргумента вычисленные для различных
частот, например
сопр ,где n - число октав вправо и влево по оси частот от
сопр или
частоты сопряжения.
n
/n
ЛФЧХ апериодического звена первого порядка имеет вид ( Рис.49)
1
T
90 0
45 0
0.01
0.1
( )
1
сопр 10
Рис.49
100
1000
1/с
46. 1.3 Позиционные (пропорциональные, статические, ) звенья второго порядка
К ним относятся звенья, описываемые уравнениями вида:d 2 y(t) d y(t) y(t) ( 2 2 p 1)y(t) kx(t)
b2 2
b1
T 2p T 1
dt
dt
K
Передаточная функция таких звеньев имеет вид: W(s)
T 22s 2 T 1s 1
(56)
В зависимости от сочетания параметров передаточной функции звена их подразделяют на 3-и типа:
- апериодические звенья второго порядка;
- колебательные звенья второго порядка;
- консервативные звенья второго порядка.
1.3.1. Апериодические звенья второго порядка
К звеньям этого типа относят позиционные звенья второго порядка, параметры передаточной функции
которых соотносятся: Т 1 2T 2 . Это условие, при котором корни характеристического уравнения звена
T 22s 2 T 1s 1 0
S1,2
будут действительными.
4T 22
4T 22
,при Т 1 2T 2 подкоренное выражение 1
T1
0
( 1 1
)
2
2
T1
2T 2
T1
В этом случае характеристическое уравнение звена может быть представлено в виде:( T 3s 1 )( T 4 s 1 ) 0 ,
где:
T 3
1
S1
,
T 4
1
S2
, а передаточная функция звена в виде:
W(s)
K
( T 3s 1 )( T 4s 1)
Такая передаточная функция соответствует последовательному соединению двух апериодических
звеньев первого порядка с передаточными функциями
1
K
и W (s)
2
W 1(s)
( T 4 s 1 )
( T 3s 1 )
поэтому эти звенья и называют апериодическими 2-го порядка или двойными апериодическими.
(57)
47.
Временные характеристики звеньев второго порядкаПереходная функция
Аналитическим выражением переходной характеристики звена второго порядка является решение
дифференциального уравнения при Х(t)=1(t). Для звеньев с Т 1 2T 2 оно имеет вид:
y t y C1es1t C2 es2t y C1e t T3 C2 e t T4
1
1
y
0
y 0 К С1 С2 0
y К
С1
С2 0
К Т3
С1
Т3 Т 4
К Т4
С2
Т 4 Т3
Т3
(58)
Т4
t
t
T
T
3
4
h ( t ) K 1
e T3 e T 4 1 ( t )
T3 T4
T4 T3
h(t)
y уст
Т 4 T 3
(59)
y( )
Вид переходной характеристики представлен на Рис.50
К
Весовая функция
Т4
Рис.50
w (t)
t
Аналитическое выражение весовой функции получим, взяв производную
от переходной функции
t
t
K
w ( t ) ph ( t )
T3 e T 4 1 ( t ),
e
T3 T4
t
0
Рис.51
(60)
T3 T4
Вид весовой функции приведен на Рис.51
48. Частотные характеристики звеньев второго порядка
Частотная передаточная функция звеньев этого типа имеет видK
K
M( )e j ( ),
(61)
2
2
1-T 2 j T 1 1 j T 3 1 j T 4
K
K
M ( )
- модуль частотной передаточной функции
2 2
2 2
2 2 1
2
2
2
1
Т
Т
3
( 1 T 2) T 1
4
W(j )
( ) arctg
T 1
arctg T 3 arctg T 4
1-T 22 2
Аналитическое выражение ЛАХ: L( ) 20lgM(
L2( )
1
T3
40дб
- аргумент частотной передаточной функции
) 20lgK-20lg(1 T 32 2)1/2 20lg( 1 T 24 2)1/2
Асимптотами ЛАХ являются:
L1( ) 20lg K при T 3 0 1
1
L 2( ) 20lg K 20lgT 3 при T 4
1
T4
1
T3
L 1 ( ) 20 lg K
(62)
L 3( ) 20lg K 20lgT 3 20lgT 4
0дб/дек
T4
при
20дб
1
Аналитическое выражение ЛФХ:
180
0.01
( ) arctg T3 arctg T4
0
1350
0.1
1
сопр
10
сопр
100
1000
L2( )
90 0
45 0
L 3( )
0.01
( )
0.1
1
10
Рис.52
100
1000
1/с
(63)
ЛФХ при
0 асимптотически
стремится к 0, а при
к значению
0 .
180
Она может быть построена как сумма ЛФХ
двух апериодических звеньев 1-го
порядка.
1/с
49.
1.3.2.Колебательные звеньяУравнение звеньев этого типа имеет тот же вид
d 2 y(t) d y(t) y(t) ( 2 2 p 1)y(t) kx(t)
b2 2
b1
T 2p T 1
dt
dt
T1
1 называют параметр затухания.
при этом Т1 2 T 2 . Величину
(64)
2T 2
При таком сочетании параметров корни характеристического уравнения звена будут комплексно-сопряженными
4T 22
T1
1
( 1 1
) ( 1 1
) j
S1,2
2
2
2T 2
T
2
T1
Передаточная функция звеньев этого типа может быть представлена в виде:
W(s)
K
K
,
2 2 s 1
2 2 2 Ts 1
T 2s T 1
T s
где:
Т Т2 , 2 Т Т 1 .
(65)
При комплексно-сопряженных корнях характеристического уравнения и х(t)=1(t) решение дифференциального
уравнения будет иметь вид:
n
y(t) yч (t ) yоб (t ) ( y уст Ci esit )1(t ) ( y уст С1e( j )t C2 e( j )t )1(t )
где:
C1иC 2
i 1
- постоянные интегрирования, находятся из начальных условий
y(t) [ y уст e j t (С1e j t C2 e j t )]1(t )
(66)
к
y(0) 0, р y(0) 0
или используя формулы Эйлера:
y t [ yуст e t (C1cos t C1 j sin t C2 cos t C2 j sin t )]1(t )
[ yуст e t ((C1 C2) cos t (C1 C2) j sin t )]1(t ).
Вводя обозначения:
получим:
C1 C2
2
2
arctg
,
C1 C 2 C12sin , C1 C 2 C12cos , C12 2 ( C1 C 2 ) ,
C1 C2
y t [ yуст e t (C12 sin cos t C12 j cos sin t )]1(t ) [ yуст e t C12 sin( t )]1(t ),
т.е. реакция звена будет иметь затухающую гармоническую составляющую.
50.
Временные характеристики колебательных звеньевПереходная характеристика звена может быть получена при подаче на его вход воздействия 1(t) или построена
по выражению
2 2
y(t) h(t) K[1 e t (cos t j sin t )]1(t ) K[1 e t
sin( t )]1(t ). (67)
h(t)
По экспериментально снятой характеристике можно найти параметры
звена
K
А1
K ( 1 e t )
t
w ( t )
К
Т
2
e
t
t
А2
Рис.54
2 2
;
К y .
Аналитическое выражение весовой функции
Рис.53
А3
2
T ;
Весовая функция колебательных звеньев
w (t)
А1
1
1
;
2
2
T1 2 T
ln А3 ;
А1
;
T2 T
А3
А2
2
K
2
T
t
e sin t 1 ( t )
(68)
Ее вид представлен на рис.54
Чем меньше
, тем меньше затухание переходных
процессов в звене и больше частота колебаний.
51.
Частотные характеристики колебательных звеньевЧастотная передаточная функция звена имеет вид:
W(j )
M ( )
K
K
M( )e j ( ),
(1-T 22 2 ) j T 1 1 T 2 2 j 2 T
K
2
( 1 2T 22) 2 T 12
( ) arctg
T 1
1-T 22 2
K
T
( 1 T )
2
arctg
2 2 4 2
2 T
2
1-T
2
2
- модуль частотной передаточной функции
2
- аргумент частотной передаточной функции
Аналитическое выражение ЛАХ: L( ) 20lgM( ) 20lgK - 20lg[(1 T 2 2 )
1
T
L2( )
L 1 ( ) 20 lg K
0 .2
0дб/дек
20дб
0 .4
0 .8
180 0
0.01
1350
90
0.1
1
( )
100
0 .8
0 .4
0 .2
0
45 0
0.01
сопр10
0.1
1
сопр 10
2
4 2T 2]1 /2
(71)
Асимптотами ЛАХ являются:
1
L1( ) 20lg K при Т
1
L 2( ) 20lg K 40lgT при Т
Вид реальной ЛАХ в значительной степени
зависит от значения особенно в области
1
частот близких к и может существенно
Т
отличаться от асимптотической ЛАХ. Поэтому
использование последних для колебательных
звеньев не всегда возможно.
1000
L2( )
100
Рис.55
2
(70)
0
0.1
40дб
(69)
1/с
При 0.4 0.7 отличие не превышает 3дб
и асимптотическими ЛАХ пользоваться
можно. В остальных случаях нужно вводить
поправки.
1/с
1000
ЛФХ также зависит от
и изменяется от
0 до
при изменении частоты от 0 до
52.
1.3.3 Консервативные звеньяУравнением движения звеньев этого типа является уравнение вида:
d 2 y(t) y(t) ( 2 2 1)y(t) kx(t), т.е. уравнение 2-го порядка при T 0
1
b2 2
T p
K
dt
W(s )
,
Передаточная функция консервативного звена:
Корнями характеристического уравнения звена
T 2s 2 1
T 2s 2 1 0 являются:
y К;
y(t) yч (t ) yоб (t ) ( yуст С1e
С1 С2 С К 2
h(t ) K (1 cos t )1(t )
Весовая функция
Аналитическое выражение весовой функции:
h(t)
t
0
C2 e j t )1(t ) ( y C cos t )1(t )
– незатухающая гармоника с амплитудой К и частотой
w ( t )
2
(73)
1
S1,2 j j
T
Эти звенья по сути являются идеализированным частным случаем колебательного звена при
Временные характеристики
Переходная характеристика консервативного звена
j
Ее уравнение
(72)
1
T
(74)
K
sin t 1 ( t ) К sin t1(t)
Т
w(t )
(75)
2
к
K
t
Рис.56
t
К
Т
Рис.57
53.
Частотные характеристики консервативного звенаЧастотная передаточная функция звена
М( )
W(j )
K
0
1 T
2
Аналитическое выражение ЛАХ:
L ( )
1-T
2
Асимптотами ЛАХ являются:
T3 0
L 2( ) 20lg K 40lgT
1
при Т
L1( ) 20lg K
0дб/дек
180 0
0.1
1
сопр 10
К
100
( ) arctg
1000
L2( )
0.1
1
сопр 10
Рис.58
100
1000
0
1 2T 2
(73)
Т1 ; 0 ( ) 0
1
о
При ; ( ) 180
Т
При
45 0
( )
1
при
Аналитическое выражение ЛФХ:
90 0
0.01
(72)
Построим ЛАХ и ЛФХ консервативного звена
20дб
1350
(71)
L( ) 20lgM( ) 20lgK - 20lg[(1 T 2 2 ) ]
40дб
0.01
2
- аргумент частотной передаточной функции
1
Т
L 1 ( ) 20 lg K
2
M( )e j ( ),
- модуль частотной передаточной функции;
1-T 2 2
( ) arctg
K
54. 2 Интегрирующие звенья
К звеньям этой группы относят три типа звеньев:- идеальные интегрирующие звенья;
- реальные интегрирующие звенья;
- изодромные звенья.
2.1 Идеальные интегрирующие звенья
Выходная переменная звеньев этого типа пропорциональна не входному воздействию, а интегралу от
входного воздействия, т. е. это звенья, которые при ряде допущений могут быть описаны уравнением
t
вида:
K
d
y(t) K X(t)dt X(t)
p
0
Передаточная функция звеньев этого типа:
y(t) py(t) KX(t).
dt
K
W( s ) .
S
или
(74)
(75)
Временные характеристики идеальных интегрирующих звеньев
Переходная функция
При Х(t)=1(t) реакция звеньев этого типа представляет собой прямую из начала координат, с углом
наклона, равным arctg K. Аналитическое выражение переходной характеристики идеальных
интегрирующих звеньев имеет вид:
(76)
y(t) h ( t ) Kt 1 ( t )
h(t)
Графическое изображение переходной характеристики приведено на рис.59
w(t )
K
arctg K
tc
Рис.59
Рис.60
tc
Весовая функция является производной от переходной характеристики, а следовательно ее
аналитическое выражение
w (t) ph ( t ) K 1 ( t )
Графическое изображение
w (t)
представлено на рис.60.
(77)
55. Частотные характеристики идеальных интегрирующих звеньев
Частотная передаточная функция (амплитудно-фазовая характеристика) звеньев этого типа имеетаналитическое выражение вида:
K
K
W( j )
j
j .
Модуль частотной передаточной функции идеальных интегрирующих звеньев
Аргумент звеньев этого типа:
K/
0
( ) arctg
0
90
ЛАХ идеальных интегрирующих звеньев описывается выражением:
L( ) 20lg M( ) 20lg
K
М( )
K
(78)
,
(79)
2
20lg K 20lg ,
(80)
{ 20lg K, 1} и { 0, К}
т.е. прямая, которая проходит через точки
и имеет наклон -20дб/дек
ЛФХ не зависит от частоты и является прямой, параллельной оси частот проходящей на уровне 90 0
L ( )
ЛАХ и ЛФХ идеального интегрирующего
звена приведены на Рис.61
40дб
20lg К
20дб
180 0
0.01
1350
0.1
1
0.1
1
10
К
100
1000
1/с
100
1000
1/с
90 0
45 0
0.01
( )
Рис.61
10
56. 2.2 Реальные интегрирующие звенья (интегрирующие с запаздыванием)
К реальным интегрирующим звеньям относят звенья, которые описываются уравнениями вида:t
dy(t) y(t) K x (t)dt или (Tp 1)y(t) K X(t) или (T p 2 p)y(t) KX(t)
b1
p
dt
0
(80)
Последнее выражение – уравнение 2-го порядка, у которого свободный член равен 0. Оно может быть
представлено:
PZ(t) KX(t)
Tp 1 py(t) KX(t), или системой двух уравнений
(Tp 1)y(t) Z(t),
т.е. уравнений идеального интегрирующего звена и апериодического звена 1-го порядка, соединенных
последовательно, или в виде:
K
1
K
KT
y(t)
p (Tp 1)
X(t)
p
X(t) -
Tp 1
X(t),
что соответствует параллельному соединению идеального интегрирующего и апериодического звена 1-го порядка.
W( s )
Передаточная функция звеньев этого типа имеет вид:
Временные характеристики реальных интегрирующих звеньев
K
.
s(Ts 1)
Переходная функция
Используя последнее представление у(t), аналитическое выражение переходной характеристики
получим как алгебраическую сумму решений уравнений идеального интегрирующего и апериодического
1-го порядка звеньев при Х(t)=1(t).
t/T
y(t) h(t) K[t - T(1 e
В графическом виде она представлена на рис.62
w (t) ph(t) K(1 e t/T ) 1 ( t ).
K
Ее графическое изображение
приведено на Рис.63.
КТ
Т
Рис.62
t
(82)
Весовая функция звена имеет выражение
w (t)
h(t)
)]1( t ).
(81)
Т
Рис.63
t
(83)
57. Частотные характеристики реальных интегрирующих звеньев
Частотная передаточная функция реальных интегрирующих звеньевW(j )
K
K
.
j (Tj 1) j - 2 T
(84)
Модуль частотной передаточной функции реальных интегрирующих звеньев
М( )
K
1 T 2 2
K
2 T 2 4
,
Аргумент частотной передаточной функции реальных интегрирующих звеньев
( ) arctg K/ arctgT - arctgT
ЛАХ строится по выражению:
0
2
L( ) 20 lg M( ) 20 lg K 20 lg 20 lg( 1 T 2 2 ) 1 /2 ,
Асимптотами ЛАХ являются:
L ( )
L1 ( )
L 1 ( ) 20 lg K 20 lg ,
1
Т
40дб
при
20дб
0.01
3.03дб
при
0
1350 0.1
1
сопр10
к 100
1000
90 0
45 0
0.01
( )
1
Т
и
1
Т
и
0
,
L 2 ( ) 20 lg K 20 lg 20 lg T ,
20 lg K
180
(85)
0.1
1
сопр10
Рис.64
100
1000
L2( )
.
ЛФХ строится по точкам, используя
выражение:
( ) .90о arctgT
(86)
ЛАХ и ЛФХ можно построить также как
сумму соответствующих характеристик
двух звеньев: идеального интегрирующего
и апериодического 1-го порядка.
58. 1.2.3 Изодромные звенья (интегрирующие с форсированием)
К звеньям этого типа относят звенья, которые описываются уравнениями вида:dy(t)
dX(t)
KX(t) K 1
dt
dt
где T K/ K 1
или в операторной форме py(t)
Передаточная функция изодромных звеньев имеет вид:
KX(t) K 1 pX(t) K(1 Tp)X(t), (87)
W(s)
K(1 Ts) K
K1
S
S
(88)
Из выражения для передаточной функции следует, что изодромное звено может быть представлено
совокупностью двух параллельно включенных звеньев, а именно идеального интегрирующего и идеального
статического с коэффициентами передачи К и К1 соответственно.
Временные характеристики изодромных звеньев
Переходная функция
Переходная характеристика изодромного звена - реакция звена на входное воздействие вида Х(t)=1(t)
может рассматриваться как сумма реакций двух звеньев: интегрирующего hи(t) и безынерционного hб(t).
Аналитическим выражением переходной характеристики является:
y(t) h(t) h и (t) h б (t) (Kt K 1 ) 1 ( t )
(89)
Графическое изображение переходной функции приведено на рис.65.
Весовая функция изодромного звена - реакция звена на входное воздействие вида Х(t)= (t) имеет
аналитическое выражение производной от h(t) и равна сумме весовых функций указанных звеньев
y(t) w (t) w и (t) w б (t) K 1 ( t ) K 1 ( t )
w (t)
Вид весовой функции
h(t)
wб(t)
hб(t)=К
К
wи(t)=К
К
t
Рис.65
изодромных звеньев
приведен на рис.66
t
Рис.66
(90)
59. Частотные характеристики изодромных звеньев
Частотная передаточная функция изодромных звеньев имеет вид:W(j )
K(1 jT )
j
Модуль частотной передаточной функции изодромных звеньев
M( )
2
K 1 T
2
Аргумент частотной передаточной функции реальных интегрирующих звеньев
( ) arctg K/ arctgT - arctgT
0
(91)
(92)
2
ЛАХ звеньев этого типа строится по выражению:
L( ) 20 lg M( ) 20 lg K 20 lg 20 lg( 1 T 2 2 ) 1 /2 ,
L 1 ( ) 20 lg K 20 lg ,
Асимптотами ЛАХ изодромного звена являются
L ( )
при
20 lg K
при
20дб
20 lg K 1 L 2 ( )
3.03дб
180 0
0.01
1350 0.1
1
10
сопр
к
100
0дб/дек
1000
1/с
45 0
( )
0.1
1
10
сопр
Рис.67
и
1
Т
и
0
100
1000
Асимптоты соответствуют:
L 1 ( ) - ЛАХ интегрирующего звена,
L 2 ( ) - ЛАХ безынерционного звена.
ЛФЧХ можно представить суммой ЛФХ
интегрирующего звена W(s) К s и
форсирующего звена W(s) 1
. Ts
L1 ( )
90 0
0.01
1
Т
L 2 ( ) 20 lg KT 20 lg K 1 ,
1
Т
40дб
(93)
1/с
ЛАХ и ЛФХ изодромного звена
приведены на рис.67
60. 3. Дифференцирующие звенья
Существуют звенья, выходная переменная которых при определенных условиях пропорциональнапроизводной от входного воздействия. Такие звенья и называют дифференцирующими.
К группе дифференцирующих звеньев относят два типа звеньев:
- идеальные дифференцирующие звенья;
- реальные дифференцирующие звенья (дифференцирующие с замедлением).
3.1 Идеальные дифференцирующие звенья
К звеньям этого типа относят звенья, которые описываются уравнениями вида:
y(t) K
d
X(t) KpX(t).
dt
(94)
Коэффициент передачи дифференцирующего звена размерная величина, которая содержит и
размерность времени (сек).
Передаточная функция идеальных дифференцирующих звеньев имеет вид:
W( s ) Ks.
(95)
Временные характеристики идеальных дифференцирующих звеньев
Переходная функция идеального дифференцирующего звена
Реакцией звена на воздействие вида 1(t) будет увеличенная в К раз производная от воздействия этого
вида, т.е. импульсом бесконечно большой амплитуды и бесконечно малой длительности, площадь
(96)
которого равна К. Аналитическое выражение переходной функции:
Графическое ее представление приведено на рис.68.
Весовая функция идеального дифференцирующего звена
Она имеет аналитическое выражение вида:
y(t) h ( t ) K ( t ).
w (t) ph ( t ) Kp ( t ) K
w( t )
h(t)
t
Рис.68
t
Рис.69
d (t)
.
dt
Это соответствует двум импульсам бесконечно
малой длительности и положительной и
отрицательной бесконечно большой амплитуды
при времени равном 0 (см.Рис.69).
(97)
61. Частотные характеристики идеальных дифференцирующих звеньев
Частотная передаточная функция (аналитическое выражение амплитудно-фазовой частотнойхарактеристики) звеньев этого типа имеет вид:
W(j ) jK
Модуль частотной передаточной функции
Аргумент частотной передаточной функции
M( ) K
( ) arctg K 90 o
0
2
(98)
(99)
ЛАЧХ идеального дифференцирующего звена имеет аналитическое выражение:
L( ) 20 lg M( ) 20 lg K 20 lg
ЛАХ имеет наклон 20дб/дек , проходит через точку
20 lg K на частоте
1
на частоте
L ( )
(100)
и пересекает ось частот
К1
.
ЛФЧХ не зависит от частоты и
проходит параллельно оси частот на
o
уровне + 90 .
40дб
20 lg K
20дб
180 0
0.01
0.1
1
10
100
1000
1/с
0.1
1
10
100
1000
1/с
1/К 1350
90 0
45 0
0.01
( )
90 o
Рис.70
ЛАЧХ и ЛФЧХ идеального
дифференцирующего звена
приведены на рис.70
62. 3.2 Реальные дифференцирующие звенья
Дифференцирующие звенья этого типа имеют некоторую инерционность, поэтому дифференцируютвходное воздействие с погрешностью, особенно ощутимой на больших частотах и при быстрых его
изменениях во времени.
Уравнение реальных дифференцирующих звеньев имеет вид:
dy(t) y(t) K d X(t)dt или (Tp 1)y(t) KpX(t) или y(t) Kp X(t).
(101)
b1
dt
Tp 1
dt
Вводя промежуточную переменную Z ( t) KpX(t), (Tp 1)y(t) Z(t) , звенья этого типа
можно представить в виде последовательно соединенных двух звеньев: -идеально дифференцирующего и
апериодического 1-го порядка, т.е они не являются элементарными типовыми звеньями.
X(t)
Z ( t)
Kp
1
(Tp 1)
y(t)
Передаточная функция реальных дифференцирующих звеньев имеет вид: W( s )
Временные характеристики реальных дифференцирующих звеньев
Ks
.
1 Тs
(102)
Переходная характеристика как решение дифференциального уравнения звена при Х(t)=1(t) имеет
выражение вида:
h(t)
K t/T
1( t )
e
T
(103)
т. е. импульс амплитудой К/Т со сглаженным задним фронтом, изменяющемся во времени по экспоненте.
.
w (t)
h(t)
Весовая функция звена
описывается выражением:
K
T
w (t)
t
Переходная и весовая функции
звена представлены на рис.71 и
рис.72 соответственно.
K
Рис.71
t
K
K
(t) - e t/T1 ( t )
T
T2
T2
Рис.72
(104)
63. Частотные характеристики реальных дифференцирующих звеньев
Частотная передаточная функция (аналитическое выражение амплитудно-фазовой частотнойхарактеристики) реальных дифференцирующих звеньев имеет вид:
jK
M ( ) e j ( )
Tj 1
K
М ( )
Модуль частотной ПФ T2 2 1
V( )
K
Аргумент частотной ПФ - ( ) arctg
arctg
arctgT arctgT
U( )
0
2
W(j )
(105)
(106)
ЛАХ звена имеет аналитическое выражение:
L( ) 20 lg M( ) 20 lg K 20 lg 20 lg( 1 T 2 2 ) 1 /2 ,
L ( )
40дб
20 lg K/T
1
Т
L2( )
20 lg K
1350 0.11 / К
L 1 ( ) 20 lg K 20 lg ,
0дб/дек
при
1
10
100
1000
1/с
45 0
0.01
45 0 0.1
сопр
90 0
( )
1
10
Рис.73
1
Т
и
0
при
1
Т
и
K
,
T
Асимптоты соответствуют:
L 1 ( ) - ЛАХ идеального
дифференцирующего звена,
(
)
L2
- ЛАХ безынерционного звена.
90 0
00
L 2 ( ) 20 lg K - 20lgT 20 lg
сопр
180 0
0.01
Асимптотами ЛАХ звена являются
L1 ( )
3.03дб
20дб
(107)
100
1000
1/с
ЛФЧХ можно представить суммой ЛФХ
идеального дифференцирующего звена и
апериодического звена 1-го порядка.
ЛАХ и ЛФХ реального дифференцирующего
звена приведены на рис.73.
64. 4. Звенья с постоянным запаздыванием
Звенья этого типа также как пропорциональные безынерционные звенья передают входноевоздействие на выход звена без искажения или увеличенное в К раз, однако вносят запаздывание
постоянной величины.
Уравнение таких звеньев имеет вид:
y(t) X(t - ) при t
t
0
(108)
при
Временное запаздывание
называют временем чистого запаздывания.
Такими свойствами обладают различного рода линии запаздывания.
Если звено усиливает, то уравнения имеют вид:
y(t)
Передаточная функция звеньев с запаздыванием
W( s)
y(s)
- s
Ke ,
X(s)
т.к.
КX(t - )
0
при
при
t
t
(109)
s
X(t) X(s), y(t) КX(t - ) y(s) K e
X(s)
(110)
Временные характеристики звеньев с запаздыванием.
Переходная функция и весовая функция рассматриваемых звеньев будут аналогичными временным
характеристикам идеальных пропорциональных звеньев, но смещенными на
по оси времени.
Аналитическими их выражениями являются:
(111)
h(t) K1(t - )
w (t) K (t - )
(112)
Графическое изображение переходной характеристики и импульсной переходной характеристики
приведены наРис.74 и Рис.75 соответственно.
w (t)
h(t)
K
0
tc
Рис.74
0
tc
Рис.75
65. Частотные характеристики звеньев с запаздыванием
X(t) XmSin t сигнал на выходе звена будетпо оси времени y(t) XmSin ( t - ) XmSin( t - )
.
При гармоническом входном воздействии
гармоническим, но сдвинутым на
Амплитуда выходного сигнала звена будет равна Хm у звеньев чистого запаздывания или KXm при
усилении звеном в К раз, следовательно модуль звена M( ) 1 или M( ) K соответственно.
Фазовое запаздывание
Т – период.
(113)
( ) 2 T,
ТT
x(t)
Xm
Частотные свойства звеньев с запаздыванием можно
представить в экспоненциальном виде
W(j ) 1e - j 1e j или
W(j ) K e - j ( ) K e j для звеньев
y(t )
3
2
t
180 0
0.01
1350 0.1
1
10
90 0
звено с усилением.
ЛФХ будет нелинейной монотонно убывающей
функцией частоты, т.к.
, а при
построении ЛФХ используется логарифмический
масштаб.
1000 1/с ЛАХ и ЛФХ звеньев с запаздыванием приведены
100
на Рис.77.
0.157
45 0
0.01
( )
с усилением
ЛАХ звена с запаздыванием имеет выражение:
( )
20дб
0.1
1
10
Рис.77
(115)
L( ) 20 lg M( ) 20 lg 1 или
L( ) 20 lg M( ) 20 lg K, если
Рис.76
L ( )
40дб
20 lg K
(114)
100
1000
1/с
66.
Неустойчивые и неминимально - фазовые звеньяРассмотренные ранее звенья называются устойчивыми и минимально – фазовыми, так как при подаче на
их вход воздействия ограниченной величины выходная переменная стремится к установившемуся значению, а
при подаче гармонического воздействия фазовый сдвиг сравнительно небольшой.
Исключение составляют интегрирующие звенья, реакция которых на скачок воздействия (переходная
функция) неограниченно возрастает при
. В тоже время производная от
стремится к
постоянному значению (как весовая функция). Такие звенья называют нейтрально устойчивыми.
t
y(t )
y(t )
t
x(t ) const
Существуют звенья, у которых
при
и
, хотя их описание с точностью
до знаков некоторых коэффициентов полинома B(s) передаточной функции будут совпадать с устойчивыми
звеньями. Такие звенья называются неустойчивыми.
Различие в поведении устойчивых и неустойчивых звеньев можно объяснить, используя решение уравнения
движения звена вида :
n
y(t) yч (t ) yоб (t ) ( y уст Ci esit ),
где:
i 1
yч(t ) y уст - частное решение,
y об (t )
si
Сi
- общее решение,
- корень характеристического уравнения В( )= 0 порядка n, для типовых звеньев n=1;2,
- постоянные интегрирования, определяются из начальных условий.
s
Характеристическим уравнением называется приравненный нулю знаменатель передаточной функции.
Корни характеристического уравнения звена называются полюсами или нулями знаменателя
передаточной функции. Эти значения Si обращают полином знаменателя передаточной функции в 0 и
являются коэффициентами в показателе степени экспонент в решении уравнения движения звена.
i 0 , если si,i 1 i j i . Это дает затухание
t
(Ci esi 0) при t , т.е. стремление y t y уст.
s 0
У устойчивых звеньев все i
составляющих под знаком суммы
или
s 0 или
У неустойчивых звеньев хотя бы один корень
i
Это дает неограниченный рост одной из составляющих
стремление
.
y (t )
имеет
i 0
sit )
(Ci e
при
, если
всех
si ,i 1 i j i.
t , а следовательно
67.
Пример устойчивого и неустойчивого звеньевРассмотрим это на примере звеньев первого порядка, уравнения движения и передаточные функции которых
имеют вид:
b1dy(t) y(t) ( Tp 1)y(t) kx(t)
Передаточная функция:
b1dy(t) y(t) (Tp 1)y(t) kx(t)
dt
Передаточная функция:
dt
или
K
Ts 1
K
(116)
W(s)
Ts 1
W(s)
Корень характеристического уравнения у первого звена будет вещественным отрицательным
а у второго звена – вещественным положительным 2
s 1 Т
s1 1 Т,
Вследствие этого переходная характеристика, т.е. реакция на единичный скачек 1(t), у первого (устойчивого)
звена имеет вид:
-t
y(t) h(t) k(1 e T ) 1 ( t ),
а у второго
неустойчивого звена -
t
T
y(t) h(t) k(e 1)1(t ),
Графический вид характеристик:
h(t)
(117)
т.е.неограниченно возрастает по
экспоненциальной зависимости.
(118)
неустойчивое
y уст
устойчивое
К
Рис.78
t
Признаком неустойчивых звеньев является отрицательное значение одного из коэффициентов полинома
знаменателя передаточной функции. Неустойчивыми будут звенья с передаточными функциями:
W(s)
K
T 22 s2 T1s 1
W(s)
K
T 2 s2 2 Ts 1
W(s)
K
K
K
W(s)
W(s)
s(Ts 1)
T 2 s2 2 Тs 1
T 2 s2 1
68.
Неминимально – фазовые звеньяОсобенностью частотных характеристик неустойчивых звеньев является то, что их амплитудно-частотные
характеристики совпадают с АЧХ устойчивых звеньев, а фазовые сдвиги значительно больше, особенно на
низких частотах.
K
K
Так у звена с передаточной функцией W(s)
частотная передаточная функция W( j )
(119)
jT 1
Ts 1
Модуль частотной передаточной функции неустойчивого звена равен модулю частотной ПФ устойчивого звена
первого порядка.
Мнуз ( ) W( j )
K
jT 1
K
T
2
2 1
М уз ( ) W( j )
K
jT 1
(120)
Следовательно АЧХ и ЛАЧХ этих звеньев будут совпадать.
( ) неустойчивого звена определяется выражением: ( ) arctg Т 180о arctgT
Аргумент
т.е. при изменении
Аргумент
от 0 до , изменяется от
до
- 2
-1
.
( ) arctgT
( ) устойчивого звена будет определяться выражением:
1
( )
L ( )
т.е. при изменении
изменяется от 0 до
T
0дб/дек
20дб
3.03дб
180 0
0.01
1350 0.1
90
1
10
100
0
( )
0.1
1
сопр10
Рис.79
от 0 до
.
2
,
W1( j ) j Т1 1 и W 2 ( j ) j Т1 1
1000
45 0
0.01
ЛАЧХ и ЛФЧХ этих звеньев приведены на Рис.79.
Большие фазовые сдвиги имеют и звенья с
положительными корнями полинома А(s)
числителя ПФ. Корни полинома числителя
называют нулями. Если
40дб
L 1 ( ) 20 lg K
(121)
100
j Т2 1
j Т2 1
1( ) arctg Т1 arctg T2
2 ( ) arctg Т1 arctg T2
1 ( ) > 2 ( )
69.
Передаточные функции САРРассмотрим применение понятия передаточной функции к линеаризованным САР.
Обобщенную схему САР, работающих по замкнутому циклу, можно представить в виде:
f (t )
Регулятор
(t )
x(t )
УУ
ИЭ
УП
U (t )
ОУ
y (t )
y (t )
ЧЭ
Условные обозначения:
ОУ – объект управления;
ИЭ – исполнительный элемент;
УП – усилитель- преобразователь;
УУ – устройство управления;
ЧЭ – чувствительный элемент;
Рис.80
x(t )
f (t )
y (t )
U (t )
(t )
- управляющее воздействие на САР;
- возмущающее воздействие на САР;
- регулируемая переменная;
- управляющее воздействие на ОУ;
- ошибка регулирования.
Предположим, что ЧЭ имеет коэффициент передачи равный 1 и пока отсоединен от регулятора.
Тогда система будет разомкнутой, и
(t ) x(t ) . Переходя к изображениям переменных по Лапласу,
выразим управляющее воздействие на ОУ и его регулируемую переменную через
и f (t ).
U (s) Wрег (s) (s) Wрег s x s
x(t )
(122)
y(s) Wou s U s Wof s f s Wou s Wрег s s Wof s f s (123)
Wрег s ; W ou s ; Wof s - передаточные функции регулятора и ОУ по U (t ) и f (t ) .
передаточной функцией разомкнутой системы
W x s Wрег s Wou s называется
по управляющему воздействию.
W f s Wof s
называется передаточной функцией разомкнутой системы
по возмущающему воздействию.
70.
y(s) W х s х s W f s f sДля оригиналов (функций времени): y (t ) W х p х t W f p f t W х p t W f p f t
С учетом введенных понятий запишем:
(124)
(125)
Передаточные функции замкнутой системы
Восстановим связь чувствительного элемента (ЧЭ) с регулятором
f(t)
РЕГУЛЯТОР
x(t)
(t)
УУ
УП
ИЭ
u(t)
ОУ
y(t)
y(t)
ЧЭ
Рис.81
Это соответствует замыканию системы, поэтому уравнение:
(t) x t y t - уравнение замыкания.
Подставляя уравнение замыкания в уравнение (125) и решая относительно регулируемой переменной получим:
Или для изображений
W х s
(
s
)
х
1 W x s
W f s
(
s
)
f
1 W x s
W f p
p
W
х
y (t )
х t
f t
1 W x p
1 W x p
W f s
s
y( s) W х
х s
f s
1 W x s
1 W x s
- называется передаточной функцией замкнутой системы по
управляющему воздействию.
- называется передаточной функцией замкнутой системы по
возмущающему воздействию.
Для замкнутой системы с учетом введенных понятий ПФ запишем
(126)
(127)
(128)
(129)
y(s) х s х s f s f s (130)
71.
Передаточные функции для ошибкиИспользуя уравнение замыкания и уравнение (125), можно получить уравнение для ошибки замкнутой САР:
W f p
p
y (t ) x t t W х
х t
f t , откуда
1 W x p
1 W x p
W f p
W f p
1
p
х t
f t ,
t [1 W х
]х t
f t
1 W x p
1 W x p
1 W x p
1 W x p
1
х р
1 W x р
1 x р - называется операторной передаточной функцией
(131)
(132)
замкнутой системы для ошибки
Переходя в уравнении (131) от переменных во времени к их изображениям по Лапласу, введем более
строгое понятие передаточных функций для ошибки
х s
1
1 W x s
f s
1 x s
W f s
,
1 W x s
- передаточная функция замкнутой системы для
ошибки по управляющему воздействию,
- передаточная функция замкнутой системы для
ошибки по возмущающему воздействию.
(133)
(134)
Уравнения (128), (129), (133) и (134) позволяют найти передаточные функции замкнутой системы при известных
передаточных функциях разомкнутой системы. Легко найти выражения и для решения обратной задачи:
х s
(
s
)
Wх
1 x s
1 х s
(
s
)
Wх
x s
W f (s)
f s
x s
Если передаточная функция разомкнутой системы представлена отношением полиномов
х (s)
А х s
В s A x s
х s
В s
B s A x s
B s A x s - характеристический полином замкнутой системы.
(135)
W х (s)
А х s
,то:
В s
72.
Структурные схемы САРПравила преобразования динамических структурных схем
1 Преобразование цепочки последовательно соединенных звеньев.
1.1 Объединение цепочки звеньев: передаточная функция цепочки последовательно соединенных
звеньев равна произведению передаточных функций этих звеньев.
x s
W1 s
y1 s x2 s
W 2 s
y2 s x3 s
W 3 s
y s
x s
W1 s W 2 s W 3 s
y s W3 s x3 s W3 s W 2 s x2 s W3 s W 2 s W1 s x s
y s
n
W s Wi s
i 1
1.2 Перестановка звеньев:
x s
W1 s
y1 s x2 s
W 2 s
y s
x s
W 2 s
y 2 s x1 s
W1 s
y s
2 Преобразование цепочки параллельно соединенных звеньев.
Передаточная функция цепочки последовательно соединенных звеньев равна
сумме передаточных функций этих звеньев.
x s
W1 s
y1 s
W 2 s
y 2 s
W 3 s
y3 s
x s
y s
W1 s W 2 s W3 s
y s
y s y1 s y 2 s y3 s
W1 s x s W 2 s x s W3 s x s
n
W
s
y s W1 s W 2 s W3 s x s
Wi s
i 1
73.
3 Преобразование контурного соединения звеньев.3.1 Объединение звеньев при контурном соединении:
x1 s
x s
( ) y 2 s
W1 s
y s
W 2 s
x1 s x s y2 s
y 2 s W 2 s y s
y s W1 s x1 s
y s
W1 s
1 W1 s W 2 s
y s W1 s [ x s W 2 s y s ]
[1 W1 s W 2 s ] y s W1 s x1 s
x s
y s
W1 s
x s W k s x s
1 W1 s W 2 s
Передаточная функция контурно соединенных звеньев равна отношению передаточной функции прямой цепи к
алгебраической сумме 1 и произведения передаточных функций звеньев прямой и обратной цепи контура.
x s
3.2 Замена звеньев прямой и обратной цепи или направления замыкания контура
( )
W1 s
y s
W 2 s
W k s
W1 s
1 W1 s W 2 s
x s ( ) x2 s
( )
y1 s
W -21 s
W1-1 s
y s
x2 s x s y1 s
y1 s W1-1 s y s
y s W-21 s x2 s W-21 s W1-1 s [ W1 s x s y s ]
[ W1 s W 2 s 1] y s W1 s x1 s
s
W -21 s
W
1
W k s
-1 s -1
1 W1 W 2 1 W1 s W 2 s
74.
4. Перенос сумматора или элемента сравнения через звено4.1 С выхода звена на его вход
х1 s
х1 s
y s
W s
х 2 s
W s
y s
s
y s W s [ x1 s x 2 ]
W s
х 2 s
W -1 s
y s W s x1 s x2 s
4.2 Со входа звена на его выход
х1 s
W s
х1 s
y s
W s
W s
х 2 s
х 2 s
y s W s [ x1 s x2 s ]
x s
y s W s x1 s W s x2 s
4.3 переход к единичной обратной связи
W1 s
y s
W 2 s
s
W
1
W k s
1 W1 s W 2 s
y s
W1 s
y s
x s
W -21 s
W1 s
W2 s
y s
W2 s
W -21 s
x s
-1 W1 s W 2 s
s
W эк
W2
1 W1 s W 2 s
75.
5. Перенос узла (точки ветвления) через звено5.1 С выхода звена на его вход
х s
W s
y s
y s
y s W s х s
5.2 Со входа звена на его выход
х s
W s
х s
y s
х s
W s
y s
W s
y s
х s
W s
y s
W -1 s
х s
6. Перенос узла (точки ветвления) через сумматор (элемент сравнения)
6.1 С выхода сумматора на вход
х1 s
х 2 s
y s
х s
y s
6.2 Со входа сумматора на выход
х1 s
y s
х1 s
х 2 s
y s
y s
х1 s
х 2 s
7. Объединение и перестановка сумматоров
От перемены мест слагаемых сумма не изменяется
х 2 s
y s
х1 s



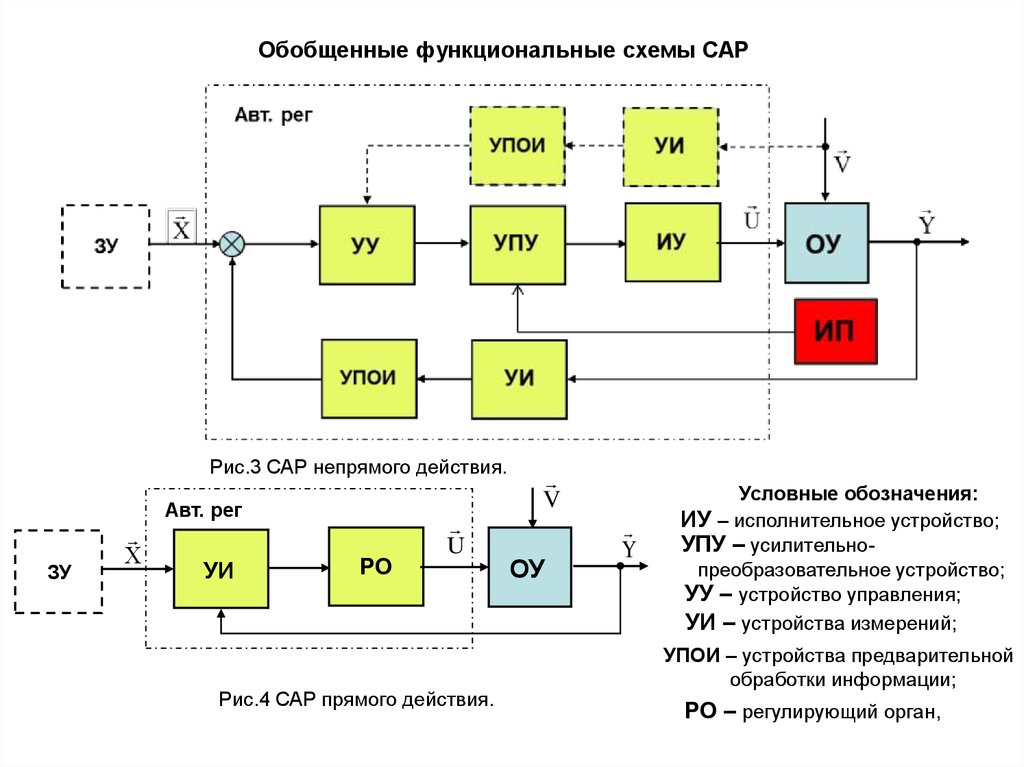

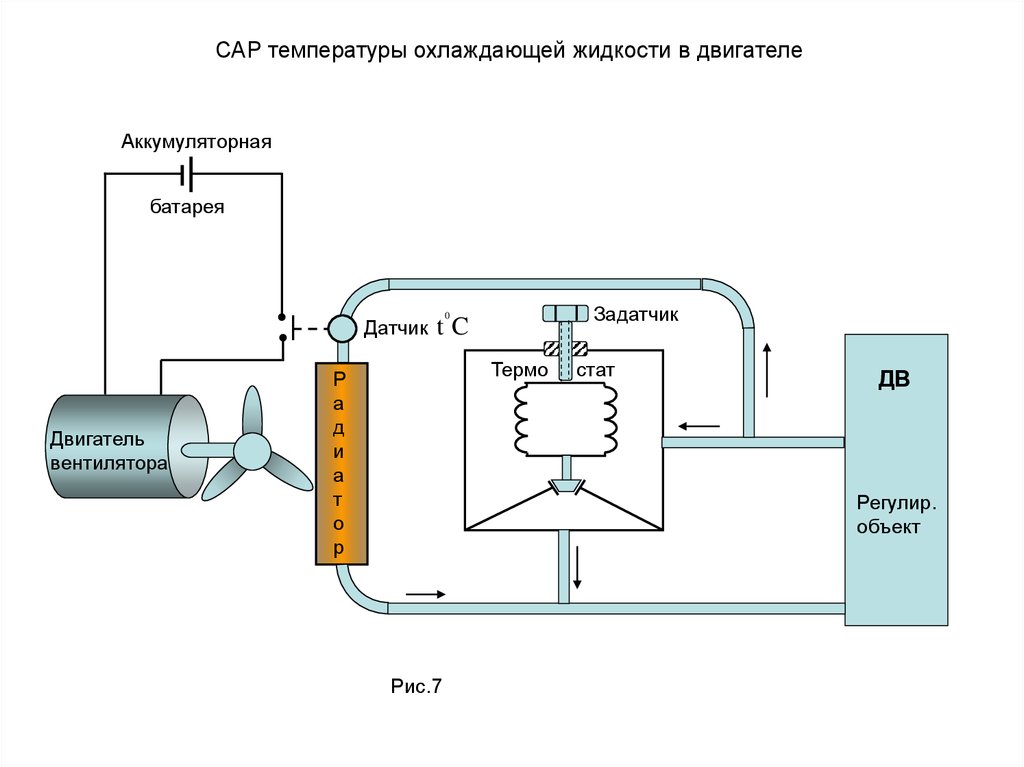

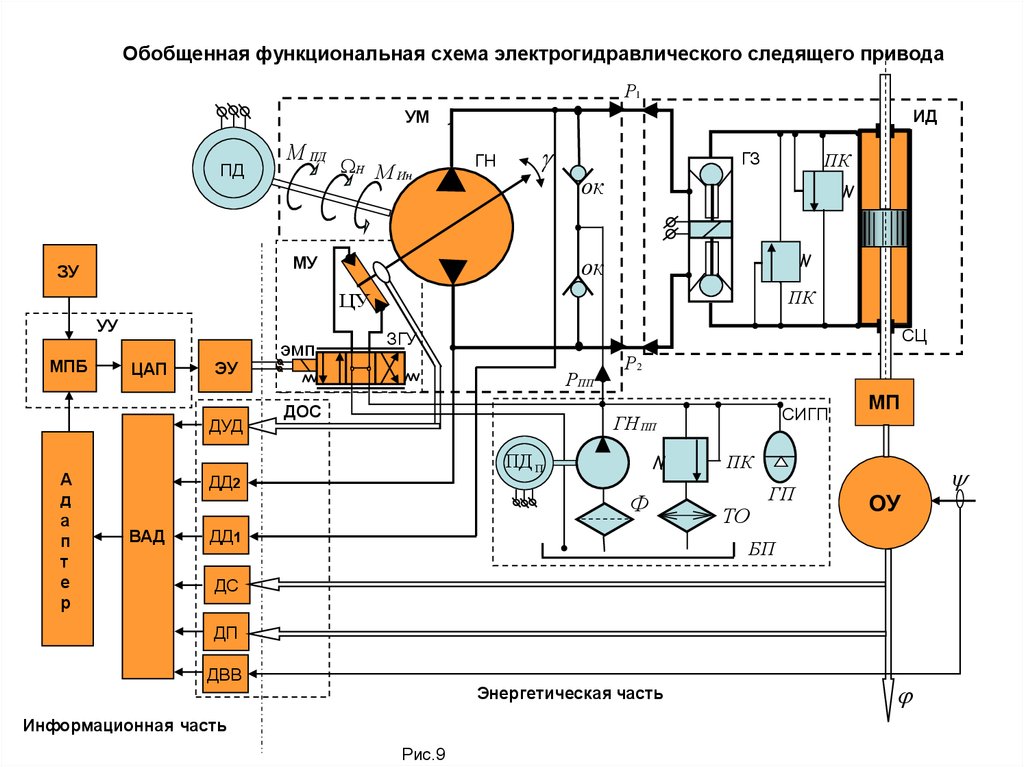


















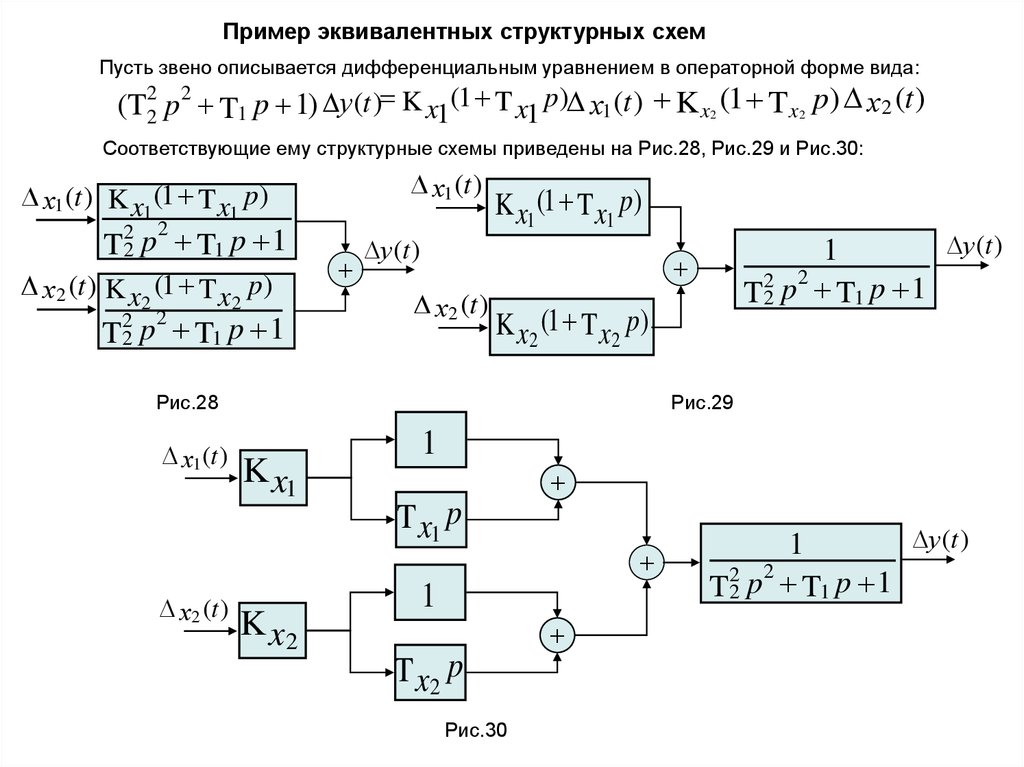



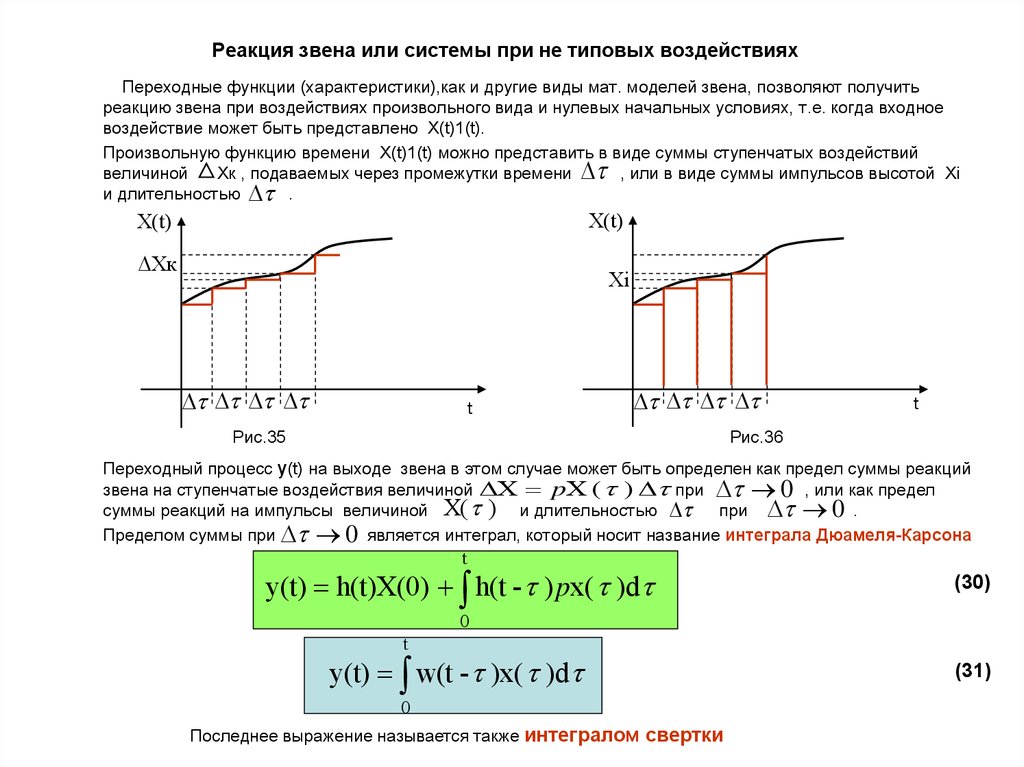



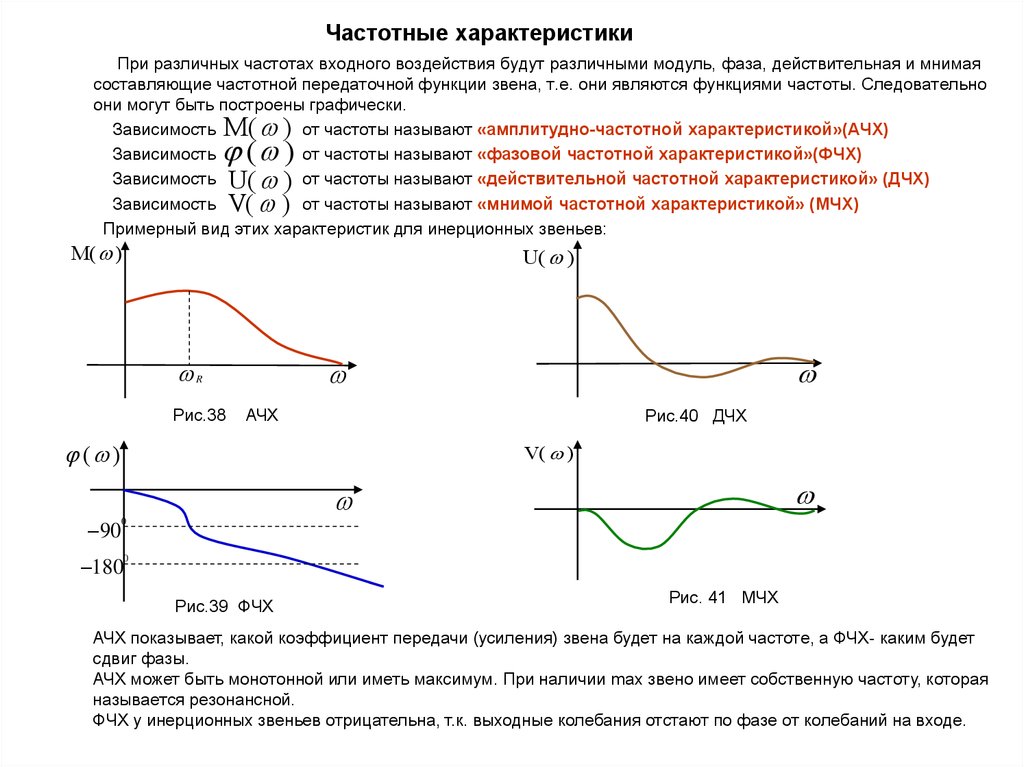






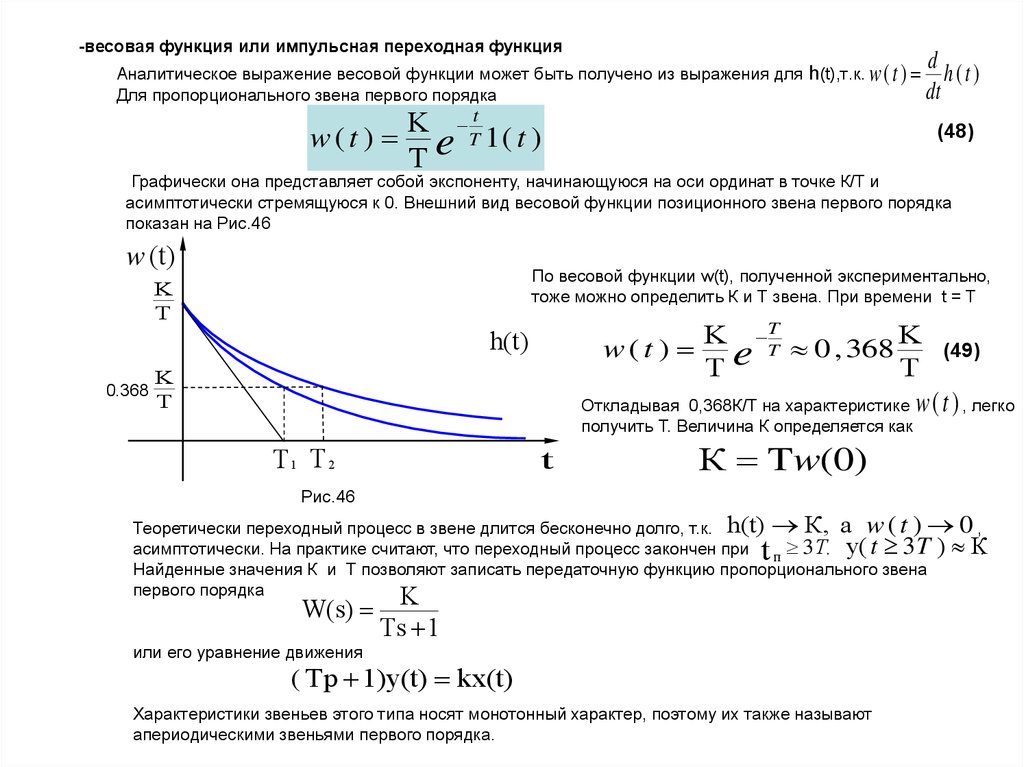

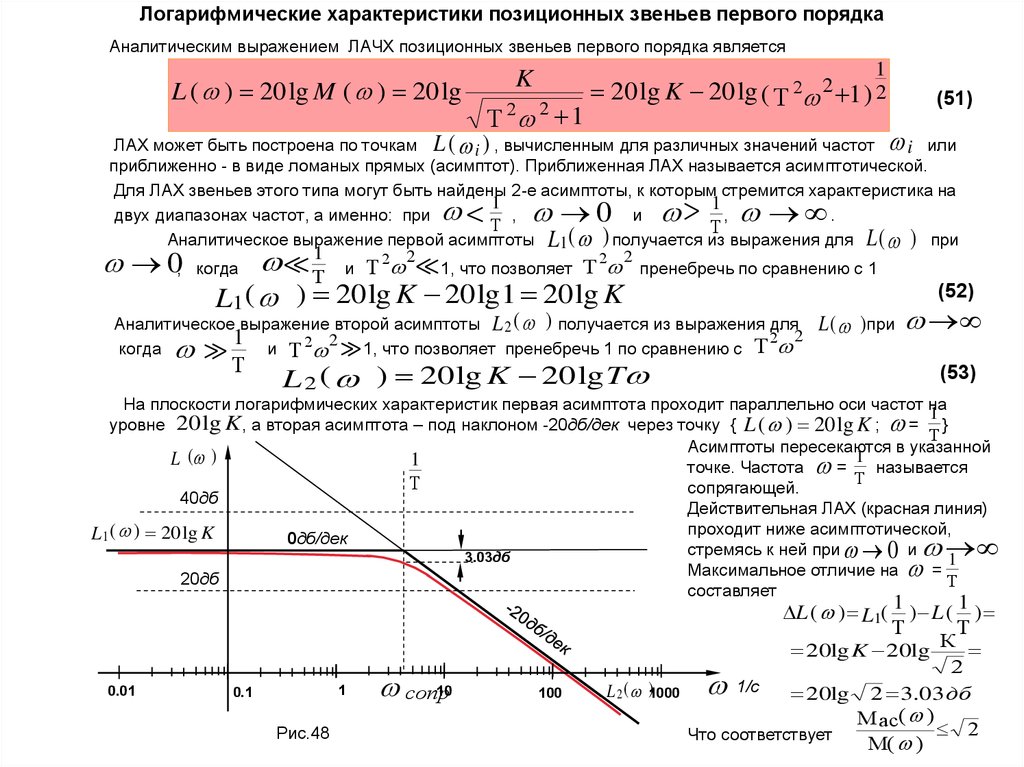
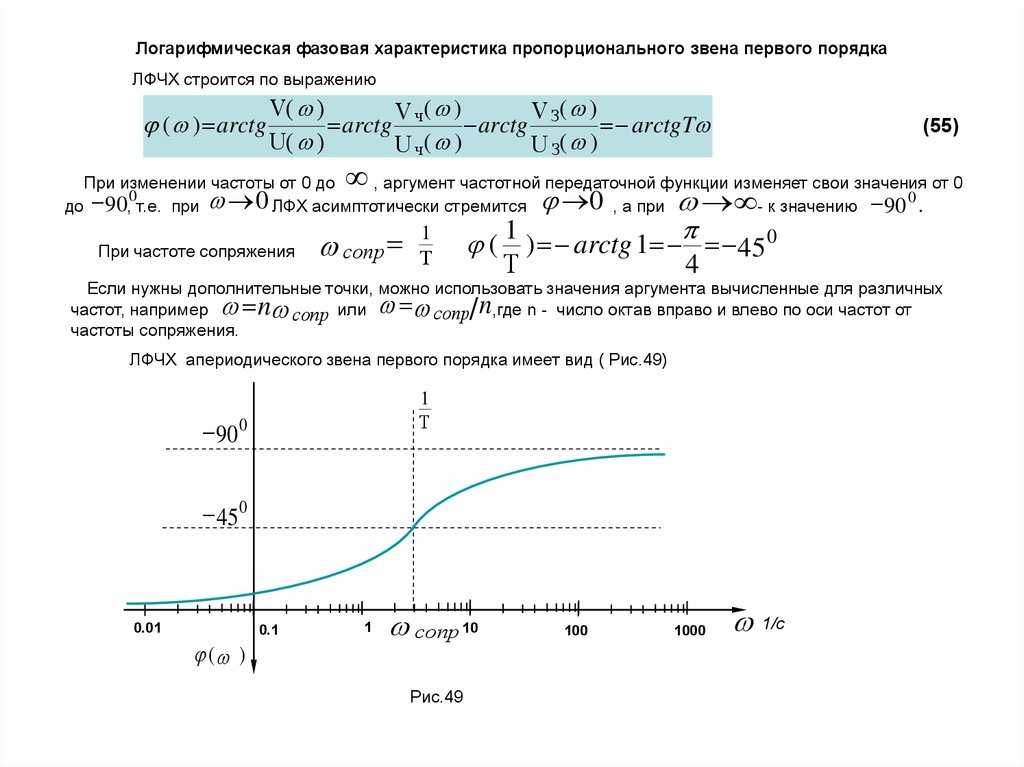

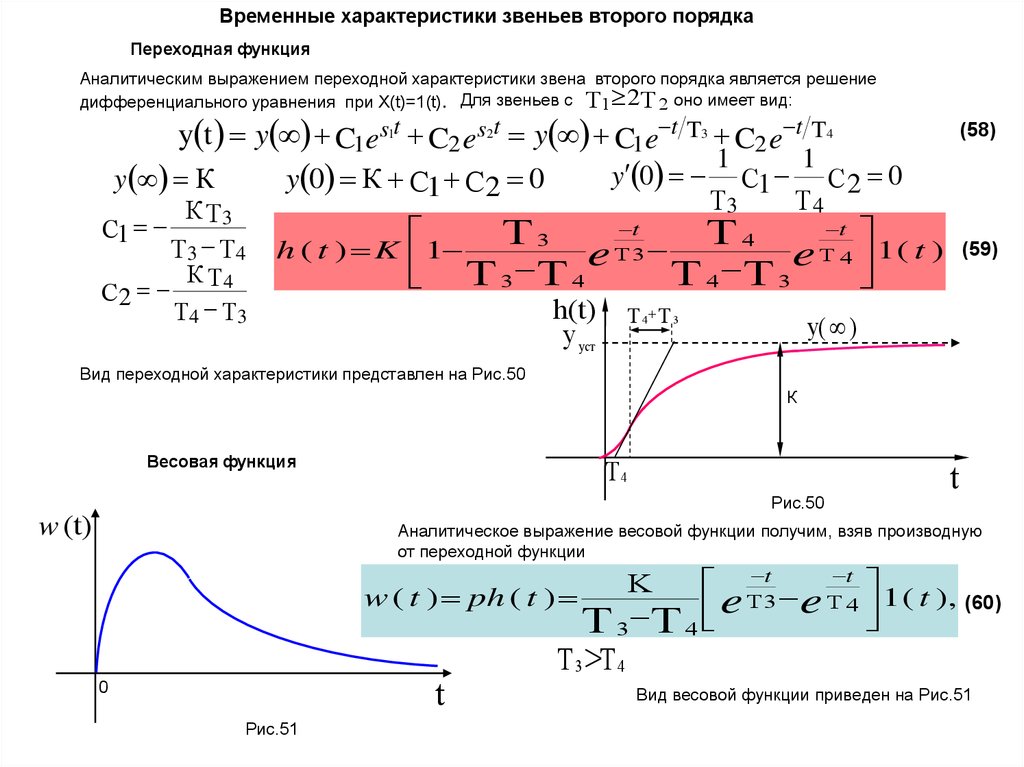
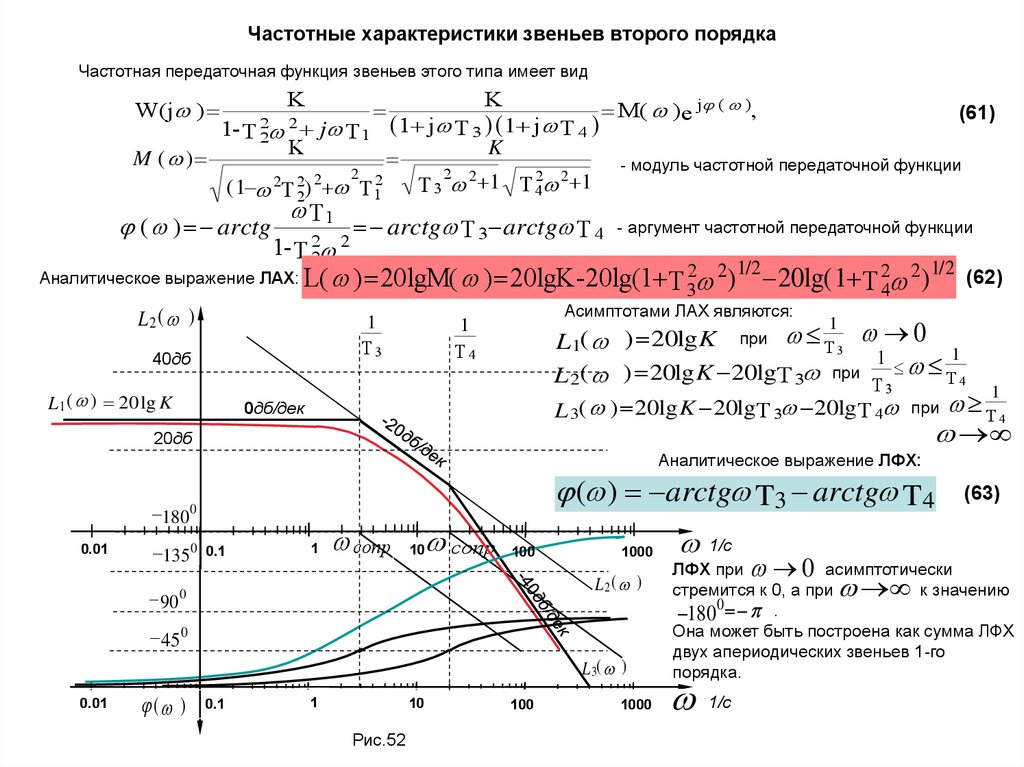


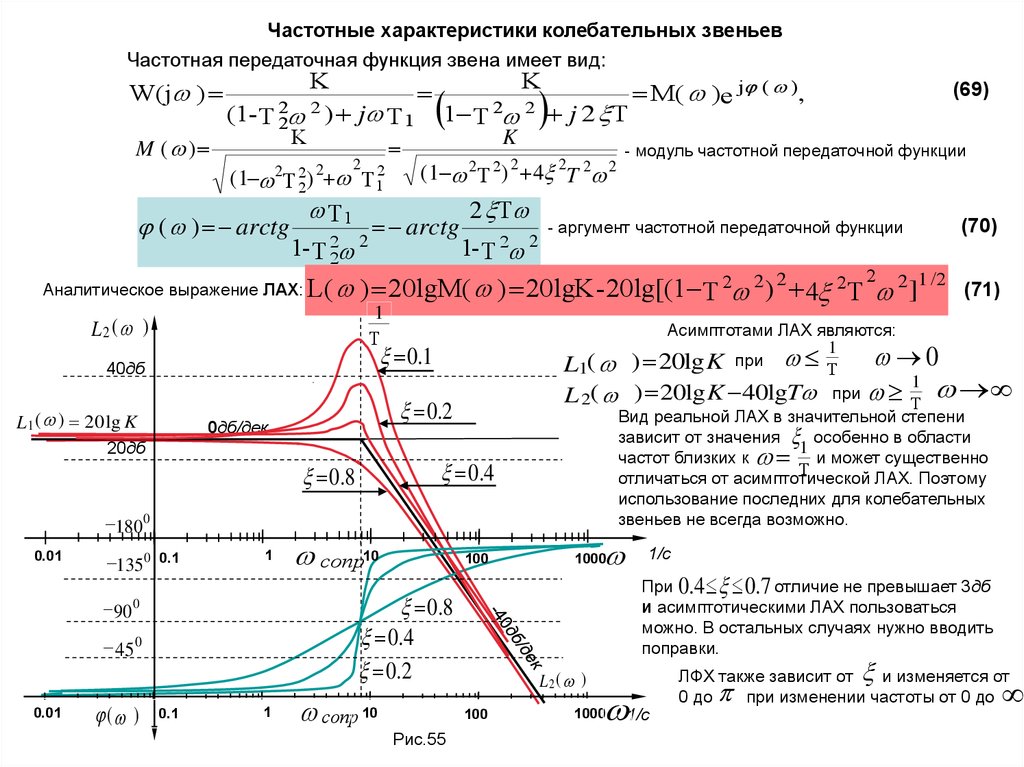
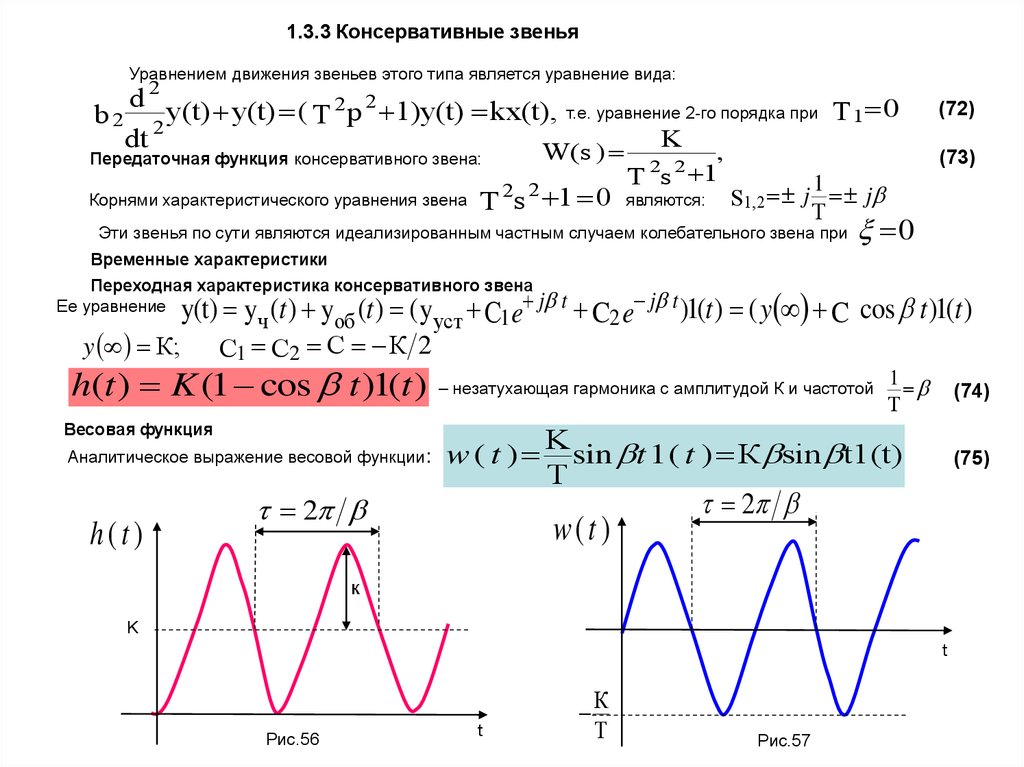
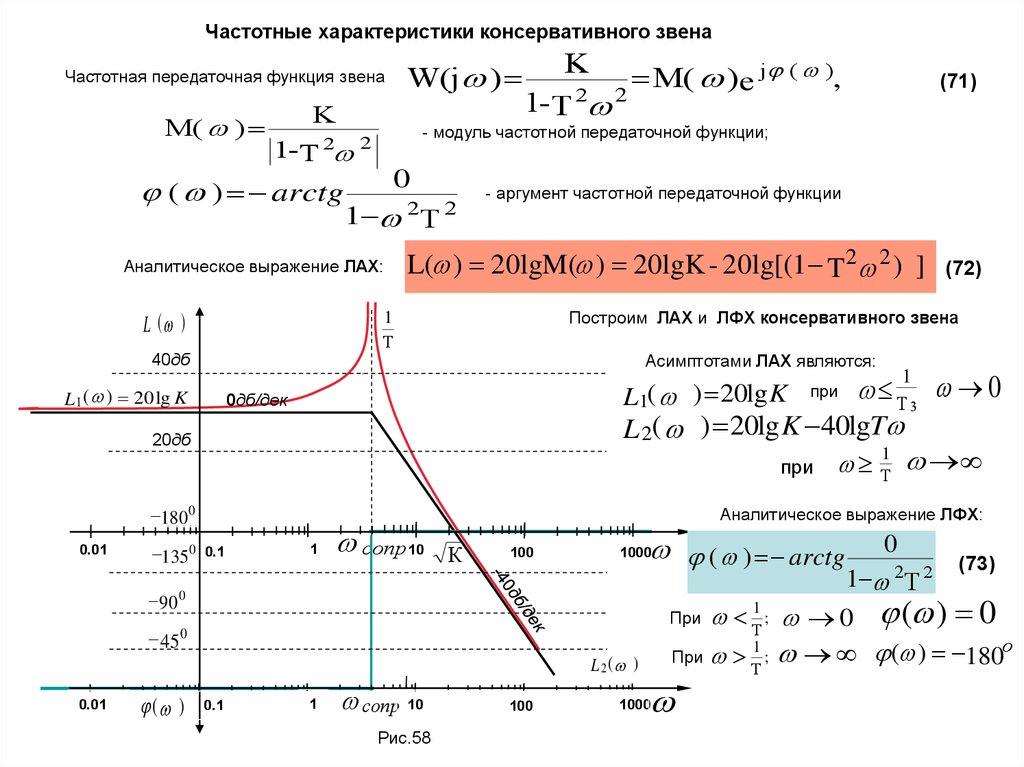

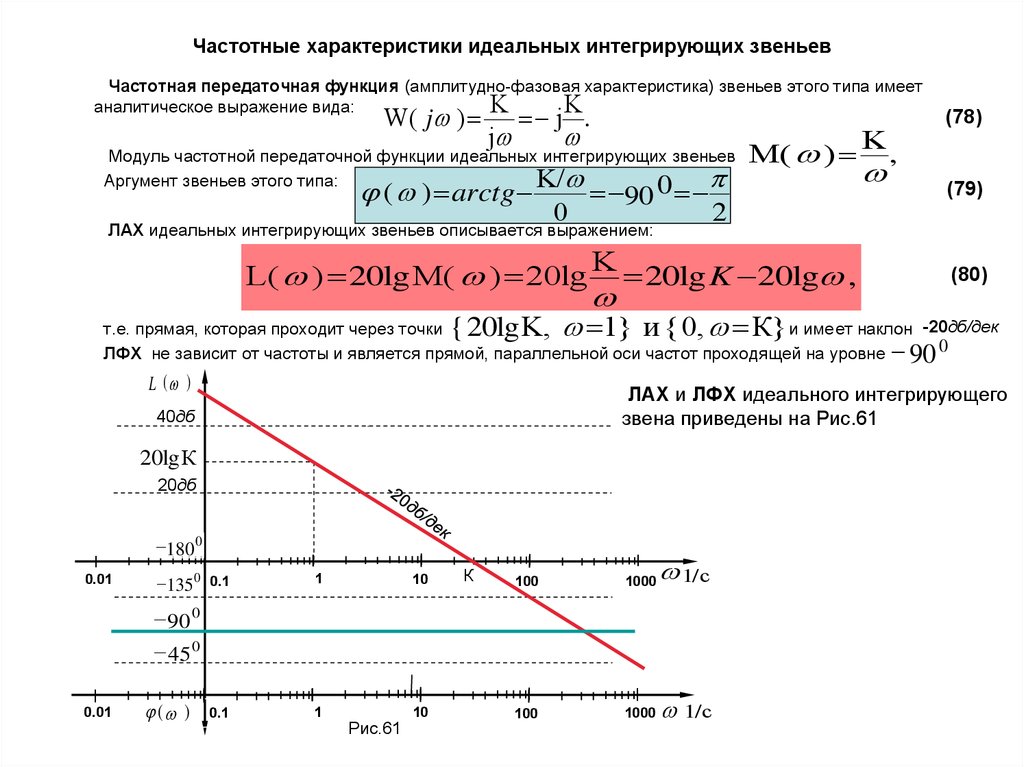
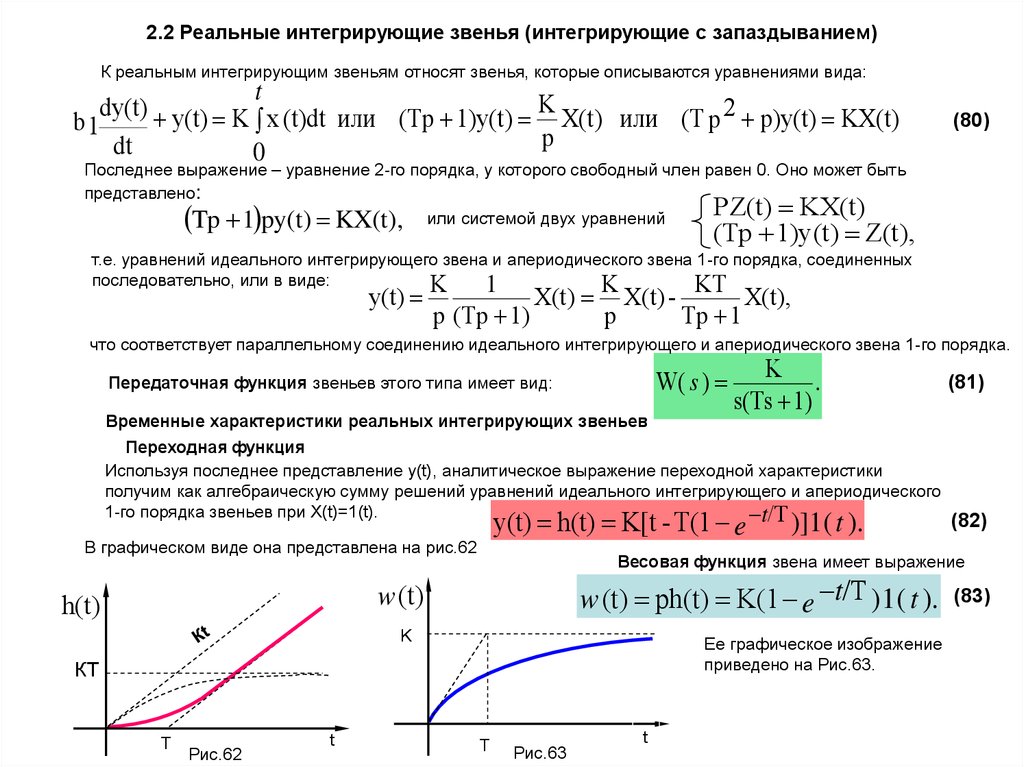
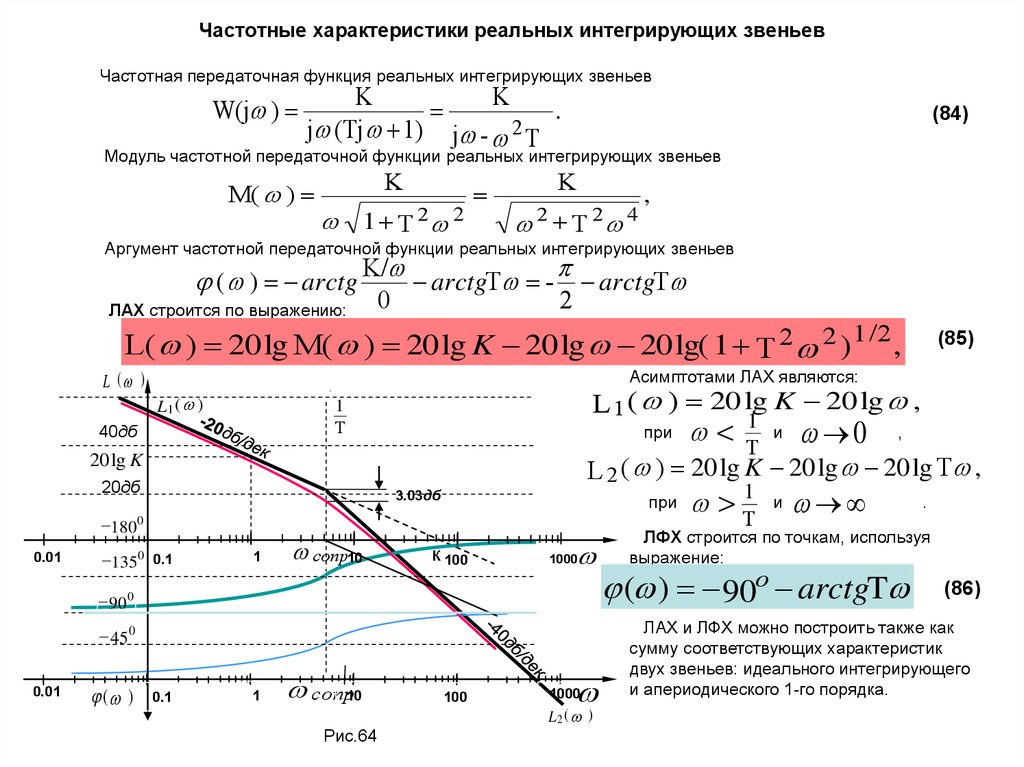
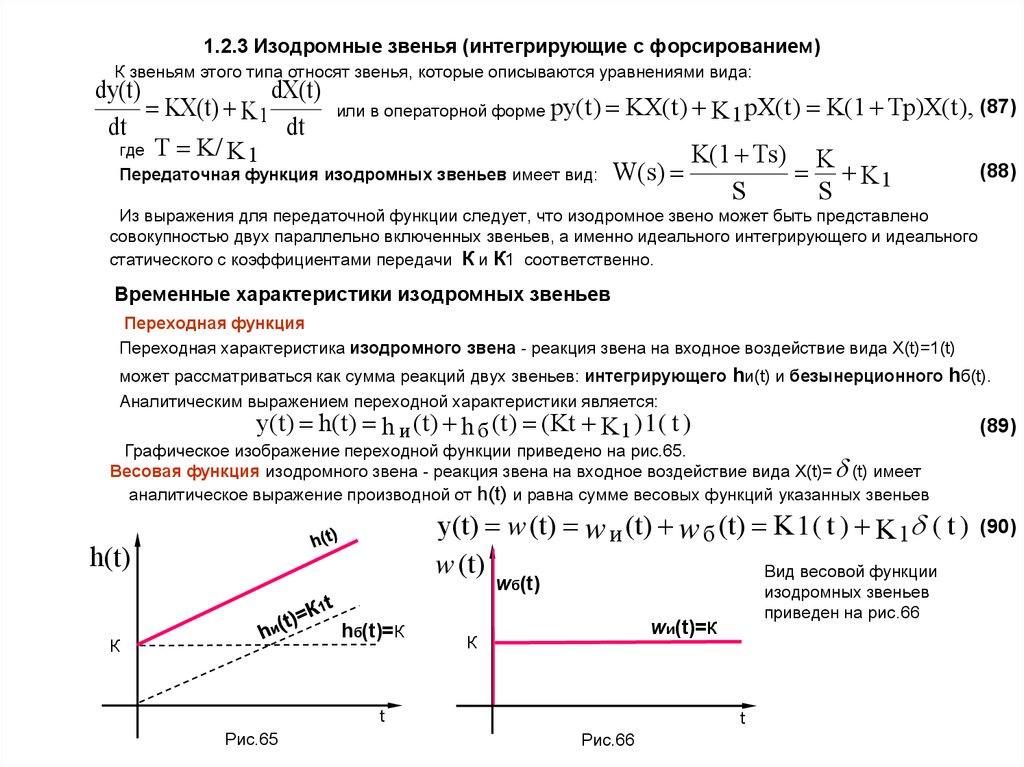
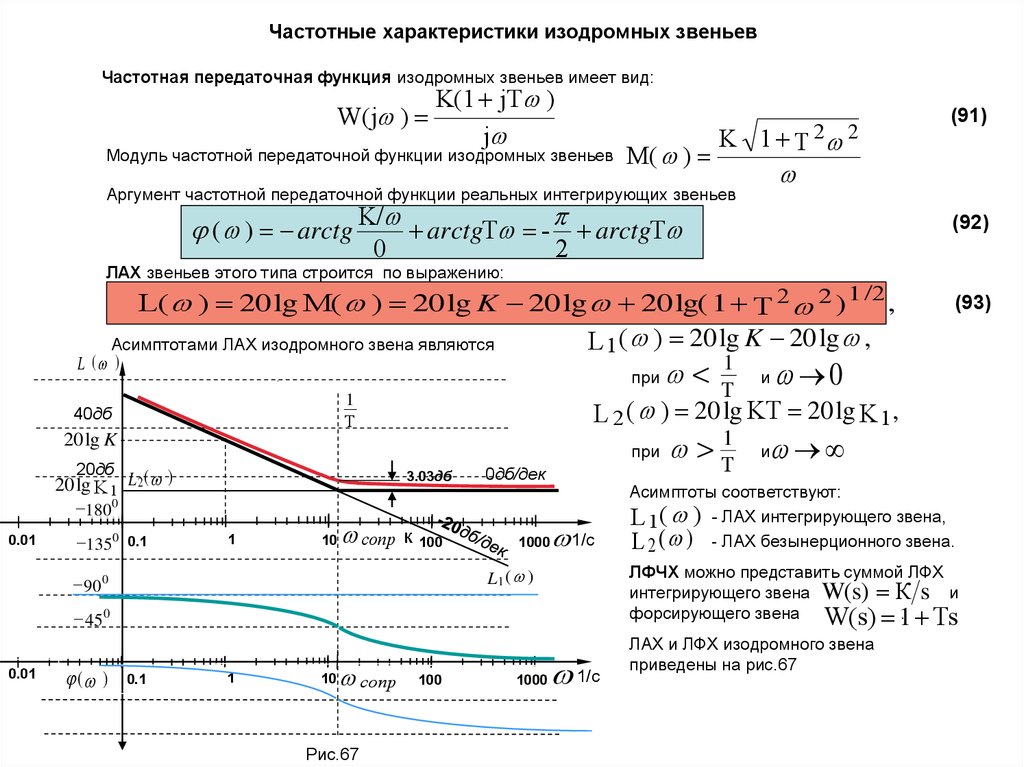

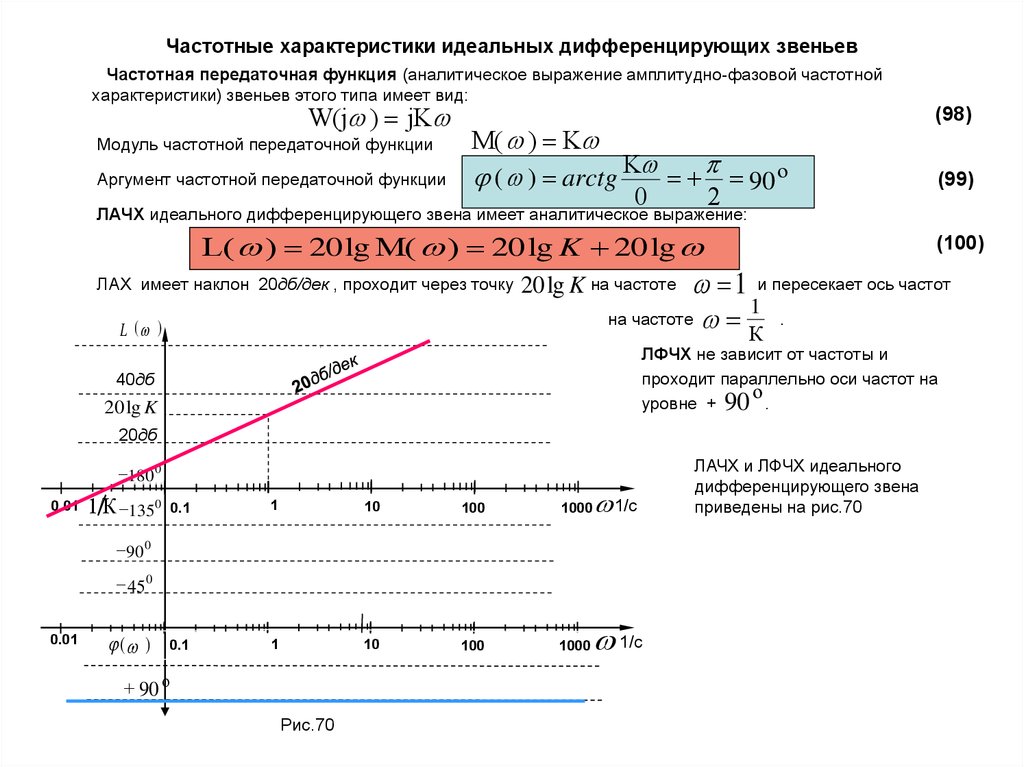

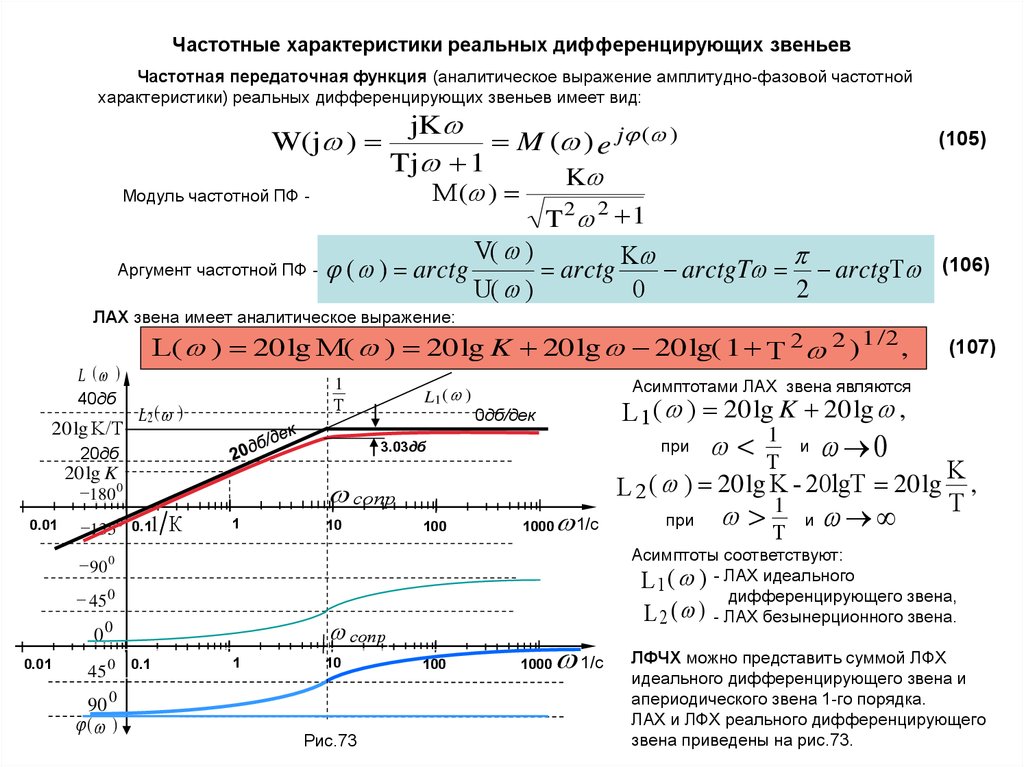
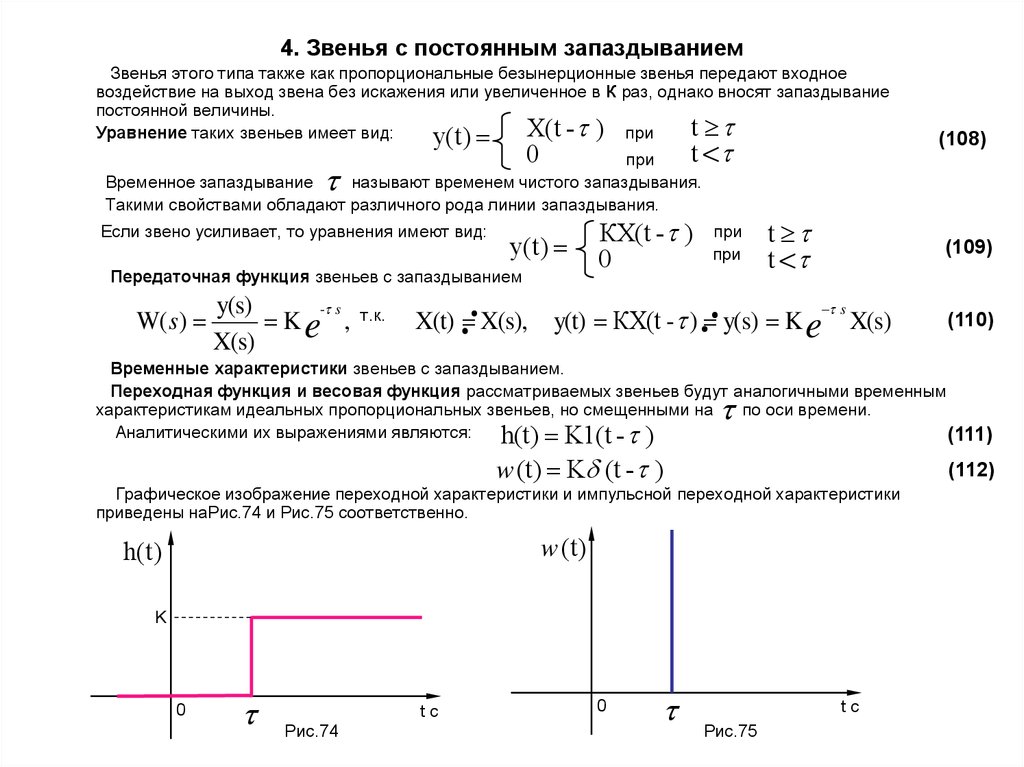
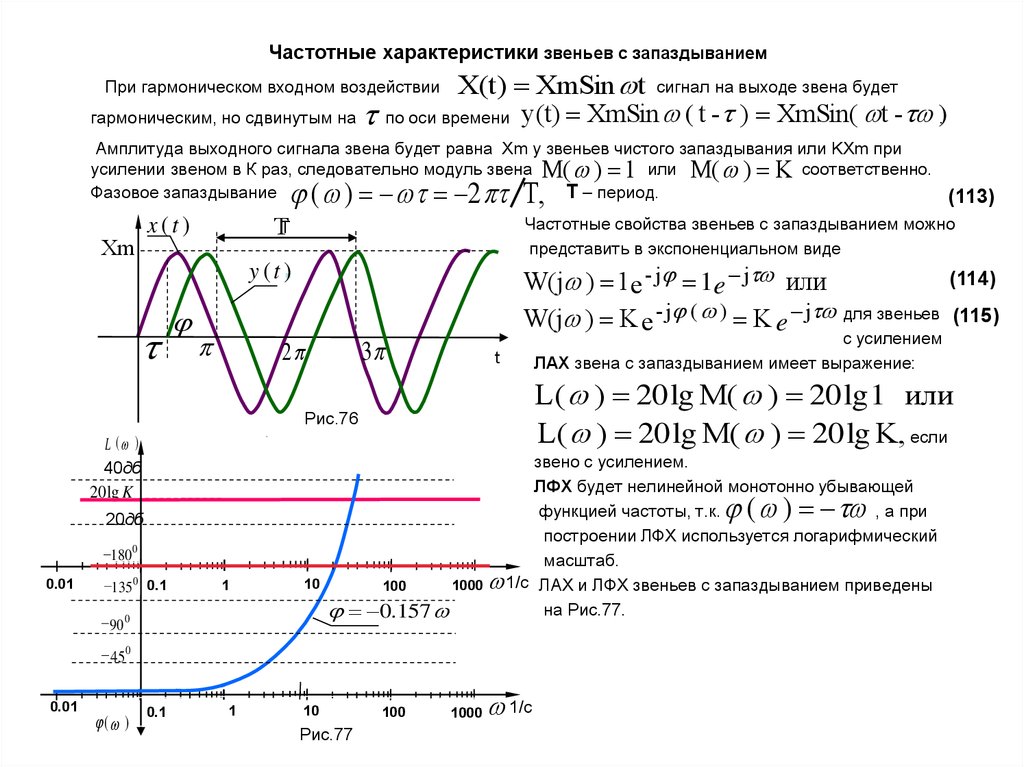

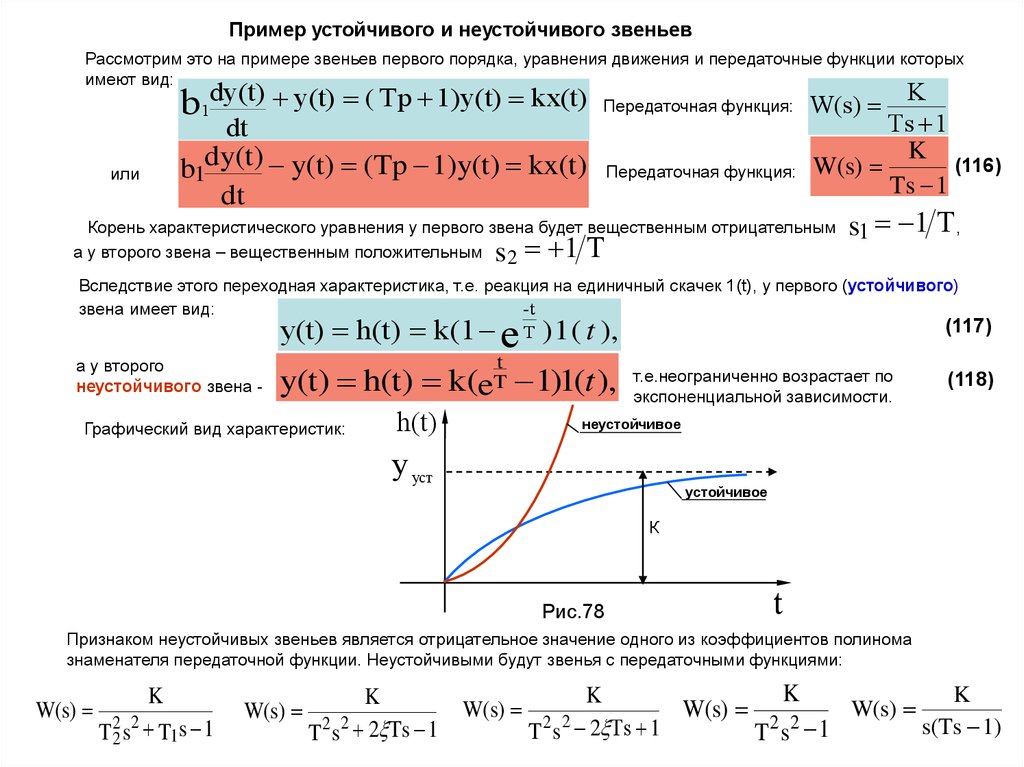
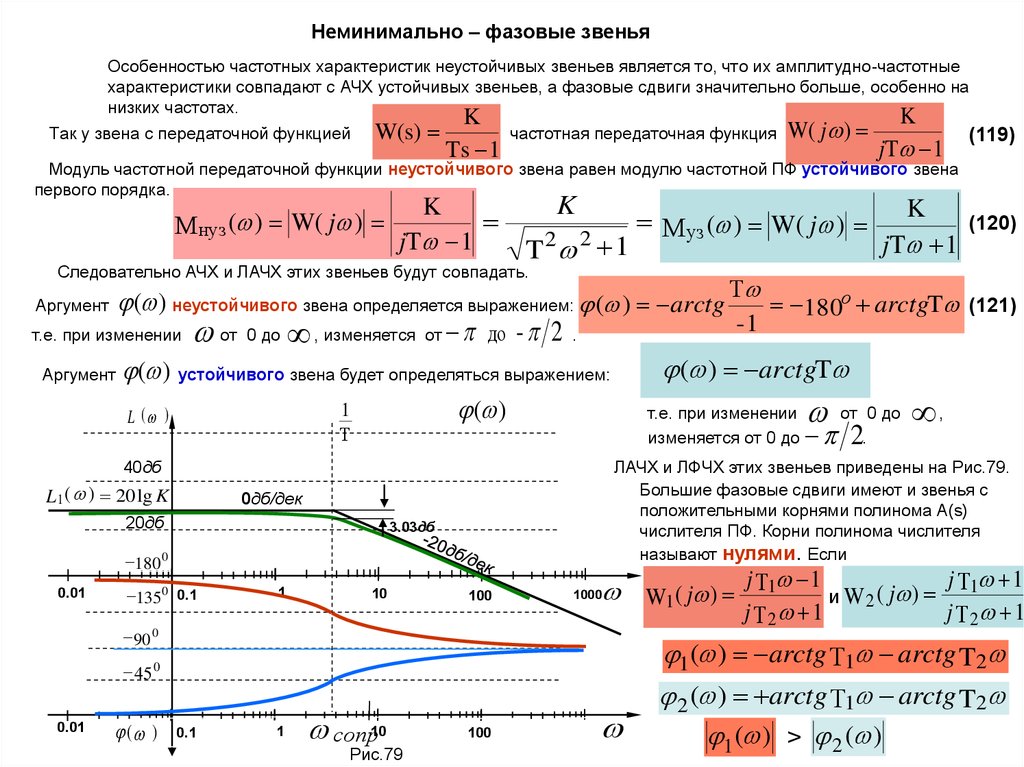
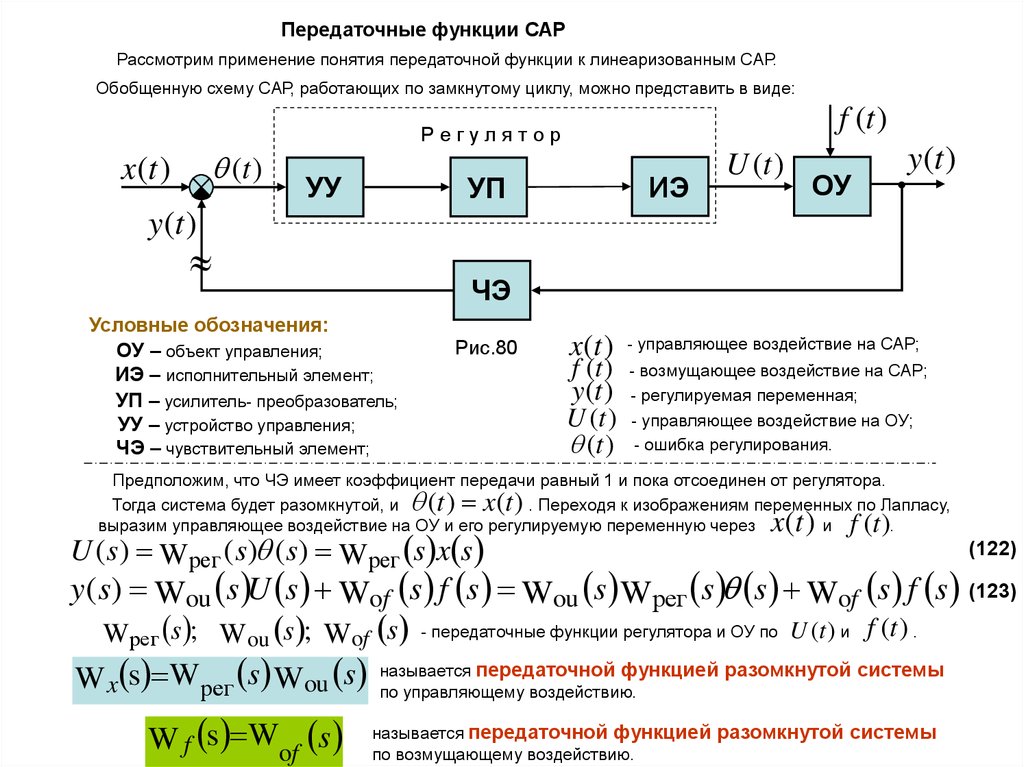



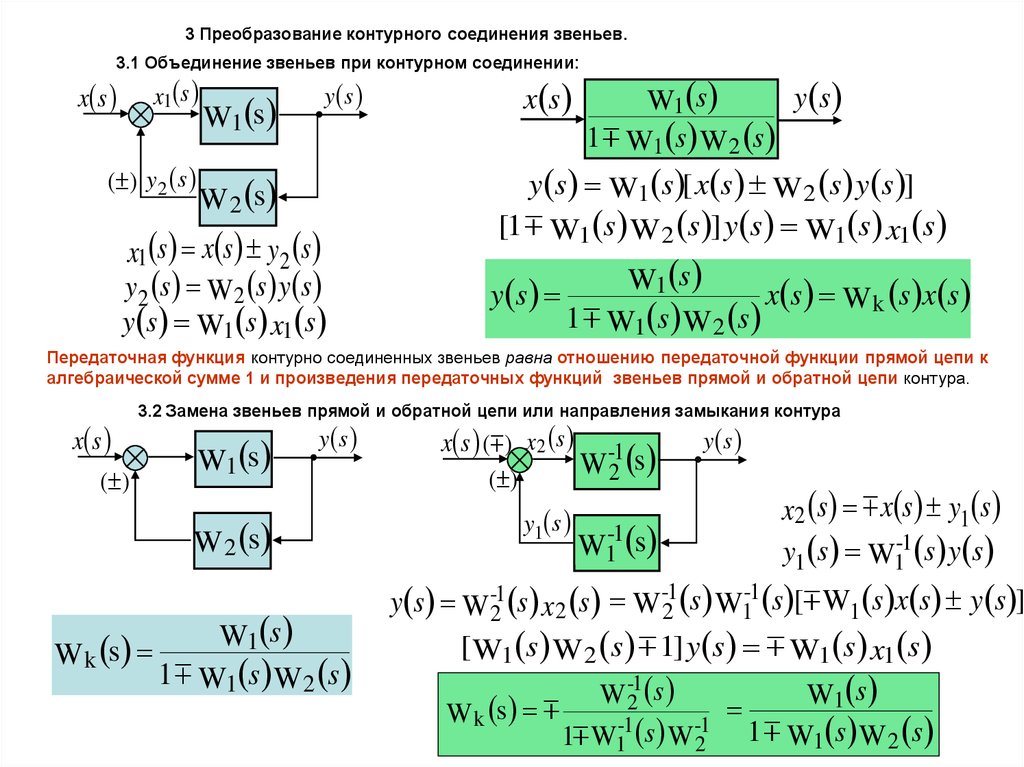
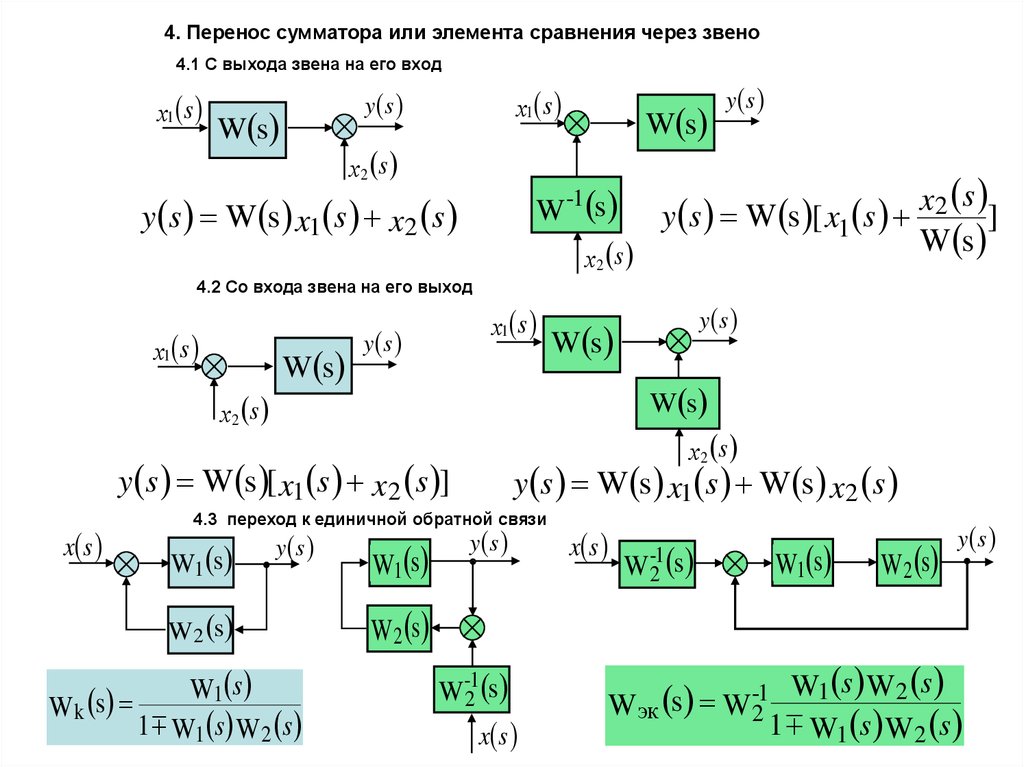
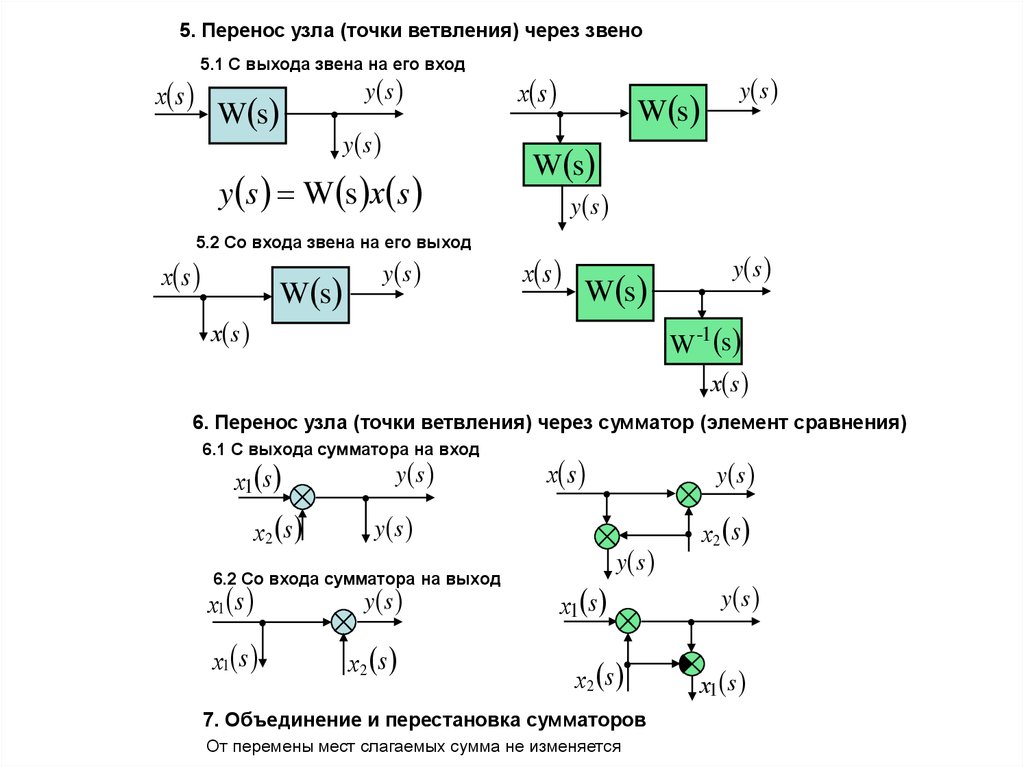
 mechanics
mechanics








