Similar presentations:
Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 1)
1.
СТРОИТЕЛЬНАЯ МЕХАНИКА.Часть I
ТЕОРИЯ ОПРЕДЕЛЕНИЯ
ПЕРЕМЕЩЕНИЙ
ДЕФОРМИРУЕМЫХ
СИСТЕМ
2.
dsa b
D
qds2
k
B
B1
D
qB1
k
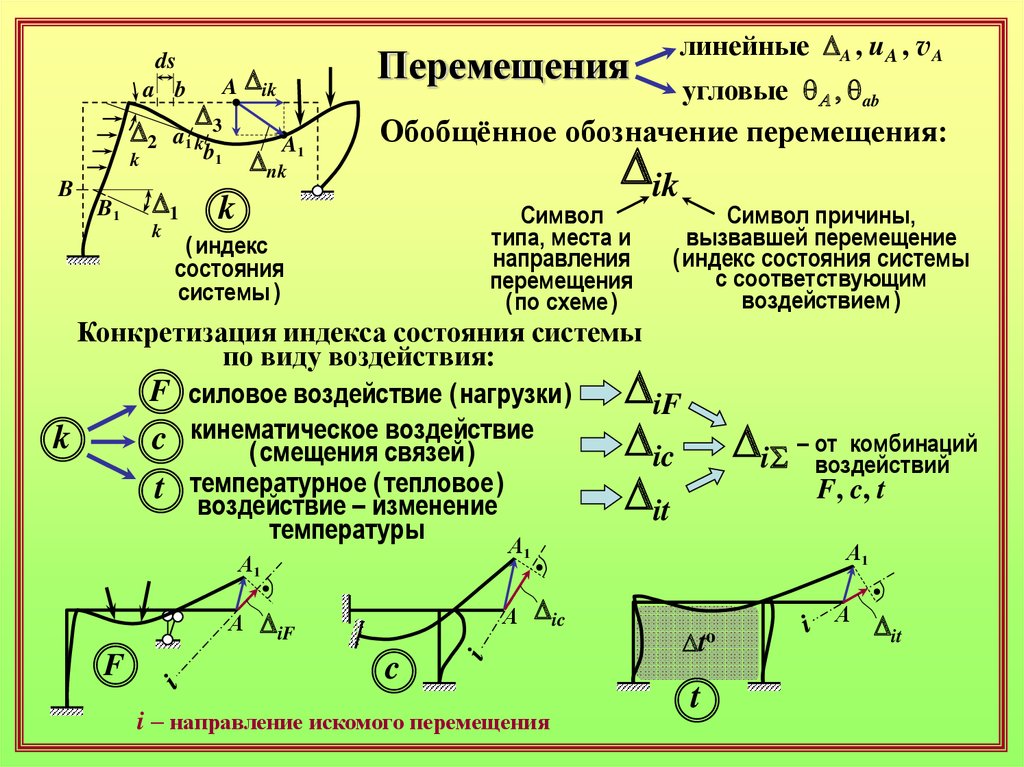
Перемещения
A Duik
A
Dv3 A
a1 k
b1
линейные DA , uA , vA
A1
DAnk
D
k
( индекс
состояния
системы )
угловые qA , qds
Обобщённое обозначение перемещения:
Dik
Символ
Символ причины,
типа, места и
вызвавшей перемещение
направления
(индекс состояния системы
с соответствующим
перемещения
воздействием )
( по схеме )
Читается: перемещение такой-то точки ( сечения )
по такому-то направлению от k–го воздействия.
Если i = k, то Dkk – собственное перемещение
( перемещение, вызванное силовым
воздействием Fk , по его направлению )
Fk
Dkk
A
A1
k
3.
dsa b
D2
k
B
B1
D1
k
D3
Перемещения
A Dik
a1 k
b1
линейные DA , uA , vA
A1
Dnk
угловые qA , qab
Обобщённое обозначение перемещения:
Dik
k
Символ
типа, места и
направления
перемещения
( по схеме )
( индекс
состояния
системы )
Символ причины,
вызвавшей перемещение
(индекс состояния системы
с соответствующим
воздействием )
Конкретизация индекса состояния системы
по виду воздействия:
F силовое воздействие ( нагрузки )
DiF
воздействие
k
c кинематическое
Dic
( смещения связей )
( тепловое)
t температурное
Dit
воздействие – изменение
температуры
F
F, c, t
А1
А1
А
комбинаций
DiS – от
воздействий
А
DiF
Dic
c
i – направление искомого перемещения
А1
Dto
t
А
Dit
4.
Единичные перемещенияПеремещения (линейные, угловые), возникающие от равных единице
механических воздействий (силовых или кинематических ),
называются единичными перемещениями.
Обозначение единичных перемещений:
Fk = 1
А1
А
δik
От единичного
силового
воздействия
k
i
( индекс состояния
системы )
i – направление искомого перемещения
Групповое перемещение
От единичного
кинематического
воздействия
δ ik
δik
Символ
типа, места и
направления
перемещения
(по схеме )
Символ причины,
вызвавшей перемещение
( индекс состояния системы
с соответствующим
единичным воздействием )
Пример: относительное ( взаимное ) линейное перемещение
точек А и В по направлению линии АВ.
А
)
Δ(A
iF
А
Δ(BiF ) Δ Δ(A) Δ(B )
iF
iF
iF
А1
F
B1
B
i
А1
i
δ ik
B
k
( индекс
B1 состояния
системы )
uB,k = 1
5.
МЕТОД МАКСВЕЛЛА – МОРАОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ
( метод вспомогательных единичных нагрузок )
J.C. Maxwell ( 1864 ), O. Mohr ( 1874 )
ИДЕЯ МЕТОДА МАКСВЕЛЛА – МОРА ( ММ-М )
В дополнение к действительному состоянию
рассчитываемой системы (при заданных воздействиях)
рассматривается вспомогательное ( фиктивное ) состояние
с единичным силовым воздействием
по направлению искомого перемещения;
силовые факторы вспомогательного единичного состояния
затем используются, вместе с соответствующими
характеристиками действительного состояния,
для вычисления искомого перемещения.
6.
МЕТОД МАКСВЕЛЛА – МОРАОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ
( метод вспомогательных единичных нагрузок )
Правило задания
вспомогательного единичного воздействия
Во вспомогательном ( фиктивном ) состоянии системы,
рассматриваемом независимо ( отдельно )
от действительного состояния,
в месте, где определяется искомое перемещение,
по его направлению прикладывается численно равное
единице силовое воздействие, тип которого
( сила, момент либо группа сил и/или моментов )
соответствует типу определяемого перемещения
( линейное или угловое, одиночное либо обобщённое ).
В общем случае вспомогательное ( фиктивное )
единичное воздействие – обобщённое, соответствующее
определяемому обобщённому ( групповому) перемещению.
Кинематическое свойство вспомогательного единичного воздействия:
оно (воздействие) таково, что способно совершить работу
на определяемом перемещении.
7.
МЕТОД МАКСВЕЛЛА – МОРАОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ
( метод вспомогательных единичных нагрузок )
Типовые случаи вспомогательных единичных состояний
а) при определении одиночных перемещений
Линейное перемещение точки ( A )
Угол поворота сечения ( 1 )
или узла
DiS= ?
Fi = 1
А
А
DiS= ?
F
F
Dt
i
1
1’
F
A1
o
S
Mi = 1
S
i
(F t)
1
q
i
(F c)
i
б) при определении групповых перемещений
Относительное ( взаимное )
линейное перемещение точек ( A и В )
А
ΔiF Δ(iFA) Δ(iFB ) ?
Δ(BiF ) А Fi = 1
Δ
(A )
iF
А1
B1
F
B
i
Относительный ( взаимный )
угол поворота сечений ( 1 и 2 )
1 2
Fi = 1
i
B
i
1’ 2’
DiF= ?
F
q
1 2
Mi = 1
i
8.
МЕТОД МАКСВЕЛЛА – МОРАОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ
( метод вспомогательных единичных нагрузок )
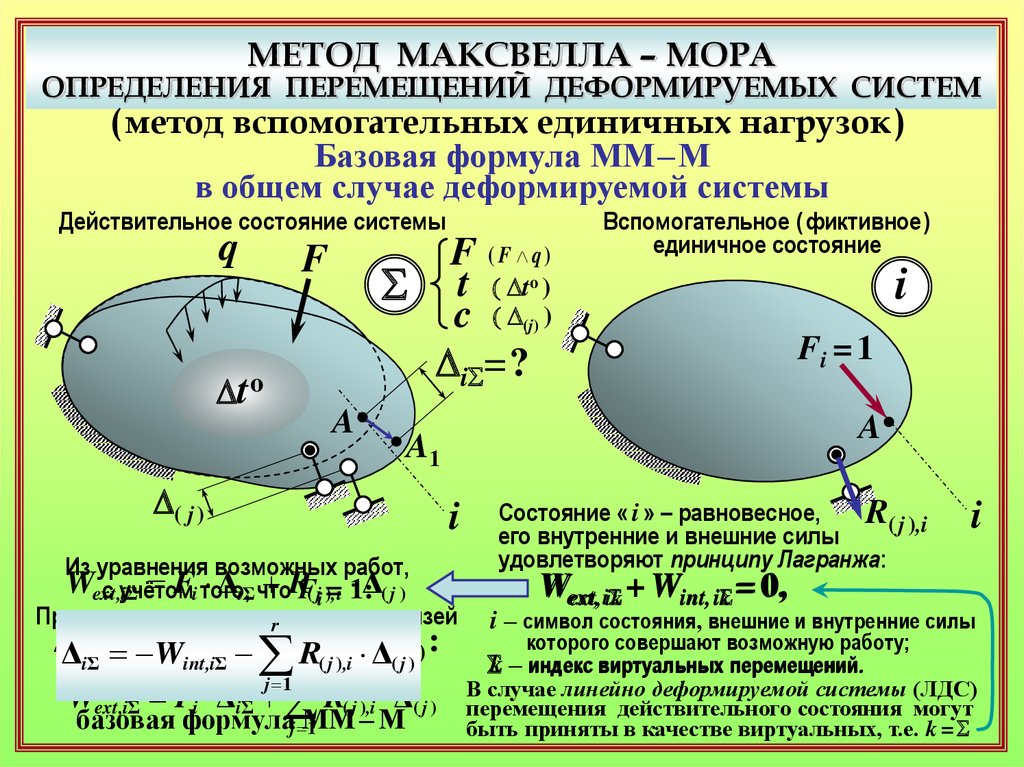
Базовая формула ММ–М
в общем случае деформируемой системы
Действительное состояние системы
q
F (F q)
S t ( Dto )
c ( D(j) )
DiS=?
F
Dt o
A
i
Из уравнения возможных работ,
Wext,
ΔiΣ что
RF( ji )=,i 1:
Δ( j )
с учётом
iΣ Fi того,
При одновременных смещениях
связей
r
DΔ( 1 ) , D
D( r ) :
2 ) ,…,
(W
D( j )R,…, Δ
W
F Δ R Δ
базовая формула
ММ – М
ext,iΣ
int,iΣ
i
j 1
iΣ
r ( j ),i
j 1
( j ),i
(j)
(j)
i
Fi = 1
A
A1
D( j )
iΣ
Вспомогательное ( фиктивное )
единичное состояние
Состояние « i » – равновесное,
R( j ),i
его внутренние и внешние силы
удовлетворяют принципу Лагранжа:
i
Wext, iS
ik + Wint, iS
ik = 0,
i – символ состояния, внешние и внутренние силы
которого совершают возможную работу;
Sk – индекс виртуальных перемещений.
В случае линейно деформируемой системы (ЛДС)
перемещения действительного состояния могут
быть приняты в качестве виртуальных, т.е. k = S
9.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Возможной работой внешних ( внутренних ) сил
называется работа, совершаемая этими силами
на перемещениях (деформациях ), вызванных
другими воздействиями ( реальными или виртуальными ).
Действительной работой внешних ( внутренних ) сил
называется работа, совершаемая ими на перемещениях
( деформациях ), вызванных самими этими силами.
Потенциальная энергия деформации – это энергия,
накапливаемая в материале системы в процессе
его деформирования заданными воздействиями
и возвращаемая в виде механической работы
при разгрузке системы ( материала ).
10.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Dkk
Fi
Fk
A
Dik
i
Возможные работы внешних
и внутренних сил i –го состояния
на перемещениях k –го состояния:
Fi
Wext,ik = – Wint,ik
Fi
0
Dik = inv( Fi )
Dik
A B
A1
Dik
Wext, ik = – Wint, ik = Fi* Dik
i
B1
k
Dkk – собственное перемещение
Dik – побочное перемещение
Действительная работа
внешних сил
Fk
k –го состояния:
F
Wext,kk
k
Fk(z)
0
z dz
Dkk
0<h<1
Dkk
Δk k
F (ζ) dζ
k
0
η Fk Δkk
11.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Dkk
Fi
Fk
A
Dik
i
Возможные работы внешних
и внутренних сил i –го состояния
на перемещениях k –го состояния:
Fi
Wext,ik = – Wint,ik
Fi
0
Dik = inv( Fi )
Dik
A B
A1
Dik
i
B1
k
Dkk – собственное перемещение
Dik – побочное перемещение
Действительная работа
внешних сил
Fk
k –го состояния:
Для ЛДС
F
k
Fk(z)
Fk(z)
0
Wext, ik = – Wint, ik = Fi* Dik U – ПЭУД
z dz
Dkk
h = 1/2
Dkk
Wext,
Wext,
U
kk kk
Δk k
1F Δ
F
2 k(ζk) dkkζ
Теорема0Клапейрона
η Fk Δ1834
( B.P.E. Clapeyron,
kk )
12.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Dkk
Fi
Fk
A
i
Dik
Возможные работы внешних
и внутренних сил i –го состояния
на перемещениях k –го состояния:
Wext, ik = – Wint, ik = Fi* Dik
Выражения возможных и действительных
работ внешних и внутренних сил и ПЭУД
через внешние силовые факторы
и перемещения
( через обобщённые нагрузки
и обобщённые перемещения ).
A B
A1
i
B1
k
Действительная работа внешних
и внутренних сил k –го состояния,
потенциальная энергия упругой
деформации (ПЭУД) ЛДС:
Wext,kk U Wint,kk 1 Fk Δkk
2
Теорема Клапейрона
13.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
txy,i
tyz,i
Fi
dy dz
dx
txz,i
sy,i
Fk
sz,i
A
i
Dkk
sx,i
Dik
A B
A1
i
ex,k
ey,k
ez,k
gxy,k
gyz,k
gzx,k
B1
k
Выражения возможных и действительных работ внешних и внутренних сил
и ПЭУД через внутренние силовые факторы ( напряжения ) и деформации
(
Wext, ik Wint, ik
σ x,i εx,k σ y,i ε y,k σz,i εz,k τ xy,i γ xy,k τ yz,i γ yz,k τzx,i γzx,k dV
V
Wext, kk Wint, kk U
1 σ x,k εx,k σ y,k ε y,k σz,k εz,k τ xy,k γ xy,k τ yz,k γ yz,k τzx,k γzx,k dV
2V
(
dV dx dy dz
14.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных и действительных работ внешних и внутренних сил
и ПЭУД через внутренние силовые факторы ( напряжения ) и деформации
(
Wext, ik Wint, ik
σ x,i ε x,k σ y,i ε y,k σz,i εz,k τ xy,i γ xy,k τ yz,i γ yz,k τzx,i γzx,k dV
V
1
2V
(
Wext, kk Wint, kk U
σ x,k ε x,k σ y,k ε y,k σz,k εz,k τ xy,k γ xy,k τ yz,k γ yz,k τzx,k γzx,k dV
Физические зависимости, связывающие деформации k –го состояния с напряжениями
(для линейно деформируемого изотропного тела, с учётом температурной составляющей )
εx,k σx,k ν (σ y,k σz,k / E α Δt ; ; εz,k σz,k ν (σx,k σ y,k / E α Δt ;
γ xy,k τ xy,k / G ; ; γzx,k τzx,k / G ; G E / 2 ( 1 ν
Wext, ik Wint, ik
Wext, kk U Wint, kk
1
2 2 σ x,i
2 σ x,k σ y,i σ y,k σ z,i σ z,k
1
1
[σ x,k σV y,kE σz,k 2ν ( σ x,k σ y,k σ y,k σz,k σz,k σ x,k
2V E
ν σ x,i 2(σ y,k 2σz,k σ2 y,i (σz,k σ x,k σz,i (σ x,k σ y,k
ττzx,k τ τzx,k
Δ t (σEx,kα
zx,k
(τ xy,iν) (ττxy,k
(σ x,i σ z,kσ y,i] dV
2 (1 2ν)(1
τ zx,iE α
τzx,k
Δσt y,k
σz,i } dV
yz,i
yz,k
15.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
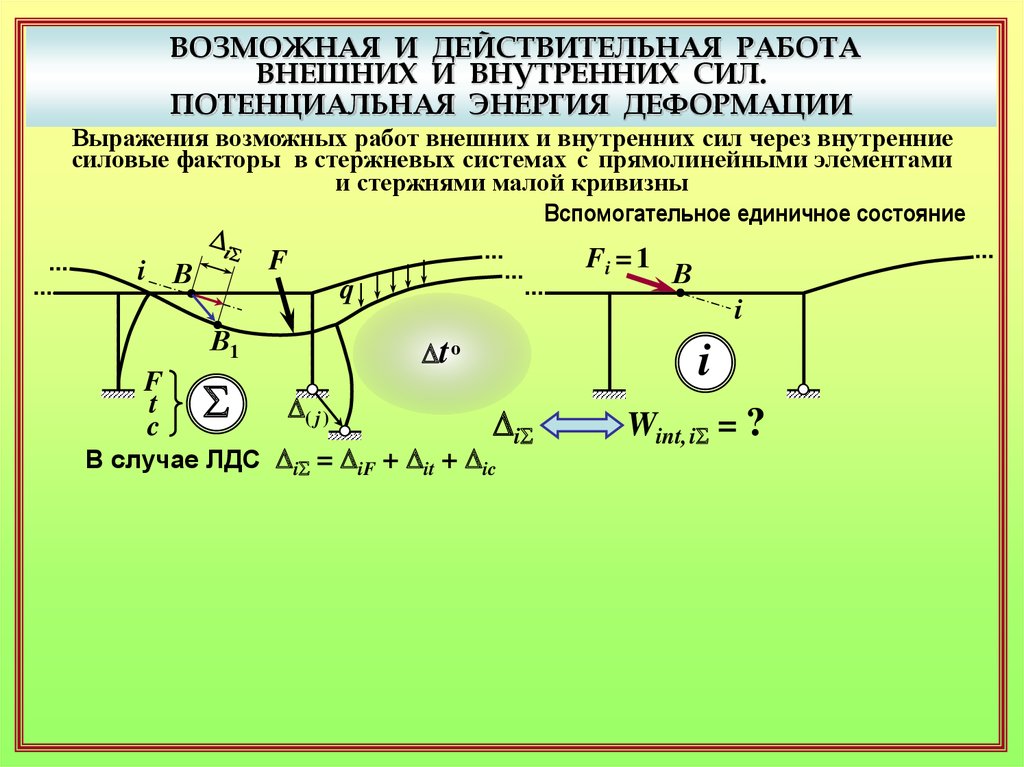
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
Вспомогательное единичное состояние
q
В1
F
t
c
Fi = 1
F
i В
S
i
Dt o
D( j )
В
i
DiS
В случае ЛДС DiS = DiF + Dit + Dic
Wint, iS = ?
16.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
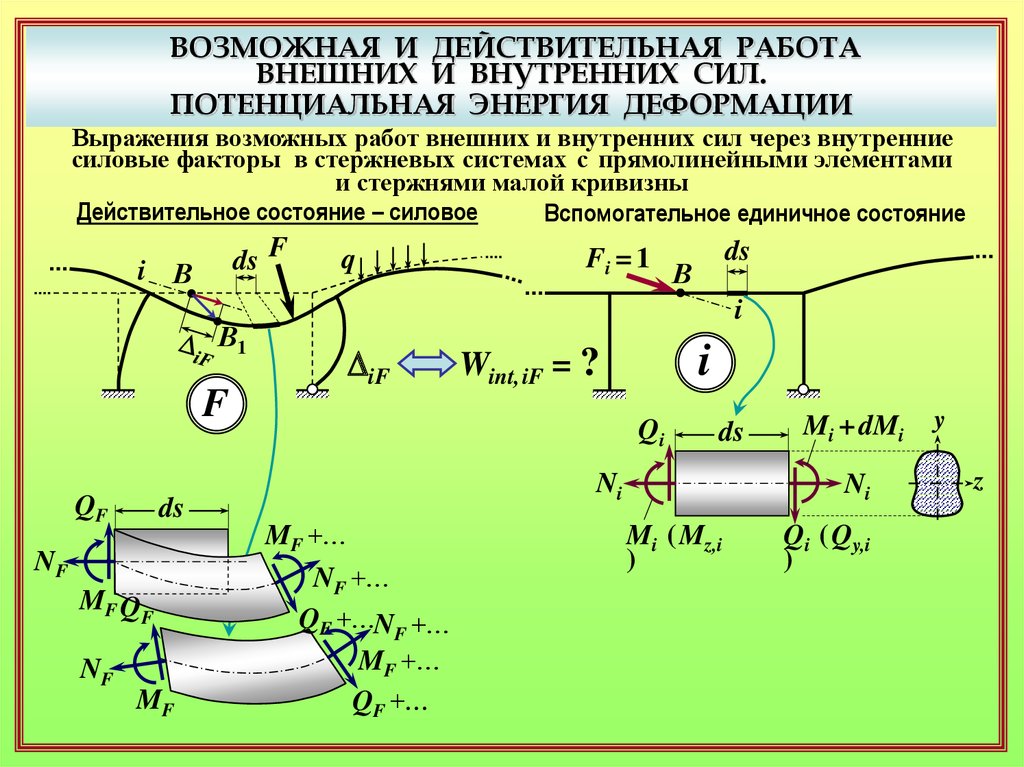
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
Действительное состояние – силовое
Вспомогательное единичное состояние
ds F
i В
В1
q
Fi = 1
ds
NF
MF Q
F
NF
MF
В
i
DiF
i
Wint, iF = ?
F
QF
ds
Qi
ds
Ni
MF +…
NF +…
QF +…NF +…
MF +…
QF +…
Mi + dMi
Ni
Mi (Mz,i
)
Qi (Qy,i
)
y
z
17.
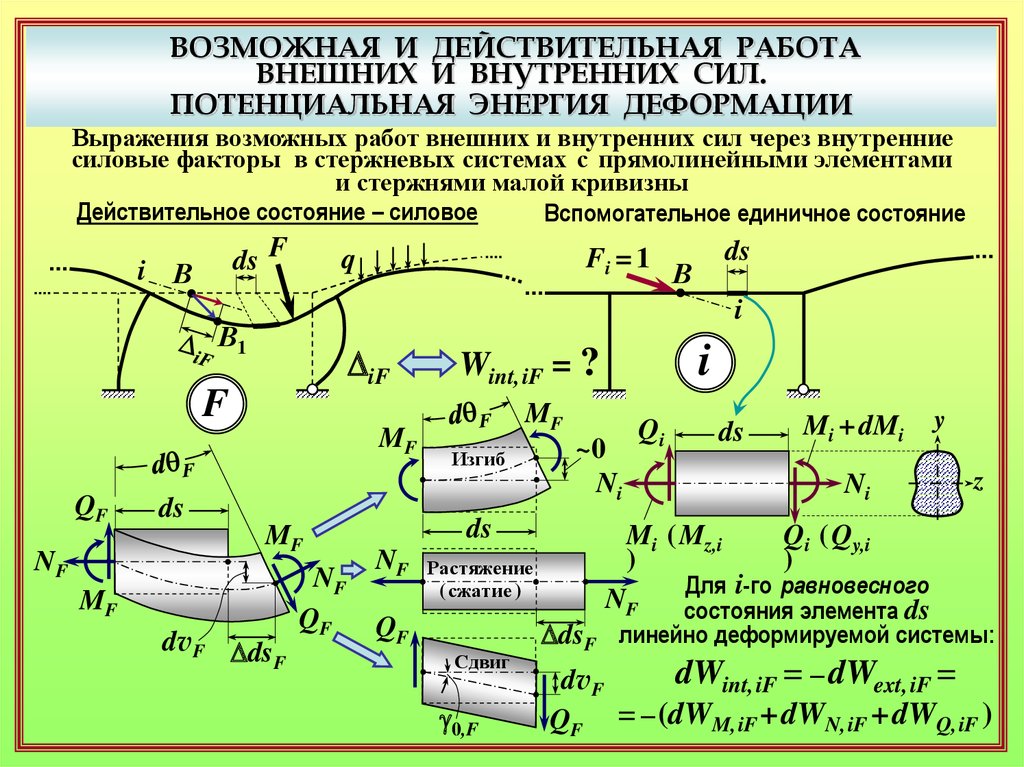
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
Действительное состояние – силовое
Вспомогательное единичное состояние
ds F
i В
Fi = 1
q
DiF
MF
ds
MF
MF
dvF Dds
F
NF
QF
MF
Изгиб
~0
Ni
ds
NF
i
Wint, iF = ?
F
NF
В
i
В1
QF
ds
Сдвиг
g0,F
ds
DdsF
Mi + dMi
Ni
Mi (Mz,i
)
Растяжение
( сжатие )
QF
Qi
y
z
Qi (Qy,i
)
Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:
NF
dWint, iF = – dWext, iF =
dvF
QF = – (dWM,iF + dWN, iF + dWQ, iF )
18.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
Действительное состояние – силовое
Вспомогательное единичное состояние
ds F
i В
В1
Fi = 1
q
В
i
DiF
MF
dWM, iF = Mi * dqF = Mi * rF * ds
M M
dWM,N,iFiF =M
Nii * Dds
dW
dθF F = Nii * eF F* ds
ds
EI
dWQ, iF = Qi * dvF = Qi * g0,F * ds
NF
По закону Гука при изгибе,Nрастяже N
нии
и сдвиге
dW(сжатии)
i F ds
N,iF N
i ΔdsFсоответственно:
rF = MF /EI; eF = NFEA
/ EA; QF
g0,F = t0,F /G = (kt* QQF /A)/G
Q
dW
Qi dнеравномерности
vF kτ i F ds
kt – Q,iF
коэффициент
распределения касательных GA
i
Wint, iF = ?
F
напряжений по сечению
ds
MF
Изгиб
~0
Ni
ds
g0,F
ds
DdsF
Mi + dMi
Ni
Mi (Mz,i
)
Растяжение
( сжатие )
Сдвиг
Qi
y
z
Qi (Qy,i
)
Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:
NF
dWint, iF = – dWext, iF =
dvF
QF = – (dWM,iF + dWN, iF + dWQ, iF )
19.
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
Действительное состояние – силовое
Вспомогательное единичное состояние
ds F
i В
В1
Fi = 1
q
DiF
MF
M MF
dWM,iF Mi dθF i
ds
EI
dWint,iF dWext,iF
NF
M MF Ni NF
i
N N
EI
dWN,iF
Ni ΔdsF EAi F ds
Qi QF EA
QF
kτ
ds
dWQ,iF
В
i
Q Q
Qi dvF kτ i F ds
GA
i
Wint, iF = ?
F
GA
ds
MF
Изгиб
~0
Ni
ds
g0,F
ds
DdsF
Mi + dMi
Ni
Mi (Mz,i
)
Растяжение
( сжатие )
Сдвиг
Qi
y
z
Qi (Qy,i
)
Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:
NF
dWint, iF = – dWext, iF =
dvF
QF = – (dWM,iF + dWN, iF + dWQ, iF )
20.
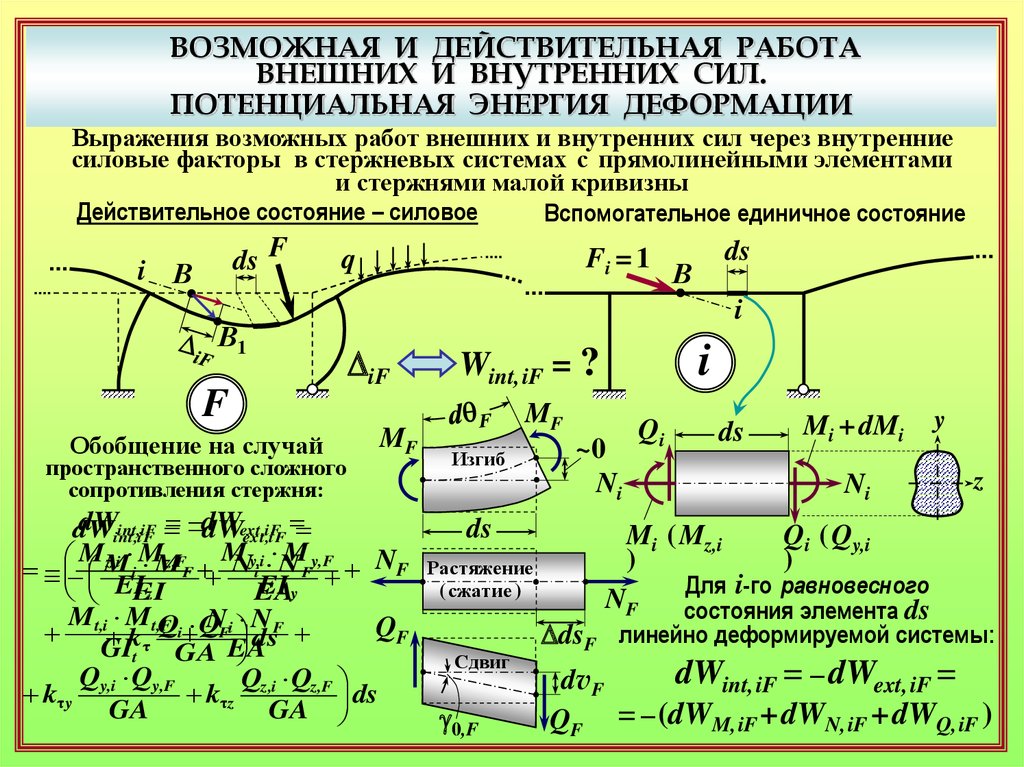
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
Действительное состояние – силовое
Вспомогательное единичное состояние
ds F
i В
Fi = 1
q
В1
пространственного сложного
сопротивления стержня:
В
i
DiF
MF
dWint,iF
dW
int,iF
dW
dWext,iF
ext,iF
M y,i M y,F
M z,i M
z,F
i MF Ni NF
M
NF
EI y
z
EIEI
EA
M M F i Q
N N
QF
t,i kτ t,Q
Fi dsF
GIt GA EA
Q Q
Q Q
kτy y,i y,F kτz z,i z,F ds
GA
GA
i
Wint, iF = ?
F
Обобщение на случай
ds
MF
Изгиб
~0
Ni
ds
g0,F
ds
DdsF
Mi + dMi
Ni
Mi (Mz,i
)
Растяжение
( сжатие )
Сдвиг
Qi
y
z
Qi (Qy,i
)
Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:
NF
dWint, iF = – dWext, iF =
dvF
QF = – (dWM,iF + dWN, iF + dWQ, iF )
21.
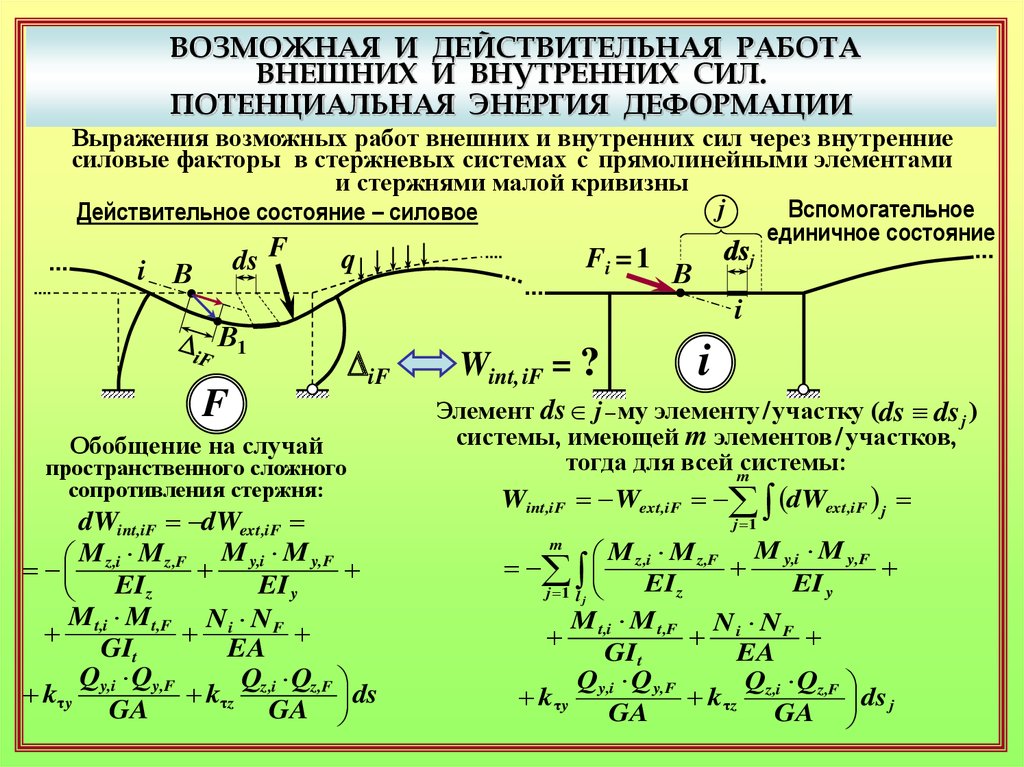
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТАВНЕШНИХ И ВНУТРЕННИХ СИЛ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через внутренние
силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны
j
Вспомогательное
Действительное состояние – силовое
единичное состояние
ds F
i В
Fi = 1
q
В1
dsj
В
i
DiF
F
Обобщение на случай
пространственного сложного
сопротивления стержня:
dWint,iF dWext,iF
M M z,F M y,i M y,F
z,i
EI
EI
z
y
M Mt,F N i N F
t,i
GIt
EA
Q Q
Q Q
kτy y,i y,F kτz z,i z,F ds
GA
GA
Wint, iF = ?
i
Элемент ds j – му элементу / участку (ds ds j )
системы, имеющей m элементов / участков,
тогда для всей mсистемы:
Wint,iF Wext,iF (dWext,iF j
j 1
M M z,F M y,i M y,F
z,i
EI
EI
z
y
j 1 l j
M M t,F N i N F
t,i
GIt
EA
Q Q y,F
Q Q
kτy y,i
kτz z,i z,F ds j
GA
GA
m
22.
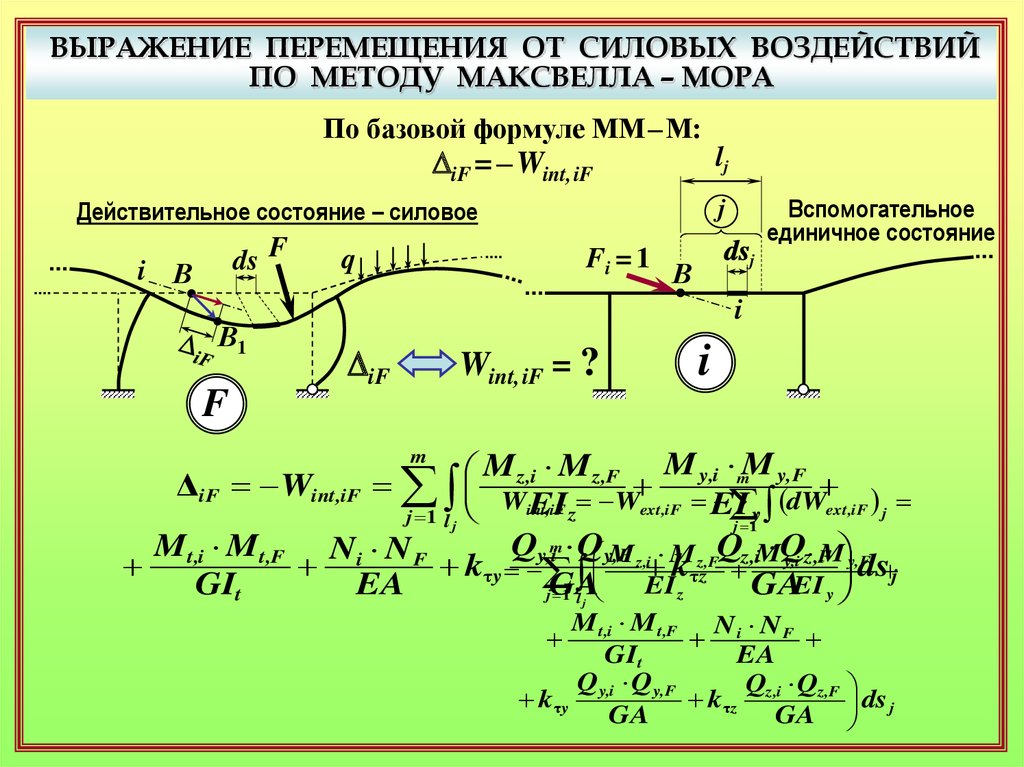
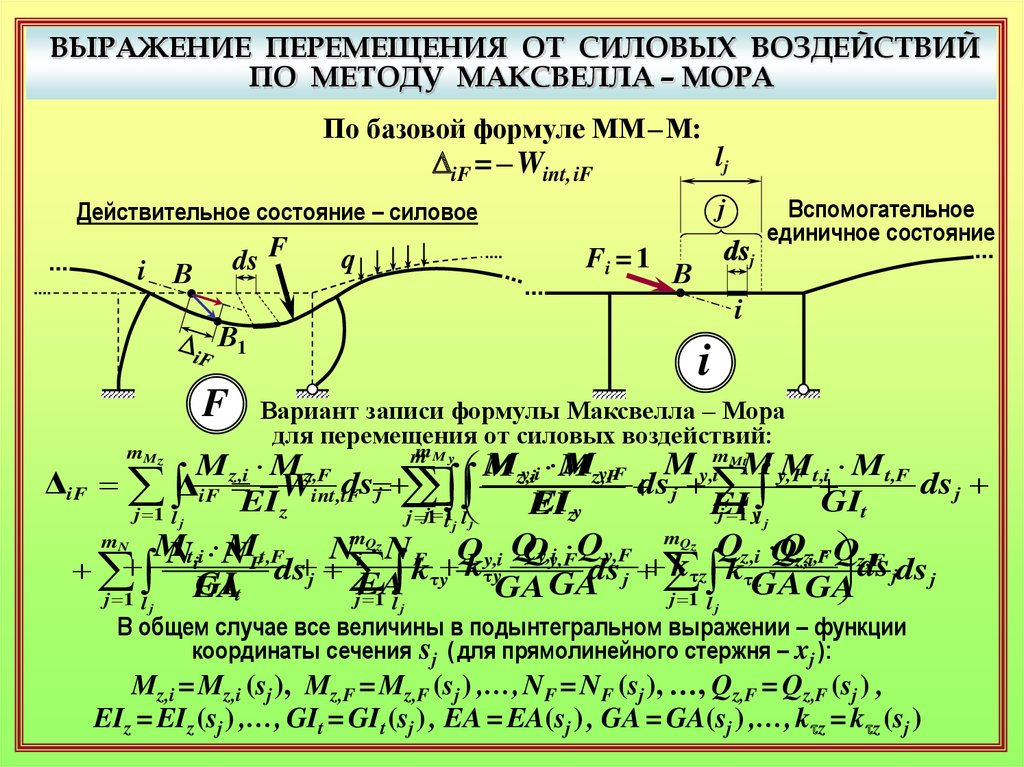
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
DiF = – Wint, iF
lj
Действительное состояние – силовое
ds F
i В
В1
j
Fi = 1
q
dsj
В
Вспомогательное
единичное состояние
i
DiF
Wint, iF = ?
i
F
M z,i M z,F M y,i mM y,F
ΔiF Wint,iF W
(
W
dW
EI
EI
int,iF
ext,iF
ext,iF j
z
y
j 1 l j
j 1
Qy,im Q y,MF z,i M z,FQz,iM Q
Mt,i Mt,F N i N F
F
kτy kτz y,i z, FM y,ds
j
EI
EI
GIt
EA
GA
GA
z
y
j 1 l
m
j
M t,i M t,F N i N F
GIt
EA
Q Q y,F
Q Q
kτy y,i
kτz z,i z,F ds j
GA
GA
23.
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
DiF = – Wint, iF
lj
Действительное состояние – силовое
ds F
i В
Fi = 1
q
dsj
В
Вспомогательное
единичное состояние
i
В1
F
j
i
Вариант записи формулы Максвелла – Мора
для перемещения от силовых воздействий:
m My
Mz,y,FF M y,im MtM y,M
M z,i M z,F
M z,iy,i M
F t,i Mt,F
ΔiF ΔiF Wint,iF
ds
ds
ds j
j
j
EI
EI
GI
EIzy
EI
z
t
j 1 l j
j 1 yl j
j j1 1
l j l j
mQz
mQz
mN M M
Q
Q
Qz,i Q
Qz,iz,F Q
N
N
Q
Q
z,ds
y,i
y,
F
t,i
t,
F
N
N
i
F
y,i
y,F
F
i
F
k
k
GI ds j
k
ds
k
τ
y
τ
z
jds j
τ
y
j
τ
z
EA
GA
GA
EA
GA
GA
t
j 1 l
j 1 l
j 1 l
mM z
j
m
j
j
В общем случае все величины в подынтегральном выражении – функции
координаты сечения sj ( для прямолинейного стержня – xj ):
Mz,i = Mz,i (sj ), Mz,F = Mz,F (sj ) ,…, NF = NF (sj ), …, Qz,F = Qz,F (sj ) ,
EIz = EIz (sj ) ,…, GIt = GIt (sj ) , EA = EA(sj ) , GA = GA(sj ) ,…, ktz = ktz (sj )
24.
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
DiF = – Wint, iF
lj
Действительное состояние – силовое
ds F
i В
j
Fi = 1
q
В
i
В1
F
dsj
Вспомогательное
единичное состояние
i
Вариант записи формулы Максвелла – Мора
для перемещения от силовых воздействий:
mM t
My
M y,i M y,F
M z,i M z,F
Mt,i Mt,F
ΔiF
ds j
ds j
ds j
EI
EI
GI
Изгиб
z Изгиб
y
t Кручение
j 1 l j
j 1 l j
j 1 l j
m
mQz
Qy
mN
Qy,i Qy,F
Qz,i Qz,F
Ni NF
ds j kτy
ds j kτz
ds j
EA
GA
GAu
j 1 l
j 1 l Сдвиг
j 1 l Сдвиг
m
mM z
j
Растяжение/сжатие
j
j
Учёт деформируемых ( нежёстких ) упругоподатливых связей в системе:
Rj
cD
Rj
cq
cq
Жёсткости линейных и угловых упругих связей
Закон Гука для
упругих связей:
Rj = cj * Dj
j 1
Rj,i Rj,F
cj
u – суммарное число
внешних и внутренних
упругих связей
25.
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
По базовой формуле ММ–М:
DiF = – Wint, iF
lj
Действительное состояние – силовое
ds F
i В
j
Fi = 1
q
В
i
В1
F
dsj
Вспомогательное
единичное состояние
i
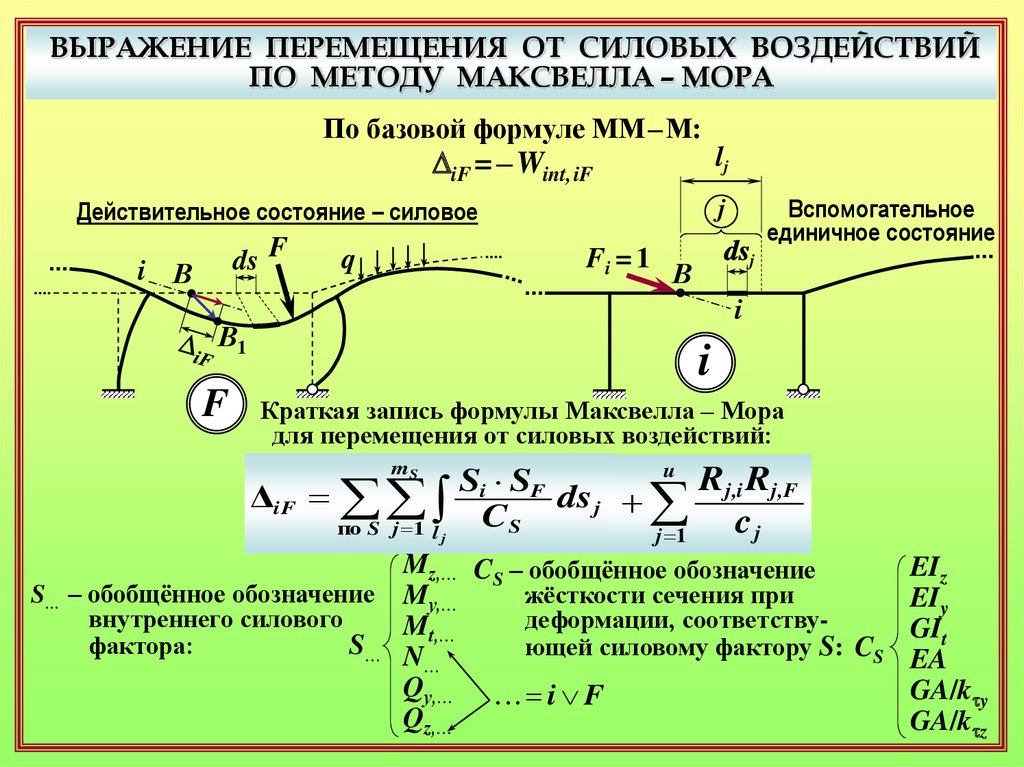
Краткая запись формулы Максвелла – Мора
для перемещения от силовых воздействий:
ΔiF
mS
по S j 1 l j
S… – обобщённое обозначение
внутреннего силового
фактора:
S…
Si SF
ds j
CS
u
Rj,i Rj,F
cj
j 1
Mz,… CS – обобщённое обозначение
жёсткости сечения при
My,…
деформации, соответствуMt,…
ющей силовому фактору S: CS
N…
Qy,… i F
Qz,…
EIz
EIy
GIt
EA
GA/kty
GA/ktz
26.
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
Приложение
К вопросу об учёте деформации сдвига при определении перемещений
1. Формула для коэффициента kt
Формула выводится путём сопоставления выражений
возможных
работ
по двум расчётным моделям элемента ds:
а) с фактическими касательными напряжениями
б) с обобщёнными силами ( поперечными
ti (y) в концевых сечениях элемента ds во вспосилами Qi ) в концевых сечениях элемогательном i-ом единичном состоянии и факмента ds в i-ом единичном состоянии
тическими деформациями сдвига gF (y) в дейсти соответствующими обобщёнными
вительном состоянии:
перемещениями ( абсолютным сдвигом
b( y)
dvF ) в действительном состоянии:
Q S ( y)
ds
tF ( y)
F
z
h
i
τi ( y)
y
γ F ( y)
dy
y
i
z
ds
b( y) Iz
Qi
y
i
τF ( y) QF Sz ( y)
G
G b ( y) Iz
По закону
Гука
при сдвиге
QF
F
dV
kτ A2
(a)
dWext,iF
τi ( y) γF ( y) b( y) ds dy I z
h
Sz ( y) 2 dy
b( y)
SzF( y) Sz ( y) 2
Qi Sz ( y) QF Sz (( ya )) Qi QF Qi Q
ds 2 ds dy
ds
dWext,iF
b( y) dy
dy
2
b
(
y
)
b
(
y
)
I
Gb
(
y
)
I
b
(
y
)
GI
GI
z
z
z
z
h
h
h
h
2
Qi
τ
Q
γ0,F 0,F F kτ
G
GA
dvF = g0,F * ds
QF
(б)
dWext,iF
Qi dvF Qi γ0,F ds
Q QF F
(б)
dWext,iF
Qii Q
k ds
GAGA τk τ ds
27.
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
Приложение
К вопросу об учёте деформации сдвига при определении перемещений
1. Формула для коэффициента kt
Формула выводится путем сопоставления выражений
возможных
работ
по двум расчётным моделям элемента ds:
а) с фактическими касательными напряжениями
б) с обобщёнными силами ( поперечными
ti (y) в концевых сечениях элемента ds во вспосилами Qi ) в концевых сечениях элемогательном i-ом единичном состоянии и факмента ds в i-ом единичном состоянии
тическими деформациями сдвига gF (y) в дейсти соответствующими обобщёнными
вительном состоянии: ё
перемещениями ( абсолютным сдвигом
b( y)
dvF ) в действительном состоянии:
Q S ( y)
ds
tF ( y)
F
z
h
i
τi ( y)
y
γ F ( y)
dy
y
i
z
ds
b( y) Iz
y
Qi
i
τF ( y) QF Sz ( y)
G
G b ( y) Iz
По закону
Гука
при сдвиге
QF
Qi
τ
Q
γ0,F 0,F F kτ
G
GA
F
S ( y) dy
kτ A2 z
Iz h b( y)
2
Значения коэффициента kt для некоторых видов сечений:
kt = 6/5
kt = 10/9
kt A/Aw
dvF = g0,F * ds
QF
28.
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙПО МЕТОДУ МАКСВЕЛЛА – МОРА
Приложение
К вопросу об учёте деформации сдвига при определении перемещений
2. Оценка влияния сдвига на перемещения от силовых воздействий
Составляющая перемещения DiF , обусловленная деформацией сдвига, – DiF,Q ;
в отношении к составляющей DiF,M от изгиба: DiF,Q /DiF,M = aQ
Для j-го участка / элемента постоянного сечения:
2
2
E
h
α j kτ( j) α(r j) j β(Sj) ,
Gj
lj
( j)
Q
где α(r j) rj / hj < 0,5 – относительный радиус инерции сечения; β(Sj)
l j2 Qi QF ds j
lj
M M
i
F
lj
Признаки необходимости учёта деформации сдвига
при определении перемещений стержневых систем:
сечение – тонкостенное ( kt > 2 );
материал – относительно низкомодульный при сдвиге ( E/G > 3…4 );
элемент достаточно массивный, «короткий» ( h/l > 1/8 );
нагрузки таковы, что вызывают значительные поперечные силы
при сравнительно небольших изгибающих моментах
( ориентировочно: средние на грузовом участке | M/Q | < ~ h ).
Подробнее см.: Себешев В.Г. Особенности работы статически неопределимых систем
и регулирование усилий в конструкциях: Учебное пособие. –
Новосибирск: НГАСУ, 2009. – 164 с.
ds j
29.
Контрольныевопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 29» )
1. Как в общем виде обозначаются перемещения? Какой смысл имеют индексы в этом
обозначении? ( 2 )
2. Что такое собственное перемещение? ( 2 )
3. Какие индексы используются для обозначения перемещений от силовых,
температурных, кинематических и комбинированных воздействий? ( 3 )
4. Какие перемещения называются единичными? ( 4 )
4. Какова основная идея метода Максвелла – Мора определения перемещений
деформируемых систем? Почему этот метод также называется методом единичных
вспомогательных нагрузок? ( 5 )
5. Правило задания вспомогательного единичного воздействия. Каков кинематический
смысл этого воздействия? ( 6 )
6. Типовые случаи вспомогательных единичных состояний в методе Максвелла – Мора.
(7)
7. Какой принцип механики лежит в основе метода Максвелла – Мора? ( 8 )
8. Через какие величины выражается искомое перемещение по базовой формуле метода
Максвелла – Мора? ( 8 )
9. Что такое возможная работа внешних или внутренних сил? ( 9 )
10. Какая работа внешних или внутренних сил называется действительной? ( 9 )
11. Что называется потенциальной энергией деформации системы? ( 9 )
12. Как связаны возможные работы внешних и внутренних сил ( 10 ) , их действительные
работы и потенциальная энергия упругой деформации (ПЭУД)? ( 12 )
_____________________________________________________
*) Только в режиме «Показ слайдов»
30.
Контрольныевопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
13. Как выражаются возможные и действительные работы внешних и внутренних сил
и ПЭУД через обобщённые нагрузки и обобщённые перемещения? Частный случай –
линейно деформируемые системы ( теорема Клапейрона ). ( 10 – 12 )
14. Какой приём используется для получения выражения возможной работы через
внутренние силовые факторы? ( 16 )
15. Как деформации действительного силового состояния выражаются через внутренние
силовые факторы? ( 18 )
16. Каков смысл величин EI, EA, GIt , GA/kt , входящих в формулу Максвелла – Мора? ( 18 )
17. Варианты развёрнутой записи формулы Максвелла – Мора для перемещения
от силовых воздействий. ( 22, 23 )
18. Какими слагаемыми в формуле Максвелла – Мора учитываются разные виды упругих
деформаций элементов ( изгиб, растяжение/сжатие, сдвиг, кручение )? ( 24 )
19. Что учитывает коэффициент kt в слагаемом формулы Максвелла – Мора, отражающем
влияние сдвига? ( 18 ) ( 27 )
20. Как учитываются в формуле Максвелла – Мора деформации упругоподатливых связей
системы? ( 24 )
21. Краткая обобщённая запись формулы Максвелла – Мора для перемещения от силового
воздействия. ( 25 )
22. Какие величины обобщённо обозначаются как Si и SF в краткой записи формулы
Максвелла – Мора? То же, СS? ( 25 )
_____________________________________________________
*) Только в режиме «Показ слайдов»




















 physics
physics mechanics
mechanics








