Similar presentations:
Строительная механика. Статически неопределимые системы
1.
СТРОИТЕЛЬНАЯ МЕХАНИКАЧасть II
СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ
СИСТЕМЫ
Расчёт СНС
смешанным методом
2.
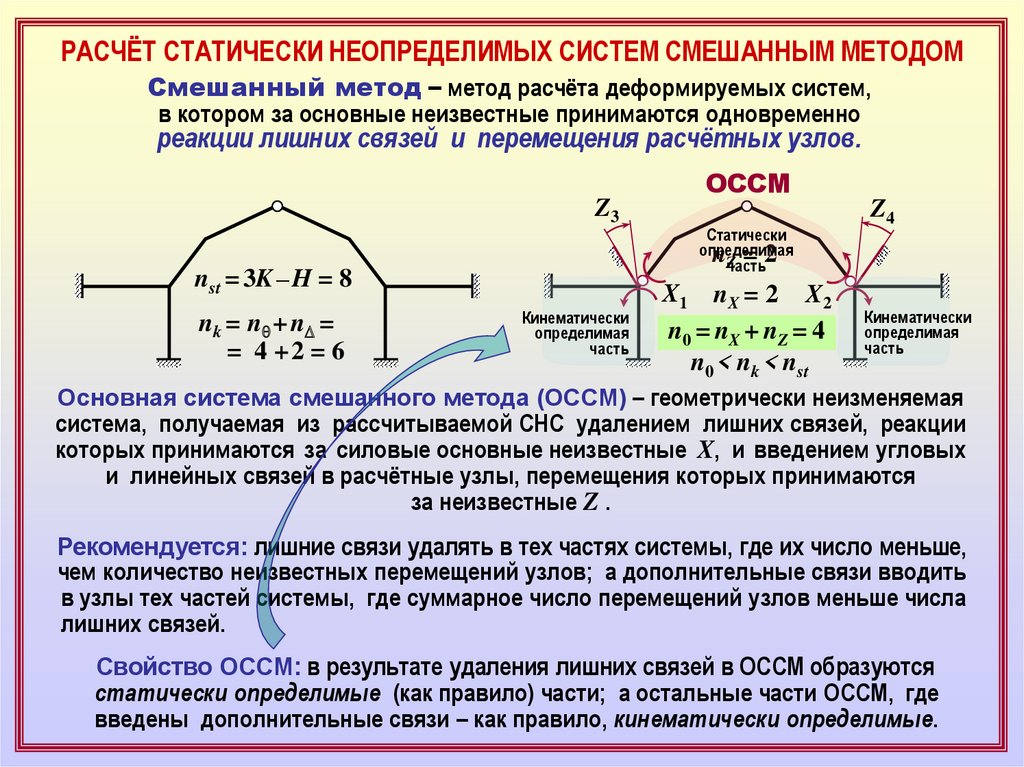
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМСмешанный метод – метод расчёта деформируемых систем,
в котором за основные неизвестные принимаются одновременно
реакции лишних связей и перемещения расчётных узлов.
ОССМ
Z3
nst = 3K – H = 8
Статически
определимая
nZчасть
=2
Z4
X1 nX = 2 X2
Кинематически
nk = nq + nD =
определимая
n0 = nX + nZ = 4
часть
= 4 +2 = 6
n0 < nk < nst
Основная система смешанного метода (ОССМ) – геометрически неизменяемая
система, получаемая из рассчитываемой СНС удалением лишних связей, реакции
которых принимаются за силовые основные неизвестные X, и введением угловых
и линейных связей в расчётные узлы, перемещения которых принимаются
за неизвестные Z .
Кинематически
определимая
часть
Рекомендуется: лишние связи удалять в тех частях системы, где их число меньше,
чем количество неизвестных перемещений узлов; а дополнительные связи вводить
в узлы тех частей системы, где суммарное число перемещений узлов меньше числа
лишних связей.
Свойство ОССМ: в результате удаления лишних связей в ОССМ образуются
статически определимые (как правило) части; а остальные части ОССМ, где
введены дополнительные связи – как правило, кинематически определимые.
3.
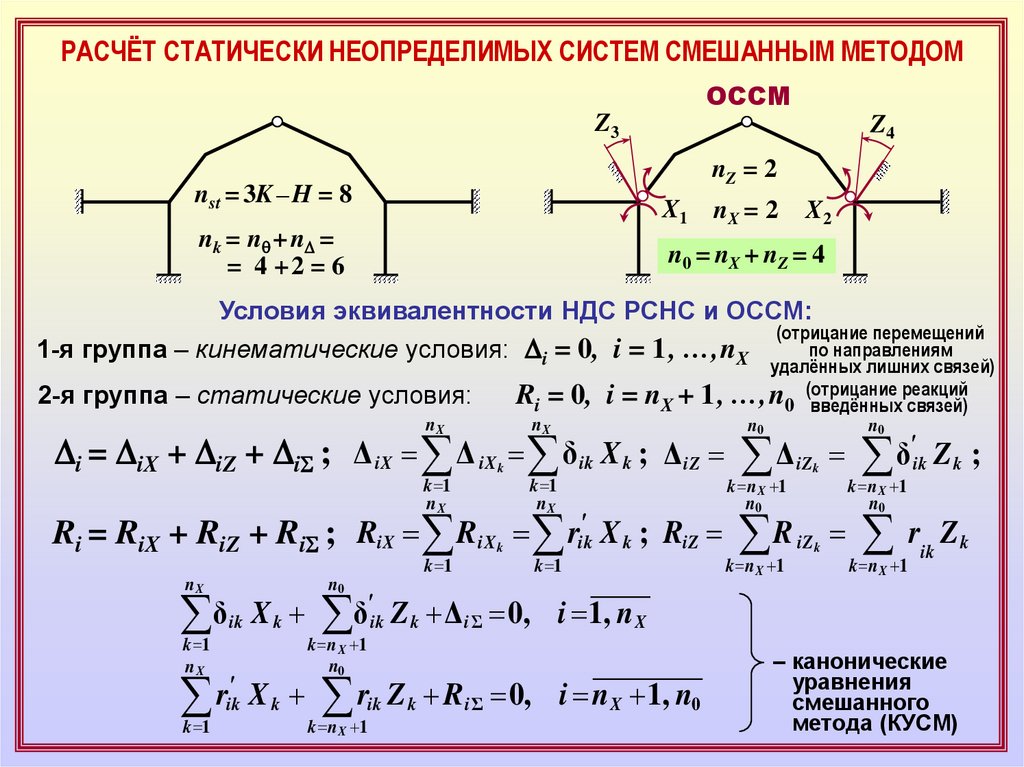
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМОССМ
Z3
Z4
nZ = 2
nst = 3K – H = 8
X1
nk = nq + nD =
= 4 +2 = 6
nX = 2
X2
n0 = nX + nZ = 4
Условия эквивалентности НДС РСНС и ОССМ:
(отрицание перемещений
по направлениям
1-я группа – кинематические условия: Di = 0, i = 1, …,nX
2-я группа – статические условия:
Ri = 0, i =
nX
удалённых лишних связей)
реакций
nX + 1, …,n0 (отрицание
введённых связей)
nX
Di = DiX + DiZ + DiS ; Δ iX Δ iX δ ik X k ; Δ iZ
k 1
nX
k
k 1
nX
Ri = RiX + RiZ + RiS ; RiX RiX rik' X k ; RiZ
k 1
nX
δ
k 1
nX
ik
Xk
'
r
ik
Xk
k 1
n0
δ'
k n X 1
n0
r
ik
ik
k n X 1
k
k 1
n0
Δ
iZ k
R
iZ k
k n X 1
n0
k n X 1
n0
δ'
k n X 1
n0
k n X 1
ik
Zk ;
rik Z k
Z k Δ i Σ 0, i 1, n X
Z k R i Σ 0, i n X 1, n0
– канонические
уравнения
смешанного
метода (КУСМ)
4.
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМδ12 X 2 ...
δ1nX X nX δ'1, nX 1 Z nX 1
δ'1,n X 2 Z nX 2 ...
δ'1n0 Z n0
Δ1Σ 0 ,
δ 21 X 1
δ 22 X 2 ...
δ 2 nX X nX δ'2, nX 1 Z nX 1
δ'2, nX 2 Z n X 2 ...
δ'2 n0 Z n0
Δ 2Σ 0 ,
δ nX 1 X 1 δ nX 2 X 2 ... δ n X nX X n X δ'nX , nX 1 Z n X 1 δ'n X , nX 1 Z nX 2 ... δ'nX n0 Z n0
Δ nX Σ 0 ,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
rn' X 1,1 X 1 rn' X 1, 2 X 2 ... rn' X 1, nX X nX rnX 1, nX 1 Z nX 1 rnX 1, nX 2 Z n X 2 ... rnX 1, n0 Z n0 RnX 1, Σ 0 ,
rn' X 2,1 X 1 rn' X 2, 2 X 2 ... rn' X 2, nX X nX rnX 2, nX 1 Z nX 1 rnX 2, nX 2 Z nX 2 ... rnX 2, n0 Z n0 RnX 2, Σ 0 ,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
rn' 0 1 X 1
rn' 0 2 X 2 ...
rn' 0 nX X n X rn0 , nX 1 Z nX 1 rn0 , nX 2 Z nX 2 ...
rn0 n0 Z n0
Rn0 Σ 0 .
2-я группа
уравнений
δ11 X 1
1-я группа
уравнений
Система канонических уравнений смешанного метода:
nZ
nX
В матричной форме:
δ11
δ12
δ 22
δ 21
. . . . .
δ
δ nX 2
nX 1
rn' 1, 1 rn' 1, 2
X
X
rn' X 2, 1 rn' X 2, 2
. . . . .
rn' 1
rn' 0 2
0
nX
A
Y
B
XZ
S
δ'1, n X 2 δ'1n0 X 1 Δ1Σ
'
δ 2nX
δ'2, n X 1 δ'2, n X 2 δ'2 n0 X 2 Δ 2Σ δ XX δ XZ X Δ Σ 0
B = 0
. . . . . . . . . . . . . . . . r'AXZr * Y +
ZX ZZ Z S RΣ
δ n X n X δ'n X , n X 1 δ'n X , n X 1 δ'n X n0
X nX Δ nX Σ
0
rn' X 1, n X rn X 1, n X 1 rn X 1, n X 2 rn X 1, n0 Z n X 1 Rn X 1, Σ
'
rn X 2, n X rn X 2, n X 1 rn X 2, n X 2 rn X 2, n0 Z n X 2 Rn X 2, Σ
. . . . . . . . . . . . . . . .
rn' 0 n X
rn0 , n X 1 rn0 , n X 2 rn0 n0 Z n0 Rn0 Σ
δ1 n X
δ'1, n X 1
nZ
5.
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМПеремещения в ОССМ по направлениям силовых основных неизвестных X
– от единичных перемещений Z = 1
– от единичных сил X = 1
δ11
δ
δ XX 21
(nX nX )
δ n X 1
δ12
δ 22
δ nX 2
δ1n X dii > 0
δ'1, n X 1 δ'1, n X 2
'
δ'
δ 2 n X dik = dki
δ
'
2, n X 1
2, n X 2
δ XZ
Вычисление dik – методом (nX nZ ) '
'
δ n X n X Максвелла – Мора
δ n X , n X 1 δ n X , n X 2
δ'ik rki'
δ'1, n0
'
т
δ'2, n0 δ'XZ (rZX
)
'
Вычисление δik –
'
δ n X , n0 только через
r'
ki
Реакции введенных связей в расчётных узлах ОССМ
– от единичных сил X = 1
– от единичных перемещений Z = 1
'
'
nZ
nX
rn' X 1, 1 rn' X 1, 2
'
r '
'
n X 2, 1 rn X 2, 2
rZX
(nZ nX )
'
'
rn0 , 1 rn0 , 2
δ11
δ12
δ 22
δ 21
δ
δ nX 2
nX 1
rn' 1, 1 rn' 1, 2
X
X
rn' X 2, 1 rn' X 2, 2
rn' 1
rn' 0 2
0
nX
rik δki
rn' X 1, n X
'
'
т
rn' X 2, n X rZX (δ XZ )
'
Вычисление rik –
или
rn' 0 , n X статическим
кинематическим
способами
δ1 n X
δ
δ 2nX
δ'2, n X 1
δ nX nX
δ'n X , n X 1
'
1, n X 1
rn' X 1, n X rn X 1, n X 1
rn' X 2, n X rn X 2, n X 1
r
'
n0 n X
rn0 , n X 1
rn X 1, n X 1 rn X 1, n X 2
r
r
rZZ n X 2, n X 1 n X 2, n X 2
(nZ nZ )
rn0 , n X 1 rn0 , n X 2
rn X 1, n0 rii > 0
rn X 2, n0 rik = rki
Вычисление rik –
rn0 n0 статическим или
кинематическим
δ'1, n X 2 δ'1n0 X 1 Δ1Σ
δ'2, n X 2 δ'2 n0 X 2 Δ 2Σ
δ'n X , n X 1 δ'n X n0 X Δ
nX nX Σ
0
rn X 1, n X 2 rn X 1, n0 Z n X 1 Rn X 1, Σ
rn X 2, n X 2 rn X 2, n0 Z n X 2 Rn X 2, Σ
rn0 , n X 2 rn0 n0 Z n0 Rn0 Σ
nZ
способами
AXZ * Y + BS = 0
δ XX δ'XZ X Δ Σ
0
'
rZX
rZZ Z RΣ
1
Y AXZ
BΣ
nX
S Sk X k
n0 k 1
S Z
k nX 1
k
k
SΣ
6.
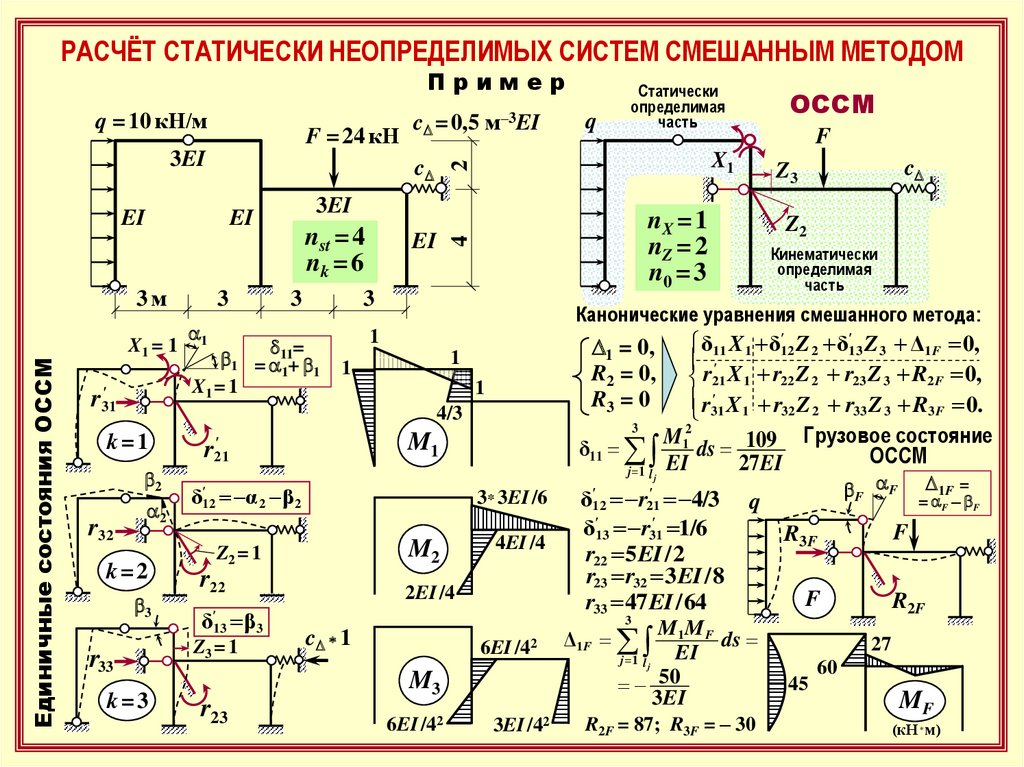
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМПример
q = 10 кН/м
F = 24 кН
3EI
Единичные состояния ОССМ
X1 = 1
'
r31
3
b1
X1 = 1
3
3
d11=
= a1+ b1
b2
a2
k=2
b3
r33
k=3
M1
δ'12 α 2 β 2
δ β3
'
13
Z3 = 1
3* 3EI /6
M2
4EI /4
2EI /4
'
δ'12 r21
4/3
'
δ'13 r31
1/6
r22 5EI / 2
r23 r32 3EI / 8
r33 47 EI / 64
b F aF
q
cD * 1
6EI /42
F
6EI /42
3EI /42
Δ1F
M1 M F
ds
EI
j 1 l j
50
3 EI
R2F = 87; R3F = – 30
D1F =
= aF – bF
F
R3F
R2F
3
M3
r23
Кинематически
определимая
часть
δ11 X 1 δ'12 Z 2 δ'13 Z 3 Δ1F 0,
'
r21 X 1 r22 Z 2 r23 Z 3 R2 F 0,
'
r31
X 1 r32 Z 2 r33 Z 3 R3 F 0.
3
Грузовое состояние
M12
δ11
ds 109
ОССМ
27 EI
j 1 l j EI
1
r22
Z2
D1 = 0,
R2 = 0,
R3 = 0
1
1
Z2 = 1
cD
Z3
Канонические уравнения cмешанного метода:
1
'
r21
F
nX = 1
nZ = 2
n0 = 3
4
EI
4/3
k=1
r32
nst = 4
nk = 6
ОССМ
X1
3EI
EI
a1
q
2
cD
EI
3м
cD = 0,5 м–3EI
Статически
определимая
часть
27
45
60
MF
(кН * м)
7.
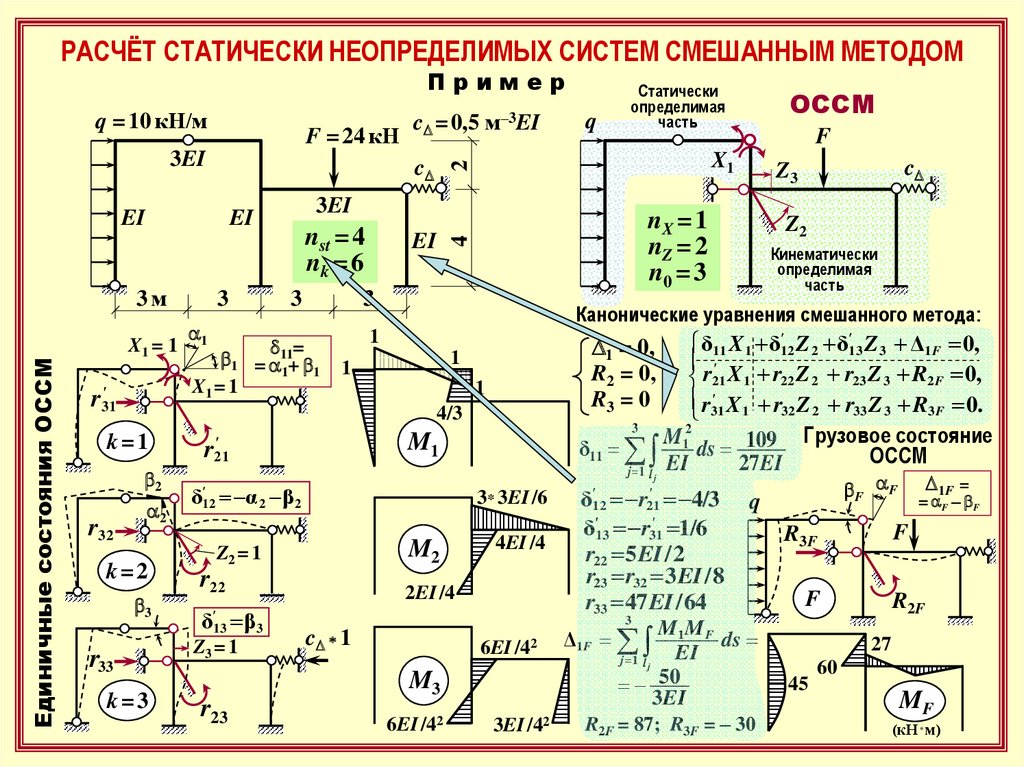
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМПример
q = 10 кН/м
F = 24 кН
3EI
Единичные состояния ОССМ
X1 = 1
'
r31
3
b1
X1 = 1
3
3
d11=
= a1+ b1
b2
a2
k=2
b3
r33
k=3
M1
δ'12 α 2 β 2
δ β3
'
13
Z3 = 1
3* 3EI /6
M2
4EI /4
2EI /4
'
δ'12 r21
4/3
'
δ'13 r31
1/6
r22 5EI / 2
r23 r32 3EI / 8
r33 47 EI / 64
b F aF
q
cD * 1
6EI /42
F
6EI /42
3EI /42
Δ1F
M1 M F
ds
EI
j 1 l j
50
3 EI
R2F = 87; R3F = – 30
D1F =
= aF – bF
F
R3F
R2F
3
M3
r23
Кинематически
определимая
часть
δ11 X 1 δ'12 Z 2 δ'13 Z 3 Δ1F 0,
'
r21 X 1 r22 Z 2 r23 Z 3 R2 F 0,
'
r31
X 1 r32 Z 2 r33 Z 3 R3 F 0.
3
Грузовое состояние
M12
δ11
ds 109
ОССМ
27 EI
j 1 l j EI
1
r22
Z2
D1 = 0,
R2 = 0,
R3 = 0
1
1
Z2 = 1
cD
Z3
Канонические уравнения cмешанного метода:
1
'
r21
F
nX = 1
nZ = 2
n0 = 3
4
EI
4/3
k=1
r32
nst = 4
nk = 6
ОССМ
X1
3EI
EI
a1
q
2
cD
EI
3м
cD = 0,5 м–3EI
Статически
определимая
часть
27
45
60
MF
(кН * м)
8.
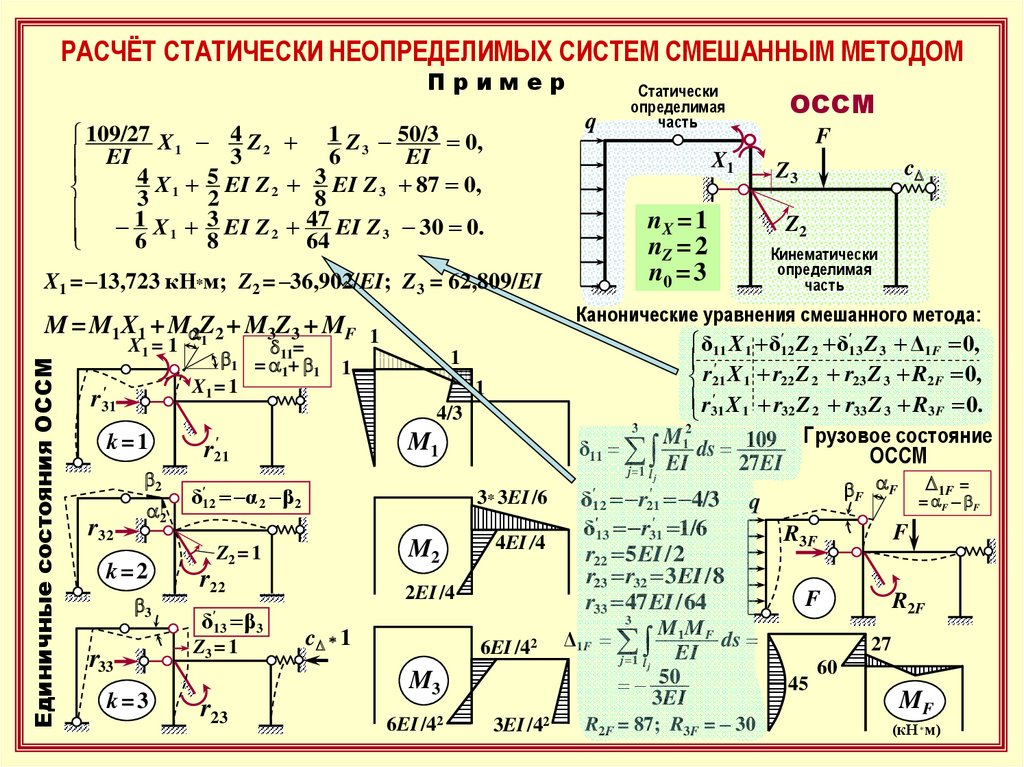
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМПример
q
109/27 X 1 4 Z 2 1 Z 3 50/3 0,
3
6
EI
EI
4 X 5 EI Z 3 EI Z 87 0,
2
3
3 1 2
8
1 X 1 3 EI Z 2 47 EI Z 3 30 0.
6
8
64
Статически
определимая
часть
Единичные состояния ОССМ
X1 = 1
'
r31
nX = 1
nZ = 2
n0 = 3
b2
a2
k=2
1
1
b3
r33
k=3
M1
δ'12 α 2 β 2
3* 3EI /6
M2
Z2 = 1
r22
δ β3
'
13
Z3 = 1
4EI /4
2EI /4
Кинематически
определимая
часть
'
δ'12 r21
4/3
'
δ'13 r31
1/6
r22 5EI / 2
r23 r32 3EI / 8
r33 47 EI / 64
b F aF
q
cD * 1
6EI /42
F
6EI /42
3EI /42
Δ1F
M1 M F
ds
EI
j 1 l j
50
3 EI
R2F = 87; R3F = – 30
D1F =
= aF – bF
F
R3F
R2F
3
M3
r23
Z2
δ11 X 1 δ'12 Z 2 δ'13 Z 3 Δ1F 0,
'
r21 X 1 r22 Z 2 r23 Z 3 R2 F 0,
'
r31
X 1 r32 Z 2 r33 Z 3 R3 F 0.
3
Грузовое состояние
M12
δ11
ds 109
ОССМ
27 EI
j 1 l j EI
1
1
'
r21
cD
Z3
Канонические уравнения cмешанного метода:
4/3
k=1
r32
b1
X1 = 1
d11=
= a1+ b1
F
X1
X1 = –13,723 кН*м; Z2 = –36,902/EI; Z3 = 62,809/EI
M = M1X1 + Ma2Z
+ M3Z3 + MF
1 2
ОССМ
27
45
60
MF
(кН * м)
9.
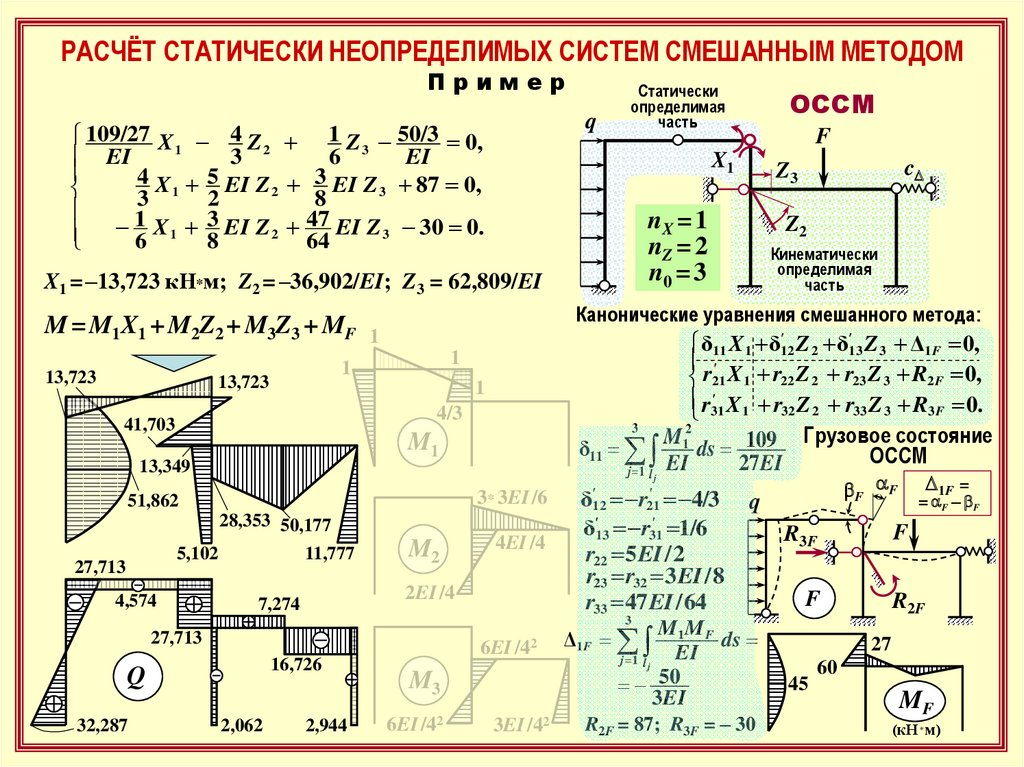
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ СМЕШАННЫМ МЕТОДОМПример
q
109/27 X 1 4 Z 2 1 Z 3 50/3 0,
3
6
EI
EI
4 X 5 EI Z 3 EI Z 87 0,
2
3
3 1 2
8
1 X 1 3 EI Z 2 47 EI Z 3 30 0.
6
8
64
Статически
определимая
часть
13,723
nX = 1
nZ = 2
n0 = 3
1
4/3
M1
13,349
3* 3EI /6
51,862
28,353 50,177
5,102
27,713
4,574
11,777
M2
4EI /4
2EI /4
7,274
Z2
Кинематически
определимая
часть
δ11 X 1 δ'12 Z 2 δ'13 Z 3 Δ1F 0,
'
r21 X 1 r22 Z 2 r23 Z 3 R2 F 0,
'
r31
X 1 r32 Z 2 r33 Z 3 R3 F 0.
3
Грузовое состояние
M12
δ11
ds 109
ОССМ
27 EI
j 1 l j EI
1
1
41,703
cD
Z3
Канонические уравнения cмешанного метода:
1
13,723
F
X1
X1 = –13,723 кН*м; Z2 = –36,902/EI; Z3 = 62,809/EI
M = M1X1 + M2Z2 + M3Z3 + MF
ОССМ
'
δ'12 r21
4/3
'
δ'13 r31
1/6
r22 5EI / 2
r23 r32 3EI / 8
r33 47 EI / 64
b F aF
q
F
R3F
F
R2F
3
27,713
16,726
Q
32,287
2,062
2,944
6EI /42
M3
6EI /42
3EI /42
Δ1F
M1 M F
ds
EI
j 1 l j
50
3 EI
R2F = 87; R3F = – 30
D1F =
= aF – bF
27
45
60
MF
(кН * м)
10.
nZnX
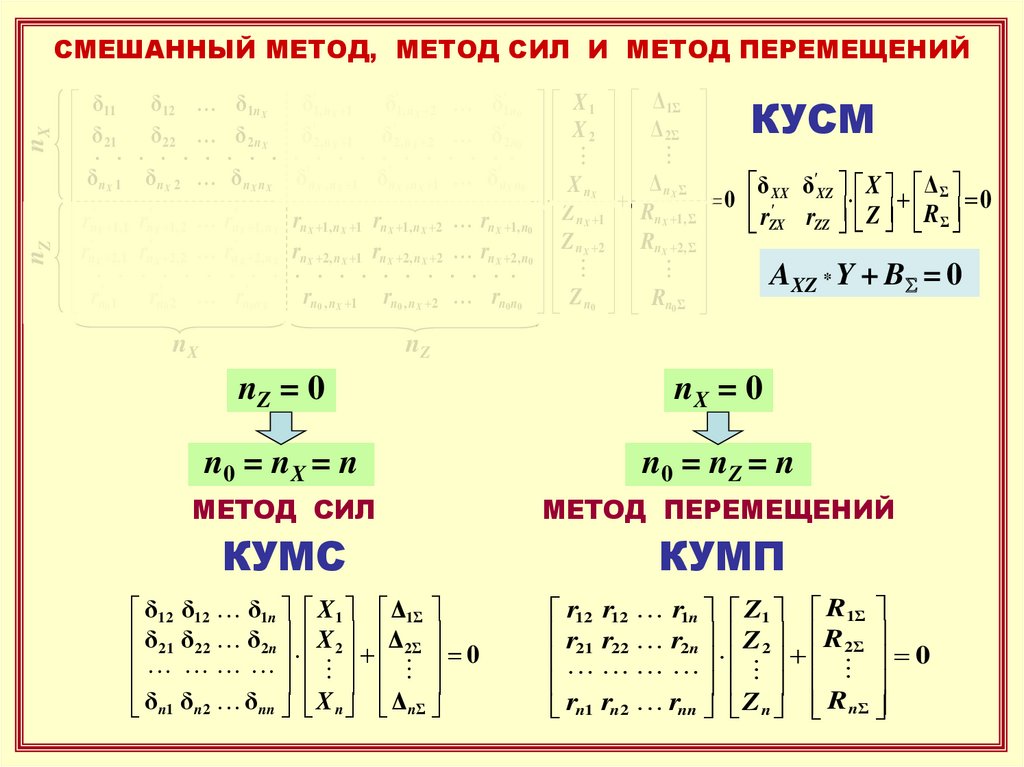
СМЕШАННЫЙ МЕТОД, МЕТОД СИЛ И МЕТОД ПЕРЕМЕЩЕНИЙ
δ11
δ
. 21.
δ nX 1
rn' X 1,1
r'
nX. 2,.1
r'
n0 1
δ'1, nX 2 δ'1n0 X 1 Δ1Σ
δ'2, nX 2 δ'2 n0 X 2 Δ 2Σ
. . . . . . . . . . . . . .
'
δ nX nX δ'nX , nX 1 δ'nX , nX 1 δ'nX n0 X n Δ n Σ
X X 0 δ 'XX δ XZ X Δ Σ 0
rZX rZZ Z R Σ
rn' X 1, nX rnX 1, nX 1 rnX 1, nX 2 rnX 1, n0 Z nX 1 RnX 1, Σ
rn' X 2, nX rnX 2, nX 1 rnX 2, nX 2 rnX 2, n0 Z nX 2 RnX 2, Σ
. . . . . . . . . . . . . .
AXZ * Y + BS = 0
rn' 0nX
rn0 , nX 1 rn0 , nX 2 rn0n0 Z n0 Rn0 Σ
δ12 δ1nX
δ 22 δ 2 nX
. . . .
δ nX 2
rn' X 1, 2
rn' X 2, 2
. . . .
rn' 0 2
КУСМ
δ'1, nX 1
δ'2, nX 1
nX
nZ
nZ = 0
nX = 0
n0 = nX = n
n0 = nZ = n
МЕТОД СИЛ
МЕТОД ПЕРЕМЕЩЕНИЙ
КУМС
КУМП
δ12 δ12 δ1n X 1 Δ1Σ
δ21 δ22 δ2n X 2 Δ2Σ
0
δ
δ
δ
X
Δ
nn n
n1 n2
nΣ
r12 r12 r1n Z1 R1Σ
r21 r22 r2n Z 2 R 2Σ
0
R
r
r
r
Z
nn n
n1 n2
nΣ
11.
nZnX
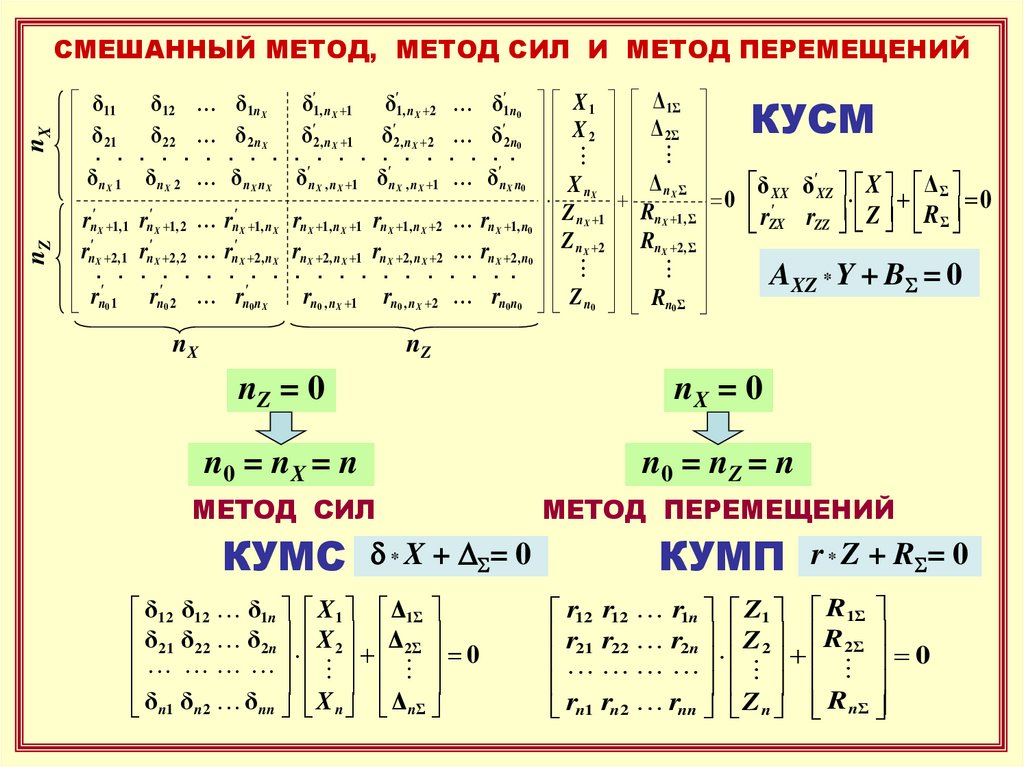
СМЕШАННЫЙ МЕТОД, МЕТОД СИЛ И МЕТОД ПЕРЕМЕЩЕНИЙ
δ11
δ
. 21 .
δ nX 1
rn' X 1,1
r'
nX. 2,.1
r'
n0 1
δ'1, nX 2 δ'1n0 X 1 Δ1Σ
δ'2, nX 2 δ'2 n0 X 2 Δ 2Σ
. . . . . . . . . . . . . .
'
δ nX nX δ'nX , nX 1 δ'nX , nX 1 δ'nX n0 X n Δ n Σ
X X 0 δ 'XX δ XZ X Δ Σ 0
rZX rZZ Z R Σ
rn' X 1, nX rnX 1, nX 1 rnX 1, nX 2 rnX 1, n0 Z nX 1 RnX 1, Σ
rn' X 2, nX rnX 2, nX 1 rnX 2, nX 2 rnX 2, n0 Z nX 2 RnX 2, Σ
. . . . . . . . . . . . . .
AXZ * Y + BS = 0
rn' 0nX
rn0 , nX 1 rn0 , nX 2 rn0n0 Z n0 Rn0 Σ
δ12 δ1nX
δ 22 δ 2 nX
. . . .
δ nX 2
rn' X 1, 2
rn' X 2, 2
. . . .
rn' 0 2
КУСМ
δ'1, nX 1
δ'2, nX 1
nX
nZ
nZ = 0
nX = 0
n0 = nX = n
n0 = nZ = n
МЕТОД СИЛ
МЕТОД ПЕРЕМЕЩЕНИЙ
КУМС
КУМП
d * X + DS= 0
δ12 δ12 δ1n X 1 Δ1Σ
δ21 δ22 δ2n X 2 Δ2Σ
0
δ
δ
δ
X
Δ
nn n
n1 n2
nΣ
r * Z + RS= 0
r12 r12 r1n Z1 R1Σ
r21 r22 r2n Z 2 R 2Σ
0
R
r
r
r
Z
nn n
n1 n2
nΣ
12.
СМЕШАННЫЙ МЕТОД, МЕТОД СИЛ И МЕТОД ПЕРЕМЕЩЕНИЙР е з ю м е:
1. Канонические уравнения любого метода ( сил, перемещений или смешанного )
являются разрешающими уравнениями задачи расчёта заданной деформимой системы, т. е. синтезом статической, геометрической и физической
сторон задачи.
Метод
сил
перемещений
смешан-
ный
Место в канонических уравнениях, где реализованы стороны задачи
( непосредственно или опосредованно )
статическая
геометрическая
физическая
В использовании условий
равновесия для определения силовых факторов
в ОСМС от единичных
основных неизвестных
и от заданных нагрузок
В изначальном статическом смысле условий эквивалентности ОСМП и РДС
а) в изначальном статическом смысле условий
эквивалентности ОССМ и
РСНС ( 1-я группа КУСМ );
б) в использовании условий равновесия для определения силовых факторов
в статически определимых
частях ОССМ от единичных основных неизвестных
и от заданных нагрузок
В изначальном геометрическом
( кинематическом ) смысле условий эквивалентности ОСМС и
РСНС
В применении закона Гука
для определения методом
Максвелла–Мора перемещений dik и DiF и закона
линейного температурного расширения для Dit
В обеспечении совместности
перемещений ( деформаций )
ОСМП в единичных состояниях и от заданных воздействий,
а также в выполнении кинематических граничных условий
а) в изначальном геометрическом
( кинематическом ) смысле условий эквивалентности ОССМ
и РСНС ( 2-я группа КУСМ );
б) в обеспечении совместности
перемещений ( деформаций ) кинематически определимых частей ОССМ в единичных состояниях и от заданных воздействий,
а также в выполнении кинематических граничных условий
В стандартных задачах
для типовых элементов
ОСМП ( решения на основе закона Гука и закона
линейного температурного расширения )
а) в статически определимых частях ОССМ – как
в методе сил;
б) в кинематически определимых частях ОССМ –
как в методе перемещений
13.
СМЕШАННЫЙ МЕТОД, МЕТОД СИЛ И МЕТОД ПЕРЕМЕЩЕНИЙР е з ю м е:
2. При выборе метода расчёта деформируемой системы в случае равных
( или близких ) количеств основных неизвестных МС, МП и СМ предпочтение следует отдавать методу перемещений из-за
а) большей в сравнении с другими методами формализованностью его
расчётных процедур вследствие использования стандартных ( табличных ) данных;
б) более высокой информативности результатов расчёта: наряду с усилиями в рассчитываемой системе определяются также и перемещения
её узлов.
3. При равных количествах основных неизвестных МС и СМ рациональным
является смешанный метод, в котором часть процедур основана на использовании тех же табличных данных, что и в методе перемещений.
4. Самый универсальный – метод перемещений: с его помощью могут рассчитываться любые деформируемые системы – как статически неопределимые, так и статически определимые.
14.
Контрольные вопросы( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 14» )
1. Какие величины являются основными неизвестными смешанного метода (СМ)? ( 2 )
2. Как формируется основная система смешанного метода (ОССМ) и какими
соображениями следует при этом руководствоваться? ( 2 )
3. Какими свойствами должна обладать рационально выбранная ОССМ? ( 2 )
4. Из каких условий получаются канонические уравнения СМ? ( 3 )
5. Какие группы уравнений входят в систему КУСМ? ( 3 )
6. Какие различные по смыслу величины являются коэффициентами КУСМ (перечислить) ( 3 ) , ( 4 ) . Какие из них не имеют аналогов в коэффициентах КУМС и КУМП?
7. Раскрыть смысл
а) системы КУСМ в целом ( 3 ) ;
б) произвольного (i-го) уравнения 1-й и 2-й групп КУМС ( 3 ) ;
в) свободных членов уравнений DiS , RiS ( 3 ) ;
г) слагаемых dik Xk , δ'ik Z k , rik' X k , rik Zk ; ( 5 ) ;
д) коэффициентов dik , δ'ik , rik' , rik ( 5 ) .
8. Свойства и способы определения коэффициентов канонических уравнений СМ ( 5 ) .
9. Какие особенности имеет определение коэффициентов δ'ik ? ( 5 ) Теорема Гвоздева
о взаимности единичных перемещений и реакций.
*)
Только в режиме «Показ слайдов».
15.
Контрольные вопросы( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 15» )
10. Почему канонические уравнения смешанного метода являются разрешающими
уравнениями задачи расчёта СНС (синтезом статической, геометрической
и физической сторон задачи)? ( 12 )
11. Как по найденным основным неизвестным смешанного метода вычисляются
искомые усилия в заданной системе? ( 5 )
12. Взаимосвязь смешанного метода, метода сил и метода перемещений ( 10 ) .
13. Можно ли получить
а) канонические уравнения СМ формальным объединением КУМС и КУМП?
б) КУМС и КУМП из уравнений смешанного метода? ( 10 )
14. Сравнительная оценка возможностей и рациональности применения методов сил,
перемещений и смешанного ( 13 ) .
*)
Только в режиме «Показ слайдов».







 mathematics
mathematics mechanics
mechanics








