Similar presentations:
Статически неопределимые системы. Строительная механика
1.
© Себешев В.Г., 2022СТРОИТЕЛЬНАЯ МЕХАНИКА
Часть II
СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ
СИСТЕМЫ
Расчёт деформируемых систем
методом перемещений
2
2.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙОсновная система метода перемещений
– это, как правило, кинематически определимая система,
получаемая из заданной деформируемой системы
путём введения в расчётные узлы минимально необходимых
угловых и линейных связей по направлениям перемещений,
принимаемых за основные неизвестные.
ОСМП = РДC + ДСРУ + Z
Угловая
связь
Шарнирная система
Линейная
связь
EA
nс = 5
nD = 5
nk = 11
EA
nж.у. = 6
Z1 Z 2
ОСМП Z3
Z4
Z11
Z9
Z7
EA
Z8
Z5
Z6
Z10
3.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙОсновная система метода перемещений (ОСМП)
Вариативность ОСМП
а) за счёт различий в выборе направлений
и точек размещения линейных связей
*
б) при использовании или неучёте гипотезы l j l j
в) за счёт выбора расчётных узлов (дополнительные РУ)
Z2
Z1
Z2
Z1
Z2
Z2 Z1
Z1
l *j l j
l *j l j
а)
Z5
Дополнительные
расчётные узлы
Z4
Z2
б)
Z1
l l
l *j l j
Z3
*
j
j
( учёт продольных деформаций стержней )
в)
Z3
l *j l j
Z5
Z2 Z 1
Z6
Z4
l *j l j
4.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙОсновная система метода перемещений (ОСМП)
Заданная
система
nq = 2
nq = 12
EA
EA
EA
EA
nD = 4
nD = 11
nD = 4
nk = 11
nk = 6
nk = 16
( nst = 0 )
( nst = 2 )
( nst = 26 )
Основная
система
Шарнирная
система
nq = 0
5.
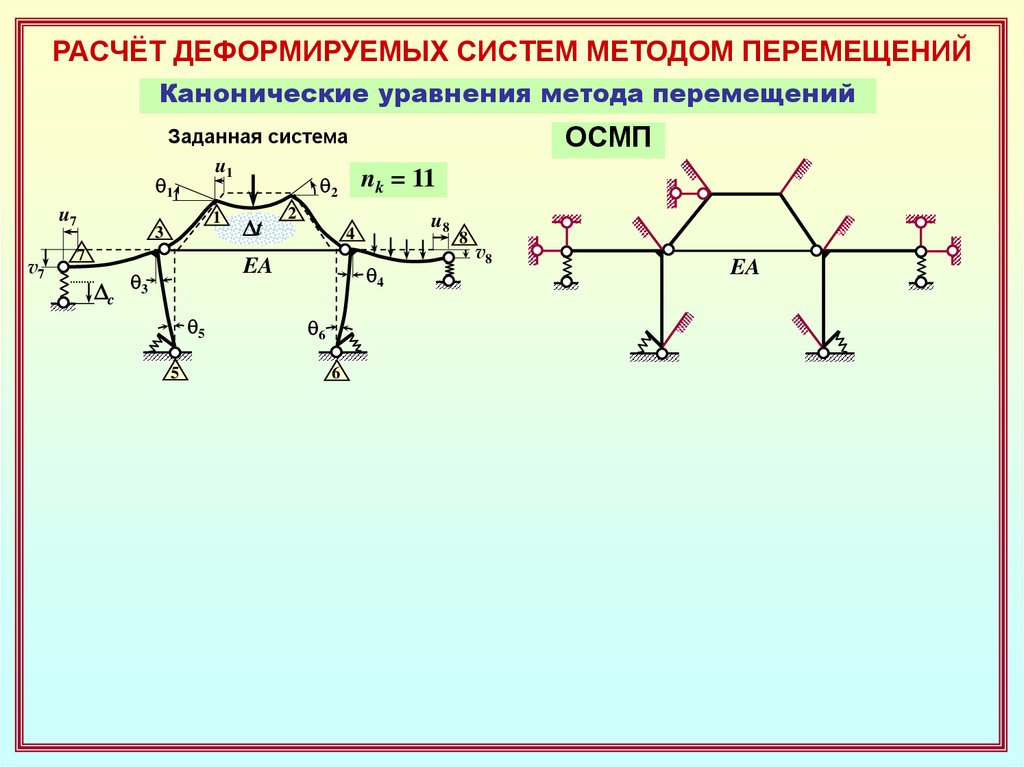
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙКанонические уравнения метода перемещений
ОСМП
Заданная система
nk = 11
Z1 Z2
Z3
Z4
Z11
Z9
Z7
EA
EA
Z8
Z5
Z6
Z10
6.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙКанонические уравнения метода перемещений
ОСМП
Заданная система
u1
q1
q2 nk = 11
u7
v7
1
3
7
Dc
Dt
2
EA
q3
q5
5
u8
4
q4
q6
6
8
v8
EA
7.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙКанонические уравнения метода перемещений
ОСМП
Заданная система
u1
q1
q2 nk = 11
u7
v7
1
3
7
Dc
Dt
2
4
EA
q3
q5
5
S
u8
q4
q6
6
R8S R9S
R3S
8
v8
R7S
Dc
R1S
R2S
Dt
EA
R5S
R6S
S
R11,S
R4S
R10,S
8.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙКанонические уравнения метода перемещений
ОСМП
Заданная система
u1
q1
q2 nk = 11
v7
1
3
7
Dc
Dt
2
4
EA
q3
q5
5
S
u8
8
q4
v8
R10,S
S
6
Z1= q1
Z7= u7
R9
R8
Z3= q3
Z8= v7
R7
7
R3
EA
Z4= q4
2
4
Z6= q6
S+Z
5
Zk
Zk=1 Z =?
k
8
R10
6
n
от Zk = 1
R4
R11
Z10= u8
R6
R5
k
RiZ RiZk ; RiZ k rik Z k
Dt
Z5= q5
RiZk
Z2= q2
R1 R2
Z9= u1
1
3
Dc
(статические условия эквивалентности); RiZ =?
Реакция
rik
i-й связи
k 1
R4S
EA
R5S
R6S
Dc
Ri 0 , i 1, n ( n nk )
n
R11,S
Dt
R7S
q6
Условия эквивалентности НДС
заданной системы и ОСМП
при одинаковых воздействиях ( S )
и перемещениях расчётных узлов ( Z ):
Ri = RiZ + RiS
R2S
Z10= v8
u7
R1S
R8S R9S
R3S
r Z R 0 , – КУМП
k 1
ik
k
i 1, n
iΣ
9.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙКанонические уравнения метода перемещений
n
r Z R 0 , i 1, n
k 1
ik
k
iΣ
r11Z1 r12Z2 r1k Zk r1n Zn R1Σ 0,
r21Z1 r22Z2 r2k Zk r2n Zn R2Σ 0,
r Z r Z r Z r Z R 0,
1 1
i2 2
ik k
in n
iΣ
i
r Z r Z r Z r Z R 0.
nk k
nn n
nΣ
n1 1 n2 2
r11 r12 r1k r1n
Z1
R1Σ
r21 r22 r2 k r2 n
Z2
R2Σ
Матричная форма:
r Z RΣ 0 r r r r r ; Z Z ; RΣ R
ik
in
i1 i 2
k
iΣ
Zn
RnΣ
rn1 rn 2 rnk rnn
Матрица внешней жёсткости
основной системы МП
по направлениям
основных неизвестных Z
Вектор
Вектор реакций
основных введённых связей
неизвестных
от заданных
воздействий
10.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙКанонические уравнения метода перемещений
r11Z1 r12Z2 r1k Zk r1n Zn R1Σ 0,
r21Z1 r22Z2 r2k Zk r2n Zn R2Σ 0,
r Z r Z r Z r Z R 0,
1 1
i2 2
ik k
in n
iΣ
i
r Z r Z r Z r Z R 0.
nk k
nn n
nΣ
n1 1 n2 2
Смысл канонических уравнений метода перемещений и их компонентов:
1. Система канонических уравнений в целом – условия статической эквивалентности
основной системы МП и заданной системы при одинаковых воздействиях ( S ) и истинных
перемещениях Z расчётных узлов.
2. Произвольное ( i -е ) уравнение – отрицание полной реакции i -й введённой связи в ОСМП
(суммарной реакции Ri от заданных воздействий ( S ) и одновременных смещений всех
введённых связей, равных истинным перемещениям Z расчётных узлов).
3. Левая часть i -го уравнения – полная реакция i -й введённой связи в ОСМП (суммарная
реакция Ri от заданных воздействий ( S ) и одновременных смещений всех введённых
связей, равных истинным перемещениям Z расчётных узлов).
4. Свободный член i -го уравнения RiS – реакция i -й введённой связи в ОСМП от заданных
воздействий ( S ).
5. Слагаемое rik Zk i -го уравнения – реакция Rik i -й введённой связи в ОСМП от смещения
k-й связи, равного истинному перемещению Zk .
6. Коэффициент rik при неизвестном Zk в i -ом уравнении – реакция i -й введённой связи
в ОСМП от единичного смещения k-й связи Zk = 1 ( единичная реакция ).
r11, r22 ,…, rii ,…, rnn – собственные единичные реакции введённых связей в ОСМП
rik ( i = k ) – побочные
11.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙЕдиничные состояния основной системы
F Z2
2
1
Z2= 1
r21
r22
q
Z1
Z1= 1
l lj
*
j
r11
r12 k = 2
k=1
r11 Z1 r12 Z 2 R1 F 0,
r Z r Z R 0.
2F
21 1 22 2
Способы определения
коэффициентов
rik
Главные
требования
и свободных
членов
к состояниям
ОСМП RiS
канонических
при единичных уравнений
смещениях
введённых связей и при
(из условий
заданных воздействиях:
M1
Грузовое состояние ОСМП
равновесия
статические совместности
а) обеспечение
узлов и частей
ОСМП)
перемещений и деформаций
элементов;
перемножением
эпюр
б) кинематические
выполнение кинематических
через работу
граничных условий.
концевых усилий
и узловых
нагрузок
M2
F
R1F
F
R2F
q
MF
12.
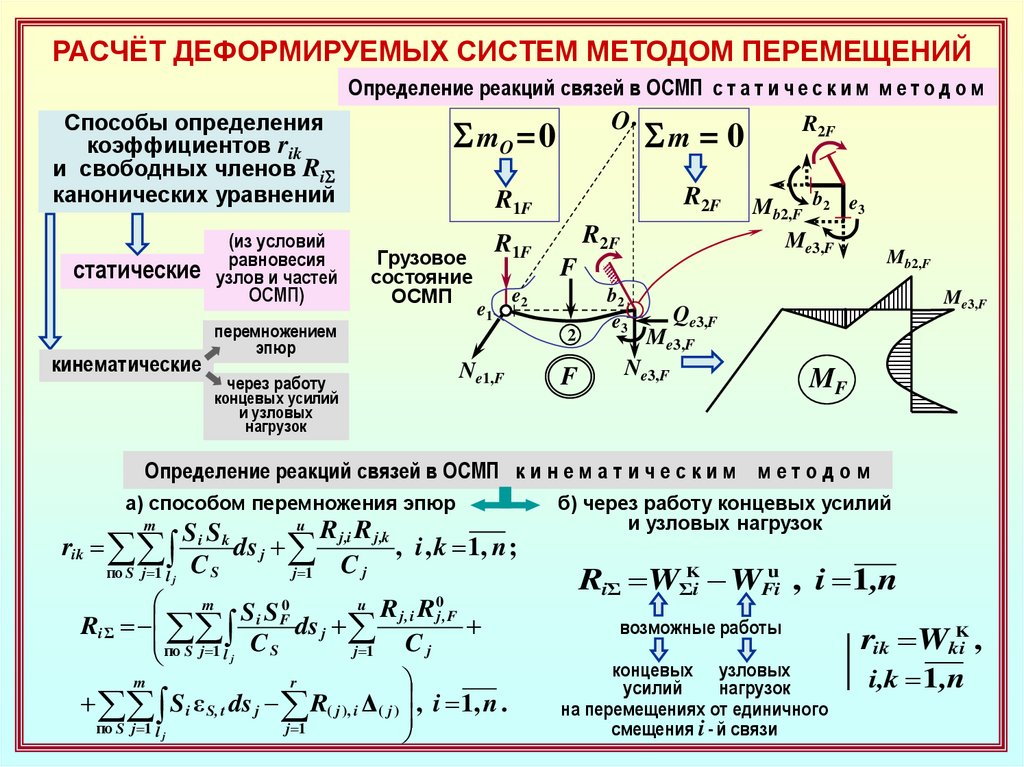
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙОпределение реакций связей в ОСМП с т а т и ч е с к и м м е т о д о м
Способы определения
коэффициентов rik
и свободных членов RiS
канонических уравнений
статические
кинематические
(из условий
равновесия
узлов и частей
ОСМП)
Грузовое
состояние
ОСМП
перемножением
эпюр
через работу
концевых усилий
и узловых
нагрузок
b1
R2F
R2F
Mb2,F b2 e3
Me3,F
R2F
F
e1
e2
2
1
Sm = 0
R1F
F
b2
e3
3
b3
q
Mb2,F
Me3,F
MF
13.
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙОпределение реакций связей в ОСМП с т а т и ч е с к и м м е т о д о м
Способы определения
коэффициентов rik
и свободных членов RiS
канонических уравнений
статические
кинематические
(из условий
равновесия
узлов и частей
ОСМП)
O
S mO = 0
Sm = 0
R2F
R2F
Mb2,F b2 e3
Me3,F
R1F
Грузовое
состояние
ОСМП
перемножением
эпюр
через работу
R1F
e1
R2F
e2
2
Ne1,F
концевых усилий
и узловых
нагрузок
Mb2,F
F
F
b2
e3
Me3,F
Qe3,F
Me3,F
Ne3,F
MF
Определение реакций связей в ОСМП к и н е м а т и ч е с к и м м е т о д о м
а) способом перемножения эпюр
u R R
Si Sk
j,i
j,k
rik
ds j
, i , k 1, n ;
C
C
S
j
по S j 1 l j
j 1
m
0
m
u R R0
S
S
j, i
j, F
i
F
Ri Σ
ds j
по S j 1 l C S
C
j
j 1
j
m
r
S i ε S, t ds j R( j ), i Δ ( j ) , i 1, n .
по S j 1 l j
j 1
б) через работу концевых усилий
и узловых нагрузок
RiΣ WΣKi WFiu , i 1,n
возможные работы
концевых узловых
усилий
нагрузок
на перемещениях от единичного
смещения i - й связи
rik WkiK ,
i,k 1,n
14.
Типовые элементы плоской основной системы метода перемещенийbj
Тип 1
ej
bj
(ej ) EIj = const (bj )
Тип 2
ej
Тип 3
bj
ej
(ej ) EАj = const (bj )
EIj = const
bj
Тип 4
ej
(ej ) EIj = const (bj )
Реакции связей и внутренние усилия в типовых элементах плоской ОСМП
а) от смещений связей ( концевых сечений )
Тип
элемента
Вид
смещения
Поворот концевого сечения на угол q
Взаимное линейное смещение концевых
сечений D
D
q
Тип 1
lj
4i j θ
6i j θ /l j
q
Тип 2
3i j θ
3i j θ /l j
Тип 3
Тип 4
2i j θ
M
6 i j D /l j
Q
12 i j D /l 2j
EI j
ij
lj
lj
6 i j D /l j
M
Q
D
M
3i j D /l j
Q
3i j D /l 2j
M = 0, Q = 0
EAj D /l j
Стержень рассматривается как
lj
жёсткая
lj
M
Q
lj
D
N
линейная связь
15.
Типэлемента
б) о т н е к о т о р ы х в и д о в в о з д е й с т в и й
Н а г р у з к и
Равномерно распределённая
Сосредоточенная сила
q
lj
2
j
Тип 1
ql / 12
F
xl l j
ql 2j / 12
M
2
j
ql j / 2 ql / 24
Q
Fl j ξl ξr
Q
F
Fξ (1 2ξr )
2
l
xl l j
lj
M
M
M ξr (2 3ξr)
M ξl [1 3ξr (2ξr 1)]
Q
6M ξ ξ
lj l r
Fl j ξl ξr
M
Q
3 ql
8 j
ξr
2
F ξ 3 ξ2 Fl j ξl ξr 1 2
r
2 r
Q
F
M 1 3ξ2
r
2
F
lj
xl l j
Fxr
Fxl
xr l j
3 M ξ 1 ξ2
r
r
2
3 M 1 ξ2
r
2 lj
Dt1j > Dt2j
0 Q
0
EAj α j D t0 j
N
hj
M
M
Q
lj
EI
3 j α D t
j
nr, j
2 hj
3 EI h 1l 1 α D t
j j j
j
nr, j
2
EAj α j D t0 j
M
Q
N
Dt2j
Dt1j
lj
N
M
D t nr, j D t1 j D t 2 j
Dt1j
xr l j
M
q
N
xl l j
hj
Dt2j
M
xr l j
Fl j
ξ ξ 1 ξr
2 l r
ql / 8
Тип 2
M
xr l j
lj
M ξl (2 3ξl) EI j
α j D t nr , j
hj
F
2
j
Тип 3
xl l j
Fl j ξ2l ξr
q
ql j / 2
xl + x r = 1
xr l j
2Fl j ξ2l ξ2r
Fξ2r (1 2ξl )
Dt2j
Dt1j
M
Fl j ξ2r ξl
ql j / 2
5 ql
8 j
Сосредоточенный момент
Изменение
температуры
EAj α j D t0 j
hj
N
16.
Свойства матрицы внешней жёсткости ОСМПrii 0 , i 1, n
rik rki ( i k ) – по теореме Рэлея (J.W. Rayleigh)
Det ( r ) > 0
Проверки коэффициентов КУМП
Используются суммарные единичные силовые факторы Ss , Rj,s – внутренние усилия и реакции
упругих связей от одновременных единичных смещений Z1 = 1 , Z2 = 1 ,… , Zn = 1.
А. Универсальная проверка коэффициентов:
u R2
n n
S s2
j,s
rss ds j
(?) rik ( 0 ).
C
C
s
j
по S j 1 l j
j 1
i 1 k 1
m
Б. Построчная проверка коэффициентов
(при отрицательном результате универсальной проверки):
m
u
n
j,i j,s
i s
is
j
ik
s
j
по S j 1 l j
j 1
k 1
R R
S S
r
ds
(?) r
C
C
( i 1, n).
Проверка свободных членов КУМП
u R R0
m
n
r
m S s S F0
j,s j,F
RsΣ
ds j
S s ε S,t ds j R( j ), s Δ( j ) (?) R i Σ
по S j 1 l C S
C
j
j 1
по S j 1 l j
j 1
i 1
j
Определение основных неизвестных: Z r
Искомые усилия: S
n
S Z S
k 1
k
k
S
1
RΣ .
n
M M k Z k M S Q dM N
ds
k 1
17.
ПроверкиГлавная
в методе
перемещений
результатов
Статическая проверка
(проверка равновесия)
а) системы в целом
б) узлов
в) выделенных частей
S s0 , R 0j,s , R(0j ) ,s – от X1 = X2 =…= Xn = 1 в ОСМС
расчёта
Кинематическая
( деформационная )
проверка
Только для
статически
неопределимой
рассчитываемой
системы
а) о б щ а я
u R0 R
S s0 S
j,s
j
D s D i
ds j
C
C
s
j
i 1
по S j 1 l j
j 1
n
m
m
r
S s,t ds j R(0j ) ,s D ( j ) 0 (?)
по S j 1 l j
0
s
j 1
б) ч а с т н ы е
0
u R R
S i0 S
j,i
j
D i
ds j
C
C
s
j
по S j 1 l j
j 1
m
S i0 , R 0j,i , R(0j ) ,i – от Xi = 1 в ОСМС
m
r
S ds j R(0j ) ,i D ( j ) 0 (?)
по S j 1 l j
j 1
( i 1, n )
0
i s,t
Ds , Di – заведомо равные нулю
перемещения по направлениям
лишних связей в СНС
18.
Контрольные вопросы( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 18» )
1. Сколько различных вариантов ОСМП может быть предложено для расчёта некоторой
заданной системы? ( 3 )
2. Какие условия (требования) положены в основу вывода уравнений метода
перемещений? ( 8 )
3. Каковы по изначальному смыслу канонические уравнения метода перемещений
(КУМП) – статические, кинематические или физические? ( 8 )
4. Варианты записи канонических уравнений метода перемещений:
а) в обычной форме – развернутое и компактное представления ( 9 ) ;
б) в матричной форме – поэлементная и укрупненная записи ( 9 ) .
5. Раскрыть смысл:
а) системы КУМП в целом ( 10 ) ;
б) произвольного (i-го) канонического уравнения ( 10 ) ;
в) левой части i-го канонического уравнения ( 10 ) ;
г) свободного члена i-го канонического уравнения RiS (RiF , Rit , Ric ) ( 10 ) ;
д) слагаемого rik Zk ( 10 ) ;
е) коэффициента rik ( 10 ) .
6. Как называется и какой смысл имеет матрица r коэффициентов КУМП? ( 9 )
7. Как называются и какой смысл имеют коэффициенты rii ? Коэффициенты rik ? ( 10 )
Обозначить на схеме ОСМП и истолковать смысл rik (i и k – по заданию) и/или RiF ( 11 ) .
8. Каким главным требованиям должны удовлетворять деформированные состояния
ОСМП при единичных смещениях связей и при заданных воздействиях? ( 11 )
9. Методы и способы определения коэффициентов и свободных членов КУМП ( 11 ) .
10. Статические способы (приёмы) определения реакций угловых и линейных связей
в ОСМП, рациональное их использование ( 12 ) .
*) Только в режиме «Показ слайдов».
19.
Контрольные вопросы( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 19» )
11. Кинематические способы определения реакций связей ( 13 ) .
12. Типы элементов ОСМП, табличные эпюры и способы их получения ( 14 – 15 ) .
13. Свойства компонентов матрицы r. Теорема о взаимности единичных реакций в ЛДС
(теорема Рэлея) ( 16 ) .
14. Какой должна быть сумма компонентов матрицы r : положительной, отрицательной,
равной 0, любой? ( 16 )
15. Проверки коэффициентов (универсальная и построчная) и свободных членов
канонических уравнений ( 16 ) .
16. Усилия в какой системе используются для проверки реакций в ОСМП от заданных
воздействий? ( 16 )
17. Почему канонические уравнения метода перемещений являются разрешающими
уравнениями задачи расчёта СНС (синтезом статической, геометрической и физической сторон задачи)? – см. лекцию «Смешанный метод расчёта СНС»
18. Определение основных неизвестных и искомых усилий ( 17 ) .
19. Полная проверка результатов расчёта системы методом перемещений, ее составные
части ( 17 ) .
20. Какая из частей полной проверки результатов расчёта – статическая или кинематическая – является главной и почему? ( 17 )
21. Содержание и приёмы статической проверки ( 17 ) . Могут ли выполняться условия
равновесия при наличии ошибок (каких?) в решении задачи?
22. Сущность и техника выполнения кинематической (деформационной) проверки
результатов расчёта методом перемещений ( 17 ) .
23. Формулы кинематической проверки (общей и частных) при силовых, температурных
и кинематических воздействиях ( 17 ) .
*) Только в режиме «Показ слайдов».

















 mechanics
mechanics








