Строительная механика. Методы определения силовых факторов в деформируемых системах

1. МЕТОДЫ ОПРЕДЕЛЕНИЯ СИЛОВЫХ ФАКТОРОВ В ДЕФОРМИРУЕМЫХ СИСТЕМАХ

СТРОИТЕЛЬНАЯ МЕХАНИКА.
Часть I
МЕТОДЫ ОПРЕДЕЛЕНИЯ
СИЛОВЫХ ФАКТОРОВ
В ДЕФОРМИРУЕМЫХ
СИСТЕМАХ

2.

внешних (опорные реакции)
Силовые факторы – реакции связей
внутренних
статический
кинематический
энергетический
Методы определения
силовых факторов
между дисками
в сечениях элементов
(внутренние силовые факторы)
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование
уравнений равновесия системы в целом и/или её частей.
Уравнения равновесия в случае
линейно деформируемой системы:
q
F1
B
A
l
M
l/2
l/2
HA
A
VC q
q
C C
HC
h
h
C
F2 F 1
A*S + BF = 0
l
MA
VC
B
F2
M
VB
l/2 l/2
VA n = 3*2 = 6 = n ;
D
yp
M A
nc = nS = 6
VA
Вектор искомых
реакций связей: S H A
VB
VC
H C
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных
размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Для системы в целом:
– число искомых усилий nS = nc ;
– количество уравнений nyp= nD .
В случае статически определимой
cистемы (W = 0) nD=nc
nyp= nS

3.

Силовые факторы – реакции связей
Методы определения
силовых факторов
внешних (опорные реакции)
внутренних
статический
кинематический
энергетический
между дисками
в сечениях элементов
(внутренние силовые факторы)
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование
уравнений равновесия системы в целом и/или её частей.
Уравнения равновесия в случае
линейно деформируемой системы:
A*S + BF = 0
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных
размеров ( дискретной системы )
h
( AC )
m
0 Уравнения
VC q
Уравнения
равновесия:
A
q
( AC )
2
равновесия:
F2
F
y 0
M
1
C C
B
S – вектор искомых усилий;
A (VACC) l HC h F1 h ql /2 0
VC
q 0l 0
V
A x
HC
А – матрица коэффициентов
M
H
2
A HC F1 0
при неизвестных S
VC
VB
M A VC l HC h F12 h ql /2 0 A
l
в уравнениях равновесия;
VC M
q
l F20 l ql /8 0
VBA l/2
H H F 0
l/2 l/2
ВF – вектор «грузовых» членов
MA
HA
VB A VC C F2 1 q l/2 0
уравнений равновесия
CB0
)
V
C (
A
Hm
n
=
3
*
2
=
6
=
n
;
(от заданных нагрузок).
0
C
D
yp
M
A
(CB)
nc = nS = 6
Для системы в целом:
y 0
VA
(CB)
Вектор
искомых
x 0
– число искомых усилий nS = nc ;
реакций связей: S H A – количество уравнений nyp= nD .
VB
VB l/2 M F2 l ql 2/8 0
VC В случае статически определимой
VB VC F2 q l/2 0
H C cистемы (W = 0) nD=nc
nyp= nS
HC 0

4.

Силовые факторы – реакции связей
Методы определения
силовых факторов
внешних (опорные реакции)
внутренних
статический
кинематический
энергетический
между дисками
в сечениях элементов
(внутренние силовые факторы)
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование
уравнений равновесия системы в целом и/или её частей.
Уравнения равновесия в случае
линейно деформируемой системы:
A*S + BF = 0
VC q
Уравнения равновесия:
q
2
F2
F
M A VC l HC h F1 h ql /2 0 1
C C
B
VA VC q l 0и достаточное
необходимое
HC
M
HC F1 0 условие
H A статическое
V
VB
C
геометрической
l
2
A
VB l/2 M F2 l ql /8 0
неизменяемости
l/2 l/2
MA
HA
q l/2 0
VB VC F2системы
VA n = 3*2 = 6 = n ;
HC 0
D
yp
2
M A
F1h ql /2
1 0 0 0 l h
nc = nS = 6
VA
0 1 0 0 1 0
ql
Вектор
искомых
реакций связей:
F1
S H A
A 0 0 1 0 0 1 BF
2
VB
0 0 0 l/2 0 0
M F l ql /8
F 2 ql/2
1
0 0 0 1 1 0
VC
2
S
A
B
F
0 0 0 0 0 1
H C
0
h
Det ( A) 0
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных
размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Для системы в целом:
– число искомых усилий nS = nc ;
– количество уравнений nyp= nD .
В случае статически определимой
cистемы (W = 0) nD=nc
nyp= nS

5.

Силовые факторы – реакции связей
Методы определения
силовых факторов
внешних (опорные реакции)
внутренних
статический
кинематический
энергетический
между дисками
в сечениях элементов
(внутренние силовые факторы)
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование
уравнений равновесия системы в целом и/или её частей.
Уравнения равновесия в случае
линейно деформируемой системы:
A*S + BF = 0
Универсальная процедура формирования
системы уравнений равновесия
( концепция конечных элементов )
1. Разделение системы на элементы и узлы
сечениями по концам стержневых элементов
( концевыми сечениями ).
2. Запись уравнений:
– 1-я группа – уравнения равновесия элементов
в локальных (собственных) осях координат –
стандартная процедура;
– 2-я группа – уравнения равновесия узлов
( включая опорные ) в общей ( глобальной )
системе координат;
– 3-я группа – статические характеристики
связей в узлах.
линейные алгебраические уравнения
для системы элементов конечных
размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).

6.

ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
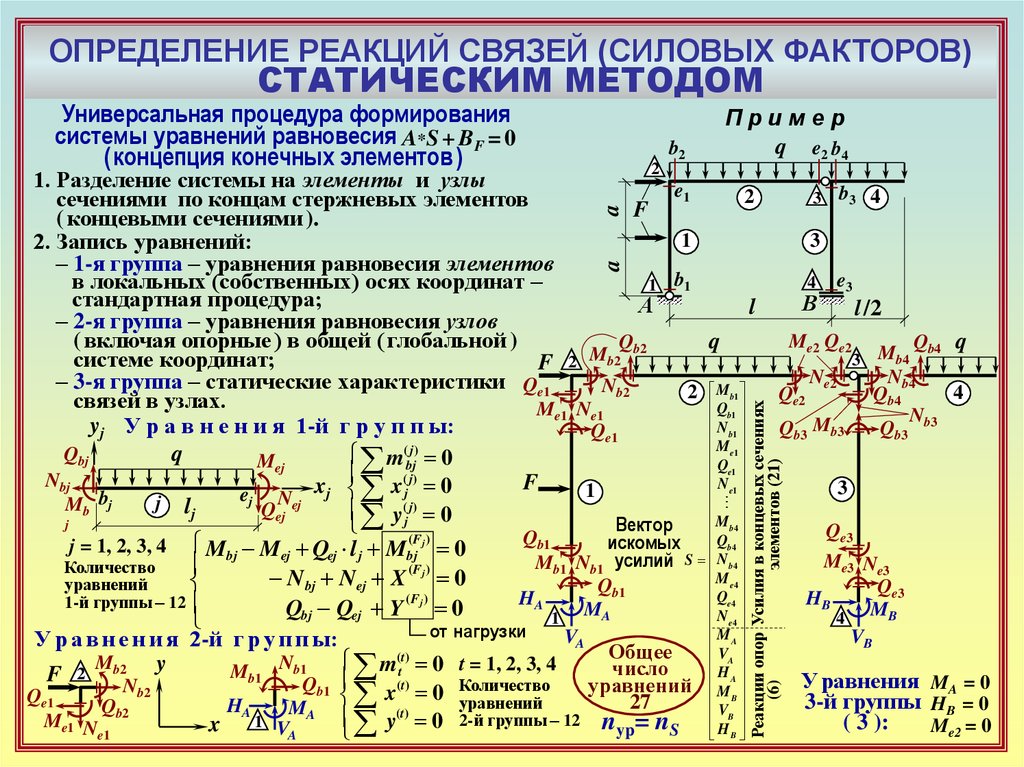
Универсальная процедура формирования
системы уравнений равновесия A*S + BF = 0
( концепция конечных элементов )
b2
Пример
q e2 b 4
2
Реакции опор Усилия в концевых сечениях
(6)
элементов (21)
a
a
1. Разделение системы на элементы и узлы
e1
2
3 b3 4
сечениями по концам стержневых элементов
F
( концевыми сечениями ).
1
3
2. Запись уравнений:
– 1-я группа – уравнения равновесия элементов
4 e3
в локальных (собственных) осях координат –
1 b1
стандартная процедура;
В
А
l
l /2
– 2-я группа – уравнения равновесия узлов
( включая опорные ) в общей ( глобальной )
Me2 Qe2
q
Q q
Qb2
Mb4 b4
M
b2
3
системе координат;
2
F
Ne2
Nb4
– 3-я группа – статические характеристики Qe1
Nb2
M b1
2
4
Q
Q
b4
e2
связей в узлах.
Qb1
Me1 Ne1
N
N
yj У р а в н е н и я 1-й г р у п п ы:
Qb3 b3
Qb3 Mb3
Qe1
b1
M e1
Qbj
q
m(bjj) 0
Mej
Qe1
( j)
N e1
Nbj
F
xj x j 0
3
1
e
N
b
j
ej
j lj
Mb j
(
j
)
Qej
yj 0
j
Вектор
M b4
Qe3
Qb1
искомых Qb4
j = 1, 2, 3, 4 Mbj Mej Qej l j Mbj(F j ) 0
Me3 Ne3
Mb1 Nb1 усилий S N b4
Количество
(F j )
M
N
N
X
0
bj
ej
уравнений
e4
Qb1
Qe3
(F j )
HA
HB
Qe 4
1-й группы – 12
Qbj Qej Y 0
MB
N e4
1 MA
4
от нагрузки
M
VA
VB
У р а в н е н и я 2-й г р у п п ы:
V A
Общее
A
m(tt) 0 t = 1, 2, 3, 4
M
число
Mb1 Nb1
F 2 b2N y
HA
У равнения MA = 0
(
t
)
Q
Количество
уравнений
b1
b2
MB
x 0 уравнений
Qe1
27
3-й группы HB = 0
HA
VB
Q
MA
(t )
2-й
группы
–
12
1
Me1 N b2
y
0
( 3 ):
nyp= nS H B
x
Me2 = 0
VA
e1

7.

ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
В случае статически неопределимой системы
W<0
nD < nc
nyp< nS
Недостающие уравнения в количестве nc – nD = nл.с. – геометрические:
AD* D + D = 0 – условия совместности перемещений
(например, описание перемещений по направлениям лишних связей)
Объединённая система уравнений:
A* S + BF = 0
AD* D + D = 0
Из физических зависимостей ( закон Гука и др. ):
D = D(S) – выражения перемещений через усилия
Разрешающие уравнения в усилиях:
A0* S + B0 = 0
Необходимое и достаточное аналитическое условие
геометрической неизменяемости системы: Det ( A0) 0

8. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ) КИНЕМАТИЧЕСКИМ МЕТОДОМ

В основе метода – принцип возможных перемещений (
принцип Лагранжа )*:
если механическая система находится в равновесии,
то сумма работ внешних сил, приложенных к системе,
и соответствующих им внутренних сил
на возможных ( виртуальных) перемещениях
равна нулю:
Wext + Wint = 0
*J.L. Lagrange ( 1788 )

9. Возможные (виртуальные) перемещения –

а) бесконечно малые ( для линейно
деформируемых систем – конечные,
но малые в сравнении с габаритами
системы );
б) не противоречащие условиям
совместности деформаций
( перемещений ) и кинематическим
граничным условиям ( условиям
закрепления );
в) отсчитываемые от исследуемого
положения равновесия.

10.

F1
q
Fn
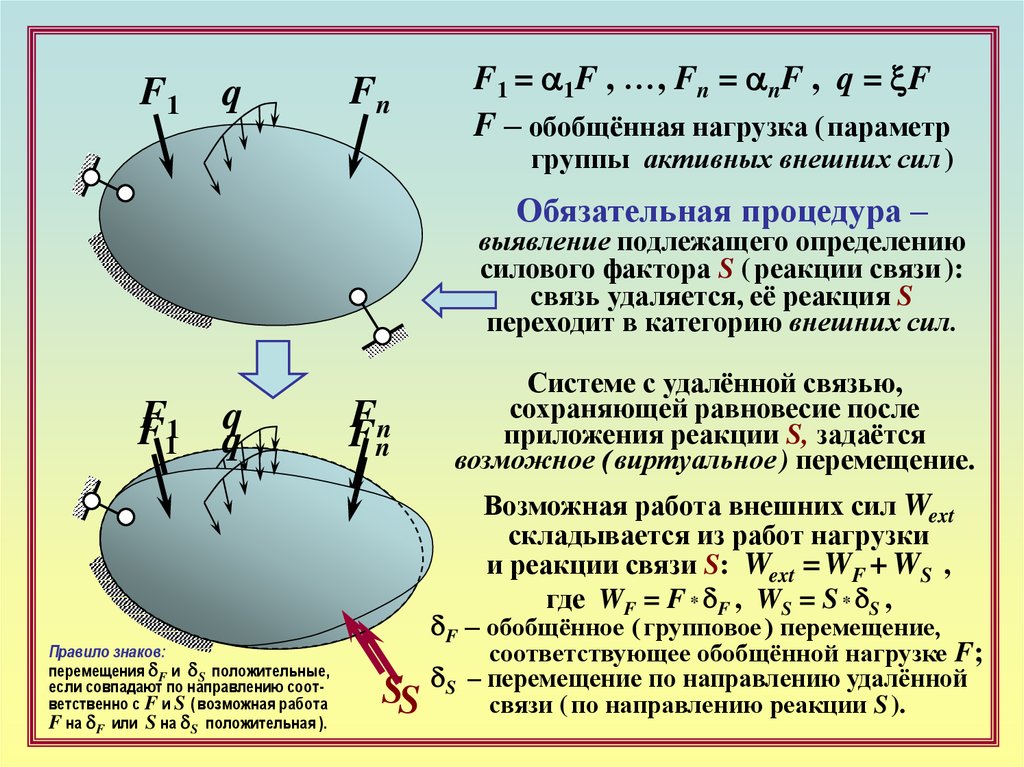
F1 = a1F , …, Fn = anF , q = xF
F – обобщённая нагрузка ( параметр
группы активных внешних сил )
Обязательная процедура –
выявление подлежащего определению
силового фактора S ( реакции связи ):
cвязь удаляется, её реакция S
переходит в категорию внешних сил.
F1
F
1
q
q
Fn
F
n
Системе с удалённой связью,
сохраняющей равновесие после
приложения реакции S, задаётся
возможное ( виртуальное ) перемещение.
Возможная работа внешних сил Wext
складывается из работ нагрузки
и реакции связи S: Wext = WF + WS ,
где WF = F * dF , WS = S * dS ,
Правило знаков:
перемещения dF и dS положительные,
если совпадают по направлению соответственно с F и S ( возможная работа
F на dF или S на dS положительная ).
dF – обобщённое ( групповое ) перемещение,
SS
соответствующее обобщённой нагрузке F;
dS – перемещение по направлению удалённой
связи ( по направлению реакции S ).

11. Алгоритм определения реакции связи кинематическим методом

1. В системе, находящейся в равновесном деформированном
состоянии при заданной нагрузке, удаляется связь, реакцию
которой S требуется определить. Взамен удалённой связи
прикладывается её реакция S, обеспечивающая сохранение
неизменным состояния равновесия системы.
2. Системе с удалённой связью, находящейся по-прежнему
в равновесном деформированном состоянии при действующей
нагрузке и реакции S, задаётся возможное (виртуальное)
перемещение.
3. Определяются (с точностью до общего неопределённого
множителя d0 ) перемещения dF и dS – соответственно
по направлениям заданной нагрузки F и искомой реакции S.
4. Из уравнения возможных работ Wext + Wint = 0 определяется
искомый силовой фактор S (реакция связи):
F δF Wint
S
δS

12. Алгоритм определения реакции связи кинематическим методом

1. В системе, находящейся в равновесном деформированном
состоянии при заданной нагрузке, удаляется связь, реакцию
которой S требуется определить. Взамен удалённой связи
прикладывается её реакция S, обеспечивающая сохранение
неизменным состояния равновесия системы.
2. Системе с удалённой связью, находящейся по-прежнему
в равновесном деформированном состоянии при действующей
нагрузке и реакции S, задаётся возможное (виртуальное)
перемещение.
3. Определяются (с точностью до общего неопределённого
множителя d0 ) перемещения dF и dS – соответственно
по направлениям заданной нагрузки F и искомой реакции S.
4. Из уравнения возможных работ Wext + Wint = 0 определяется
искомый силовой фактор S (реакция связи):
F δF Wint
S
δS

13.

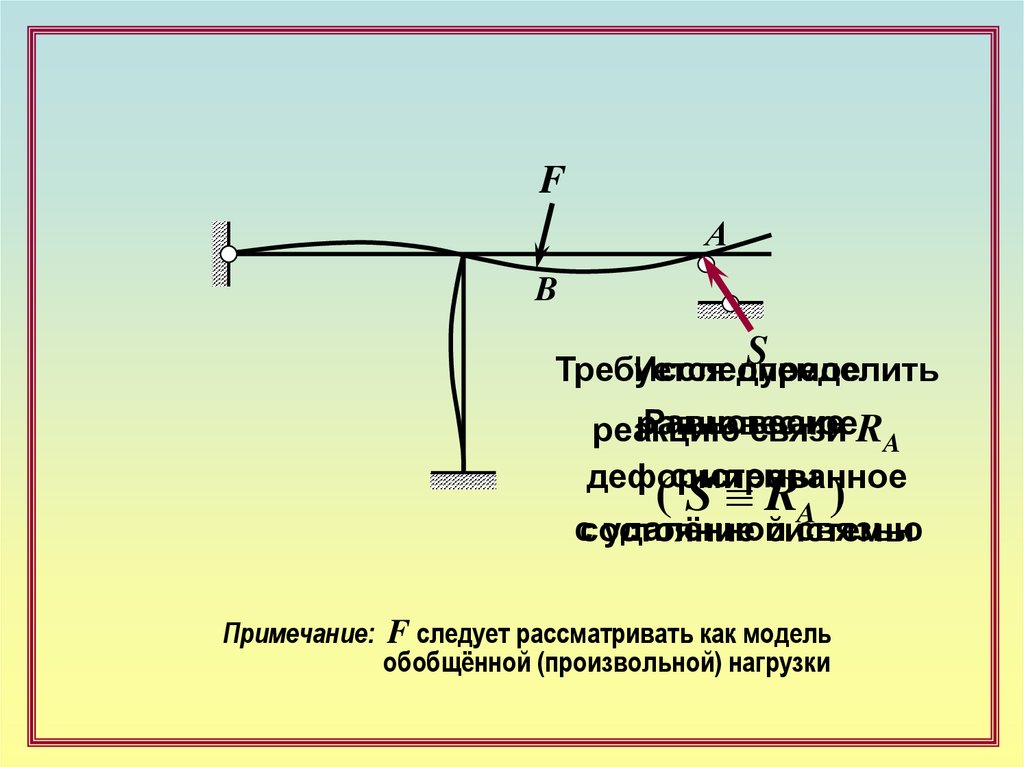
F
А
B
S
Требуется
Исследуемое
определить
Равновесие
равновесное
реакцию
связи RA
системы
деформированное
( S RA )
ссостояние
удалённой
связью
системы
Примечание: F следует рассматривать как модель
обобщённой (произвольной) нагрузки

14.

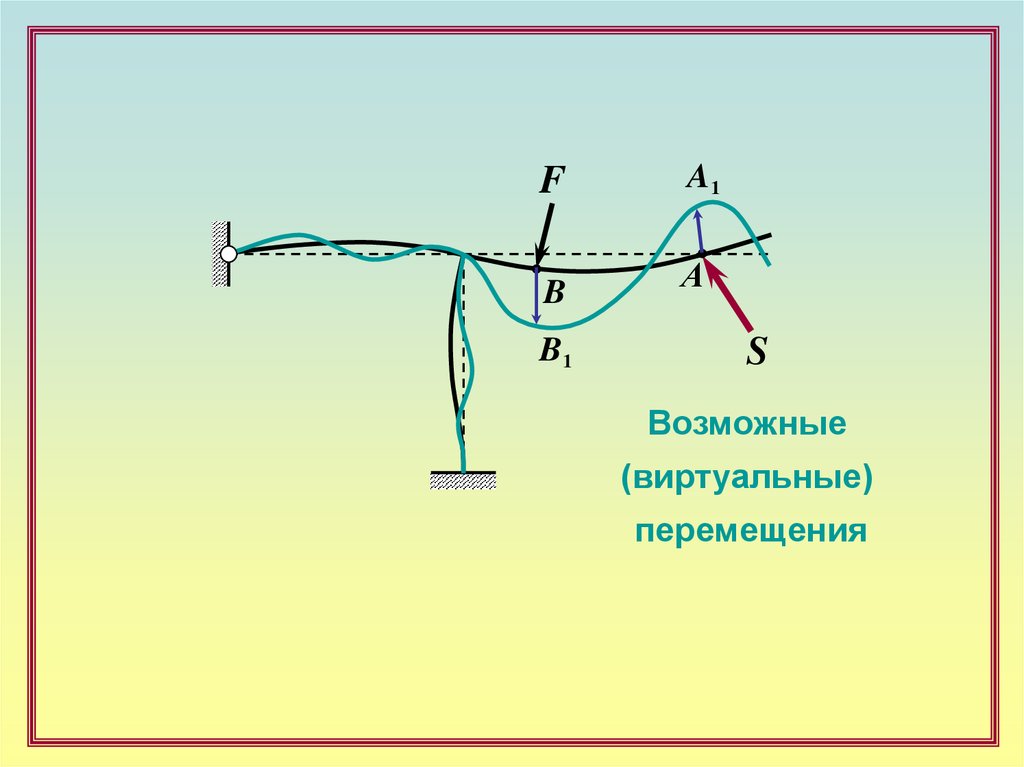
F
A1
B
А
B1
S
Возможные
(виртуальные)
перемещения

15.

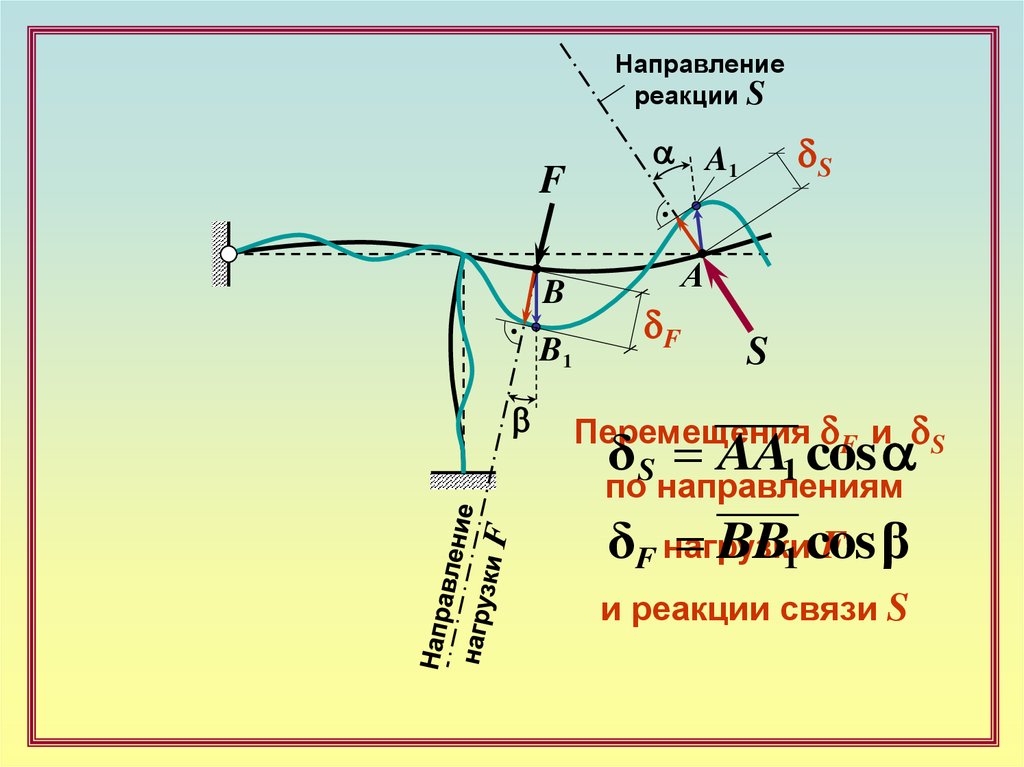
Направление
реакции S
F
B
B1
b
dS
a A1
А
dF
S
Перемещения dF и dS
δS AA1 cos a
по направлениям
δF нагрузки
BB1 cos
F β
и реакции связи S

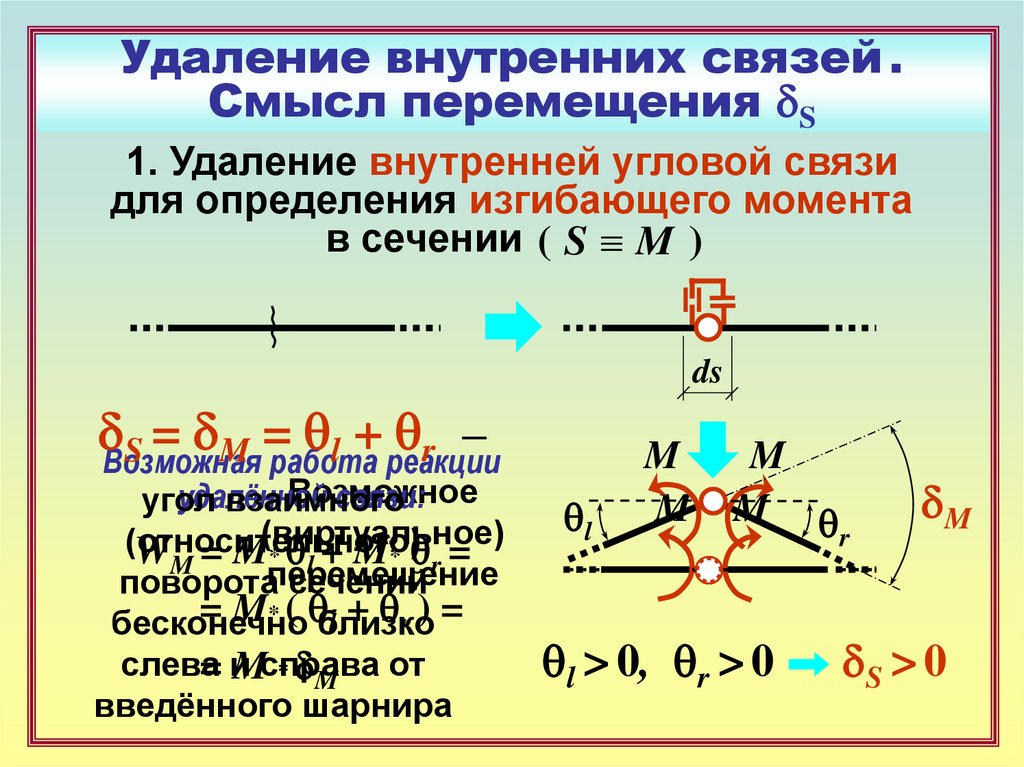
16. Удаление внутренних связей . Смысл перемещения dS

1. Удаление внутренней угловой связи
для определения изгибающего момента
в сечении ( S M )
ds
dВозможная
q
+
q
–
S = dM =
l
r
работа реакции
Возможное
удалённой
связи:
угол
взаимного
(виртуальное)
(относительного)
WM = M* ql + M* qr =
поворотаперемещение
сечений
= M* ( qблизко
l + qr ) =
бесконечно
слева
от
= иMсправа
* dM
введённого шарнира
ql
M
M
M
M q
r
ql > 0, qr > 0
dM
dS > 0

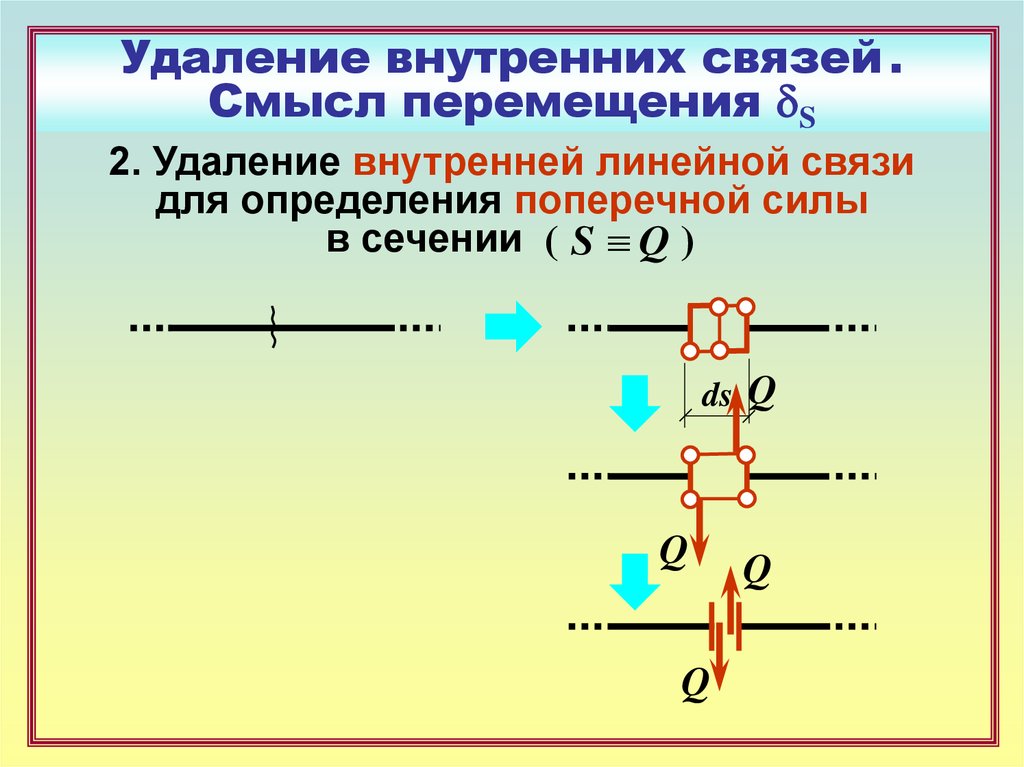
17. Удаление внутренних связей . Смысл перемещения dS

2. Удаление внутренней линейной связи
для определения поперечной силы
в сечении ( S Q )
ds Q
Q
Q
Q

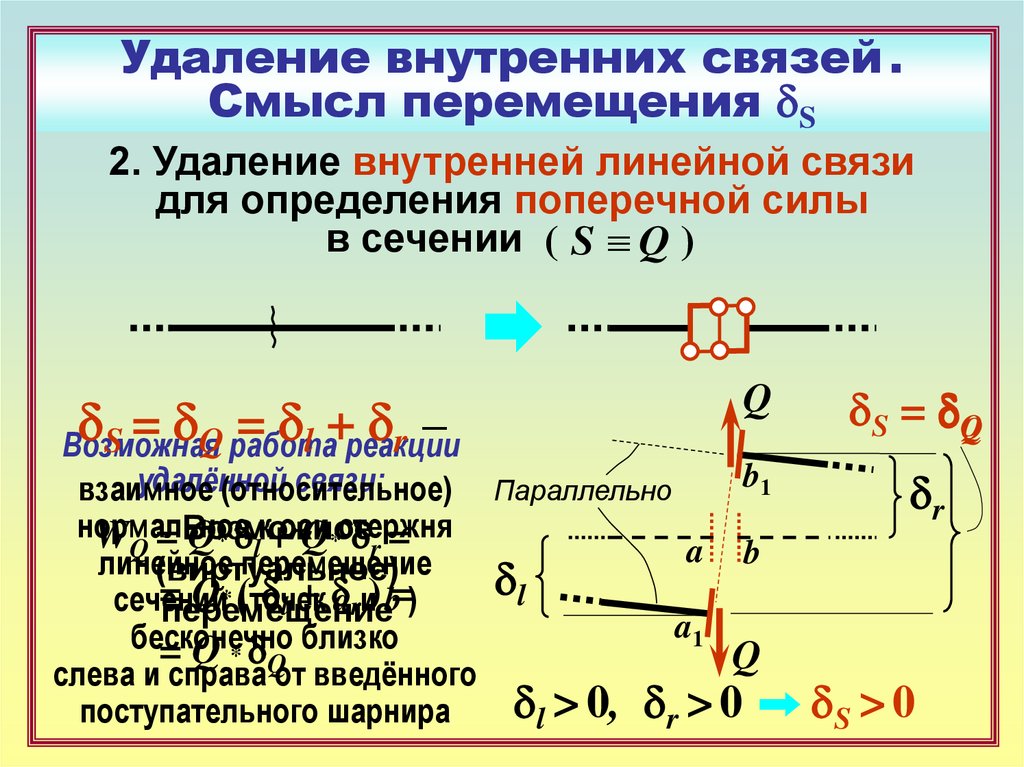
18. Удаление внутренних связей . Смысл перемещения dS

2. Удаление внутренней линейной связи
для определения поперечной силы
в сечении ( S Q )
dS = dQ работа
= dl +реакции
dr –
Возможная
Q
b1
удалённой
связи:
Параллельно
взаимное
(относительное)
нормальное
WQ = Возможное
Q* dlк+оси
Q*стержня
dr =
a b
линейное
перемещение
(виртуальное)
d
=
Q
* ((точек
d
+
d
)
=
l
сечений
a
и
b
)
l
r
перемещение
a1
бесконечно
близко
= Q * dQ
Q
слева и справа от введённого
dl > 0, dr > 0
поступательного шарнира
dS = dQ
dr
dS > 0

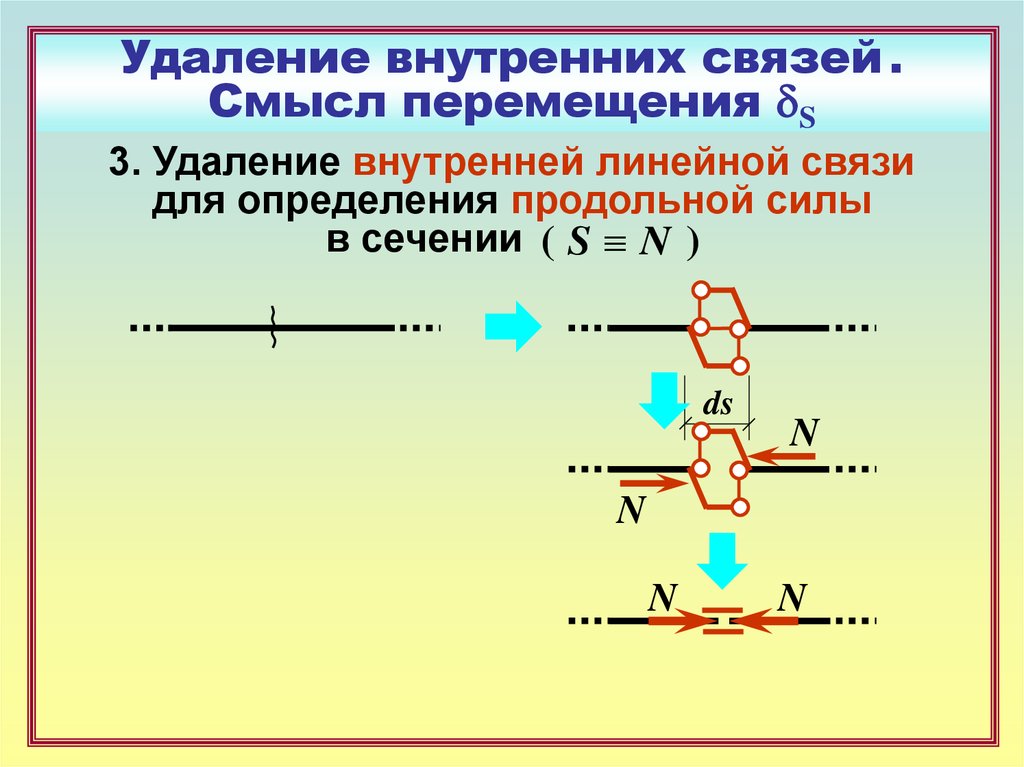
19. Удаление внутренних связей . Смысл перемещения dS

3. Удаление внутренней линейной связи
для определения продольной силы
в сечении ( S N )
ds
N
N
N
N

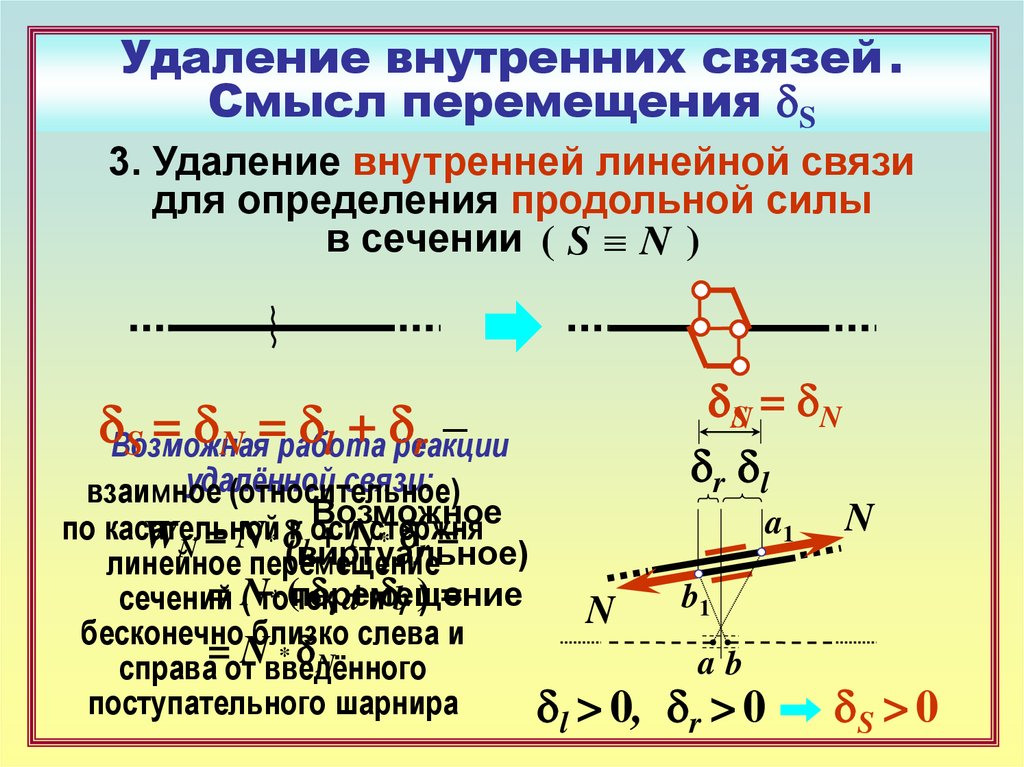
20. Удаление внутренних связей . Смысл перемещения dS

3. Удаление внутренней линейной связи
для определения продольной силы
в сечении ( S N )
dВозможная
dl + dреакции
S = dN =работа
r –
удалённой
связи:
взаимное
(относительное)
Возможное
по касательной
к
оси
стержня
WN = N* d(виртуальное)
l + N* dr =
линейное перемещение
=N
* (перемещение
dl a+иdbr ) =
сечений
( точек
N
бесконечно близко слева и
* dN
справа=отNвведённого
поступательного шарнира
d > 0,
l
dNS = dN
dr dl
a1
N
b1
ab
dr > 0
dS > 0

21.

ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
Силовой фактор S в линейно деформируемой системе
определяется как производная потенциальной энергии
упругой деформации U (ПЭУД) по соответствующему
перемещению DS по направлению S
( т е о р е м а Л а г р а н ж а ):
S dU
dΔ S

22.

Контрольные
вопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 22» )
1. Какие силовые факторы определяются в расчётах сооружений и конструкций? ( 2 )
2. Перечислить основные методы определения силовых факторов. ( 2 )
3. В чём сущность статического метода определения реакций связей и внутренних
усилий? ( 2 )
4. Какими уравнениями описывается равновесие
а) дифференциально-малого элемента ( 2 )
б) дискретной ( конечно-элементной ) линейно деформируемой системы? ( 2 )
5. Каково соотношение между числом уравнений равновесия и количеством искомых
силовых факторов в случае статически определимой системы? ( 2 )
6. В чём суть универсальной процедуры формирования уравнений равновесия,
реализующей концепцию конечных элементов? ( 5 )
7. Из каких групп состоит система уравнений равновесия, формируемых с помощью
универсальной процедуры? ( 4 ) ( 6 )
8. Какие особенности имеет применение статического метода к статически
неопределимым системам? ( 7 )
9. Каково необходимое и достаточное аналитическое ( статическое ) условие
геометрической неизменяемости системы? ( 4 ) ( 7 )
10. На чём основан кинематический метод определения реакций связей ( силовых
факторов )? Дать формулировку принципа Лагранжа. ( 8 )
11. Что такое возможные ( виртуальные ) перемещения? – три их свойства. ( 9 )
12. Какая обязательная процедура предшествует заданию виртуальных перемещений
при реализации кинематического метода определения реакции некоторой связи? ( 10 )
13. Что такое обобщённая нагрузка и обобщённое перемещение? ( 10 )
_____________________________________________________
*) Только в режиме «Показ слайдов»

23.

Контрольные
вопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 23» )
14. Изложить алгоритм определения реакции связи кинематическим методом. ( 11 )
15. Основная формула кинематического метода для определения
силового фактора S . ( 11 )
16. Что такое dF и dS в основной формуле кинематического метода? ( 10 )
17. Каково правило знаков для перемещений dF и dS? ( 10 )
18. Какие связи должны удаляться при определении внутренних силовых факторов
кинематическим методом? ( самостоятельно )
19. Какая связь удаляется при определении кинематическим методом изгибающего
момента в определённом сечении стержневого элемента? Что появляется в сечении
в результате удаления связи? ( 16 )
20. Какой смысл имеет величина dS в случае определения изгибающего момента М ? ( 16 )
21. Какая связь удаляется при определении кинематическим методом поперечной силы
в сечении стержневого элемента? Что появляется в сечении в результате удаления
связи? ( 17 )
22. Какой смысл имеет величина dS в случае определения поперечной силы Q ? ( 18 )
23. Какая связь удаляется при определении кинематическим методом продольной силы
в сечении стержневого элемента? Что появляется в сечении в результате удаления
связи? ( 19 )
24. Какой смысл имеет величина dS в случае определения продольной силы N ? ( 20 )
25. На чём основан энергетический метод определения силовых факторов
в деформируемых системах? ( 21 )
26. Аналитическая запись энергетической теоремы Лагранжа для определения силового
фактора S . ( 21)
_____________________________________________________
*) Только в режиме «Показ слайдов»