Similar presentations:
Энергетические методы определения перемещений
1. Энергетические методы определения перемещений
Работа внешних силРастяжение-сжатие
L
PX
dL
1
APX PX L
2
Кручение
φ
MX
L
1
AM X M X
2
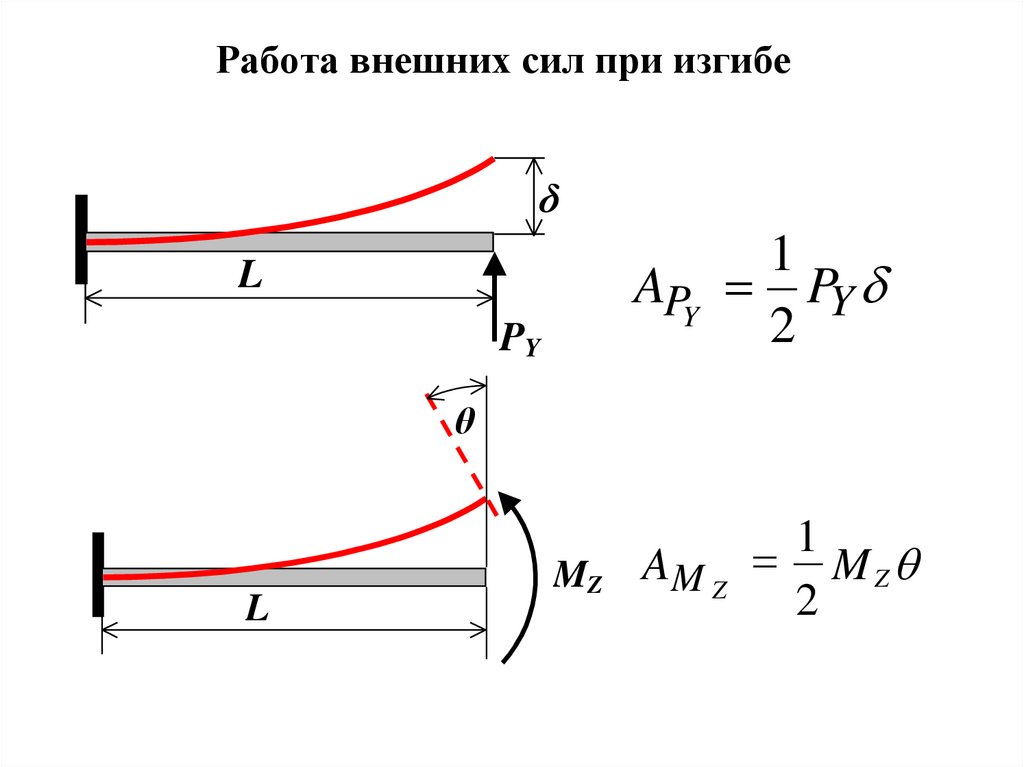
2. Работа внешних сил при изгибе
δ1
APY PY
2
L
PY
θ
L
MZ
1
AM Z M Z q
2
3. Обобщенная работа внешних сил
Формулы можно обобщитьAPОБ
1
PОБ ОБ
2
где РОБ – обобщенная сила, т.е. любое силовое воздействие,
любой силовой фактор;
δОБ - обобщенное перемещение, т.е. тот вид перемещения,
на котором РОБ совершает работу.
Каждый из шести известных силовых факторов совершает работу на
своем перемещении
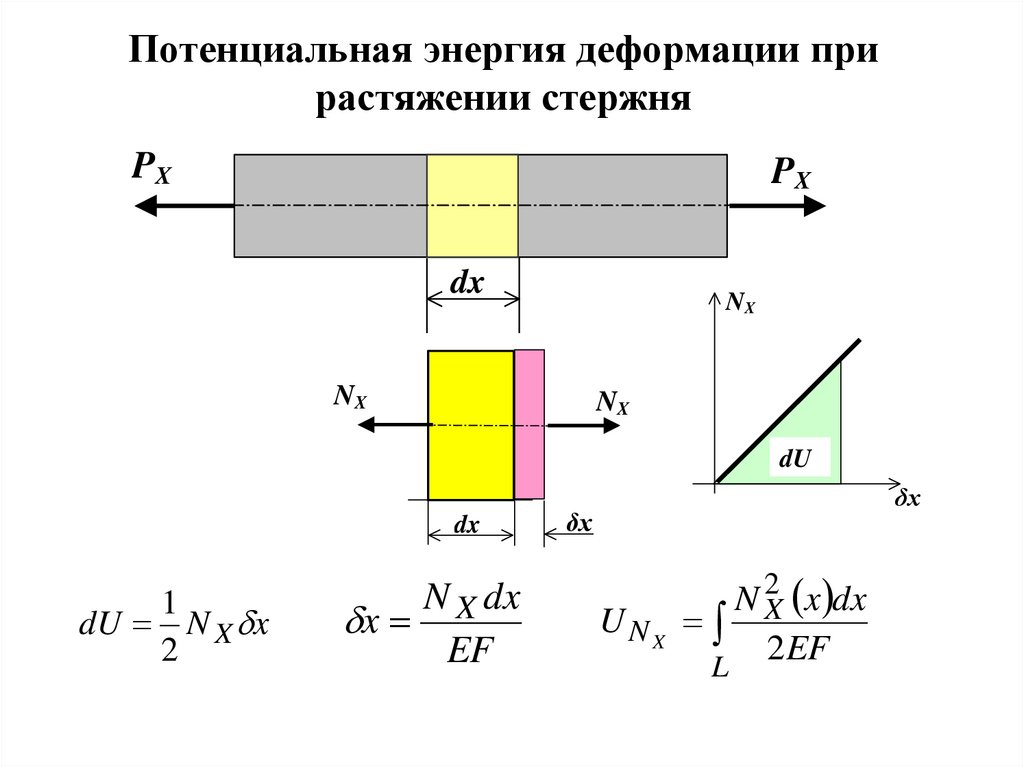
4. Потенциальная энергия деформации при растяжении стержня
PXPX
dx
NX
NX
NX
dU
dx
1
dU N X x
2
N X dx
x
EF
δx
δx
2
x dx
NX
UNX
2 EF
L
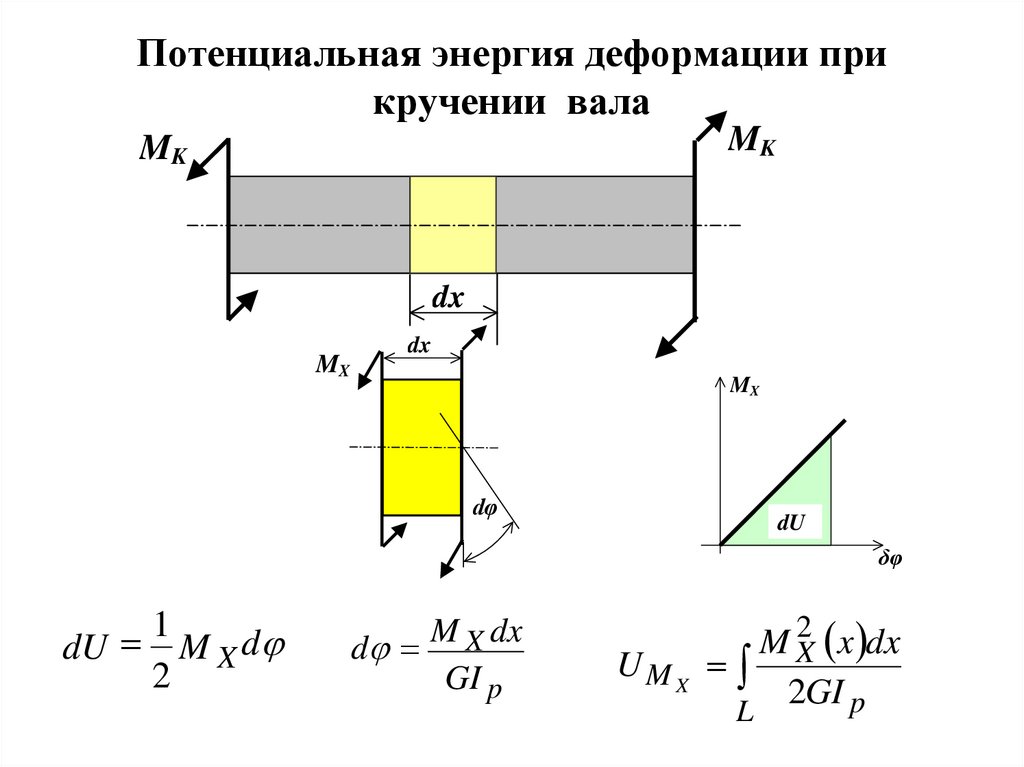
5. Потенциальная энергия деформации при кручении вала
MKMK
dx
MX
dx
MX
dφ
dU
δφ
1
dU M X d
2
M dx
d X
GI p
2
MX
x dx
UMX
2GI p
L
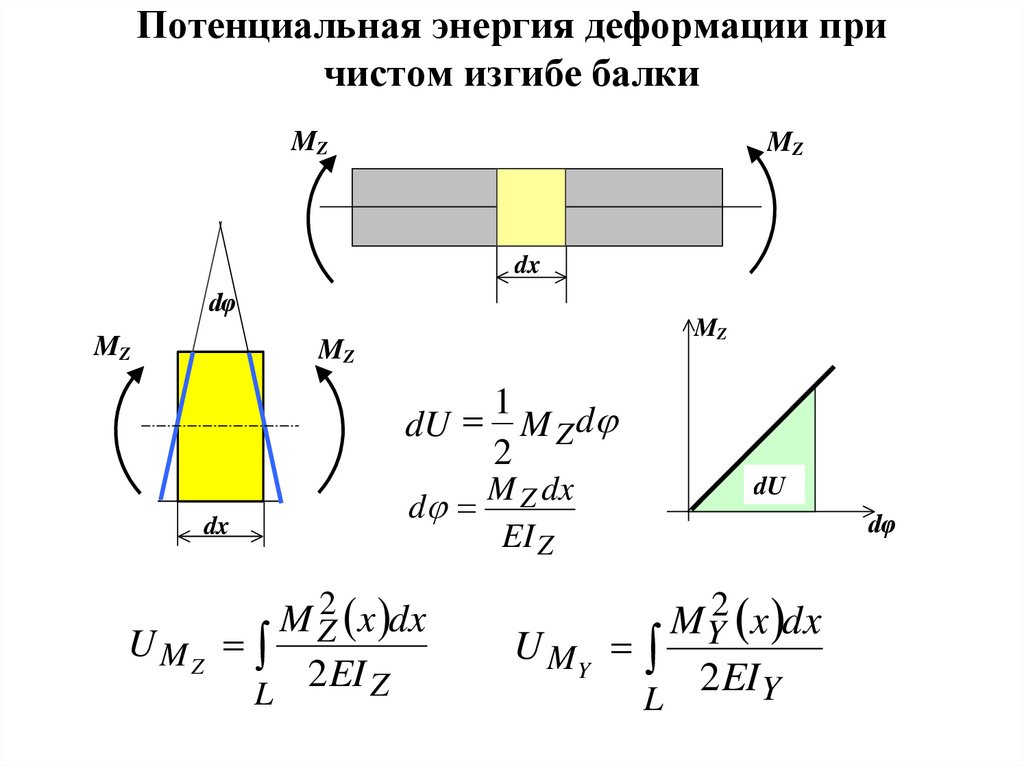
6. Потенциальная энергия деформации при чистом изгибе балки
MZMZ
dx
dφ
MZ
MZ
MZ
dx
1
dU
M Z d
2
M dx
d Z
M Z2 x dx
UMZ
2 EI Z
L
dU
EI Z
M Y2 x dx
U MY
2 EI Y
L
dφ
7. Потенциальная энергия бруса при сложном нагружении
Каждому силовому фактору соответствуют перемещения, накоторых остальные силовые факторы не совершают работу.
Поэтому потенциальная энергия деформации при сложном
нагружении равна сумме потенциальных энергий шести отдельных
факторов. Пренебрегая энергией деформации, связанной с
поперечными силами, получаем для полной энергии деформации
U U N X U M X U MY U M Z ,
2
2
NX
x dx
MX
x dx
M Y2 x dx
M Z2 x dx
U
.
2
EF
2
GI
2
EI
2
EI
p
Y
Z
L
L
L
L
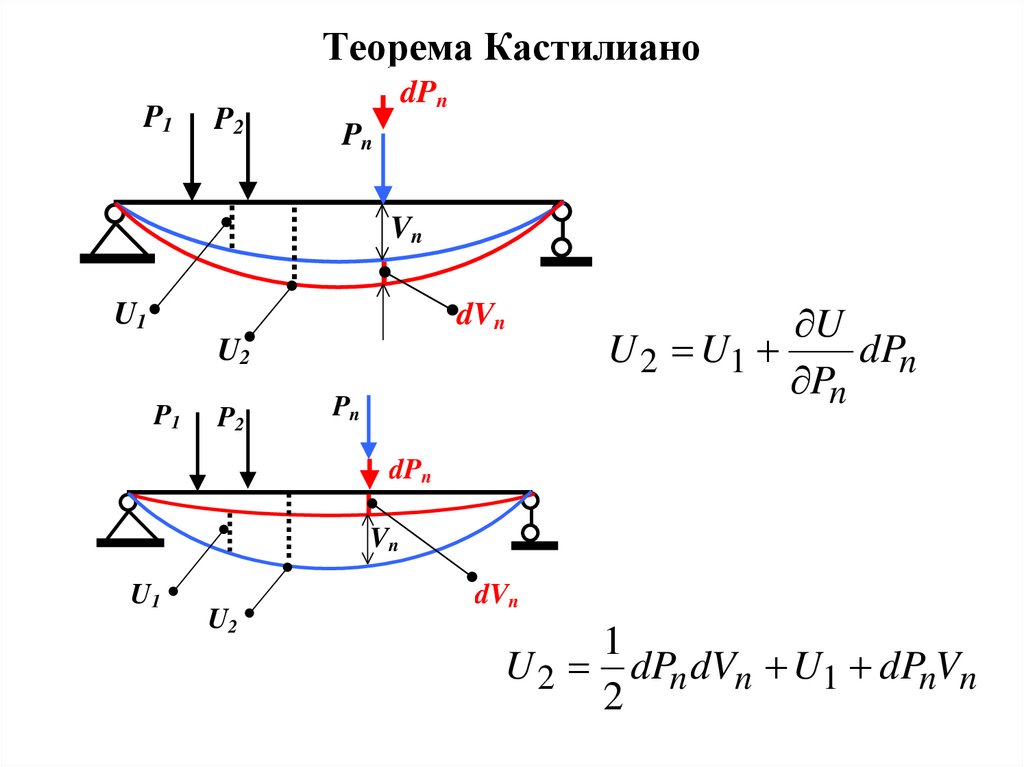
8. Теорема Кастилиано
P1P2
dPn
Pn
Vn
U1
dVn
U2
P1
P2
Pn
U
U 2 U1
dPn
Pn
dPn
Vn
U1
U2
dVn
1
U 2 dPn dVn U1 dPnVn
2
9. Теорема Кастилиано (продолжение)
U1
U1
dPn dPn dVn U1 dPnVn .
Pn
2
1
Пренебрегая членом второго порядка малости dPn dVn , получаем
2
аналитическую формулировку теоремы Кастилиано
U
Vn
Pn
или
U
VОБ
PОБ
Частная производная от потенциальной энергии системы
по силе равна перемещению точки приложения силы вдоль
направления действия этой силы.
10. Пример применения теоремы Кастилиано
Mx
O
A
L
Требуется найти угол поворота сечения θA и прогиб конца балки δA .
M Z2 x dx 1 M 2 L
MZ (x) = M = const
U
2 EI Z
2 EI Z
L
U
ML
qА
M EI Z
Но как найти прогиб конца балки δA ?
11. Пример применения теоремы Кастилиано (метод фиктивной силы)
MPФ
x
O
A
L
M Z M PФ x
M PФ x 2 dx 1 M 2 L MPФ L2 PФ2 L3
U
2 EI
2 EI
2 EI
6 EI
L
Z
Z
Z
Z
U
ML2
А
PФ PФ 0 2 EI Z
Отмерим, что можно дифференцировать и под знаком интеграла.
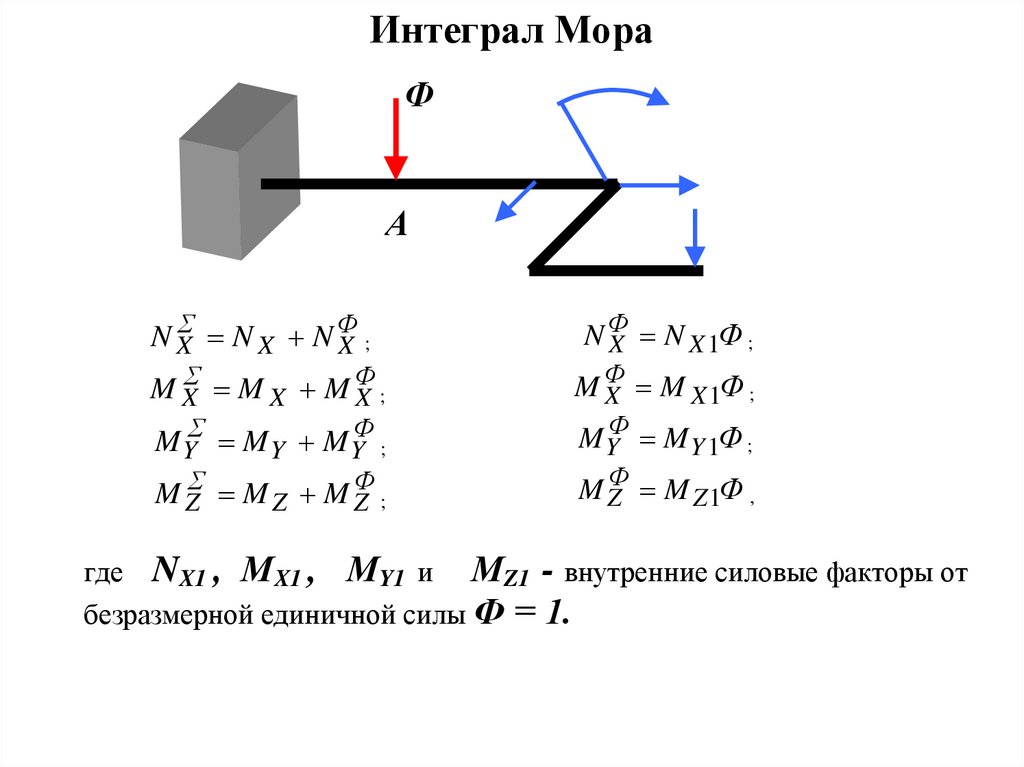
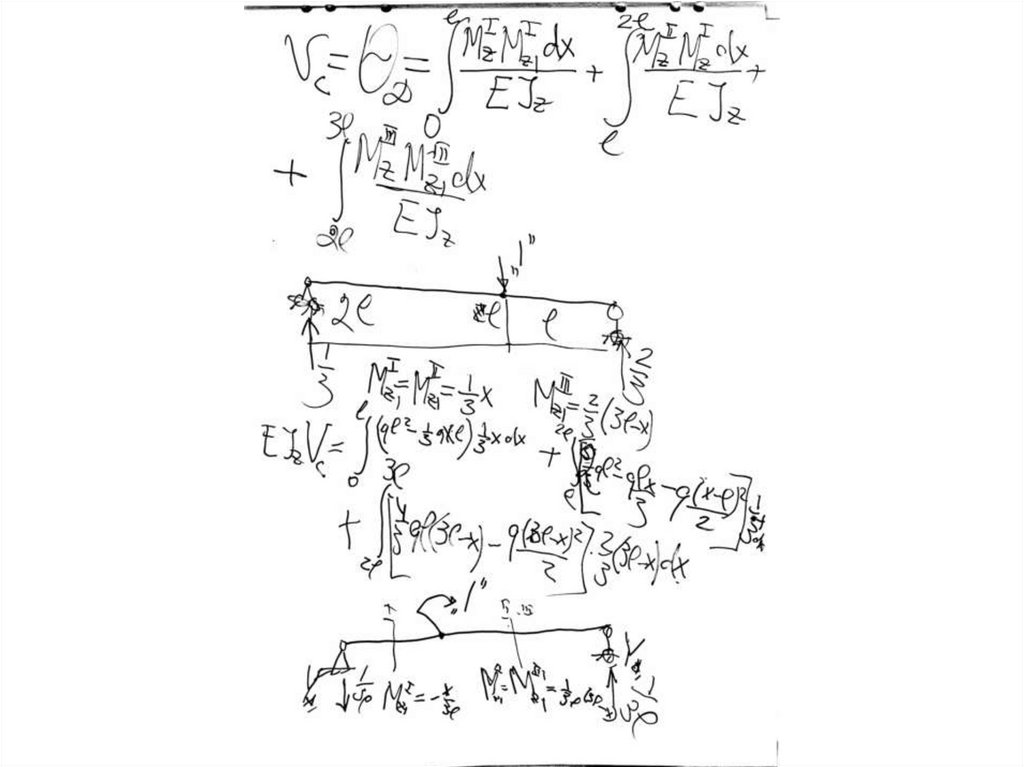
12. Интеграл Мора
ФА
N NФ
NX
X
X ;
NФ
X N X 1Ф ;
M MФ
MX
X
X;
MФ
X M X 1Ф ;
M Z M Z M ZФ ;
M ZФ M Z 1Ф ,
M Y M Y M YФ ;
M YФ M Y 1Ф ;
где NX1 , МX1 , МY1 и МZ1 - внутренние силовые факторы от
безразмерной единичной силы Ф = 1.
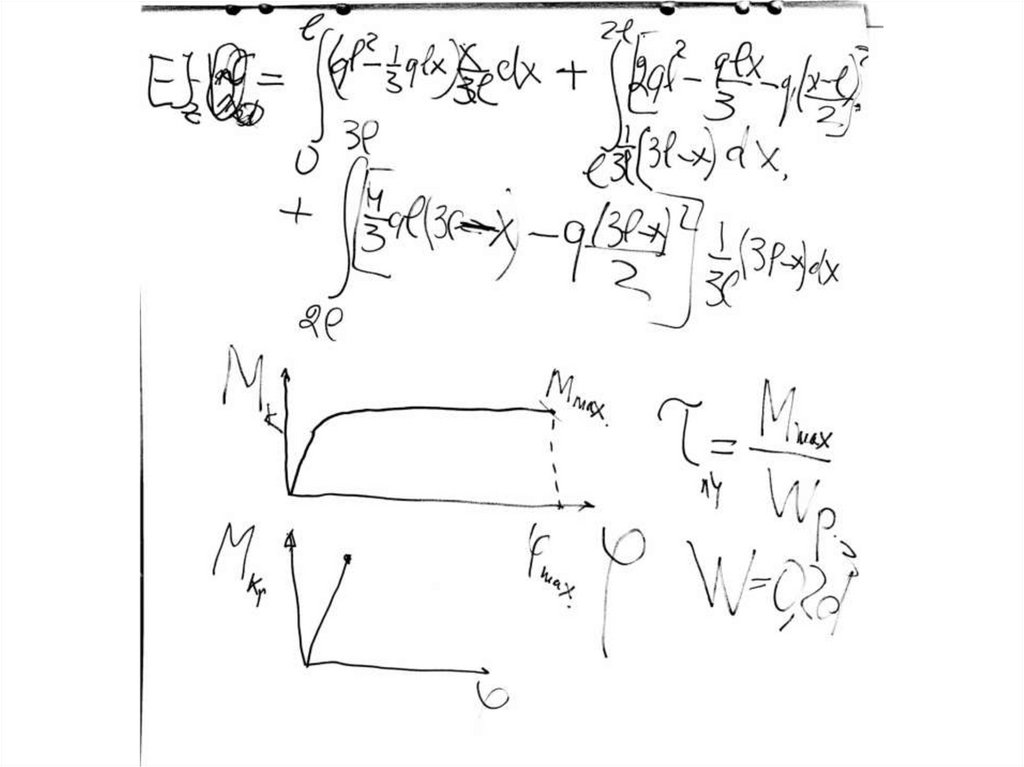
13. Интеграл Мора (продолжение)
N X N1X Ф 2 dxM X M X 1Ф 2 dx
U
...
2 EF
2GI
L
p
L
M Y M1Y Ф 2 dx
M Z M Z1Ф 2 dx
2 EI
2 EI
L
Y
L
Z
N X N1 X dx
M X M 1X dx
U
А
...
2GI p
Ф Ф 0 L 2 EF
L
M Y M 1Y dx
M Z M 1Z dx
2 EI Y
2 EI Z
L
L
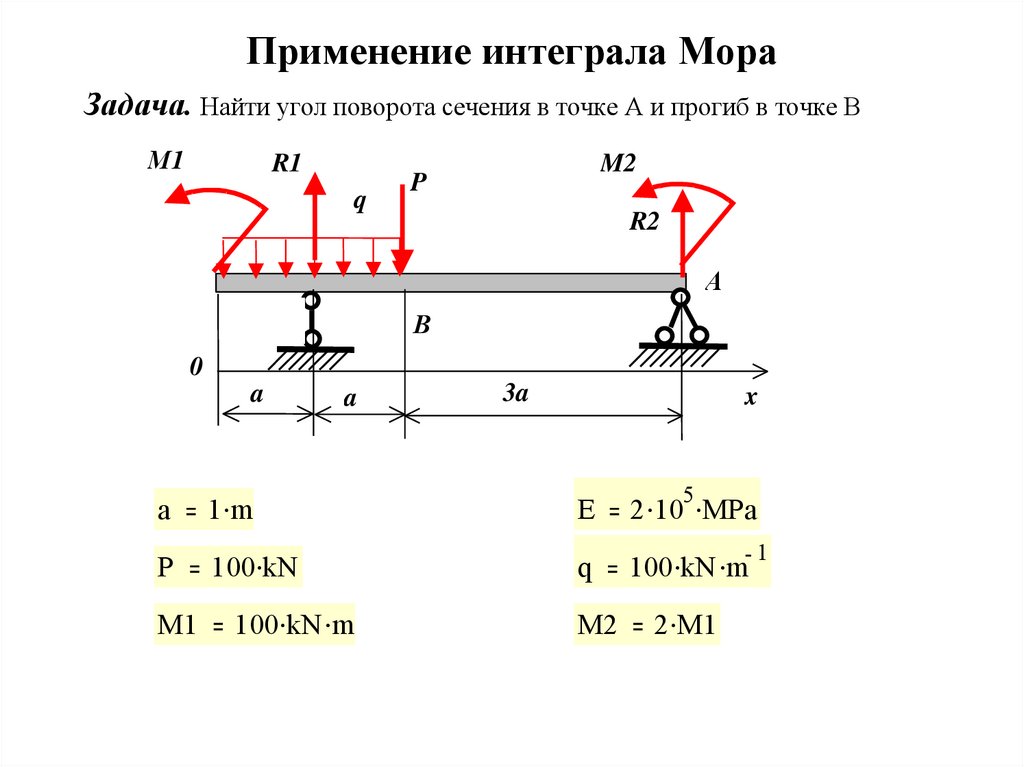
14. Применение интеграла Мора
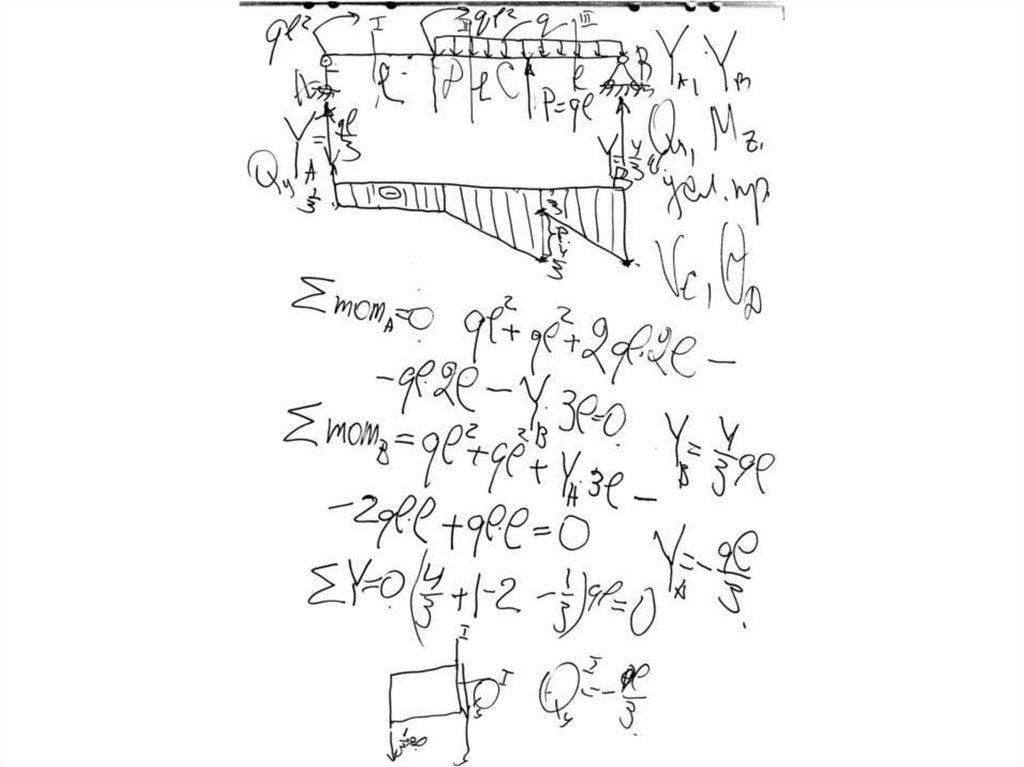
Задача. Найти угол поворота сечения в точке А и прогиб в точке ВМ1
R1
q
M2
P
R2
А
В
0
a
a
3a
x
a
1 m
E
5
2 10 MPa
P
100 kN
q
1
100 kN m
M2
2 M1
M1
100 kN m
15. Применение интеграла Мора
• Определим опорные реакции• Отметим, что M1=Pa, M2=2M1, тогда R2=-P/2
и R1=7P/2, то есть
16. Применение интеграла Мора (продолжение 1)
Найдем опорные реакцииGiven
R2
M1
q 2 a 4 a
R1
R2
P
q 2 a 0
R1
R1 4 a
P 3 a
M2 0
Find ( R1 R2 )
R1 350 kN
R2 50 kN
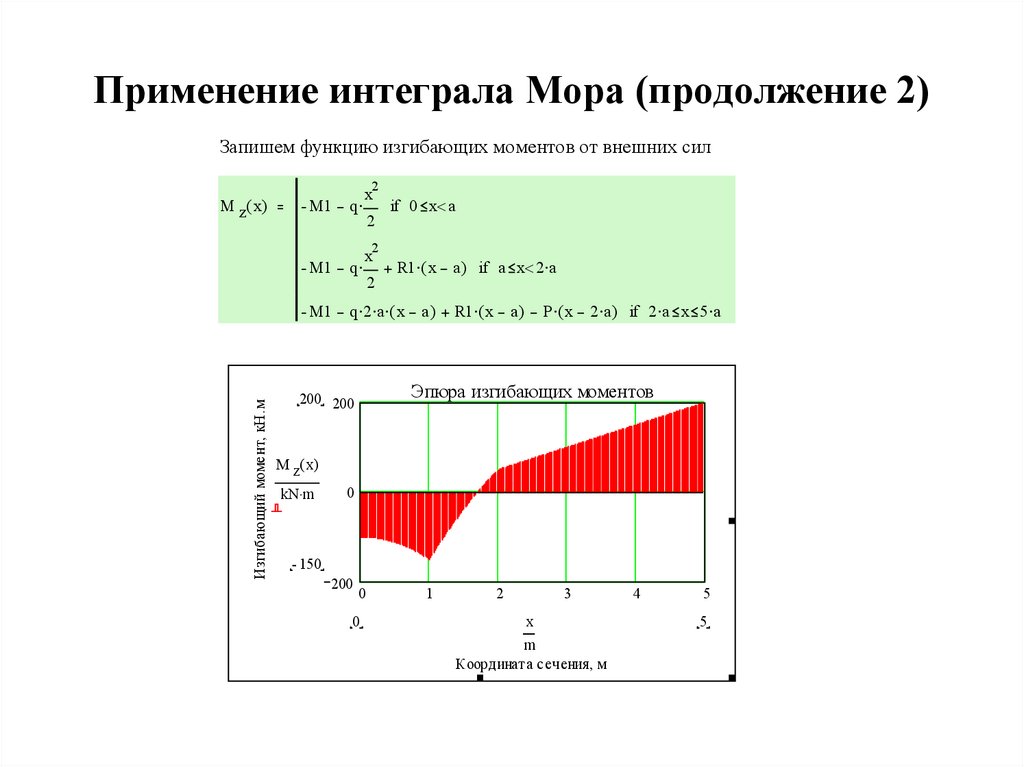
17. Применение интеграла Мора (продолжение 2)
Запишем функцию изгибающих моментов от внешних сил2
M z( x)
M1
x
q
if 0 x a
2
2
M1
Изгибающий момент, кН.м
M1
x
q
R1 ( x a ) if a x 2 a
2
q 2 a ( x a ) R1 ( x a ) P ( x 2 a ) if 2 a x 5 a
Эпюра изгибающих моментов
200 200
M z( x)
kN m
0
150
200
0
0
1
2
3
x
m
Координата сечения, м
4
5
5
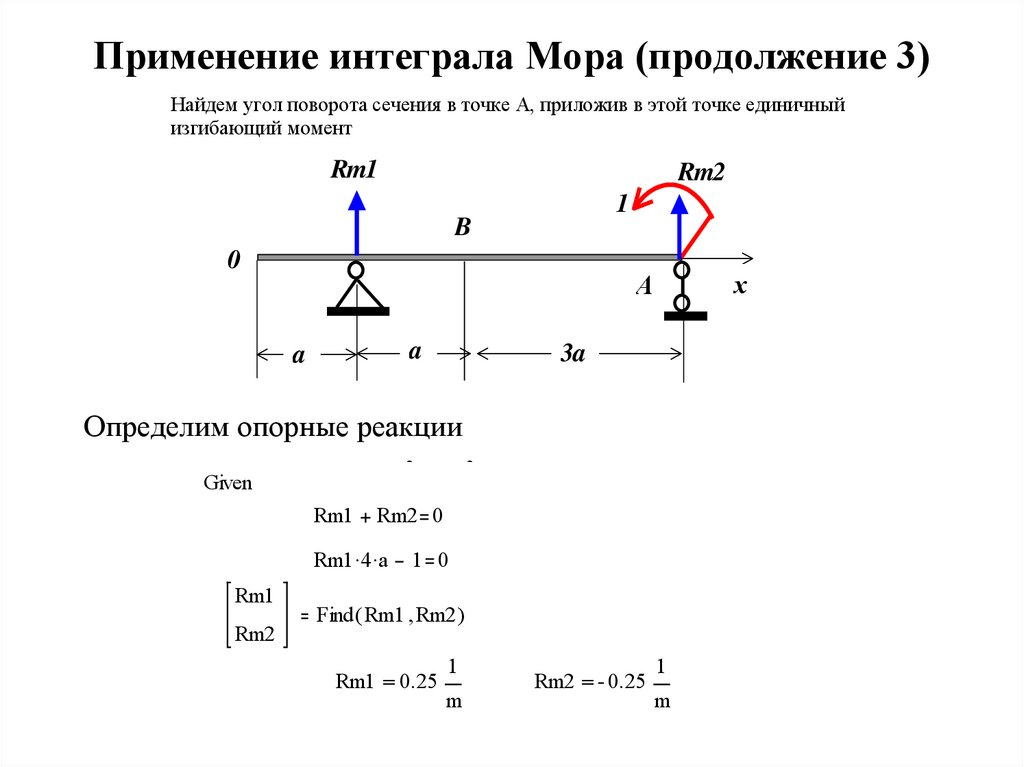
18. Применение интеграла Мора (продолжение 3)
Найдем угол поворота сечения в точке А, приложив в этой точке единичныйизгибающий момент
Rm1
Rm2
1
B
0
х
А
a
a
3a
Определим опорные реакции
Найдем опорные реакции
Given
Rm1
Rm2 0
Rm1 4 a
Rm1
Rm2
1 0
Find ( Rm1 Rm2 )
Rm1 0.25
1
m
Rm2 0.25
1
m
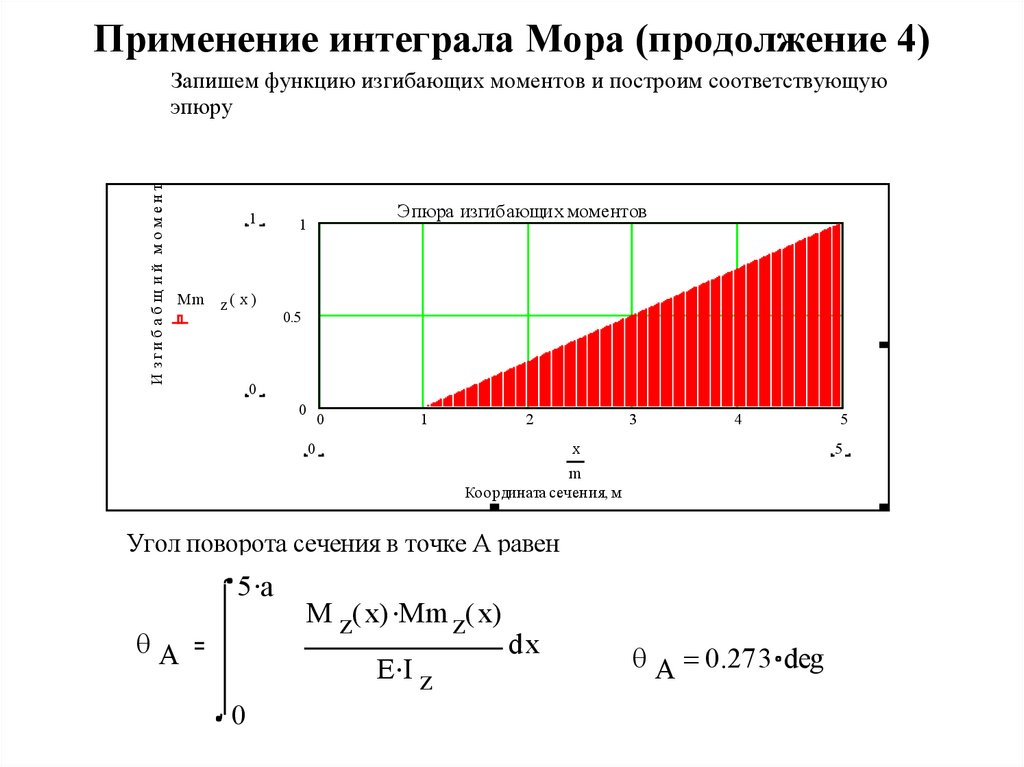
19. Применение интеграла Мора (продолжение 4)
И зги б а б щ и й м о м е н тЗапишем функцию изгибающих моментов и построим соответствующую
эпюру
1
Mm
z( x )
Эпюра изгибающи х моментов
1
0.5
0
0
0
1
2
0
3
4
x
5
m
Координата сечения, м
Угол поворота сечения в точке А равен
5 a
qA
M z( x) Mm z( x)
E I z
0
dx
5
q A 0.273 deg
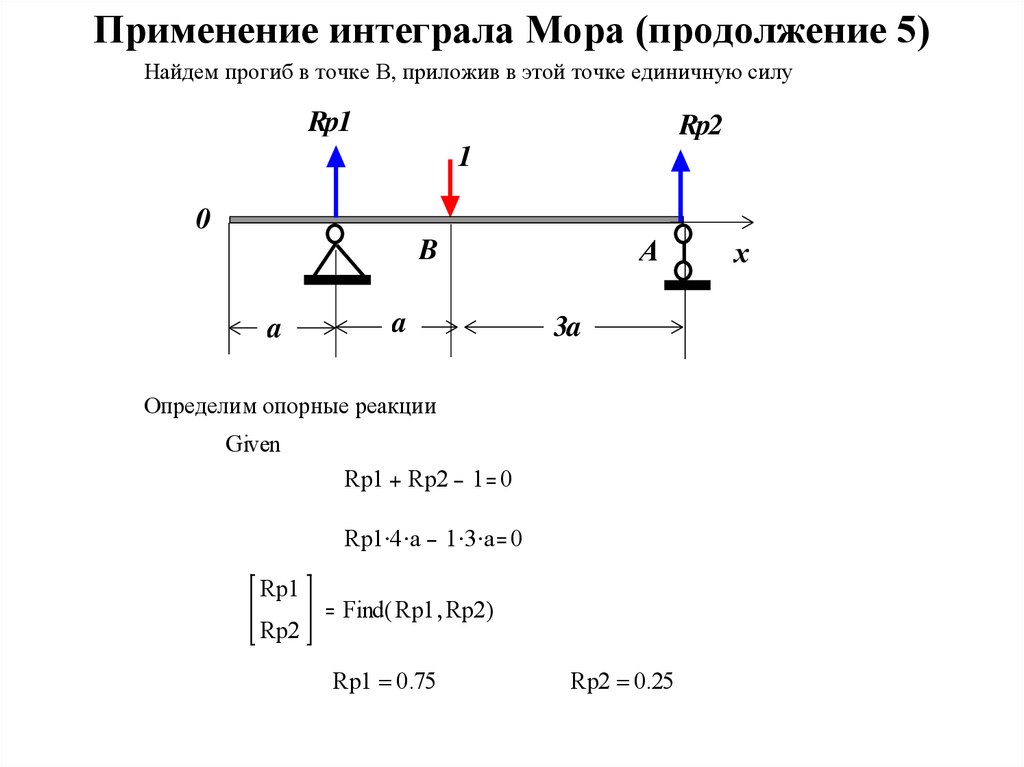
20. Применение интеграла Мора (продолжение 5)
Найдем прогиб в точке В, приложив в этой точке единичную силуRp1
Rp2
1
0
А
B
a
a
3a
Определим опорные реакции
Given
Rp1
Rp2 1 0
Rp1 4 a
Rp1
Rp2
1 3 a 0
Find( Rp1 Rp2)
Rp1 0.75
Rp2 0.25
х
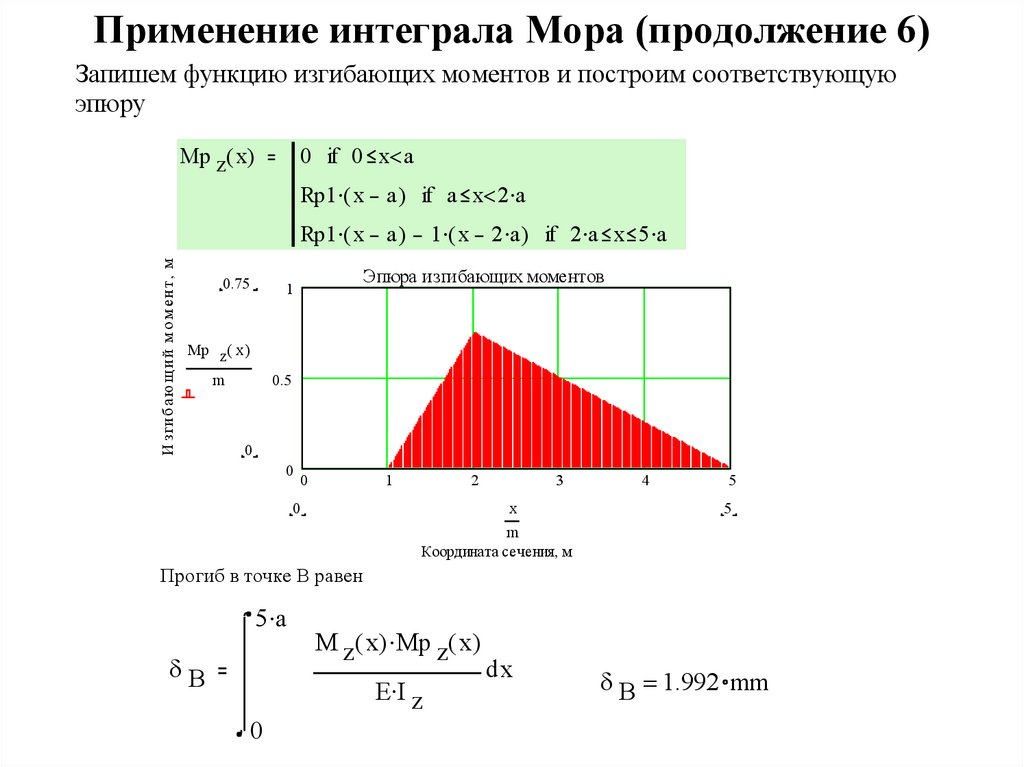
21. Применение интеграла Мора (продолжение 6)
Запишем функцию изгибающих моментов и построим соответствующуюэпюру
0 if 0 x a
Rp1 ( x a ) if a x 2 a
Mp z( x)
И зги б а ю щ и й м о м е н т , м
Rp1 ( x a )
0.75
1 ( x 2 a ) if 2 a x 5 a
Эпюра изгибающих моментов
1
Mp z( x )
m
0.5
0
0
0
1
2
0
3
x
4
5
5
m
Координата сечения, м
Прогиб в точке В равен
5 a
B
M z( x) Mp z( x)
E I z
0
dx
B 1.992 mm











 mechanics
mechanics








