Формула Мора. Правило Верещагина

1.

Формула Мора.
Правило Верещагина.

2. 1. Интеграл Мора

Используется в тех случаях, когда требуется найти перемещение в
направлении не совпадающем с направлением действия сил.
Сущность интеграла Мора в следующем идеальном построении:
1. Прикладываем в интересующем направлении внешнюю силу Ф.
2. Составляем для системы выражение для потенциальной энергии
деформации U.
3. Дифференцируем выражение для U по Ф и получаем выражение для
перемещения в направлении действия Ф (то есть в интересующем
направлении)
4. В полученном выражении приравниваем Ф=0, получаем окончательное
выражение.

3.

Фиктивную силу Ф представляем в виде произведения
скалярной величины Ф на единичный силовой фактор в
соответствующем направлении.
Таким образом фиктивная сила в зависимости от
интересующего нас направления будет выражена:
N1Ф - в случае продольной силы. Определяем продольное
перемещение. N1 – единичная продольная сила
приложенная в интересующей нас точке.
Qz1Ф - в случае горизонтальной перерезывающей силы.
Определяем прогиб в горизонтальной плоскости. Qz1 –
единичная горизонтальная перерезывающая сила
приложенная в интересующей нас точке.
Q y1Ф - в случае вертикальной перерезывающей силы.
Определяем прогиб в вертикальной плоскости. Qy1 –
единичная горизонтальная перерезывающая сила
приложенная в интересующей нас точке.

4.

M K1Ф - в случае крутящего момента. Определяем угол
закручивания. MK1 – единичный крутящий момент
приложенный в интересующей нас точке.
M y1Ф - в случае момента изгибающего в горизонтальной
плоскости. Определяем угол поворота сечения в
горизонтальной плоскости. My1 – единичный
изгибающий момент в горизонтальной плоскости
приложенный в интересующей нас точке.
M z1Ф - в случае момента изгибающего в вертикальной
плоскости. Определяем угол поворота сечения в
вертикальной плоскости. Mz1 – единичный изгибающий
момент в вертикальной плоскости приложенный в
интересующей нас точке.

5.

После приложения фиктивной силы Ф значения силовых
факторов в интересующем сечении будут равны сумме
значений силовых факторов от исходной системы сил и от
силы Ф.
N N P N1Ф; Qу QуP Qу1Ф; Qz QzP Qz1Ф;
M K M KP M K 1Ф; M y M yP M y1Ф; M y M zP M z1Ф.
N P , QyP , QzP , M KP , M yP , M zP - значения силовых факторов
до приложения силы Ф. (То есть в реально существующей
системе)
Подставляем в формулу для внутренней энергии:
N P N1Ф dx
U
l
0
l
0
2
2 EA
0
M KP M K 1Ф dx
2
2GI K
k y QyP Q y1Ф dx
2
l
l
0
2GA
M M Ф dx
2
yP
y1
2 EI y
l
0
l
0
k z QzP Qz1Ф dx
2
2GA
M zP M z1Ф 2 dx
2 EI z

6.

Дифференцируя по Ф, и принимая после этого Ф=0, находим
перемещение.
(формулы громоздкие, поэтому на примере одного
слагаемого)
l
2
N P N1Ф dx
Ф 0
2 EA
l
2
N P dx
Ф 0 2 EA
Ф 0
l
2
2
N P 2 N P N1Ф N1Ф dx
Ф 0
2 EA
2 N P N1Фdx
Ф 0
2 EA
l
Ф 0
N1Ф dx
Ф 0 2 EA
l
Ф 0
l 2 N P N1Ф
l N1Ф 2
0
dx
dx
0 Ф 2 EA Ф 0 0 Ф 2 EA
Ф 0
l
l N P N1
l 2 N1Ф
N P N1
dx
dx
dx
0 EA
Ф 0 0 2 EA Ф 0 0 EA
Ф 0
2
Ф 0

7.

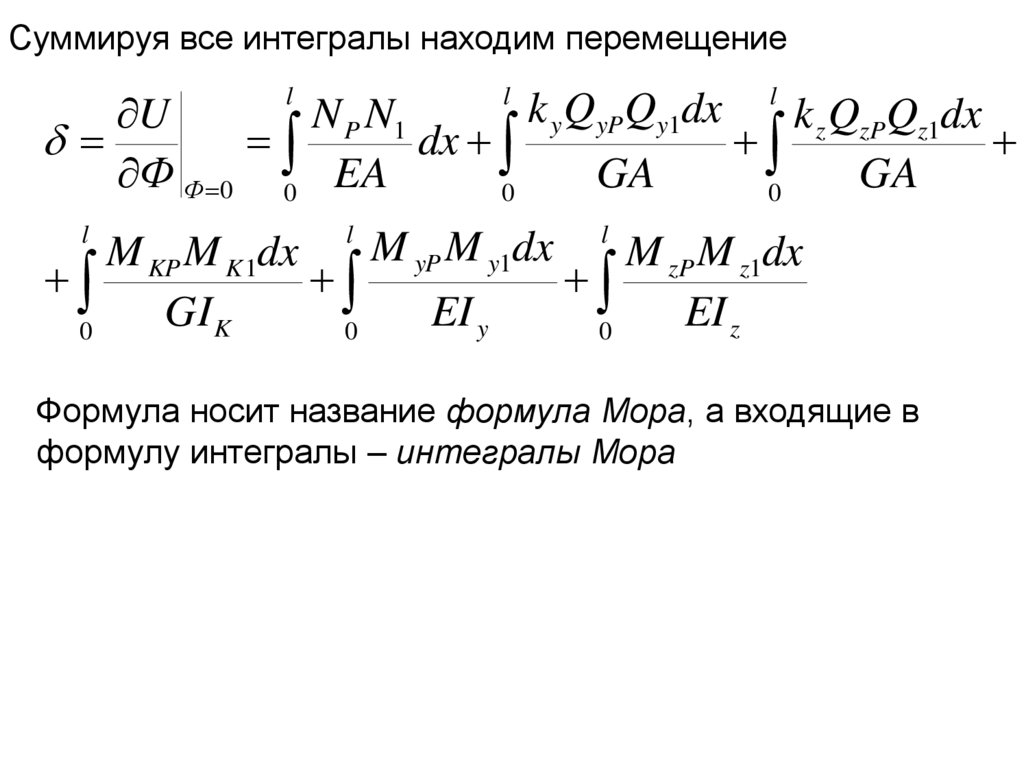
Суммируя все интегралы находим перемещение
l
k
Q
Q
dx
U
N P N1
k z QzPQz1dx
y yP y1
dx
Ф Ф 0 0 EA
GA
GA
0
0
l
l
l
l
l
M
M
dx
M KP M K 1dx
M zP M z1dx
yP
y1
GI K
EI y
EI z
0
0
0
Формула носит название формула Мора, а входящие в
формулу интегралы – интегралы Мора

8.

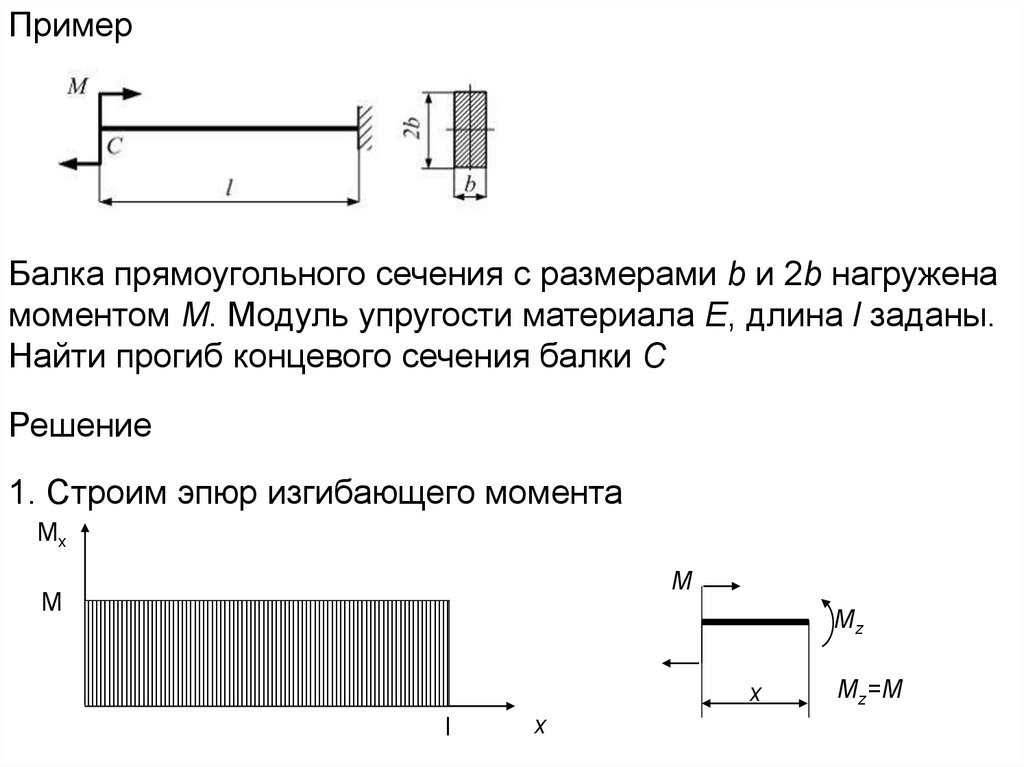
Пример
Балка прямоугольного сечения с размерами b и 2b нагружена
моментом М. Модуль упругости материала Е, длина l заданы.
Найти прогиб концевого сечения балки С
Решение
1. Строим эпюр изгибающего момента
Мx
M
М
Mz
x
l
x
Mz=M

9.

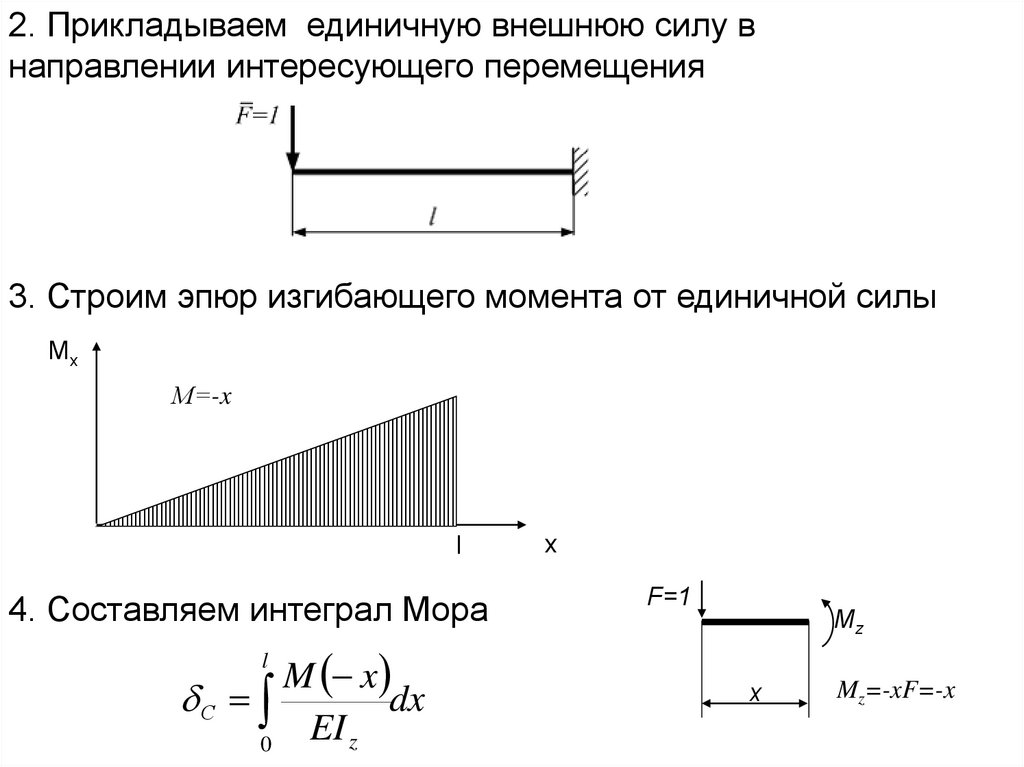
2. Прикладываем единичную внешнюю силу в
направлении интересующего перемещения
3. Строим эпюр изгибающего момента от единичной силы
Мx
М=-x
l
4. Составляем интеграл Мора
M x
С
dx
EI z
0
x
F=1
Mz
l
x
Mz=-xF=-x

10.

5. Вычисляем интеграл
b 2b
Iz
12
3
12 M x
3 M
3 Ml 2
x dx
С
dx
4
4
4
E
8
b
2
Eb
4
Eb
0
0
l
l

11.

Интеграл Мора можно использовать для определения перемещений как
прямолинейных, так и криволинейных стержневых систем.
Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней
вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ
где ρ - радиус кривизны стержня, который может быть постоянным, а может быть
функцией от угловой координаты φ.
ρ
2
M zP M z1
d
EI z
1
dφ
φ1
φ
φ2
ds

12.

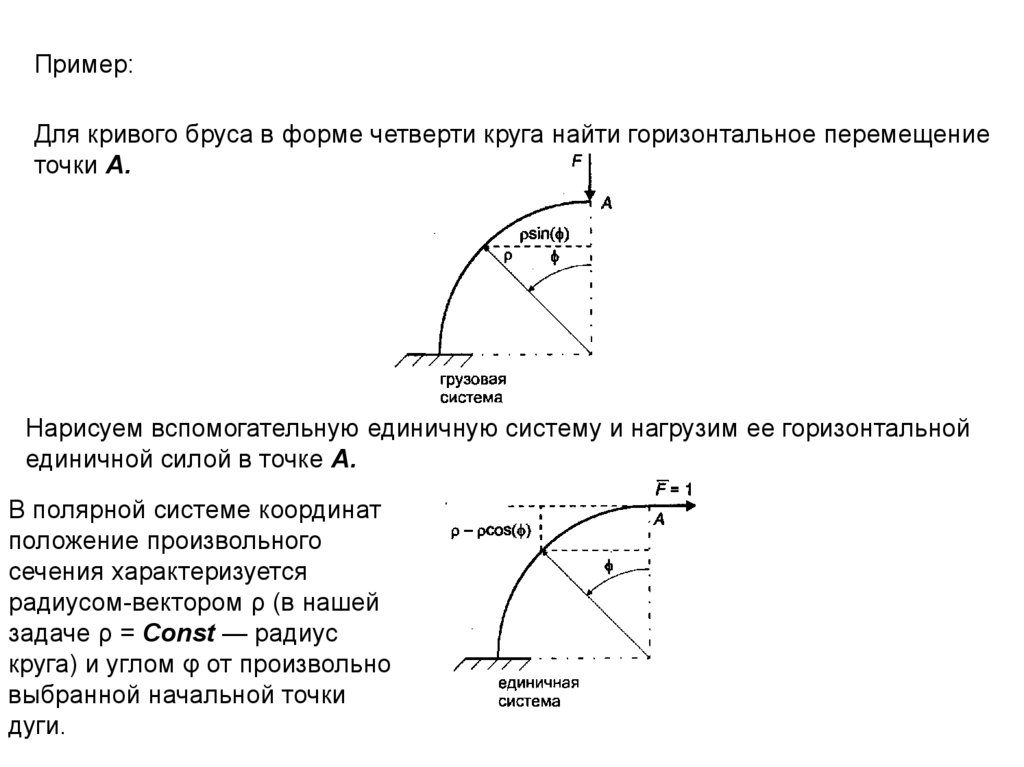
Пример:
Для кривого бруса в форме четверти круга найти горизонтальное перемещение
точки А.
Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной
единичной силой в точке А.
В полярной системе координат
положение произвольного
сечения характеризуется
радиусом-вектором ρ (в нашей
задаче ρ = Const — радиус
круга) и углом φ от произвольно
выбранной начальной точки
дуги.

13.

M F F sin
Изгибающий момент от внешних сил
1 1 cos 1 cos
Изгибающий момент от единичной силы M1
Горизонтальное перемещение точки А
M F M1
F sin 1 cos
F 3
Aгор
d
d
EI z
EI z
2 EI z
1
0
2
2
2
sin ( ) ( 1 cos ( ) )
d 0.5
1
0

14.

Правило Верещагина
Правило Верещагина – графо-аналитический метод,
позволяющий упростить вычисления интегралов, входящих в
формулу Мора. Упрощение основано на том, что эпюры от
единичных силовых факторов на прямолинейных участках
оказываются линейными.
Предположим, что необходимо взять интеграл от
произведения двух функций
l
J f1 ( z ) f 2 ( z )dz
0
Пусть вторая из этих функций - линейная f 2 ( z ) b kz
Тогда
l
l
J b f1 ( z )dz k zf1 ( z )dz
0
0
Первый интеграл – площадь эпюры f1(z)
l
f ( z)dz
1
0
Второй интеграл – статический момент этой эпюры
относительно оси ординат
1

15.

По свойству статического момента
l
zЦТ – координата
0 zf1 ( z)dz 1 zЦТ центра тяжести
первого эпюра
В сумме получаем
J 1b k 1 z ЦТ 1 (b kzЦТ )
Выражение в скобках – значение функции f2 под центром
тяжести первой фигуры
J 1 f 2 ( z ЦТ )
ЦТ
h
ЦТ
h
ЦТ
h
l
l
l
l/2
lh / 3
lh / 2
lh
l /3
l/4

16.

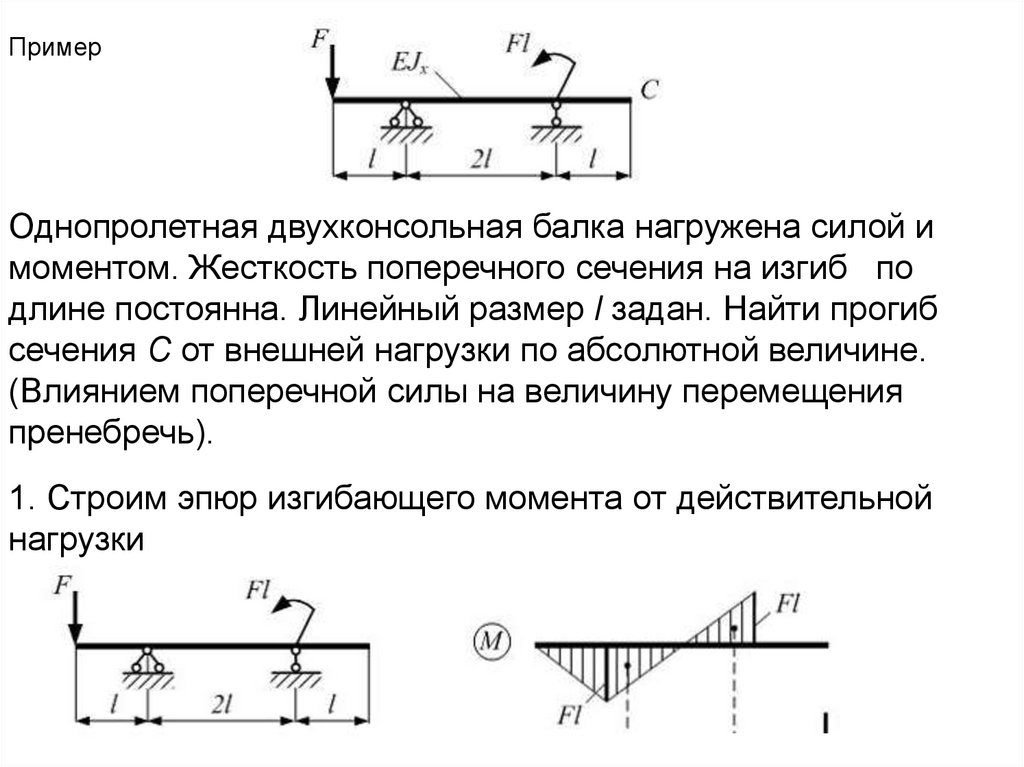
Пример
Однопролетная двухконсольная балка нагружена силой и
моментом. Жесткость поперечного сечения на изгиб по
длине постоянна. Линейный размер l задан. Найти прогиб
сечения С от внешней нагрузки по абсолютной величине.
(Влиянием поперечной силы на величину перемещения
пренебречь).
1. Строим эпюр изгибающего момента от действительной
нагрузки

17.

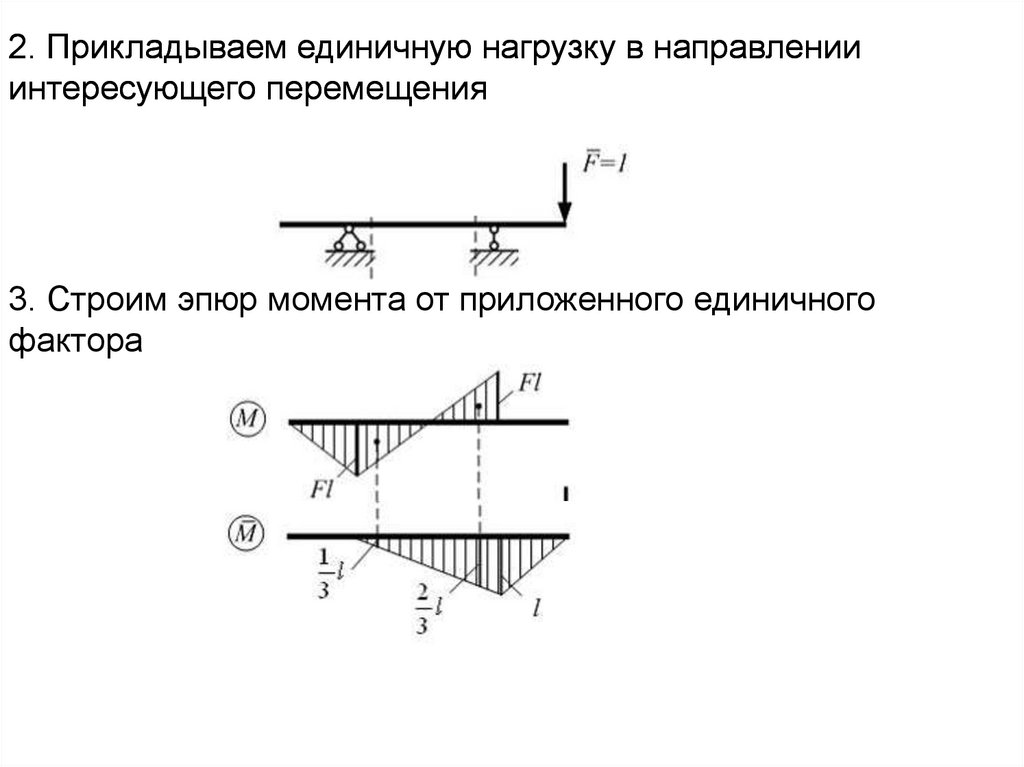
2. Прикладываем единичную нагрузку в направлении
интересующего перемещения
3. Строим эпюр момента от приложенного единичного
фактора

18.

4. Находим интеграл Мора по правилу Верещагина
1 1 2 2 1 2 1
1 Fl 3
с
Fl l Fl l
EJ 2
3 2
3
6 EJ x

19. 3. Формула Мора для определения температурных перемещений сечения по заданному направлению

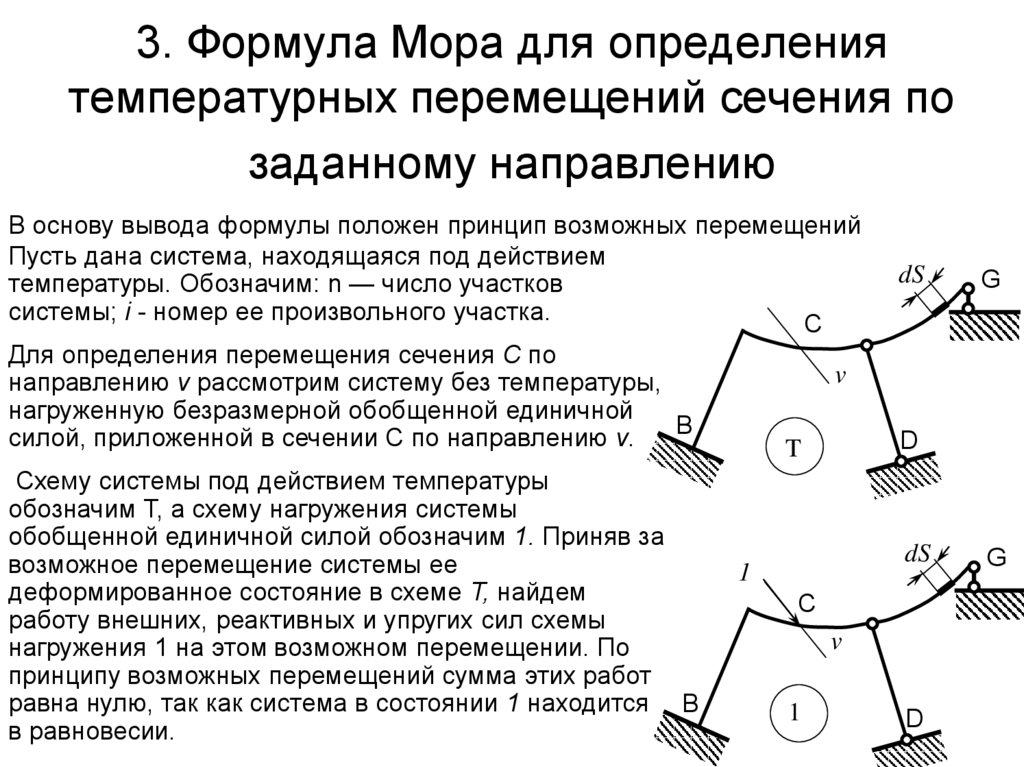
В основу вывода формулы положен принцип возможных перемещений
Пусть дана система, находящаяся под действием
температуры. Обозначим: n — число участков
системы; i - номер ее произвольного участка.
C
Для определения перемещения сечения С по
направлению v рассмотрим систему без температуры,
нагруженную безразмерной обобщенной единичной
B
силой, приложенной в сечении С по направлению v.
Схему системы под действием температуры
обозначим Т, а схему нагружения системы
обобщенной единичной силой обозначим 1. Приняв за
возможное перемещение системы ее
деформированное состояние в схеме Т, найдем
работу внешних, реактивных и упругих сил схемы
нагружения 1 на этом возможном перемещении. По
принципу возможных перемещений сумма этих работ
равна нулю, так как система в состоянии 1 находится B
в равновесии.
dS
G
v
D
T
dS
1
C
v
1
D
G

20.

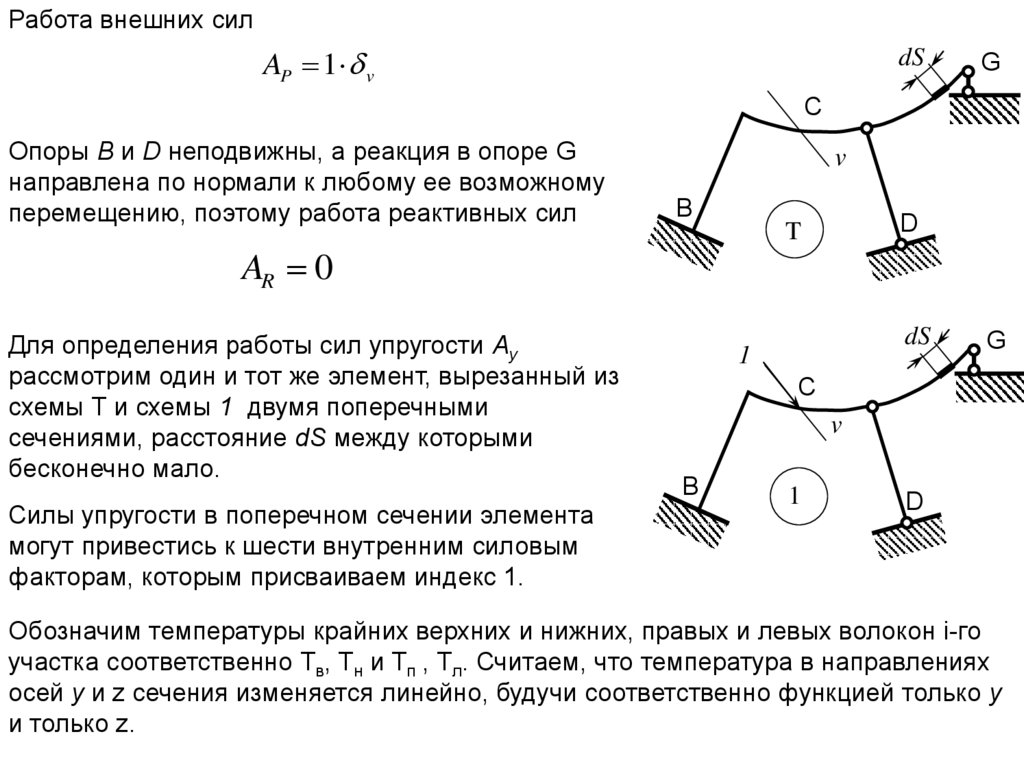
Работа внешних сил
AP 1 v
dS
G
C
Опоры В и D неподвижны, а реакция в опоре G
направлена по нормали к любому ее возможному
перемещению, поэтому работа реактивных сил
v
B
AR 0
Для определения работы сил упругости Ау
рассмотрим один и тот же элемент, вырезанный из
схемы Т и схемы 1 двумя поперечными
сечениями, расcтояние dS между которыми
бесконечно мало.
Силы упругости в поперечном сечении элемента
могут привестись к шести внутренним силовым
факторам, которым присваиваем индекс 1.
D
T
dS
1
G
C
v
B
1
D
Обозначим температуры крайних верхних и нижних, правых и левых волокон i-го
участка соответственно Тв, Tн и Тп , Tл. Считаем, что температура в направлениях
осей у и z сечения изменяется линейно, будучи соответственно функцией только у
и только z.

21.

Законы изменения температуры по поперечному сечению показаны на рис.
TB
y z
Очевидно, что
TC
a
C N1
y
C
C'
x
x
z
b
M21
B B'
TC T y y 0 T z z 0
TH
dS
dδT
dS
B
TП
или
A
T(y)
A'
TЛ
Температура на оси
элемента
A
hy
T T
T b TH a
T y B Н y B
a b
a b
T TЛ
T с TЛ d
T z П
z П
с d
c d
TB b TH a TП с TЛ d
a b
c d
c
d
h2
T(z)
Пусть dδT — возможное перемещение центра тяжести поперечного сечения в
схеме от изменения температуры элемента.
d T TC dS
где α - коэффициент линейного расширения материала элемента.
Пусть dθTz - возможный относительный поворот концевых сечений элемента около
оси z в схеме от изменения температуры
T y
d zT
dS
hy
где T y TВ TН , h y - наибольший размер поперечного сечения в направлении оси
у.

22.

По аналогии, возможный относительный поворот концевых сечений элемента
вокруг оси y
Tz
d yT
dS
hz
где Tz TП TЛ , hz - наибольший размер поперечного сечения в направлении оси z.
1. dAy — работа сил упругости в элементе dS по абсолютной величине равна
работе внутренних силовых факторов состояния на возможных перемещениях
состояния и противоположна ей по знаку, так как силы упругости всегда
направлены в сторону, противоположную направлению изменения расстояния
между точками тела.
2. Работа МК1, Qy1 и Qz1 равна нулю, так как концевые сечения элемента при
нагреве относительно оси х не поворачиваются, a Qy1 и Qz1 перпендикулярны
направлению dδT, поэтому
dAy M z1d zT M y1d yT Nd T
Подставляя сюда полученные ранее выражения и интегрируя полученное
выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.
Ty
Tz
Ayi M z1
M y1
N1 Tc ds
hy
hz
si

23.

Суммируя эти интегралы по всем участкам системы, найдем Aу.
Ty
Tz
Ay M z1
M y1
N1 Tc ds
hy
hz
i 1 si
n
Складывая Ар с Ау и приравнивая сумму нулю, получим формулу Мора для
определения температурных перемещений сечений стержневой системы по
заданному направлению:
Ap Ay 0;
Ty
Tz
1 v M z1
M y1
N1 Tc ds 0;
hy
hz
i 1 si
n
Ty
Tz
v M z1
M y1
N1 Tc ds;
hy
hz
i 1 si
n