Метод Максвелла – Мора определения перемещений. Правило Верещагина (лекция 2)

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Лекция 2.
Метод Максвелла – Мора определения
перемещений. Правило Верещагина
Авторы:
к.т.н., Войтко Александр Михайлович
1

2.

Обобщённой силой называется любое однопараметрическое силовое
воздействие: это может быть и сосредоточенная сила, и сосредоточенный момент, и
распределенная нагрузка, и группа сил, связанных между собой.
Обобщенным перемещением, соответствующим заданной обобщенной
силе, называется то перемещение, на котором обобщенная сила совершает
работу.
Два варианта обобщенных сил
и соответствующих им
обобщенных перемещений
2

3.

Деформации балок при изгибе
Приближенная формула Максвелла –
Мора, которая используется для
определения перемещений в
изгибаемых плоских стержневых
системах и не учитывает влияния на
перемещения продольной и
поперечной сил:
(4.21)
Чтобы воспользоваться формулой Максвелла –
Мора, надо:
1) определить изгибающий момент на каждом
участке от заданной нагрузки;
2) освободить конструкцию от заданной нагрузки и
загрузить ее единичной обобщенной силой,
соответствующей искомому перемещению, то есть:
• если мы хотим определить вертикальное
перемещение какой-то точки, то в этой точке следует
приложить сосредоточенную силу, положить ее
равной единице и найти изгибающий момент,
вызванный действием только этой силы;
• если требуется найти угол поворота какого-то
сечения, то в этом сечении надо приложить
сосредоточенную пару, равную единице, и найти
изгибающий момент от этой пары;
3) подставить произведение изгибающих моментов
от нагрузки и от единичной обобщенной силы в
интеграл (4.21) и проинтегрировать по всей длине
конструкции.
3

4.

Введем правило знаков в методе Максвелла – Мора: полученный по формуле
Максвелла – Мора положительный знак перемещения показывает, что искомое
перемещение происходит по направлению, совпадающему с принятым направлением
единичной обобщенной силы, отрицательный знак перемещения говорит о том, что
точки оси перемещаются (сечения поворачиваются) в сторону, противоположную
направлению единичной обобщенной силы.
Правило Верещагина состоит в следующем:
1. Разбиваем эпюру М на простые фигуры, для которых известно положение центра
тяжести (прямоугольники, треугольники и т. п.).
2. Находим площади этих фигур ωk . При определении площадей учитываем знаки
ординат.
3.Под центрами тяжести этих фигур находим ординаты ηk на эпюре Mi (с учетом
знаков).
4. Искомый интеграл будет равен (при постоянной жесткости балки EI = const ) сумме
произведений площадей ωk на соответствующие им ординаты под центрами тяжести ηk
, то есть:
где n – количество фигур, на которые разбита эпюра М.
4

5.

Некоторые полезные формулы для перемножения эпюр
(4.23)
(4.24)
где ординаты a, b, c и d на эпюрах М и Мi
показаны на рисунке, б (берутся с учетом
знаков); l – длина перемножаемого участка эпюр.
5

6.

Пример №1
Выражения для
изгибающих моментов на
трех участка:
участок1: 0≤x1≤a;
M(x1)=F1 x1 −q1 x1 x1 /2;
участок2: 0≤x2≤b;
M(x2)=F 1(a+x2)−q1
a(a/2+x2)−F2 x2 +q2 x2 x2 /2;
участок3: 0≤x3≤c;
M(x3)=MA +RAx3.
6

7.

Подставим записанные выражения в интеграл Максвелла – Мора (4.21) и проинтегрируем
(на первых двух участках интегралы в рассматриваемом примере равны нулю):
(4.21)
7

8.

Чтобы найти прогиб сечения С , приложим в точке С новую единичную обобщенную силу –
сосредоточенную силу, положив ее равной единице (рисунок, в).
Выражения для изгибающих моментов M2(x) на каждом участке от единичной
сосредоточенной силы будут такими:
8

9.

После подстановки функций M(x) и M2(x) в интеграл (4.21) и интегрирования на
каждом участке получим
9

10.

Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила
Верещагина
10

11.

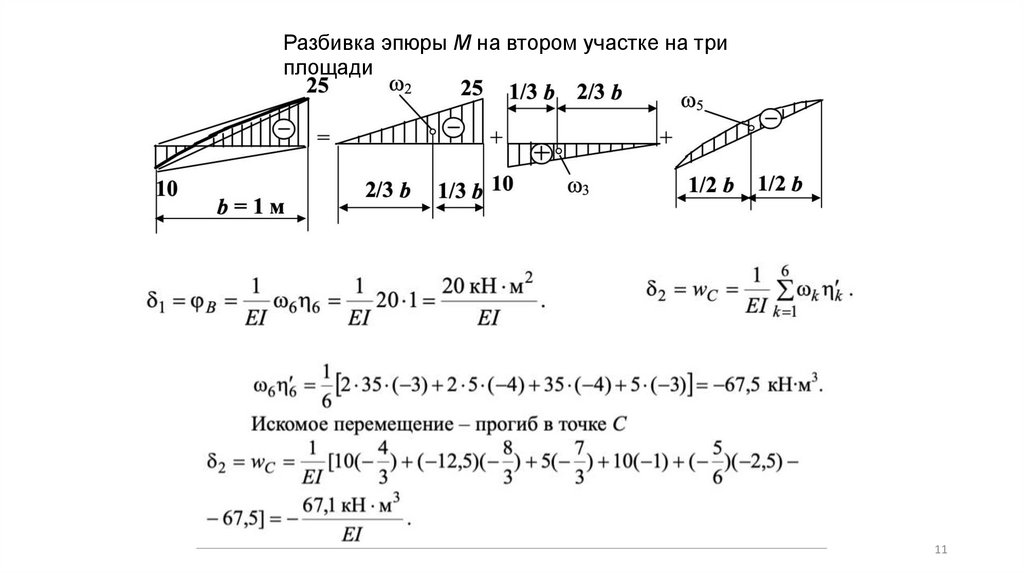
Разбивка эпюры М на втором участке на три
площади
11

12.

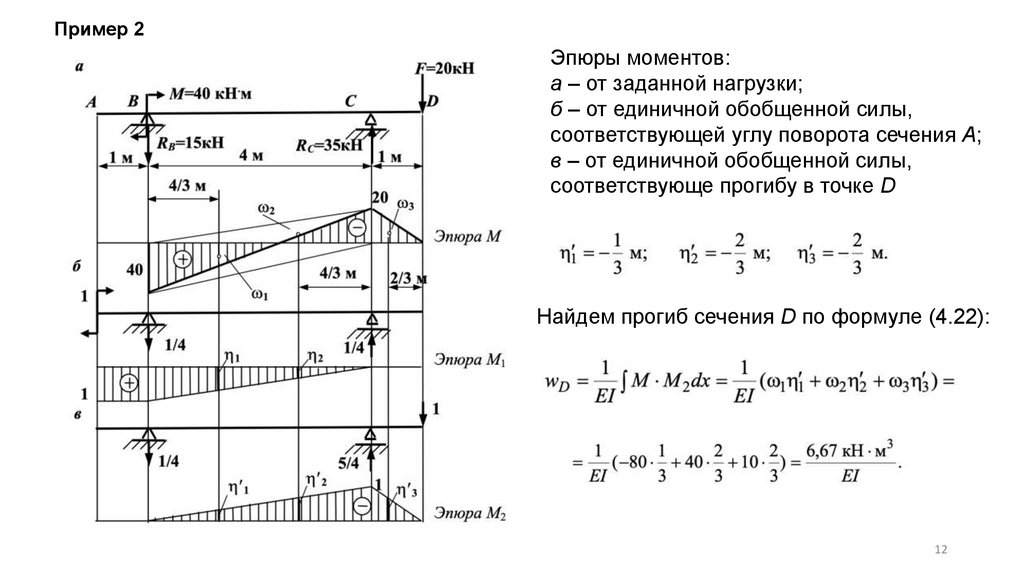
Пример 2
Эпюры моментов:
а – от заданной нагрузки;
б – от единичной обобщенной силы,
соответствующей углу поворота сечения А;
в – от единичной обобщенной силы,
соответствующе прогибу в точке D
Найдем прогиб сечения D по формуле (4.22):
12

13.

13

14.

14

15.

15

16.

Примеры разложения сложных фигур на простейшие для случая однозначных
эпюр
16

17.

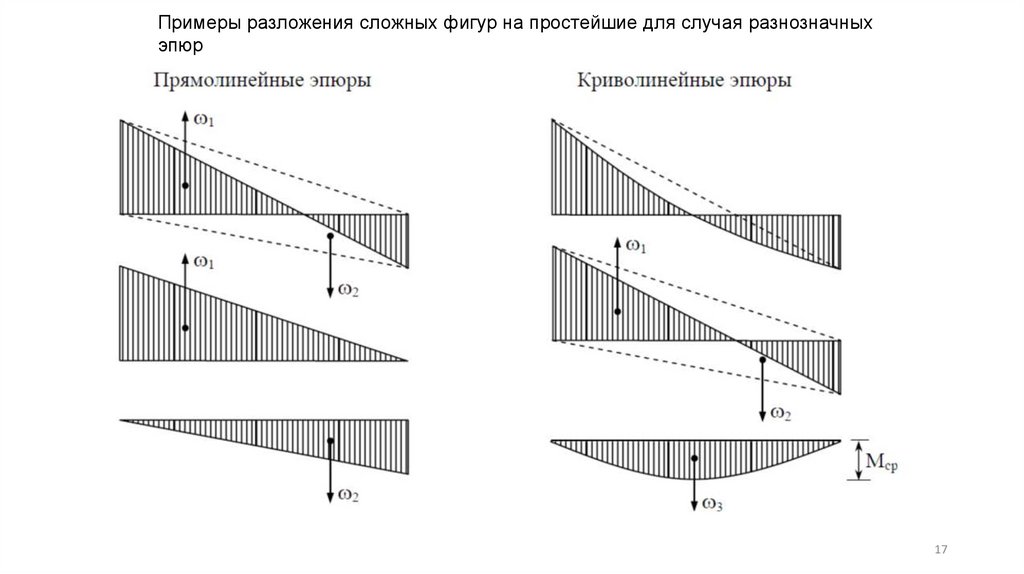
Примеры разложения сложных фигур на простейшие для случая разнозначных
эпюр
17

18.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
[email protected]
18