АГиТДУ Лекция 6 -25

1.

АГиТДУ
Лекция 6 Линейное пространство.
Структура решения ОСЛУ и НСЛУ.
Лектор курса
Поторочина К.С.
Доцент ДИТиА, ИРИТ-РТФ

2.

Линейное пространство
Пусть L – непустое множество элементов, P – числовое поле. L
называется линейным пространством над полем P , если на L определены две операции:
- сложение – правило, по которому любой упорядоченной паре x, y L
ставится в соответствие единственный элемент из L , называемый суммой
и обозначаемый x y , и
- умножение элемента из L на число из P , т.е. указан закон (правило), по которому каждому элементу x из L и любому числу из P поставлен
в соответствие единственный элемент из L , называемый произведением
элемента на число и обозначаемый x .

3.

Аксиомы линейного пространства
При этом выполнены следующие аксиомы:
10. x, y L
x y y x
(коммутативность);
20. x, y, z L x y z x y z (ассоциативность);
30. L : x L
x x (существование нулевого элемента);
40. x L ! x L : x x (существование противоположного элемента).
50 . x L , , P
60 . x L
x x ;
1 x x для единицы 1 поля P ;
70 . x L , , P
x x x ;
80 . x , y L , P
x y x y .

4.

Аксиомы линейного пространства
Простейшие следствия из аксиом линейного пространства
1. Нулевой элемент единственен.
Доказательство.
От противного. Допустим, что существуют раз-
личные нулевые элементы 1 и 2 . Тогда по аксиоме 3
имеем
2 2 1 1 2 1 , то есть 2 1 , что противоречит нашему предполо-
жению. Значит, нулевой элемент единственен.
2. x L
0 x .
Доказательство. x 0 x 1 0 x x 0 x .
3. P
.
Доказательство. x x x в силу единственности нулевого элемента.

5.

Аксиомы линейного пространства
4. x L, P
x x .
Доказательство. x x x 0 x .
5. m N , x L mx x
x.
m
x 1
Доказательство. x
m
6. Если P, x L
1 x mx .
m
x 0 x .
Доказать самостоятельно.

6.

Аксиомы линейного пространства
Замечания.
1)
Элементы
линейного
пространства
будем
часто
называть
пространство
будем
называть
векторами.
2)
Если
P
,
то
линейное
вещественным линейным пространством.
линейное
пространство
пространством.
называется
Если же
комплексным
P
, то
линейным

7.

Примеры линейных пространств
1. В геометрии множество V3 всех геометрических векторов (направленных
отрезков) в трехмерном пространстве с общим началом в некоторой точке пространства с операциями сложения векторов и умножения вектора на число есть
линейное пространство над полем
.
2. Множество Pm n всех матриц размера m n с элементами из P с операциями
сложения матриц и умножения матрицы на число из P является линейным пространством над P .
3. Множество Pn x всех многочленов с элементами из P с операциями сложения
матриц и умножения многочлена на число из P является линейным пространством над P .

8.

Линейная зависимость и независимость
Пусть L – линейное пространство над полем P .
Пусть A a1 , , an – система элементов из L .
Определение. Линейной комбинацией элементов a1 , , an системы A с коэффициентами
1 , , n называется элемент вида 1a1 n an .
n
Если b i ai , то говорят, что элемент b линейно выражается через элементы a1 , , an
i 1
системы A (обозначение b ⊣ A )
Определение. Говорят, что система векторов А линейно зависима, если существует
некоторый ненулевой набор чисел 1, , n из P , такой что 1a1
n an ;
система векторов А линейно независима, если равенство 1a1
лишь при условии 1 ... n 0 .
n an возможно

9.

Аксиомы линейного пространства
Справедливы следующие утверждения:
1) Если среди векторов a1,
, an есть нулевой вектор, то система А
линейно зависима.
2) Если к линейно зависимой системе прибавить любое число векторов, то система останется линейно зависимой.
3) Если система А линейно независима, то всякая ее подсистема линейно независима.

10.

Аксиомы линейного пространства
Критерий
пространство
линейной
над полем P ,
зависимости.
Пусть
L
–
линейное
A a1 , , an – система элементов из L .
Система A линейно зависима тогда и только тогда, когда один из векторов
системы является линейной комбинацией остальных векторов.
Замечание. В арифметическом пространстве
n
решение задач о
линейной зависимости системы арифметических векторов сводится к
решению системы линейных уравнений.

11.

Аксиомы линейного пространства
Определение. Пусть L – л.п. над P . Пусть A a1 , , an – система
элементов из L . Подсистема A системы А называется максимальной линейно независимой системой (МЛНС) в А, если выполнены условия:
1) A – линейно независима;
2) a A система A a линейно зависима.
Свойства МЛНС.
1) Если A – МЛНС в A , то любой вектор из A линейно выражается
через A .
2) Если A1 и A2 – МЛНС в A , то число элементов систем A1 и A2
одинаково, то есть A1 A2 .
Определение. Рангом системы элементов называется количество
элементов ее МЛНС.

12.

Базис и размерность
Линейное пространство L называется n-мерным, если в нём существуют n линейно
независимых векторов, а любая система из (n + 1) вектора является линейно зависимой.
Число n называется размерностью пространства L (обозначение: dim L = n).
Определение. Упорядоченная МЛНС линейного пространства L называется базисом L.
Итак, если система элементов e1, , en – базис Ln , то
e1,
, en линейно независима;
x Ln
x
e1,
n
, en , т.е. x i ei .
i 1

13.

Аксиомы линейного пространства
Теорема 1 (о базисе). Любую линейно независимую систему конечномерного
линейного пространства можно дополнить до его базиса.
Следствие 1. В n -мерном пространстве любая система из n 1 элементов линейно
зависима.
Следствие 2. В n -мерном пространстве любую линейно независимую систему из n
элементов можно принять за базис этого пространства.
Теорема 2 (об единственности разложения элемента по базису).
Если e1,
, en – базис в Ln , то любой элемент из Ln единственным образом линейно выра-
жается через элементы этого базиса.

14.

Аксиомы линейного пространства
Определение. Коэффициенты 1, , n разложения элемента x по
базису x 1e1
e1,
nen называются координатами вектора x в базисе
, en .
Вектор x можно представить в матричном виде столбцом X его
1
координат: X . Тогда запись разложения элемента x по базису
r
e1, , en :
1
x i ei e1,..., en ... e1,..., en X X
i 1
n
n

15.

Решение ОСЛУ, НСЛУ. ФСР.
Структура решения однородной и неоднородной СЛУ.
Фундаментальная система решений (ФСР)
Общая теория ОСЛУ
Рассмотрим однородную систему m линейных уравнений с n
неизвестными:
AX = B
(1)
т.е. bi = 0 (i =1, 2,…, m). Обозначим B = О.
Однородная система всегда совместна, она имеет нулевое
(тривиальное) решение х1= х2=…= хn= 0.

16.

Аксиомы линейного пространства
Теорема 1. Для того, чтобы ОСЛУ имела ненулевые решения, необходимо и
достаточно, чтобы ранг r ее основной матрицы был меньше числа неизвестных n.
Свойства решений ОСЛУ
1. Если X1, X2 – решения ОСЛУ, то X1 + X2 решение ОСЛУ.
2. Если X0 – решения ОСЛУ, то λ X0 решение ОСЛУ.

17.

Аксиомы линейного пространства
Пусть {X1, X2,…, Xn} – множество решений СЛУ.
Выражение вида λ1 X1+ λ2 X2+…+ λn Xn называют линейной комбинацией
решений.
Говорят, что X1, X2,…, Xn линейно независимы, если
λ1 X1+ λ2 X2+…+ λn Xn= O только при условии, что все λi = 0.
Если λ1 X1+ λ2 X2+…+ λn Xn= O и λi 0, то X1, X2,…, Xn линейно зависимы.

18.

Аксиомы линейного пространства
Любое упорядоченное множество (n − r) линейно независимых решений системы
(1) образует фундаментальную систему решений (ФСР).
Теорема 2 (о структуре общего решения ОСЛУ).
Общее решение ОСЛУ с n неизвестными ранга r < n есть линейная комбинация
векторов ее ФСР с (n − r) произвольными коэффициентами вида:
n r
X общее ci X i .
решение
ОСЛУ
i 1

19.

Аксиомы линейного пространства
Общая теория НСЛУ
Рассмотрим НСЛУ:
AX = B (B О).
(2)
Система AX = θ (3) называется соответствующей ОСЛУ для данной НСЛУ.
Теорема 3. Сумма любого решения системы (2) и любого решения системы (3) есть
решение НСЛУ (2).
Теорема 4. Разность двух решений НСЛУ (2) есть решение ОСЛУ (3).
Теорема 5 (о структуре общего решения НСЛУ).
Общее решение НСЛУ (2) есть сумма общего решения ОСЛУ (3) и некоторого
(частного) решения НСЛУ, т.е.
Х общее X общее Х частное .
решение
НСЛУ
решение
ОСЛУ
решение
НСЛУ

20.

Пример
Пример. Решить ОСЛУ и найти ФСР
а)
6 x1 2 x2 2 x3 5 x4 7 x5 0,
9 x 3x 4 x 8 x 9 x 0,
1
2
3
4
5
6 x1 2 x2 6 x3 7 x4 x5 0,
3x1 x2 4 x3 4 x4 x5 0.
x2 4 x3 11x5
x
,
1
3
3
3
x4 2 x3 3x5

21.

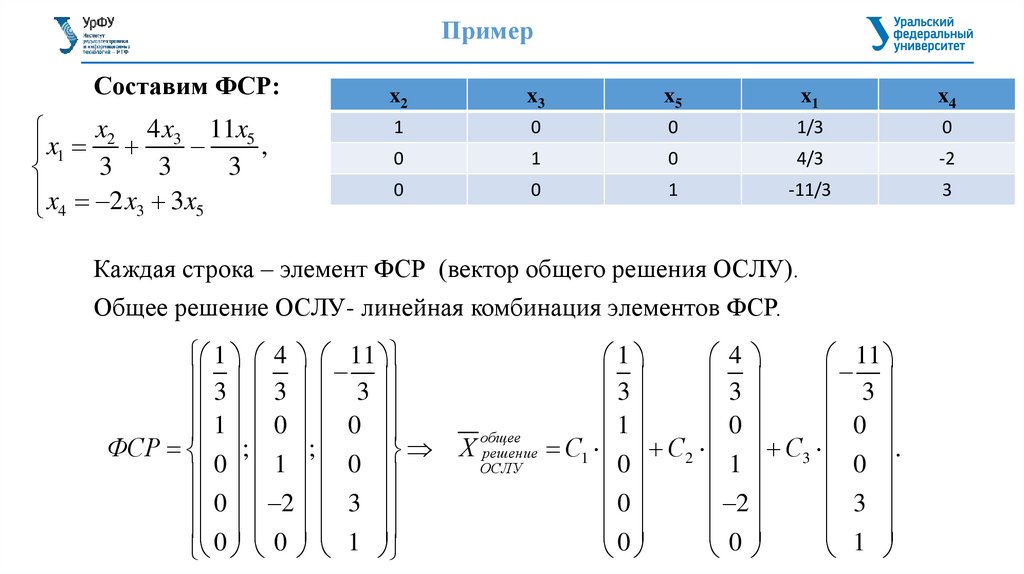
Пример
Составим ФСР:
x2 4 x3 11x5
,
x1
3
3
3
x4 2 x3 3x5
x2
x3
x5
x1
x4
1
0
0
1/3
0
0
1
0
4/3
-2
0
0
1
-11/3
3
Каждая строка – элемент ФСР (вектор общего решения ОСЛУ).
Общее решение ОСЛУ- линейная комбинация элементов ФСР.
1 4 11
3 3 3
1 0 0
ФСР ; ;
0
1
0
0 2 3
0
0
1
1
4
11
3
3
3
1
0
0
общее
X решение С1 С2 С3
.
0
1
0
ОСЛУ
0
2
3
0
0
1

22.

Пример
x2 4 x3 11x5
,
x1
3
3
3
x4 2 x3 3x5

23.

Пример
3 x1 5 x2 2 x3 0,
б) 4 x1 7 x2 5 x3 0,
x1 x2 4 x3 0,
2 x1 9 x2 6 x3 0.