Similar presentations:
Алгебра и аналитическая геометрия
1.
Опорный конспект лекций на сайте skif@donstu.ru библиотекаэлектронных ресурсов ДГТУ факультет ИВТ кафедра
прикладной математики А.В. Братищев Лекции по
мптематике. Семестр 1.
ЛИТЕРАТУРА
1. Пантелеев А.В., Якимова А.С. Теория функций
комплексного переменного и операционное исчисление в
примерах и задачах.
2. Нефёдов В.Н., Осипов В.А. Курс дискретной математики.
3. Тишин В.В. Дискретная математика в примерах и задачах.
4. Сборник задач по алгебре и аналитической геометрии. Ред.
А.С.Феденко.
Сайт www. techlibrary
2.
КАЛЕНДАРНЫЙ ПЛАН 2021-2022 уч.г.Алгебра и аналитическая геометрия ВИ-11,12,13
Неделя
Тема лекции
Практика
1. 1.09 Арифметические операции над комплексными чис
Арифметические операции над комплексными
лами и комплексная плоскость.
числами и комплексная плоскость.
2. 6.09 Элементы теории множеств и математич. логики
Формы задания комплексного числа. Возведение в
степень. Уравнение z n a .
3. 13.09 Матрицы. Определители.
Самостоятельная работа 1.
4. 20.09 Определенные и совместные СЛАУ. Метод Гаусса
Линейные операции над векторами. Скалярное
произведение.
5. 27.09 Векторное пространство. Базисы. Примеры.
Векторное и смешанное произведения.
Отображения, линейные операторы.
6. 04.10 Евкл. прост-во. Декартова и другие системы
Прямые на плоскости.
координат. Проекция и ее свойства.
7. 11.10 Векторная алгебра.
Самостоятельная работа 2.
8. 18.10 Прямая и плоскость.
Кривые второго порядка.
9. 25.10 Прямая и плоскость.
Плоскость в пространстве.
10. Кривые второго порядка.
Прямая в пространстве.
01.11
11. Поверхности второго порядка.
Плоскость и прямая.
08.11
12. Движения.
Самостоятельная работа 3.
15.11
13. Группы подгруппы, циклической группы. Смежного Группы подгруппы, циклической группы.
22.11 класса, нормального делителя группы, фактор-группы
14.
Кольца, поля. Конечного поля, идеала кольца и
Конечного поля
29.11 факто-кольца
15. Алгебр. кривые третьего порядка. Эллиптические
Эллиптич. кривые над конечными полями.
06.12 кривые. Эллиптич. кривые над конечными полями.
16. Теоретическая контрольная
Самостоятельная работа 4
13.12
3.
Вопросы к курсу, 2021-2022 уч. год., ВИ1. Опр. комплексной плоскости. Пр. 2. Опр. модуля, сопряженного числа, главного
значения аргумента. Пр. 3. Опр. тригонометрической, показательной форм компле
ксного числа. 4. Опр. произведения, частного комплексных чисел, корня n-ой степе
ни. Пр. 5. Опр. матрицы, транспонированной матрицы и алгебраического дополнения
элемента матрицы. Пр. 6.Опр. суммы матриц, произведения матрицы на число и про
изведения матриц. Пр. 7. Опр. определителя, минора и ранга матрицы. Пр. 8. Опр.
СЛАУ, совместной и определенной СЛАУ. Пр.
9. Опр. векторного прост-ва (ВП). 10. 5 примеров векторных прост-в. 11. Опр. декартова произведения множеств и векторных прост-в. Пр. 12. Опр. линейной комби
нации элементов, линейно независимых элементов и базиса в ВП. Пр. 13. Опр. ска
лярного произведения и нормы в векторном прост-ве. Пр. 14. Опр. отображения мно
жеств, линейного и полилинейного отображений ВП. Пр. 15. Опр. n-мерных евклидо
ва векторного и евклидова (точечного) прост-в. 16. Опр. ДСК и полярной системы
координат. 17. Опр. символа Кронекера, ортонормированного базиса и прямоуголь
ной ДСК. 18. Опр. компонент элемента, радиуса-вектора и координат точки.
19. Опр. проекции вектора на ось. Свойства. 20. Опр. правой тройки и векторного
произведения. 21. Опр. смешанного произведения и геом. смыслы модулей
векторного и смешанного произведений
22. Опр. плоскости и три аналитических способа ее задания. 23. Опр. прямой и
три способа ее задания в пространстве. 24. Опр. кривой второго порядка и эллипса.
Уравнение. 25. Опр. гиперболы и параболы. Уравнение. 26. Опр. и рисунки
эллипсоида, одно- и двуполостных гиперболоидов. 27. Опр. и рисунки эллиптиче
ского, гиперболического параболоидов и конуса.
28. Алгебр. кривые третьего порядка. Эллиптические кривые. 29. Опр. группы
подгруппы, циклической группы. Пр. 30. Опр. смежного класса, нормального делите
ля группы, фактор-группы. Пр. 31. Опр. кольца, поля. Пр. 32. Опр. конечного поля,
идеала кольца и факто-кольца. Пр. 33. Опр. эллиптич. кривой над конечными полями.
4.
§ 1 Комплексные числа. Топология расширеннойкомплексной плоскости.
Мнимая единица- выражение вида i : 1 со свойством i 2 i i : 1
Пр. Решить уравнение x2 1 0 x2 1 x1,2 1 i .
Комплексное число (в алгебраической форме) - выражение вида
z : a bi , a, b R .
Пр. Решить уравнение
x 2x 5 0
2
Проверка
2 4 20 2 16 ( 1)
x1,2
1 2 1 1 2i .
2
2
ЗАМЕЧАНИЕ Обозначение i - Декарт,1637 Эйлер,1777 Гаусс.
Понятие комплексного числа – Кардано, 1545, Бомбелли, 1572.
Термин «комплексное число» - Карно, 1803.
Теория комплексных чисел - Гауссом, 1831.
5.
Сципион дель Ферро (1465 - 1526) – итальянский математик,открывший общий метод решения неполного кубического
уравнения
, где
(задача много веков не поддавалась
лучшим математикам древней Греции и стран ислама).
Закончил Болонский университет, где с 1496 г. работал
профессором математики.
После многолетних усилий он сумел найти формулу решения
кубического уравнения вида
2
3
2
b
b
b a
b a
x 3 3
2
2
2 3
2 3
3
-
формула Кардано. Метод решения нигде не опубликовал, но
сообщил его своему зятю Аннибалу делла Наве и ученику
Антонио Марио Фиоре.
Фиоре использовал новый алгоритм на популярных тогда
математических турнирах (турнир в 1535 г. с Н.Тартальей).
Наве ознакомил Д.Кардано с рукописью дель Ферро в 1545 г.
6.
Лодовико Феррари (1522-1565) - итальянский математик, ученикКардано. Нашёл общее решение уравнения четвёртой степени (1540).
ЗАДАЧА 1 Найти корни уравнения x3 2 x 2 3x 10 0 с помощью
2
3
2
3
формулы дель Ферро x 3 b b a 3 b b a , приведя его
2
2
2 3
2 3
предварительно заменой переменных к уравнению вида x3 ax b .
ЗАДАЧА 2 Найти корни уравнения x4 2 x3 2 x2 10 x 25 0 методом
Феррари, как корни двух квадратных уравнений
a2
2 a
y1
y12
a
x x b y1 x y1 c x
d ,
2
2
4
2
4
2
где y1 есть корень кубического уравнения
y 3 by 2 (ac 4d ) y a 2 d 4bd c 2 0 .
7.
Никколо Тарталья (1499 -1557) – итальянский математик. Родился в очень бедной семье
В 14 лет пошел в школу, но проучился 15 дней,
дойдя в изучении алфавита до буквы К.
Самоучка, зарабатывал на хлеб преподаванием
математики. Консультировал по различным во
просам математики и техники «мастеров, инже
неров, купцов, артиллеристов и архитекторов».
Представитель нового направления, поставившего целью
подчинить науку практическим нуждам. Впервые установил, что
наибольшая дальность стрельбы орудия достигается при угле
наклона ствола = 450 . Занимался задачами увеличения меткости и
эффективности огнестрельного оружия («Новая наука», 1537г.).
Переоткрыл формулу Сципиона дель Ферро (1535).
Пр.
.
8.
Джерола́мо Карда́но (1501 -1576) - итальянский математик, инженер, философ, медик, астролог. Автор 130
монографий.
В его честь названы
карданный подвес (для уменьшения воздействия на
компас морской качки) и карданный вал.
В трактате «Великое искусство» («Ars magna»,1545)
впервые опубликовал формулу, рассказанную ему
Тартальей. Там же приведена формула решения уравне
ния четвёртой степени, найденная его учеником Лодовико Феррари.
1) Первым в Европе стал использовать отрицательные корни уравнений.
2) Обнаружил, что кубическое уравнение может иметь три веществен
ных корня (этот факт остался незамеченным даже в трудах Омара
Хайяма), причём сумма этих корней всегда равна коэффициенту при с
противоположным знаком (одна из формул Виета).
9.
Рафаэль Бомбелли (1526 -1572) - итальянский математик,инженер-гидравлик. Главный труд «Алгебра» (L’Algebra,
написана в 1560 г., издана в 1579 г.).
Б. первым в Европе приводит правила работы с отрицате
льными числами, включая правило знаков для умножения.
Б. первым оценил пользу комплексных чисел, в частности
для решения уравнений третьей степени по формулам
Кардано.
Пр. Уравнение
имеет вещественный корень
x = 4, однако по формулам Кардано получаем:
. Б. обнаружил, что
, откуда
сразу получается нужный вещественный корень.
Определил произведение комплексных чисел.
Б.
придумал первые скобки; они имели вид прямой и
перевёрнутой буквы L. Привычные нам круглые скобки
появились в том же XVI веке, однако в общее употребление
их ввели только Лейбниц и Эйлер.
Б. первый стал использовать числовое (а не словесное, как
ранее) обозначение для показателя степени, помечаемое
специальной дужкой снизу. Современное обозначение показателя ввёл в широкое
обращение Декарт.
Применилцепные дробидля вычисления квадратных корней из натуральных чисел
10.
Менее чем за 50 лет (1526-1572) математикам итальянской школы(Ферро, Тарталья, Кардано, Бомбелли) удалось исчерпать
возможности алгебраического метода решения уравнений. Лишь
в 1826 г. Абель установил невозможность решения уравнения 5ой степени в радикалах.
11.
ЗАМЕЧАНИЕ (геометрический смысл комплексного числа.Вессель, 1799, Арган, 1806) Каждой точке с радиусом-вектором
OM {a, b} евклидовой плоскости R 2 с ПДСК
Y
R
сопоставим комплексное число z : a bi . Тем
M
b
самым устанавливаем взаимно однозначное
соответствие между векторами R 2 и множестX
a
O
вом комплексных чисел C . Ось абсцисс назыC
вается вещественной осью и обозначается Re ,
Im
z a bi
ось ординат - мнимой осью и обозначается Im bi
Единицей измерения на мнимой оси будет i .
Re
Комплексная плоскость - совокупность
a
0
точек и так переименованных осей.
Обозначение C .
2
Re z : a - вещественная часть комплексного числа z : a bi ;
Im z : b - коэффициент мнимой части числа z : a bi .
Сумма (разность) комплексных чисел z1 a1 b1i , z2 a2 b2i это
комплексное число z1 z2 : (a1 a2 ) (b1 b2 )i .
12.
Лаза́р Карно́ 1753- 1823) — французский государственный и военный деятель, инженер и учёный.
Предложил название «Комплексное число» (1803).
Издал (1797) свои «Размышления о метафизике ис
числения бесконечно малых». Выступал с критикой
теории аналитических функций Ж.Лагранжа.
Сади Карно (1796 - 1832) - французский физик и математик. Внук Л.Карно. В 1824 году вышла первая и
единственная работа С. Карно - «Размышления о
движущей силе огня и о машинах, способных раз
вивать эту силу». Считается основополагающей в
термодинамике. В ней был произведён анализ суще
ствовавших в то время паровых машин (паровая ма
шина Уатта, 1770-е годы), и были выведены условия,
при которых КПД достигает максимального значения
(в паровых машинах того времени КПД не превышал
2 %). Помимо этого там же были введены основные
понятия термодинамики: идеальная тепловая машина (см. тепловая
машина), идеальный цикл (см. цикл Карно), обратимость и
необратимость термодинамических процессов. Умер о холеры.
13.
Каспар Вессель (1745 — 1818) — датско-норвежский математик, по профессииземлемер. Автор сочинения «Об аналитическом представлении направлений» (1799),
посвященного теории векторов на плоскости и в пространстве, в котором впервые дано
геометрическое представление комплексных чисел. В течение столетия сочинение
Весселя оставалось неизвестным, а его результаты открывались вновь.
Жан Робер Аргáн (1768 —1822) был непрофессиональным математиком. Арган родился
в Женеве, Швейцария. В 1806 году, управляя книжным магазином в Париже, он издал
свое «Эссе о методе представления мнимых величин», где развил идею
геометрической интерпретации комплексных чисел. Ввёл термин «модуль комплексного
числа» (1814—1815).
Иоганн Карл Фри́дрих Га́усс (1777 — 1855) - великий немец
кий математик, астроном и физик, считается одним из величай
ших математиков всех времён, «королём математиков».
Творчество Гаусса было чрезвычайно разносторонним. Его
исследования посвящены высшей алгебре, теории чисел,
дифференциальной геометрии, геодезии, небесной механике,
теоретической астрономии, теории электричества и
магнетизма. Разработал новую арифметическую теорию
квадратичных формы. Доказал основную теорему алгебры,
исследовал уравнения, к которым приводит задача деления
круга на равные части. Строго изложил теорию комплексных
чисел. Заложил основы теории сходимости рядов. В 1818
Гаусс пришел к идее о возможности неевклидовой геометрии. Доказал возможность
построения с помощью циркуля и линейки правильных 17- и 257-угольников.
14.
ЗАМЕЧАНИЕ Сложению (вычитанию) комплексных чиселz1 a1 b1i , z2 a2 b2i соответствует сложение (вычитание)
векторов {a1, b1}, {a2 , b2} евклидовой плоскости R 2 .
Произведением комплексных чисел z1 a1 b1i , z2 a2 b2i называет
ся комплексное число z1 z2 : (a1a2 b1b2 ) (a1b2 a2b1 )i (Бомбелли,1572)
Пр.
Комплексное число z : a bi называется сопряженным к
комплексному числу z a bi (Коши, 1831).
Пр. z z (a bi )(a bi ) a 2 b 2i 2 a 2 b 2 0 .
15.
Модулем комплексного числа z a bi называется числоz : a 2 b 2 (Арган, 1814).
Пр. z z a 2 b2 z 2 .
ЗАМЕЧАНИЕ (геометрический смысл модуля разности комплексных чисел) z2 z1 (a2 a1 )2 (b2 b1 ) 2 модуль разности комп
лексных чисел совпадает с расстоянием между соответствующими
точками z1 , z2 комплексной плоскости C .
Пр. D( z1 , R) : z : z z1 R .
16.
Частное от деления комплексных чисел z1 a1 b1i , z2 a2 b2i этокомплексное число
z1
zz
zz
: 1 2 1 22 .
z2 z2 z2 z2
Пр.
Главным значением аргумента комплексного числа z : a bi 0
называется величина угла arg z [0;2 ) между положительным
направлением вещественной оси и направлением на точку z ,
отсчитываемого против часовой стрелки (argumentum – лат. знак)
(Коши,1847).
ЗАМЕЧАНИЕ 1 Иногда предполагается, что arg z .
ЗАМЕЧАНИЕ 2 Функция arg z , определена на C \{0}, и
определяет бесконечнозначную функцию Arg z : arg z 2 k , k .
Пр. Arg (1 i)
17.
Огюсте́н Луи́ Коши́ (1789 - 1857) — великий французский математик, член Парижской Петербургской и других академий наук, Лондонского королевского общества.
К. написал свыше 800 работ. Много работал в
области комплексного анализа, в частности, создал теорию интегральных вычетов. В математической физике
глубоко изучил краевую задачу с начальными условиями,
которая с тех пор называется «задача Коши».
К. заложил основы математической теории
упругости. Он рассматривал тело как сплошную среду и
вывел систему уравнений для напряжений и деформаций в каждой точке. В
работах по оптике Коши дал математическую разработку волновой теории
света и теории дисперсии.
Ему принадлежат также исследования по геометрии (о многогранниках), по
теории чисел, алгебре, астрономии и во многих других областях науки.
Впервые дал строгое определение основным понятиям математического
анализа — пределу, непрерывности, производной, дифференциалу, интегралу,
сходимости ряда и т. д. Его определение непрерывности опиралось на понятие
бесконечно малого, которому он придал новый смысл: у К. бесконечно малое —
переменная величина, стремящаяся к нулю. Ввёл понятие радиуса сходимости
ряда. Курсы анализа К., основанные на систематическом использовании понятия
предела, послужили образцом для большинства курсов позднейшего времени.
18.
Если z a bi, : arg z, r : a 2 b 2 z , то выражение z r cos ir sinr (cos i sin ) -тригонометрическая форма комплексного числа
Обозначение ei : cos i sin - формула Эйлера (1740).
z rei - показательная форма комплексного числа.
Пр.
19.
Леона́рд Э́йлер (Leonhard Euler; 1707,Базель,Швейцария - 1783, Санкт-Петербург, Россий
ская империя) – выдающийся математик,
механик, физик, астроном XVIII века.
Э. - автор более чем 800 работ по
математическому анализу,
дифференциальной геометрии,
теории чисел,
приближённым вычислениям,
небесной механике,
математической физике,
оптике,
баллистике,
кораблестроению,
теории музыки и др.
Почти полжизни провёл в России (1726-1741; 1776-1783).
Внёс существенный вклад в становление российской науки.
Первые русские академики-математики (С. К. Котельников) и
астрономы (С. Я. Румовский) были учениками Эйлера.
Некоторые потомки Э. живут в России.
20.
ТЕОРЕМА 1 Пусть zk rk (cos k i sin k ), k 1,2 . Тогда:1) z1 z2 r1r2 cos( 1 2 ) i sin( 1 2 ) ;
2)
z1 r1
cos( 1 2 ) i sin( 1 ) ;
z2 r2
3) алгебраическое уравнение z n a 0 имеет ровно n комплексных
корней, которые вычисляются по формуле
2 k
2 k
zk n a cos
i sin
, где a a (cos i sin ), k 0,...n 1.
n
n
21.
ЗАМЕЧАНИЕ В 1813 г. Н.И.Лобачевским (1792-1856) представлена работа — «О разрешении алгебраического уравнения xm 1 0 ».
Пр. 3 1
ЛЕКЦИЯ 2 ВИ 22.09.21
ЗАМЕЧАНИЕ 1 (геометрический смысл умножения комплексного
числа на e i ) Умножение точек комплексной плоскости на e i
равносильно повороту вокруг начала координат на угол .
Если z re i , то w : ze i re( )i .
ЗАМЕЧАНИЕ 2 Множество таких отображений e i образует группу
22.
23.
§ 2 Системы линейных алгебраическихуравнений (СЛАУ). Матрицы. Определители.
Матрицы
Матрица размера m n - совокупность чисел, расположенных
в виде таблицы из m строк и n столбцов. ЛЕКЦИЯ 2 13.09.18
a11 ... a1n a11 ... a1n
Обозначение A ... ... ... ... ... ... aij aij .
a
m1 ... amn am1 ... amn
Матрицы A (aij ), B (bij ) называются равными A B ,
если они имеют одинаковые размеры и i j aij bij .
ЗАМЕЧАНИЕ Понятие матрицы впервые появилось в середине
XIX века в работах Уильяма Гамильтона и Артура Кэли.
Термин «матрица» (от matrix - лат. источник, начало –изначальная фор
ма или структура какого-либо объекта) ввел Джеймс Сильвестр в 1850 г.
24.
А́ртур Кэ́ли (1821-1895) - английский математик.Основные математические работы относятся к
алгебре алгебраической геометрии, теории
инвариантов
Начал разработку теории матриц: определил сумму,
умножение матриц и произведение матрицы на число,
Обнаружил ассоциативность и некоммутативность мат
Риц. «Понятие матрицы предшествует идее
детерминанта»
Заложил основы теории алгебраических инвариантов Установил
существование связи между теорией инвар иантов и проективной
геометрией. Разработал осно вные понятия абстрактной теории
конечных групп.
Изучал геометрию в пространстве n измерений, теорию
дифференциальных уравнений. Занимался теорией эллипти ческих
функций, небесной механикой, кинематикой механизмов: доказал,
что шатунная кривая шарнирного четырехзвенника является кривой
шестого порядка. Принимал участие в развитии теории кватернионов,
однако отрицал ее полезность для прикладной математики.
25.
Джеймс Джозеф Сильвестр (1814 - 1897) - английский математик. Основные работы относятся калгебре,
теории инвариантов,
теории матриц,
математической физике,
теоретической и прикладной кинематике.
Развивая идеи А. Кэли в области теории инвари
антов, предложил терминологию этой теории –инва
риант, ковариант, дискриминант, коммутант.
Развил теорию канонических форм.
Внес вклад в теорию вероятностей.
Совместно с А. Б. Кемпе построил инверсор. Изобрел пантограф.
Сыграл важную роль в деле организации исследовательской работы
в области математики в США. Основатель (1878) и первый редактор
первого американского математического журнала «The American
Journal of Mathematics».
26.
Матрица квадратная, если m=n.- главная
диагональ
- побочная
диагональ
Квадратная матрица единичная, если все элементы главной
диагонали равны 1, а остальные элементы равны 0.
1 0 0
1 0
,...
Пр. E (1),
,
0
1
0
0
1
0 0 1
Квадратная матрица нулевая, если все ее элементы равны нулю.
0 0 0 0 0 0
Пр. E (0), (0 0), , ,
,...
0 0 0 0 0 0
27.
Сумма двух матриц A (aij ), B (bij ) размера m n этоматрица, которая обозначается и вычисляется по формуле
a11 b11 ... a1n b1n
A B : (aij bij ) ............................
a b ... a b
mn
mn
m1 m1
Пр. 1 1 0 .
1 1 0
Произведение матрицы A (aij ) на число это матрица вида
a11 ... a1n
A : ( aij ) ..................
a ... a
mn
m1
1
1
0
1 0 1
2
1 0
1 0 1 0
2
Пр. 2
.
;
:
(
1)
1
2 4
0 1
0 1 0 1
1 1 2
2
4
28.
Произведение матрицы A (aij ) размера m p на матрицуB (bij ) размера p n - это матрица A B : (ci j ) размера m n ,
элементы которой вычисляются по правилу
p
cij : ai1b1 j ... aip bpj aik bkj
k 1
1 0
1 0 0
0 1
,
B
Пр. A
0
1
0
0 0
2 3
1 0 0
1 0
0 1 0
AB
,
BA
0
1
0 0 0
2 2
3 2
3 3
Обратная к квадратной матрице A (ai j ) размера n n квадратная матрица A 1 (bi j ) размера n n со свойством
AA 1 A 1 A E .
ЛЕКЦИЯ 2 23.09.19
29.
Фу, Гонсалес, Ли Робототехника. М.: Мир, 198930.
ОпределительОпределитель (детерминант) первого порядка квадратной
матрицы A (a11 ) размера 1 1 - число, обозначаемое и
вычисляемое по формуле
det A a11 : a11
Пример
det( 10) 10 10 .
Determinacio – лат. определять.
31.
Определитель n-го порядка квадратной матрицы A (aij )размера n n - число, обозначаемое
a11 ... a1n
det A ... ... ... ,
an1 ... ann
которое находится по формуле
n
det( A) : ai1 ( 1) M i1 ... ai n ( 1) M i n ai k ( 1)i k M i k ,
i 1
i n
k 1
где M i k - определитель (n-1)-го порядка матрицы, которая получается вычеркиванием из матрицы A i-той строки и k-го столбца.
ЗАМЕЧАНИЕ Данная формула вычисления - разложение определителя по i- ой строке.
Формула разложения по j-ому столбцу:
n
det A ak j ( 1) k j M k j a1 j ( 1)1 j M1 j ... an j ( 1) n j M n j .
k 1
32.
Пример 1a11 a12
2
3
a11 1 a22 a12 1 a21 a11a22 a12 a21
a21 a22
1 0 1
Пример 2 Вычислим определитель 0 2 1
1 3 0
разложением по второй строке и по третьему столбцу.
1 0 1
1
1
0
3 0
4 1
5 1
0 2 1 0 1
2 1
1 1
3 0
1 0
1 3
1 3 0
0 2 1 3 1
1 0 1
2
0
0
4 0
5 1
6 1
0 2 1 1 1
1 1
0 1
1 3
1 3
0 2
1 3 0
2 3 1
33.
ТЕОРЕМА 2.1 (свойства определителей)1) Если в определителе поменялись местами две строки (два
столбца), то новый определитель будет отличаться от
исходного только знаком.
2) Если элементы одной строки (или столбца) умножить на одно и
тоже число , то полученный новый определитель будет в
раз больше исходного.
3) Если к одной строке (столбцу) прибавить поэлементно
другую строку (столбец), то полученный новый определитель
совпадет с исходным.
4) Пусть два определителя одинакового порядка различаются
только одной строкой (столбцом). Тогда их сумма совпадает с
определителем, у которого соответствующая строка (столбец)
есть сумма строк (столбцов) слагаемых определителей.
34.
◄ 1) Ограничимся случаем n =2.a21
a11
a22
a
a21a12 a11a22 a11a22 a12 a21 11
a12
a21
a12
.
a22
2) По определению определителя
a11 ... a1n
a21
...
an1
...
...
...
a11
a2 n
a
a11 ( 1)1 1 M 11 ... a1n ( 1)1 n M 1n 21
...
...
ann
an1
... a1n
... a2 n
.
... ...
... ann
3) Пусть n=2 и к первой строке прибавлена вторая. Тогда
a11 a21 a12 a22
a
a
a11a22 a21a22 a21a12 a21a22 a11a22 a12a21 11 12 .
a21
a22
a21 a22
1 0
1 3
1 5
1 8
4) (пример)
17 .
2 1
2 2
2 0
2 1
a11
a21
...
an1
... a1n
a11
... a2 n a21
... ...
...
... ann an1
... a1 n
a11 a11
... a2 n
a21
)( 1)1 1 M 11 ... (a1n a1 n )( 1)1 n M 1n
(a11 a11
... ...
...
... ann
an1
... a1n a1 n
...
a2 n
.%
...
...
...
ann
35.
Минор порядка k матрицы A - определитель матрицы,элементы которой стоят на пересечении каких-либо k строк и
k столбцов матрицы A.
1 0 2
Пр.1 Матрица
имеет 3 минора порядка 2,
2 3 4
6 миноров порядка 1 и не имеет миноров порядка 3.
4 6
1 2
1 4 6
Пр.2 0 1 1 1 det 0 1 1 2 rangA 3 .
0 0 2 1
0 2 1
Ранг матрицы - самый большой порядок у не равных нулю
миноров этой матрицы.
1 1 1
1 1 1
Пр. A 2 2 2 det A 2 2 2 0 rangA 3.
3 3 3
3 3 3
1 1
1 1
2 2
0;
0;
0 rangA 2.
1 1 rangA 1
2 2
3 3
3 3
36.
Квадратная матрица A невырожденная, если rang A n , тоесть когда det A 0 . ЛЕКЦИЯ 3 9.09.16
a11 ... am1
Матрица AT A : ... ... ... называется транспонированной
a ... a
mn
1n
a11 ... a1n
к матрице A ... ... ... .
a
m1 ... amn
2
Пр. A AT 2 1 . ЛЕКЦИЯ 2 12.09.17 16.09.21
1
Ai j : ( 1)i j M ij - алгебраическое дополнение элемента aij
матрицы A.
ЛЕКЦИЯ 3 14.09.15
( Ai j )T - присоединенная матрица к матрице A.
37.
ЗАМЕЧАНИЕ Если матрица A не вырождена, то существуетобратная матрица A 1 , которая вычисляется по формуле
A
где Ai j : ( 1)i j M ij
1
1
( Aij )T ,
det A
a22
T
Пусть n 2 ( Aij )
a12
◄
a21 a22 a12
.
a11 a21 a21
T
0
1 a11 a12 a22 a12
1 a11a22 a12a21
AA
0
a21a12 a11a22
det A a21 a22 a21 a11 det A
1
0 1 0
1 det A
E.
det A 0 1
det A 0
Аналогично доказывается, что A 1 A E .
38.
a11 x1 ... a1n xn b1...
...
...
- система линейных алгебраических
a x ... a x b
m
mn n
m1 1
уравнений (СЛАУ), где известные числа ai j - коэффициенты
СЛАУ, известные числа b1 ,..., bm - свободные члены, ЛЕКЦИЯ 3 2014
неизвестные, искомые числа x1 ,..., xn - решение СЛАУ.
b1
a11 ... a1n
A : ... ... ... - матрица коэффициентов, B ...
b
a
m
m1 ... amn
x1
матрица свободных членов, X ... - матрица неизвестных
x
n
ВИ ЛЕКЦИЯ 3 24.09.21
39.
a11 ... a1n x1 b1... ... ... ...
am1 ... amn xn bm
AX B - матричная запись СЛАУ.
a11 ... a1n b1
A : ... ... ... ... - расширенная матрица СЛАУ.
a
m1 ... amn bm
x1 x2 1
x1
1 1
1
1 1 1
Пр.
A
, X , B , A
x
x
2
x
1
1
2
1
1
2
1 2
2
СЛАУ совместная, если она имеет хотя бы одно решение.
В противном случае СЛАУ несовместная.
1 1 x1 1
Пр. Матричное уравнение СЛАУ имеет вид
.
1 1 x2 2
1 1
1 1 1
1, rang
2.
СЛАУ несовместная и rang
1 1
1 1 2
40.
Две СЛАУ с одинаковым числом неизвестных называютсяэквивалентными, если они обе несовместные или обе совместные и имеют одинаковые множества решений.
ЗАМЕЧАНИЕ СЛАУ переходит в эквивалентную при
следующих элементарных преобразованиях:
1) перестановка местами двух уравнений,
2) умножение какого-либо уравнения на неравное нулю число,
3) поэлементное прибавление к одному уравнению другого
уравнения.
СЛАУ определенная, если она имеет ровно одно решение и
неопределенная, если решений больше одного.
Пр.
41.
ТЕОРЕМА 2.2ЛЕКЦИЯ 3 14.09.18
1) (критерий Кронекера-Капелли совместности СЛАУ)
СЛАУ совместна тогда и только тогда, когда ранг матрицы этой
СЛАУ равен рангу расширенной матрицы.
2) (критерий определенности СЛАУ)
Для того чтобы СЛАУ была определенной необходимо и
достаточно, чтобы она была совместной и ранг матрицы
коэффициентов совпадал с числом неизвестных:
rang A rang A n .
3) (формулы Крамера) Определенная СЛАУ с помощью
элементарных преобразований приводится к СЛАУ, у которой
матрица коэффициентов A квадратная и det A 0. В этом случае
решение СЛАУ вычисляется по формулам Крамера
n
1
x1
, ... , xn
,
где : det A, i -определитель, получаемый из заменой в
нем i-ого столбца на столбец свободных членов.
42.
Леопо́льд Кро́некер (1823-1891) - немецкий математик,профессор университета в Берлине. Иностранный членкорреспондент Петербургской Академии наук (1872).
Основные труды по алгебре и теории чисел, где
продолжил работы своего учителя Э. Куммера по
теории квадратичных форм и теории групп. Большое
значение имеют его исследования по арифметической
теории алгебраических величин.
Альфре́до Капе́лли (1855-1910) – итальянский математик, зав.
кафедрой алгебры Неаполитанского университета.
Занимался представлениями групп Ли.
43.
a11 x1 a12 x2 b13)
a21 x1 a22 x2 b2
a11 a12
x1
b1
A
, X , B
a21 a22
x2
b2
44.
◄ Ограничимся доказательством того, что из совместностиСЛАУ следует равенство rang A rang A .
Так как все миноры матрицы A являются минорами матрицы A ,
то по определению ранга rang A rang A .
Пусть X есть ненулевое решение СЛАУ: AX=B. Если c1 ( A),..., cn ( A)
- матрицы, образованные из столбцов матрицы A, то равенство AX=B
n
можно переписать в виде xk ck ( A) B Любой минор матрицы
k 1
A есть либо минор матрицы A, либо (в силу теоремы 2.1.4) алгебраиче
ская сумма миноров матрицы A. Порядок минора матрицы A
самого большого порядка будет не больше порядка какого-либо
минора матрицы A. rang A rang A . rang A rang A
СЛЕДСТВИЕ СЛАУ с m=n определенная rang ( A) n det A 0 .
45.
Элементарные преобразования матрицы:1) перестановка двух строк;
2) поэлементное умножение какой-либо строки на не равное нулю
число;
3) прибавление к одной строке соответствующих элементов другой
строки.
ЗАМЕЧАНИЕ СЛАУ преобразуется в эквивалентную СЛАУ,
если ее расширенную матрицу подвергнуть элементарным
преобразованиям.
46.
Метод Гаусса это метод решения СЛАУ с помощьюэлементарных преобразований по следующему правилу:
0
b1'
...
0
bm'
0
1
x1 x10
b1"
0 x10
... .. 1 .. ... ...
0
0
0
bm"
1
x
x
x
n
n
n
Пр.1 ЛЕКЦИЯ 4
3x1 x2 2
3 1 2 1 2 3
1 2 3 5 I 2 II
~
~
~
1 2 3 3 1 2 II 3I 0 5 7
x1 2 x2 3
5 0 1 15
~
1
0 5 7 5
x1 0, 2
1 0 0, 2
0 1 1, 4 x 1, 4 .
2
Гаусс
47.
мx1 - x2 + 2 x3 - x4 + 2 x5 = 1
п
п
Пример Найти общее решение СЛАУ н
.
п
п
о- 2 x1 + 2 x2 - 3 x3 + x4 - x5 = 2
ЛЕКЦИЯ 4 16.09.16
ЛЕКЦИЯ 3 15.09.17 ЛЕКЦИЯ 3 14.09.18 ЛЕКЦИЯ 3 25.09.19
ж 1 - 1 2 - 1 2 1ц
ж1 - 1 2 - 1 2 1ц
I - 2 ЧII
ч
ч
з
з
ч
ч
: з
:
зз
ч
ч
з
ч
ч
и- 2 2 - 3 1 - 1 2шII + 2 ЧI
и0 0 1 - 1 3 4ш
ж1 - 1 0 1 - 4 - 7ч
ц
ж1 0ч
ц
з
з
ч Ю det з
: з
ч= 1 Ю x1 , x3 - базисные
зи0 0 1 - 1 3 4 ч
зи0 1ч
ч
ш
ш
переменные. x2 , x4 , x5 - свободные переменные.
м
x1 - x2 + x4 - 4 x5 = - 7
п
п
п
п
x3 - x4 + 3x5 = 4
п
п
Ю п
Ю
нx2 = a
п
п
x4 = b
п
п
п
п
п x5 = g
о
решение СЛАУ.
мx1 = a - vb + 4g - 7
п
п
п
п
x2 = a
п
п
п
, a , b, g О R , - общее
н x3 = b- 3g + 4
п
п
x4 = b
п
п
п
п
п
о x5 =
ЛЕКЦИЯ 4 16.09.14
48.
мx1 - x2 + 2 x3 - x4 + 2 x5 = 1
п
п
н
п
п
о- 2 x1 + 2 x2 - 3 x3 + x4 - x5 = 2
49.
50.
3x1 6 x2 3x3 2 x4 4Пр.2 Решить СЛАУ 2 x1 4 x2 2 x3 x4 x5 0 .
x x 2 x 1
5
1 4
51.
x1 x2 x3 4x x 2
Пр.3 Решить СЛАУ 2 3
ЛЕКЦИЯ 3 ВИС 1.10.18
x1 x2 1
x1 x3 5
52.
§ 3 Векторное пространство и его свойства.Векторное (линейное) пространство - множество, для
элементов которого определены операции сложения и умножения
на число, удовлетворяющие следующим аксиомам (Пеано):
1) x, y E x y y x ,
2) x, y, z E ( x y ) z x ( y z ) ,
3) 0 E x E 0 x x ,
4) x E ( x) E x ( x) 0 ,
5) , R x E ( ) x ( x) ,
6) , R x E ( ) x x x ,
7) R x, y E ( x y ) x y ,
8) x E 1 x x .
ЛЕКЦИЯ 4 18.09.15 ВИ 29.09.21
Пр. Множество чисел R - векторное пространство, а множества чисел
N., Z, Q, I - нет.
Линейная комбинация элементов e1 , ..., en E - это сумма вида 1e1 ... nen ,
где 1,..., n - действительные числа, называемые коэффициентами разложения.
53.
История формирования понятия пространстваБернард Больцано (1781 -1848) - чешский математик,
философ и теолог. Ввел термины «неопределенные элемен
ты» и «произвольные допущения» (аксиомы) (1804 г.).
Энрико Бэтти(1823 -1892) - итальянский математик и физик
Ввел современную геометрическую терминологию в статье
«О пространстве любого числа измерений» (1871).
Сальваторе Пинкерле (1853-1936) - итальянский математик.
Один из основателей современного функционального анализа
В статье «Замечание о геометрии функц. простран ства» (1896)
впервые использовал термины «функциональное пространст
во», «линейное пространство». В работах П. и Вольтерра кри
сталлизуются понятия функционала и линейного оператора.
Джузеппе Пеано (1858-1932) - итальянский математик. Внёс
вклад в математическую логику, аксиоматику, философию
математики. Более всего известен как автор стандартной
аксиоматизации натуральной арифметики, в частности,
системы аксиом векторного пространства.
54.
История формирования понятия вектораГамильтон (1840-ые) опубликовал развитые операции с
векторами как часть своего кватернионного исчисления
(вектор образовывали мнимые компоненты кватерниона).
Гамильтон предложил термин вектор (лат. vector, несущий).
Максвелл использовал этот формализм в работах по
электромагнетизму, тем самым обратив внимание учёных
на новое исчисление.
Гиббс в 1880-ых г.г. выпустил «Элементы векторного
анализа».
Хэвисайд (1903) придал векторному анализу
современный вид.
55.
ЛЕКЦИЯ 4 21.09.18Элементы e1 , ..., en E линейно зависимы, если существует равная
нулю линейная комбинация этих элементов, в которой не все
коэффициенты равны нулю.
В противном случае элементы
линейно независимы.
Пр. Орты в евклидовой плоскости:
ЗАМЕЧАНИЕ Элементы линейно зависимы хотя бы один из
них представим в виде линейной комбинации остальных.
Последовательность элементов e1 ,..., en E полная (является
базисом) в векторном пространстве E, если каждый элемент из
E представим (единственным образом) в виде линейной
комбинации этих элементов.
ЗАМЕЧАНИЕ Базис является полной системой. Обратное,
вообще говоря, неверно.
Пр.
56.
ТЕОРЕМА 3.1 1) Последовательность элементов e1 ,..., enявляется базисом в векторном пространстве Е она является
полной и линейно независимой системой.
2) Базисы в векторном пространстве имеют одинаковое число
элементов.
Если в векторном пространстве существует базис, то число
элементов n этого базиса - размерность пространства E, а
пространство называется n- мерным.
Обозначение dim E : n (от лат. dimension- размерность).
Термин «n-мерное пространство» ввел Грассман (1844).
Векторное пространство называется бесконечномерным,
если в нём не существует базис с конечным числом элементов.
{
Пр. Пространство P : a0 x n a1 x n 1 ... an 1 x an : ak R , n N {0}
всех многочленов бесконечномерное.
57.
◄ 1) Доказательство от противного. Пусть e1 ,...en линейнозависимы и, например, 1 0 . Тогда нулевой элемент имеет два
различных разложения 0 1 e1 ... n en и 0 0 e1 ... 0 en ,
что противоречит определению базиса.
(от противного). Пусть какой-либо элемент имеет два
различных разложения: x 1e1 ... n en , x 1e1 ... n en и,
например, 1 1 . Тогда ( 1 1 )e1 ... ( n n )en 0 , что проти
воречит условию линейной независимости элементов e1 ,..., en .
58.
2) Пусть f1 ,..., f m , e1 ,...en - два базиса в Е. Пусть дляe1 11 f1 ... m1 f m
определенности m n . По условию . . . . . . . . .
e f ... f
1n 1
mn m
n
a11 x1 ... a1n xn 0
Покажем, что СЛАУ . . . . . . . . имеет единственное
a x ... a x 0
mn n
m1 1
(нулевое) решение. Пусть, от противного, есть ненулевое
решение x10 ,..., xn0 . Умножая строки предыдущей системы на
соответствующие xi0 и почленно их складывая, получим:
x10 e1 ... xn0en ( 11 x10 ... 1n xn0 ) f1 ...
( m1 x10 ... mn xn0 ) f m 0
Так как e1 ,..., en базис, то x10 ... xn0 0 . Это противоречит
предположению, и значит СЛАУ имеет единственное
решение. Это возможно только в случае m n .
59.
Декартово произведение множеств E и F называетсямножество пар элементов
E F : {x, y}: x E , y F ,
Декартово произведение векторных пространств E и F - это
декартово произведение соответствующих множеств
E F : {x, y}: x E , y F ,
на котором определены операции сложения элементов и
умножения их на число по правилу: {x, y}: { x, y},
{x1 , y1} {x2 , y2 }: {x1 x2 , y1 y2 }.
ЗАМЕЧАНИЕ 1 Аналогично определяются декартовы
произведения n пространств E1 ... En и E n : E ... E .
n
ЗАМЕЧАНИЕ 2 Операции над элементами декартова произве
дения удовлетворяют 8 аксиомам.
.
60.
ПРИМЕР 1 Пространство векторов V3 с общим началом.ЗАМЕЧАНИЕ 3 вектора образуют базис в V3 они не
компланарные.
dim(V3 ) 3.
61.
ПРИМЕР 2 Пространство комплексных чисел .i : 1 - мнимая единица. z : a b i -комплексное число, a, b R
(a1 b1i ) (a2 b2i ) : (a1 a2 ) (b1 b2 ) i
(a bi) (0 0i) (a 0) (b 0)i a bi ЛЕКЦИЯ 5
Пр.1 (c 0 i)(a bi) (ca 0 b) (cb 0 a) i ca cbi c(a bi) c 0i c
ЗАМЕЧАНИЕ Множество комплексных чисел удовлетворяет
аксиомам 1)-8) векторного пространства относительно операций
сложения и умножения на действительное число.
Пр.2 Число a bi : a ( b)i противоположное числу z : a bi .
Последовательность 1, i образует базис в dim 2 .
z a bi - сопряженное число к комплексному числу z : a bi .
z z a 2 b2 R .
Пр.3 x 2 4 x 5 0 x1,2 2 4 5 2 i .ЛЕКЦИЯ 5 19.09.16
Проверка. 2 i 4 2 i 5 4 4i i 2 8 4i 5 0 .
2
62.
ПРИМЕР 3 Пространство M m,n матриц размера m n .a11 ... a1n
ЗАМЕЧАНИЕ Матрица A : ... ... ... является противопо
a
m1 ... am,n
ложной к матрице A (aij ) . Попарно различные матрицы размера
m n в количестве m n штук, у каждой из которых один элемент
равен 1, а остальные равны 0, образуют базис в пространстве M m,n
1 0 0 1 0 0 0 0
Пр.
- базис в M 2,2 .
,
,
,
0 0 0 0 1 0 0 1
& A M 2,2
1 0
0 1
0 0
0 0
A a11
a12
a21
a22
0 0
0 0
1 0
0 1
a11 0 0 a12 0 0 0 0 a11 a12 0 0
0 0 0 0 a21 0 0 a22 a21 a22 0 0
a11 a12 a21 a22 0 .
dim(M m,n ) mn.
63.
ПРИМЕР 4 Пространство Pn многочленов степени n .[ p q]( x) (a0 b0 ) (a1 b1 ) x ... (an bn ) x n
( a0 b0 ) ( a1 b1 ) x ... ( an bn ) x n ЛЕКЦИЯ 4 19.09.17
( a0 ... an x n ) ( b0 ... bn x n ) p( x) q( x) .
ЗАМЕЧАНИЕ 1 Множество Pn удовлетворяет аксиомам 1)-8), и
потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Последовательность многочленов x 0 : 1, x, ,..., x n
является базисом в Pn . Поэтому dim Pn n 1.
полна в P .
Пусть p( x) a 1 a x ... a x 0 0 1 0 x ... 0 x .
◄ p( x) : a01 a1 x ... an x n 1, x, ,..., x n
n
0
1
n
n
n
По определению равенства двух многочленов k n ak 0 .
1, x, ,..., x n линейно независима в Pn .
Остается воспользоваться теоремой 2.3.1.
64.
ПРИМЕР 5 Арифметическое пространство n ЛЕКЦИЯ 5Ввели Кэли и Грассман (1946).
ЗАМЕЧАНИЕ 1 Множество n удовлетворяет аксиомам 1)-8), и
потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Элементы
e1 : {1,0,...,0}, e2 : {0,1,0,...,0}, ... , en : {0,...0,1}
образуют естественный базис в n . Следовательно, dim n n .
◄ 1) a n a1e1 ... an en {a1 , a2 ,..., an } a , то есть
последовательность e1 ,..., en полна в n .
2) По определению равенства двух n-ок в n
a1e1 ... an en {a1 ,..., an } {0,...,0} a1 ... an 0 .
Следовательно, условия теоремы 2.3.1 выполнены.
ЗАМЕЧАНИЕ 3 Аналогично определяется пространство C n над
полем комплексных чисел C .
65.
§ 4 Линейные операторы. Евклидово пространство.Отображение множества A в множество B - правило,
сопоставляющее каждому элементу из A один элемент из B .
В случае A B отображение называется преобразованием
пространства. ЛЕКЦИЯ 5 20.09.14
Обозначение: F : A B .
A - область определения.
B - область значений.
y F ( x) - образ элемента.
Множество значений (образ отображения)
F ( A) : y B : x A y F ( x) .
Пр. y sin x .
66.
Отображение L из векторного пространства E в векторное пространство F называется линейным оператором (отображением), если
, R a, b E L( a b) La Lb .
(впервые изучались Гамильтоном и Кэли, 1853-1862 г.)
(позднелатинское operator — работник).
Пр.1 Функции, имеющие производную в фиксированной точке,
образуют векторное пространство. Операция дифференцирования
d
в таком пространстве является линейным оператором.
dx
d
d
d
(2 x 2 3sin x) 2 x 2 3 sin x .
dx
dx
dx
Пр. 2 Каждая матрица A (aij ) размера m n определяет линейный
оператор L :
n
m
по следующему правилу: если a {x1 , ..., xn } ,
y1 a11 ... a1n x1
... .
то La : { y1 , ..., yn }, где ... : ....................
y a
x
....
a
m n
m m1
Такой оператор называется матричным.
67.
Термин «функция» (в некотором более узком смысле) былвпервые использован Лейбницем (1692 год). Иоганн Бернулли в
письме к Лейбницу употребил этот термин в смысле, более
близком к современному. Первоначально, понятие функции было
неотличимо от понятия аналитического представления.
Определение функции, данное Эйлером (1751 год), затем —
у Лакруа (1806 год) — уже практически в современном виде.
Общее определение функции (в современной форме, но для
числовых функций) было дано Лобачевским (1834 год)
и Дирихле (1837 год).
К концу XIX века понятие функции переросло рамки
числовых систем. Первыми это сделали векторные функции,
вскоре Фреге ввёл логические функции (1879), а после
появления теории множеств Дедекинд (1887) и Пеано (1911)
сформулировали современное универсальное определение
отображения.
68.
Готфрид Вильгельм Лейбниц (1646 - 1716) –немецкий философ, логик, математик, механик,
физик, юрист, историк, дипломат, изобретатель
и языковед.
Основатель и первый президент
Берлинской Академии наук.
Л., независимо от Ньютона, создал математический анализ - дифференциальное и интегральное исчисления, основанные на бесконечно малых величинах.
Л. создал комбинаторику как науку.
Заложил основы математической логики.
Описал двоичную систему счисления с цифрами 0 и 1, на
которой основана современная компьютерная техника.
В механике ввёл понятие «живой силы» (прообраз современного понятия кинетической энергии) и сформулировал закон
сохранения энергии.
В психологии развил учение о бессознательной психической
жизни.
69.
Ю́лиус Вильге́льм Ри́хард Дедеки́нд (1831- 1916) немецкий математик, известный работами пообщей алгебре и основаниям вещественных чисел.
В 1871 году, обобщив теорию многочленов и ал
гебраических чисел, вводит в математику абстракт
ые алгебраические структуры: кольца, идеалы
и модули.
Д., наряду с Вейерштрассом, создал обоснование теории веще
ственных чисел (1876).
Совместно с Кронекером он создаёт общую теорию делимости
Д. был редактором посмертных изданий избранных трудов
Дирихле, Гаусса и Римана.
70.
L : E F - изоморфизм векторных пространств E и F, если:1) L переводит разные элементы в разные:
ЛЕКЦИЯ 6 21.09.15
x1 , x2 E ( x1 x2 ) ( Lx1 Lx2 ) ,
2) каждый элемент из F является образом некоторого элемента из E:
y F x E Lx y .
При этом пространства E, F называются изоморфными.
Пр. Пространства
n
и M n1 изоморфны.
71.
(в ) называется линейнойЛинейный оператор из E в
формой (линейным функционалом).
b
Пр. Определённый интеграл f ( x)dx на векторном пространстве
a
интегрируемых на [a, b] функций является линейным
функционалом. Лекция 4 2.10.19
Отображение F ( x1 ,..., xn ) : F ({x1 ,..., xn }) из декартова
произведения векторных пространств E n E ... E
в векторное пространство F называется n-линейным
(полилинейным) отображением, если оно является линейным
отображением из E в F по каждой переменной xk , k 1,.., n , при
фиксированных остальных. n- линейное отображение из E n в
называется n- линейной (полилинейной) формой.
ЗАМЕЧАНИЕ 2-линейное отображение F ( x1 , x2 ) : E 2 F
принято называть билинейным отображением.
72.
Билинейная форма B( x, y ) : E 2 называется скалярнымпроизведением на векторном пространстве E, если она обладает
свойствами:
1) x, y E B( y, x) B( x, y ) ,
2) x E если ( y E B ( x, y ) 0), то ( x 0) ,
3) x 0 B( x, x) 0 .
Обозначение x, y ( x, y ) : B( x, y ) .
Пр.1 Определенное в школе скалярное произведение векторов
порождает билинейную форму B ( x , y ) : V 32 по правилу
B( x , y ) : x y cos x y , и для нее выполняются свойства 1)-3).
Пр.2 Пусть x : x1 ,..., xn , y : y1 ,..., yn n . Тогда отображение
B( x, y) x, y : x1 y1 ... xn yn : n
является билинейной формой со свойствами 1) - 3). Мы будем
называть его естественным скалярным произведением в n .
73.
Отображение : Eсвойствами:
1) x 0 x 0 ,
2) x E R x x ,
3) x, y E x y x y .
называется нормой, если обладает
ЗАМЕЧАНИЕ 1 Понятие нормы обобщает понятие длины
(модуля) вектора в V3 . Гаусс ввел (1831) понятие и термин норма
комплексного числа как z z . Гамильтон ввел независимо (1843)
понятие и термин норма кватерниона термин норма вектора.
Обозначение - Шмидт (1908). ЛЕКЦИЯ 4 ВИС 15.10.18
ЗАМЕЧАНИЕ 2 Каждое скалярное произведение x, y : E 2
порождает норму в E по правилу x :
x, x .
ЛЕКЦИЯ 6
СЛЕДСТВИЕ Естественное скалярное произведение в R n
2
обладает свойством : x, y R n x1 y1 ... xn yn x12 ... xn2 y12 ... yn2
(неравенство Коши-Буняковского). ЛЕКЦИЯ 5 26.09.18
74.
Виктор Яковлевич Буняко́вский (1804-1889) – российскийматематик, вице-президент академии наук (1864—1889).
Из семи лет пребывания за границей в течение двух лет
в Париже слушал лекции в Сорбонне и общался с Лапласом,
Пуассоном, Фурье, Ампером, Лежандром и другими знамени
тыми учёными. Больше всего Б. работал у Коши.
С 1846 года Б. читал лекции по аналитической механике
в санкт-петербургском университете, дифференциальное и
интегральное исчисление, теорию вероятностей, а позднее,
уже в пятидесятых годах интегрирование дифференциальных
уравнений, вариационное исчисление, исчисление конечных
разностей.
Изобрел планиметр и вариант арифмометра.
Б. больше всего работал в теории чисел и теории вероятностей. В 1846 году появилась
всемирно известная монография «Основания математической теории вероятностей»
Разрабатывал по преимуществу практические приложения математической теории
вероятностей. Его труды (1958) по проектированию эмеритальной кассы послужили к
учреждению целого ряда подобных касс на выработанных им началах. Сделав в 1869
году исследование «выводы эмпирического закона о смертности», Б. упростил этим
решение вопросов относительно страхования капиталов и пожизненных доходов.
В 1885 году вышла статья Б. «О вероятной числительности контингентов русской
армии в 1883—1885 годах», являвшаяся очень ценным руководством при решении
вопросов, связанных с всеобщей воинской повинностью.
Лекции Б. отличались поразительной ясностью, увлекательностью и в то же время
литературной красотой изложения, делали легко доступными самые сложные
математические положения и увлекали даже безучастных слушателей
75.
n-мерное евклидово (точечное) пространство - тройка объектовEn ( E , . , . , P) : n-мерное векторное пространство E, какое-либо
скалярное произведение x, y на нём и множество “точек” P.
Объекты согласованы следующим образом:
1) каждой упорядоченной паре точек A, B P поставлен в
соответствие один элемент x E , который обозначают x AB ;
2) x E A P существует единственная точка B со свойством
x AB ;
3) A, B, C P AB BC AC (правило треугольника).
ЗАМЕЧАНИЕ Пеано - основатель концепции, по которой основными
ми элементами евклидова пространства являются вектор и точка.
Расстояние между двумя точками M1 , M 2 P
определяется по формуле ЛЕКЦИЯ 6 23.09.16
M 1 , M 2 :
M 1 M 2 , M 1M 2 M 1M 2 .
n-мерное евклидово векторное пространство - пара E , , .
n-мерное аффинное пространство - пара (E,P) со свойствами 1) -3)
76.
Пр. n- мерное арифметическое евклидово пространство n тройка объектов: арифметическое пространство n , естественноескалярное произведение x, y : x1 y1 ... xn yn и множество
«точек» P : ( x1,..., xn ) : x1,..., xn . При этом точки A ( x1 ,..., xn ) ,
B ( y1 ,..., yn ) P свяжем с вектором из n по правилу
AB : { y1 x1 ,..., yn xn }.
Тогда расстояние между этими точками вычисляется по формуле
( A, B) :
AB, AB ( y1 x1 ) 2 ... ( yn xn ) 2 .
2
3
ЛЕКЦИЯ 6
77.
Декартова система координат (ДСК) в n-мерномевклидовом пространстве E - это совокупность каких-либо
точки O P и базиса e1 ,..., en E .
Символ Кронекера – отображение i j : 2 {0,1},
определяемое по правилу i j : 1, если i j и i j : 0 , если i j .
Базис e1 ,..., en E называется ортонормированным, если
i, j n ei , e j ij .
ЗАМЕЧАНИЕ Элементы ei ортонормированного базиса попарно
перпендикулярны: i j ei , e j 0 и их нормы равны единице:
i n ei
ei , ei 1. ЛЕКЦИЯ 5 ВИ 6.10.21
Прямоугольная декартова система координат (ПДСК) ДСК, в которой выделенный базис является ортонормированным.
Если a x1e1 ... xn en , то числа x1 ,..., xn называются координатами (компонентами) элемента (вектора) a в базисе e1 ,..., en .
78.
Рене́ Дека́рт (Картезий, 1596-1650) –французский философ, математик, механик, физик и физиолог, создатель
аналитической геометрии, современной алгебраической
символики, автор метода радикального сомнения в
философии (картезианство), механицизма в физике.
Сформулировал свой метод познания: дедуктивные
(математические) рассуждения над результатами
воспроизводимых опытов.
«Рассуждение о методе, позволяющем направлять
свой разум и отыскивать истину в науках» (1637). Здесь переработана мате
матическая символика Виета в близкую к современной. Коэффициенты он
обозначал a, b, c…, а неизвестные - x,y, z. Натуральный показатель степени
принял современный вид (дробные и отрицательные утвердились благодаря
Ньютону). Появилась черта над подкоренным выражением. Уравнения
приводятся к канонической форме (в правой части - ноль).
Классификация алгебраических кривых. Новый способ задания кривой с помощью уравнения - был решающим шагом к понятию функции.
Сформулировал (хотя и не доказал) основную теорему алгебры: общее
число вещественных и комплексных корней уравнения равно его степени.
Труды математиков второй половины XVII века отражают сильнейшее
влияние Декарта.
79.
Радиусом-вектором точки М и ПДСК называется вектор OM .Если OM x1e1 ... xn en , то n- ка ( x1 ,..., xn ) называются
координатами точки M P в ПДСК.
Пусть даны матрица A (aij ) размера (n k ) n , rang A n k ,
и последовательность чисел b1 ,..., bn k . k-мерная плоскость
(k-плоскость) в n-мерном евклидовом пространстве E с фиксированной ПДСК - это множество точек Ì ( x1 ,..., xn ) , координаты
a11 x1 . . . a1n xn b1
которых удовлетворяют СЛАУ
.
. . .
a x ... a
n k n xn bn k
n k 1 1
1-плоскость в E называется прямой. ЛЕКЦИЯ 5 26.09.17
Пр.1 2-плоскость (плоскость) в V3 - это множество точек,
координаты которых ( x1 , x2 , x3 ) удовлетворяют СЛАУ
a11 x1 a12 x2 a13 x3 b1 или проще Ax By Cz D 0 .
80.
Пр.2 Прямая в V3 - это множество точек, координаты которыхa11 x1 a12 x2 a13 x3 b1
( x1 , x2 , x3 ) удовлетворяют СЛАУ
,
a21 x1 a22 x2 a23 x3 b2
a11
где rang
a21
a12
a22
a13
2 . Или проще
a23
A1 x B1 y C1 z D1 0
.
A2 x B2 y C2 z D2 0
81.
Полярная система координат в V2 - совокупность точки O(- полюс) и луча с началом в этой точке (- полярная ось).
Полярные координаты точки M - пара чисел (r , ) , где угол между полярной осью и вектором OM , отсчитываемый
против часовой стрелки, r OM . ЛЕКЦИЯ 6 27.09.2014
Совместим прямоугольную
декартову и полярную систеM y
M
мы координат так, чтобы наr
чало координат совпадало с
X
полюсом, а ось OX - с полярx
O
O
ной осью, как на рисунке.
Декартовы координаты (x,y) точки M и ее полярные координаты
r x 2 y 2
x r cos
связаны равенствами:
.
,
y
y r sin arctg
x
Пр. r=1 есть уравнение единичной окружности в полярной
системе координат.
Y
82.
§ 5 Векторная алгебра в пространстве V3Даны ось l (-направленная прямая) и
вектор. Опустим перпендикуляры из
его концов на ось. ЛЕКЦИЯ 7 28.9.15
b
a
c
l
Проекция вектора a на ось l - это расстояние между
основаниями этих перпендикуляров, взятое со знаком "+", если
0 l a
, со знаком "-", если
l a и равное нулю, если
2
2
a l . Правило, сопоставляющее каждому вектору его проекцию
на ось, называется операцией проектирования.
Пр. Если a l , то прl a 0 .
Если вектор a и ось l параллельны и сонаправлены, то прl a a .
Если вектор a и ось l параллельны и разнонаправлены, то
прl a a .
83.
Проекция (лат. projectio - выбрасывание вперёд). Термин проекция употребляется и в отношении самойоперации проектирования, и в отношении её результата.
Центр проекции + Предмет + Картинная (проекционная) плоскость.
Аксонометрическая проекция (от др.-греч. ἄξων «ось»+μετρέω «измеряю»)
Центральная проекция
Стереографическая проекция
А́льбрехт Дю́рер (1471- 1528) - немецкий живописец и график.
Один из величайших мастеров западноевропейского Ренессанса.
Первый североевропейский теоретик искусства , автор
практического руководства для художников на немецком языке.
Основоположник сравнительной антропометрии.
Первый из европейских художников, написавший автобиографию
84.
ТЕОРЕМА 5.1 (свойства проекции)1) прl a a cos(l a ) .
ВИ-11 ЛЕКЦИЯ 4 29.09.21
2) a , b V3 прl (a b ) прl a прl b .
3) a V3 l прl ( a ) прl a . То есть операция
проектирования является линейным функционалом в V3 .
4) Фиксируем ПДСК в V3 . Тогда проекции вектора на оси
координат OX,OY,OZ совпадают с компонентами этого вектора
в базисе i , j , k
: если a {x, y, z}, то
x прi a , y пр j a , z прk a .
5) Косинусы cos( i a ), cos( j a ), cos(k a ) называются
направляющими косинусами вектора a и связаны
равенством cos 2 ( i a ) cos 2 ( j a ) cos 2 (k a ) 1.
85.
◄4) Подействуем на равенство a xi yj zk линейной опера-
цией проектирования на ось OX: прi a x прi i y прi j z прi k x ,
прk a x прk i y прk j z прk k z .
5) По свойству гипотенузы прямоугольного
параллелепипеда и пунктам 1), 4)
2
a x 2 y 2 z 2 a 2 cos 2 i a a 2 cos2 j a a 2 cos 2 k a
1 cos 2 cos 2 cos 2 , ЛЕКЦИЯ 7 30.09.16
где : i a , : j a , : k a .
86.
Скалярное произведение векторов a , b это числоa b (a, b) a b cos ab .
ЛЕКЦИЯ 7
ЛЕКЦИЯ 6 28.09.18
ТЕОРЕМА 5.2 (свойства скалярного произведения)
1) a a = a 2 , где a = a . 2) ab = 0 Ы (a = 0) Ъ (b = 0) Ъ (a ^ b) .
3) a b = b a . 4) a b = a Чпр a b = b Чпр b a .
5) Скалярное произведение является билинейной формой на V32 .
6) Если a x1 , y1 , z1 , b x2 , y2 , z2 , то a b x1 x2 y1 y2 z1 z2 .
Физическое приложение
Работой постоянной силы F по
перемещению материальной точки из
начала в конец вектора s называется
величина A : F s .
S
F
F
F
F
F
F
A : F s
87.
Упорядоченная тройка некомпланарных векторовa, b, c с общим началом называется правой (левой),
если из конца вектора c движение от a к b по
кратчайшему из двух углов происходит против
(по) часовой стрелки.
ЗАМЕЧАНИЕ Обычно предполагается, что орты i , j , k в ПДСК
образуют правую тройку.
Векторное произведение векторов a , b это вектор 0 , если
(a 0) (b 0) (a || b) . В противном случае
[a,b]
c
векторное произведение это вектор c , который
вполне определяется свойствами:
a
b
1) | c | a b sin ab ,
2) c a , b ,
3) a , b, c - правая тройка векторов.
Пр. [ i , j ] k , [ j, k ] i, [k , i] j, [ j , i ] k , [k , j ] i, [i, k ] j .
88.
Смешанное произведение трёх векторов a , b, c - это числоa b c : ([a , b ], c) .
ЗАМЕЧАНИЕ 1 ЛЕКЦИЯ 6 29.09.17
1) (геометрический смысл модуля векторного произведения)
| [a , b] | численно равен площади параллелограмма, построенного
на векторах a , b как на сторонах.
2) (геометрический смысл модуля смешанного произведения)
| a b c | численно равен объему призмы, построенной на векторах
a , b, c как на ребрах. ВИС ЛЕКЦИЯ 6 12.10.18
·
| a b c |= | [a , b ] | Ч| c | Ч| cos([a , b] c) |= | [ a , b ] | Чпр[ a ,b ]c = Sпар Чh = Vприз .
ЗАМЕЧАНИЕ 2 Тройка a , b, c правая векторы [a , b ], c находят
ся в одном полупространстве, определяемом плоскостью векторов
·
a , b [a , b ] c / 2 a b c = | [a , b ] | Ч| c | Чcos([a , b] c) > 0
смешанное произведение a b c положительное.
ЗАМЕЧАНИЕ 3 a bc bc a c a b b a c a c b c b a .
89.
Уи́ льям Ро́ уэн Га́мильтон (1805 - 1865) - выдающийся ирландскийматематик и физик XIX века. Основные работы посвящены мате
матической оптике, механике, вариационному исчислению.
Развил (1830—1837) математическую оптику, а затем
распространил свои методы на механику.
Привел дифференциальные уравнения произвольной
материальной системы к каноническому виду.
Разрабатывал теорию комплексных чисел. Идею комплексных чисел
распространил на пространство, определив четыре единицы: 1, i, j, k. Ввел
понятие кватерниона, термин вектор.
Г. ввел (1846) скалярное произведение как скалярную часть и векторное
произведение как векторную часть произведения двух кватернионов.
Работал также в области геометрии, алгебры и теории дифференциальных
уравнений. Именем Гамильтона названы: 1) функция, определяющая движение
механической системы, 2) дифференциальный оператор, 2) канонические
уравнения механики.
Установил (1833) для консервативных систем общий интегральный
вариационный принцип классической механики.
90.
ТЕОРЕМА 5.3 (свойства векторного произведения)1) a , b b , a .
2) Векторное произведение является билинейным отображением из
V32 в V3 .
i
3) Если a x1 , y1 , z1 , b x2 , y2 , z2 , то a , b x1
x2
j
y1
y2
k
z1 .
z2
СЛЕДСТВИЕ Ненулевые векторы a = {x1 , y1 , z1}, b = {x2 , y2 , z2 }
x
y
z
параллельны Ы 1 = 1 = 1 . ЛЕКЦИЯ 7 30.09.14 ЛЕКЦИЯ 8 2.10.15
x2
y2 z 2
Физический смысл векторного произведения:
F
Моментом относительно точки A силы FB ,
приложенной к точке B, называется вектор A
M A [ FB ] : [ AB, FB ].
M A [ FB ]
B
91.
Физический смысл векторного произведения:Пусть материальная точка A вращается по
окружности (с центром O) с линейной
O
скоростью v A . Вектор угловой скорости
r
вращения точки A относительно цента O
это расположенный на оси вращения вектор
, определяемый равенством vA [ , r ] .
Равенство называется формулой Эйлера. ЛЕКЦИЯ 6 9.10.19
vA
A
ТЕОРЕМА 2.7 (свойства смешанного произведения)
1) abc 0 (a 0) (b 0) (c 0) (векторы a , b , c
компланарны).
2) Смешанное произведение является 3– линейной формой:
a b c : V33 .
3) Если a {x1 , y1 , z1}, b {x2 , y2 , z2 }, c {x3 , y3 , z3} в ПДСК, то
x1
a bc x2
x3
y1
y2
y3
z1
z2 .
z3
92.
§ 6 Прямые и плоскости ЛЕКЦИЯ 8 3.10.16в евклидовых пространствах V2 , V3 ЛЕКЦИЯ 8
L : Ax + By + Cz + D = 0 - общее уравнение плоскости в V3
:= {( x, y, z ) : Ax + By + Cz + D = 0}.
(A,B,C 0 одновременно). L=
ЗАМЕЧАНИЕ Уравнение впервые встречается у Клеро (1731).
Вектор нормали к плоскости - вектор, перпендикулярный любому
вектору, начало и конец которого лежат в этой плоскости.
Пр.1 Вектор n := { A, B, C} является вектором нормали к
плоскости L : Ax + By + Cz + D = 0 .
Пр.2 Орт i является вектором нормали к координатной плоскости
YOZ : x 0 .
Угол между плоскостями - угол между их векторами нормалей.
В зависимости от выбранных векторов нормалей этот угол имеет
два значения.
ЛЕКЦИЯ 8.12
93.
Алекси́ Клод Клеро́ (1713-1765) -французский математик, механик и астроном, иностранный член
Петербургской АН (1754).
В возрасте 12 лет он поразил парижских академи
ков своей работой о некоторых кривых 4-ого поряд
ка. В 16-лет представил академии трактат: «Иссле
дования о кривых двоякой кривизны», который поло
жил начало 3-ём дисциплинам: аналитической геометрии в про
странстве, дифференциальной геометрии и начертательной геометрии.
Ввёл понятия криволинейного интеграла (1743), полного дифферен
циала, а также общего и особого решения дифференциальных урав
нений 1-го порядка (1736). Подготовил блестящие учебники
«Начала геометрии» и «Начала алгебры».
Создал динамическую теорию относительного движения в
механике. Определил соотношение между силой тяжести и
сжатием Земли.
94.
Лаза́р Карно́ 1753- 1823) — французский государственный и военный деятель, инженер и учёный.
Предложил название «Комплексное число» (1803).
Издал (1797) свои «Размышления о метафизике ис
числения бесконечно малых». Выступал с критикой
теории аналитических функций Ж.Лагранжа.
Сади Карно (1796 - 1832) - французский физик и математик. Внук Л.Карно. В 1824 году вышла первая и
единственная работа С. Карно - «Размышления о
движущей силе огня и о машинах, способных раз
вивать эту силу». Считается основополагающей в
термодинамике. В ней был произведён анализ суще
ствовавших в то время паровых машин, и были выве
дены условия, при которых КПД достигает максима
льного значения (в паровых машинах того времени
КПД не превышал 2 %). Помимо этого там же были
введены основные понятия термодинамики:
идеальная тепловая машина (см. тепловая машина), идеальный цикл
(см. цикл Карно), обратимость и необратимость термодинамических
процессов. Умер о холеры.
95.
ТЕОРЕМА 6.1 (свойства плоскости в V3 ) Пусть заданы 3 плоскосA1 B1 C1
A1 B1 C1 D1
ти L ii : Ai x Bi y Ci z Di 0, i 1,2,3, A : A2 B2 C2 , A : A2 B2 C2 D2
A B C
A B C D
3
3
3
3 3
3 3
A1 B1 C1
A1 B1 C1
rang
1) L 1 || L 2
1.
A
B
C
A2 B2 C2
2
2
2
A1 B1 C1 D1
A1 B1 C1 D1
rang
1.
2) L 1 L 2
A
B
C
D
A2 B2 C2 D2
2
2
2
2
3) Плоскости L 1 , L 2 , L 3 пересекаются по одной прямой тогда и
только тогда, когда rangA rangA 2.
4) Плоскости L 1 , L 2 , L 3 пересекаются в одной точке т огда и только
тогда, когда rang A 3 det A 0 . ВИС ЛЕКЦИЯ 7 26.10.18
5) cos L 1L 2
A1 A2 B1B2 C1C2
A B C A B C
2
1
2
1
2
1
2
2
2
2
2
2
. ЛЕКЦИЯ 7 3.10.17
6) Расстояние от точки M 0 x0 , y0 , z0 до плоскости L 1 вычисляется
по формуле M 0 , L 1
A1 x0 B1 y0 C1 z0 D1
A B C
2
1
2
1
2
1
. ЛЕКЦИЯ 8 4.10.14
96.
Пр.1 Составить уравнение плоскости, проходящей через триточки M i ( xi , yi , zi ), i 1, 2,3, не лежащие на одной прямой.
M3
M1
M
M2
Пр.2 Найти общий вид уравнения плоскости, проходящей через
заданную точку M 0 ( x0 , y0 , z0 ) .
97.
Пусть векторы a : { 1, 1, 1}, b : { 2 , 2 , 2} не коллинеарны, изадана точка M 0 ( x0 , y0 , z0 ) . Система уравнений
x 1u 2v x0
измерять одну вещь
y 1u 2v y0 , u , v R ,
с
помощью
другой
.
Термин
Лейбница
,1684
z u v z
1
2
0
определяющая множество точек с координатами ( x, y, z ) в V3 ,
называется параметрическим уравнением плоскости.
ЗАМЕЧАНИЕ а) Если плоскость задана параметрическим
уравнением, то ее общее уравнение имеет вид
1 1
1 1
1
( x x0 )
( y y0 )
2 2
2 2
2
1
( z z0 ) 0 .
2
б) Если плоскость задана уравнением A( x x0 ) B( y y0 ) C ( z z0 ) 0
и для определенности A 0 , то ее параметрическое уравнение
B
C
x A u A v x0
можно задать, в виде: y u y0
, u, v R .
98.
ЗАМЕЧАНИЕ 1Пусть в какой-либо ПДСК евклидовой плоскости V2 заданы две прямые l1 , l2 уравнениями Ai x Bi y Ci 0, i 1,2Тогда справедливы утверждения.
1) l1 || l2
2) l1 l2
A1 B1
.
A2 B2
A1 B1 C1
.
A2 B2 C2
3) cos l1 l2
A1 A2 B1B2
A B A B
2
1
2
1
2
2
2
2
.
4) Расстояние от точки M 0 ( x0 , y0 ) до прямой l1 вычисляется по
формуле ( M 0 , l1 )
A1 x0 B1 y0 C1
A B
2
1
2
1
.
ЗАМЕЧАНИЕ 2 В современной форме основные задачи на
прямую впервые изложил Лакруа (1799).
99.
Сильве́стр Франсуа́ де Лакруа́ (17651843) - французский математик.Профессор парижских нормальной и
политехнической школ, декан факультета наук, профессор в Collège de France.
Известен по составленному им курсу
дифференциального и интегрального
исчисления: «Traité du calcul différentiel et
intégral». На русский язык не переводился.
В Российской империи учебниками Лакруа широко
пользовались при чтении лекций в университетах, и они же
вместе с пособиями Луи-Бенжамена Франкёра служили для
составителей русских учебников главными источниками и
образцами.
100.
Множество точек, координаты которых ( x, y, z ) удовлетворяютA1 x B1 y C1 z D1 0
A1
СЛАУ l :
, где rang
A2 x B2 y C2 z D2 0
A2
B1
B2
C1
2,
C2
называется общим уравнением прямой в V3 .
A1 x B1 y C1 z D1 0
l : ( x, y, z ) V3 :
.
A2 x B2 y C2 z D2 0
Множество точек, координаты которых ( x, y, z ) удовлетворяют
СЛАУ
A1 ( x x0 ) B1 ( y y0 ) C1 ( z z0 ) 0
A2 ( x x0 ) B2 ( y y0 ) C2 ( z z0 ) 0
A1
где rang
A2
B1
B2
(1),
C1
2 , называется общим уравнением прямой в
C2
V3 , проходящей через точку M 0 ( x0 , y0 , z0 ) .
101.
Пусть дан вектор k {m, n, p} 0 и точка M 0 ( x0 , y0 , z0 ) .x x0 y y0 z z0
Система уравнений вида
2
m
n
p
называется каноническим уравнением прямой (Коши, 1826).
Вектор k - направляющий вектор прямой l (Лагир, 1685) .
Формула, определяющая множество точек в V3 с координатами
x mt x0
y nt y0 , t R
z pt z
0
(3) ,
называется параметрическим уравнением прямой (Коши,
1826). ЛЕКЦИЯ 9 7.10.16
102.
Огюсте́н Луи́ Коши́ (1789 - 1857) — великий французский математик, член Парижской Петербургской и других академий наук, Лондонского королевского общества.
К. написал свыше 800 работ. Много работал в
области комплексного анализа, в частности, создал теорию интегральных вычетов. В математической физике
глубоко изучил краевую задачу с начальными условиями,
которая с тех пор называется «задача Коши».
К. заложил основы математической теории
упругости. Он рассматривал тело как сплошную среду и
вывел систему уравнений для напряжений и деформаций в каждой точке. В
работах по оптике Коши дал математическую разработку волновой теории
света и теории дисперсии.
Ему принадлежат также исследования по геометрии (о многогранниках), по
теории чисел, алгебре, астрономии и во многих других областях науки.
Впервые дал строгое определение основным понятиям математического
анализа — пределу, непрерывности, производной, дифференциалу, интегралу,
сходимости ряда и т. д. Его определение непрерывности опиралось на понятие
бесконечно малого, которому он придал новый смысл: у К. бесконечно малое —
переменная величина, стремящаяся к нулю. Ввёл понятие радиуса сходимости
ряда. Курсы анализа К., основанные на систематическом использовании понятия
предела, послужили образцом для большинства курсов позднейшего времени.
103.
ЗАМЕЧАНИЕ 1 Направляющий вектор k параллелен любомувектору, начало и конец которого лежат на этой прямой.
ЗАМЕЧАНИЕ 2 Уравнения (1), (2), (3), в которых
B1 C1
C1
m :
, n :
B2 C2
C2
A1
A1 B1
,
, p :
A2
A2 B2
задают одну и ту же прямую в V3 .
ЛЕКЦИЯ 7 16.10.19
____
Угол между двумя прямыми - угол между направляющими
векторами этих прямых. Этот угол принимает два значения.
104.
ТЕОРЕМА 6.2 (свойства прямых) Пусть даны две прямыеx2 x1 y2 y1 z2 z1
x xi y yi z zi
n1
p1 . Тогда :
li :
, i 1, 2 и A : m1
mi
ni
pi
m
n2
p2
2
m n p
1) l1 l2 m1 n1 p1 rang 1 1 1 1;
ЛЕКЦИЯ 9.13
m2 n2 p2
m2 n2 p2
m1 n1 p1 x2 x1 y2 y1 z2 z1
2) l1 l2
rang A 1;
m
n
p
m
n
p
2
2
1
1
1
2
m n p
3) l1 , l2 пересекаются rangA rang 1 1 1 2 ;
m2 n2 p2
4) l1 , l2 скрещиваются det A 0 rang A 3 ;
5) cos l1 l2
m1m2 n1n2 p1 p2
p12 n12 p12
m22 n22 p22
;
6) Расстояние от точки
M 0 ( x0 , y0 , z0 ) до прямой l1 вычисляется по формуле ( M 0 , l1 )
[ M 0 M 1 , k1 ]
| k1 |
;
7) Расстояние между двумя прямыми l1 , l2 вычисляется по формуле
(l1 , l2 )
(k1 , k2 , M 1M 2 )
| [k1 , k2 ] |
. ЛЕКЦИЯ 9 05.10.15
105.
6) Расстояние от точки до прямой.M0
h
l1
k1
M1
ЛЕКЦИЯ 9
7) Расстояние между двумя прямыми.
k2
M2
h
l2
l1
O
M1
L
k1
106.
ЗАМЕЧАНИЕ 1) Ax By C 0 - общее уравнение прямой.x x1 y y1
, k : {m, n}, - каноническое уравнение прямой.
2)
m
n
x x1
y y1
3)
- уравнение прямой, проходящей через две
x2 x1 y2 y1
точки M1 ( x1, y1 ), M 2 ( x2 , y2 ) .
x mt x0
, t R - параметрическое уравнение прямой.
y nt y0
4)
5)
x y
1 - уравнение прямой "в отрезках на осях".
a b
6) cos x sin y p 0 - нормальное уравнение прямой, где
n {cos , sin } - единичный вектор нормали к прямой, а
p cos x sin y (n , OM ) прn OM есть проекция радиусоввекторов точек M прямой на направление вектора нормали.
107.
§ 7 Алгебраические кривые второго порядкав евклидовой плоскости V2 ЛЕКЦИЯ 9 11.10.14
Кривая второго порядка в V2 - множество точек, координаты
которых в какой-либо ПДСК удовлетворяют уравнению
a11 x 2 2a12 xy a22 y 2 b1x b2 y c 0
где a11 , a12 , a22 0 одновременно. ЛЕКЦИЯ 8 10.10.17
Пр. Окружность в ПДСК в V2 задается уравнением
( x x0 )2 ( y y0 )2 R 2 ,
и имеет параметрическое уравнение x R cos t x0 , t [0,2 ].
y R sin t y
0
Кпр. Уравнение x2 y 2 1 0 задает пустое множество точек в V2 .
ЗАМЕЧАНИЕ Невырожденных кривых второго порядка 3 типа.
Невырожденных кривых третьего порядка – десятки типов
(классификация Ньютона).
Литература: Савёлов А.А. Плоские кривые.
108.
Прямая l , проходящая через точку M 0 кривой,называется касательной к кривой в точке M 0 ,
l
M
M0
если расстояние от переменной точки M кривой
до прямой l стремится к нулю быстрее, чем расстояние от M до M 0 :
(M , l )
0.
M M 0 ( M , M )
0
lim
Эллипс – множество точек в V2 , сумма
расстояний 2a от каждой из которых
до двух заданных точек F1, F2 (фокусов)
есть величина постоянная.
ЛЕКЦИЯ 8 10.10.18
109.
ТЕОРЕМА 7.11) Пусть F1 ( c,0), F2 (c,0) , b := a 2 - c 2 , b < a .
x2 y 2
Тогда каноническое уравнение эллипса имеет вид 2 + 2 = 1.
a
b
c
b2
2) Эксцентриситет эллипса e := = 1- 2 О (0,1) . Если
a
a
a const и 1, то эллипс сжимается к отрезку [ a, a ] оси OX;
Если 0 , то эллипс выпрямляется в окружность x2 y 2 a 2 .
3) Уравнение касательной к эллипсу в точке M ( x0 , y0 ) имеет вид
x0
y0
x 2 y 1.
2
a
b
[ a,0], [0, a] OX - большие полуоси.
[ b,0], [0, b] OY - малые полуоси.
110.
cb2
Пр. (геометрический смысл эксцентриситета) e := = 1- 2
a
a
Если 0 , то уравнение эллипса
x2 y 2
2 1.
2
a
a
3
x2
y2
Если , то уравнение эллипса 2
1.
2
2
a (a 2)
Если 1, то «уравнение эллипса»
ЛЕКЦИЯ ВИС 10.12.18
x2 y 2
2 1.
2
a
0
111.
Прямая l называется асимптотой кнеограниченной кривой, если
расстояние от переменной точки
кривой до этой прямой стремится к
нулю, когда точка неограниченно
удаляется по кривой.
Гипербола – множество точек в V~2 , модуль разности расстояний от
каждой из которых до двух заданных точек (фокусов) есть величина
постоянная: d 2 d1 2a .
112.
ТЕОРЕМА 7.2 1) Пусть F1 ( c,0), F2 (c,0) , b := c 2 - a 2 , b < a . Тогдаx2 y 2
каноническое уравнение гиперболы имеет вид 2 - 2 = 1.
a
b
b
a
2) y x - уравнения асимптот ветвей гиперболы. ЛЕКЦИЯ 10.13
c
b2
3) Эксцентриситет гиперболы e := = 1 + 2 О (1, Ґ ) . Если a const
a
a
и 1, то ветви гиперболы сжимаются к отрезкам ( , a], [a, ) .
Если , то ветви гиперболы разгибаются в прямые x a .
4) Уравнение касательной к гиперболе в точке M ( x0 , y0 ) имеет вид
x0
y0
x
y 1.ЛЕКЦИЯ 10 12.10.15
2
2
a
b
[ a,0], [a,0] OX -
вещественные полуоси.
[0, b], [0, b] OY -
мнимые полуоси.
113.
x2y2
a 2 a 2 1 1, a 1,
c 1 2
2
x
y
1 b 0,1
b 2 1 b 2
ЛЕКЦИЯ 8 21.10.19
114.
Парабола - множество точек в V2 , расстоянияот которых до заданной точки F (фокуса) и до
заданной прямой l (директрисы) совпадают.
p
p
ТЕОРЕМА 7.3 1) Пусть F ,0 , l : x .
2
2
Y
l
M ( x, y )
X
p 2
0
F p 2 ,0
Тогда каноническое уравнение параболы
имеет вид y 2 2 px .
ЛЕКЦИЯ 10 14.10.14
2) Точка параболы 0,0 является ближайшей к директрисе и
называется вершиной параболы.
3) y0 y p( x x0 ) - уравнение касательной к параболе y 2 2 px в
точке ( x0 , y0 ) . ЛЕКЦИЯ 11 17.10.16
(M , l )
M M 0 ( M , M )
0
3) lim
1
lim
| y0 y p ( x x0 ) |
y02 p 2 M M 0 ( x x0 ) 2 ( y y0 ) 2
115.
116.
ТЕОРЕМА 7.4 (классификация геометрических объектов,задаваемых общим уравнением кривой второго порядка)
2
2
Уравнение кривой второго порядка a11 x 2a12 xy a22 y b1x b2 y c 0
с помощью последовательно: а) преобразования поворота ПДСК
вокруг начала координат, б) сдвига ПДСК на некоторый вектор и,
возможно, в) отражения относительно какой-то из осей координат,
может быть приведено к одному из простейших видов:
1) каноническому уравнению эллипса, гиперболы, параболы;
2) уравнению пары прямых
Y
M
x 2 y 2 0, x 2 a 2 ;
y
Y1
3) уравнению, которому
удовлетворяют координаты
j
2
2
j
1
одной точки x y 0 ;
X1
i1
4) уравнению, которому не
удовлетворяют координаты ни
x
i
O
X
одной точки x 2 y 2 1.
117.
ЗАМЕЧАНИЕ Исключение слагаемого 2a12 xy из уравненияa11 x 2 2a12 xy a22 y 2 b1 x b2 y c 0
поворотом ПДСК на угол j .
2a12
1
j = arctg
Ю
2
a11 - a22
м
x = cos j x1 - sin j y1
п
п
н
п
п
о y = sin j x1 + cos j y1
м
i1 = {cos j , sin j }
п
п
. OM = x i + y j = x1 i1 + y1 j1 Ю
н
п
j
=
{
sin
j
,
cos
j
}
п
о 1
выражение старых координат ( x, y) точки M
через ее новые координаты ( x1 , y1 ) в OX1Y1 . ЛЕКЦИЯ 10
Y
жx1 ч
ц
жx ц
жcos j - sin j ц
ч
з
зз ч
з
Ы X = AX 1 .
ч
ч
зз ч
зз
ч
ч= и
ч
зиyш
sin j
cos j шиy1 ш
жcos j - sin j ц
T
- 1
ч
A = зз
.
A
=
A
Ю
ч
ч
зиsin j
cos j ш
A - ортогональная матрица.
Y1
M
y
j
j1
i1
O
i
x
X1
X
118.
Пр. Привести уравнение кривой x 2 - 2 xy + y 2 - 2 x - 2 y + 3 = 0к каноническому виду и изобразить ее.
1
- 2 p
j = arctg
=
2
1- 1 4
м
п
2
2
п
x
=
x
y1
п
1
п
2
2
Ю п
Ю
н
п
2
2
п
п
y=
x1 +
y1
п
2
2
п
о
Ю 2 y - 2 2 x1 + 3 = 0 Ю y =
2
1
2
1
м
п
3 2
п
x
=
x
+
2
Ю п
н1
4
п
п
п
о y1 = y2
Y
Y1
X1
4
Ю
X
0
ж
3 2ц
ч
з
ч
2 зз x1 Ю
ч
ч
зи
4 ш
Y
X 1, X 2
Y2
Ю
Y1
Ю y22 =
3 2 4
0
- уравнение параболы.
X
2 x2 -
119.
Кривые третьего порядка.Кривые четвертого порядка.
ЛЕКЦИЯ 9 12.10.18
120.
§ 8 Поверхности второго порядка в евклидовомпространстве V3 . Движение. Квадратичная форма.
Поверхность второго порядка - множество точек в V3 ,
координаты которых удовлетворяют уравнению вида
a11 x 2 a22 y 2 a33 z 2 2a12 xy 2a13 xz 2a23 yz b1x b2 y b3 z c 0 ,
b1
x
или в матричной записи X AX BX c 0, где X : y , B : b2 , а
z
b
3
A (aij ) 0 - симметричная матрица.
Пример 1 Эллипсоид – множество
точек в V3 , координаты которых
x2 y 2 z 2
удовлетворяют уравнению 2 2 2 1 .
a
b
c
Отрезки [ a,0], [0, a] OX , [ b,0], [0, b] OY ,
[ c,0], [0, c] OZ - полуоси эллипсоида.
ЛЕКЦИЯ 11.13
121.
Пример 2 Коническая поверхность (конус) множество точек,x2 y 2 z 2
координаты которых удовлетворяют уравнению 2 + 2 - 2 = 0 .
a
b
c
Пример 3 Однополостный гиперболоид – множество точек,
x2 y 2 z 2
координаты которых удовлетворяют уравнению 2 + 2 - 2 = 1.
a
b
c
Пример 4 Двуполостный гиперболоид – множество точек в V%3 ,
координаты которых удовлетворяют уравнению
z
x2 y 2 z 2
+ 2 - 2 = - 1.
2
a
b
c
z
0
x
0
x
y
y
122.
В 2017 году исполнится 95 лет со дня постройки башни Шухова.Инженер Владимир Шухов в 1886 году для Всероссийской промышленной и
художественной выставки в Н.Новгороде построил 25-метровую сетчатую башню
Так как возведённая в 1914 году Ходынская радиостанция уже не справлялась
с постоянно растущим объёмом радиограмм, в 1919 году было принято постано
вление о строительстве новой башни. По первоначальному проекту Шухов
ская радиобашня на Шаболовке достигала 350 метров и весила лишь 2200 тонн.
Например, башня Эйфеля при высоте 305 метров весит
7300 тонн. Но первоначальные замыслы Шухова в условиях
гражданской войны и блокады реализовать не удалось, поэ
тому инженер откорректировал свой проект: вместо 9 секций
оставил только 6, а высоту снизил до 150 метров. На возве
дение такой башни потребовалось всего 240 тонн металла.
Секции башни представляют
собой однополостные гипербо
лоиды вращения, сделанные из
прямых
балок,
упирающихся
концами в кольцевые основания.
На международной научной
конференции «Heritage at Risk.
Сохранение архитектуры XX века
и Всемирное наследие» 2006 года
шуховская
башня
объявлена
объектом всемирного наследия. ЛЕКЦИЯ 11 16.10.2015
123.
Пример 5 Эллиптический параболоид - множество точек,x2 y 2
координаты которых удовлетворяют уравнению 2 + 2 = z
a
b
Пример 6 Гиперболический параболоид (седло) –множество точек, координаты которых удовлетворяют уравнению
x2 y2
- 2 = z . От гр. Παραβολή - парабола + ε’ι̃δος 2
a
b
вид, сходство.
ЛЕКЦИЯ 9 23.10.19
z
0
x
y
124.
Пример 7 Эллиптический цилиндр - множество точек, координаты которых удовлетворяют уравнению
x2
y2
+
= 1.
a 2 b2
z
y
x
Шарообразную форму здания,
расположенного в густонаселенном районе
Токио, образуют 24 овальных кольца,
закрепленных вокруг полого
эллиптического цилиндра.
ЛЕКЦИЯ 11 19.10.14
125.
Пример 8 Гиперболический цилиндр - множество точек в V%3 ,x2 y 2
координаты которых удовлетворяют уравнению 2 - 2 = 1.
a
b
Пример 9 Параболический цилиндр - множество точек в V%3 ,
координаты которых удовлетворяют уравнению y 2 = 2 px .
z
z
y
y
x
x
Пример 10 Уравнение пары прямых ЛЕКЦИЯ 10 13.10.17
( A1x B1 y C1z D1 ) ( A2 x B2 y C2 z D2 ) 0 .
Пример 11 Прямая или точка, например, , , 0 ,
( x x0 )2 ( y y0 )2 0, ( x x0 )2 ( y y0 )2 ( z z0 ) 2 0 .
Пример 12 Пустое множество, например,
x2 y 2 z 2 1, где , , 0 .
126.
§ 9 Элементы теории групп.Группа – множество элементов G , на котором определена бинарная
операция со свойствами:
1) x, y, z G ( x y) z x ( y z ) - свойство ассоциативности;
2) e E x E e x x e x - есть нейтральный элемент;
3) x E y E x y y x e - каждый элемент имеет симметричный.
Группа G называется коммутативной (абелевой) если выполнено
свойство
4) x, y G x y y x .
Пр. Векторное пространство E является коммутативной группой
относительно операции сложения.
ЗАМЕЧАНИЕ В абелевой группе операция обозначается + ,
нейтральный элемент называется нулем и обозначается 0, а
симметричный элемент – противоположным и обозначается –x .
Пр. Перестановка (подстановкой) n-ой степени называется
множества {1, 2, …, n} на себя и результат биекции. Множество
перестановок (биекций) образует группу. Которая 1 2 3 4 5
называется симметрической группой степени n и 3 2 4 5 1
обозначается S .
127.
Пр. Перестановка (подстановкой) n-ой степени называется множества{1, 2, …, n} на себя и результат биекции. Множество перестановок
(биекций) образует группу. Которая называется симметрической
группой степени n и обозначается .
128.
Нильс Хе́нрик А́бель (1802 - 1829) норвежский математик1823: Абель закончил блестящее исследование древней
проблемы: доказал невозможность решить в общем виде (в
радикалах) уравнение 5-й степени.
1823: публикует расширенный вариант своей первой
работы об уравнениях: уравнения любой степени выше 4й, вообще говоря, неразрешимы в радикалах. Причём он
привёл конкретные примеры неразрешимых уравнений.
Нашёл необходимое условие для того, чтобы корень
уравнения выражался «в радикалах» через коэффициенты этого уравнения.
Достаточное условие вскоре открыл Галуа, чьи достижения опирались на труды
Абеля.
1828: Абель избран членом Королевского научного общества Норвегии.
Продолжает активно развивать теорию эллиптических функций. Ждёт
обещанного приглашения на работу в Берлин.
1829: умирает от туберкулёза.
129.
130.
Эвари́ст Галуа́ (1811-1832) - французский математик,основатель современной высшей алгебры. Радикальный революционер-республиканец, был застрелен на
дуэли в возрасте двадцати лет.
Галуа исследовал проблему нахождения общего
решения уравнения произвольной степени, то есть
задачу, как выразить его корни через коэффициенты,
используя только арифметические действия
и радикалы.
Нильс Абель несколькими годами ранее доказал, что
для уравнений степени 5 и выше решение «в радикалах» невозможно, однако
Галуа продвинулся намного дальше: он нашёл необходимое и достаточное ус
ловие для того, чтобы корни уравнения допускали выражение через радикалы.
Но наиболее ценным был даже не этот результат, а те методы, с помощью кото
рых Галуа удалось его получить. Решая эти задачи, он заложил основы современной алгебры, вышел на такие фундаментальные понятия, как группа (Галуа
первым использовал этот термин, активно изучая симметрические группы)
и поле (конечные поля носят название полей Галуа).
131.
Группа, в которой операция называется умножением, называетсямультипликативной. При этом операция обозначается « » , нейтральный
элемент называется единицей и обозначается 1, а симметричный элемент –
обратным и обозначается x-1.
Пр.
Группа с конечным числом элементов называется конечной, а число
элементов – порядком группы.
Пр.
Пр.
Подмножество H группы G называется подгруппой, если оно замкнуто
относительно операций умножения и взятия обратного элемента:
1) h1, h2 H h1h2 H , 2) h H h 1 H .
Пр.
132.
Для любого g G множество g : g k : k называется циклическойподгруппой. Элемент g называется образующим элементом
подгруппы.
Обозначение циклической подгруппы g .
Пр.
Элемент g имеет бесконечный порядок, если k l , k , l , g k g l и
имеет конечный порядок p , если g p 1 и 1 m p g m 1.
Пр.1
Пр.2
ЗАМЕЧАНИЕ 1) У бесконечной циклической подгруппы только 2
циклических элемента g и g 1.
2) Элемент g m циклической группы порядка p будет образующим
тогда и только тогда, когда числа m и p взаимно простые.
133.
Группы G1 , G2 с операциями соответственно , называютсяизоморфными, если существует биективное отображение f : G1 G2
со свойством:
a, b G1 f (a b) f (a) f (b)
f называется изоморфизмом групп G1 , G2 .
Пр.
Если G1 G2 : G , то f называется автоморфизмом группы G .
Пр.
134.
Пусть подгруппа H мультипликативной группы G , и элемент a G .Множество aH : ah : h H называется левым смежным классом
группы G по подгрупп H , содержащем a . Множество Ha : ha : h H
называется правым смежным классом группы G по подгруппе H .
ЗАМЕЧАНИЕ (свойства смежных классов)
1) b aH bH aH a 1b H ;
2) bH aH или bH aH ;
3) a aH .
4) Аналогичные свойства имеют место для правых смежных классов
Ha .
СЛЕДСТВИЕ Группа представима в виде объединения (всех) попарно
непересекающихся смежных классов по подгруппе H . Такое
представление называется левым (правым) разложением (разбиением)
группа G по подгруппе H .
Пр.
135.
Индекс подгруппы H в группе G - это число G : H смежных классов вкаждом (правом или левом) из разложений группы по этой подгруппе
H (в бесконечном случае это мощность множества этих классов).
ЗАМЕЧАНИЕ 1) (теорема Пуанкаре) Пересечение конечного числа
подгрупп конечного индекса само имеет конечный индекс.
2) (теорема Лагранжа) Произведение порядка подгруппы H на ее
индекс G : H равно порядку группы G . Это соотношение имеет место как
для конечной группы G , так и в случае бесконечной G - для
соответствующих мощностей.
СЛЕДСТВИЯ
1) порядок любого элемента группы G делит порядок группы.
2) Всякая группа простого порядка является циклической.
3) Если G - нециклическая группа порядка n , то существует такой
собственный делитель l числа, что a G a l 1.
Пр.
136.
Подгруппа G называется нормальным делителем группы H , еслиa G aH Ha .
ЗАМЕЧАНИЕ Подгруппа будет нормальным делителем группы H
тогда и только тогда, когда a, h G aha 1 H .
Пр.
Пусть подгруппа G является нормальным делителем группы H . На
множестве смежных классов группы H по подгруппе G можно задать
операцию умножения по правилу aH bH : (ab) H . Множество смежных
классов является группой относительно этой операции с нейтральным
элементом H . Оно называется факторгруппой группы H по подгруппе G ,
и обозначается G / H .
Пр.
137.
Группы G1 , G2 с операциями соответственно , называютсягомоморфными, если существует отображение f : G1 G2 со
свойством:
a, b G1 f (a b) f (a) f (b) .
f называется гомоморфизмом групп G1 , G2 .
Пр.
Ядром гомоморфизма f называется множество
ker f : a G1 : f (a ) e ,
где e - нейтральный элемент группы.
ЗАМЕЧАНИЕ 1) Ядро гомоморфизма ker f является нормальным
делителем группы G1 .
2) (теорема о гомоморфизмах групп) Если f : G1 G2 - гомоморфизм
групп, то F (G1 ) G1 / ker f .
Пр.
138.
§ 10 Элементы теории поля.Тройка R, , , где R - множество с определенными на нем двумя
бинарными операциями – сложением « » и умножением « »,
называется кольцом, если
1) R является абелевой группой по сложению,
2) R содержит единицу по умножению и для него справедливы законы
ассоциативности и дистрибутивности:
a, b, c R ab c a bc , a b c ac bc, a b c ab ac .
Кольцо называется коммутативным, если оно коммутативно
относительно умножения: a, b R ab ba .
Пр. Множество квадратных матриц M 2,2 является некоммутативным
1 2
1 0
, B
кольцом. A
.
3 4
0 2
139.
Не равные нулю элементы кольца a, b R называются делителяминуля, если ab 0 .
Пр. М
Кольцо относительно операции сложения является группой,
которая называется аддитивной группой кольца.
Элемент кольца a R называется обратимым, если он имеет
обратный в этом кольце: a 1 R aa 1 a 1a 1.
ЗАМЕЧАНИЕ Множество всех обратимых элементов является
мультипликативной подгруппой. Она называется
мультипликативной группой кольца и обозначается R .
Пр. Мультипликативной группой кольца матриц M 2,2 является
множество всех невырожденных матриц из M 2,2 .
140.
Непустое подмножество S R называется подкольцом, если оноявляется аддитивной подгруппой и замкнуто относительно операци
умножения.
Пр.
Пусть заданы 2 кольца R1 , R2 . Биективное отображение f : R1 R2
называется изоморфизмом кольца R1 на кольцо R2 , если
a, b R1 f (a b) f (a) f (b), f (ab) f (a) f (b) .
Если изоморфизм существует. То кольца называются изоморфным
ЗАМЕЧАНИЕ Если изоморфизм существует, то
f (0) 0, x f ( x) f ( x), f (1) 1, x K f ( x 1 ) f ( x) 1 .
Пр.
141.
Коммутативное кольцо F с более чем одним элементом. называетсяполем, если каждый ненулевой элемент в нём обратим.
Пр.
Если единица поля 1 является элементом бесконечного порядка в
аддитивной группе поля, то поле имеет характеристику ноль:
charF 0 .
Пр.
Характеристикой поля F называется порядок p единицы поля в его
аддитивной группе: charF p .
Пр.
Подкольцо поля называется подполем поля, если оно содержит 0 и 1,
и 0 a S a 1 S .
Пр.
142.
Подкольцо I кольца R называется левым (правым) идеалом кольца,если r R a I ra I ar I . Подкольцо I называется
двусторонним идеалом кольца R , если оно является и левым и
правым идеалом кольца.
Пр.
Пусть M R . Наименьший идеал (левый, правый, двусторонний)
кольца, содержащий M , называется идеалом, порожденным
множеством M . Он обозначается ( M ) .
ЗАМЕЧАНИЕ ( M ) совпадает с пересечением всех (левых, правых,
двусторонних) идеалов кольца, содержащих M .
Идеал (левый, правый, двусторонний), порожденный одним
элементом a , называется главным идеалом. Обозначается
соответственно (a)l ,(a)r ,(a) .
Пр.
143.
Коммутативное кольцо без делителей нуля называется кольцомглавных идеалов.
Пусть I двусторонний идеал кольца. Элемент a R сравним с
элементом b R кольца по модулю идеала I (по идеалу), если
a b I . a b mod( I )
ЗАМЕЧАНИЕ Сравнения по модулю идеала можно почленно
складывать и умножать.
Смежный класс a I аддитивной группы кольца R по подгруппе
называется классом вычетов кольца R по модулю идеала I (по
идеалу).
ЗАМЕЧАНИЕ На множестве всех классов вычетов кольца R по
модулю идеала I определена операции сложения и умножения по
правилу (a I ) (b I ) : (a b) I , (a I ) (b I ) : ab I . Это
множество является кольцом, называется факторкольцом кольца R по
идеалу I , и обозначается R / I .
Пр.
144.
Идеал I кольца называется максимальным, если I R и несуществует промежуточного идеала между I и R .
Пусть R1 , R2 кольца. Отображение f : R1 R2 со свойством:
a, b R1 f (a b) f (a) f (b), f (ab) f (a) f (b)
называется гомоморфизмом колец R1 , R2 .
ЗАМЕЧАНИЕ Если R - коммутативное кольцо, то идеал I будет
максимальным тогда и только тогда, когда факторкольцо R / I
является полем.
Пр.
Ядром гомоморфизма f кольца R1 в кольцо R2 называется
множество ker f : a r1 : f (a) 0 ,
ТЕОРЕМА 1) Ядро ker f является двусторонним идеалом кольца
R . 2) (теорема о гомоморфизмах колец) Если f : R1 R2 гомоморфизм колец, то f ( K1 ) K1 / ker f .
Пр.
145.
Виктор Фёдорович Шаталов (род. 1.05.1927) - педагог- новатор. Народныйучитель СССР (1990). Почётный доктор АПН Украины. Создатель нового
направления в педагогике «педагогика сотрудничества». Разработал систему обучения с использованием опорных сигналов - взаимосвязанных 1) ключевых слов, 2) условных знаков, 3) рисунков и 4) формул с кратким выводом.
Оригинальная система интенсивного обучения Шаталова, разработанная
для средних и старших классов общеобразовательной школы включает около
200 педагогических открытий, самые важные из которых:
1) Авторские учебные пособия, представляющие программный материал
главным образом в вербально-графических формах, упрощающих процесс
изложения, восприятия и запоминания.
2) Принцип открытых перспектив, ориентированный на развитие творческого мышления.
3) Принцип систематической обратной связи, на базе разнообразных нестандартных форм
объективного учёта и контроля знаний каждого учащегося на каждом уроке, позволяющий
отказаться от ученических дневников и классных журналов.
4) Вместо традиционных домашних заданий учащиеся получают обширные «предложения», объём
и сложность которых варьируются на этапах обучения с учётом индивидуальных особенностей, а к
окончанию курса приближаются к конкурсным и олимпиадным.
5) Практикуются оригинальные формы взаимопроверки учащихся, в том числе в интересах
увеличения времени для решения задач высокой сложности и развития продуктивного мышления.
6) Традиционные экзамены заменены работами по «листам группового контроля» и так называемыми релейными, выявляющими результат самостоятельной деятельности над всеми видами заданий.
7) Устранению дидактических противоречий способствует принцип бесконфликтности учебной ситу
ации, то есть создание соответствующих условий для занятий при участии родителей школьников
8) Широко используются игровые формы учебных занятий.
Многие находки Шаталова
используются не только школьн. учителями, но педагогами вузов, при обучении некоторым сложным профессиям
146.
Учитель-экспериментатор Виктор Шаталов о реформах образованияВладимир Губайловский, Александр Костинский
Опубликовано 12.05.2004 16:00
Александр Костинский: Виктор Федорович, вы считаете, что нужно учить всех детей, и всех
можно выучить? Это главный тезис вашей системы преподавания?
Виктор Шаталов: То что учить нужно, это не я так считаю, так считает вся страна и каждая
семья и каждый ребенок. А относительно того, что можно научить - да, я так считаю.
Александр Костинский: То есть каждого можно сделать отличником?
Виктор Шаталов: Скажу одно, что мою школу все дети заканчивали на пять, и все как один
поступали в институты. Я совершенно уверен - детей можно учить не более 9 лет. Это
доказано. У меня сдавали курс 9 класса семилетние дети.
Я обратился к Путину с письмом, а мне ответил какой-то, извините, деятель о том, что
они приняли к сведению. Кто принял к сведению? Я ведь не к тебе обращался, я обратился к
Владимиру Владимировичу. Речь идет о колоссальной работе, которую нужно зачинать где-то
в самых высоких сферах. Те, кто чуть ниже, они будут идти только по следу, а сами по себе
ничего не решат. Поэтому я очень надеюсь на встречу с министром просвещения Российской
Федерации. Новый министр, кажется, математик, я надеюсь, мы найдем общий язык.
147.
5Опорные конспекты - это было не главное. Гораздо важнее были система оценивания, система контроля, система объяснения. Наши опорные конспекты в табеле о рангах того, что я сегодня несу, находятся на шестом месте, на самом последнем. Они существенны, значимы, но они
не определяют результатов работы. Значительно выше стоит 4система инспекций, контроля,
опроса, то есть то, что сейчас низвергнуто. Еще на порядок выше стоит 3спортивная работа.
Во-первых, мы в моей школе учимся пять дней в неделю, а в четверг у нас второй выходной
день. Во-вторых, у нас физкультура каждый день. Пусть узнает об этом министр просвещения,
пусть узнает государственная система власти. На ступеньку выше опорных конспектов стоит и
2решение задач. Конспекты - это чистая теория, это уверенное владение теоретическим материалом, а закреплять этот материал нужно задачами. И только задачами и упражнениями можно подтвердить теорию. Вы понимаете, что это выше, чем конспекты. И, наконец, еще важнее:
можно научить теории, можно научить решать задачи, но трагедия современной школы в том,
что в ней нет разумно продуманной 1системы повторения. Я хочу спросить тех, кто сейчас
слушает нас, что вы помните о химии, которой вас учили школе? Кто сумел выучить в школе
иностранный язык? А ведь обучению отдано по 7-8 лет. Спросите любого прохожего, он ни
английского, ни немецкого, ни французского не знает. Почему? Потому что 1повторение было
заброшено. Давайте просто рассуждать: ребенок в полтора года - молчун, "папа, мама, баба" он знает несколько слов. А в два с половиной года - это болтун, с ним можно свободно побесе
довать. Стало быть, ребенок за один год изучил иностранный язык. Потому что этот язык для
него иностранный. Если бы он родился в Китае, он бы говорил по-китайски, родился в Арген
тине - говорил бы по-испански и так далее. Значит за один год ребенок изучает иностранный
язык. А мы десятками лет трудимся. Почему? Потому что нет системы повторения. Нужно погружение в языковую среду, и только тогда решается проблема. Не интернатами, не специаль
ными курсами. Итак, выше стоит 1абсолютно новая система повторения. Повторение при ко
тором - я здесь отвечаю за каждое слово - ребенок ни по одному предмету ничего не забывает.
148.
Макаренко – формирование из беспризорника с помощью элементов воинскойдисциплины выпускника, обладающего необходимым объемом знаний, умений и
навыков для дальнейшего обучения, работы и жизни в гражданском обществе.
Шаталов – формирование из запущенного школьника из семьи (с помощью самой
семьи и 7 приемов обучения) выпускника, подготовленного для дальнейшей
успешной учебы в Вузе.
Приоритеты приемов в системе «педагогика сотрудничества» Шаталова
Абсолютно новая система повторения
Решение задач
Спортивная работа
Система контроля знаний, опросы
Опорный конспект

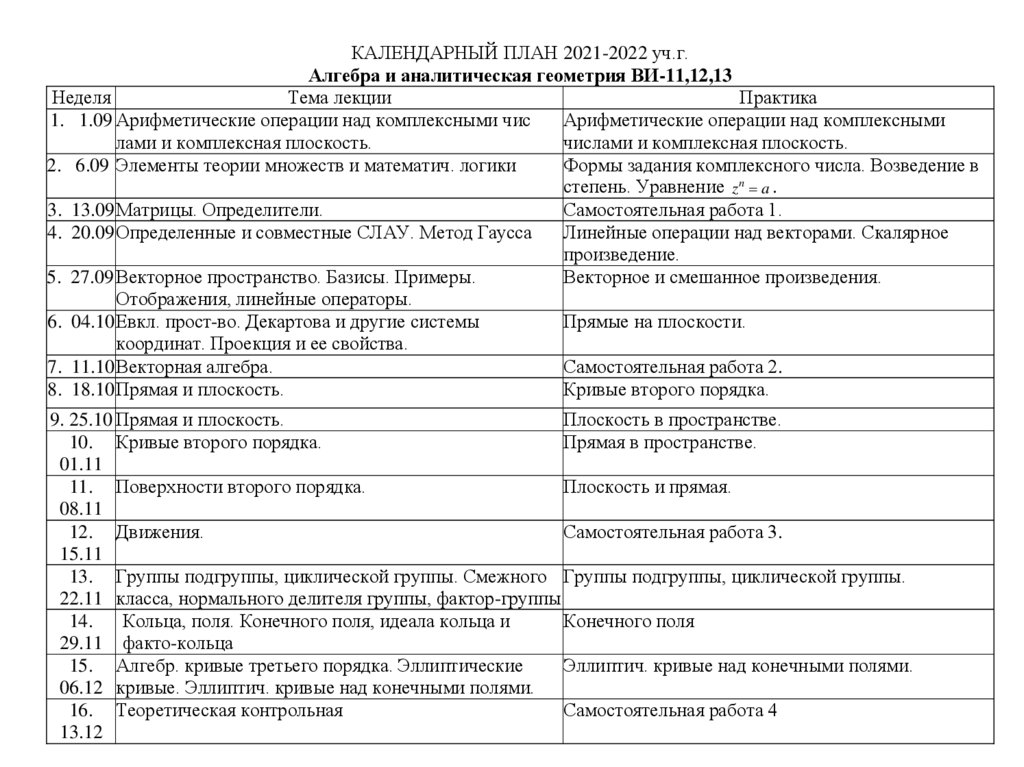












































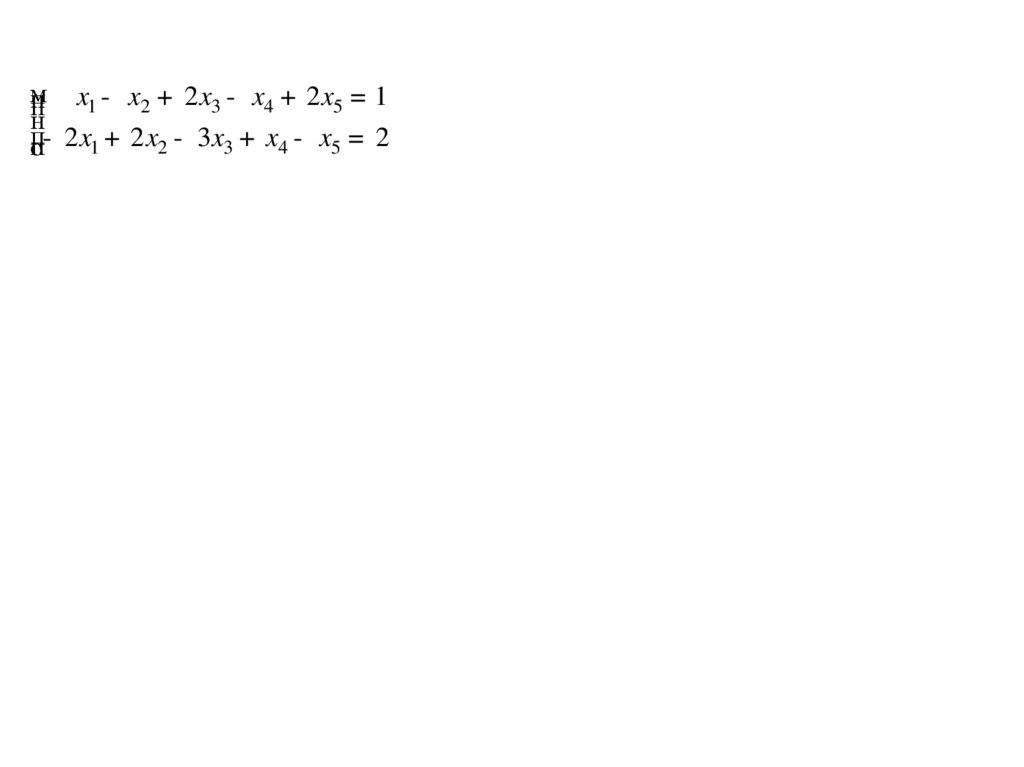



























































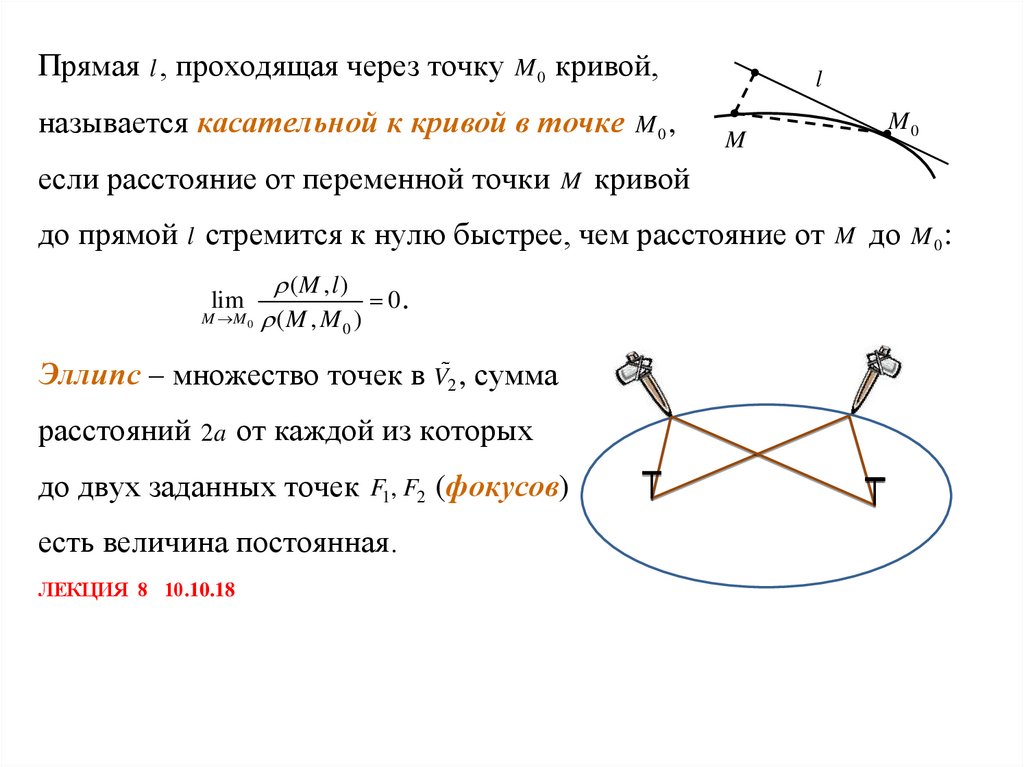


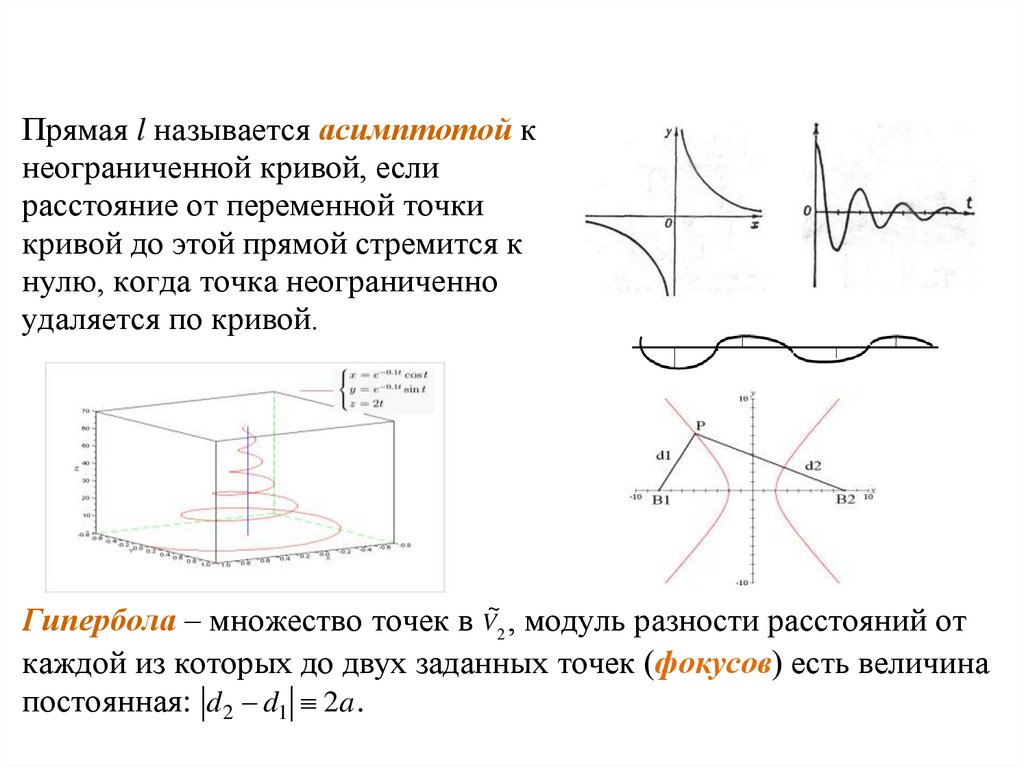



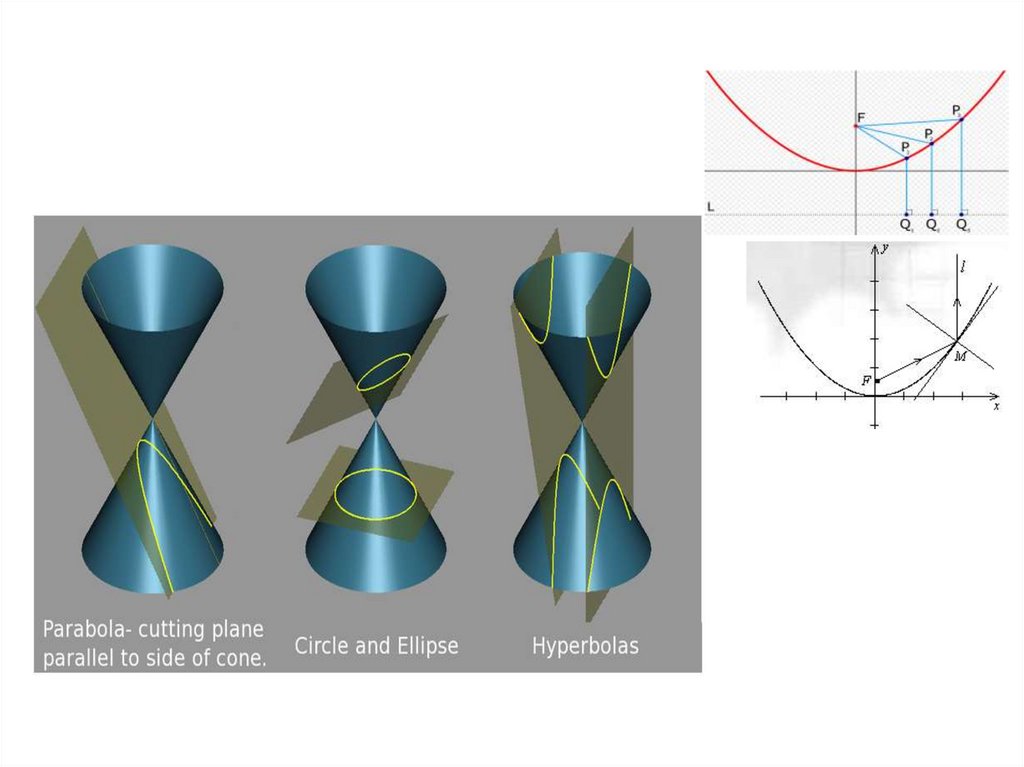






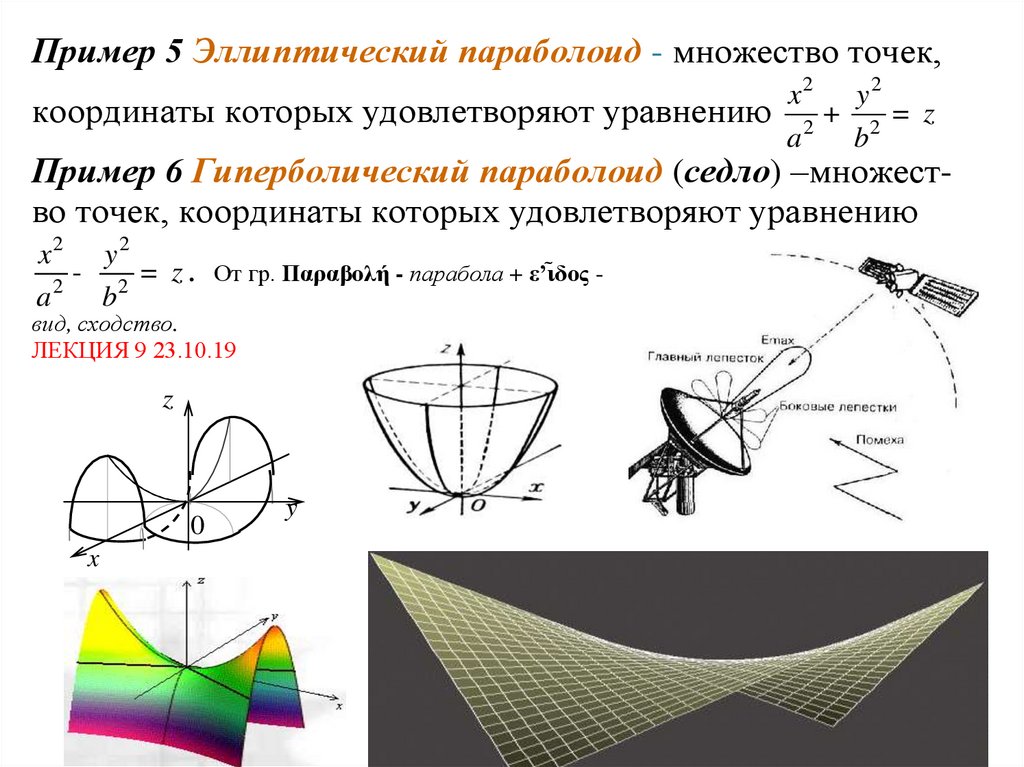

























 mathematics
mathematics








