Линейная алгебра и аналитическая геометрия

1.

Линейная алгебра и аналитическая геометрия
• Определители
• Миноры
• Обратная матрица
• Ранг матрицы
• Теорема о базисном миноре
• Системы линейных уравнений
• Матричный метод
• Метод Крамера
• Метод Гаусса
• Системы линейных однородных уравнений

2.

Определение. Матрицей размера m n называется
таблица, образованная из элементов некоторого
множества и имеющая m строк и n столбцов.
Если m n , то матрицу называют прямоугольной,
а если m n – квадратной порядка n.
Элементы, из которых составлена матрица, называют
элементами матрицы.
Пример:
a24 – элемент второй строки и четвертого столбца
a13 – элемент первой строки и третьего столбца

3.

a11
a
A 21
am1
a12
a22
am 2
a1n
a2 n
amn
A ( aij ) ( i 1, m , j 1, n ) прямоугольная, m n
A ( aij ) ( i, j 1, n ) квадратная порядка n
Две матрицы A и B считаются равными, если они
одинакового размера, и элементы, стоящие в A и B
на одинаковых местах, равны между собой, т.е.
aij=bij .

4.

1.
a11
a
A 21 ( ai1 )
am1
размера m 1
матрица – столбец длины m
2. A a11 a12 a1n ( a1i ) размера 1 n
матрица – строка длины n
3.
0
0
O
0
0
0
0
0
0
0
нулевая матрица

5.

4. Условную линию в квадратной матрице порядка n,
на которой расположены элементы a11, a22, … , ann,
называют главной диагональю этой матрицы.
Условную линию в квадратной матрице порядка n,
на которой расположены элементы a1n, a2n-1, … ,
an1, называют побочной диагональю.
a11
0
A
0
1
0
E=
0
0
a22
0
0
1
0
0
0
диагональная матрица
ann
0
0
единичная матрица
1

6.

5.
a11 a12
0 a
22
A 0 0
0 0
a13
a23
a33
0
a1n
b11 0 0
b b
0
a2 n
21
22
a3 n B b31 b32 b33
b b b
ann
n1 n2 n3
0
0
0
bnn
треугольные матрицы
6.
a11 a12
0 a
22
A 0 0
0 0
a13
a23
a33
0
a1m
a2 m
a3 m
amm
a1n
a2 n
a3 n
amn
трапециевидная матрица

7.

7.
Прямоугольную матрицу размера m n будем
называть ступенчатой, если первый ненулевой
элемент каждой строки находится правее первого
ненулевого элемента предыдущей строки.
1
0
0
0
2 3 4 5 6
1 2 3 4 5
0 0 1 2 3
0 0 0 0 0
– ступенчатая
1
0
0
0
2 0 0
1 2 0
1 2 0
0 1 2
– не ступенчатая

8.

Определение. Произведением матрицы A=(aij) на
число называется такая матрица B=(bij), элементы
которой равны произведениям соответствующих
элементов матрицы A на число , т.е. bij aij
A
(-1)A – противоположная матрице A
-A
Определение. Суммой двух матриц A=(aij) и B=(bij)
одинакового размера называется такая матрица
C=(cij), элементы которой равны суммам соответствующих элементов матриц A и B, т.е. cij aij bij
A B

9.

1.
A B B A
2. ( A B) C A ( B C )
3. A O A
4. A ( A ) O
5. ( A ) ( )A
6. ( )A A A
7. ( A B ) A B
8. 1A A

10.

Определение. Пусть A и B – матрица-строка и
матрица-столбец одинаковой длины. Произведением
матрицы-строки A на матрицу-столбец B
называется число с, (т.е. матрица
),1
равное
сумме
1
произведений их соответствующих элементов:
c a11 b11 a12 b21 a13 b31 a1n bn1
Определение. Пусть A – матрица размера m n , B –
матрица размера n k (т.е. количество столбцов в
матрице A совпадает с количеством строк в матрице
B). Произведением матрицы A на матрицу B
называется матрица С размера m k такая, что
каждый её элемент cij является произведением i-той
строки матрицы A на j-тый столбец матрицы B:
cij ai1 b1 j ai 2 b2 j ai 3 b3 j ain bnj

11.

AB BA
Матрицы A и B, для которых AB=BA, называют
перестановочными.
1.
AE= EA=A
AO=OA= O
2. ( AB )C A( BC)
3. ( A B)C AC BC
4. C( A B ) CA CB

12.

Определение. Пусть A – матрица размера m n .
Матрица размера n m , полученная из A заменой
каждой ее строки столбцом с тем же номером,
называется транспонированной к A.
T
A
Операция нахождения матрицы AT называется
транспонированием матрицы A.
1. (AT)T= A
2. (A+B)T= AT+BT
3. ( A ) A
T
T
T
T
T
4. ( A B ) B A

13.

Факториал натурального числа n:
n! 1 2 3 n
0!= 1
Расположение n чисел 1, 2, 3, …, n в любом порядке
называется перестановкой этих чисел.
Пусть дана некоторая перестановка чисел 1, 2, 3, …, n:
1, 2 , , i , , k , , n
Говорят, что два числа i и k образуют инверсию в
перестановке, если большее число стоит левее
меньшего, т.е. если i k .
Количество пар, образующих инверсию в перестановке, называется числом инверсий в перестановке.

14.

Определение. Пусть A – квадратная матрица порядка
n. Определителем матрицы A (определителем
порядка n) называется сумма n! членов, составленных следующим образом: членами определителя
служат всевозможные произведения n элементов
матрицы, взятых по одному из каждой строки и
каждого столбца матрицы, причём произведение
берется со знаком «плюс», если число инверсий в
перестановке первых индексов сомножителей и
число инверсий в перестановке вторых индексов
сомножителей в сумме дают четное число, в
противном случае – со знаком «минус».

15.

A
det A
a11
a21
an1
a12
a22
an 2
a1n
a2 n
ann

16.

Определение. Пусть A – квадратная матрица порядка
n. Определителем матрицы A (определителем
порядка n) называется сумма n! членов,
составленных следующим образом: членами определителя служат всевозможные произведения n
элементов матрицы, взятых по одному из каждой
строки и каждого столбца матрицы, причём
произведение берется со знаком «плюс», если число
инверсий в перестановке первых индексов
сомножителей и число инверсий в перестановке
вторых индексов сомножителей в сумме дают четное
число, в противном случае – со знаком «минус».

17.

a11 a12
a11a22 a12 a21
a21 a22
a11 a12 a13
a11a22 a33 a12 a23 a31 a13 a21a32
a21 a22 a23
a13 a22 a31 a12 a21a33 a11a23 a32
a31 a32 a33
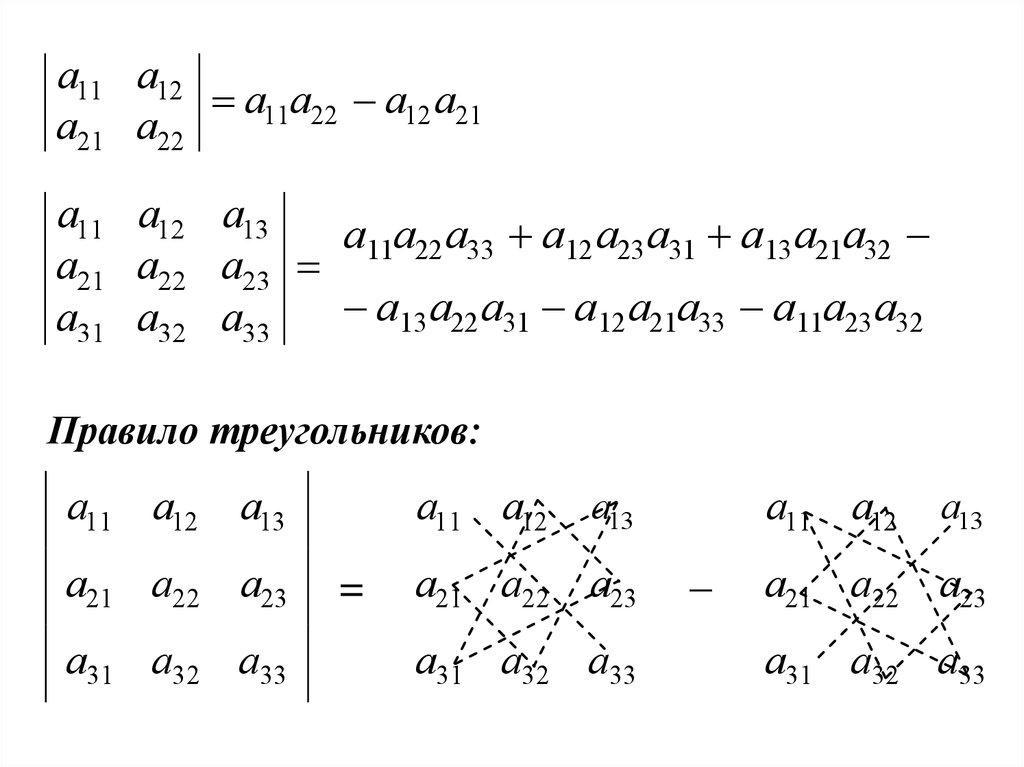
Правило треугольников:
a11 a12 a13
a21 a22 a23
a31 a32 a33
a11 a12
=
a11 a12
a13
a21 a22 a23
a31 a32 a33
–
a13
a21 a22 a23
a31 a32 a33

18.

1. При транспонировании матрицы ее определитель не
меняется.
2. При перестановке любых двух строк (столбцов)
определитель меняет знак.
3. Общий множитель элементов любой строки
(столбца) можно выносить за знак определителя.
4. Если все элементы k-той строки определителя |A|
являются суммами двух элементов, то определитель равен сумме двух определителей |A1| и |A2|, у
которых все строки кроме k-той совпадают со строками |A|, а k-тая строка в определителе |A1| состоит
из первых слагаемых, а в определителе |A2| – из
вторых слагаемых.

19.

5. Определитель равен нулю если:
а) он имеет строку (столбец), состоящую из нулей;
б) он имеет хотя бы две одинаковые строки (столбца);
в) он имеет хотя бы две пропорциональные (т.е.
отличающиеся множителем) строки (столбца);
г) хотя бы одна строка (столбец) является линейной
комбинацией нескольких других строк (столбцов).
Определение. Если некоторая строка (столбец) может
быть представлена в виде суммы других k строк,
умноженных соответственно на числа 1 , 2 , , k , то
будем говорить, что данная строка (столбец) является
линейной комбинацией указанных строк (столбцов).

20.

6. Определитель не изменится, если к каждому
элементу i-й строки (столбца) прибавить соответствующий элемент k-й строки (столбца), умноженный на число 0.
7. Если A и B – квадратные матрицы порядка n, то
AB BA A B

21.

Пусть A – матрица размера m n
k – некоторое число, 1 k min{ m, n}
Определение. Выберем в матрице A произвольно k
строк и k столбцов. Из элементов, стоящих на
пересечении выбранных строк и столбцов,
составим определитель Mk. Этот определитель
называют минором k-го порядка матрицы A (ее
определителя).

22.

Определение. Пусть A – квадратная матрица
порядка n. Выберем в A минор k-го порядка Mk
(выберем строки с номерами i1,i2,…,ik и столбцы с
номерами j1, j2,…, jk). Вычеркнем из матрицы A
строки и столбцы, из элементов которых состоит
минор Mk. Определитель Mk*, составленный из
оставшихся элементов, называется дополнительным минором к минору Mk.
i1 i2 ik j1 j2 jk
*
Число
Ak ( 1)
M k
называют алгебраическим дополнением минора Mk.
aij
Mij – дополнительный минор (порядок n-1)
i j
Aij – алгебраическое дополнение: ( 1) M ij

23.

Теорема (Лапласа). Пусть в определителе порядка n
выбрано k строк (столбцов) (где 1 k n 1 ). Тогда
определитель равен сумме произведений всех миноров k-го порядка, содержащихся в выбранных строках (столбцах), на их алгебраические дополнения.
Следствие (теоремы Лапласа). Определитель равен
сумме произведений всех элементов любой строки
(столбца) на их алгебраические дополнения, т.е.
|A| ai1 Ai1 ai 2 Ai 2 ain Ain
|A| a1 j A1 j a2 j A2 j anj Anj
(разложение определителя по i-той строке и j-тому
столбцу соответственно)

24.

1
1
A
1
2
2
2
1
3
3 4
1 2
3 4
1 1
A 1 A11 ( 1) A21 ( 1) A31 2 A41
2 1 2
2 3 4
1 ( 1)1 1 1 3 4 ( 1) ( 1)2 1 1 3 4
3 1 1
3 1 1
2 3 4
2 3 4
( 1) ( 1)3 1 2 1 2 2 ( 1) 4 1 2 1 2
3 1 1
1 3 4
= –102

25.

Определение. Обратной к матрице А называется
матрица, обозначаемая А-1, такая, что
1
1
A A A A E
Если А имеет обратную, то
1. А – квадратная.
2. Обратная матрица единственная.
3. Определитель матрицы А отличен от нуля.

26.

Теорема. Пусть А – квадратная матрица порядка n.
Матрица A имеет обратную тогда и только тогда,
когда ее определитель |A| отличен от нуля. Причем
обратная матрица A-1 может быть найдена по
формуле:
1
A 1
A
S
T
где S – матрица из алгебраических дополнений
элементов матрицы A, т.е.
A 11 A 12
A 21 A 22
S
A
n1 A n2
A 1n
A 2n
A nn

27.

Определение. Рангом матрицы называют максимальный порядок ее миноров, отличных от нуля.
Базисным минором матрицы называют её отличный от нуля минор, порядок которого равен рангу
матрицы.
Строки и столбцы, на пересечении которых стоят
элементы базисного минора, называются базисными.
r(A )

28.

Определение. Элементарными преобразованиями
матрицы называются преобразования следующего
вида:
2.
умножение некоторой строки (столбца) на
ненулевое число;
прибавление к одной строке (столбцу) другой
строки (столбца), умноженной на произвольное число;
3.
перестановка двух строк (столбцов);
4.
вычеркивание нулевой строки (столбца).
1.

29.

Определение. Матрица В называется эквивалентной
матрице А, если она может быть получена из А элементарными преобразованиями.
A~ B
Теорема (об инвариантности ранга матрицы относительно элементарных преобразований). Ранг матрицы инвариантен относительно элементарных преобразований (эквивалентные матрицы имеют равные
ранги).
1) с помощью элементарных преобразований строк
получаем для матрицы А эквивалентную матрицу В,
имеющую ступенчатый вид;
2) находим в матрице В базисный минор и определяем ранг матрицы В и, следовательно, матрицы А.

30.

Пример
2 1 2 2 3 2 1 2 2 3
A 6 3 7 4 8 ~ 0 0 1 2 1
2 1 1 4 4 0 0 1 2 1
~ 2 1 2 2 3 B
0 0 1 2 1
r( B ) 2
r(A) = 2
1
2
M2
0 1
– базисный минор

31.

S1, S2, … , Sk – строки (столбцы) матрицы А
α1, α2, … , αk – некоторые числа
α1S1 + α2S2 + … + αkSk – линейная комбинация
Определение. Строки (столбцы) S1, S2, … , Sk
называют линейно зависимыми, если существуют
числа α1, α2, … , αk, не все равные нулю
одновременно, такие, что линейная комбинация
α1S1 + α2S2 + … + αkSk = 0 (нулевой матрице).
Если же равенство α1S1 + α2S2 + … += αkSk = 0
возможно только при условии α1 = α2 = … = αk = 0,
=O
то строки (столбцы) S1, S2, … , Sk называют
S1, S2, S4 – линейно
линейно независимыми.
зависимы

32.

Лемма (о линейной зависимости). Строки (столбцы)
S1, S2, … , Sk линейно зависимы тогда и только
тогда, когда хотя бы одна из них является линейной
комбинацией других.
Теорема (о базисном миноре). 1. Базисные строки
(столбцы) матрицы линейно независимы.
2. Любая строка (столбец) матрицы является
линейной комбинацией базисных строк (столбцов).
Следствие (критерий равенства нулю определителя). Определитель матрицы A равен нулю тогда и
только тогда, когда его строки (столбцы) линейно
зависимы.

33.

Линейное уравнение
a1 x1 a 2 x 2 a n x n b
a1 , a 2 , , a n , b – числа.
a1 , a 2 , , a n – коэффициенты уравнения
b – свободный член
Если b 0, то уравнение называют однородным.
Если b 0, то уравнение называют неоднородным.

34.

Система m линейных уравнений с n неизвестными,
т.е. система вида
a11x1 a12 x2 a1n xn b1 ,
a x a x
a 2 n xn b 2 ,
21 1
22 2
am1 x1 am 2 x2 amn xn bm .
a11
a
A 21
am1
a12
a22
am 2
x1
b1
x
b
2
X B 2
xn
bm
a1n
a2 n
amn
a11
A* a21
am1
a12
a22
am 2
a1n
a2 n
amn
(*)
b1
b2
bm
Тогда система принимает вид:
AX = B

35.

Упорядоченный набор чисел c1, c2, …, cn называется
решением системы (*), если он обращает в тождество каждое уравнение системы.
c1
c2
C – решение системы
c
n

36.

Теорема (Кронекера – Капелли). Система линейных
уравнений (*) совместна тогда и только тогда, когда
ранг матрицы системы равен рангу ее расширенной
матрицы, т.е.
r( A ) r( A* )
Теорема (критерий единственности решения).
Система линейных уравнений (*) имеет единственное решение тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы и
равен числу переменных, т.е.
r( A ) r( A* ) n

37.

1) Матричный метод
Пусть m = n и A 0.
Системы такого вида называются невырожденными.
A 0
r ( A* ) n r ( A) r ( A* ) n
1. r ( A) n
решение единственно.
2. по теореме об обратной матрице А имеет обратную.
1
X A B

38.

2) Метод Крамера
Теорема (Крамера). Если в системе линейных уравнений число уравнений m и число неизвестных n
совпадает и A 0 , то система совместна и имеет
единственное решение, которое может быть найдено
по формулам
i
xi
i 1,2, n
где A , а i – определитель, получаемый из
определителя заменой его i-го столбца на столбец
свободных членов.

39.

Пример
2 x 1 3x 2 1
3x 4 x 1
1
2
2 3
3 4
1
8 9 1 0
1 3
1 4
1
1
1
x1
1
1
2
2 1
3 1
1
2
1
x2
1
1

40.

Определение. Элементарными преобразованиями
системы линейных уравнений называются преобразования следующего вида:
1. умножение обеих частей уравнения на
ненулевое число;
2. прибавление к одному уравнению другого,
умноженного на произвольное число;
3.
перестановка двух уравнений;
4.
вычеркивание одного из двух пропорциональных или одинаковых уравнений.
Определение. Две системы называются эквивалентными (равносильными), если их решения совпадают.

41.

Схема метода Гаусса.
Прямой ход
1. Элементарными преобразованиями приводим
систему к эквивалентной системе, имеющей
расширенную матрицу ступенчатого вида.
2. Выясняем, будет ли система совместна, сравнивая
ранги основной и расширенной матриц полученной
системы.
3. Выбираем в основной матрице полученной системы
базисный минор треугольного вида.
4. Переносим в правую часть системы слагаемые с
неизвестными, коэффициенты которых не вошли в
базисный минор.

42.

Обратный ход
5. Начиная с последнего уравнения (в обратном
порядке) выражаем все зависимые переменные через
свободные. Система, в которой зависимые переменные выражены через свободные, называется
общим решением системы.
6. Придавая свободным переменным конкретные
числовые значения, получаем бесконечно много
решений исходной системы. Каждое из этих решений
называют частным решением системы.

43.

2 x 1 7x 2 3x 3 x 4 6 ,
3x 1 5 x 2 2 x 3 2 x 4 4 ,
9x 1 4 x 2 x 3 7x 4 2 .
1. 2 7 3 1 6 ~ 1 2 1 1 2
3 5 2 2 4
0 11 5 1 10
9 4 1 7 2
x 1 2 x 2 x 3 x 4 2 ,
11x 2 5 x 3 x 4 10 .
2. r( A) r( A* ) 2 система совместна
3. 1 1
4. x 1 x 4 2 2 x 2 x 3 ,
0 1
x 4 10 11x 2 5 x 3 .
5. x 4 10 11x 2 5 x 3
x1 2 2 x 2 x 3 x 4 2 2 x 2 x 3 10 11x 2 5x 3
x 1 8 9x 2 4 x 3 ,
– общее решение
x 4 10 11x 2 5 x 3

44.

a11x 1
a21x 1
am1x 1
a12 x 2
a22 x 2
am 2 x 2
a1n x n
a2 n x n
amn x n
0,
0,
0.
(**)
x 1 x 2 x n 0 – решение., т.е. система совместна
Это решение называют нулевым или тривиальным.
Другие решения называют нетривиальными.
r (A) r (A* )
Теорема (критерий существования нетривиальных
решений). Система линейных однородных уравнений
обладает нетривиальным решением тогда и только
тогда, когда ранг её основной матрицы меньше числа
неизвестных, то есть r(A ) n .

45.

С1, С2, … , Сk – матрицы-столбцы, являющиеся
решениями системы (**)
α1, α2, … , αk – некоторые числа
α1С1 + α2С2 + … + αkСk – линейная комбинация
Теорема (свойство решений системы линейных
однородных уравнений). Любая линейная комбинация конечного числа решений системы (**)
является решением этой системы.

46.

Теорема
(существования
фундаментальной
системы решений). Пусть r – ранг матрицы
системы (**). Если система имеет нетривиальные
решения, то найдутся n – r линейно независимых
решений таких, что любое другое её решение будет
их
линейной
комбинацией.
Эти
решения
называются фундаментальной системой решений
системы (**).
1. Находим общее решение системы.
2. Записываем любой отличный от нуля
определитель порядка n – r.
3. Записываем n – r решений системы, беря в
качестве значений для свободных неизвестных
элементы строк поочередно.

47.

x1
2 x
1
x
1
x 1
x2
3x 2
x2
2x 2
x 3 2x 4
2 x 3 5x 4
x3
x3 x4
2x 5
4x 5
2x 5
2x 5
0,
0,
0,
0.
x 1 x 3 x 4 2 x 5 , – общее решение
x4
x 2
1) x 3 1 x 4 0
2) x 3 0 x 4 1
3) x 3 0 x 4 0
1 0 0
0 1 0
0 0 1
x2 0
x5 0
x 1 1
x5 0
x 1 1 x 2 1
x2 0
x1 2
x5 1
(1, 0, 1, 0, 0), (– 1, 1, 0, 1, 0), (2, 0, 0, 0, 1)
– фундаментальная система решений

48.

Пусть система АХ = В совместна и r(A) < n.
Установим связь между решениями системы АХ = В и
соответствующей ей системы АХ = 0.
Теорема 1. Сумма любого решения линейной неоднородной системы и любого решения соответствующей
ей однородной системы является решением неоднородной системы.
Теорема 2. Разность двух произвольных решений линейной неоднородной системы является решением
соответствующей однородной системы.
Теорема 3. Общее решение линейной неоднородной
системы равно сумме любого частного решения этой
системы и общего решения соответствующей однородной системы.