Дисциплина ЛААГ (линейная алгебра и аналитическая геометрия)

1. Дисциплина ЛААГ (линейная алгебра и аналитическая геометрия)

Кафедра высшей
математики
ТПУ
Лектор:
доцент
Тарбокова
Татьяна
Васильевна
1

2. СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ ЛААГ

• Тема 1. Линейная алгебра
• Тема 2. Векторная алгебра
• Тема 3. Аналитическая
геометрия на плоскости
• Тема 4. Аналитическая
геометрия в пространстве
2

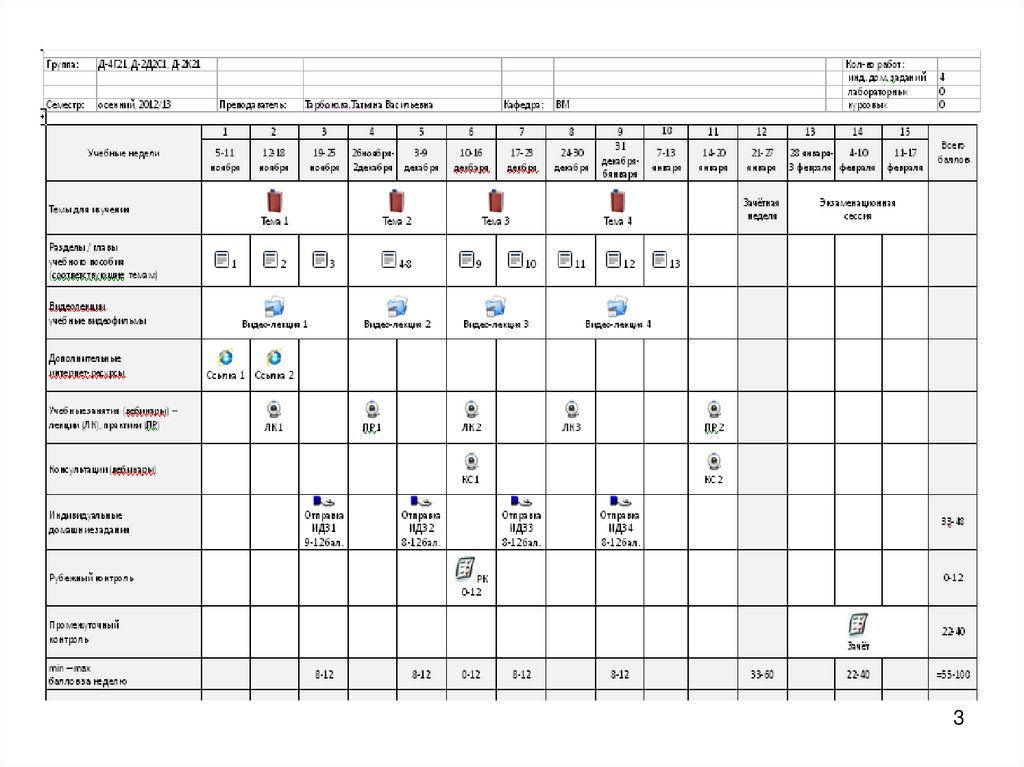
3.

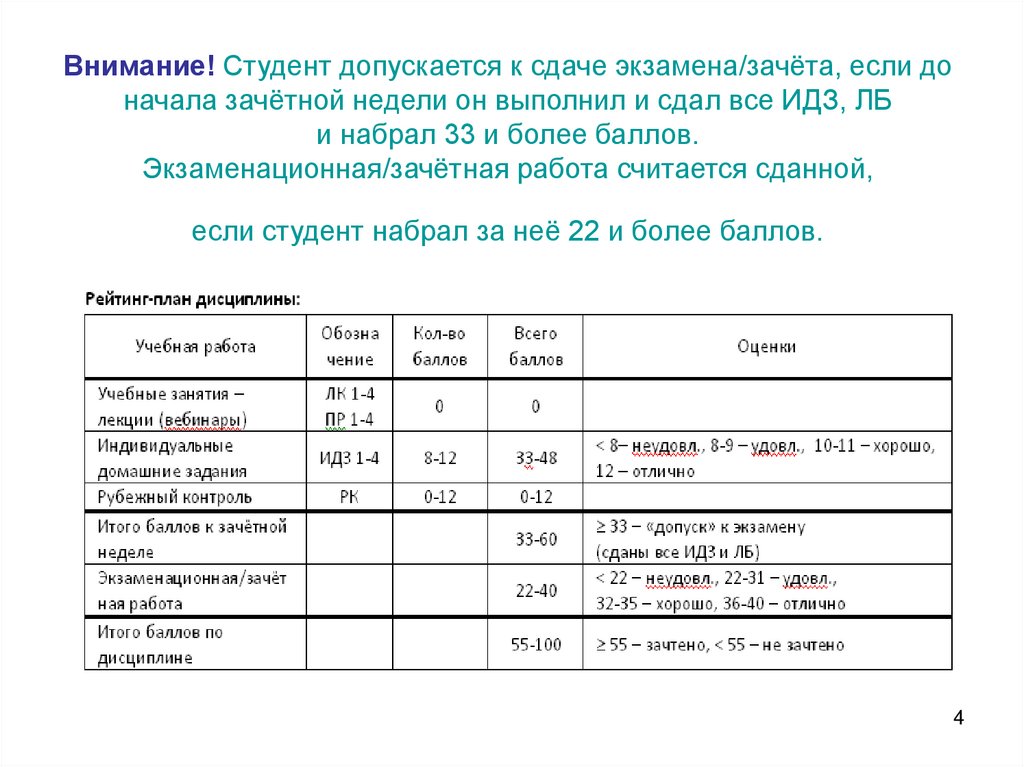
3

4. Внимание! Студент допускается к сдаче экзамена/зачёта, если до начала зачётной недели он выполнил и сдал все ИДЗ, ЛБ и набрал

33 и более баллов.
Экзаменационная/зачётная работа считается сданной,
если студент набрал за неё 22 и более баллов.
4

5. Дополнительные Интернет- ресурсы Ссылка 1. http://portal.tpu.ru/SHARED/t/TOKTV/page_3

5

6. Дополнительные Интернет-ресурсы Ссылка 2. http://portal.tpu.ru/SHARED/t/TOKTV/Page_121

6

7. Тема 1. Линейная алгебра Разделы

• 1. Матрицы и действия над ними
• 2. Определители и их вычисление
• 3. Системы линейных уравнений
7

8. Матрицы, определители и действия над ними

8

9. Виды матриц

9

10. Виды матриц

10

11. Произведение матриц

11

12. Произведение матриц

12

13. Произведение матрицы-строки на матрицу-столбец

Произведение матрицы-строки на матрицустолбец
13

14. Пример

• Можно ли умножить матрицы:
• (ответьте: 1) да или нет, 2)…)?
• 1) A (3, 1, 0, 8) B (9, 4, 2, 5)
• 2)
• 3)
0
A ( 6, 1, 0) B 2
10
4
A (5, 0, 3) B
5
14

15. Произведение матриц

15

16. Пример произведения матриц

Задание.
Найдите произведение матриц
1
2
0 3
5 1
16

17. Решение.

1 0 3 ( 1) ( 3) 0 1 3
2 5 1 2 ( 3) 5 1 1
17

18. § Определители, их вычисление и свойства

• 1. Понятие определителя
• Определителем порядка n
квадратной матрицы n-го порядка
называют число , соответствующее
этой квадратной матрице.
• Определитель числовой матрицы
первого порядка равен числу,
являющемуся элементом этой матрицы.
18

19.

Определитель матрицы A обозначают |A| ,
detA или
a11 a12 a1n
a21 a22 a2 n
an1 an 2 ann
Элементы, строки, столбцы матрицы
называются соответственно элементами,
строками, столбцами определителя
матрицы.
19

20.

• Минором M ij элемента a ij
определителя n-го порядка называется
определитель (n–1)-го порядка,
полученный из данного определителя
вычеркиванием элементов
i-й строки и j-го столбца.
20

21.

• Алгебраическим дополнением Aij
элемента a ij называется
• минор этого элемента,
( i j )
• умноженный на ( 1)
:
Aij ( 1)
(i j )
M ij
21

22.

Теорема Лапласа. Определитель равен
сумме произведений всех элементов
любой строки (столбца) на их
алгебраические дополнения, т.е.
|A|=ai1Ai1+ai2Ai2+…+ainAin
|A|=a1jA1j+a2jA2j+…+anjAnj
22

23. Определитель второго порядка равен разности произведений элементов главной диагонали и элементов побочной диагонали.

A ai1 Ai1 ai 2 Ai 2 ... ain Ain
Aij ( 1) (i j ) M ij
23

24. Вычисление определителя третьего порядка

A a1 j A1 j a2 j A2 j ... anj Anj
Aij ( 1) (i j ) M ij
a11 a12 a13
a 23
a13
a13
1 2 a 21
2 2 a11
3 2 a11
a 21 a 22 a 23 a12 1
a 22 1
a32 1
a 31 a 33
a 31 a 33
a 21 a 23
a 31 a 32 a 33
a12 a21a33 a31a23 a22 a11a33 a31a13 a32 a11a23 a21a13 .
24

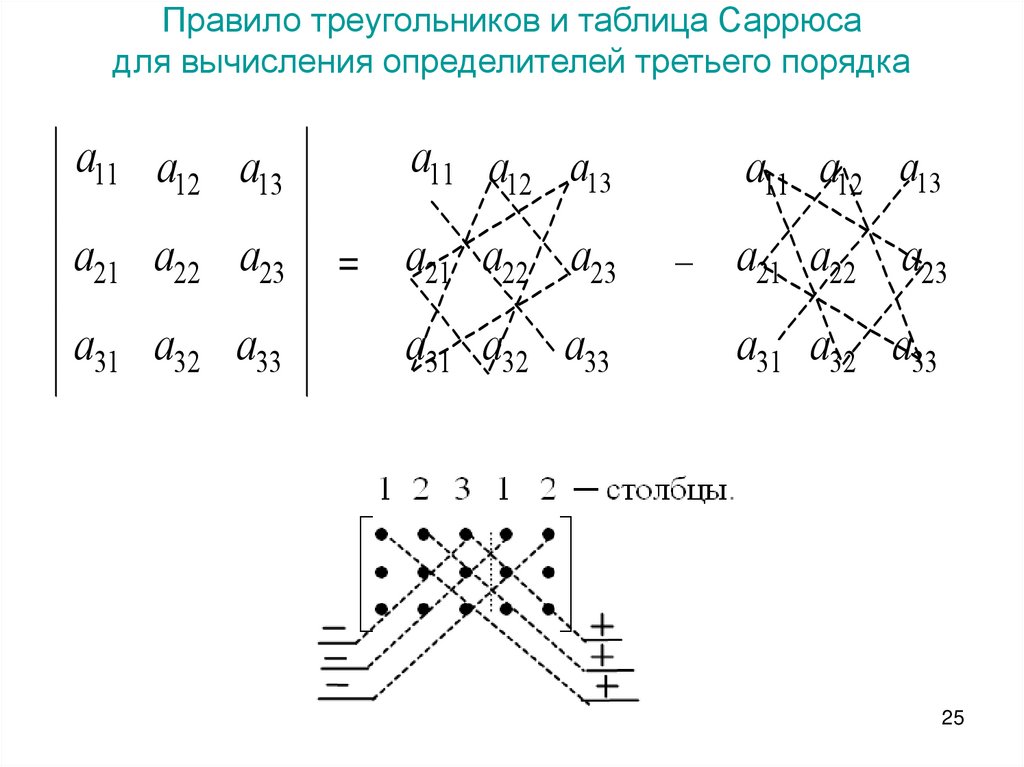
25. Правило треугольников и таблица Саррюса для вычисления определителей третьего порядка

a11 a12 a13
a21 a22 a23
a31 a32 a33
a11 a12 a13
=
a21 a22 a23
a31 a32 a33
a11 a12 a13
–
a21 a22 a23
a31 a32 a33
25

26. Определитель треугольного вида равен произведению элементов главной диагонали

a11
0
0
...
0
a12
a 22
0
...
0
a13
a 23
a33
...
0
...
...
...
...
0
a1n
a2n
a3n a11a 22 a33 ...a nn .
...
a nn
26

27. § Ранг матрицы 1. Понятие ранга матрицы. Теорема о базисном миноре

Минором M k порядка k
матрицы А называется любой
определитель k-го порядка этой
матрицы,
составленный из элементов,
стоящих на пересечении любых
её «к» столбцов
и любых её «к» строк.
27

28.

Минор Mk матрицы A называется её
базисным минором,
если он отличен от нуля,
а все миноры матрицы A более
высокого порядка k+1, k+2, …, t
равны нулю или не существуют.
Строки (столбцы) базисного минора
называют базисными строками
(столбцами)
Рангом матрицы A называется
порядок её базисного минора.
Обозначают: r(A) или rang(A).
28

29. 2. Методы нахождения ранга матрицы

1) Метод окаймляющих миноров.
Пусть Ms – минор порядка s. Окаймляющим минором
для минора Ms называется любой минор порядка
s+1, содержащий минор Ms .
ТЕОРЕМА. Если в матрице A есть минор
k-го
порядка, отличный от нуля, а все окаймляющие его
миноры равны нулю или не существуют, то ранг
матрицы A равен k .
Найти ранг матрицы можно по следующей схеме
(Метод окаймляющих миноров):
а) Находим в матрице минор Mk порядка k, отличный
от нуля (где k 1).
б) Ищем его окаймляющий минор Mk+1 отличный от
нуля. Если такого минора не существует, то ранг
матрицы равен k. Если окаймляющий минор Mk+1 0,
то рассматриваем окаймляющие миноры для Mk+1 29
и
т.д.

30. Схема метода окаймляющих миноров

30

31.

2) Метод элементарных преобразований.
Элементарными
преобразованиями
матрицы
называются преобразования следующего вида:
а) умножение строки (столбца) на число 0;
б) прибавление к i-й строке (столбцу) k-й строки
(столбца),
умноженной на число 0;
в) перестановка i-й и k-й строки (столбца);
г) вычеркивание одной из двух пропорциональных или
равных строк (столбцов);
д) вычеркивание нулевых строк (столбцов).
Матрица B называется эквивалентной матрице A ,
если она может быть получена из A элементарными
преобразованиями.
Обозначают: A ~ B.
31

32.

ТЕОРЕМА. Эквивалентные матрицы имеют
равные ранги.
ТЕОРЕМА. Любая матрица A эквивалентна
некоторой треугольной или
трапециевидной матрице, не содержащей
нулевых и пропорциональных строк. Причем
эта треугольная или трапециевидная
матрица может быть получена из A
элементарными преобразованиями только
строк.
Найти ранг матрицы можно по следующей
схеме (метод элементарных
преобразований):
1) с помощью элементарных преобразований
строк получаем для матрицы A
эквивалентную треугольную или
32
трапециевидную матрицу B;

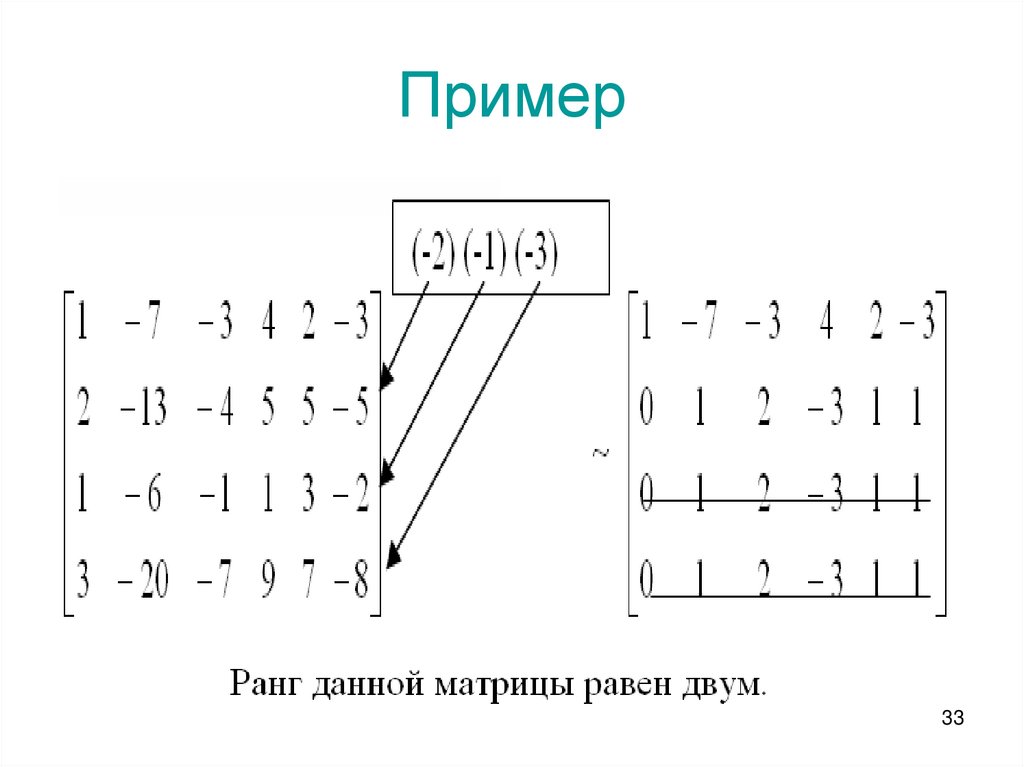
33. Пример

33

34. Свойства матриц и определителей

34

35. Вычисление определителей четвёртого и более высоких порядков

• 1. Выбрать рабочую строку (столбец) такую, где есть
хотя бы одна единица. Рабочую строку (столбец) не
изменяем.
• 2. Выбрать столбец (строку), в котором нужно
получить нули вместо всех элементов, кроме
элемента в рабочей строке. Обычно - это столбец
(строка) с нулями или числами, близкими к единице.
• 3. Каждый элемент рабочей строки (столбца)
умножить на число, противоположное элементу, на
месте которого надо получить ноль,
• и соответствующие элементы рабочей строки
(столбца) и изменяемых строк (столбцов) сложить
(элементарные преобразования строк (столбцов)).
• 4. Разложить определитель по элементам столбца
(строки), в котором получили нули, применяя теорему
Лапласа. Порядок определителя при этом
понижается на единицу.
35

36. § Системы линейных уравнений 1. Основные понятия

Уравнение называется линейным, если
неизвестные в нём содержатся только в
первой степени
и между собой не перемножаются,
т.е. если оно
a1 x1имеет
a2 x2вид
... an xn b
,
где
,b –x известные заданные числа,
x1 , x2a, i...,
n
- неизвестные уравнения.
ai называются коэффициентами уравнения,
b называется свободным членом.
Если bb =00, то уравнение называется
однородным.
Если
, уравнение называется
неоднородным.
36

37. Рассмотрим систему m линейных уравнений с n неизвестными, т.е. систему вида

a11 x1 a12 x2 a1n xn b1 ,
a21 x1 a22 x2 a2 n xn b 2 ,
am1x1 am 2 x2 amn xn bm .
(1)
37

38. Обозначим через A и A* следующие матрицы:

a11
a
A 21
a
m1
a12 a1n
a22 a2n
am 2 amn
a11
a
A* 21
a
m1
a12 a1n
a22 a2 n
am 2 amn
b1
b2
bm
Матрицу A называют основной матрицей системы (1),
матрицу A* – расширенной матрицей системы (1).
Пусть X – матрица-столбец неизвестных,
x1
b1
B – матрица-столбец свободных членов,
x
b2
2
т.е.
X
B
x
n
b
m
Тогда систему (1) можно записать в виде матричного
уравнения AX=B. Его называют матричной формой
системы (1).
38

39.

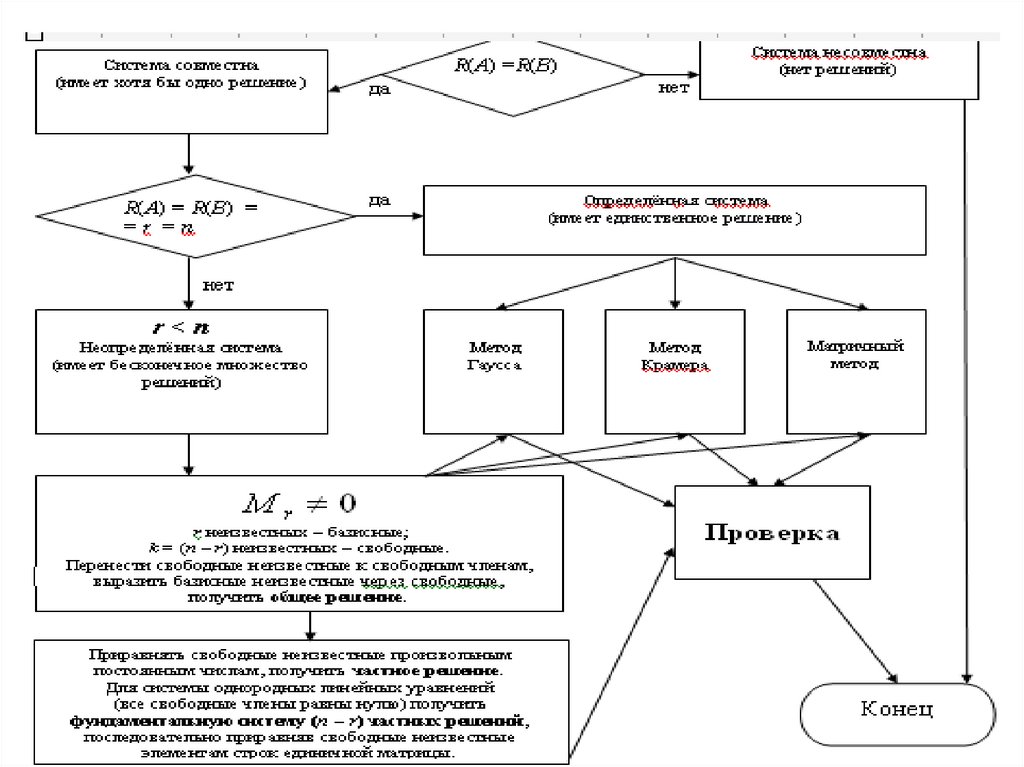
ТЕОРЕМА Кронекера –
Капелли.
Система линейных
уравнений (1) совместна
тогда и только тогда,
когда ранг основной
матрицы системы равен
рангу её расширенной
матрицы, т.е. r(A) = r(A*).
39

40. 2. Методы решения систем линейных уравнений

Матричный метод.
ОПРЕДЕЛЕНИЕ. Обратной к матрице A называется матрица,
обозначаемая A-1, такая, что A·A-1=A-1 · A=E.
Преобразование матричных уравнений
AX C ( A 1 A) X A 1C X
XB C X ( BB 1 ) CB 1 X
AXB C ( A 1 A) X ( BB 1 ) A 1CB 1 X
AX 2B C AX C 2B.
Квадратная матрица, определитель которой
отличен от нуля, называется невырожденной.
40

41. ТЕОРЕМА. Пусть A – квадратная матрица. Матрица A имеет обратную тогда и только тогда, когда её определитель |A| отличен от

нуля. Причем обратная
матрица A-1 может быть найдена по формуле:
A
s
1
1
ST
A
где
– матрица из алгебраических дополнений
элементов матрицы A, т.е.
A A
A
T
12
1n
11
A
A
A
22
2n
S 21
A
A
A
n
1
n
2
nn
Матрица S
называется союзной
(или присоединенной, или взаимной) для матрицы A.
Нахождение решения по формуле X A 1 B
называют матричным методом решения
41
системы.

42. Пример

• Решить систему уравнений x1 5 x2 11,
• матричным методом.
3x1 2 x2 1
• Решение.
1 5
2 3
2 5
T
17 0, S
, S
3 2
5 1
3 1
x1 1 2 5 11 1 22 5 1
X
.
x2 17 3 1 1 17 33 1 2
• Проверка!!!
42

43. Метод Крамера

ТЕОРЕМА (Крамера). Если в системе
линейных уравнений число уравнений m и
число неизвестных n совпадает, и |A| 0,
то система совместна и имеет
единственное решение, которое может
быть найдено по формулам
Di
xi
(i 1,2, n)
( )
D
D
где D=|A|, а
i – определитель, получаемый
из определителя D заменой его i-го столбца
на столбец свободных членов.
Формулы ( ) называются формулами Крамера.
43

44. Пример

• Решить систему уравнений
• методом Крамера.
• Решение.
x1 5 x2 11,
3x1 2 x2 1
11 5
1 11
1 2
3 1 1 33 34
22 5 17
x1
1; x 2
2;
1 5
1 5
2 15 17
2 15
17
3 2
3 2
• Проверка!!!
44

45. Метод Гаусса (метод исключения неизвестных)

• Две системы называются
эквивалентными (равносильными),
если их решения совпадают.
• К эквивалентной системе можно
перейти с помощью элементарных
преобразований расширенной
матрицы этой системы.
45

46.

Исключение неизвестных обычно
осуществляют элементарными
преобразованиями строк
расширенной матрицы СЛУ.
В результате расширенная матрица
СЛУ приводится к
трапецеидальному виду,
который позволяет легко выделить
базисный минор основной матрицы
системы.
46

47.

• Неизвестные, коэффициенты
при которых вошли в базисный
минор называются базисными
неизвестными.
• Неизвестные, коэффициенты
при которых не вошли в
базисный минор, называются
свободными неизвестными.
47

48.

• Если n – число неизвестных
системы, r – её ранг, то
• r неизвестных системы –
базисные,
• k = n – r свободные.
48

49.

• Если ранг основной и расширенной
матриц СЛУ совпадает с числом
неизвестных СЛУ, то свободных
неизвестных нет. В этом случае СЛУ
имеет единственное решение
(определённая СЛУ).
Если ранги основной и расширенной
матриц СЛУ равны, но меньше числа
неизвестных СЛУ, то СЛУ
неопределённая. В этом случае находят
общее решение СЛУ.
49

50.

• Решение СЛУ, в котором базисные
неизвестные выражены через
свободные неизвестные,
называется общим решением
СЛУ.
Решение, которое получается из
общего путём присваивания
свободным неизвестным числовых
значений, называется частным
решением СЛУ.
50

51.

• Общее решение системы линейных
уравнений можно получить, руководствуясь,
например, следующим планом:
• а) выбрать базисный минор (обычно это
минор, под главной диагональю которого –
все нули);
• б) перенести свободные неизвестные к
свободным членам, то есть в правые части
уравнений;
• в) обратным ходом метода Гаусса выразить
базисные неизвестные через свободные
неизвестные.
51

52.

52

53. Пример

• Решить систему уравнений x1 5 x2 11,
3x1 2 x2 1
• методом Гаусса.
Решение.
( 3)
1 5 : 11
1 5 : 11
;
3 2 : 1
0 17 : 34
x1 5 x 2 11,
x 2 2, x1 1.
17 x 2 34,
Проверка!!!
53

54.

54

55. Найти общее решение СЛУ и какое-либо частное решение СЛУ

55

56. Запишем эквивалентную СЛУ:

56

57. СПАСИБО ЗА ВНИМАНИЕ

57