Линейная алгебра

1.

Линейная алгебра
Определители второго порядка
Системы из двух линейных уравнений с двумя неизвестными
Определители n – ого порядка
Методы вычисления определителей
Системы из n линейных уравнений с n неизвестными.

2.

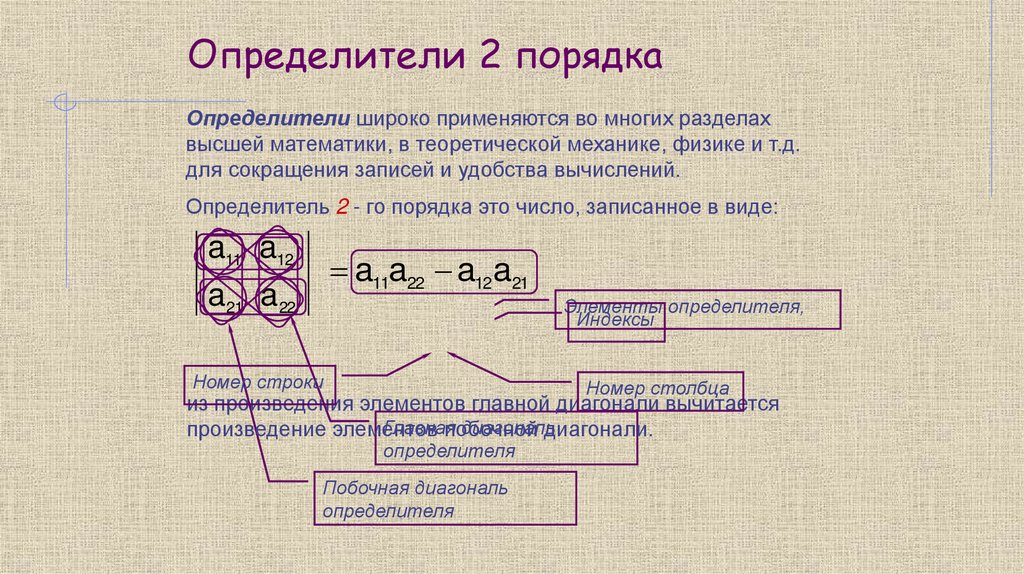
Определители 2 порядка
Определители широко применяются во многих разделах
высшей математики, в теоретической механике, физике и т.д.
для сокращения записей и удобства вычислений.
Определитель 2 - го порядка это число, записанное в виде:
a11 a12
a11a22 a12a21
a 21 a 22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя

3.

Определители n – ого порядка
Определителем n – ого порядка называется число:
a11 a12
a21 a 22
an1 an 2
a1n
a 2n
ann
Методы вычисления определителей n – ого порядка рассмотрим
на примере вычисления определителей третьего порядка.

4.

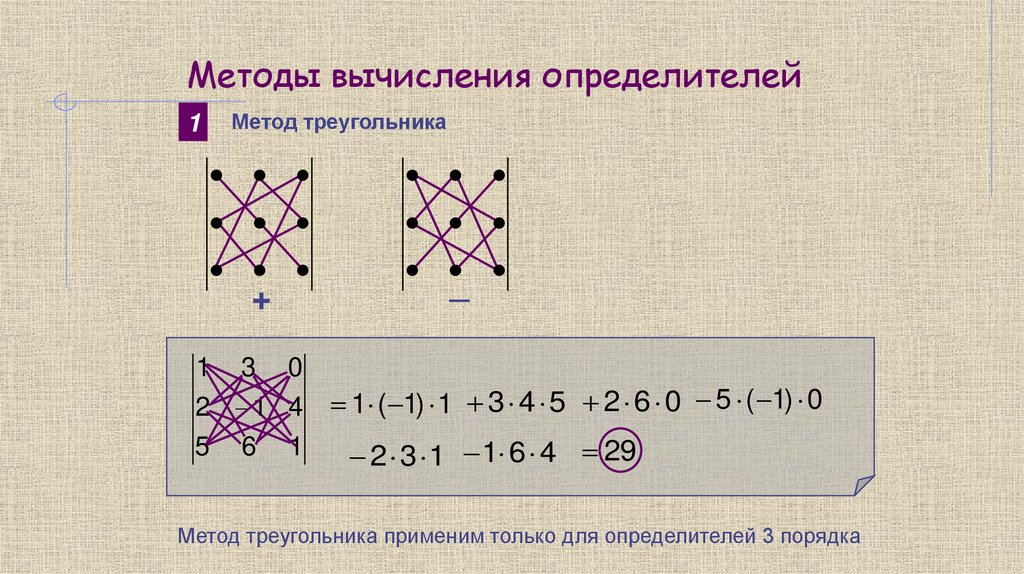
Методы вычисления определителей
1
Метод треугольника
+
1 3 0
2 1 4
5 6 1
_
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29
Метод треугольника применим только для определителей 3 порядка

5.

Методы вычисления определителей
2
Метод разложения определителя по элементам строки
(столбца)
Определитель второго порядка, который получается из определителя
3 - го порядка путем вычеркивания i - й строки и j - го столбца, т.е.
строки и столбца, на пересечении которых стоит элемент ai j
называется минором элемента и обозначается Mi j
Алгебраическим дополнением элемента ai j называется
Ai j Mi j ( 1)i j
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
aa2211 aa2312
MM1123
aa3231 aa3332
1 1 2 3
A
M
(
M23
A11 23 M11 23( 1) 1) M
11

6.

Методы вычисления определителей
Величина определителя равна сумме произведений элементов
какой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
0 1
0 3
3 1
1 2
1 1
0 3 1 2
( 1) 0
( 1)1 3
( 1) 1
2 1
2 5
5 1
2 5 1
2 (3 1 5 1) 1 (0 1 2 1) 2

7.

Методы вычисления определителей
3
Использование свойств определителя
Свойства определителя:
Величина определителя:
равна нулю, если элементы какого - либо столбца или строки
равны нулю:
0 0
0 a22 0 a21 0
a21 a22
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
a11 a12 a11 a12 0

8.

Методы вычисления определителей
меняет знак, если поменять местами строки (столбцы):
a11 a12
a21 a22
a11 a22 a12 a21 a12 a21 a11a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого - либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k a11 a22 k a12 a21 k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
a11 a12
a21 a22
a11 a21
a12 a22

9.

Методы вычисления определителей
не меняется, если к элементам какой-либо строки (столбца)
прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
a11
a12
a21 ka11 a22 ka12
a11a22 a21a12
a11a22 a11ka12 a21a12 ka11a12
a11 a12
a21 a22
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали: a a a
11
12
13
0 a22 a23 a11a22 a33
0 0 a33

10.

Методы вычисления определителей
1 3 1
1
3 1 1 3 1
5 1
2 1 3 0 5 1 0 5 1 1
( 1)1 1
7 2
1 4 1
1 4 1 0 7 2
5 2 7 1 17
Выберем 1
К элементам
2
Разложим
столбец
и
К элементам
3
строки
прибавим
определитель
по
превратим
второй
строки
прибавим
элементы 11строки,
элементам
столбца
и третий
элементы
1
строки
умноженные на (-2)
элементы в нули
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.

11.

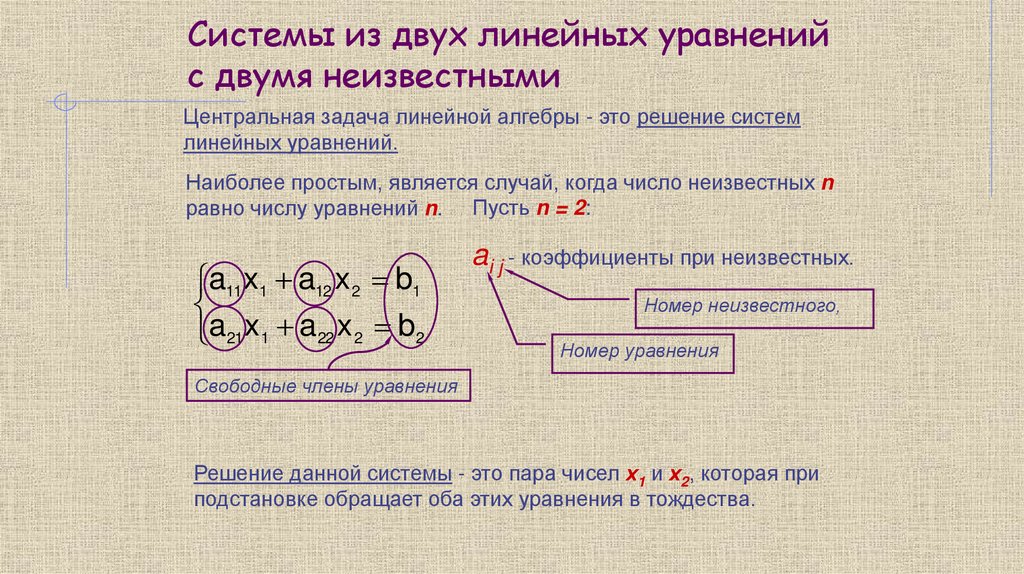
Системы из двух линейных уравнений
с двумя неизвестными
Центральная задача линейной алгебры - это решение систем
линейных уравнений.
Наиболее простым, является случай, когда число неизвестных n
равно числу уравнений n. Пусть n = 2:
a11x1 a12 x 2 b1
a21x1 a22 x 2 b2
ai j - коэффициенты при неизвестных.
Номер неизвестного,
Номер уравнения
Свободные члены уравнения
Решение данной системы - это пара чисел х1 и х2, которая при
подстановке обращает оба этих уравнения в тождества.

12.

Системы из двух линейных уравнений
с двумя неизвестными
a11x1 a12 x 2 b1
a21x1 a22 x 2 b2
a11 a22 x1 a12 a22 x 2 b1 a22
a12 a21 x1 a12 a22 x 2 a12 b2
a a a a x a b a b
11
22
Обозначим:
1
b1 a12
b2 a22
12
21
1
a11 a12
a 21 a 22
22
1
12
2
a11 a22 a12 a21
b1 a22 a12 b2
x1 1

13.

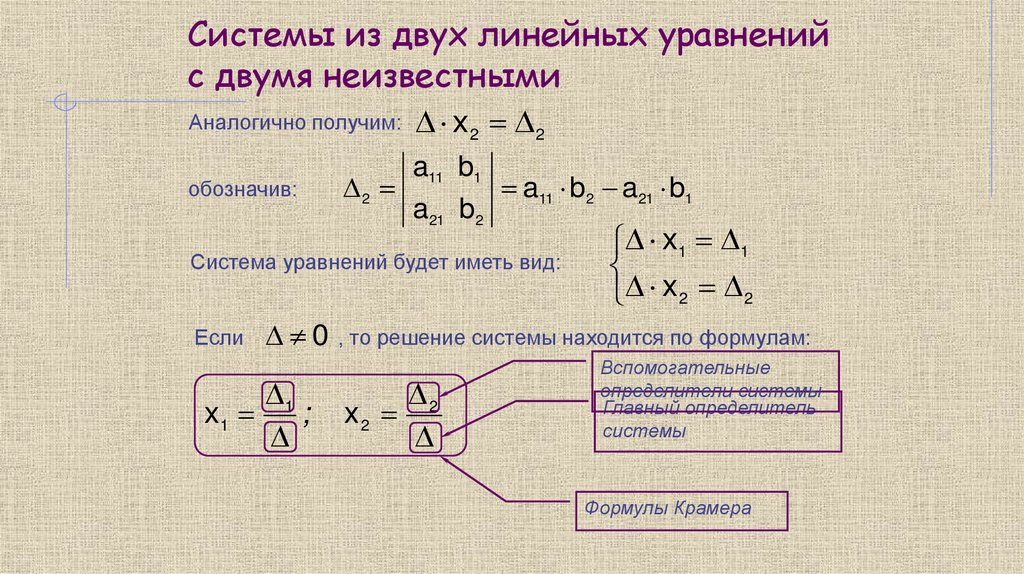
Системы из двух линейных уравнений
с двумя неизвестными
Аналогично получим: x 2 2
обозначив:
2
a11 b1
a21 b2
a11 b2 a21 b1
Система уравнений будет иметь вид:
Если
x1 1
x 2 2
0 , то решение системы находится по формулам:
1
x1
;
2
x2
Вспомогательные
определители системы
Главный определитель
системы
Формулы Крамера

14.

Системы из n линейных уравнений с n
неизвестными
Рассмотрим общую квадратную систему линейных уравнений:
a11x1 a12 x 2 a1n x n b1
a21x1 a22 x 2 a2n x n b2
an1x1 an2 x 2 ann x n bn
Система линейных уравнений называется совместной, если она
имеет решение и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет
единственное решение и неопределенной, если она имеет
бесконечное множество решений.
Система называется однородной, если b1 b2 bn 0
Однородная система совместна, так как всегда имеет нулевое
решение.

15.

Системы из n линейных уравнений с n
неизвестными
Для сокращения выкладок запишем систему из трех уравнений с
тремя неизвестными:
a11x1 a12 x 2 a13 x 3 b1
a21x1 a22 x 2 a23 x 3 b2
a x a x a x b
33 3
3
31 1 32 2
a11 a12 a13
a 21 a 22 a 23
a31 a32 a33
Вспомогательные определители получаются из главного
определителя, если заменить соответствующий столбец столбцом
свободных членов:
b1 a12 a13
a11 b1 a13
a11 a12 b1
1 b 2 a 22 a 23
2 a 21 b 2 a 23
3 a 21 a 22 b 2
b3 a32 a33
a31 b3 a33
a31 a32 b3

16.

Системы из n линейных уравнений с n
неизвестными
По величине главного и вспомогательных определителей можно
судить о характере системы:
Если
0 то система совместна и определенна.
Если 0, 1 2 3 0
неопределенна.
то система совместна и
Если 0, но 1 0 или 2 0 или 3 0 то
система несовместна.
В общем случае будем иметь n +1 определителей n – ого порядка
, 1, 2 , 3 , , n 2 , n 1, n
и, если 0 , то решение системы находится по формулам
Крамера:
1
x1 ;
2
x2
;
n
xn

17.

Линейная алгебра
Матрицы. Основные понятия.
Действия над матрицами
Метод обратной матрицы решения систем линейных уравнений

18.

Матрицы. Основные понятия
Матрицей называется прямоугольная таблица, составленная
из каких – либо элементов и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические
выражения, функции и т.д.
a11
a 21
A
a
m1
a12 ... a1n
a 22 ... a 2n
am 2 ... amn
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов

19.

Матрицы. Основные понятия
Если m n , то матрица называется прямоугольной.
Если m n
порядка).
, то матрица называется
квадратной (n - ного
Любое число (скаляр) можно представить как матрицу первого
порядка, размерностью 1 1 .
Матрица типа 1 n называется матрица-строка:
a a
11
12
a13 ... a1n
Матрица типа m 1 называется матрица-столбец:
a11
a 21
...
a
m1

20.

Матрицы. Основные понятия
Квадратная матрица называется единичной, если ее элементы,
расположенные на главной диагонали, равны единице,
остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
Если все элементы квадратной матрицы равны нулю, то она
называется нуль-матрицей и обозначается символом 0.
0 0 0
O 0 0 0
0 0 0

21.

Матрицы. Основные понятия
Для каждой квадратной матрицы n - ного порядка существует
определитель n - ного порядка, элементы которого равны
соответствующим элементам матрицы.
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
a11 a12
det A a21 a 22
a31 a32
a13
a 23
a33
Определитель любой единичной матрицы равен единице.
Если определитель матрицы равен нулю, то
называется вырожденной, в противном случае
невырожденная.
матрица
матрица

22.

Действия над матрицами
Равенство матриц
Матрицы равны, если они имеют одинаковую размерность и их
соответствующие элементы равны.
A B
dim A dimB;
aij bij
Сложение (вычитание) матриц
Сумма и разность матриц существуют только для матриц
одинакового размера, при этом соответствующие элементы
матриц складываются или вычитаются.
C A B
dim A dimB dim C
c ij aij bij

23.

Действия над матрицами
Умножение матрицы на число
При умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
B k A
dim A dimB; bij aij k
Найти значение выражения: C A 5 B
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
0 5 ( 5) 1 5 0 4 5 2 25 1 14

24.

Действия над матрицами
Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij
на матрицу B размера [n k ] с элементами bjq называется
матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1

25.

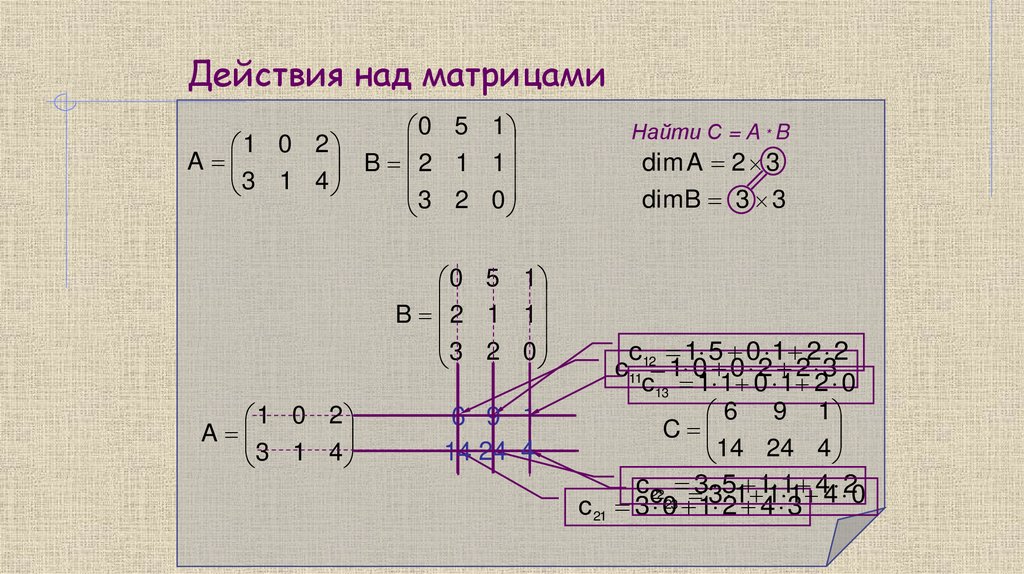
Действия над матрицами
1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
6 9 1
14 24 4
Найти С = A * B
dim A 2 3
dim B 3 3
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3

26.

Действия над матрицами
Свойства операции произведения матриц:
2) AB A B ;
3) A B C AC BC ;
1) A BC AB C ;
4) В общем случае для произведения матриц не действует
переместительный закон: A B B A
иногда АВ существует, а ВА не имеет смысла. В случае, когда
АВ = ВА, матрицы А и В называются коммутативными.
5) Единичная матрица является коммутативной для любой
квадратной матрицы того же порядка:
EA AE A
6) Для двух квадратных матриц А и В одного порядка произведение
определителей равно определителю произведения .
det A det B det AB

27.

Действия над матрицами
Нахождение обратной матрицы
Обратной матрицей по отношению к данной невырожденной
квадратной матрице A n - ного порядка, называется матрица,
которая, будучи умноженной как слева, так и справа на данную
матрицу, дает единичную матрицу.
Обратная матрица обозначается символом А-1. Таким образом,
согласно определению: АА-1=А-1А=Е.
1
A
A A
A det A 0 A
det A
T
1
Транспонированная матрица
Присоединенная матрица
получается из матрицы А Если определитель матрицы
получается путем замены каждого
путем замены строк т
равен нулю, то обратная
элемента матрицы А на его
соответствующими
матрица не существует
алгебраическое дополнение
столбцами

28.

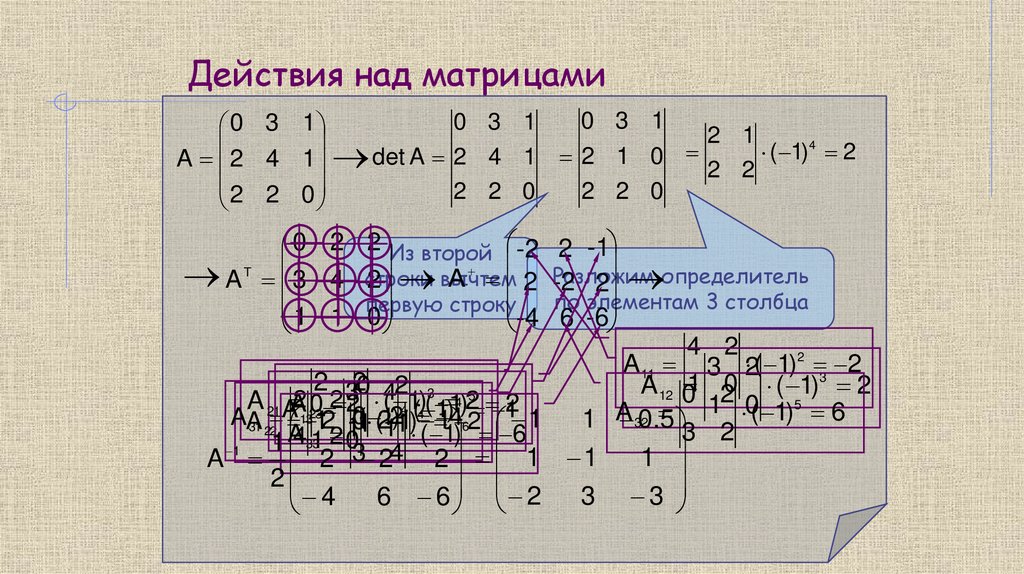
Действия над матрицами
0 3 1
0 3 1
0 3 1
2 1
4
(
1
)
2
2
1
0
det
A
2
4
1
A 2 4 1
2 2
2 2 0
2 2 0
2 2 0
0 2 2 Из второй -2 2 -1
T
A 3 4 строки
A 2 Разложим
2 вычтем
-2 2 определитель
по элементам
3 столбца
строку
1 1 первую
0
-4 6 -6
4 2
A 11 3 2
( 1)2 3 2
2 320 42 3 5
A 12 0
1 20 ( 1) 2
2 23
2 2 ( 4 1( 4) (
A 21 A
)14)2 1
A
2
0
1 0( 1)5 6
1
A
13
0
2
AA
(
1
)
4
1 320.5 3 2
12 101 (21 11) ( 11 ) 62 6 1
31 22
A
1 4331 2 03 4
1
1
A 2 2
2 1 1
2
2
3
3
4
6
6

29.

Метод обратной матрицы решения
систем линейных уравнений
Метод обратной матрицы рассмотрим на примере
решения квадратной системы 3 порядка.
a11x1 a12 x 2 a13 x 3 b1
a21x1 a22 x 2 a23 x 3 b2
a x a x a x b
33 3
3
31 1 32 2
Запишем эту систему в матричном виде. Обозначим:
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
x1
X x2
x3
b1
B b2
b3
Основная матрица
Матрица - столбецМатрица - столбец
системы свободных членов
неизвестных

30.

Метод обратной матрицы решения
систем линейных уравнений
Тогда систему можно записать так:
a11 a12
A X a21 a 22
a
31 a32
a13 x1 a11 x1 a12 x 2 a13 x 3 b1
a23 x 2 a 21 x1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
a33 x 3 31 1 32 2
3
33 3
A X B
Найдем решение системы в матричном виде.
Предположим, что det A отличен от нуля и, следовательно,
существует обратная матрица А-1.
Умножим слева матричную запись системы на обратную матрицу:
A 1 A X A 1 B
E X A 1 B X A 1 B
Метод обратной матрицы применим для решения квадратных
систем с невырожденной основной матрицей.

31.

Метод обратной матрицы решения
систем линейных уравнений
Решить систему методом обратной матрицы.
3x 2 x 3 1
2x1 4x 2 x 3 2
2x 2x 3
2
1
X A 1 B
1 0.5
1
1
A 1 1
1
2
3
3
x1
0 3 1
A 2 4 1 X x 2
2 2 0
x3
1
B 2
3
1
B 2
3
-0,5
2
-5
0.5
X 2
5

32.

Линейная алгебра
Метод Гаусса решения систем линейных уравнений
Ранг матрицы
Исследование систем линейных уравнений
Однородные системы линейных уравнений

33.

Метод Гаусса решения систем
линейных уравнений
Рассмотрим задачу решения системы линейных уравнений
размерностью (m x n). Запишем систему в матричном виде: A X B
Если закрепить раз и
a11 a12 a13 a1n x1 b1 навсегда нумерацию
a 21 a22 a23 a2n x 2 b2 неизвестных, то можно
неизвестные в
опустить
системы и
записи
a a a a x b записать ее в виде
mn n
m матрицы, отделяя
m1 m 2 m3
b1
a11 a12 a13 a1n
a21 a22 a23 a2 n b2
B A B
a a a a b
m
mn
m1 m 2 m 3
столбец свободных
членов вертикальной
чертой.
Расширенная матрица
системы

34.

Метод Гаусса решения систем
линейных уравнений
Следующие действия над расширенной матрицей системы
называются элементарными преобразованиями.
Умножение или деление элементов строк на одно и то же
число, не равное нулю
Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки,
умноженных на произвольный множитель.
Конечной целью элементарных преобразований является
получение верхнетреугольной матрицы, у которой все элементы,
стоящие под главной диагональю равны нулю. Преобразования
стараются производить так, чтобы на главной диагонали
появлялись единицы.
a11 a12
a 21 a 22
a
31 a32
a13
a 23
a33
b1
1 c 12
b2 0 1
0 0
b3
c 13
c 23
1
d1
d2
d3

35.

Метод Гаусса решения систем
линейных уравнений
5x 2y 4z 5
2x 3y z 7
3x y 2z 3
Ко второй строке
Запишем
прибавим третью строку,
расширенную
умноженную на (-5)
матрицу системы
( 2)
5 2 4 5 ( 2) 1 8 6 9 ( 3)
~
1 строке
7 прибавим
2 К3первой
~
2 3 1 7
строку,
3 1 вторую
3 1 2 3
2
3
умноженную
на (-2)
6
9 1Ко второй
8
6строке
9 ( 5)
1 8
прибавим
первую
строку,
вычтем
Из третьей строки
0 19 13на (-2),
25
~
0 19 13 25 ~ умноженную
вторую строку
строке
0 23 16 30
0 К третьей
4 первую
3 строку,
5
прибавим
умноженную на (-3).

36.

Метод Гаусса решения систем
линейных уравнений
( 1)
: 5
~
1 8 6 9 4 1 8 6 9
0
~
0 1 2
0 1 2 0
строке
0 4 3 5
0 К0третьей
прибавим
5
5
вторую строку,
умноженную на 4
1 8 6 9
Вторую строку умножим
на (-1), третью
строку
Восстановим
систему:
0 1 2 0
разделим на 5
0 0
1
1
x 8y 6z 9
x 9 8y 6z
x 9 16 6 1
y
2
z
0
y 2
y 2z 2
z 1
z 1
z
1
x 1 y 2
z 1

37.

Ранг матрицы
Рассмотрим прямоугольную матрицу размерностью (m x n).
a11 a12
a 21 a 22
a
a32
31
am1 am 2
a13
a 23
a33
am 3
a1n
aa1111 a12 aa131n
a 2n
a1112 aa121n
22aa 3121 a3222 aa233n
M33M
a3n M
a 2132 aa223n
aam311 aam322 a33mn
amn
Выделим в этой матрице произвольное число k строк и k столбцов.
Элементы матрицы А, стоящие на пересечении выделенных строк
и столбцов, образуют определитель k - того порядка.
Минором k-того порядка матрицы А называют определитель,
полученный из А выделением произвольных k строк и k столбцов.

38.

Ранг матрицы
Рангом матрицы называется наибольший порядок отличного от
нуля минора этой матрицы.
2 3 4 5
A 0 2 3 1
0 2 2 4
Матрица А имеет 4 минора 3 - его порядка,
например:
18 миноров 2 - го порядка, например:
2 3 4
0 2 3 20
0 2 2
2 3
4
0 2
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора
этой матрицы равен 3, поэтому: r ( A ) 3

39.

Ранг матрицы
Определитель, порядок которого равен рангу матрицы, называется
базисным минором. Он может быть не единственным.
Можно показать, что эквивалентные преобразования не меняют
ранга матрицы. Поэтому, когда требуется вычислить ранг матрицы,
ее приводят к треугольному виду.
Ранг матрицы равен числу ненулевых строк матрицы,
приведенной к треугольному виду
1 3 2 1 3 2 ( 2) 1 3 2
A 0 5 4 ~ 0 5 4
0 5 4
~
1 7 6
0 0 0
0 10 8
r( A ) 2

40.

Исследование систем линейных
уравнений
Теорема Кронекера - Капелли.
Для того, чтобы система линейных алгебраических уравнений
была совместна (имела решение ), необходимо и достаточно,
чтобы ранг расширенной матрицы
системы равнялся рангу
матрицы коэффициентов: r (B) r ( A )
Если r (B) r ( A ) n (числу неизвестных), то система
совместна и определенна (имеет единственное решение).
Если r(B) r( A ) n ,то система совместна и неопределенна
(имеет бесконечное множество решений).
Если r (B) r ( A ) ,то система несовместна (не имеет решений).
При решении систем линейных алгебраических уравнений нет
необходимости заранее вычислять ранги основной и расширенной
матриц. Их определение производится автоматически при
выполнении метода исключения Гаусса.

41.

Исследование систем линейных
уравнений
2x1 2x 2 2x 3 4
x1 x 2 x 3 0
3 x1 3 x 2 x 3 2
x1 x 2 3 x 3 2
1 1 1 2 ( 3) 1
0
1 1 1 0 V
~
0
3 3 1 2
0
1 1 3 2
2 2 2 4
:2
1 1 1 0
3 3 1 2 ~
1 1 3 2
1 1
2
0 2 2
0 4 4
0 4
4
: ( 2)
: ( 4)
V : 4
~

42.

Исследование систем линейных
уравнений
1
0
0
0
1
0
0
0
1
1
1
1
2 1
1 V 0
~
0
1
0
1
r(B) r( A ) 2
1
0
0
0
1
1
0
0
2
1
0
0
система совместна
n 3 - число неизвестных
r(B) n система неопределенна
n r 3 2 1 - число свободных переменных
Восстановим систему:
Пусть x 2 t.
x1 1 t
x1 2 t x 3 1 t
x 1 t x 3 2
x2 t
x3 1
x3 1
x 1
3

43.

Исследование систем линейных
уравнений
( 2)
1 2 4 1
2 1 5 1
~
1 1 1 3
1 2 4 1 1 2 4 1
~
0 3 3 3
0 3 3 3
0 3 3
0 0
2
0
5
r(B) 3
r( A ) 2
r(B) r( A ) система несовместна
x 2y 4z 1
2x y 5z 1
x y z 3

44.

Однородные системы линейных уравнений
Система линейных уравнений называется однородной, если все
свободные члены ее равны нулю.
a11x1 a12 x 2 a1n x n 0
a21x1 a22 x 2 a2n x n 0
am1x1 am2 x 2 amn x n 0
Однородная система всегда имеет решение:
x1 0
x 2 0 xn 0
Это решение называется тривиальным. Оно является
единственным решением системы в случае, когда r( A ) n
Если r( A ) n , то система имеет бесконечное множество
решений.

45.

Однородные системы линейных уравнений
Пусть: r ( A ) r n
Тогда система имеет r базисных переменных и n – r свободных
переменных.
Общее решение системы запишется в виде:
x1( t1,..., t n r )
...
x r ( t1,..., t n r )
X
t1
...
t
n r
Базисные переменные,
зависящие от свободных
переменных
Значения свободных
переменных
t1 xr 1; t 2 xr 2 ; tn r xn

46.

Однородные системы линейных уравнений
Выберем n - r частных решений однородной системы, полученных
из общего решения следующим образом: полагаем одно из
значений свободных переменных равным 1, а остальные равными
0 :
x1(1,0,..., 0)
x1(0,0,...,1)
x1(0,1,..., 0)
x r (0,0,...,1)
x r (1,0,..., 0)
x r (0,1,..., 0)
0
1
0
X
X1
X2
n r
0
0
1
1
0
0
Эти решения образуют фундаментальную систему решений
однородной системы (ФСР).

47.

Однородные системы линейных уравнений
( 2)
1 1 5 7 ( 3)
~
1
2 1 4
3 2 1 6
Найти фундаментальную систему решений:
x1 x 2 5 x 3 7 x 4 0
2x1 x 2 4 x 3 x 4 0
3 x 2x x 6 x 0
2
3
4
1
1 1 5 7 1 1 5 7 ( 1)
~
~
0 1 14 15
0 1 14 15
0 0
0 1 14 15
0
0
1 1 5 7
0 1 14 15
r( A ) 2
n 4
n r 4 2 2 - число свободных переменных

48.

Однородные системы линейных уравнений
Обозначим:
x 3 t1
x4 t2
(в качестве свободных переменных обычно берут те,
которые имеют 0 на главной диагонали)
x 1 x 2 5t 1 7t 2
x 1 x 2 5t 1 7t 2 0
x 2 14t1 15t 2
x 2 14t1 15t 2 0
x1 14t1 15t 2 5t1 7t 2 11t1 12t 2 Фундаментальная
система решений
x 2 14t1 15t 2
11t1 12t 2
14t1 15t 2
X
t1
t
2
11 решение
12
Общее
15
14
X2
X1
0
1
1
0