Similar presentations:
Линейная алгебра
1.
Линейнаяалгебра
2.
Лекцию читаетдоцент
кафедры математики и информатики
Романова
Юлия Станиславовна
3. Структура дисциплины
-линейная алгебра;-векторный анализ;
-аналитическая геометрия;
4. Список литературы
Письменный Д. Т. Конспект лекций по высшейматематике: Полный курс. М:Айрис-пресс,2009.
Кремер Н. Ш.и др. Высшая математика для
экономического бакалавриата : учебник и
практикум М. : Юрайт, 2012.
Шипачев В. С. Высшая математика : учебное
пособие для бакалавров. М. : Юрайт, 2012.
Данко П. Е. и др. Высшая математика в
упражнениях и задачах. Ч.1,2 –М.:Оникс:2008.
Романова Ю.С. Линейная алгебра: УМК, 2013
5. Системы линейных уравнений
6. Системой n линейных уравнений называются n уравнений, содержащих искомые переменные в первой степени
a11 x1 a12 x2 b1a21 x1 a22 x2 b2
Переменные, коэффициенты системы,
свободные члены, решение СЛУ, совместность,
определенная и неопределенная СЛУ
7.
Матрицей системы двух линейных уравненийназывается таблица чисел, составленная из
коэффициентов системы
a11 a12
A
a21 a22
Элементы М, порядок, квадратная М, главная
и побочная диагонали, определитель М 2-го
порядка
a11
a12
a21
a22
a11a22 a12 a21
8.
a11 x1 a12 x2 b1a21 x1 a22 x2 b2
b1
b2
a12
D1,
a22
D1
x1
;
D
a11 a12
D,
a21 a22
a11 b1
D2
a21 b2
D2
x2
.
D
Формулы Крамера для системы двух
линейных уравнений с двумя неизвестными
9.
Теорема Крамера1. Если определитель СЛУ отличен от нуля
D 0 , то система совместна и имеет
единственное решение, которое находится по
формулам Крамера.
D=0:
2. Если хотя бы один из определителей D1 или
D2 отличен от нуля, то система уравнений
несовместна.
3. Если оба определителя D1 =D2 =0, то СЛУ
имеет бесконечное множество решений.
10.
Пример.D
3
2
5 1
3x1 2 x2 12
5x1 x2 7
3 ( 1) 2 5 13.
D1
12
2
7 1
12 ( 1) 2 7 26;
D 2
D1 26
x1
2,
D 13
3 12
5
7
3 7 12 5 39.
D2 39
x2
3.
D 13
11.
Пример.x1 3x2 2
2 x1 6 x2 4
D
D1
D2
1 3
2
6
2 3
4
6
1
2
2 4
x1 2 3x2 ,
6 6 0;
12 12 0;
4 ( 4) 0.
x2 R.
12. Пример.
2 x1 3x2 2,4 x1 6 x2 7
Пример.
D
D1
2
3
4
6
2 3
7
6
2 6 ( 4) 3 0
12 21 33
Система несовместна
13.
a11 a12A a21 a22
a13
a23
a31 a32
a33
Минор элемента aik матрицы третьего порядка: M ik
a21
M 12
a31
a23
a33
14.
Алгебраическое дополнение элемента aik :Aik ( 1)
2 1
Пример.
A
A21 ( 1)
1 0
0 1
1;
M ik
0
1 3 1
2
2 1
i k
0
1
A33 ( 1)
3 3 2
1
1 3
5.
15.
Определитель матрицы третьего порядка:a11
a21
a12
a22
a13
a23 a11 A11 a12 A12 a13 A13
a31
a32
a33
Правило треугольника
+
-
16.
Пример. Вычислить определитель двумяспособами: по определению и по правилу
треугольника
2 1 1
1-й способ:
1
2 3
1
1 1
2 1
1
1
1
3 2 A11 ( 1) A12 1A 13 2( 1)
1 1
1
1 3 1 2
1 2 1 3
1( 1)
( 1)( 1)
1 1
1 1
2
1
1 1
2 1 1 2 1( 1) 3.
2 3
17.
2-й способ:2 1
1
1
2
1
1
3
1
2 2( 1) ( 1)( 3)1 1 1 1
1 2 1 ( 1)1( 1) 2( 3) 1
4 3 1 2 1 6 3
18.
Матрицы19.
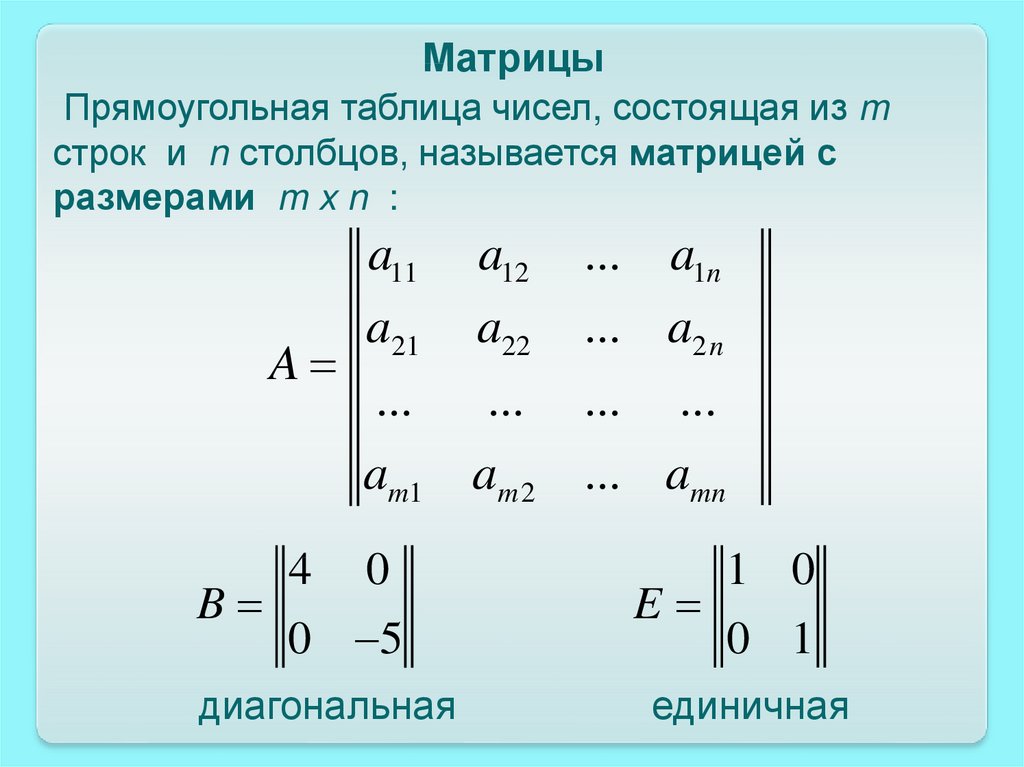
МатрицыПрямоугольная таблица чисел, состоящая из m
строк и n столбцов, называется матрицей с
размерами m x n :
a11
a21
A
...
am1
4 0
B
0 5
диагональная
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
E
1 0
0 1
единичная
20.
Операции с матрицами:-равенство;
-транспонирование;
3 2 4
A
1 0 2
-сложение;
-произведение на число;
-перемножение.
3
1
AТ 2 0
4
2
21.
Пример.3 2 4
1 3 2
A 3B
3
1 0 2
0 1 5
3 2 4 3 9 6
3 3 2 9 4 6
1 0 2 0 3 15
1 0 0 3 2 15
6 7 10
1 3 17
22.
Произведением матрицы A размера m n наматрицу B размера n p называется матрица C
размера m p :
cik ai1b1k ai 2b2 k aimbmk .
Пример. Вычислить произведение матриц А на
В и В на А.
A
2
3 0
3 1 1
1
,
2
B 0
3
2
1
23.
1B A 0
2
2
3
1
2 3 0
3 1 1
( 1) ( 2) 2 3 ( 1) 3 2 ( 1) ( 1) 0 2 1
0 ( 2) ( 3) 3 0 3 ( 3) ( 1) 0 0 ( 3) 1
2 ( 2) 1 3
2 3 1 ( 1)
8
5
2
9
3
3
1
5
1
2 0 1 1
24.
A B2
3 0
3 1 1
1
0
2
2
3
1
( 2) ( 1) 3 0 0 2 ( 2) 2 3 ( 3) 0 1
3 ( 1) ( 1) 0 1 2 3 2 ( 1) ( 3) 1 1
2 13
1 10
25.
Обратная матрица: A 1A A A A E.
1
1
Теорема. Для того, чтобы матрица А имела
обратную матрицу, необходимо и достаточно,
чтобы ее определитель был не равен нулю:
A11
1
1
A
A12
D( A)
A13
A21
A22
A23
A31
A32
A33
26.
Решение системы линейных уравненийматричным методом
a11 x1 a12 x2 a13 x3
a11 x1 a12 x2 a13 x3 b1
a21 x1 a22 x2 a23 x3 b2 .
a x a x a x b
31 1 32 2 33 3 3
a21 x1 a22 x2 a23 x3 b2 .
a31 x1 a32 x2 a33 x3
x1
a11 a12 a13
A a21 a22 a23 ,
A 1 A E ,
b1
X x2 , B b2 .
x3
a31 a32 a33
AX B,
b1
b3
A 1 AX A 1B,
EX X ,
X A 1B.
b3
27.
Пример. Решить систему уравнений матричнымметодом 7 x1 2 x2 3x3 13,
1
X A B
9 x1 3x2 4 x3 15 ,
5 x x 3x 14.
3
1 2
7
2
3
9
3
4 ;
5
1
3
7
2
3
D( A) 9
3
4 63 40 27 45 28 54 3.
5
1
3
A
x1
X
13
x2 ; B 15 .
x3
14
28.
A7
2
3
9
3
4
5
1
3
1 1
A11 ( 1)
A12 ( 1)1 2
1 3
A13 ( 1)
A21 ( 1)
2 1
A22 ( 1)
A23 ( 1)
2 3
1 3
2 2
2 3
(6 3) 3;
7 3
5 3
7 2
5 1
21 15 6;
(7 10) 3;
3 4
1 3
9 4
5 3
9 3
5 1
A31 ( 1)
3 1
A32 ( 1)
A33 ( 1)
3 2
3 3
9 4 5;
(27 20) 7;
9 15 6;
2 3
8 9 1;
3 4
7 3
(28 27) 1;
9 4
7 2
21 18 3.
9 3
29.
5 3 1A
1
1
7
3
6
6 1 .
3
3
5 3 1
1
X A B 7
3
6
1
65 45 14
13
6 1 15
3
3
14
6
2
1
1
91 90 14
15 5 .
3
3
78 45 42
9
3
x1 2, x2 5, x3 3.
30. Самостоятельная работа
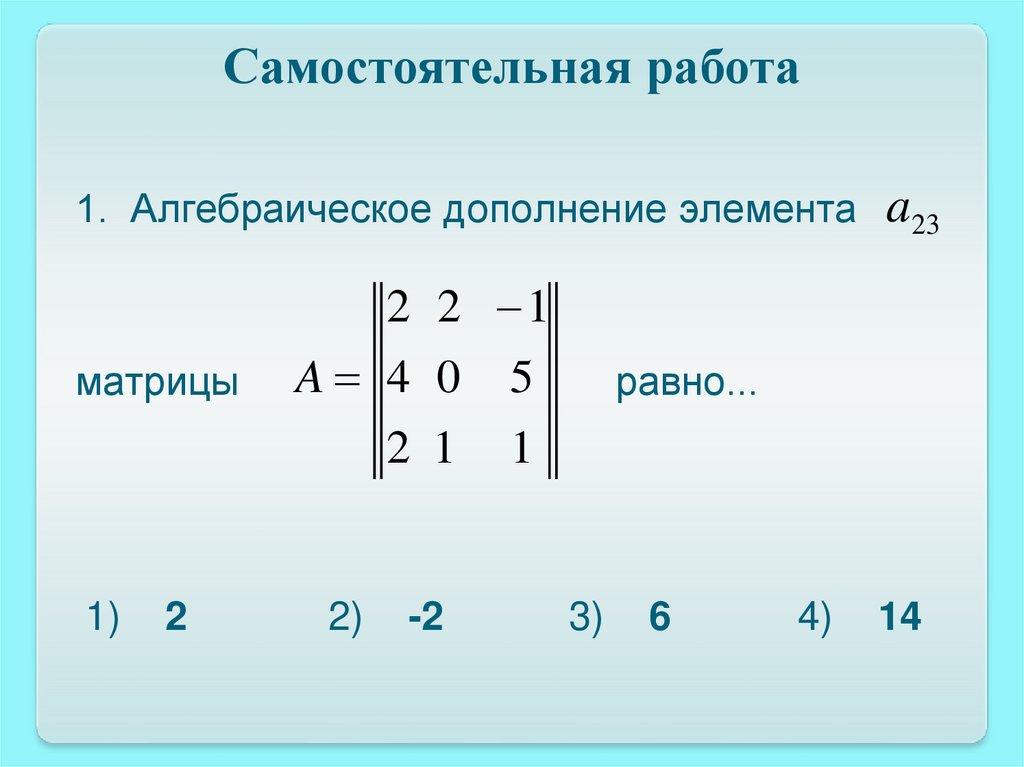
1. Алгебраическое дополнение элементаматрицы
2 2 1
A 4 0 5
2 1
1)
2
2)
-2
a23
равно...
1
3)
6
4)
14
31.
Самостоятельная работа3 1
2. Определитель
1)
-1
2)
2
-5
равен .....
1
3)
5
4)
1
3. Если определитель системы не равен нулю,
то система имеет…..
1) единственное решение;
2) бесконечное число решение;
3) не имеет решений;
4) два решения.
*
32. Самостоятельная работа
4. МатрицаA
1 1
0 1
1) квадратной;
3) нулевой;
5. С матрицами
является.....
2) единичной;
4) диагональной
A
5
2
3
4
и
можно выполнить операцию......
1) A+ В
3) А х В
2) А - В
4) В х А
B
0
1
33. Самостоятельная работа
6. Решение матричного уравненияимеет вид......
B
1) X
A
A X B
1
2) X B A
1
3) X A B
4) X A B
1































 mathematics
mathematics








