Similar presentations:
Линейная алгебра и аналитическая геометрия. Дифференциальное исчисление
1.
Преподаватель:Филипенко Николай Максимович
доцент кафедры
Высшей математики и математической физики ТПУ
2.
3.
http://mph.phtd.tpu.ruИли
http://mph.phtd.tpu.ru/methmat.php
4.
Учебно-методическое обеспечение дисциплиныОсновная литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. Том 1. М.: Наука, 1985. - 429с.
2. Ильин В.А., Поздняк Э.Г. Линейная алгебра. - М.: Наука, 1985
3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука,
1998.
5. Апатенок Р.Ф., Маркина А.М. и др. Элементы линейной алгебры и
аналитической геометрии. - Минск: Высшая школа, 1986.
6. Берман Г.Н. Сборник задач по курсу математического анализа. М.:
Наука, 1985.
Дополнительная литература (Задачники с решениями).
1.Каплан И.А. Практические занятия по высшей математике. -Харьков:
ХТУ, 1974.-ч.1
2. Сборник задач по курсу высшей математики( под ред. Г.Н. Кручковича ),
М. Наука, 1973г.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
примерах и задачах. –М. : ВШ, 1980.-ч.1
4. Терехина Л.И., Фикс И.И. Линейная алгебра и аналитическая геометрия.
2008, 2009, ….
5.
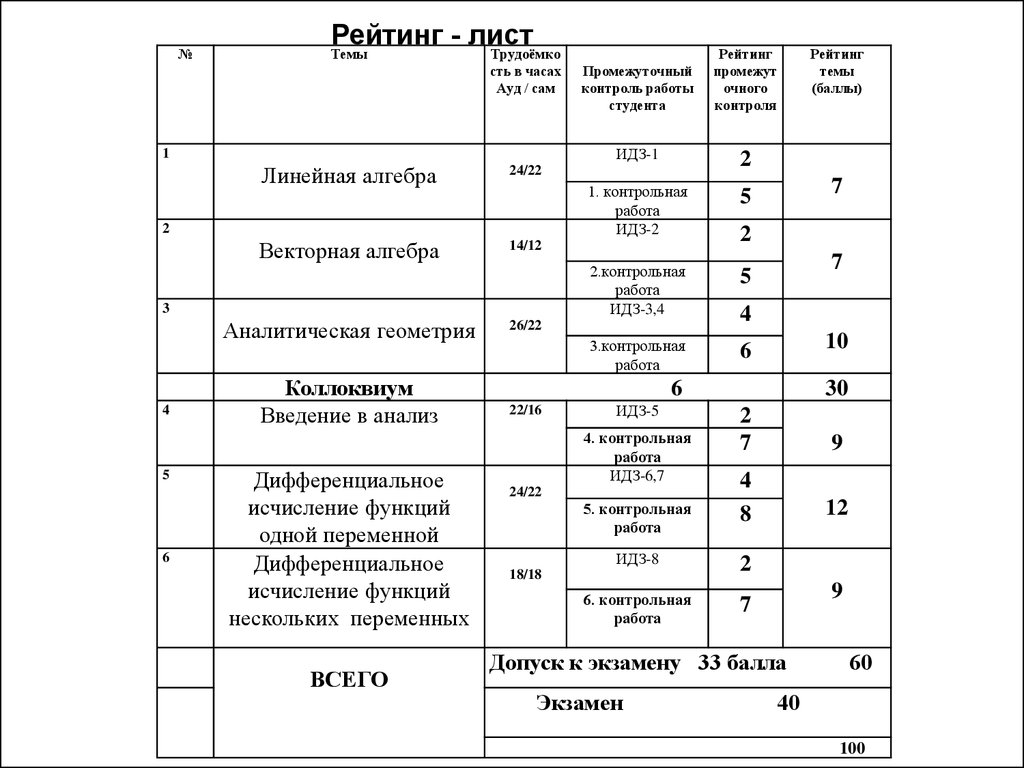
№Рейтинг - лист
Темы
Трудоёмко
сть в часах
Ауд / сам
1
Линейная алгебра
Аналитическая геометрия
4
5
6
Коллоквиум
Введение в анализ
Дифференциальное
исчисление функций
одной переменной
Дифференциальное
исчисление функций
нескольких переменных
ВСЕГО
2
1. контрольная
работа
ИДЗ-2
5
2.контрольная
работа
ИДЗ-3,4
5
3.контрольная
работа
6
14/12
3
Рейтинг
промежут
очного
контроля
ИДЗ-1
24/22
2
Векторная алгебра
Промежуточный
контроль работы
студента
26/22
7
2
7
4
10
6
22/16
ИДЗ-5
4. контрольная
работа
ИДЗ-6,7
24/22
5. контрольная
работа
30
2
7
9
4
8
12
ИДЗ-8
2
6. контрольная
работа
7
18/18
9
Допуск к экзамену 33 балла
Экзамен
Рейтинг
темы
(баллы)
60
40
100
6.
• Матрицы, действия над ними.Рассмотрим систему двух
a x a x b
11 1
12 2
1
инейных алгебраических
равнений с двумя неизвестными: a21x1 a22 x2 b2
ешением такой системы называется
ара значений: x b1a22 b2a12 , x b2a12 b1a21 .
1
a a a a
11 22
21 12
2
a22
a12
a21
a11
a a a a
11 22
21 12
одстановка которых вместо x1 и x2 обращает оба уравнения в
тождества. Видно, что решение зависит от знаменателя. Если
н неравен 0, то мы получим единственное решение для x1 и x2 .
наменатель получаем в результате действий с
коэффициентами при неизвестных, из которых можно
составить таблицу:
a11 a12
a
a
21 22
сли мы будем иметь более сложную систему уравнений, с
большим количеством неизвестных и уравнений, то
7.
система линейных уравненийa11 x1 a12 x2 ... a1n xn b1
имеет вид:
a21 x1 a22 x2 ... a2 n xn b2
Таблица, составленная из
.........................................
коэффициентов при неизвестных,
am1 x1 am 2 x2 ... amn xn bm
называется матрицей.
Определение: матрицей размером m на n называется
прямоугольная таблица чисел или буквенных выражений,
состоящая из m строк и n столбцов.
a11 a12 ... a1n
Для данной системы основная матрица:
a 21 a 22 ... a 2 n
обозначается большой буквой A.
A
...
... ... ...
Числа aij , образующие матрицу,
называются элементами матрицы.
a m1 a m 2 ... a mn
Частные виды матриц: строка, столбец, квадратная,
диагональная, единичная, треугольная, ступенчатая и др.
8.
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
• Системой m линейныхуравнений с n неизвестными
называется система вида:
• Матрицей размером m на n
называется прямоугольная таблица
чисел или буквенных выражений,
состоящая из m строк и n столбцов.
Для данной системы основная
матрица обозначается большой
буквой A. Числа aij, образующие
матрицу, называются элементами
матрицы.
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1 22 2
2n n
2
...........................................
am1 x1 am x2 ... amn xn bm .
2
a11 a12 ....a1n
a21 a22 ....a2 n
A
..................
a a ....a
m1 m 2 mn
В матричной форме систему можно
записать в виде : AX B.
10.
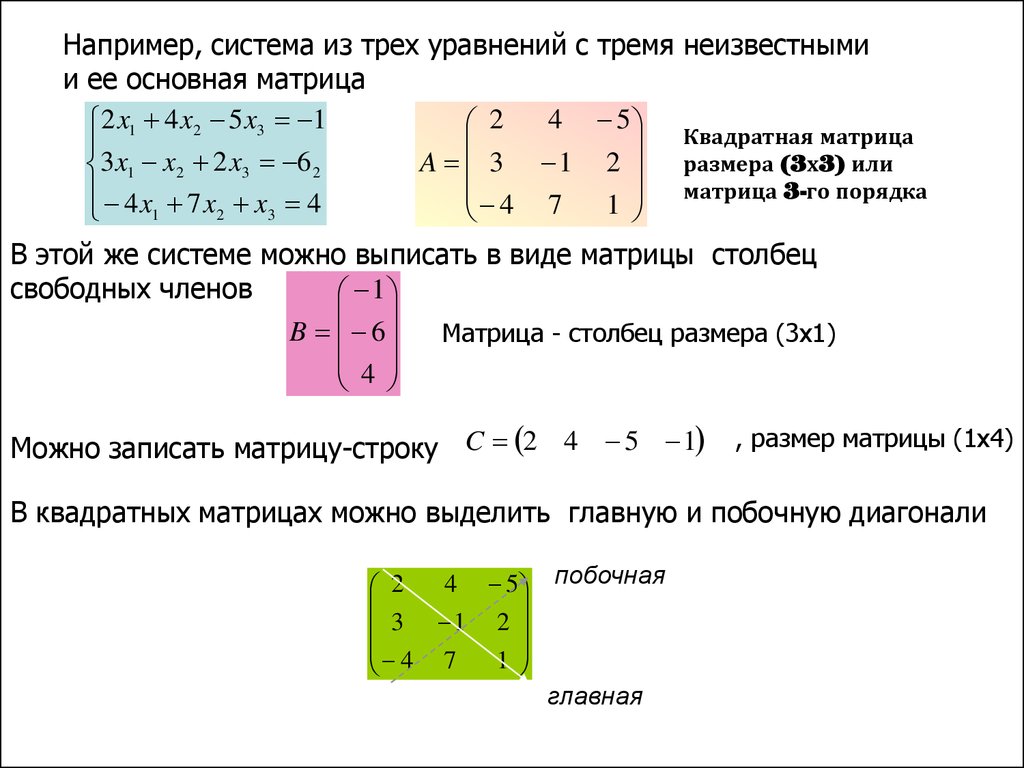
Например, система из трех уравнений с тремя неизвестнымии ее основная матрица
4 5
2 x1 4 x2 5 x3 1
2
Квадратная матрица
A 3 1 2 размера (3х3) или
3 x1 x2 2 x3 6 2
4 7
матрица 3-го порядка
4x 7x x 4
1
1
2
3
В этой же системе можно выписать в виде матрицы столбец
свободных членов
1
B 6
Матрица - столбец размера (3х1)
4
Можно записать матрицу-строку C 2 4 5 1
, размер матрицы (1х4)
В квадратных матрицах можно выделить главную и побочную диагонали
4 5 побочная
2
3
1
2
4 7
1
главная
11.
СуммойA B
- матриц A и B называется матрица C размера m n , каждый
элемент которой равен сумме соответствующих элементов матриц A и B :
cij aij bij ,( i 1,2, , m; j 1,2, , n ).
Произведением A матрицы A на число называется матрица B,
которая получается из матрицы A умножением всех элементов на :bij aij .
Например: A B 3 2 3 4 3 3 2 4 6 2
5 2 2 5 5 2 2 5 7 3
3 2 2 3 2 2 6 4
2A 2
2 5 2 2 10 4
5
2
Умножение матриц возможно, если число столбцов n матрицы A равно
числу столбцов n матрицы B.
Правило умножения: При умножении матриц каждый элемент
матрицы произведения находится как сумма произведений элементов
строки первой матрицы на соответствующие элементы столбца второй
матрицы.
Например:
3 2 3 4 3 3 2 2 3 4 2 5 5 2
A B
2 5 5 3 2 2 5 4 2 5 11 10
5
2
12.
13.
Для квадратных матриц можно вычислить определитель.Определитель квадратной матрицы есть некоторое число, которое
вычисляется по элементам матрицы согласно правилу, которое будет
сформулировано после введения понятий миноров и алгебраических
дополнений элементов определителя.
Минором элемента определителя называется определитель,
полученный после вычеркивания из исходного строки и столбца,
на пересечении которых стоит этот элемент.
Алгебраическое дополнение элемента – это минор этого элемента,
взятый со знаком (+), если сумма номеров строки и столбца,
на которых находится элемент – четная,
и со знаком (-), если эта сумма – нечетная.
2
M 11 3
4
2
M 23 3
4
5
4
1
2
7
1
4
5
1
2
7
1
2
1 2
7
1
4
4 7
A11 ( 1)
1 1
M 11
A23 ( 1) 2 3 M 23
1 2
7
1
2
4
4 7
M 11
M 23
14.
Вычисление определителей1. Определитель 1-го порядка равен самому элементу
1 a11 a11
1 2 2,
Например:
1 7 7
2. Определитель 2-го порядка находится по правилу
2
a
b
c
d
a d b c
Определитель 2-го порядка равен разности произведений
элементов главной и побочной диагонали.
2
2 3
4
Например:
2
5
2 5 ( 3) 4 10 ( 12) 10 12 22
6 2
3
7
( 6) 7 ( 2) ( 3) 42 6 48
15. Определитель 3-го порядка.
a11 a12a13
a21 a22 a23 a11a22 a33 a21a32 a13 a12 a23 a31 a31a22 a13
a31 a32 a33
a21a12 a33 a32 a23 a11.
a11 a12
a 21 a 22
a
31 a32
a13
a 23
a 33
" "
a11 a12
a 21 a 22
a
31 a 32
a13
a 23
a 33
" "
.
5 1 2
3 2
1 3
4 5 2( 1) 1 4 1 3 3( 2) 1 2( 2) 3 1( 1)
1
3 4 5 10 4 18 4 3 60 77.
16.
Определитель 3-го можно найти путем разложенияопределителя по элементам строки или столбца.
При этом используется
Основное правило вычисления определителя:
Определитель равен сумме произведений элементов
какой-либо строки или столбца
на соответствующие им алгебраические дополнения
Например, разложение определителя по элементам 1-ой строки
будет иметь вид
a11 a12 a13
a21 a22 a23 a11 A11 a12 A12 a13 A13
a31 a32 a33
a11 ( 1)
1 1
a22 a23
a32 a33
a12 ( 1)
1 2
a21 a23
a31 a33
a13 ( 1)
1 3
a21 a22
a31 a32
17.
Теорема Лапласа. Определитель равен сумме произведений всехэлементов любой строки (столбца) на их алгебраические
дополнения.
18.
Пример вычисления определителя путем разложенияпо элементам первой строки:
1 4
2
2 1 ( 1)
1 1
5
3
4
1
6
3
2
1
6
( 4) ( 1)
1 2
5 2
4
6
2 ( 1)
1 3
5
3
4 1
(3 6 ( 2) ( 1)) 4 (5 6 ( 2) 4) 2 (5 ( 1) 3 4)
(18 2) 4 (30 8) 2 ( 5 12) 16 152 34 134
Наиболее простым, очевидно, является разложение определителя
по элементам того ряда, в котором все элементы, кроме одного,
равны нулю
Например, следующий определитель наиболее просто разложить
по элементам 2-й строки
5
3
1 4
0
0 3 ( 1)
6 2 7
2 1
1 4
2 7
0 0
3 (( 1) 7 ( 2) 4) 3 ( 7 8) 3 1 3
19. 2. Свойства определителей
1) При транспонировании матрицы её определительне меняется.
2) При перестановке любых двух строк (столбцов)
определитель меняет знак.
3) Общий множитель элементов любой строки
(столбца) можно выносить за знак определителя.
4) Если все элементы k-й строки определителя |A|
являются суммами двух элементов,
то определитель равен
сумме двух определителей |A1| и |A2|,
у которых все строки, кроме k-й, совпадают со
строками определителя |A|,
k-я строка в определителе |A1| состоит из первых
слагаемых,
а в определителе |A2| – из вторых слагаемых.
20.
5) Определитель равен нулю если:а) он имеет строку (столбец), состоящую из
нулей;
б) он имеет хотя бы две одинаковые строки
(столбца);
в) он имеет хотя бы две пропорциональные
(т.е. отличающиеся множителем) строки (столбца);
aij 1 ai1 j 2 ai2 j k aik j , j 1, n
г) хотя бы одна строка (столбец) является
линейной
комбинацией нескольких других строк
(столбцов).
( a ji 1 a ji1 2 a ji 2 k a ji k , j 1, n )
21.
• 6) Определитель не изменится,если к каждому элементу i-й строки
(столбца) прибавить
соответствующий элемент k-й
строки (столбца),
умноженный на число α 0.
22.
Согласно свойству определителей: Величина определителяне изменится, если к элементам какого-либо ряда прибавить
соответствующие элементы другого ряда, предварительно
умноженные на число.
1
2
3
4
1
2
3
4
2
3
4
1
2 2
4 3
6 4
8 1
3
1
2
5
3 3
6 1
9 2
12 5
4
3
1
2
4 4
8 3
12 1
16 2
1
2
3
4
0
1
10
9
0
7
7
17
0
5
13
18
1
7 7
5 5
10
1
10
1 ( 1) 2 7
7
5
9
9
17
13
1
18
10
9
70 7
63 17 0
63
46
50 13
45 18
37
27
( 1) ( 1)
2
63
46
37
27
(1701 1702) 1
0
( 63 ( 27) ( 46) ( 37))
23. § Обратная матрица
ОПРЕДЕЛЕНИЕ. Обратной к матрице Aназывается матрица, обозначаемая A-1,
такая, что A·A-1=A-1 · A=E.
СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
1) Если матрица A имеет обратную, то A и
A-1 – квадратные матрицы одного порядка.
2) Если обратная матрица существует, то
она единственная.
3) Если матрица A имеет обратную, то
определитель матрицы A отличен от нуля.
Квадратная матрица, определитель которой
отличен от нуля, называется невырожденной.
24. ТЕОРЕМА. Пусть A – квадратная матрица. Матрица A имеет обратную тогда и только тогда, когда её определитель |A| отличен от нуля. Причем обратн
ТЕОРЕМА. Пусть A – квадратная матрица. МатрицаA имеет обратную тогда и только тогда, когда её
определитель |A| отличен от нуля. Причем обратная
матрица A-1 может быть найдена по формуле:
A
s
1
1
ST
A
где
– матрица из алгебраических дополнений
элементов матрицы A, т.е.
A A
A
T
12
1n
11
A
A
A
22
2n
S 21
A
n1 A n 2 A nn
Матрица S
называется союзной
(или присоединенной, или взаимной) для матрицы A.
25. Схема нахождения обратной матрицы
1) Находится определитель матрицы.
Если он отличен от нуля det A ,0то обратная матрица существует.
• 2) Составляется союзная матрицаA * , элементами которой являются
алгебраические дополнения элементов исходной матрицы.
• 3) Полученную союзную матрицу транспонируем, т.е. меняем ролями
строки и столбцы матрицы. Получаем матрицу A*T .
• 4) Матрицу A*T делим на определитель матрицы и получаем обратную
матрицу. (При делении матрицы на число все ее элементы нужно
разделить на это число)
1
A
A*T
det A
1
Рассмотрим примеры.
2 3
4
5
1. Найти матрицу, обратную данной A
1)
det A
2 3
4
5
5 4
2) A*
3 2
2 5 ( 3) 4 22
*T
3) A
5 3
4 2
1 5 3
1
A
4)
22 4 2
26. Нахождение обратной матрицы
2. Найти матрицу, обратную данной1) Находим определитель матрицы
2
4 5
18 0 1
3
4
4 5
2
A 3 1 2
4 1 1
1 2 1
0
3 1 ( 1) 3 2
4
1
1
1
1
18
1 3
2) Составляем союзную матрицу
3 2
1 2
3
2
A12 ( 1)
(3 8) 11
A11 ( 1)
1 2 3
4 1
1 1
A21 ( 1)
3
A31 ( 1) 4
4 5
1 1
4
(4 5) 1 A22 ( 1)
4
5
1 2
8 5 13 A32 ( 1) 5
3 11 1
*
A 1 22 18
13 11 14
2
5
4 1
2 5
3 2
1
(18 3 1) 55 0
Т.о. обратная матрица существует.
A13 ( 1) 4
2 20 22 A23 ( 1)
5
3
1
4
1
2
4
4 1
(4 15) 11 A33 ( 1) 6
2
3 4 1
(2 16) 18
4
3 1
2 12 14
3) Полученную матрицу транспонируем 4) Обратная матрица
1
13
1
13
3
3
1
A*T 11 22
11
A 1 11 22
11
55
1 18 14
1 18 14
27. Матричные уравнения
Матричные уравнения – это уравнения, в которых участвуюткак известные матрицы, так и неизвестная матрица, которую
и нужно найти. Существуют два основных типа матричных уравнений.
1 тип (левое умножение)
A X B
A 1 A X A 1 B
E X A 1 B
X A 1 B
2 тип (правое умножение)
X A B
X A A 1 B A 1
X E B A 1
X B A 1
В виде матричного уравнения A X B может быть
записана
система линейных уравнений, решение которой
1
X A B
существует, если определитель основной
матрицы отличен от нуля.
Если в системе количество уравнений и неизвестных разное,
то нельзя говорить об определителе основной матрицы и решать
систему матричным методом нельзя.
Для решения таких систем применяется метод Гаусса



























 mathematics
mathematics








