Similar presentations:
Тесты смудс демо. Линейная алгебра 020. Системы линейных уравнений
1.
ТЕСТЫ СМУДСДЕМО
Линейная алгебра
020. Системы линейных уравнений
2.
2 Системы линейных уравнений(Число заданий в тесте – 3)
• Основные понятия: совместность, решение, общее
решение, однородная СЛУ (ОСЛУ), неоднородная
СЛУ (НСЛУ)
• Правило Крамера решения СЛУ
• Признак совместности СЛУ (теорема КронекераКапелли)
• Решение СЛУ методом Гаусса, понятия базисных и
свободных переменных
• Структура общего решения НСЛУ
• Структура общего решения ОСЛУ, фундаментальная
система решений
• Формы записи: стандартная, матричная
3.
Правило Крамера решения СЛУ3x y 2 z 7
Решить систему: x 2 y z 4
2 x 3 y 2 z 7
2
1
0
4.
Правило Крамера решения СЛУРешить систему уравнений а) методом Крамера; б) методом
Гаусса; в) методом обратной матрицы
2 x y z 2,
3 x 2 y 2 z 2,
x 2 y z 1.
(2; 1; 3)
5.
Правило Крамера решения СЛУx 2 y 3z 5,
2 x y z 1,
x 3 y 4 z 6.
(1; 1;2)
6.
Правило Крамера решения СЛУ3x y 2 z 0,
2 x 3 y 5 z 0,
x y z 0.
(0;0;0)
7.
Правило Крамера решения СЛУРешить систему:
3x 5 y z 7
x 4 y 5 z 12
2 x y 3z 10
1
3
5
8.
Правило Крамера решения СЛУРешить систему:
2 x 3 y z 5
3x y 2 z 7
4 x 2 y 2 z 2
1
2
3
9.
Правило Крамера решения СЛУ10.
11.
12.
Правило Крамера решения СЛУСумма корней x1 x2 x3 системы линейных уравнений
x 2 x3 4
x1 2 x2 x3 2
2 x1 x3 7
равна….
13.
Правило Крамера решения СЛУСумма корней x1 x2 x3 системы линейных уравнений
x1 x3 1
2 x1 x2 x3 5
x 2 x 3
3
1
равна….
14.
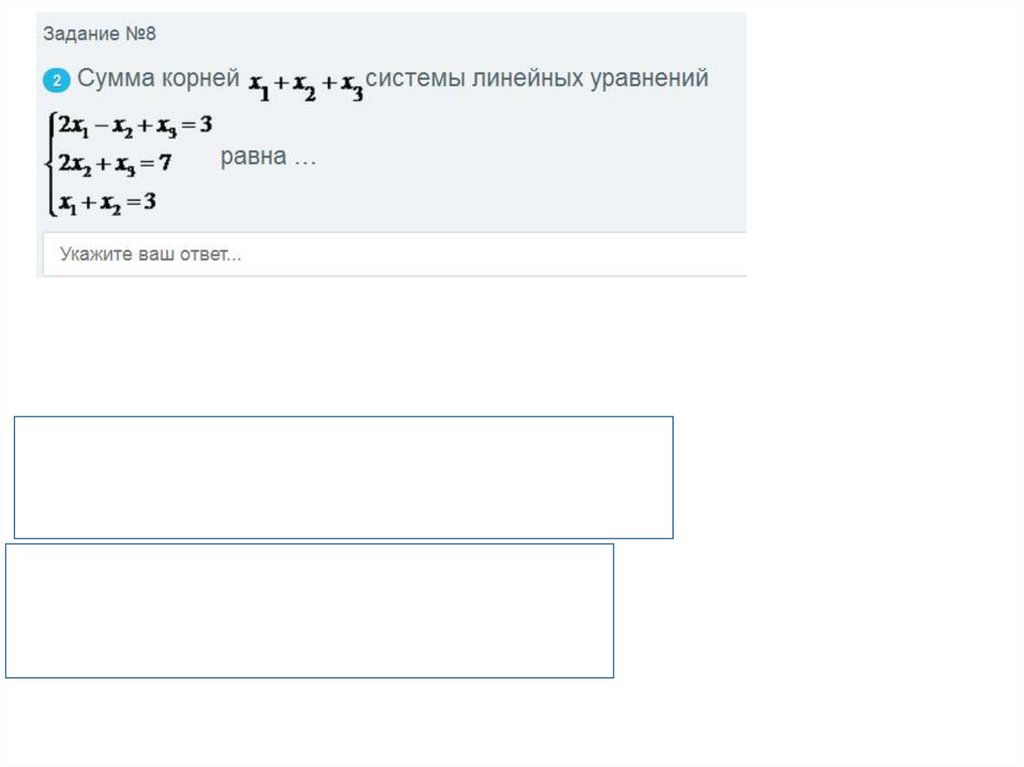
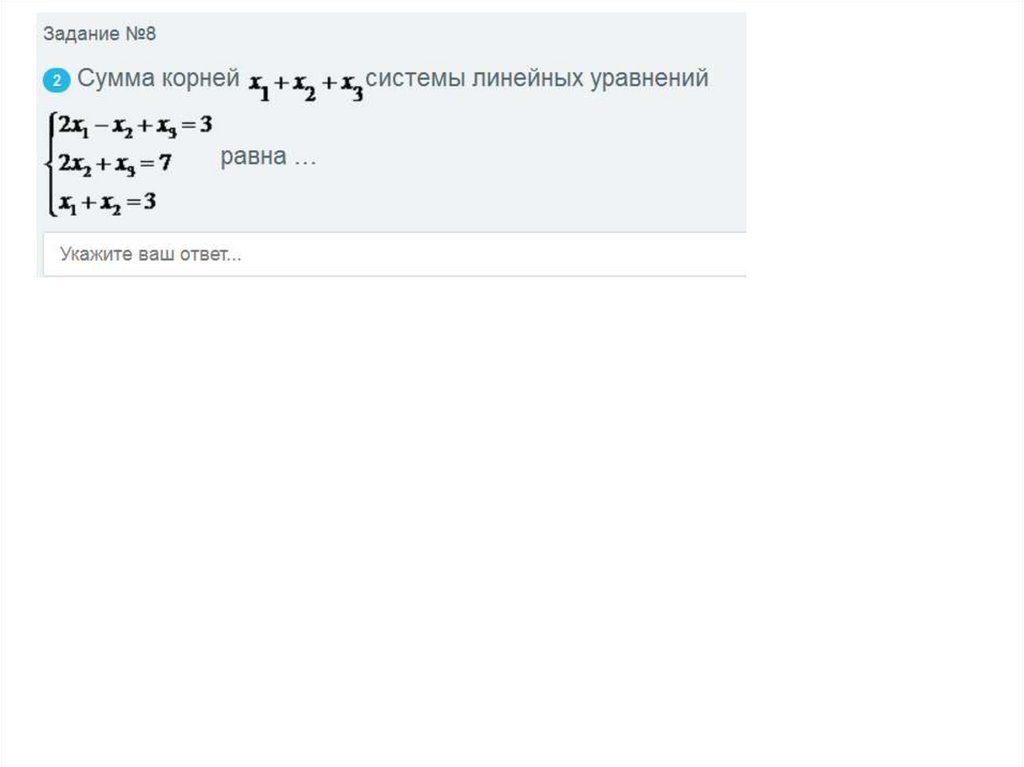
Правило Крамера решения СЛУСумма корней x1 x2 x3 системы линейных уравнений
равна….
-4
15.
16.
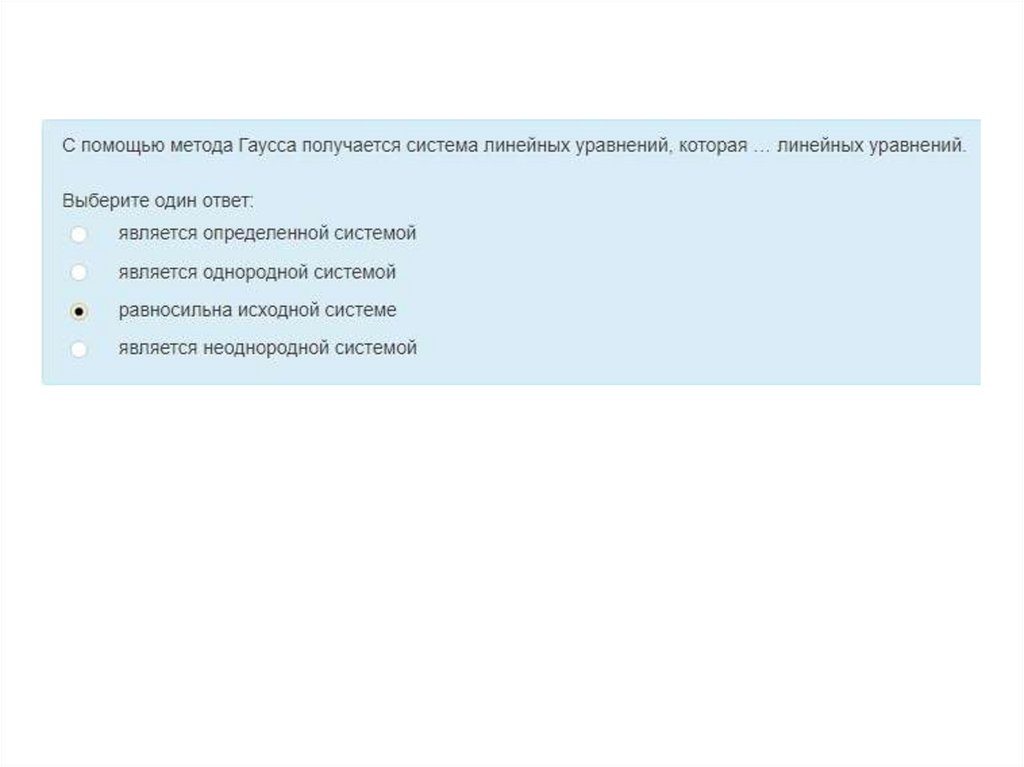
Решение СЛУ методом Гаусса, понятиябазисных и свободных переменных
Системы m линейных уравнений с n неизвестными
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
am1 x1 am 2 x2 amn xn bm
A X B
,
a11
a
21
...
am1
a12
a22
...
am 2
... a1n
... a2 n
... ... - основная матрица системы,
... amn
a11
a
A 21
...
am1
a12
a22
...
am 2
... a1n b1
... a2 n b2
... ... ... - расширенная матрица системы,
... amn bm
17.
Решение СЛУ методом Гаусса, понятиябазисных и свободных переменных
b1
x1
b2
x
2
... - столбец свободных членов.
... - столбец неизвестных,
bm
xn
Система неоднородная, если матрица B не является
нуль матрицей , однородная, если B .
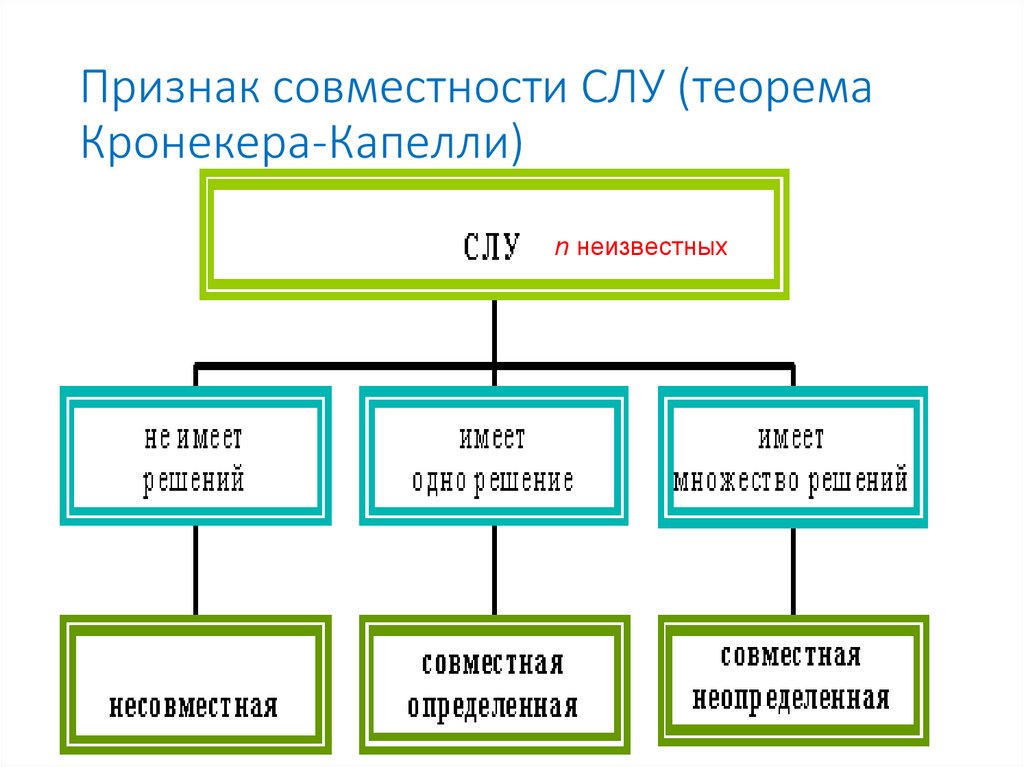
Система совместная, если она имеет решения,
несовместная - в противном случае.
Система определенная, если она имеет единственное решение,
неопределенная, если она имеет бесконечное множество решений.
18.
Признак совместности СЛУ(теорема Кронекера-Капелли)
Теорема Кронекера Капелли
Для того, чтобы система m
линейных уравнений с n
неизвестными была совместной, необходимо и достаточно, чтобы
rang ( ) rang .
19.
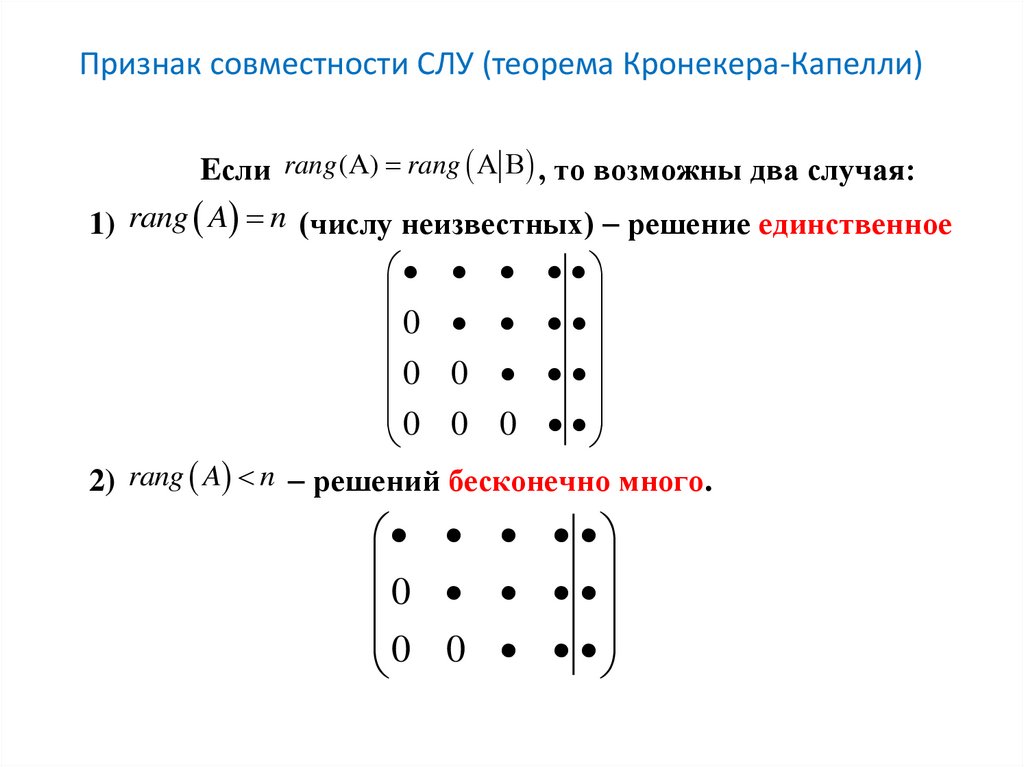
Признак совместности СЛУ (теорема Кронекера-Капелли)Eсли rang ( ) rang , то возможны два случая:
1) rang A n (числу неизвестных) решение единственное
0
0
0
0
0
0
2) rang A n решений бесконечно много.
0
0 0
20.
Признак совместности СЛУ (теоремаКронекера-Капелли)
n неизвестных
.
21.
Признак совместности СЛУ (теоремаКронекера-Капелли)
Система линейных уравнений
совместна при
o =-3
o -3
o =-2
o -2
o любом значении
x1 x2 x3
x x x 1
1
2
3
x1 x2 x3 1
22.
Признак совместности СЛУ (теоремаКронекера-Капелли)
23.
Признак совместности СЛУ (теоремаКронекера-Капелли)
24.
Признак совместности СЛУ(теорема Кронекера-Капелли)
25.
Решение СЛУ методомГаусса, понятия базисных
и свободных переменных
Структура общего решения НСЛУ
26.
27.
Общее решение неоднородной системы имеет вид:x1 c1 , c2 , ..., cn r
x2 c1 , c2 , ..., cn r
...........................
X xr c1 , c2 , ..., cn r
c
1
...
cn r
Если свободным неизвестным придавать поочередно значение 1,
полагая остальные равными 0, то из общего решения получаем
фундаментальную систему решений:
Х1 , Х 2 ,........, Х n r ,
28.
x1 (1, 0, ..., 0)x1 (0, 1, ..., 0)
x1 (0 , 0 , ..., 1)
x
(1
,
0
,
...,
0)
x
(0
,
1
,
...,
0)
x
(0
,
0
,
...,
1)
2
2
2
....................
....................
...................
xr (1, 0, ..., 0)
xr (0, 1, ..., 0)
xr (0, 0, ..., 1)
Х1
, Х2
, ..... Х n r
1
0
0
0
1
0
...
...
...
0
0
1
X c1 ,c2 ,...cn r c1 Х1 c2 Х 2 ... cn r Х n r
29.
Структура общего решения НСЛУТеорема о структуре общего решения
неоднородной системы линейных уравнений
Общее решение совместной неоднородной системы
линейных уравнений равна сумме какого-либо ее
частного решения и общего решения однородной
системы, соответствующей данной неоднородной.
Х Х 0 c1 Х1 c2 Х 2 ... cn r Х n r
Частное решение неоднородной системы можно
получить, приравняв нулю все свободные
неизвестные. Такое решение называется базисным
решением (в выбранном базисе).
30.
31.
Структура общего решенияНСЛУ
Решите систему
x1 4 x2 2 x3 1,
2 x1 3x2 x3 5 x4 7,
3x 7 x x 5 x 8.
2
3
4
1
Задача 1
32.
Структура общего решения НСЛУx1 4 x2 2 x3 1,
Решение задачи 1 2 x1 3x2 x3 5 x4 7,
3x 7 x x 5 x 8.
2
3
4
1
Рассмотрим расширенную матрицу системы:
1 4 2 0 1
1 4 2 0 1
2 2 1
( A B) 2 3 1 5 7 ~
0 5 5 5 5 ~
3 7 1 5 8 3 3 1 0 5 5 5 5
33.
Структура общего решения НСЛУРешение задачи 1
1 4 2 0 1
1 0 2 4 5
~ 3 2 0 1 1 1 1 ~ 1 4 2 0 1 1 1 1
0 0 0 0 0
0 0 0 0 0
Следовательно,
r ( ) r ( A B) 2, r(A)<n,
поэтому система совместна и не определена. Ранг равен
2, поэтому 2 базисных и 4-2=2 свободных переменных, а
также 2 строки ФСР.
34.
Структура общего решения НСЛУРешение задачи 1
Выберем в качестве базисных неизвестных
x1
и
x2
и запишем преобразованную систему:
35.
Структура общего решения НСЛУРешение задачи 1
,
x1 5 2 x3 4 x4 ,
x2 1 x3 x4 .
Полагая х3 = , х4 = , где и
произвольные числа,
получаем общее решение системы:
36.
Структура общего решения НСЛУФормы записи: стандартная,
матричная, векторная
Решение задачи 1
x1 5 2 4 5
2 4
x2 1 1
1 1
X
x3
0
1
0
0
0 1
x4
или
X 5, 1,0,0 2,1,1,0 4,1,0,1
37.
Формы записи: стандартная,матричная, векторная
Векторная форма общего решения НСЛУ с
расширенной матрицей 1 2 3 3
(1, 2,0) ( 1,2,1)
(1,0,1) ( 1,2,1)
(0,0,1) ( 1,2,1)
(0,0,1) (1,2,1)
1 1 1 1
3 4 5 5
38.
Формы записи: стандартная,матричная, векторная
Смотрим, какое из частных решений НСЛУ подходит для данной системы.
39.
Решение СЛУ методом Гаусса, понятиябазисных и свободных переменных
задача 2 Найти общее решение системы
линейных уравнений
x1 2 x2 4 x3 3x4 1
3x1 5 x2 6 x3 4 x4 2
2 x 3x 2 x x 1.
2
3
4
1
40.
Решение СЛУ методом Гаусса, понятия базисныхи свободных переменных
Решение задачи 2
Эквивалентная система содержит два уравнения:
x1 2 x2 4 x3 3 x4 1
3 x1 5 x2 6 x3 4 x4 2.
В качестве главных (базисных) неизвестных возьмем x1 , x2 . Тогда x3 , x4 свободные неизвестные.
1. Найдем частное решение системы, приравняв свободные
неизвестные нулю:
41.
Решение задачи 2x1 2 x2 1
3 x 5 x 2
1
2
x3 0
x4 0,
Решение e0 ( 1,1,0,0) - базисное решение в базисе из неизвестных ( x1 , x2 ).
Это частное решение данной системы.
42.
43.
e1 (8, 6,1,0).- первое решение фундаментальной системы решений.
44.
Второе решение из ФСР найдем, взяв x3 0, x4 1:x1 2 x2 3
3 x1 5 x2 4,
3 2
1 3
1, 1
7, 2
5,
4 5
3 4
x1 7, x2 5
e1 ( 7,5,0,1).
Фундаментальная система решений однородной системы линейных
уравнений найдена.
Общее решение однородной системы, соответствующей данной неоднородной
системе, имеет следующий вид:
c1e1 c2e2 ,
где c1 , c2 - произвольные постоянные.
45.
46.
Решение СЛУ методом Гаусса, понятия базисныхи свободных переменных
Задача 3. Исследовать совместность и найти общее
решение системы:
x 2 y z 4,
2 x 3 y z 3,
4 x y z 11.
x C,
y 7 3C ,
z 18 7C ,
C R.
47.
Решение СЛУ методом Гаусса, понятия базисныхи свободных переменных
№ 4. Исследовать совместность и найти общее решение
системы:
3x1 2 x2 x3 1
x 3x 2 x 5
1
2
3
5 x1 8 x2 3x3 11
x1 x2 1
48.
Решение СЛУ методом Гаусса, понятия базисныхи свободных переменных
№ 5 Исследовать совместность и найти общее решение
системы:
x1 x2 x3 2 x4 1
x1 x2 2 x3 x4 2
5 x 5 x 8 x 7 x 3
2
3
4
1
49.
1 способ: подстановка вариантов в СЛУ2 способ: решение
50.
51.
52.
53.
54.
55.
№ 5.1 Найти фундаментальную систему решений иобщее решение однородной системы уравнений:
x1 x2 3x3 0
x x x 2x 0
1 2 3
4
2 x1 x2 4 x3 x4 0
x1 2 x2 5 x3 x4 0
56.
№ 5.2 Найти фундаментальную систему решений иобщее решение однородной системы уравнений:
3x1 2 x2 x3 3x4 5 x5 0
6 x 4 x 3 x 5 x 7 x 0
1
2
3
4
5
9 x1 6 x2 5 x3 7 x4 9 x5 0
3x1 2 x2 4 x4 8 x5 0
57.
Вопросы для самоконтроля ифорума по разделу Линейная
алгебра.
Какая матрица называется прямоугольной? квадратной? диагональной?
единичной?
Какие матрицы складываются и умножаются?
Какая матрица имеет свою обратную матрицу?
Что называется определителем второго порядка?
По какому правилу вычисляется определитель третьего порядка?
Каковы основные свойства определителей?
Что называется минором?
Что называется алгебраическим дополнением?
Какая система уравнений называется линейной?
Какая СЛУ называется несовместной?...совместной?
…однородной?...неоднородной?
Когда неоднородная система 3-х линейных уравнений с тремя
неизвестными имеет единственное решение? не имеет решения? имеет
множество решений.






















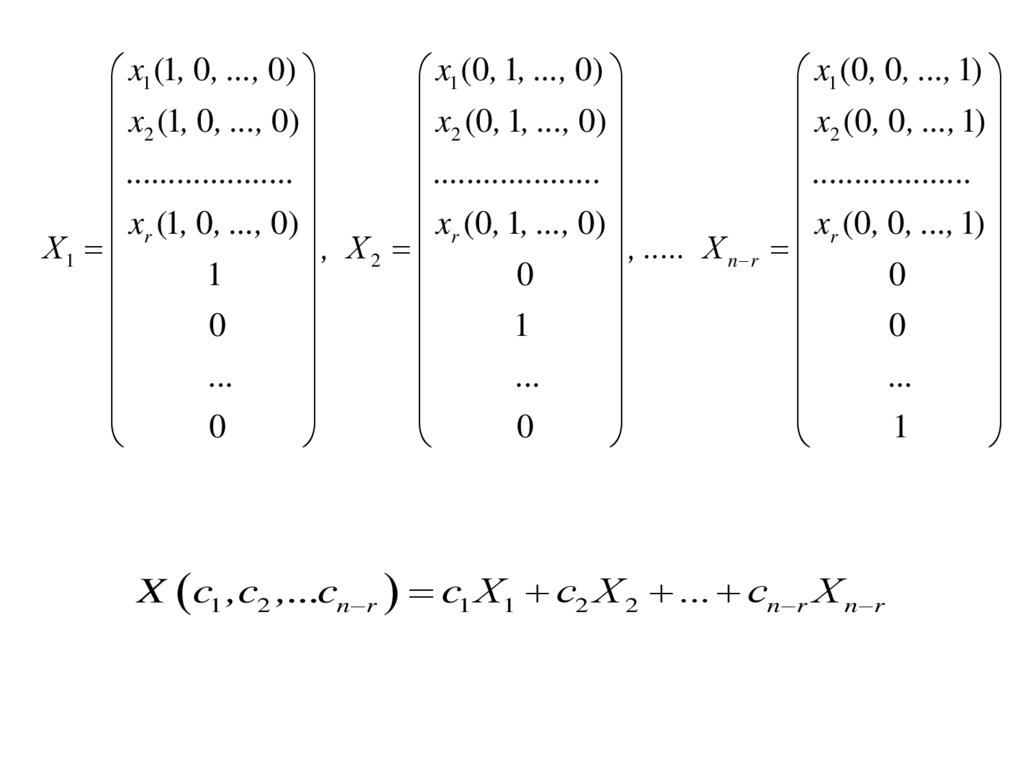

































 mathematics
mathematics








