Similar presentations:
Системы линейных алгебраических уравнений (СЛАУ). Лекция 4
1.
ЛЕКЦИЯ 4СИСТЕМЫ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
(СЛАУ)
2.
Матричный способ решения СЛАУСистемой n линейных алгебраических
уравнений с n неизвестными называется
совокупность уравнений вида:
a x a x ... a x b ,
12 2
1n n
1
11 1
a x a x ... a x b ,
22 2
2n n
2
21 1
an1 x1 an 2 x2 ... an n xn bn ,
.................................,
где ai j- коэффициенты системы, i 1, ..., n, j 1, ..., n,
x j - неизвестные, j 1, ..., n,
bi - свободные члены, i 1, ..., n.
Решением СЛАУ называется упорядоченное
множество действительных чисел {α1, α2,…, αn},
обращающее каждое уравнение СЛАУ
в числовое равенство.
3.
Представим СЛАУa11 x1 a12 x2 ... a1n xn b1 ,
матрица-столбец
a x a x ... a x b ,
свободных
22 2
2n n
2
21 1
членов
..........
..........
..........
..........
....,
матрица
матрица
столбец
коэффициентов неизвестных
an1 x1 an 2 x2 ... an n xn bn
в виде произведения матриц
Матричная
записи
a11 a12 ... a1 n
x1
b1 форма
СЛАУ
b2
a21 a22 ... a2 n
x2
A
, X , B : A X B.
... ... ... ...
...
...
Как найти Х?
a a
xn
n1 n 2 ... an n
bn
форме
X A B - решение СЛАУ в матричной
Сколько решений
1
При каких условиях решение СЛАУ
в матричной форме существует?
СЛАУ в матричной
форме существует
и почему?
4.
Пример. Решить систему уравнений матричнымспособом:
3x x 2 x 13,
1
2
3
x1 3x2 x3 11,
матрица
коэффициентов 4 x 2 x 3 x 12.
2
3
1
Решение.
обратная матрица
11 7 5
1 2
3
1
1
1
A 1
3 1 , A 1 1 1 , X A B,
6
4 2 3
14
10
8
11 7 5 13
6 1
1
1
X 1 1 1 11 12 2 .
6
6
4
14
10
8
12
24
Ответ:
{-1, -2, 4}.
5.
РешениеСЛАУ по формулам Крамера
При
каких
Сколько
1
11
1 1
Запишем
равенство
виде
1
12
условиях
решений
11
1n
X1n A B 1в, n 1 следующем
решение
A11 A21 ... An 1 b1 СЛАУ по
x1
СЛАУ
2 22
21 2 n
2 , n 1 21 2 2 формулам2 n
по формулам
Крамера
x
A
A
...
A
b
2 1 n 12
22
n2 2
1 Крамера
2
существует
Чем
.
существует?
... A ... ... ... ... ... и почему?
является
выражение
Формулы
n1 nn
n2 A
nn
A
... n , n 1An1 n n в скобках?
xn
Крамера
b a ... a a ... a a b b ... a
b a
... a a ... a а b b ... a
... ... ... ...... ... ... ... ... ... ... ...
b a
... a a ... a a b b ... a
1n
2n
nn b
n
n
Тогда
1
Определитель,
1
x
( A11b1 A21b2 ... An1bn ),
1
x
,
1
полученный
A
из
определителя
2
А,
xматрицы
2
заменой
первого
столбца
n
столбцом
xсвободных
.
n
членов
...,
1
x2 A ( A12b1 A22b2 ... An 2bn ),
..................................................,
1
xn A ( A1nb1 A2 nb2 ... Annbn ).
6.
Пример. Решить систему уравнений поформулам Крамера:
3 x1 x2 1,
2 x1 x2 5.
Решение.
1 1
3 1
3 1
5 0, 1
13,
6, 2
2 1
2 5
5 1
1 6
x1
,
5
6 13
Ответ: ; .
5 5
2 13
x2
.
5
7.
Системы m линейных алгебраическихуравнений с n неизвестными и их исследование
Системой m линейных алгебраических
уравнений с n неизвестными называют
совокупность уравнений вида:
a11x1 a12 x2 ... a1n xn b1 ,
a21x1 a22 x2 ... a2 n xn b2 ,
..........................................,
am 1 x1 am 2 x2 ... am n xn bm ,
где ai j- коэффициенты системы, i 1, ..., m, j 1, ..., n,
xj
- неизвестные,
j 1, ..., n,
- свободные члены, i 1, ..., m.
bi
8.
СЛАУ называется совместной, если она имеетхотя бы одно решение, и несовместной, если она
не имеет ни одного решения.
Расширенной матрицей СЛАУ называется
матрица, полученная дополнением матрицы
коэффициентов столбцом свободных членов:
a11 a12
a21 a22
C
... ...
a
m 1 am 2
... a1 n
... a2 n
... ...
... am n
b1
b2
.
...
bm
9.
Теорема Кронекера-КапеллиСЛАУ совместна тогда и только тогда,
когда ранги её матрицы коэффициентов и
расширенной матрицы совпадают ( rA = rC ).
Если при этом они равны числу неизвестных,
то СЛАУ имеет единственное решение (rA = rC = n).
Если ранг матрицы коэффициентов меньше
числа неизвестных, то СЛАУ имеет
бесконечное множество решений, зависящее
от n - r параметров ( rA < n ).
10.
Пример. Исследовать на совместность систему:x1 x2 1,
2 x1 2 x2 2.
11.
Метод Гаусса решения систем m линейныхалгебраических уравнений с n неизвестными
те же решения,
Суть метода Гаусса: имеющей
что и исходная СЛАУ
элементарными преобразованиями СЛАУ
прямой ход
приводится к трапециевидной СЛАУ, метода
Гаусса
эквивалентной исходной, из которой находится
обратный ход
решение (если оно существует). метода
Гаусса
Элементарные преобразования СЛАУ:
– перестановка двух любых уравнений;
– умножение уравнения на ненулевое число;
– удаление уравнений, все коэффициенты
которых и свободный член равны нулю;
– прибавление к уравнению другого уравнения,
умноженного на любое число.
Как определить число решений СЛАУ?
12.
СЛАУ не имеет решений, если в ходепреобразований получилось уравнение
0 xk 0 xk 1 ... 0 xn b,
b 0.
СЛАУ имеет единственное решение, если в ходе
преобразований получилась треугольная СЛАУ.
СЛАУ имеет бесконечное множество решений,
если в ходе преобразований получилась
трапециевидная СЛАУ.
13.
Пример. Решить систему методом Гаусса:x1 2 x2 x3 5,
3x3 1,
2 x1
x 4 x 3x 1.
Решение.
1
2
3
1
5 1 2
1 5
1 2
C 2
0
3 1 ~ 0 4
5
9 ~
1
0
4
3
1
6
2
4
Ранг матрицы системы А
рангу
расширенной
1
5 матрицы
x1 2
xсистемы
x3С, тогда
5,
1 2
равен
2
по теореме Кронекера~ 0 4
5
9 , Капелли
x2 5 xсовместна
9,
4система
3
При
этом ранги равны числу
0
38 xпо
38.
0 38 38 неизвестных,
тогда
3 теореме
Кронекера-Капелли система
2. Ответ:{решение
rA rC 3 n, x3 1, x2 имеет
1, x1 единственное
2; 1; 1}
14.
Пример. Решить систему: x1 3 x2Решение.
1
C 2
0
1
0
~
0
3
0
2
3
6
0
14,
2 x1
3 x3 7,
Ранг матрицы системы А
рангу2расширенной
равен
x2 С,x3тогда
7.
системы
матрицы
0 14 по теореме
Кронекера1
3
0
14
Капелли
система
совместна
3
7 При
этом
~
0 ранги
6меньше
3 числа
21 ~
неизвестных, тогда по теореме
система имеет
1
7Кронекера-Капелли
2
1решение
7
0 множество
бесконечное
0
14
rA rC 2 n 3,
3 21 ,
Выражаем базисные
неизвестные через свободные
0
0
14,
x1 3x2
2 x2 x3 7.
Базисные
неизвестные
Свободные
неизвестные
БН: x1 , x2 ; СН: x3 .
15.
14,x1 3x2
БН: x1 , x2 ;
СН: x3 .
2 x2 x3 7. Выражаем базисные неизвестные через
свободные. Начинаем с последнего уравнения
2 x2 7 x3 ,
7 1
x2 x3 ;
2 2
x1 14 3 x2 ,
7 1
x1 14 3 x3 ,
2 2
21 3
x1 14 x3 ,
2 2
7 3
x1 x3 .
2 2
7 3 7 1
Ответ: x3 ; x3 ; x3 R
2 2 2 2
16.
Системы линейных однородных уравнений(СЛОУ)
Системой линейных однородных уравнений
называется совокупность уравнений вида:
a11 x1 a12 x2 ... a1n xn 0,
a21 x1 a22 x2 ... a2 n xn 0,
............................................,
a x a x ... a x 0,
mn n
m1 1 m 2 2
где ai j - коэффициенты системы, i 1, ..., m, j 1, ..., n,
x j - неизвестные, j 1, ..., n.
СЛОУ всегда совместна, так как она имеет,
по крайней мере, нулевое (тривиальное) решение:
xn 0.
x1 0, x2 0, ...,
17.
Теорема 4.2. СЛОУ имеет ненулевое решениетогда и только тогда, когда ранг матрицы системы
меньше числа неизвестных ( rA < n ).
Следствие 1. СЛОУ имеет ненулевое решение
тогда и только тогда, когда число уравнений
меньше числа неизвестных ( rA < n ).
Следствие 2. СЛОУ имеет ненулевое решение
тогда и только тогда, когда число уравнений
равно числу неизвестных и матрица системы
вырождена ( rA < n ).
18.
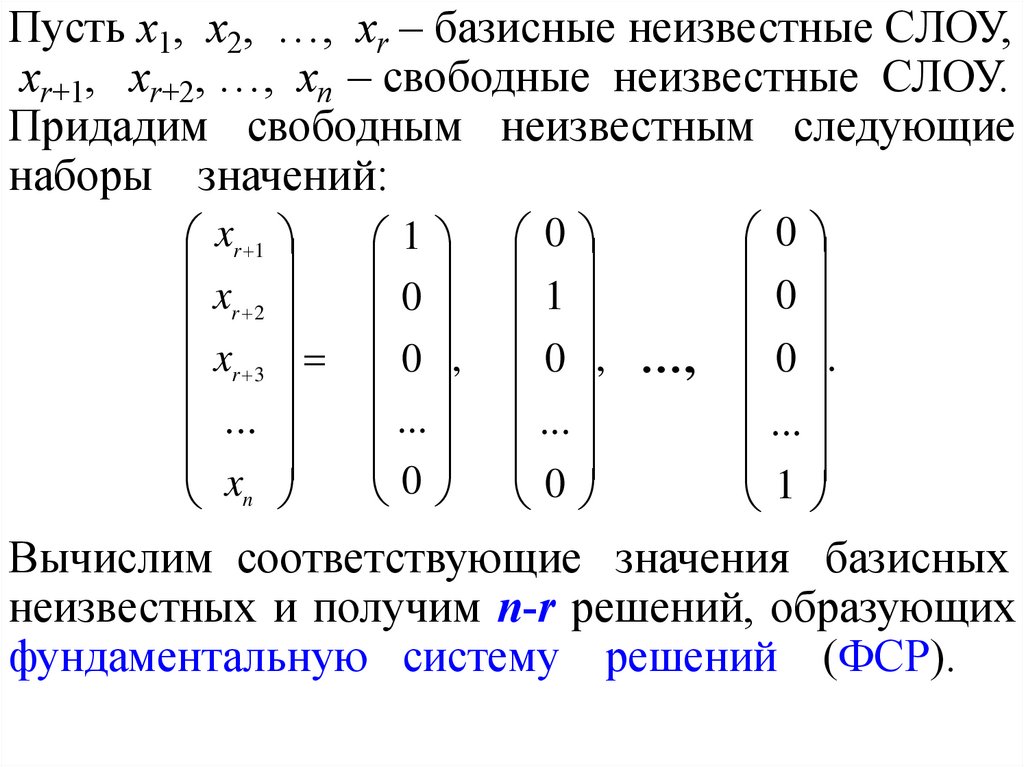
Пусть x1, x2, …, xr – базисные неизвестные СЛОУ,xr+1, xr+2, …, xn – свободные неизвестные СЛОУ.
Придадим свободным неизвестным следующие
наборы значений:
xr 1
xr 2
x
r 3
...
x
n
1
0
0 ,
...
0
0
1
0 ,
...
0
...,
0
0
0 .
...
1
Вычислим соответствующие значения базисных
неизвестных и получим n-r решений, образующих
фундаментальную систему решений (ФСР).
19.
Пример. Найти фундаментальную системурешений системы линейных однородных
уравнений:
x1 2 x2 4 x3 3 x4 0,
3 x 5 x 6 x 4 x 0,
1
2
3
4
4 x1 5 x2 2 x3 3 x4 0,
3 x1 8 x2 24 x3 19 x4 0.


















 mathematics
mathematics








