Система линейных алгебраических уравнений (СЛАУ)

1.

Система линейных алгебраических уравнений (СЛАУ).
В общем виде СЛАУ можно записать в следующем виде
a11x1
.
a12 x 2 ....... a1m x m
b1
a 21x1 a 22 x 2 ....... a 2 m x m b 2
.........
..........
.......
...........
....
a n1x1 a n 2 x 2 ....... a nm x m b n
Совокупность коэффициентов
a ij,
i =1,2,3,…,n; j=1,2,3,….,m системы
можно представить в виде матрицы:
a11 a12 a13
a
a 22 a 23
A A 21
a
n1 a n 2 a n 3
a1m
a 2m
a nm
1

2.

Совокупность неизвестных
Совокупность неизвестных
x j,
j 1,2,3,..., m
bi , i 1,2,3,..., n
- в виде вектора
- в виде вектора
x1
x
x 2
...
x
m
b1
b
b 2
...
b
n
Используя выше приведенные определения, запишем СЛАУ в матричном виде:
Ax b
Решить СЛАУ значить найти такие значения вектора
x *1
*
x 2
x*
...
*
x m
подстановка которого в систему, обращает каждое уравнение этой системы в тождество.
2

3.

Классификация СЛАУ
СЛАУ называется:
1. Переобусловленной, если n>m
2. Недообусловленой, если n<m
3. Нормальной, если n=m
4. Однородной, если вектор
b 0
5. Неоднородной, если вектор
b 0
6. Если система, имеет хотя бы одно решение, она называется совместной.
Система, не имеющая решений, называется несовместной.
7. Совместная система, имеющая единственное решение, называется определенной, а
имеющая бесчисленное множество решений, называется неопределенной.
Очевидно, что однородная система всегда совместна, так как имеет хотя бы одно
решение
x 0 , которое называется тривиальным.
3

4.

Методы решения СЛАУ
Все методы решения СЛАУ можно разделить на две группы: точные и
итерационные.
Точные методы позволяют получить решение путем выполнения
определённого и точного количества арифметических операций. При этом
погрешность решения определяется лишь точностью представления исходных
данных и точностью вычислительных операций.
Итерационные методы дают некоторую последовательность приближений к
решению. Пределом этой последовательности является решение системы
уравнений. Решение, возможно, определить лишь с некоторой, как правило,
заданной степенью точности . Количество итераций для достижения требуемой
точности решения определяется величиной , выбором начального приближения
и видом системы уравнений.
Точные методы
Метод обратной матрицы
A x b
1
1
A A x A b
1
E x A b
Метод Гаусса
*
1
x A b
x=inv(A)*b
x=A\b
Метод Гаусса включает два этапа.
4

5.

Первый этап (прямой ход) заключается в последовательном исключении неизвестных
из системы уравнений и состоит из n–1 шага. На первом шаге с помощью первого
уравнения исключается x1 из всех последующих уравнений начиная со второго, на
втором шаге с помощью второго уравнения исключается x2 из последующих уравнений
начиная с третьего и т.д. Последним исключается xn-1 из последнего n-го уравнения так,
что последнее уравнение будет содержать только одно неизвестное xn. Такое
последовательное исключение неизвестных равносильно приведению матрицы
коэффициентов к треугольному виду. Строка, с помощью которой исключаются
неизвестные, называется ведущей строкой, а диагональный элемент в этой строке –
ведущим элементом.
Второй этап (обратный ход) заключается в последовательном вычислении искомых
неизвестных и состоит из n шагов. Решая последнее уравнение, находим
неизвестное xn. Далее используя это значение из предыдущего уравнения
вычисляем неизвестное xn-1 и т.д. Последним найдем неизвестное x1 из первого
уравнения.
Матрица, содержащая помимо. коэффициентов при неизвестных A
столбец свободных членов b , называется расширенной C A b
5

6.

1. Строим расширенную матрицу С
вектор
b
С A b
c11 c1, 2
c
c
С A b 21 22
...
...
c n1 c n 2
Алгоритм.
размерностью n на n+1, приписав, справа к матрицы A
т.е. ci,j=ai,j , ci,n+1=bi , где i=1,2,3,…,n j=1,2,3,…,n
... c1n c1,n 1
... c 2n c 2,n 1
...
... ...
... c nn c n ,n 1
Задаем номер ведущей строки k = 1
2. Преобразуем все строки, расположенные ниже k-ой так, чтобы элементы cik=0,
для этого вычисляем множитель =-сi,k/ck,k и каждую i-ую строку заменяем суммой i–ой
и k-ой умноженной на , т.е. ci,j=ci,j+ *ck,j
где i = k+1,k+2,k+3,….,n и j =
k,k+1,k+2,…,n+1
3. Проверяем k = n-1 если нет, то выбираем новую ведущую строку k=k+1 и переходим
на пункт 2, иначе выполняем пункт 4.
4. Обратный ход. Из последнего n-ого уравнения определяем последнее n-ое
неизвестное. xn=cn,n+1/cn,n Последовательно, из предыдущих уравнений начиная с i=n1, вычисляем соответствующие неизвестные xi. Последним, определяется первое
неизвестное из первого уравнение.
n
(ci,n 1 ci, j * x j )
xi
j i 1
ci,i
6

7.

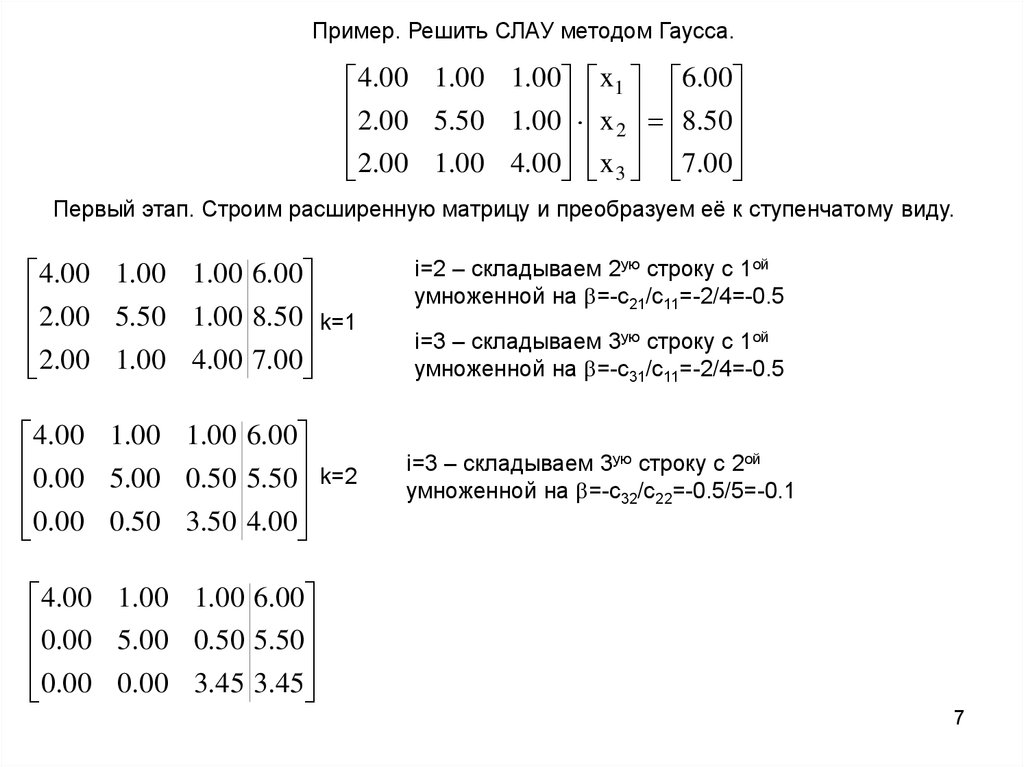
Пример. Решить СЛАУ методом Гаусса.
4.00 1.00 1.00 x1 6.00
2.00 5.50 1.00 x 8.50
2
2.00 1.00 4.00 x 3 7.00
Первый этап. Строим расширенную матрицу и преобразуем её к ступенчатому виду.
4.00 1.00 1.00 6.00
2.00 5.50 1.00 8.50
k=1
2.00 1.00 4.00 7.00
4.00 1.00 1.00 6.00
0.00 5.00 0.50 5.50
0.00 0.50 3.50 4.00
k=2
i=2 – складываем 2ую строку с 1ой
умноженной на =-c21/c11=-2/4=-0.5
i=3 – складываем 3ую строку с 1ой
умноженной на =-c31/c11=-2/4=-0.5
i=3 – складываем 3ую строку с 2ой
умноженной на =-c32/c22=-0.5/5=-0.1
4.00 1.00 1.00 6.00
0.00 5.00 0.50 5.50
0.00 0.00 3.45 3.45
7

8.

Второй этап. Вычисляем неизвестные
3.45
1.00
3.45
(5.50 (0.50 1.00))
x2
1.00
5.00
x3
x1
(6.00 (1.00 1.00 1.00 1.00))
1.00
4.00
1.00
x 1.00
1.00
8

9.

Для уменьшения погрешности вычислений используют модификации метода Гаусса,
которые определяются выбора«ведущего» элемента. В модификации с частичным выбором
на каждом k-м шаге прямого хода в качестве «ведущего» выбирается наибольший по
модулю элемент из неприведённой части k-го столбца матрицы, т.е.
c kk max cik , i k, k 1, k 2,..., n
i
Строка, содержащая этот элемент, переставляется с k-й строкой расширенной матрицы.
При полном выборе в качестве «ведущего» элемента выбирается максимальный по
модулю элемент из всей неприведённой части матрицы коэффициентов системы:
c kk max cij , i, j k, k 1, k 2,..., n
i, j
Для этого осуществляется необходимая перестановка как строк, так и столбцов в
расширенной матрице коэффициентов. При этом следует помнить, что перестановка
столбцов равносильна переименованию неизвестных.
•Пример. Решить СЛАУ методом Гаусса с частичным выбором.
1.000
2.000
5.000
6.000
1.000
1.000
1.000 x1 0.000
5.000 x 2 10.000
2.000 x 3 10.000
9

10.

Первый этап. Строим расширенную матрицу и преобразуем её к ступенчатому виду.
1
2
5
6
1
1
1
0
5 10
2 10
На первом шаге преобразования к=1
наибольший по абсолютной величине
элемент в первом столбце (5) расположен
в третьей строке матрицы, поэтому
меняем первую и третью строки и
производим необходимые преобразования.
На втором шаге преобразования к=2
наибольший по абсолютной величине 5
элемент во втором столбце (6.2) 0
расположен в третьей строке матрицы,
поэтому меняем вторую и третью строки 0
и
производим
необходимые
преобразования.
Второй этап.
Вычисляем неизвестные.
10 (( 1) 1 2 3)
x1
3
5
1
2 10
1 5 10
6 1 0
5
2
1
1
2 10
6.2 1.4
2
1.4
4.2 14
5 1
0 1.4
0 6.2
2 10
4.2 14
1.4
2
1
10
1.4
2
4.516 13 . 548
5
0
0
6.2
0
2
(2 1.4 3) 6.2
13.548
x
1
x3
3 2
6.2
6.2
4.516
3
ответ x 1
10
3

11.

Обусловленность систем линейных алгебраических уравнений.
Если система плохо обусловлена, то это значит, что погрешности коэффициентов
матрицы и свободных членов или погрешность округления при расчетах могут сильно
исказить решение.
A x b
Исходную систему уравнений
Запишем как
A x b
A ( x x ) b b
с учетом погрешности в векторе
Абсолютная погрешность
определим, как норму ошибки
1
1
A x b A x b
или
b
и тогда
x A b
отсюда можно выразить ошибку
|| x || || A b ||
|| x ||
|| x ||
|| x || || A || || b ||
или
1
Определим относительную погрешность
1
|| A || || b ||
.
|| x ||
1
Определим
|| x ||
11

12.

из исходной системы
A x b
|| A || || x || || b ||
получим
далее определим
1
|| x ||
|| A ||
|| b ||
и подставим в определение относительной погрешности получим
|| x ||
1
|| A || || A ||
|| b ||
|| x ||
|| b ||
Вводим понятие числа обусловленности:
1
K об Cond(A) || A || || A ||
и тогда
|| x ||
|| x ||
K об
|| b ||
|| b ||
12

13.

Метод простых итераций
Алгоритм метода состоит из трёх этапов.
Первый этап. Приведение СЛАУ к итерационному виду, для этого разрешим каждое
уравнение относительно соответствующего неизвестного:
a11x1
.
a12 x 2 ....... a1n x n
b1
a 21x1 a 22 x 2 ....... a 2 n x n b 2
.........
..........
.......
...........
....
a n1x1 a n 2 x 2 ....... a nn x n b n
b1
a11
b2
x2
a 22
....... ........
dn
xn
a nn
x1
где d i
bi
a ii
Тогда итерационную
запишем в виде:
( 0 x1
a
( 21 x1
a 22
...........
a
( n1 x1
a nn
a12
x2
a11
0 x2
..........
a
n2 x2
a nn
a13
a
x 3 ..... 1n x n )
a11
a11
a
a
23 x 3 ..... 2n x n )
a 22
a 22
........... .........
...........
a
n 3 x 3 ..... 0 x n ),
a nn
0 при i j
cij a ij
a при i j
ii
формулу
k
i 1,2,3, , n; j 1,2,3, , n
k 1
x d C x
; k 1,2,3,
13

14.

где вектор
d
C
– приведенный столбец свободных членов,
матрица
– приведенная матрица коэффициентов.
Второй этап. Проверяем условие сходимости
|| C || 1
если условие не выполняется, то преобразуем исходную систему и выполняем 1-й этап.
Третий этап. Осуществляем уточнение решения по полученной итерационной формуле.
k
k 1
x d C x
0
; k 1,2,3,
За начальное приближение принимается
x d
Условием окончания итерационного процесса является выполнение условия
k
k 1
|| x x
||
где величина ε определяет точность получаемого решения
а
k
k 1
x и x
– смежные приближения к решению.
14

15.

Пример. Решить СЛАУ методом простых итераций ε=0.4
4.00 1.00 1.00 x1 6.00
2.00 5.50 1.00 x 8.50
2
2.00 1.00 4.00 x 3 7.00
Преобразуем исходную систему к итерационному виду.
k
k 1
x d C x
,
k 1,2,3,
0.00 0.25 0.25
C 0.36 0.00 0.18
0.50 0.25 0.00
1.50
d 1.55
1.75
С 0.78 1
0
x d
15

16.

(k )
x
(1)
x
( 2)
x
( 3)
x
( 4)
x
( k 1)
(k )
C
x
x
d
1.50 0.00 0.25 0.25 1.50 0.68
1.55 0.36 0.00 0.18 1.55 0.68
1.75 0.50 0.25 0.00 1.75 0.61
1.50 0.00
1.55 0.36
1.75 0.50
1.50 0.00
1.55 0.36
1.75 0.50
0.25 0.25 0.68 1.18
0.00 0.18 0.68 1.19
0.25 0.00 0.61 1.24
0.25 0.25 1.18 0.89
0.00 0.18 1.19 0.89
0.25 0.00 1.24 0.86
1.50 0.00 0.25 0.25 0.89 1.06
1.55 0.36 0.00 0.18 0.89 1.06
1.75 0.50 0.25 0.00 0.86 1.08
1.06
Ответ:
x 1.06
1.08
x
x
0.82
0.86 1.65
1.14
0.50
0.51
0.95
0.63
0.28
0.30 0.56
0.38
0.17
0.17
0.22
0.32
16