Системы линейных уравнений

1. Линейная алгебра

Лекция 3
Системы линейных уравнений

2. План лекции

Система линейных алгебраических уравнений
Совместность, определенность и равносильность
систем
Методы решения систем:
– Метод Крамера;
– Метод обратной матрицы;
– Метод Гаусса.
Количество решений системы
Случай однородных систем
2

3. Системы линейных уравнений (СЛУ)

Под системой линейных уравнений (СЛУ) будем понимать:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
................................................
am1 x1 am 2 x2 ... amn xn bm
где
– «неизвестные» системы,
a11, a12 , ... , amn , b1 , ..., bm R – коэффициенты системы,
m – число уравнений, n – число неизвестных.
x1 , x2, ...xn
3

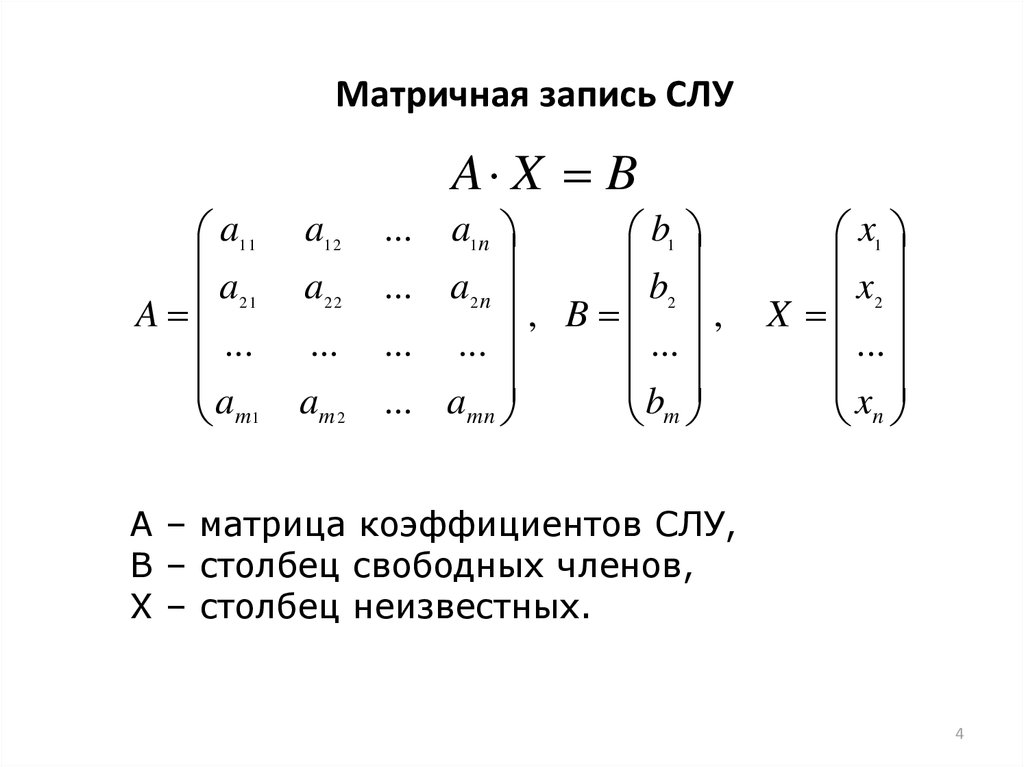
4. Матричная запись СЛУ

A X B
a1 1
a2 1
A
...
a
m1
a1 2
a2 2
...
am 2
a1n
b1
... a2 n
b2
, B ,
... ...
...
b
... amn
m
...
x1
x2
X
...
x
n
A – матрица коэффициентов СЛУ,
B – столбец свободных членов,
X – столбец неизвестных.
4

5. Решение СЛУ

Решением СЛУ называется совокупность чисел
x10 , x20 ,..., xn0 R ,
удовлетворяющая всем уравнениям системы, т.е.
обращающая их в верные числовые равенства:
a11x10 a12 x20 ... a1n xn0 b1
0
0
0
a21x1 a22 x2 ... a2 n xn b2
................................................
a x 0 a x 0 ... a x 0 b
m2 2
mn n
m
m1 1
5

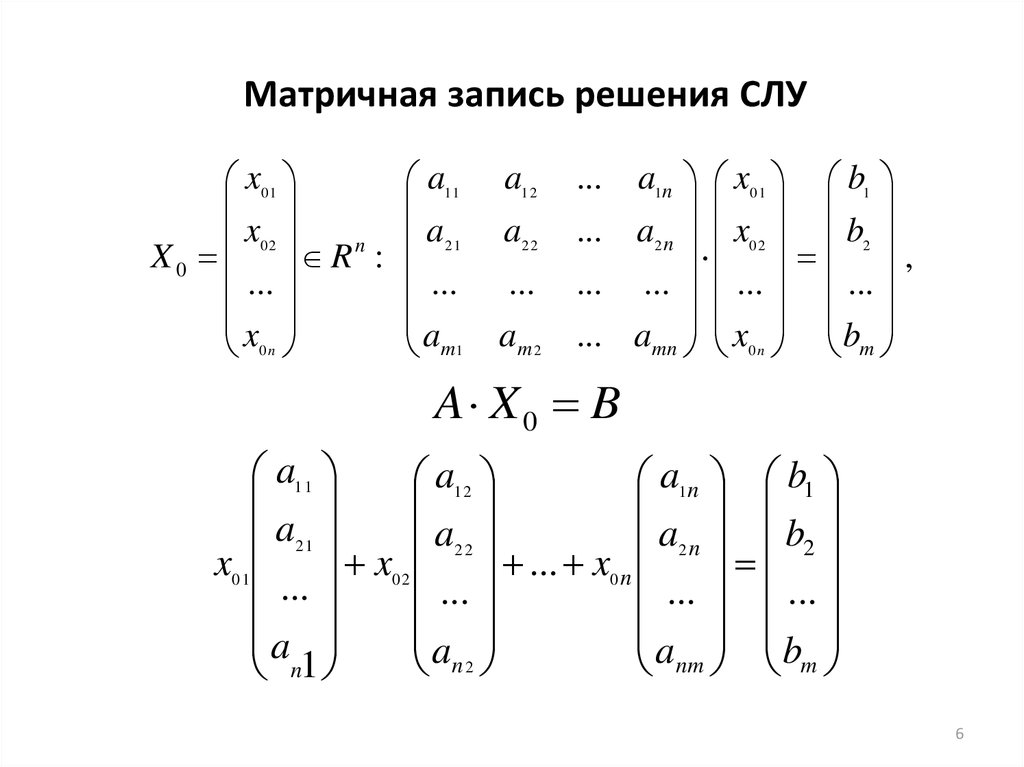
6. Матричная запись решения СЛУ

x0 1
x0 2
X 0 Rn :
...
x
0n
a1 1
a2 1
...
a
m1
a1 2
a2 2
...
am 2
a1n x0 1 b1
... a2 n x0 2 b2
,
... ...
...
...
... amn x0 n bm
...
A X0 B
a1 1
a1 2
a1n b1
a2 1
a2 2
a2 n b2
x0 1 x0 2 ... x0 n
...
...
...
...
b
a
a
a
n2
nm m
n1
6

7. Типы СЛУ

СЛУ называется совместной, если у неё имеется хотя бы
одно решение, в противном случае СЛУ называется
несовместной.
Совместная СЛУ называется определённой, если она имеет
одно единственное решение и неопределённой в
противном случае.
Две системы называются равносильными, если их
множества решений совпадают.
СЛАУ A.X=B называется однородной, если B=0 , в
противном случае СЛУ называется неоднородной.
7

8. Расширенная матрица СЛУ

Вся информация о СЛУ
A.X=B
содержится в
расширенной матрице системы:
a11
a21
A1
...
a
m1
a12
... a1n
a22
... a2 n
...
...
...
am 2 ... amn
b1
b2
...
bm
8

9. Совместная СЛУ

Пусть дана совместная определенная СЛАУ от
n неизвестных.
1.
2.
Тогда:
если система однородна, то она имеет только
тривиальное решение xi = 0, i=1,…,n;
если система не однородна, то она имеет
единственное решение, которое может быть
найдено
• по правилу Крамера,
• методом обратной матрицы,
• методом Гаусса.
9

10. Правило Крамера решения СЛУ

Пусть дана совместная СЛУ от n неизвестных
A X B , det( A) 0 .
Тогда система имеет единственное решение
i
xi , i 1, 2, ..., n ,
где
i – определитель, получаемый из
определителя заменой i-го столбца на столбец
свободных членов.
10

11. Правило Крамера. Пример 1

x1 2 x2 3 x3 2
3 x1 x2 x3 3
2 x 5 x 2 x 9
2
3
1
Найти решение СЛУ
1 2
2 2
x1 3
9
3
1
2
5
1 2 45 4 (6 12 5) 62 0 ,
2
3
1 1 62 ,
5
3
1
1 2 2
3
x2 3
3 1 62 , x2 3
2 9 2
2
2
Следовательно,
2
x1
x1
1 , x2
x2
1, x3
1 3 62 .
5 9
x3
1 .
11

12. Метод обратной матрицы решения СЛУ

Пусть дана совместная СЛАУ от n неизвестных
A X B , det( A) 0 .
Тогда существует A-1 и
X A B
1
1
A A X A B
(т.к.
1
).
Пример (тот же).
1 2 3
7 19 1
1 1
62 0 , A 3 1 1 , A 8 4 10 .
62
2 5 2
13
9
7
7 19 1 2 1
1
1
X A B 8 4 10 3 1 .
62
13 9 7 9 1
12

13. Метод Гаусса решения СЛУ

Суть метода состоит в последовательном исключении
неизвестных: сначала исключается x1 из всех уравнений системы,
начиная со 2-го, далее исключается x2 из всех уравнений,
начиная с 3-го, и т. д., пока в последнем уравнении останется
только xn (прямой ход схемы Гаусса). Затем из последнего
уравнения находится xn , с помощью этого значения из
предпоследнего уравнения вычисляется xn-1 и т. д., пока из 1-го
уравнения не найдется x1 (обратный ход схемы Гаусса).
13

14. Метод Гаусса решения СЛАУ. Пример

Пример (тот же):
x1 2 x2 3 x3 2
3 x1 x2 x3 3
2 x 5 x 2 x 9
2
3
1
1 2 3 2 II 3 I 1 2
3 2 1 2 3 2
x1 1
III 2 I
3 1 1 3 0 7 10 3 0 7 10 3 x2 1
2 5 2 9
0 9 4 5 0 0 62 62
x3 1
или
1
0
0
2 1
7 10 3 0
0 1
1 0
2
3
2 0 1 1 2 0 1 1 0 0 1
7 0 7 0 1 0 1 0 1 0 1
0 1 1 0 0 1 1 0 0 1 1
14

15. Алгоритм решения произвольной СЛУ

1. Приведем СЛУ к системе с матрицей A1 трапециевидного
(ступенчатого) вида:
a) полагая
a11 0, исключим неизвестную переменную x1
из всех уравнений системы, начиная со 2-го. Для этого
a21
к 2-му уравнению прибавим 1-ое, умноженное на
,
a11
a31
к 3-му уравнению прибавим 1-ое, умноженное на
,
a11
.........,
an1
к n-ому уравнению прибавим 1-ое, умноженное на
.
a11
15

16.

В результате преобразований система примет вид
a1n xn b1
a11 x1 a12 x2 ...
(1 )
(1 )
(1 )
a
x
...
a
x
b
22
2
2n
n
2
............................................................
an(12) x2 ...
arn(1) xn br(1)
ai1
aij aij a1 j , i 2,3,..., n, j 2,3,..., n
a11
(1 )
ai1
bi bi b1 , i 2,..., n
a11
(1 )
16

17.

б) полагая
a22(1) 0 , исключим неизвестную переменную x2
из всех уравнений системы, начиная с третьего. Для этого
(1 )
a32
к 3-му уравнению прибавим 2-ое, умноженное на (1) ,
(1 ) a 22
a42
к 4-му уравнению прибавим 2-ое, умноженное на (1) ,
a22
........ .,
an(12)
к n-ому уравнению прибавим 2-ое, умноженное на (1) .
a22
в) и т.д.
17

18. 2. Укороченная система

2. Отбросив последние n – r уравнений, запишем
укороченную систему, равносильную исходной:
a1, n xn b1
a11 x1 a12 x2 ...
(1 )
(1 )
(1 )
a
x
...
a
x
b
22
2
2 ,n n
2
............................................................
( r 1 )
( r 1 )
( r 1 )
a
x
...
a
x
b
r ,r
r
r ,n
n
r
18

19. 3. Свободные и базисные неизвестные

3. Назовем неизвестные x1, x2,…,xr базисными,
xr+1, xr+2,…,xn – свободными.
Запишем укороченную систему в виде
a11 x1 a12 x2 ... a1, r xr b1 a1,r 1 xr 1 a1, n xn
(1 )
(1 )
(1 )
(1 )
(1 )
a
x
...
a
x
b
a
x
a
x
22
2
2,r r
2
2 , r 1 r 1
2,n n
...................................................................................
( r 1 )
( r 1 )
( r 1 )
( r 1 )
a
x
b
a
x
a
r ,r r
r
r , r 1 r 1
r , n xn
19

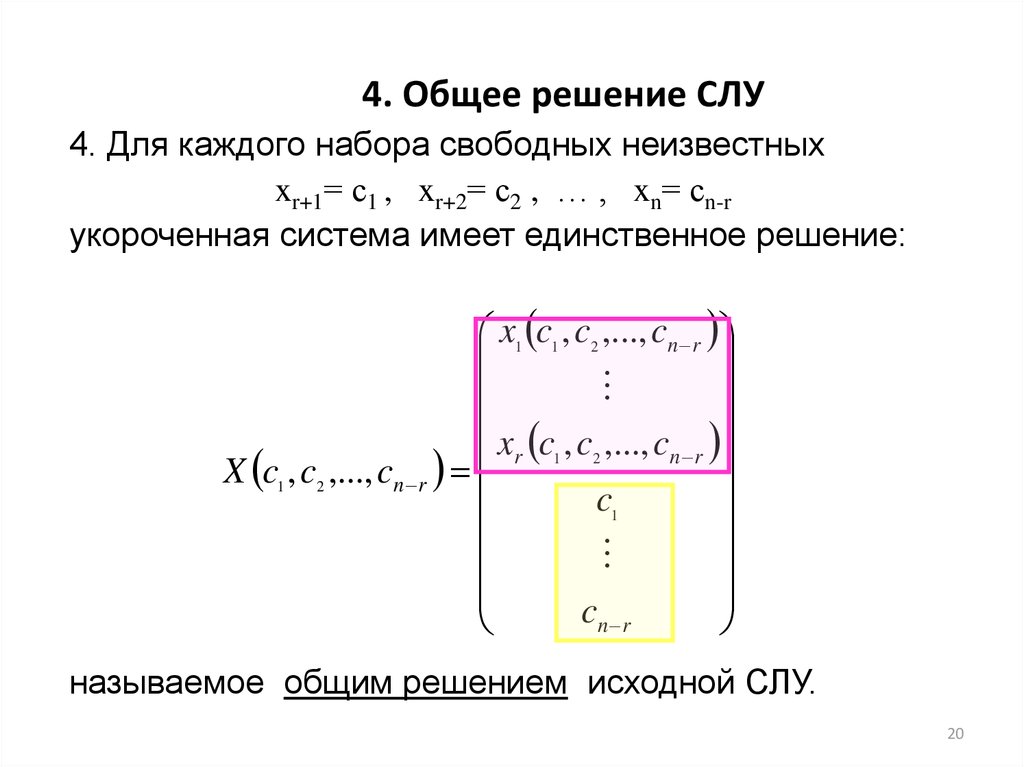
20. 4. Общее решение СЛУ

4. Для каждого набора свободных неизвестных
xr+1= с1 , xr+2= с2 , … , xn= сn-r
укороченная система имеет единственное решение:
x1 c1 , c2 ,..., cn r
x c , c ,..., c
r 1 2
n r
X c1 , c2 ,..., cn r
c1
c
n r
называемое общим решением исходной СЛУ.
20

21. Общее решение СЛУ. Пример 2

Найти общее решение СЛУ
x1 2 x2 3x3 0
2 x1 4 x2 6 x3 0
1 2 3 0 1 2 3 0
.
A1
2
4
6
0
0
0
0
0
Положим
x3=c1, x2=c2 .
Укороченная система имеет вид
откуда
x1 2c2 3 c1
Общее решение
x1 2 x2 3x3 0
,
.
2c2 3c1
X c1 , c2 c2 , c1 , c2 R .
c
1
21

22. Теорема о числе решений СЛУ

Пусть дана совместная СЛУ от n неизвестных с матрицей
коэффициентов , которая при приведении к ступенчатому виду
имеет r ненулевых строк.
Тогда:
1. если r = n , то система имеет единственное решение;
2. если r < n , то система имеет бесконечно много решений,
причем (n – r) неизвестным можно присвоить произвольные
значения, а остальные r неизвестных выражаются через них
единственным образом.
22

23. Следствия из теоремы о числе решений СЛУ

1.
Система n линейных уравнений с n неизвестными имеет
единственное решение тогда и только тогда, когда матрица
коэффициентов системы невырожденная.
2.
Однородная система A.X= 0 всегда совместна, т.к. имеет
тривиальное решение X= 0. Для существования
нетривиального решения однородной системы необходимо и
достаточно, чтобы выполнялось r < n.
23

24. Фундаментальное множество решений однородной СЛУ

Общее решение однородной системы имеет вид
X c1 E 1 c2 E 2 ... cn r E n r ,
где
с1, с2,…,сn-r
– произвольные постоянные.
Фундаментальное множество решений
E1, E 2, ..., E n r
может быть получено из общего решения, если
свободным неизвестным придавать поочередно
значение 1, полагая остальные равными 0.
24

25. Фундаментальное множество решений однородной СЛУ. Пример 2 (продолжение)

Найти фундаментальное множество решений СЛУ
x1 2 x2 3x3 0
2 x1 4 x2 6 x3 0
3c2 2c1
X c1 , c1 , c2 R
c
2
Общее решение
При c1=1, c2=0
E
2
1
1
0
,
при c2=1, c1=0
E
3
0
2
1
.
25

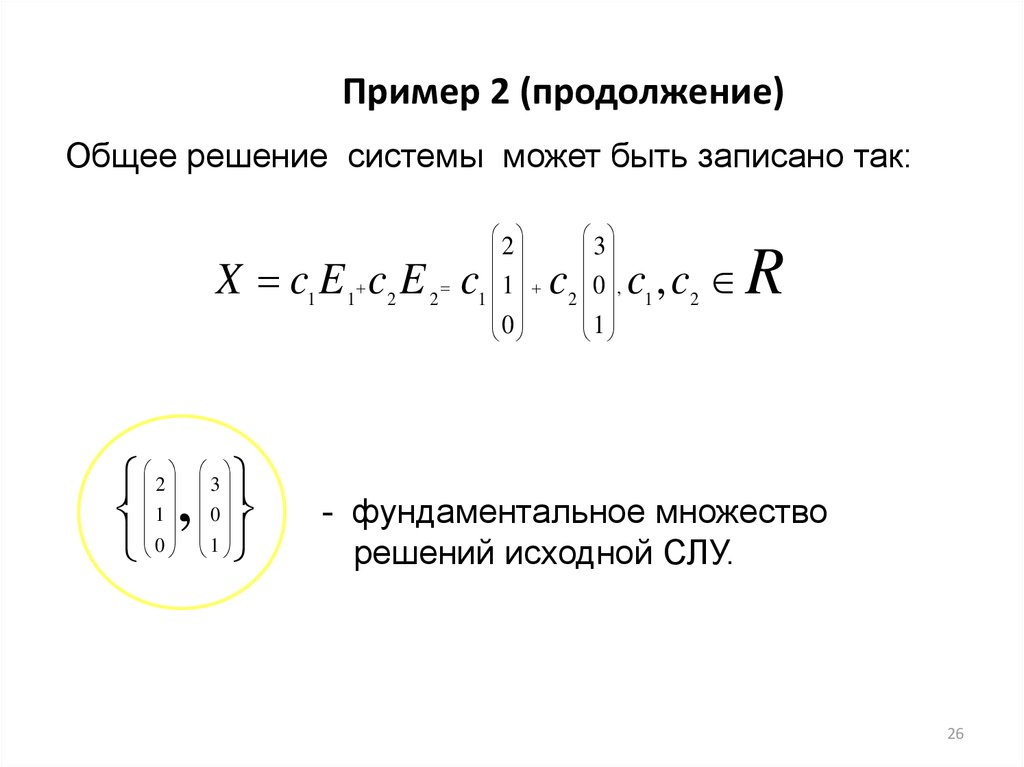
26. Пример 2 (продолжение)

Общее решение системы может быть записано так:
2
1
1
0
X c1 E 1 c2 E 2 c
2
1
0
,
3
0
1
c
3
0 ,
2
1
c1 , c2 R
- фундаментальное множество
решений исходной СЛУ.
26

27. Структура общего решения неоднородной СЛУ

Общее решение неоднородной системы
A.X = B
может быть найдено как сумма общего решения
соответствующей однородной системы
A. X = 0
и произвольного частного решения неоднородной
системы.
~
X X одн X неодн
27

28. Структура множества решений неоднородной СЛУ. Пример 3

Найти множество решений СЛУ
x1 x2 2 x3 x4 1
x4 0
2 x1 3 x2
3 x 4 x 2 x 2 x 1
2
3
4
1
1 1 2 1 1 1 1 2 1 1 1 1 2 1 1
A1 2 3 0 1 0 ~ 0 1 4 1 2 ~ 0 1 4 1 2 .
3 4 2 2 1 0 1 4 1 2 0 0 0 0 0
Укороченная система имеет вид
x1 x2 2 x3 x4 1
x2 4 x3 x4 2
n-r = 2 . Полагаем x3 = c1 , x4 = c2 , тогда
x2 2 4с1 с2
x1 1 2 4с1 с2 2с1 с2 3 6с1 2с2
28

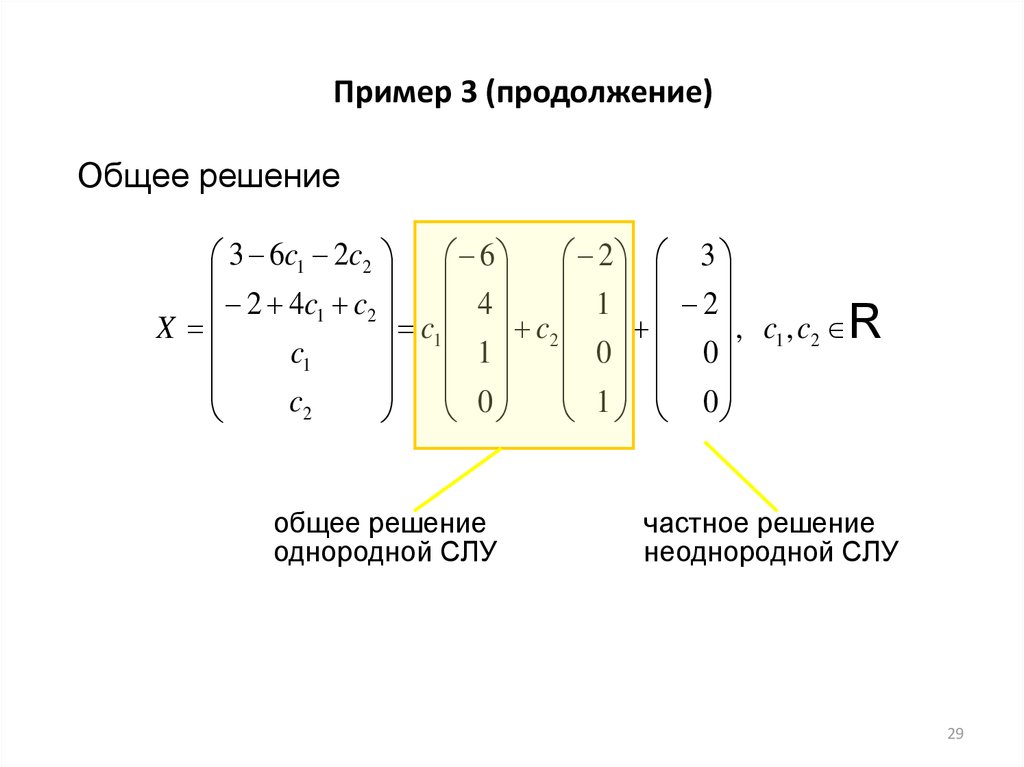
29. Пример 3 (продолжение)

Общее решение
3 6c1 2c2
6
2 3
2 4c1 c2
4
1 2
X
c1 c2
, c1 , c2 R
c1
1
0
0
c2
0
1 0
общее решение
однородной СЛУ
частное решение
неоднородной СЛУ
29