Однородные системы линейных алгебраических уравнений

1.

Однородные системы линейных
алгебраических уравнений

2.

• О п р е д е л е н и е 1. Однородной системой линейных
алгебраических уравнений (СЛАУ), состоящей из m
уравнений с n неизвестными х1,…,хn, называется система
вида:
a11 x1 a1n xn 0
a x a x 0
21 1
2n n
am1 x1 amn xn 0
А x b , (1)
2

3.

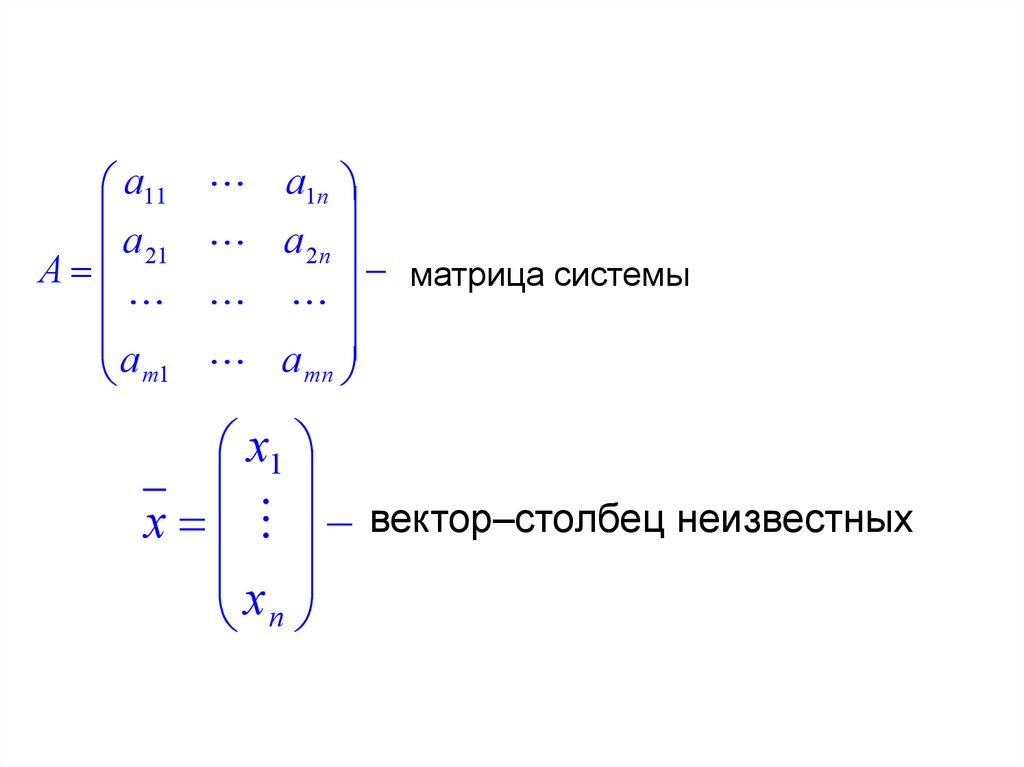
a11
a 21
A
a
m1
a1n
a 2n
матрица системы
a mn
x1
x вектор–столбец неизвестных
x
n

4.

Система линейных однородных
уравнений всегда совместна, т. к. она
всегда имеет, по крайней мере, нулевое
решение x (0; 0; .....0).
Если в системе, А x b , m n а ее
определитель отличен от нуля, то такая
система имеет только нулевое
решение, b=0.

5.

Теорема1: Система линейных однородных уравнений
имеет ненулевое решение тогда и только тогда,
когда ранг ее матрицы меньше количества
неизвестных, r A n .
В этом случае система имеет k n r A свободных
неизвестных, которые обозначают с1 , , с k .

6.

Однородная система линейных алгебраических уравнений
Фундаментальная система решений
x1 k1, x2 k2,.....xn kn
Обозначим решение системы
виде строки
e1 k1, k2,.....kn
Теорема 2: Если
- решение
системы, то
e1 k1, k2,....
kn
- также решение этой системы.
e1 k1, k2,.... kn
Теорема 3: Если
и
e l-, l ,....l
e1 k1, k2,....kn
2
решения системы (1), то при любых
линейная комбинация
данной системы.
1
2
n
1 и 2
- также решение
1e1 2 e2

7.

Фундаментальная система решений (ФСР)
Определение . Система линейно независимых
ek
решений e1 , e2 ,....называется
фундаментальной,
если каждое решение системы (1) является линейной
e1 , e2 ,.....ek
комбинацией решений
Теорема 4: Если ранг матрицы А r меньше числа
переменных n, то всякая фундаментальная система
решений системы (1) состоит из
nрешений.
r

8.

Фундаментальная система решений
Пример. Найти общее решение и ФСР однородной системы
2 x1 x2 3 x3 x4 0
3 x1 2 x2 x3 0
x 3x 4 x x 0
2
3
4
1
Решение. Приведем систему к ступенчатому виду с помощью метода
Гаусса. Для этого записываем матрицу системы (в данном случае, так как
система однородная, то ее правые части равны нулю, в этом случае
столбец свободных коэффициентов можно не выписывать, так как при
любых элементарных преобразованиях в правых частях будут получаться
нули):

9.

Ранг матрицы равен 2, свободные неизвестные,
0 0 0
2 1 3 1
11
0 1
7
3 2 1 0
1 3 4 1
5
1
0
7
5
2
x
x
1 7 3 7 x4 0
x 11 x 3 x 0
2 7 3 7 4
0
3
7
2
7
x3 , x4 .
x3 7c1 , x4 7c2
x1 5c1 2c2
x1
5
2
x 11c 3c
x
11
3
2
1
2
2
c1
c2
0
x3
7
x3 7c1
x4 7c2
x
0
7
4

10.

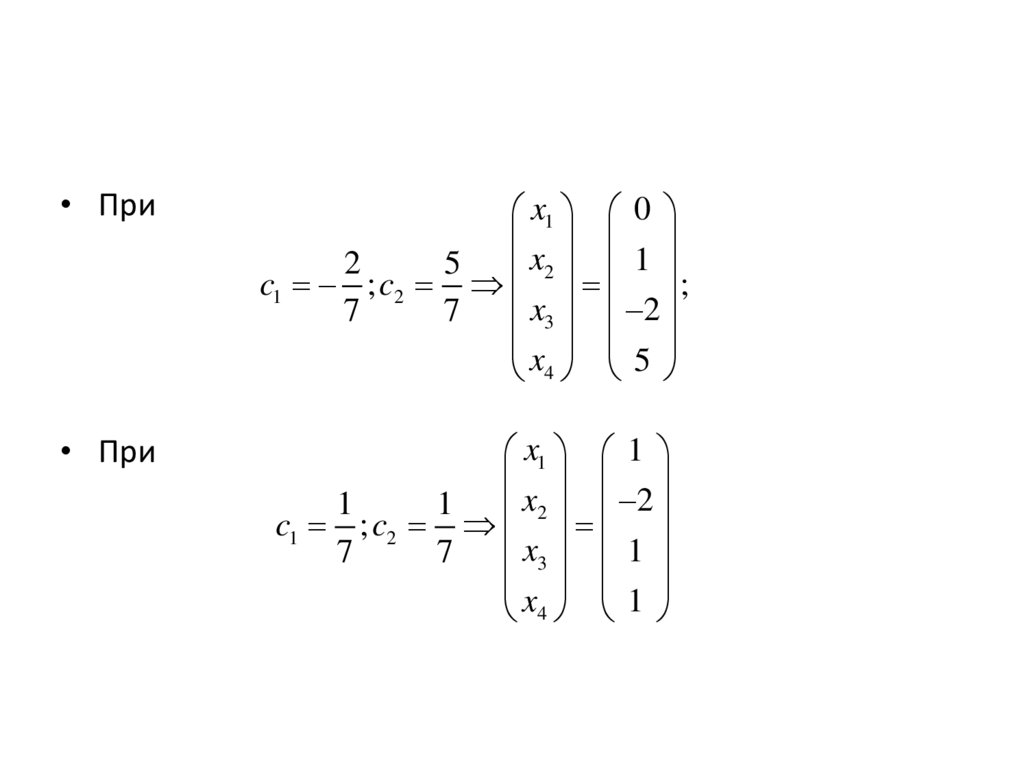
• При
x1 0
2
5 x2 1
c1 ; c2
;
7
7 x3 2
x4 5
• При
x1 1
1
1 x2 2
c1 ; c2
7
7 x3 1
x4 1