Лекция 3

1. Лекция 3

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Сжимаемость
Скорость звука
Число Маха
Распространение слабых возмущений давления
Физический смысл числа Маха
Примеры сверхзвуковых течений
Теплообмен
Теплопроводность
Конвекция
Радиация
Стандартная атмосфера
Кинематика жидкости
Ускорение жидкой частицы
Полные производные от термодинамических параметров
Уравнение линии тока
Вращательное движение жидкой частицы
Деформационное движение жидкой частицы
Деформация скашивания при движении жидкой частицы
Деформация скашивания при движении жидкой частицы
Уравнение неразрывности
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
1

2.

Сжимаемость
Сжимаемостью называется свойство среды изменять объём
при изменении давления.
Скорость звука может служить характеристикой сжимаемости.
(3.01)
(3.02)
(3.03)
– удельная газовая постоянная
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
2

3.

Скорость звука в воздухе
– показатель адиабаты, для воздуха κ=1,4
a κRT 1,4 287,26 T 20,054 T 20,05 T
a 20,05 T
(3.04)
Инженерная формула
скорости звука для воздуха
Стандартное значение
скорости звука для
воздуха
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
(3.05)
3

4.

Число Маха
Мерой сжимаемости движущегося воздуха является
число Маха – безразмерная величина (критерий подобия),
равная отношению скорости течения к местной скорости звука
V
M
a
(3.06)
M 1 - Дозвуковое течение
M 1 - Сверхзвуковое течение
M 1 - Трансзвуковое или околозвуковое течение
M 1 - Звуковое течение
M 5 - Гиперзвуковое течение
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
4

5.

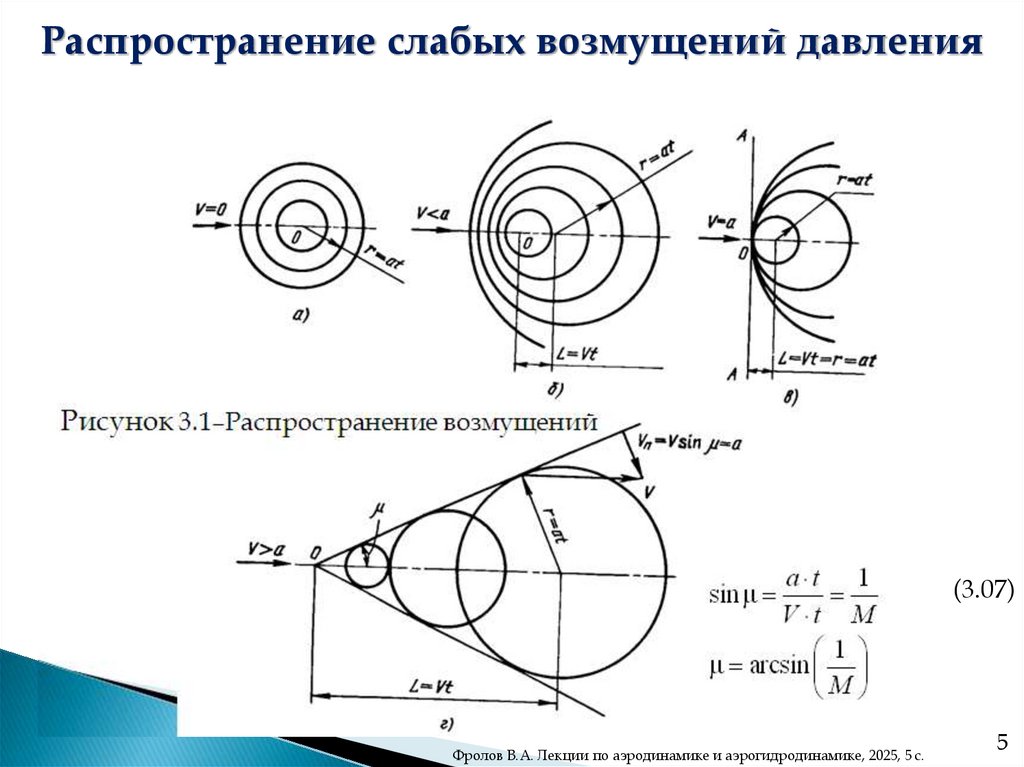
Распространение слабых возмущений давления
Рисунок 3.1–Распространение возмущений
a t
1
V t M
1
μ arcsin
M
sin μ
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
(3.07)
5

6.

Физический смысл числа Маха
cp
R
c p cv R cv 1 R cv
κ 1
cv
V2 2 V2 2
V2 2
V 2 2 κ
V 2 2 κ κ κ 1
2
(4.5)
M
2
R
R
a
e
cvT
2
T
T κ
κ 1
κ 1
κ 1
(3.08)
(3.09)
(3.10)
Квадрат числа Маха – это мера, характеризующая отношение
кинетической энергии движения газа вдоль определённого
направления к хаотическому движению молекул этого газа.
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
6

7.

Примеры сверхзвуковых течений
Рисунок 3.2 -Течение около комбинации конуса и цилиндра М=1,84 θ=12,5°
[http://nashaucheba.ru/docs/55/54032/conv_1/file1_html_m49482e0.jpg]
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
7

8.

Примеры сверхзвуковых течений
Рисунок 3.3 - Течение около комбинации оживало и цилиндра М=2,58
[http://cs625726.vk.me/v625726828/81161/HRcE5b_TpTM.jpg]
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
8

9.

Примеры сверхзвуковых течений
Рисунок 3.4 - Течение около шара М=1,53
https://im1-tub-ru.yandex.net/i?id=18f7c48944f00ad31433ad41122c011a&n=33&h=190&w=158
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
9

10.

Теплообмен
Перенос тепла из одной области газового потока в
другую называется теплообменом.
Процессы теплообмена возникают между телами,
если температура их различна. Тело или среда, имеющие
более высокую температуру T1, называются
теплоотдающими. Соответственно, тело или среда
с температурой T2<T1 называются тепловоспринимающими.
Количество тепла, проходящее через данную
контрольную поверхность в единицу времени,
называется тепловым потоком (Q). Тепловой
поток, приходящийся на единицу площади
поверхности, называется плотностью теплового потока
или удельным тепловым потоком (q).
Теплопроводность: закон Фурье (1822 г.)
q T
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
(3.11)
10

11.

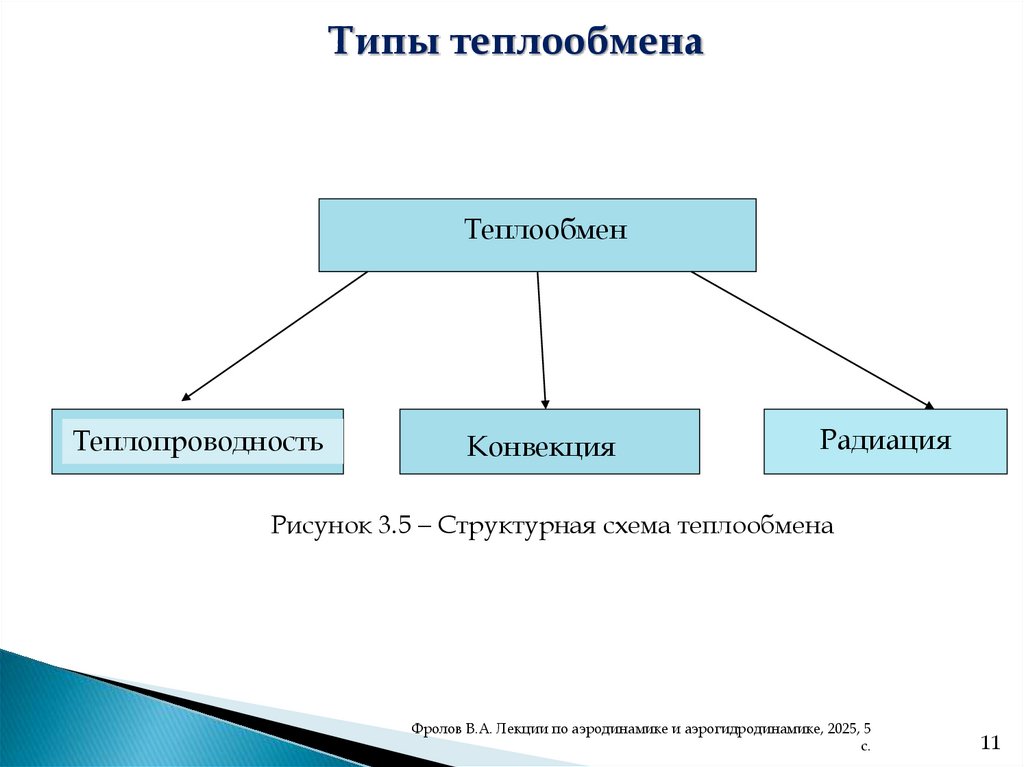
Типы теплообмена
Теплообмен
Теплопроводность
Конвекция
Радиация
Рисунок 3.5 Структурная схема теплообмена
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5
c.
11

12.

Теплопроводность
Соотношение молекулярного переноса и тепла в газе характеризуется
числом Прандтля
cp
(3.12)
Pr
Число Pr зависит от температуры. В случае воздуха, его можно принять
постоянным и равным 0,7 .
При турбулентном режиме течения тепловой поток определяется
также законом Фурье, но с другим коэффициентом пропорциональности:
(3.13)
где
- турбулентная теплопроводность. Безразмерный параметр
-турбулентное число Прандтля.
Уравнение теплопроводности ΔT=0
(3.14)
T
T
T
T gradT
i
j
k
x
y
z
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
12

13.

Конвекция
Конвективным теплообменом называют обмен теплотой между
различно нагретыми областями воздуха или воздухом и твёрдым телом,
обусловленный относительным движением макрообъёмов воздуха.
Тепловой поток при теплоотдаче определяется формулой
Ньютона
(3.15)
где
коэффициент теплоотдачи, численно равный
количеству теплоты, получаемой или отдаваемой единицей площади
стенки за единицу времени при разности температур между стенкой и
воздухом, равной 1 K.
.
Рисунок 3.6 – Точки на теле и вблизи поверхности, по
которым определяется конвективный теплообмен
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
13

14.

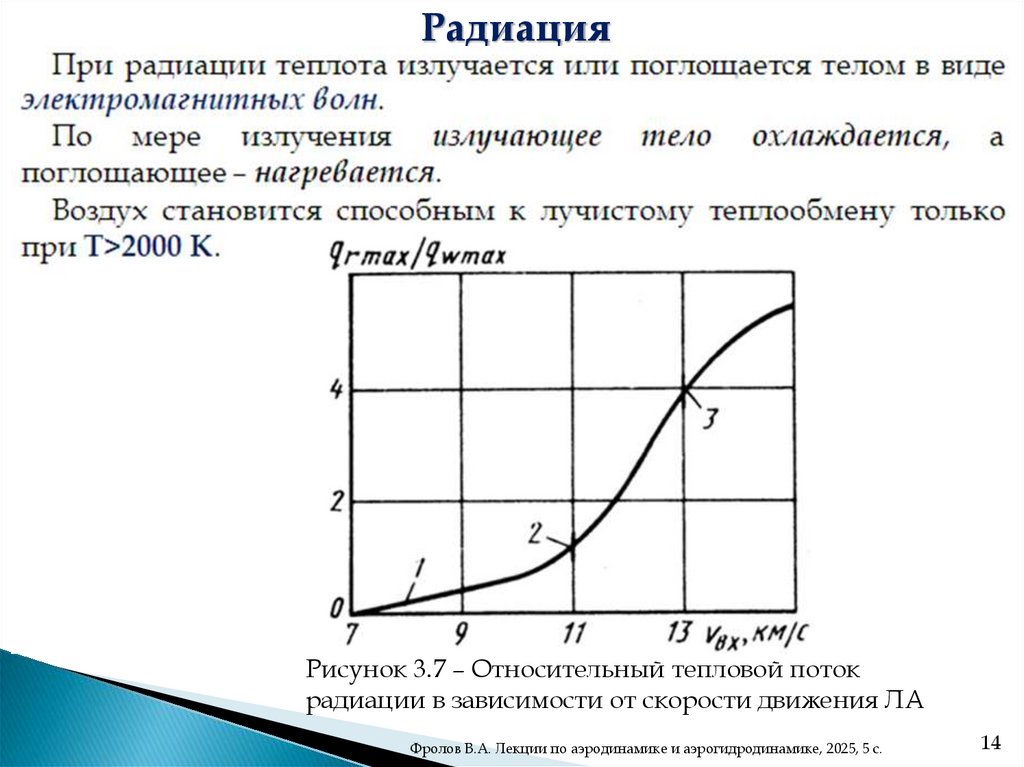
Радиация
При радиации теплота излучается или поглощается телом в виде
электромагнитных волн.
По мере излучения излучающее тело охлаждается, а
поглощающее – нагревается.
Воздух становится способным к лучистому теплообмену только
при T>2000 K.
Рисунок 3.7 – Относительный тепловой поток
радиации в зависимости от скорости движения ЛА
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
14

15.

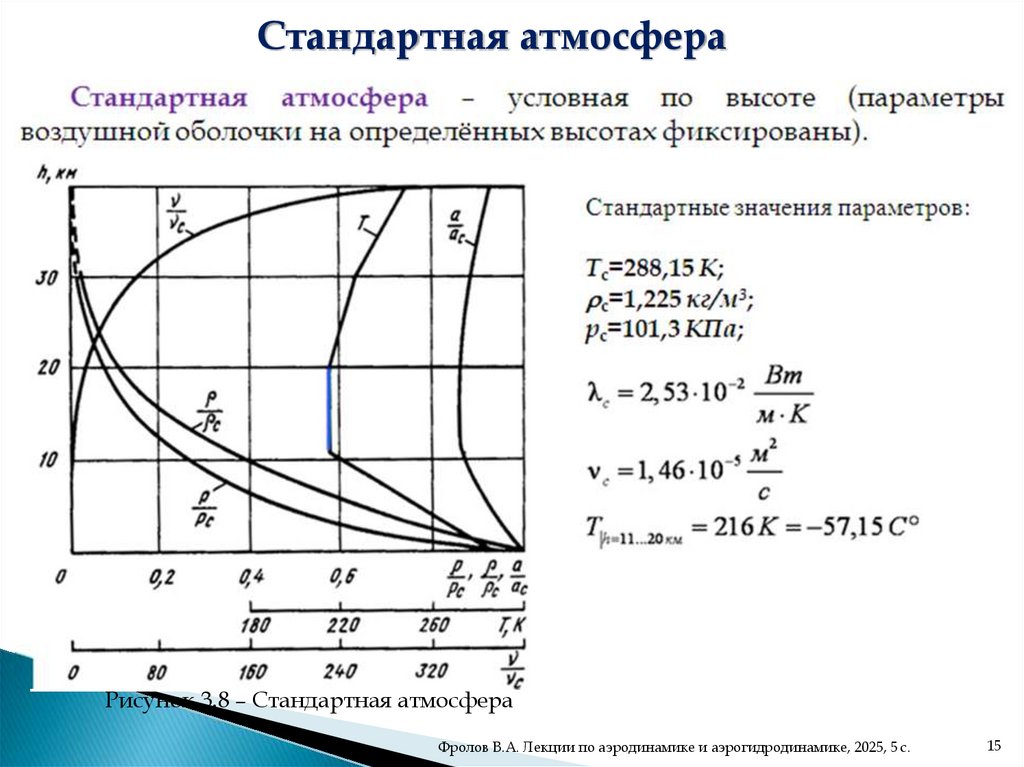
Стандартная атмосфера
Стандартная атмосфера – условная по высоте (параметры
воздушной оболочки на определённых высотах фиксированы).
Стандартные значения параметров:
Tc=288,15 K;
c=1,225 кг/м3;
pc=101,3 КПа;
Рисунок 3.8 – Стандартная атмосфера
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
15

16.

Кинематика жидкости. Ускорение
Кинематика жидкости – раздел механики, который
рассматривает поле скорости, ускорения и не рассматривает
силовое воздействие между телом и средой.
V V x, y, z , t ; V Vxi Vy j Vz k
dV V V dx V dy V dz
a
;
dt
t x dt y dt z dt
dx
dy
dz
Vx ,
Vy ,
Vz ;
dt
dt
dt
V
V
V
V
a
Vx
Vy
Vz
;
t
x
y
z
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
(3.16)
(3.17)
(3.18)
(3.19)
16

17.

Кинематика жидкости. Частные производные
(3.20)
(3.21)
(3.22)
(3.23)
d dx dy dz dx dy dz
dt
t x dt y dt z dt t dt x dt y dt z
Vx
Vy
Vz
t
x
y
z
(3.24)
(3.25)
(3.26)
(3.27)
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
17

18.

Кинематика жидкости. Ускорение
Скалярное произведение двух векторов:
(3.28)
(3.29)
Vx
V
V
V
V
Vy
Vz
V V a
V V
x
y
z
t
(3.30)
(3.31)
- локальное (субстанциональное) ускорение
- конвективное ускорение
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
18

19.

Частные производные по времени
температуры, энтальпии и энтропии
(3.32)
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
19

20.

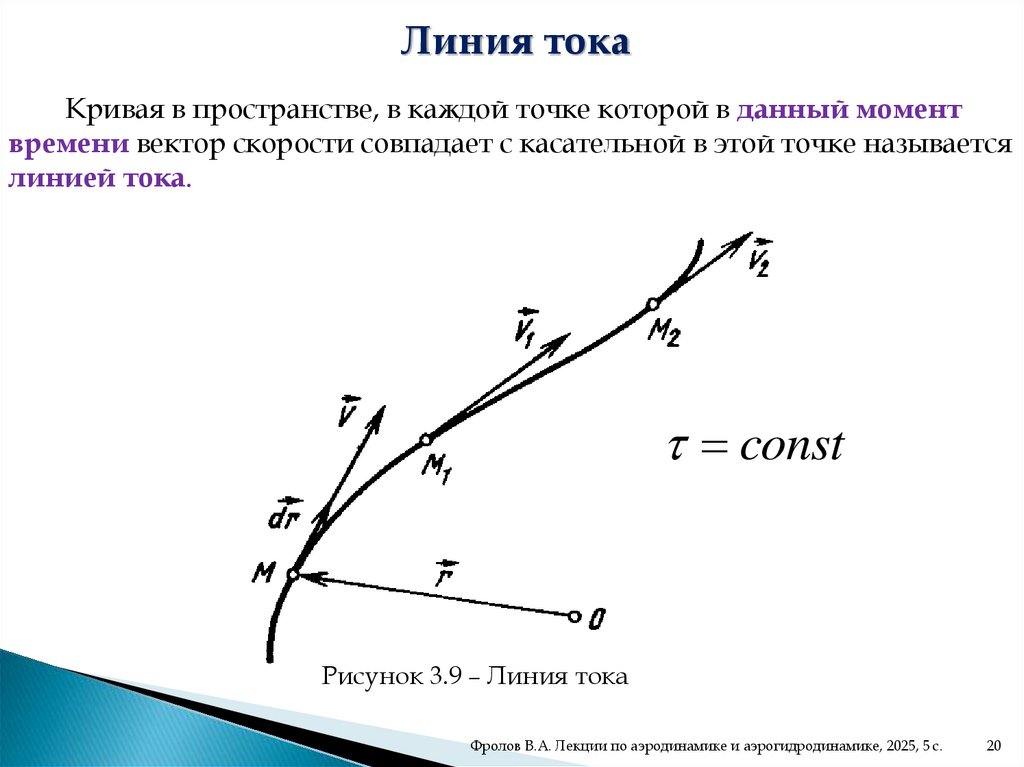
Линия тока
Кривая в пространстве, в каждой точке которой в данный момент
времени вектор скорости совпадает с касательной в этой точке называется
линией тока.
const
Рисунок 3.9 – Линия тока
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
20

21.

Дифференциальное уравнение линии тока
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
21

22.

Уравнение линии тока и траектории
Траектория это след частицы в пространстве.
Если рассматривать установившееся (стационарное) течение, линия
тока и траектория совпадают. Обратное не выполняется.
Дифференциальное уравнение линии тока:
(3.33)
Система дифференциальных уравнений траектории:
dx
dt Vx
dy
Vy
dt
dz
dt Vz
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
(3.34)
22

23.

Спасибо за внимание!
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
23

24.

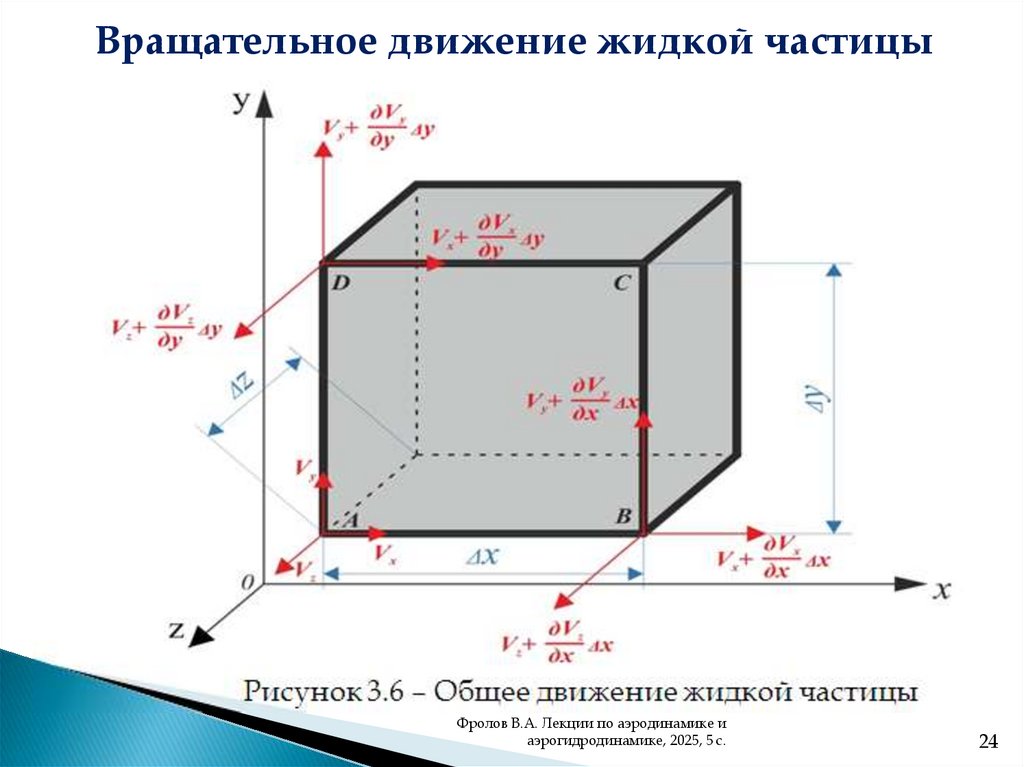
Вращательное движение жидкой частицы
Рисунок 3.6 – Общее движение жидкой частицы
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
24

25.

Вращательное движение жидкой частицы
Будем полагать вектор скорости непрерывной функцией координат и
времени.
Непрерывная функция является дифференцируемой функцией.
Дифференцируемая функцией может быть разложена в ряд Тейлора.
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
25

26.

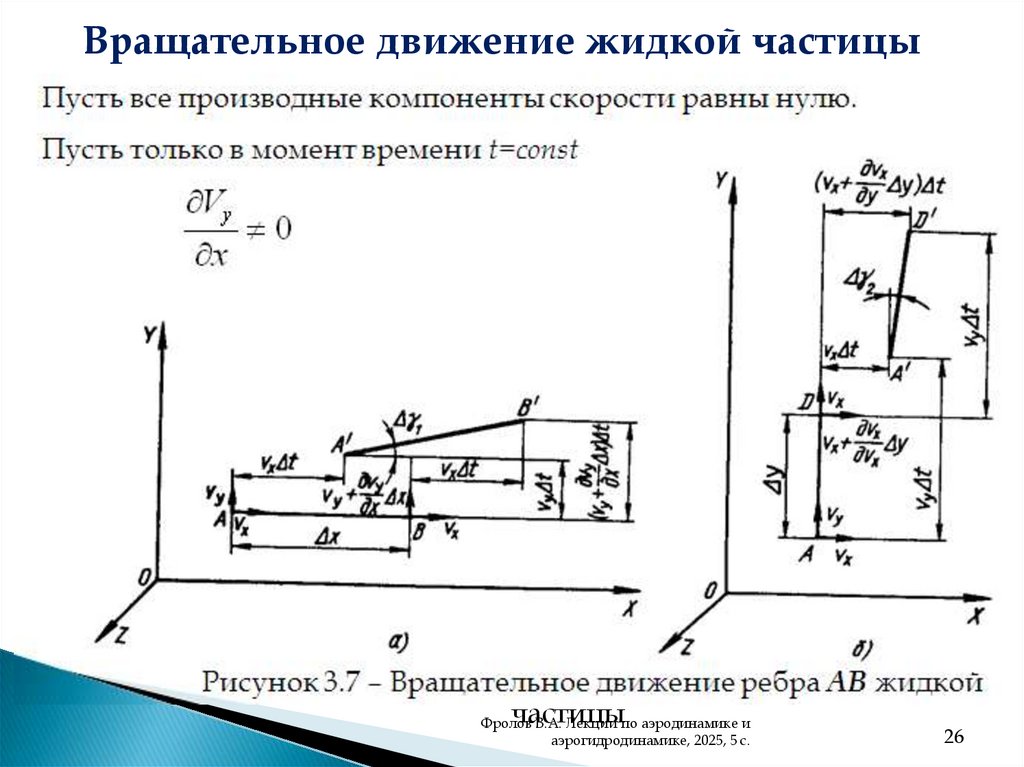
Вращательное движение жидкой частицы
Пусть все производные компоненты скорости равны нулю.
Пусть только в момент времени t=const
Vy
x
0
Рисунок 3.7 – Вращательное движение ребра АВ жидкой
частицы
Фролов
В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
26

27.

Вращательное движение жидкой частицы
(3.24)
Vx
0
y
(3.25)
Правило знаков: вращение против часовой стрелки «+», а по часовой – «-»
(3.26)
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
27

28.

Вращательное движение жидкой частицы
(3.27)
(3.28)
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
28

29.

Деформационное движение жидкой частицы
Рисунок 3.8 – Деформационное движение ребра АВ жидкой частицы
(3.29)
(3.30)
(3.31)
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
29

30.

Деформация скашивания при движении
жидкой частицы
(4.28)
Vz Vy
2ezy 2eyz
;
y
z
Vx Vz
2exz 2ezx
.
z
x
(4.29)
exx exy exz
Тензор скоростей деформаций S e
yx e yy e yz
e
e
e
zx zy zz
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
(4.30)
30

31.

Уравнение неразрывности в полных производных
Относительное изменение объёма по времени равно
(4.31)
(4.32)
(4.33)
(4.34)
(4.35)
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
31

32.

Уравнение неразрывности в частных
производных
(4.36)
ρ
div ρ V 0
t
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
(4.37)
32

33.

Уравнение неразрывности
Частные случаи уравнения
неразрывности
1) Установившиеся течение
(4.38)
2) Несжимаемое течение
Vx Vy Vz
ρ const divV 0 divV
x
y
z
Vx Vy Vz
0
x
y
z
(4.39)
divV 0
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
33

34.

Спасибо за внимание!
Фролов В.А. Лекции по аэродинамике и
аэрогидродинамике, 2025, 5 c.
34

35.

Спасибо за внимание!
Фролов В.А. Лекции по аэродинамике и аэрогидродинамике, 2025, 5 c.
35