лекция 2 по ЭиЭА (1)

1. Лекция 2. 1.Электродинамические усилия в электрических аппаратах. 2.Методы расчета электродинамических усилий. 3.Усилия и

моменты, действующие на элементы Э и ЭА при работе в цепях постоянного
тока.
4.Усилия и моменты, действующие на элементы Э и ЭА при работе в цепях переменного
тока.
1. При КЗ в сети через токоведущую часть аппарата могут проходить токи, в десятки раз превышающие
номинальный. При взаимодействии этих токов с магнитным полем других токоведущих частей аппарата
создаются электродинамические усилия (ЭДУ). Эти усилия стремятся деформировать как проводники
токоведущих частей, так и изоляторы, на которых они крепятся. При номинальных токах эти усилия малы и
ими можно пренебречь.
Электродинамической стойкостью аппарата называется
противостоять ЭДУ, возникающим при прохождении токов КЗ.
его
способность
Эта величина может выражаться либо непосредственно амплитудным значением тока iдин, при котором
механические напряжения в деталях аппарата не выходят за пределы допустимых значений, либо
кратностью этого тока относительно амплитуды номинального тока
k дин iдин /( 2I ном )
Иногда электродинамическая стойкость оценивается действующим значением тока за один период (T =
0,02 с, f = 50 Гц) после начала КЗ.

2. 2. Для расчета ЭДУ используются два метода. В первом ЭДУ определяется как результат взаимодействия проводника с током и

магнитного поля по
правилу Ампера. На элементарный проводник длиной dl, с током i, находящийся в магнитном поле с
индукцией В, созданной другим проводником (рис.2а), действует усилие
dP idlB iBdl sin ,
где — угол между векторами элемента dl и индукции В, измеряемый по кратчайшему расстоянию между
ними.
За направление dl принимается направление тока в элементе. Направление индукции В, создаваемой
другим проводником, определяется по правилу буравчика, а направление усилия — по правилу левой руки.
Для определения полного электродинамического усилия, действующего на проводник длиной l, необходимо
просуммировать усилия, действующие на все его элементы:
l
l
P dP iB sin dt
0
0
В случае произвольного расположения
проводников в одной плоскости =90° и
l
P iBdl
0
,Н
Описанный метод рекомендуется применять
тогда, когда индукцию в любой точке проводника
можно найти аналитически, используя закон
Био-Савара - Лапласа.
Рис. 2. Направление ЭДУ, действующего на элемент с током

3. Второй метод основан на использовании энергетического баланса системы проводников с током. Если пренебречь электростатической

энергией системы и принять, что при деформации токоведущих контуров или их
перемещении под воздействием ЭДУ токи в них неизменны, то усилие можно найти как частную производную от
электромагнитной энергии данной системы по координате, в направлении которой оно действует. Тогда усилие
взаимодействия между двумя контурами
P dW / dx i1i2 dM / dx
, Н
где W=(1/2)L1i12+(1/2)L2i22+Mi1i2 — электромагнитная энергия двух взаимосвязанных контуров; L1, L2 —
индуктивности изолированных контуров; i1, i2 — токи, протекающие в них; М — взаимная индуктивность; x —
возможное перемещение в направлении действия усилия.
При расчете усилия взаимодействия контуров считается, что энергия изменяется только в результате изменения
взаимного расположения контуров, а энергия, обусловленная их собственной индуктивностью - неизменна. При
расчете можно считать, что токи в контурах не зависят от их деформаций или их перемещения под действием
усилий.
Таким образом, эта формула получила название энергетической. Энергетический метод удобен, когда известна
аналитическая зависимость индуктивности или взаимной индуктивности от геометрических размеров.
3.
При проектировании аппаратов важно определить
направление действия ЭДУ. При определении
направления усилия учитывается индукция, создаваемая
всеми остальными проводниками, за исключением того
проводника, для которого оно находится.
В качестве примера рассмотрим методику
определения усилий для случаев параллельного,
перпендикулярного и кольцевого расположения
проводников.
Рассмотрим бесконечно тонкие проводники
конечной длины (рис.3).
Индукция в любой точке пространства в этом случае легко
определяется аналитически.
Рис.3. ЭДУ между
параллельными проводниками

4. Для определения усилия воспользуемся первым методом. Согласно закону Био-Савара—Лапласа элементарная индукция от элемента тока

i1dy в месте расположения элемента dx
0 i1dy
dB d H
sin
2
4 r
где — магнитная постоянная, равная 4 10
Гн/м; - угол между током i и лучом r, проведенным от dy к dx.
0
-7
1
Полная индукция от проводника l1 в месте расположения элемента dх
l1
1
0
0
1
1
1
2
0
2
где
0 cоs 1 cоs 2
sin
sin
B
i
dy
i
d i
4
r
4
a
4
a
a
a
a
y
;r
; dy 2 d
tg
sin
sin
Усилие взаимодействия между проводником l1 и элементом dx
0 cos 1 cos 2
dPx Bi 2 dx
i1i2 dx
4
a
и после замены переменной на l (при условии равенства l1=l2=l)
2
2
l
a
a
7
Px 10 i1i2 1 10 7 ki1i2
a
l
l
где k – коэффициент контура, зависящий только от размеров проводников.
В реальных условиях при отличии сечения проводника от круга (например, при прямоугольной форме) при
расчете ЭДУ необходимо учитывать поверхностный эффект, для чего можно воспользоваться кривыми Двайта.

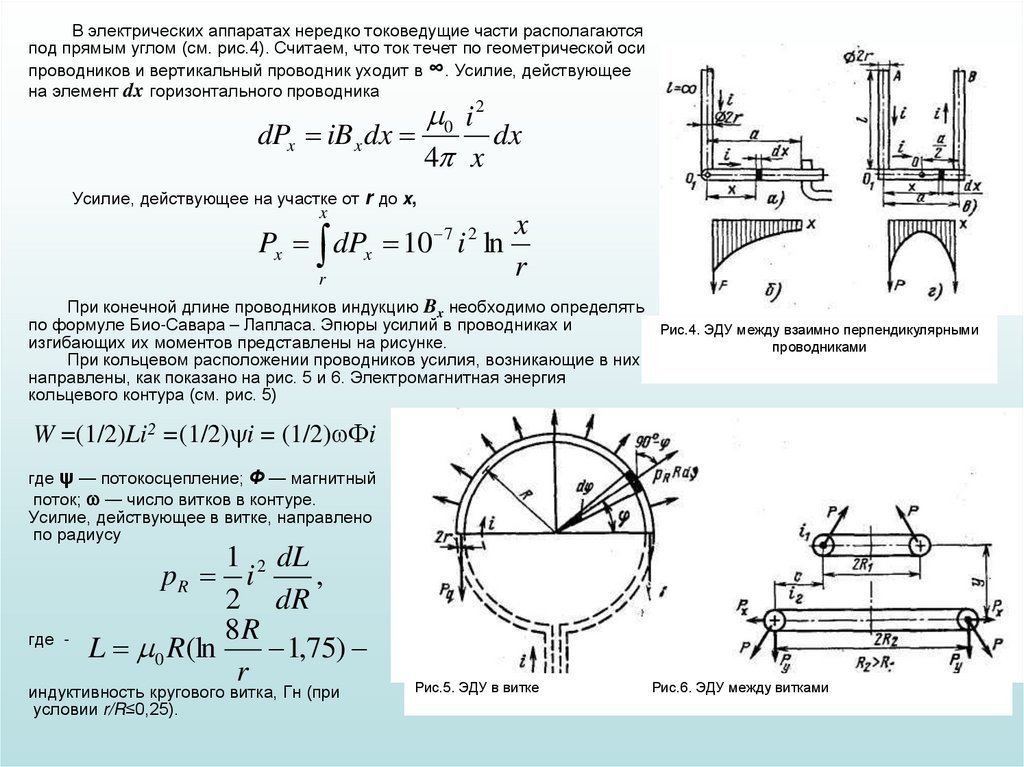
5. В электрических аппаратах нередко токоведущие части располагаются под прямым углом (см. рис.4). Считаем, что ток течет по

геометрической оси
проводников и вертикальный проводник уходит в ∞. Усилие, действующее
на элемент dx горизонтального проводника
2
0
x
x
dP iB dx
Усилие, действующее на участке от r до x,
x
i
dx
4 x
Px dPx 10 7 i 2 ln
r
x
r
При конечной длине проводников индукцию Bx необходимо определять
по формуле Био-Савара – Лапласа. Эпюры усилий в проводниках и
Рис.4. ЭДУ между взаимно перпендикулярными
изгибающих их моментов представлены на рисунке.
проводниками
При кольцевом расположении проводников усилия, возникающие в них,
направлены, как показано на рис. 5 и 6. Электромагнитная энергия
кольцевого контура (см. рис. 5)
W =(1/2)Li2 =(1/2) i = (1/2) Фi
где ψ — потокосцепление; Ф — магнитный
поток; — число витков в контуре.
Усилие, действующее в витке, направлено
по радиусу
1 2 dL
i
,
2 dR
8R
где L 0 R(ln
1,75)
r
pR
индуктивность кругового витка, Гн (при
условии r/R≤0,25).
Рис.5. ЭДУ в витке
Рис.6. ЭДУ между витками

6. Полное усилие в витке: Усилие РR приложено к окружности длиной 2R. При расчете электродинамической стойкости необходимо знать

Полное усилие в витке:
0 2
8R
PR
i (ln
0,75)
2
r
Усилие РR приложено к окружности длиной 2 R. При расчете электродинамической стойкости необходимо знать
усилие Рq, действующее в сечении витка и стремящееся его разорвать. Для определения Рq рассмотрим уравнение
равновесия полувитка. Очевидно, что
2
Pq p R Rd sin
где
и после интегрирования
0
8R
Pq 10 i (ln
0,75),
r
7 2
pR — усилие, действующее на единицу длины, равное РR /(2 R).
Если катушка насчитывает w витков, то , то усилие возрастает в w2 раз.
4.
При расчете контакторов, автоматов защиты и ряда других электрических аппаратов необходимо учитывать
большие ЭДУ, действующие в их токоведущих частях при режиме КЗ. В однофазной цепи при одинаковом
направлении тока проводники притягиваются с усилием
P 10 7 kIm2 sin 2 t
Pm
(1 cos 2 t )
2
Таким образом, усилие имеет постоянную составляющую Рm /2 и переменную составляющую двойной частоты
(Рm /2)cos 2 t. Среднее значение усилия за период
T
P
1
Pср Pdt m cI 2
T0
2
где I – действующее значение тока.
Среднее значение ЭДУ пропорционально квадрату действующего значения тока. Изменение усилия во времени
при переменном токе в однофазной цепи (рис.7) происходит без изменения своего знака.

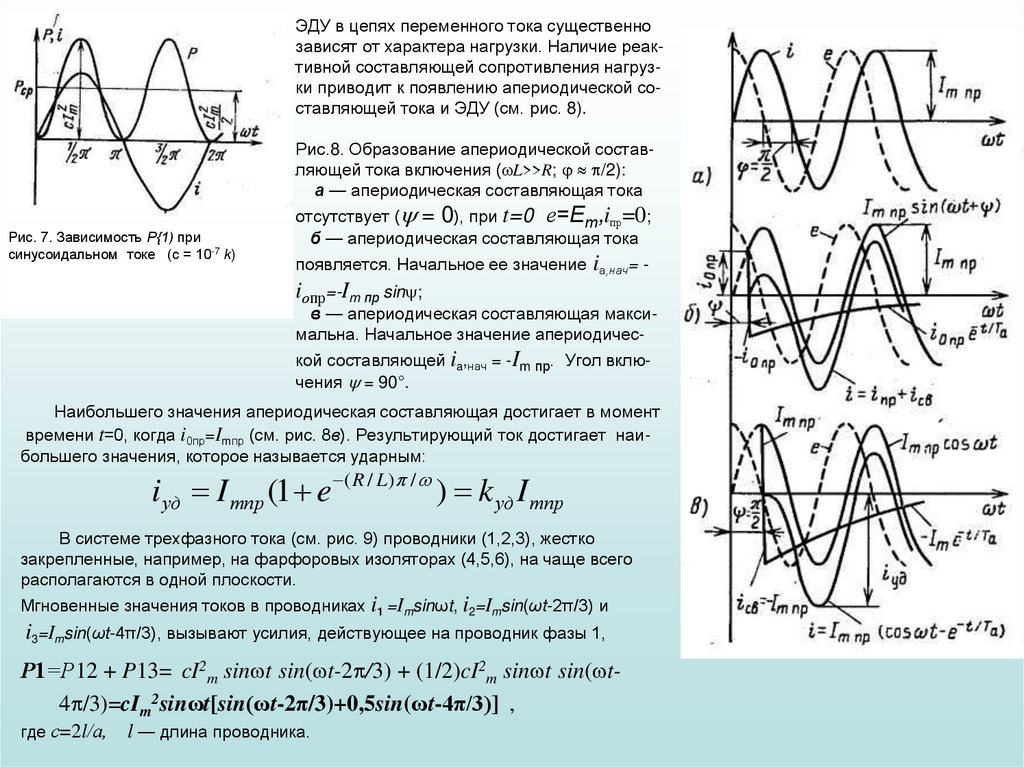
7. ЭДУ в цепях переменного тока существенно зависят от характера нагрузки. Наличие реак-тивной составляющей сопротивления

ЭДУ в цепях переменного тока существенно
зависят от характера нагрузки. Наличие реактивной составляющей сопротивления нагрузки приводит к появлению апериодической составляющей тока и ЭДУ (см. рис. 8).
Рис.8. Образование апериодической составляющей тока включения ( L>>R; /2):
а — апериодическая составляющая тока
Рис. 7. Зависимость Р{1) при
синусоидальном токе (с = 10-7 k)
отсутствует ( = 0), при t=0 е=Ет,iпр=0;
б — апериодическая составляющая тока
появляется. Начальное ее значение iа,нач= -
iопр=-Im пр sin ;
в — апериодическая составляющая максимальна. Начальное значение апериодической составляющей ia,нач = -Im пр. Угол включения = 90°.
Наибольшего значения апериодическая составляющая достигает в момент
времени t=0, когда i0пр=Imпр (см. рис. 8в). Результирующий ток достигает наибольшего значения, которое называется ударным:
i уд I mпр (1 e ( R / L) / ) k уд I mпр
В системе трехфазного тока (см. рис. 9) проводники (1,2,3), жестко
закрепленные, например, на фарфоровых изоляторах (4,5,6), на чаще всего
располагаются в одной плоскости.
Мгновенные значения токов в проводниках i1 =Imsinωt, i2=Imsin(ωt-2π/3) и
i3=Imsin(ωt-4π/3), вызывают усилия, действующее на проводник фазы 1,
Р1=Р12 + P13= cI2m sin t sin( t-2 /3) + (1/2)cI2m sin t sin( t4 /3)=cIm2sinωt[sin(ωt-2π/3)+0,5sin(ωt-4π/3)] ,
где с=2l/а,
l — длина проводника.

8. Изменение усилия, действующего на проводники, показано на рис. 9. Усилие меняет знак и достигает в определенные моменты времени

максимальных значений отталкивания и
притягивания.
Исследовав Р1 на максимум, получим максимальное
значение отталкивающего усилия
P1от max = - 0,805cIm2
Максимальное притягивающее усилие
P1прит max = - 0,055cIm2
Мгновенное значение усилия, действующего на фазу 2,
P2=P21+P23= cIm2{sin( t - 2 /3)[sin t + sin( t 4 /3)]}
Исследование показывает, что максимальные значения
притягивающего и отталкивающего усилия
P2 от max = P2прит max =0,87cIm2
Проведя аналогично расчет ЭДУ для фазы 3, получим
Рис. 9. ЭДУ в трехфазной системе
и
P3от max = - P1от max
P3прит max = - P1прит max
Наибольшее усилие действует на проводник средней фазы.
По нему и производится расчет.
При расчете электродинамической стойкости аппарата
необходимо учитывать возможность появления резонанса
между гармонически меняющимся ЭДУ и собственными
механическими колебаниями токоведуших деталей.