Электрические и электронные аппараты. Лекция № 2

1. Электрические и электронные аппараты

Лекция № 2
Электродинамические усилия в аппаратах при
переменном токе. Механический резонанс.
Электрические контакты. Контактные системы
коммутационных аппаратов.

2.

Электродинамические усилия в КА при переменном токе
Если токи в проводниках равны, то мгновенное значение ЭДУ будет
определяться выражением:
f 10 7 k12k фi 2
где
(2.1)
i – мгновенные значения токов в проводниках, описываемое
выражением:
i I m sin( t )
(2.2)
где ω – угловая частота тока;
Im – амплитуда тока.
После подстановки (2.2) в (2.1) и преобразования получим:
7
f 10 k12k фIm sin ( t ) 10
2
2
7
2 1 cos(2 t )
k12k фIm
(2.3)
2
2

3.

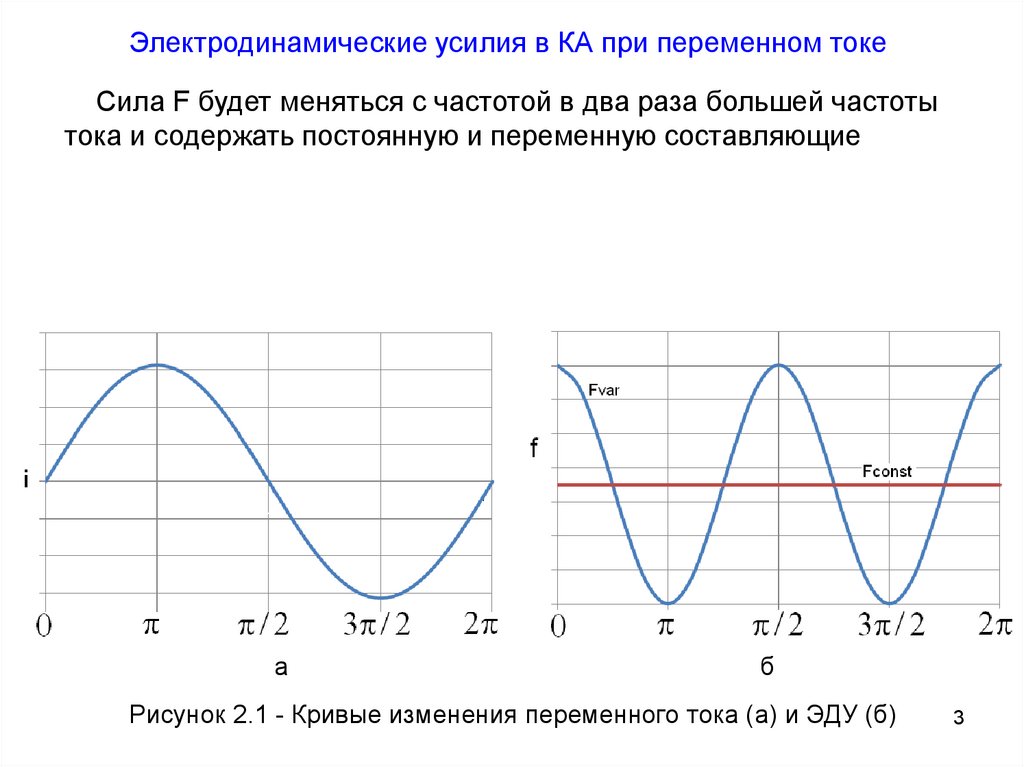
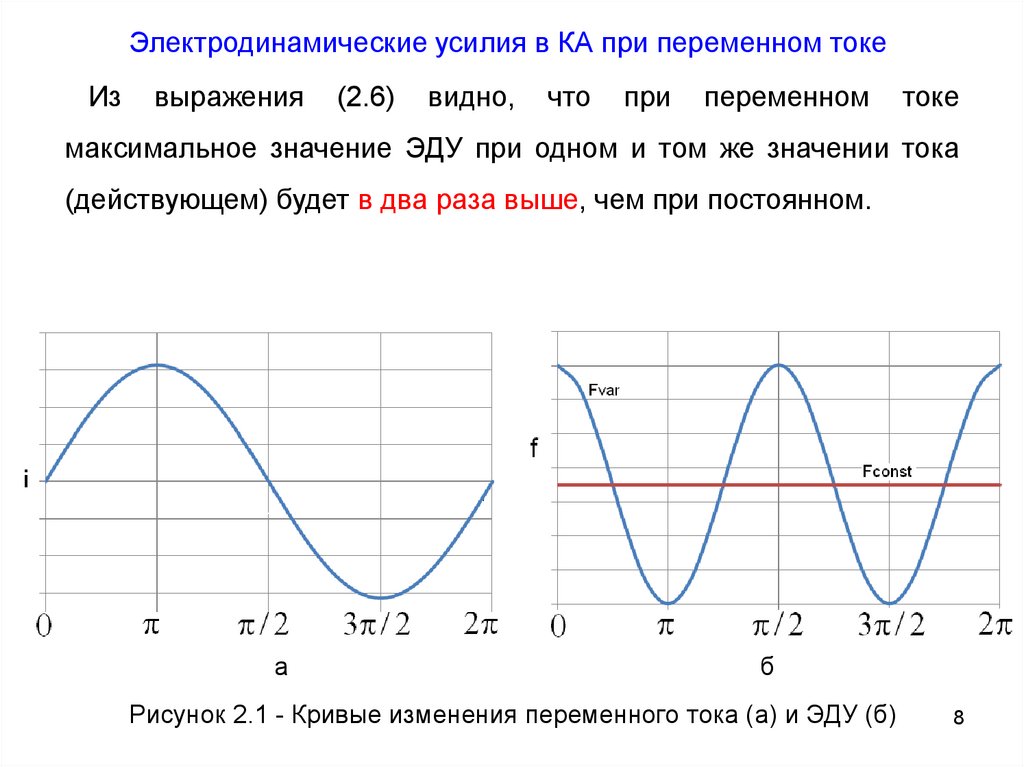
Электродинамические усилия в КА при переменном токе
Сила F будет меняться с частотой в два раза большей частоты
тока и содержать постоянную и переменную составляющие
а
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
3

4.

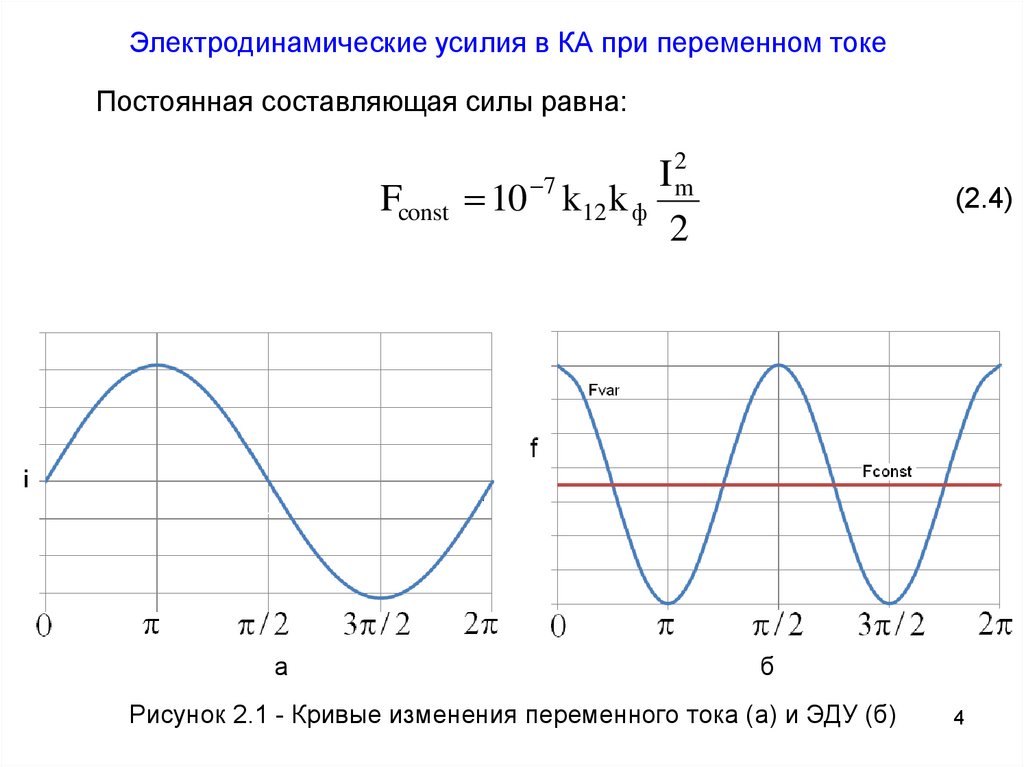
Электродинамические усилия в КА при переменном токе
Постоянная составляющая силы равна:
2
I
Fconst 10 7 k12 k ф m
2
а
(2.4)
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
4

5.

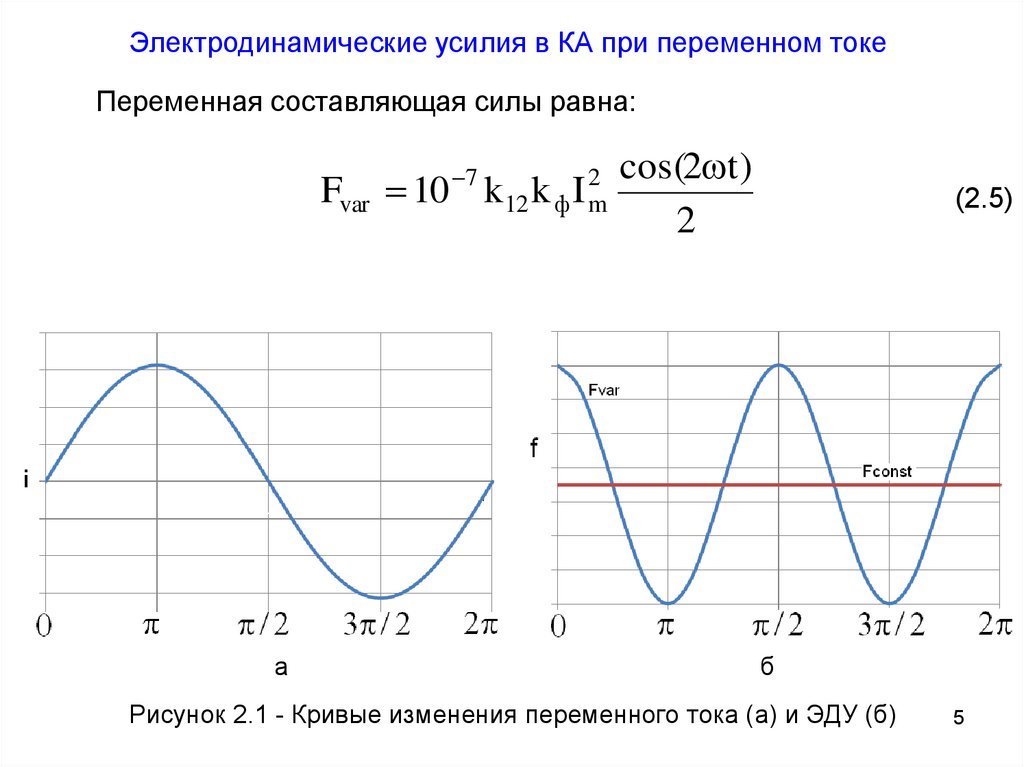
Электродинамические усилия в КА при переменном токе
Переменная составляющая силы равна:
Fvar 10
а
7
2 cos(2 t )
k12 k ф I m
(2.5)
2
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
5

6.

Электродинамические усилия в КА при переменном токе
Так как косинус угла принимает значения от +1 до –1, то сила
будет изменяться от своего максимального значения до 0, не
меняя своего знака
а
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
6

7.

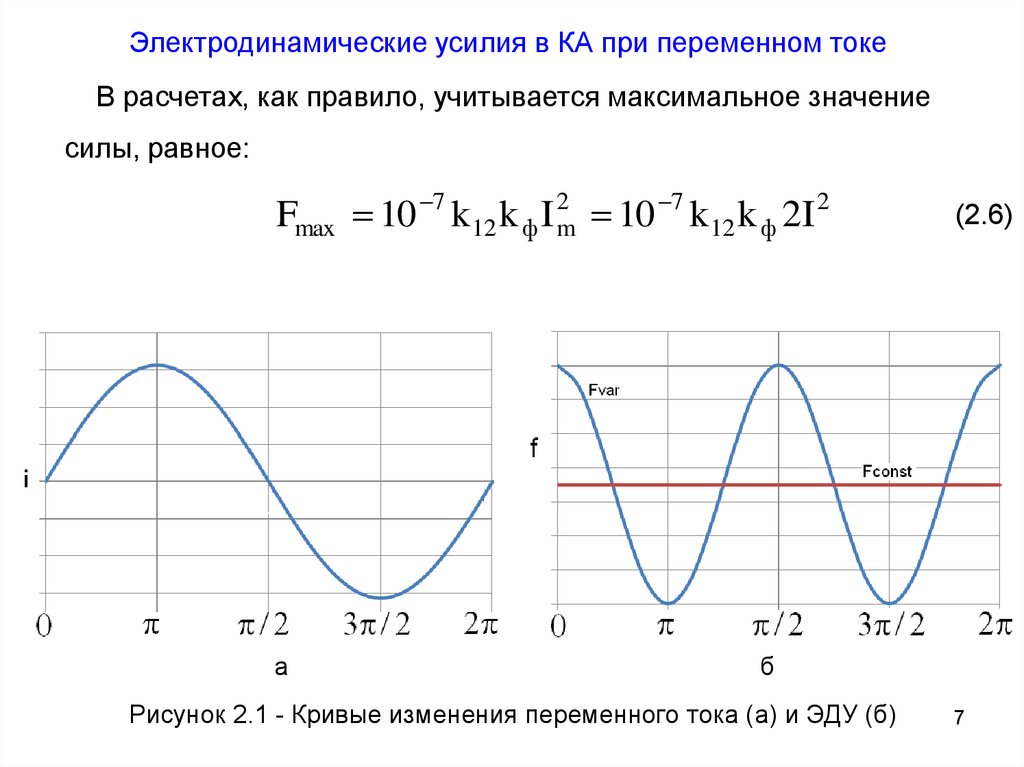
Электродинамические усилия в КА при переменном токе
В расчетах, как правило, учитывается максимальное значение
силы, равное:
Fmax 10 7 k12 k ф I 2m 10 7 k12 k ф 2I 2
а
(2.6)
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
7

8.

Электродинамические усилия в КА при переменном токе
Из
выражения
(2.6)
видно,
что
при
переменном
токе
максимальное значение ЭДУ при одном и том же значении тока
(действующем) будет в два раза выше, чем при постоянном.
а
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
8

9.

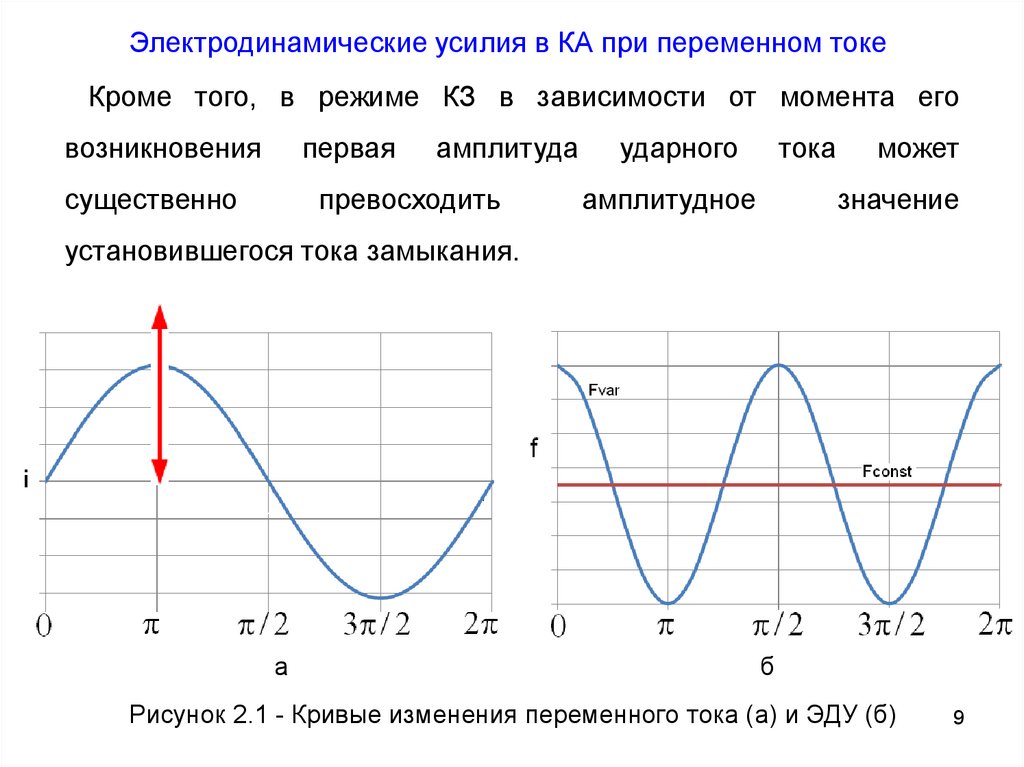
Электродинамические усилия в КА при переменном токе
Кроме того, в режиме КЗ в зависимости от момента его
возникновения
первая
амплитуда
существенно
превосходить
ударного
тока
амплитудное
может
значение
установившегося тока замыкания.
а
б
Рисунок 2.1 - Кривые изменения переменного тока (а) и ЭДУ (б)
9

10.

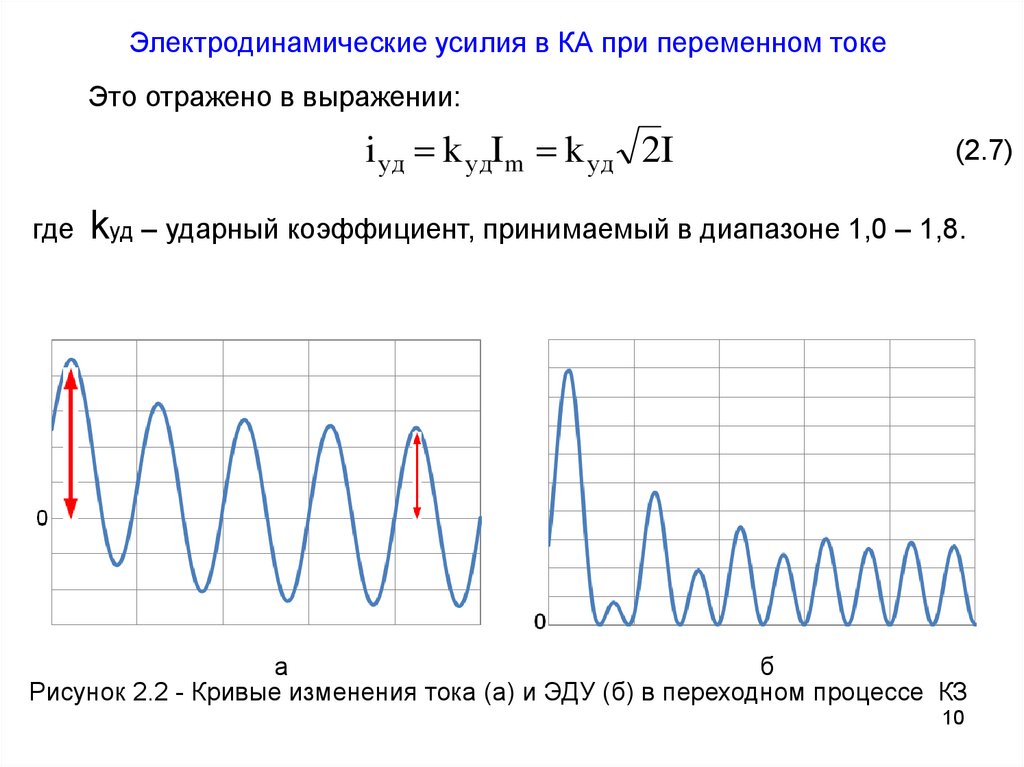
Электродинамические усилия в КА при переменном токе
Это отражено в выражении:
i уд k удIm k уд 2I
(2.7)
где kуд – ударный коэффициент, принимаемый в диапазоне 1,0 – 1,8.
а
б
Рисунок 2.2 - Кривые изменения тока (а) и ЭДУ (б) в переходном процессе КЗ
10

11.

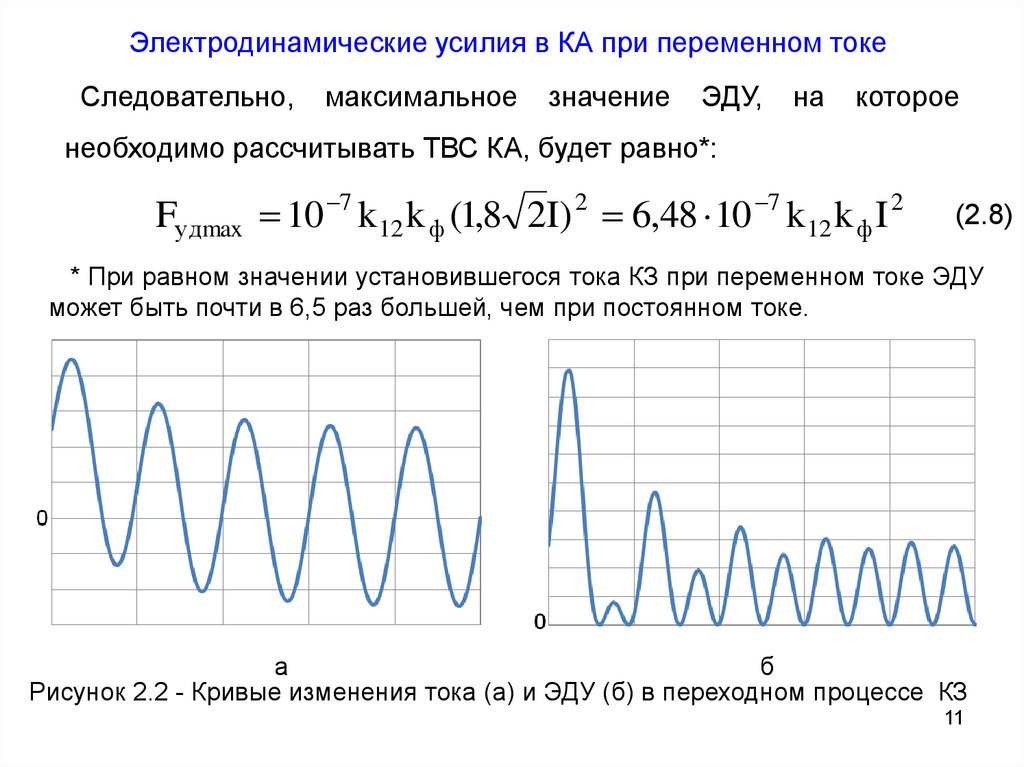
Электродинамические усилия в КА при переменном токе
Следовательно,
максимальное
значение
ЭДУ,
на
которое
необходимо рассчитывать ТВС КА, будет равно*:
Fудmax 10 7 k12 k ф (1,8 2I) 2 6,48 10 7 k12 k ф I 2
(2.8)
* При равном значении установившегося тока КЗ при переменном токе ЭДУ
может быть почти в 6,5 раз большей, чем при постоянном токе.
а
б
Рисунок 2.2 - Кривые изменения тока (а) и ЭДУ (б) в переходном процессе КЗ
11

12.

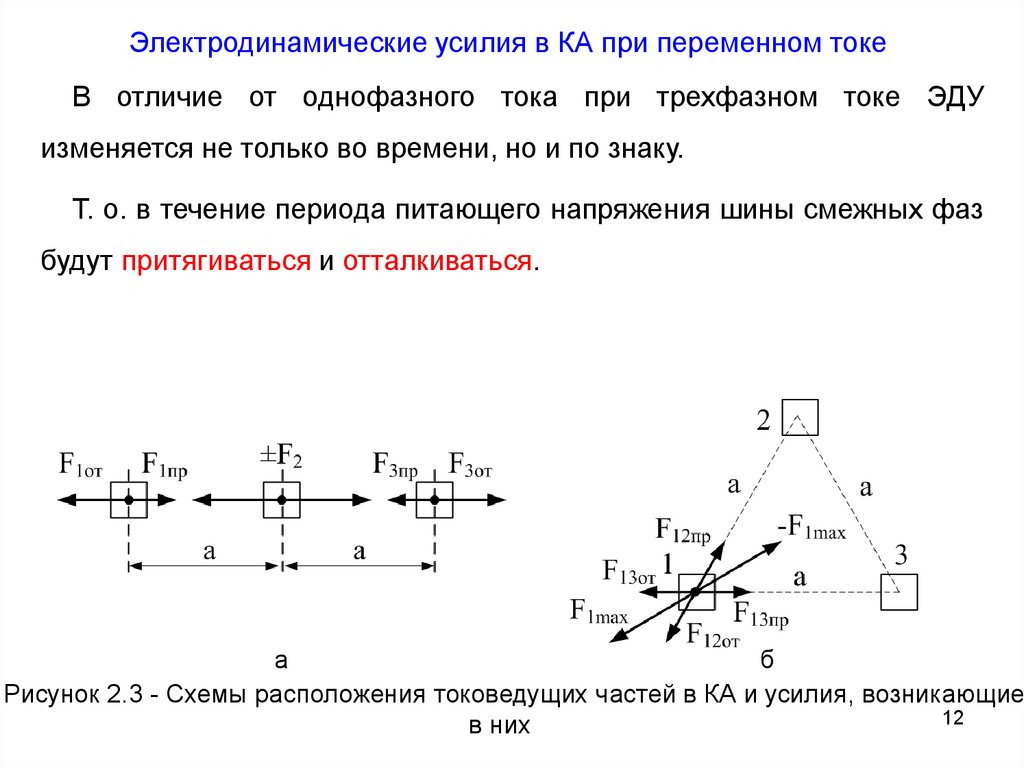
Электродинамические усилия в КА при переменном токе
В отличие от однофазного тока при трехфазном токе ЭДУ
изменяется не только во времени, но и по знаку.
Т. о. в течение периода питающего напряжения шины смежных фаз
будут притягиваться и отталкиваться.
а
б
Рисунок 2.3 - Схемы расположения токоведущих частей в КА и усилия, возникающие
12
в них

13.

Электродинамические усилия в КА при переменном токе
В
установившемся
отталкивающая
силы,
режиме
максимальные
действующая
на
притягивающая
крайние
и
проводники,
расположенные в одной плоскости (см. рис. 2.3, а) будут равны:
Fпр 0,055 10 7 k 12 k ф I 2m 0,055 10 7 k 12 k ф 2I 2
(2.9)
Fот 0,805 10 7 k12 k ф I 2m 0,805 10 7 k 12 k ф 2I 2
(2.10)
а
б
Рисунок 2.3 - Схемы расположения токоведущих частей в КА и усилия, возникающие
13
в них

14.

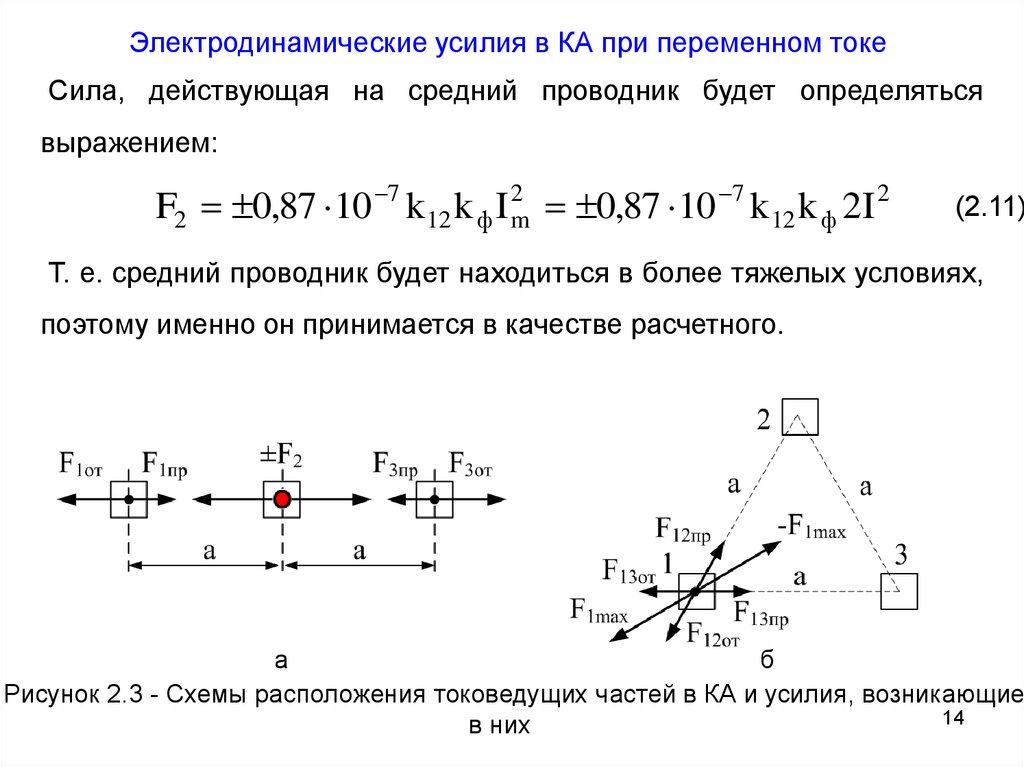
Электродинамические усилия в КА при переменном токе
Сила, действующая на средний проводник будет определяться
выражением:
F2 0,87 10 7 k 12 k ф I 2m 0,87 10 7 k 12 k ф 2I 2
(2.11)
Т. е. средний проводник будет находиться в более тяжелых условиях,
поэтому именно он принимается в качестве расчетного.
а
б
Рисунок 2.3 - Схемы расположения токоведущих частей в КА и усилия, возникающие
14
в них

15.

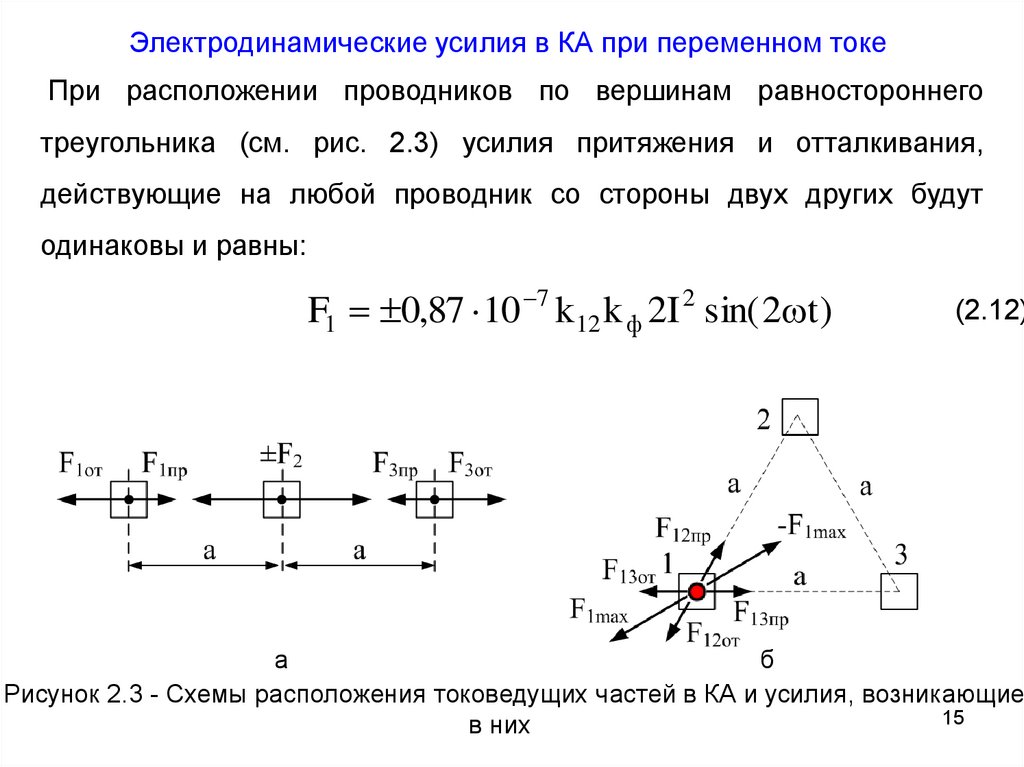
Электродинамические усилия в КА при переменном токе
При расположении проводников по вершинам равностороннего
треугольника (см. рис. 2.3) усилия притяжения и отталкивания,
действующие на любой проводник со стороны двух других будут
одинаковы и равны:
F1 0,87 10 7 k 12 k ф 2I 2 sin( 2 t )
(2.12)
а
б
Рисунок 2.3 - Схемы расположения токоведущих частей в КА и усилия, возникающие
15
в них

16.

Электродинамические усилия в КА при переменном токе
При
расчете
коммутационных
аппаратов
на
динамическую
стойкость в качестве наихудшего режима рекомендуется всегда
рассматривать режим трехфазного короткого замыкания.
Расчет ведется на максимальное усилие, получаемое при ударном
токе.
Учитывая, что сила переменна и ее максимум существует очень
короткое время, для допустимых напряжений в материале ТВС берут
большие
значения,
чем
при
постоянно
действующих
силах,
возникающих в установившемся режиме.
16

17.

Механический резонанс
Если какая-либо сила выведет механическую упругую систему из
равновесия, а затем перестанет действовать, то система будет
некоторое время колебаться около своего положения равновесия.
Частота этих колебаний называется собственной частотой
колебаний системы (или частотой собственных колебаний (ЧСК))
Скорость их затухания зависит от упругих свойств и массы системы
и не зависит от силы, вызывающей колебание.
Если сила, выводящая механическую систему из равновесия, будет
изменяться с частотой, равной частоте собственных колебаний, то на
деформацию одного периода будет накладываться деформация
следующего периода, что, в конечном итоге, приведет к разрушению
конструкции.
17

18.

Механический резонанс
Совпадение ЧСК с частотой изменения ЭДУ называется механическим
резонансом (МР).
Для исключения МР необходимо, чтобы ЧСК отличалась от частоты
воздействующей силы.
Значение ЧСК шины ТВС можно определить по формуле, Гц:
2
k
f СК
2 L2
EJ
m
(2.13)
где L – длина шины, м;
J – момент инерции поперечного сечения, м4;
E – модуль упругости материала шины, Па. Для алюминия и
алюминиевых сплавов E = 7∙1010 Па, для меди E = 10∙1010;
m – масса шины на единицу длины, кг/м;
k – коэффициент основной частоты собственных колебаний шины,
зависящий от характера крепления шины.
18

19.

Контактные системы коммутационных аппаратов
Общие требования, которым должна удовлетворять любая КС КА:
1) малое переходное сопротивление в контакте;
2) возможно более низкая температура нагрева контактов в режиме
длительного протекания номинального тока;
3) минимальное эрозионное и механическое разрушение контактов
в процессе включения и отключения цепи;
4) отсутствие вибрации контактов, их сваривания и отброса в
режиме КЗ.
Конструктивные параметры КС определяются коммутируемым
током и напряжением сети.
19

20.

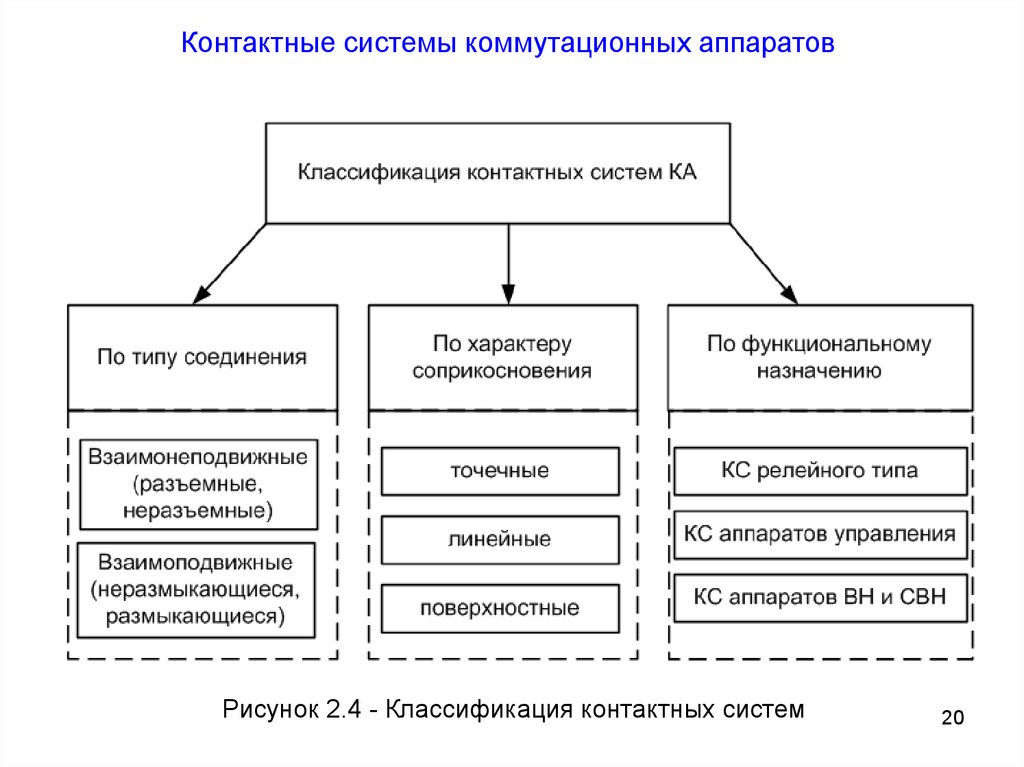
Контактные системы коммутационных аппаратов
Рисунок 2.4 - Классификация контактных систем
20

21.

Контактные системы коммутационных аппаратов
По виду соединения контакты бывают:
- взаимонеподвижные неразъемные (сварные, паяные) и разъемные
(болтовые);
- взаимоподвижные неразмыкающиеся, предназначенные для
передачи ЭЭ с неподвижной части установки на подвижную и
наоборот (щеточные скользящие, роликовые), и размыкающиеся,
расходящиеся в процессе работы (розеточные, мостиковые,
пальцевые, ножевые, с плоскими пружинами).
21