2.77M

Category: $mathematics$ mathematics

Векторы

1. 2. Историческая справка

Термин вектор (от лат.
Vector – “ несущий “)
впервые появился в 1845
г. у ирландского
математика Уильяма
Гамильтона (1805 –
1865) в работах по
построению числовых
систем.

3. Что такое вектор?

Понятие вектора возникает там,
где приходится иметь дело с объектами,
которые характеризуются величиной и
направлением: например, скорость,
сила, давление. Такие величины
называются векторными
величинами или векторами.

4.

скалярные
векторные
Время,
путь,масса
Сила, скорость,
ускорение

5.

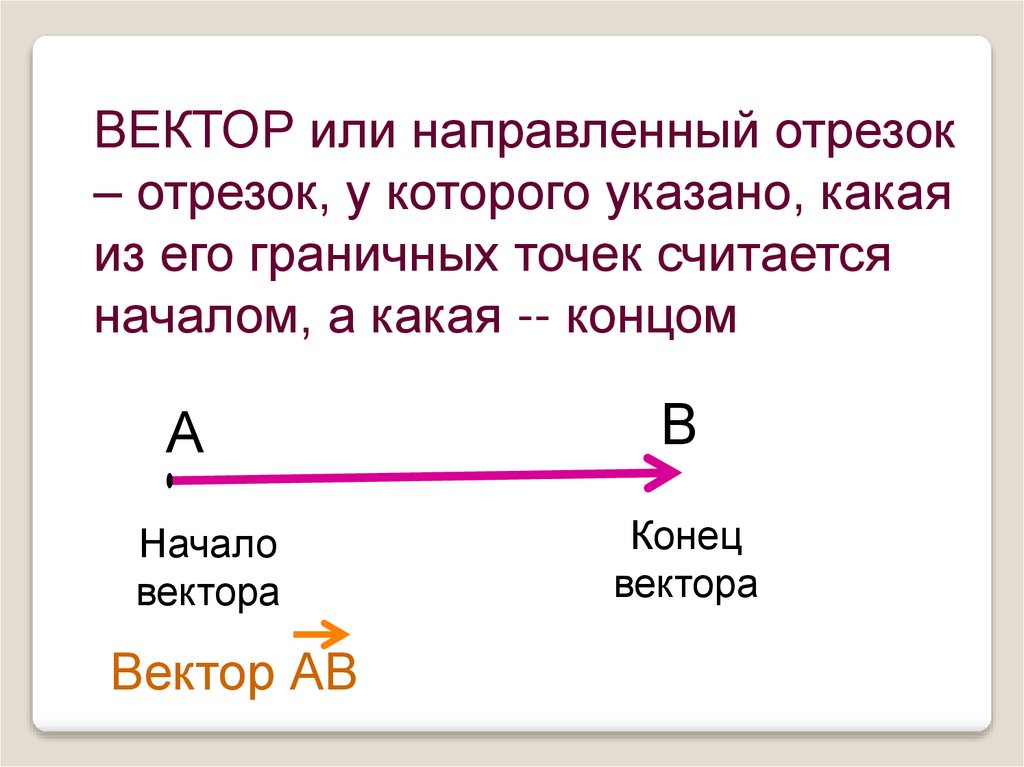
ВЕКТОР или направленный отрезок
– отрезок, у которого указано, какая
из его граничных точек считается
началом, а какая -- концом
А
В
Начало
вектора
Конец
вектора
Вектор АВ

6.

векторы обозначают двумя заглавными
латинскими буквами со стрелкой над ними или
одной строчной латинской буквой со стрелкой
над ней
любая точка плоскости является нулевым
вектором
длиной или модулем ненулевого вектора АВ
называется длина отрезка АВ

7. Длина вектора

Расстояние между началом и концом вектора
называется длиной или модулем вектора.
Длина вектора обозначается |а| или |АВ|.
Длина нулевого вектора считается равной
нулю.
A
B
C
a
D
N
|AB| = 6
|CD| = 5
|a| = 5
|NN| = 0
(каждая клетка на рисунке
имеет сторону, равную единице
измерения отрезков)

8.

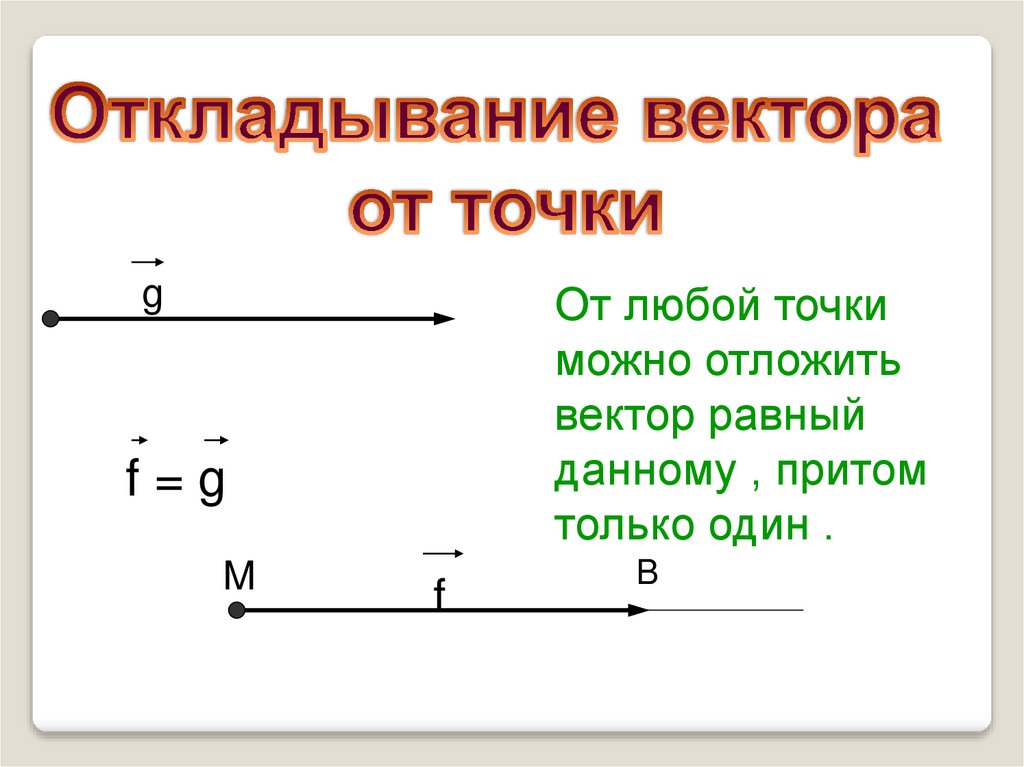
g
От любой точки
можно отложить
вектор равный
данному , притом
только один .
f=g
M
f
B

9.

• ненулевые векторы называются
коллинеарными, если они лежат либо
на одной прямой, либо на
параллельных прямых
• коллинеарные векторы могут быть
направлены одинаково и называются
сонаправленными или противоположно
направлены и называются
противоположно направленными

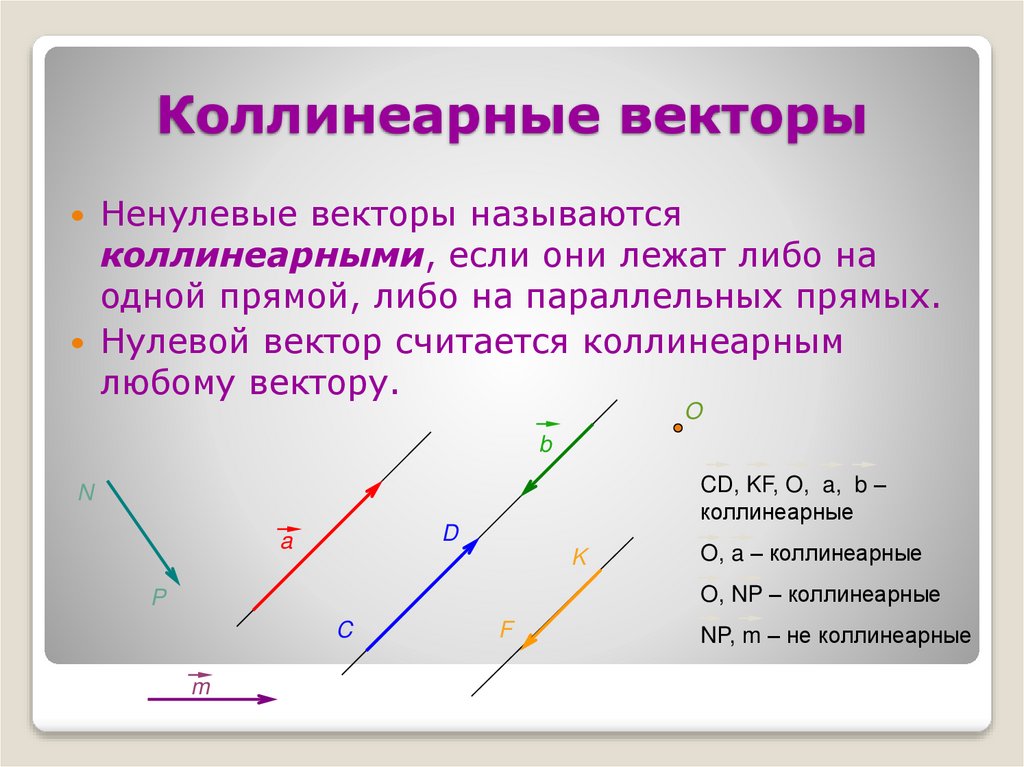
10. Коллинеарные векторы

Ненулевые векторы называются
коллинеарными, если они лежат либо на
одной прямой, либо на параллельных прямых.
Нулевой вектор считается коллинеарным
любому вектору.
O
b
CD, KF, O, a, b –
коллинеарные
N
D
a
K
O, a – коллинеарные
O, NP – коллинеарные
P
C
m
F
NP, m – не коллинеарные

11.

f
a
f=a
h
n
n=h
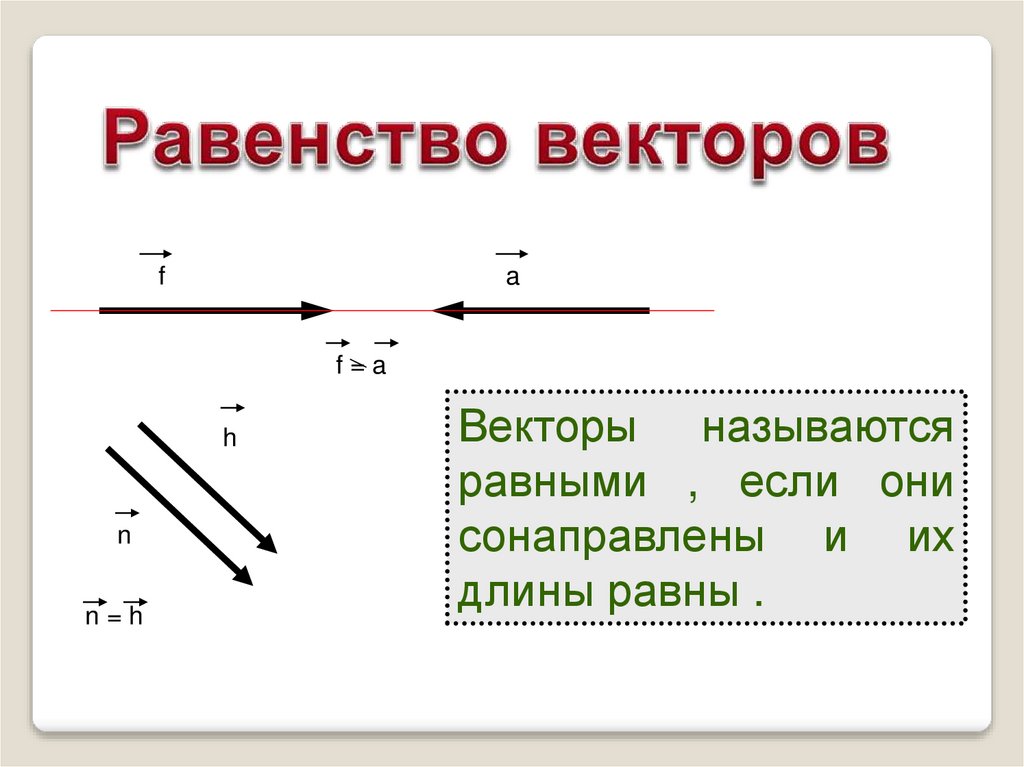
Векторы называются
равными , если они
сонаправлены и их
длины равны .

12. Задача

Какие из векторов,
изображенных на
рисунке:
1) коллинеарны;
2) сонаправлены;
3) противоположно
направлены;
4) имеют равные
длины?
Отложите эти
векторы от одной
точки.
d
c
a
b

13. Задача

На рисунке изображена равнобедренная
трапеция KLMN.
а) Укажите сонаправленные, противоположно
направленные, равные вектора.
б) Укажите векторы, длины которых равны.
Равны ли при этом сами векторы?
L
K
M
N