Similar presentations:
Историческая справка. Векторы
1. Векторы 8 класс
2. Историческая справка
Термин вектор (от лат.Vector – “ несущий “)
впервые появился в 1845 г.
у ирландского математика
Уильяма Гамильтона (1805 –
1865) в работах по
построению числовых
систем.
3. Что такое вектор?
Понятие вектора возникает там, гдеприходится иметь дело с объектами, которые
характеризуются величиной и направлением:
например, скорость, сила, давление. Такие
величины называются векторными
величинами или векторами.
4. Геометрическое понятие вектора
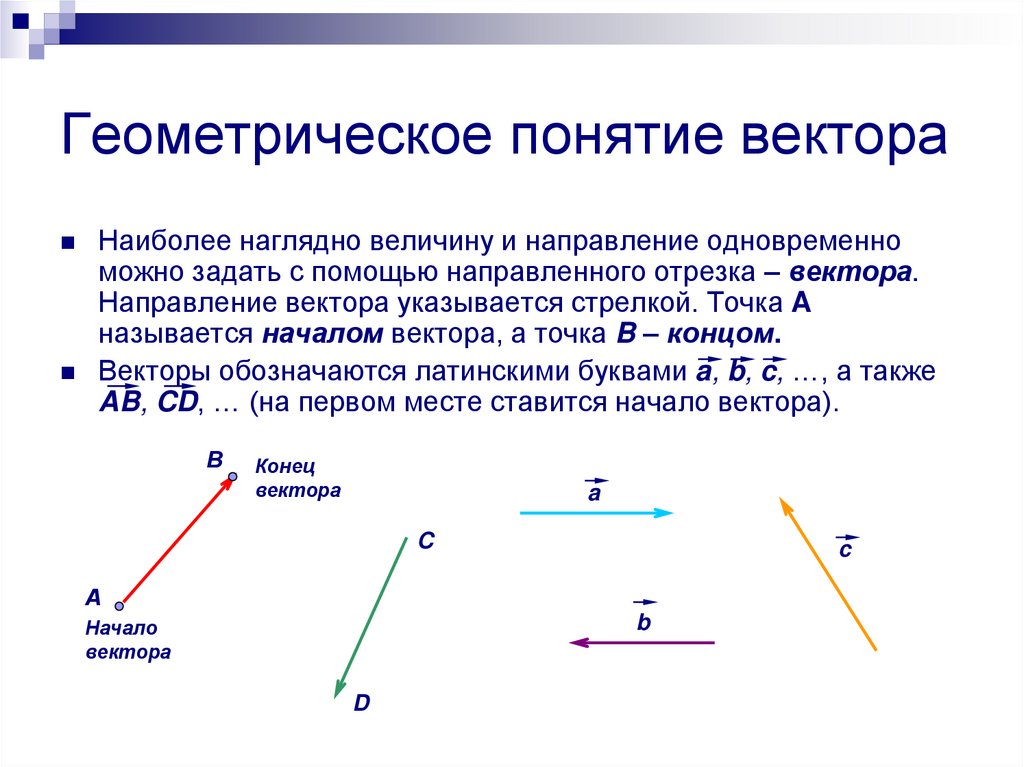
Наиболее наглядно величину и направление одновременноможно задать с помощью направленного отрезка – вектора.
Направление вектора указывается стрелкой. Точка A
называется началом вектора, а точка B – концом.
Векторы обозначаются латинскими буквами a, b, c, …, а также
AB, CD, … (на первом месте ставится начало вектора).
В
Конец
вектора
a
C
c
А
b
Начало
вектора
D
5. Нулевой вектор
Любую точку плоскостиможно считать вектором.
Такой вектор называется
нулевым.
Начало нулевого вектора
совпадает с его концом.
Нулевой вектор
обозначается 0 или СС.
М
MM - нулевой вектор
С
CC - нулевой вектор
6. Длина вектора
Расстояние между началом и концом вектораназывается длиной или модулем вектора. Длина
вектора обозначается |а| или |АВ|.
Длина нулевого вектора считается равной нулю.
A
B
C
a
D
N
|AB| = 6
|CD| = 5
|a| = 5
|NN| = 0
(каждая клетка на рисунке
имеет сторону, равную
единице измерения отрезков)
7. Коллинеарные векторы
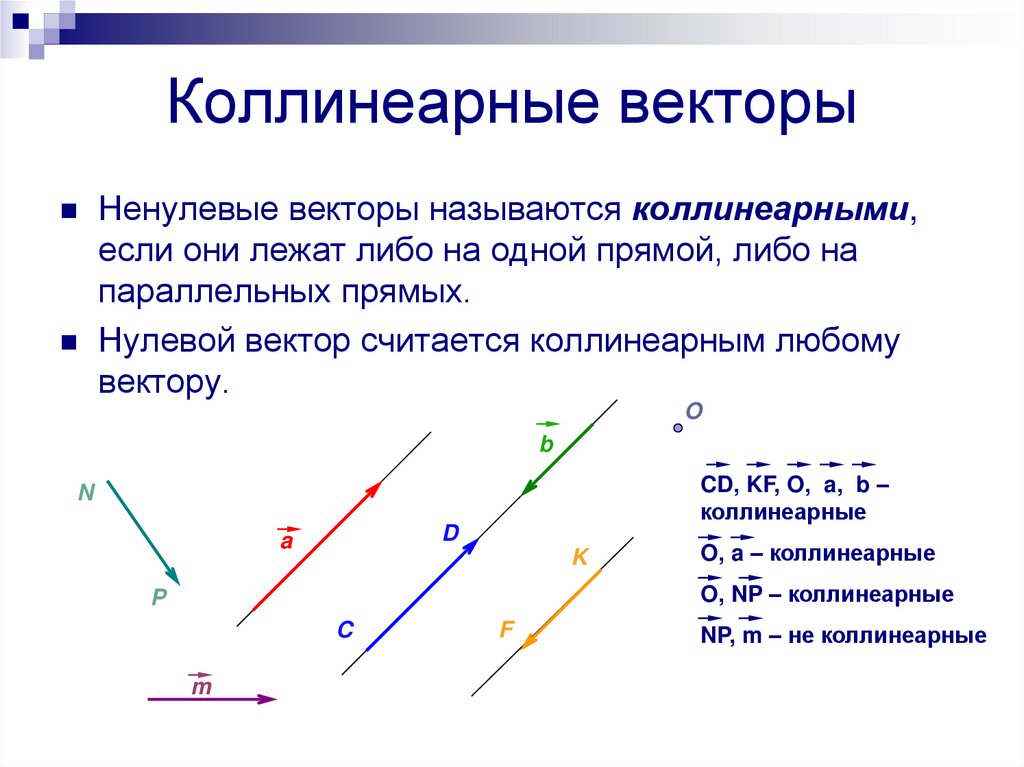
Ненулевые векторы называются коллинеарными,если они лежат либо на одной прямой, либо на
параллельных прямых.
Нулевой вектор считается коллинеарным любому
вектору.
O
b
CD, KF, O, a, b –
коллинеарные
N
D
a
K
O, a – коллинеарные
O, NP – коллинеарные
P
C
m
F
NP, m – не коллинеарные
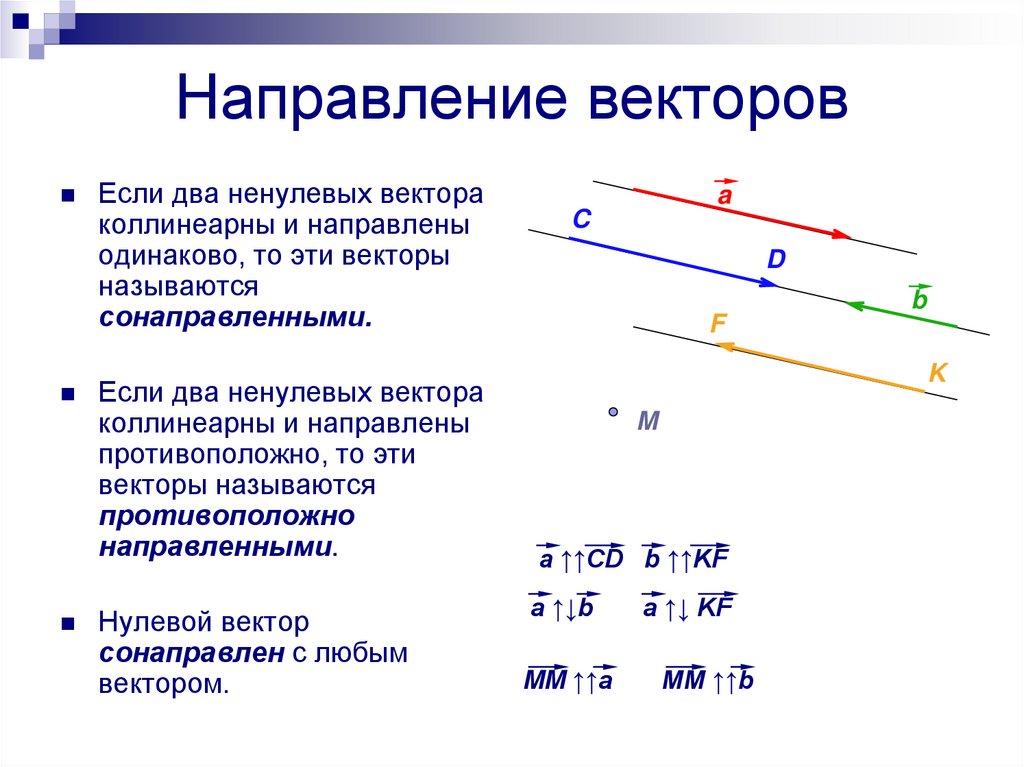
8. Направление векторов
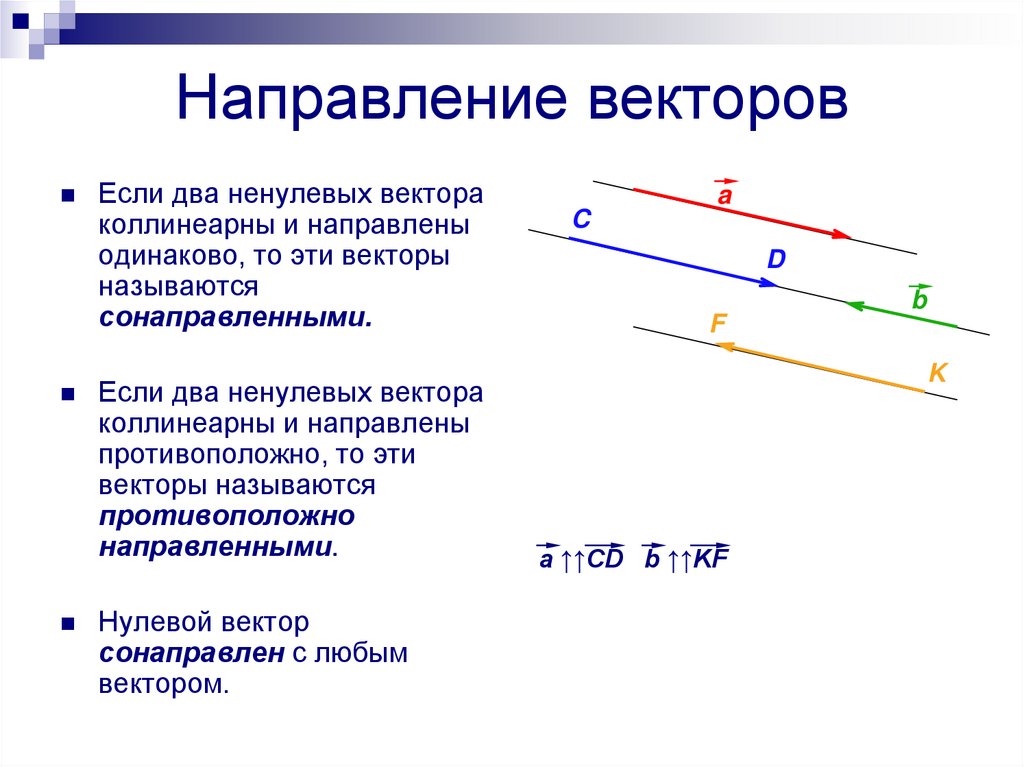
Если два ненулевых вектораколлинеарны и направлены
одинаково, то эти векторы
называются
сонаправленными.
Если два ненулевых вектора
коллинеарны и направлены
противоположно, то эти
векторы называются
противоположно
направленными.
Нулевой вектор
сонаправлен с любым
вектором.
a
C
D
b
F
K
a ↑↑CD b ↑↑KF
9. Направление векторов
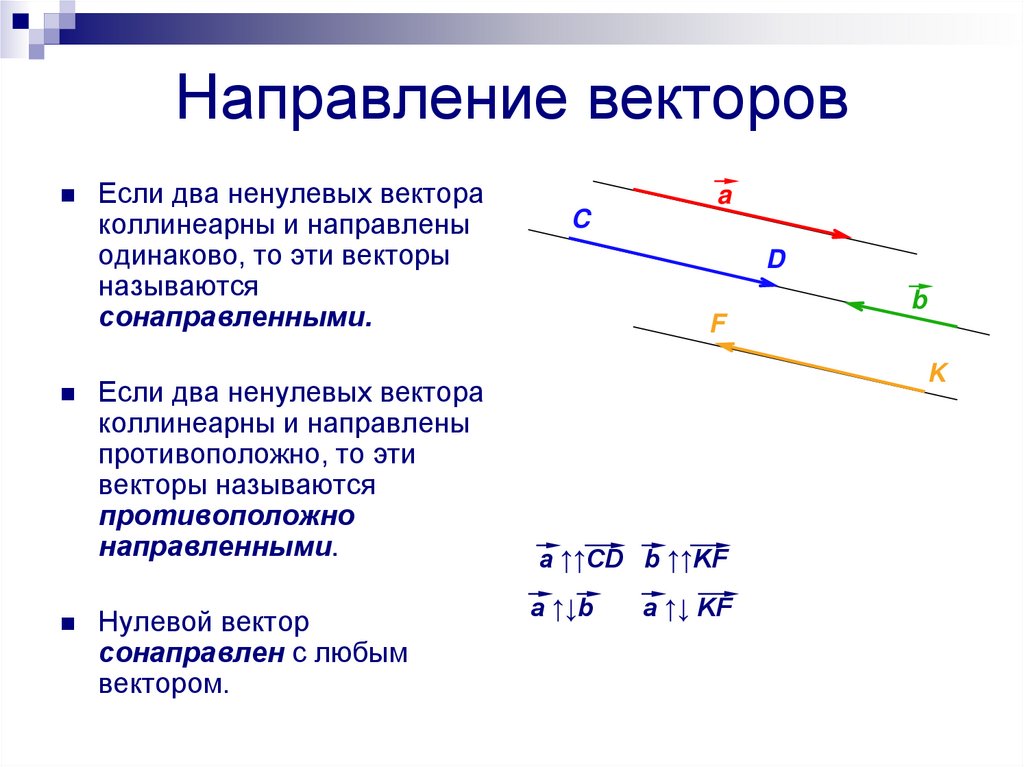
Если два ненулевых вектораколлинеарны и направлены
одинаково, то эти векторы
называются
сонаправленными.
Если два ненулевых вектора
коллинеарны и направлены
противоположно, то эти
векторы называются
противоположно
направленными.
Нулевой вектор
сонаправлен с любым
вектором.
a
C
D
b
F
K
a ↑↑CD b ↑↑KF
a ↑↓b
a ↑↓ KF
10. Направление векторов
Если два ненулевых вектораколлинеарны и направлены
одинаково, то эти векторы
называются
сонаправленными.
Если два ненулевых вектора
коллинеарны и направлены
противоположно, то эти
векторы называются
противоположно
направленными.
Нулевой вектор
сонаправлен с любым
вектором.
a
C
D
b
F
K
M
a ↑↑CD b ↑↑KF
a ↑↓b
MM ↑↑a
a ↑↓ KF
MM ↑↑b
11. Равенство векторов
Векторы называются равными, если они сонаправлены и ихдлины равны.
Равенство векторов обозначается: a = b
Все нулевые векторы равны друг другу.
C
a
ab
│a │=│b │
b
M
CC = MM
a=b
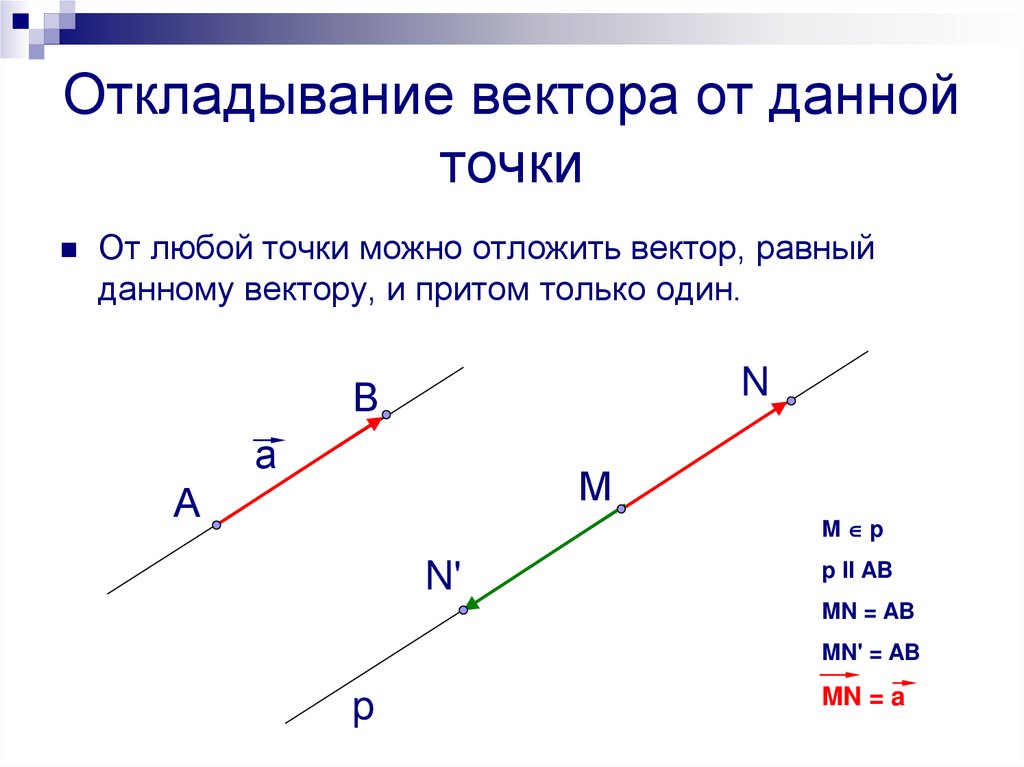
12. Откладывание вектора от данной точки
От любой точки можно отложить вектор, равныйданному вектору, и притом только один.
N
В
а
М
А
M p
N'
p II AB
MN = AB
MN' = AB
p
MN = a
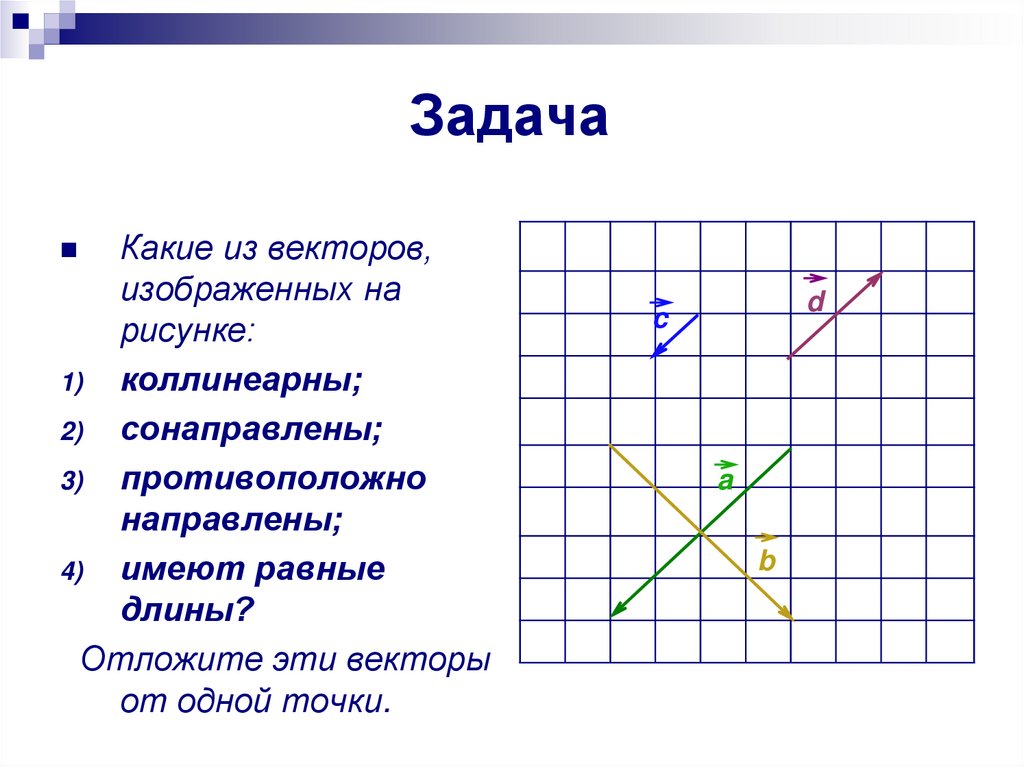
13. Задача
Какие из векторов,изображенных на
рисунке:
1) коллинеарны;
2) сонаправлены;
3) противоположно
направлены;
4) имеют равные
длины?
Отложите эти векторы
от одной точки.
d
c
a
b






 mathematics
mathematics








