Векторы в пространстве. Понятие вектора

1. Векторы в пространстве

ГПОУ
НОВОАЗОВСКИЙ ИНДУСТРИАЛЬНЫЙ ТЕХНИКУМ

2. Понятие вектора

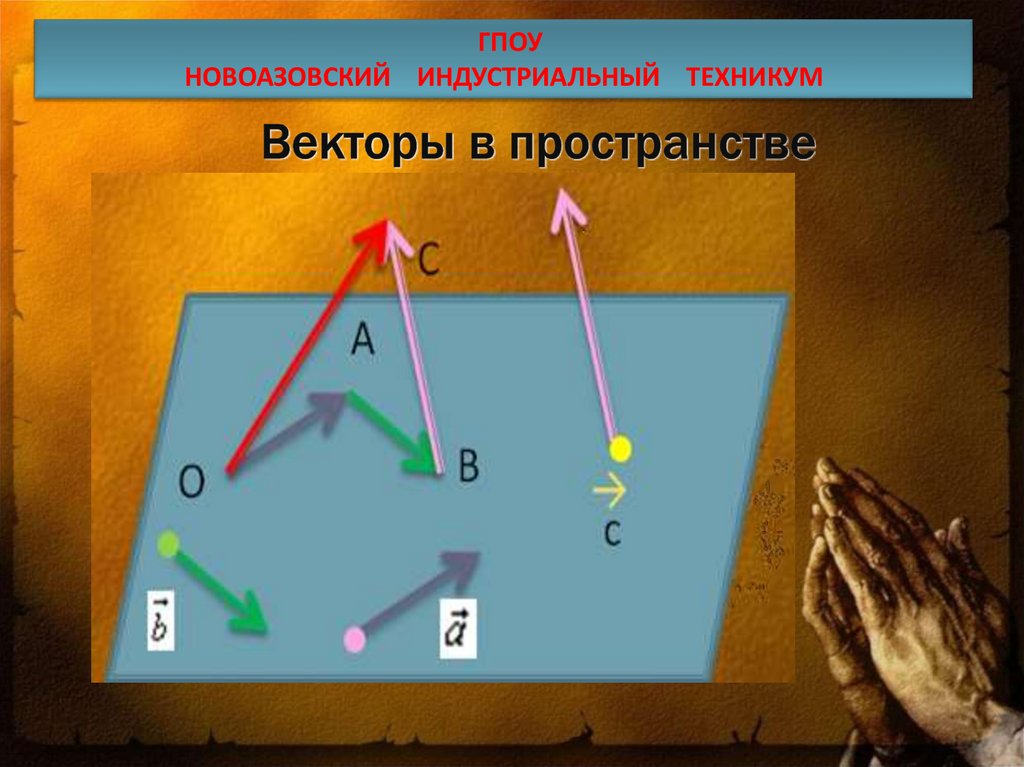
Вектор (от лат. vector, буквально — несущий, перевозящий), в геометрическом
смысле — направленный отрезок, то есть отрезок, у которого указаны начало и
конец.
Вектор характеризуется
следующими элементами:
1) начальной точкой
(точкой приложения); векторы
2 )направлением;
3) длиной («модулем вектора»).
A
T
α
Если начало вектора — точка А, а его конец — точка В, то вектор
обозначается
или
C

3.

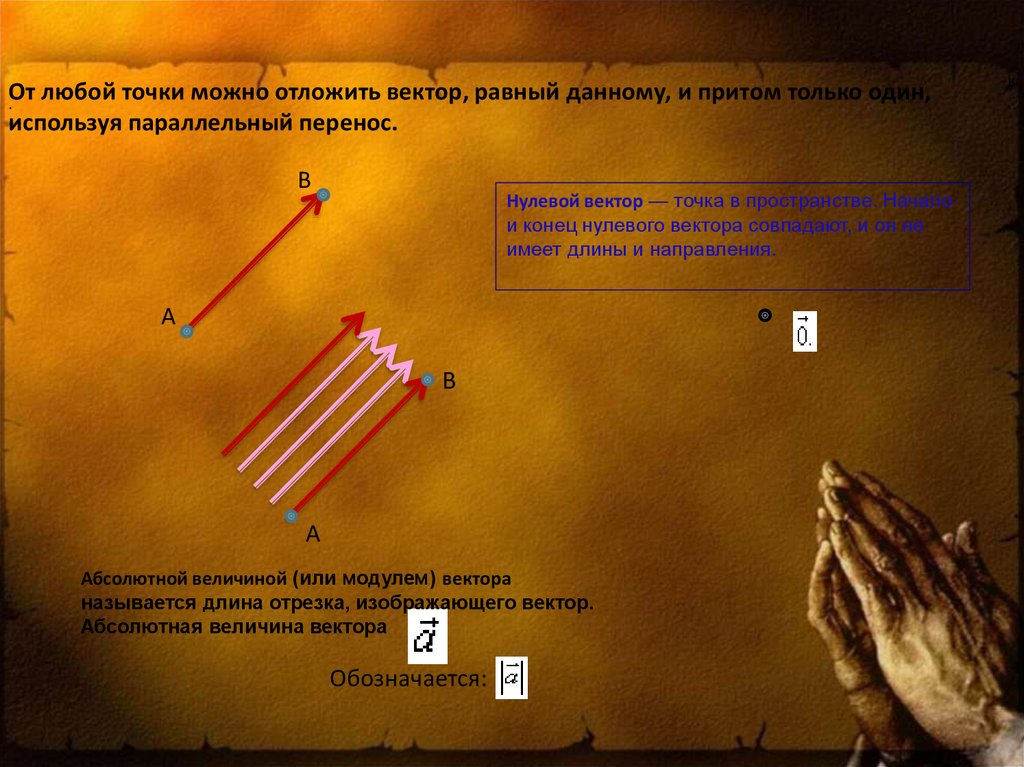
B
Нулевой вектор — точка в пространстве. Начало
и конец нулевого вектора совпадают, и он не
имеет длины и направления.
A
B
A
Абсолютной величиной (или модулем) вектора
называется длина отрезка, изображающего вектор.
Абсолютная величина вектора
Обозначается:
.
я
От
любой точки можно отложить вектор, равный данному, и притом только один,
.
используя параллельный перенос.

4.

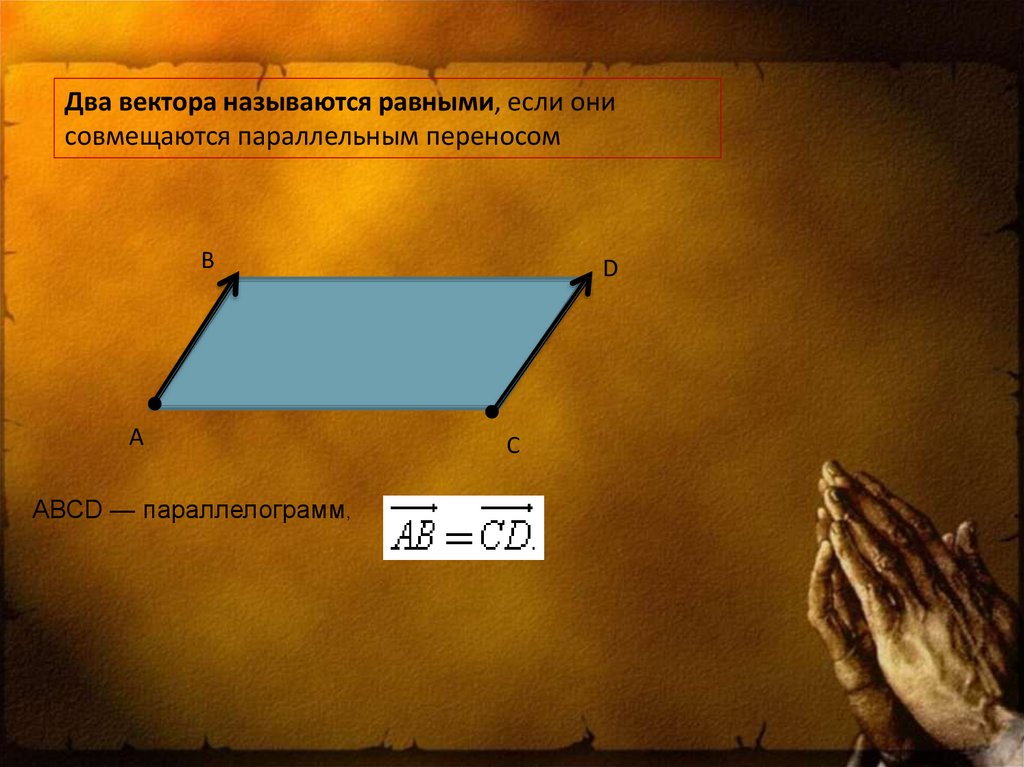
Два вектора называются равными, если они
совмещаются параллельным переносом
B
A
АВСD — параллелограмм,
D
C

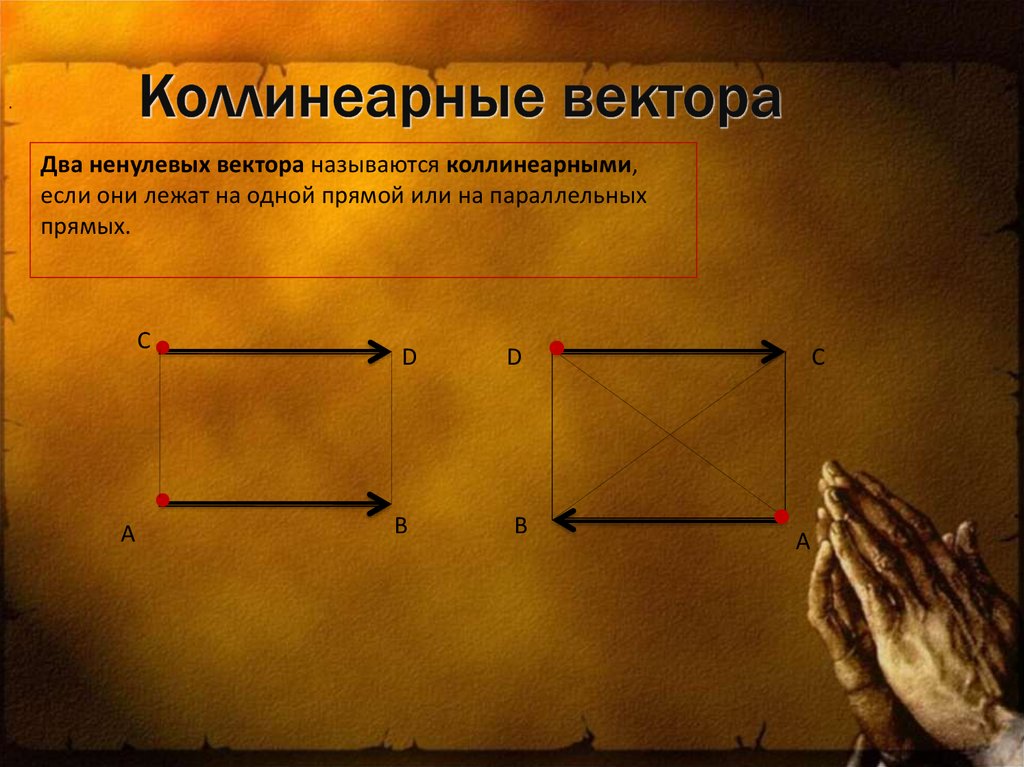
5. Коллинеарные вектора

.
Два ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или на параллельных
прямых.
C
A
D
B
D
B
C
A

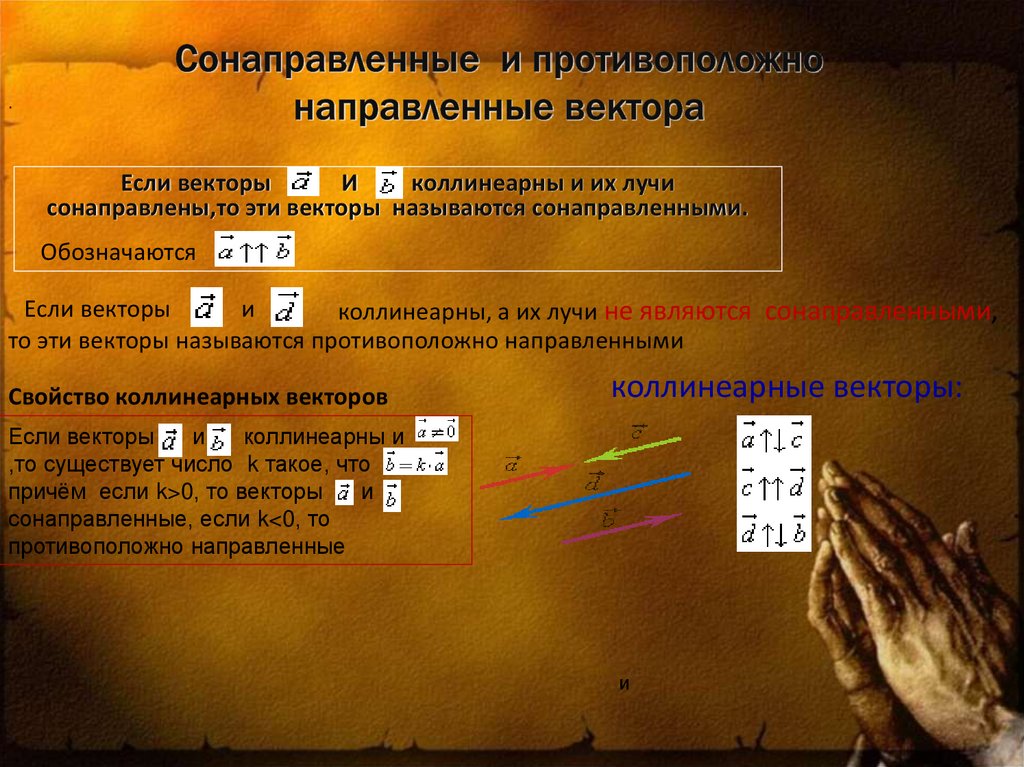
6. Сонаправленные и противоположно направленные вектора

.
Если векторы
И
коллинеарны и их лучи
сонаправлены,то эти векторы называются сонаправленными.
Обозначаются
Если векторы
и
коллинеарны, а их лучи не являются сонаправленными,
то эти векторы называются противоположно направленными
Свойство коллинеарных векторов
коллинеарные векторы:
Если векторы
и
коллинеарны и
,то существует число k такое, что
причём если k>0, то векторы
и
сонаправленные, если k<0, то
противоположно направленные
и

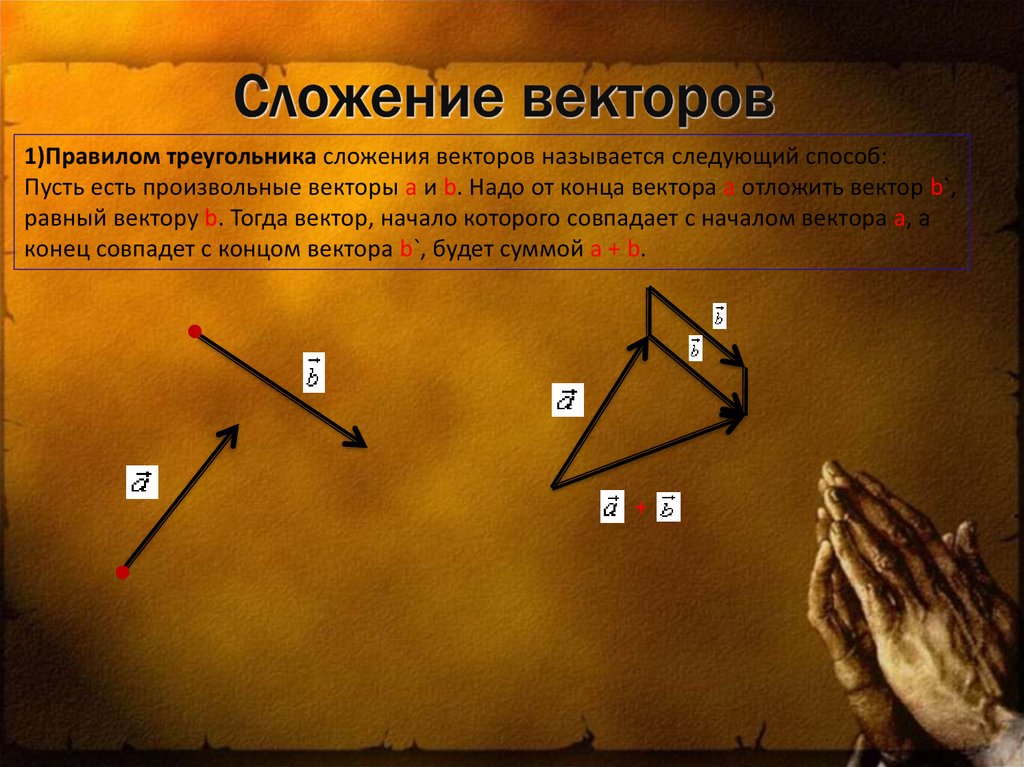
7. Сложение векторов

1)Правилом треугольника сложения векторов называется следующий способ:
Пусть есть произвольные векторы a и b. Надо от конца вектора a отложить вектор b`,
равный вектору b. Тогда вектор, начало которого совпадает с началом вектора a, а
конец совпадет с концом вектора b`, будет суммой a + b.
+

8.

2)Правило параллелограмма
A
B
C
Правилом параллелограмма сложения векторов называется следующий способ:
Пусть есть векторы AB и AC у которых начало вектора совпадает, а концы не совпадают
D
B
A
C
Достроим данный угол до параллелограмма, так что AC = BD и AB = CD.
B
A
D
Тогда AB + BD = AD, а так как BD = AC,
то AB + AC = AD
C

9. Свойства сложения векторов

Для любых векторов
заданных в пространстве, справедливы равенства
Переместительный закон
Сочетательный закон

10.

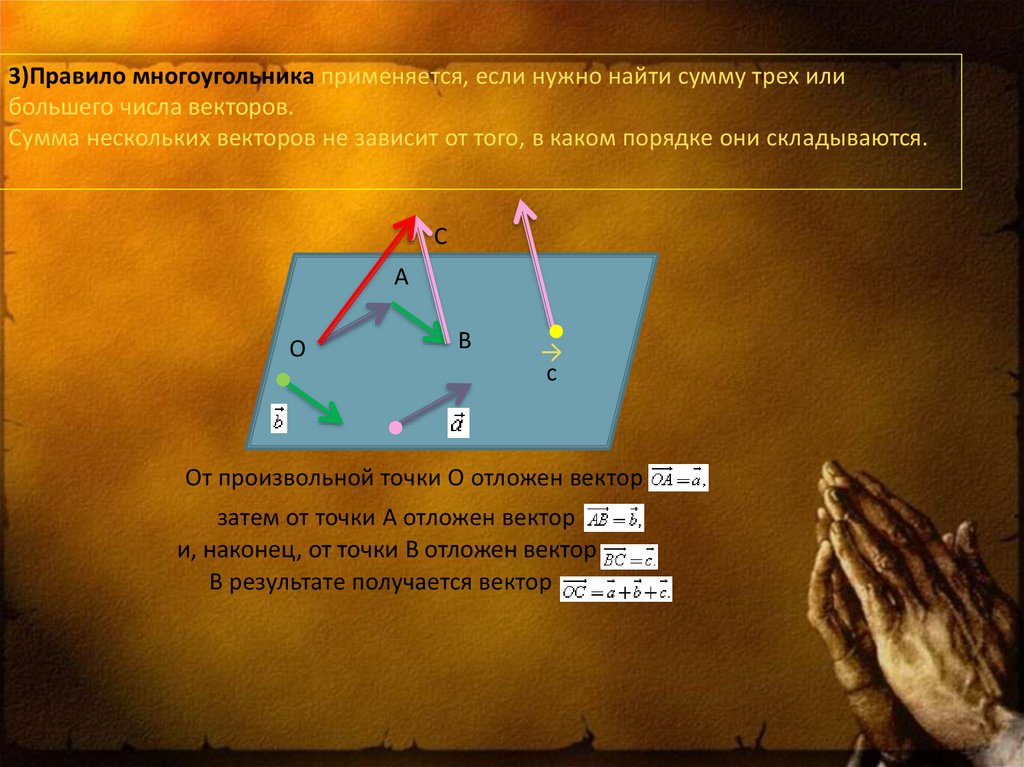
3)Правило многоугольника применяется, если нужно найти сумму трех или
большего числа векторов.
Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
С
А
О
В
→
с
От произвольной точки О отложен вектор
затем от точки А отложен вектор
и, наконец, от точки В отложен вектор
В результате получается вектор

11. Умножение вектора на число

Произведением ненулевого вектора
, длина которого равна,
на число k называется такой вектор,
причем векторы
и
сонаправлены при
и противоположно направлены при k < 0.
Произведением нулевого вектора на любое число считается нулевой вектор.

12. Свойства умножения вектора на число

Для любых векторов
и
и любых чисел k, m справедливы равенства:
Сочетательный закон
Первый распределительный закон
Второй распределительный закон