Понятие вектора в пространстве

1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ

2.

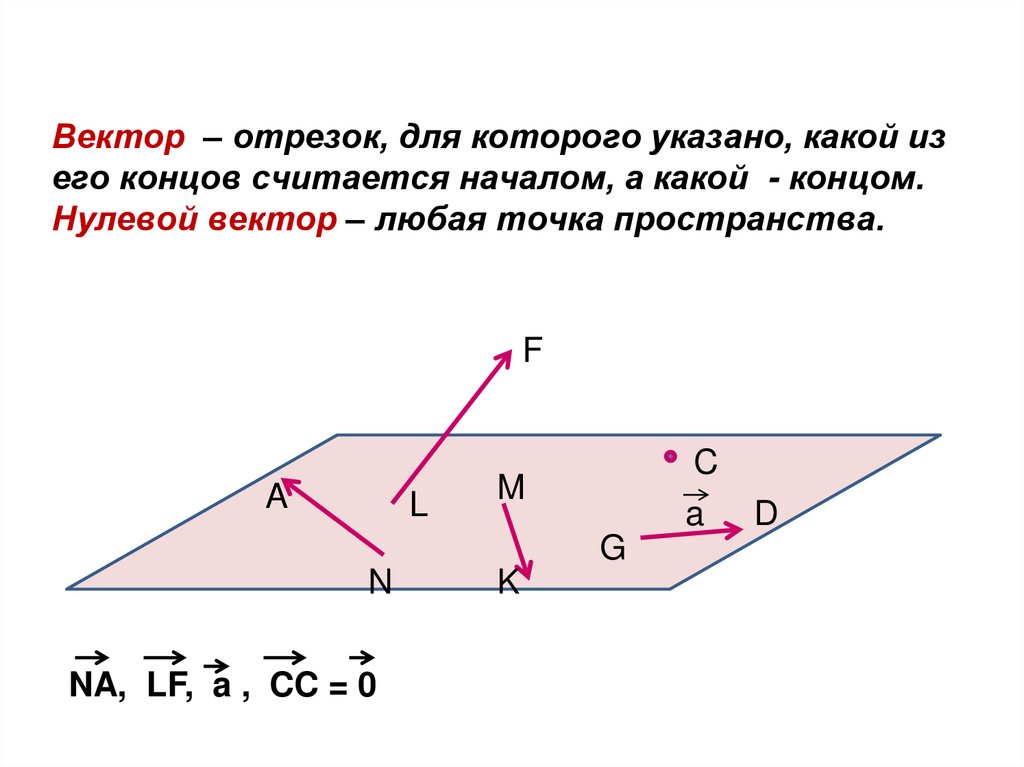
Вектор – отрезок, для которого указано, какой из
его концов считается началом, а какой - концом.
Нулевой вектор – любая точка пространства.
F
A
L
C
M
a
G
N
NA, LF, a , CC = 0
K
D

3.

• Длиной ненулевого вектора АВ
называется длина отрезка АВ
Обозначение :
| a | или | АВ |
B
a
А
• Длина нулевого вектора равна 0
С
| 0 | =0, │СС│=0

4.

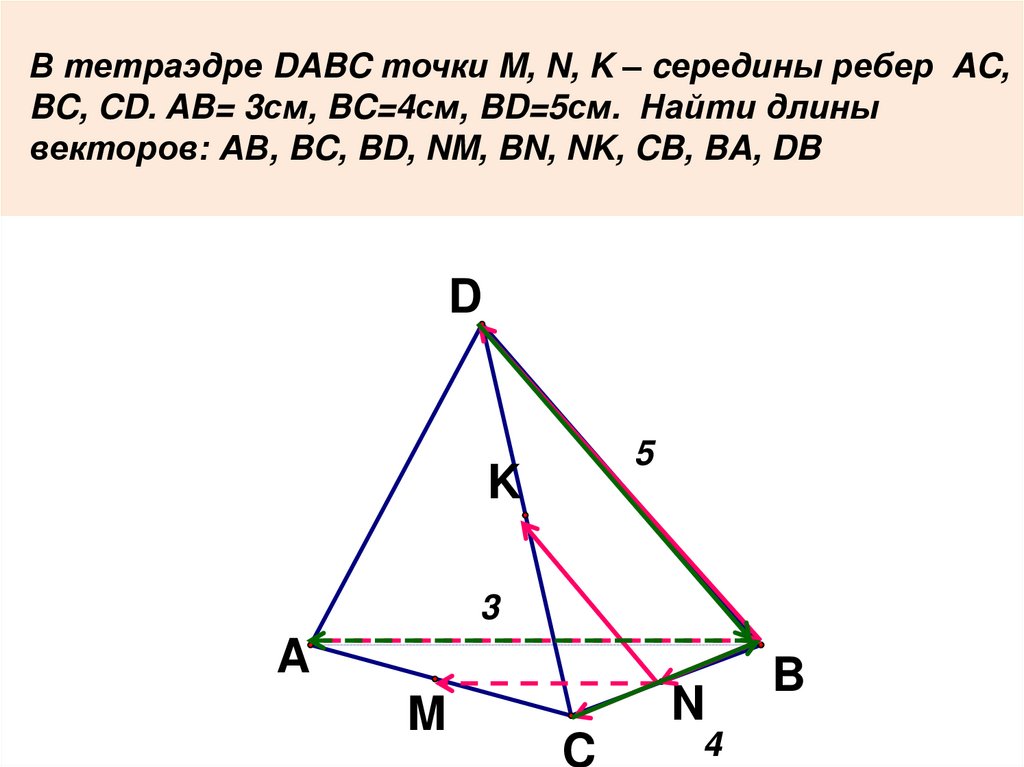
В тетраэдре DABC точки M, N, K – cередины ребер AC,
BC, CD. AB= 3см, BC=4см, BD=5см. Найти длины
векторов: АВ, BC, BD, NM, BN, NK, CB, BA, DB
D
5
K
3
A
M
N
C
4
B

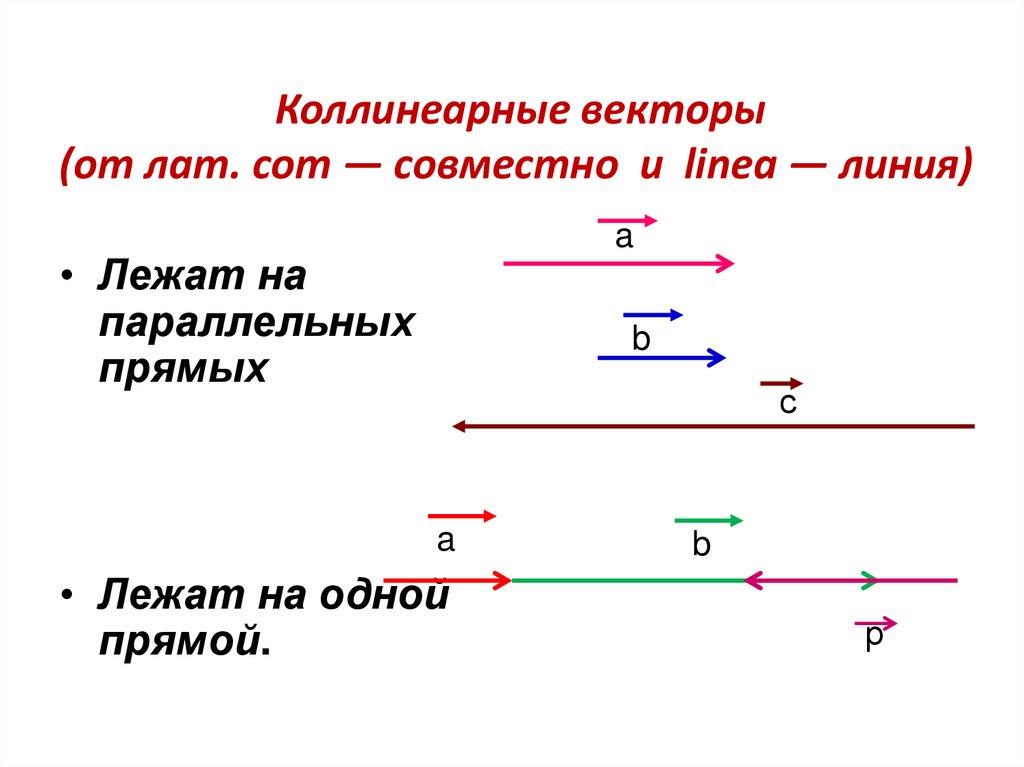
5. Коллинеарные векторы (от лат. com — совместно и linea — линия)

a
• Лежат на
параллельных
прямых
b
с
a
• Лежат на одной
прямой.
b
р

6.

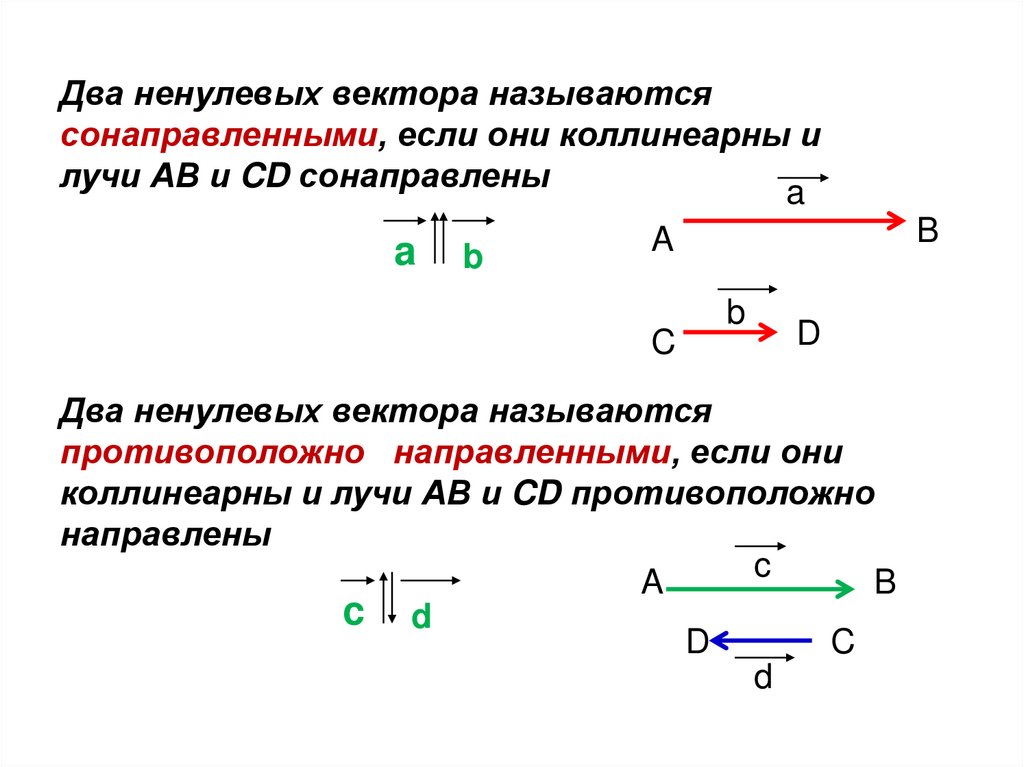
Два ненулевых вектора называются
сонаправленными, если они коллинеарны и
лучи АВ и CD сонаправлены
a
a
b
B
A
C
b
D
Два ненулевых вектора называются
противоположно направленными, если они
коллинеарны и лучи АВ и CD противоположно
направлены
c
A
B
c d
D
C
d

7.

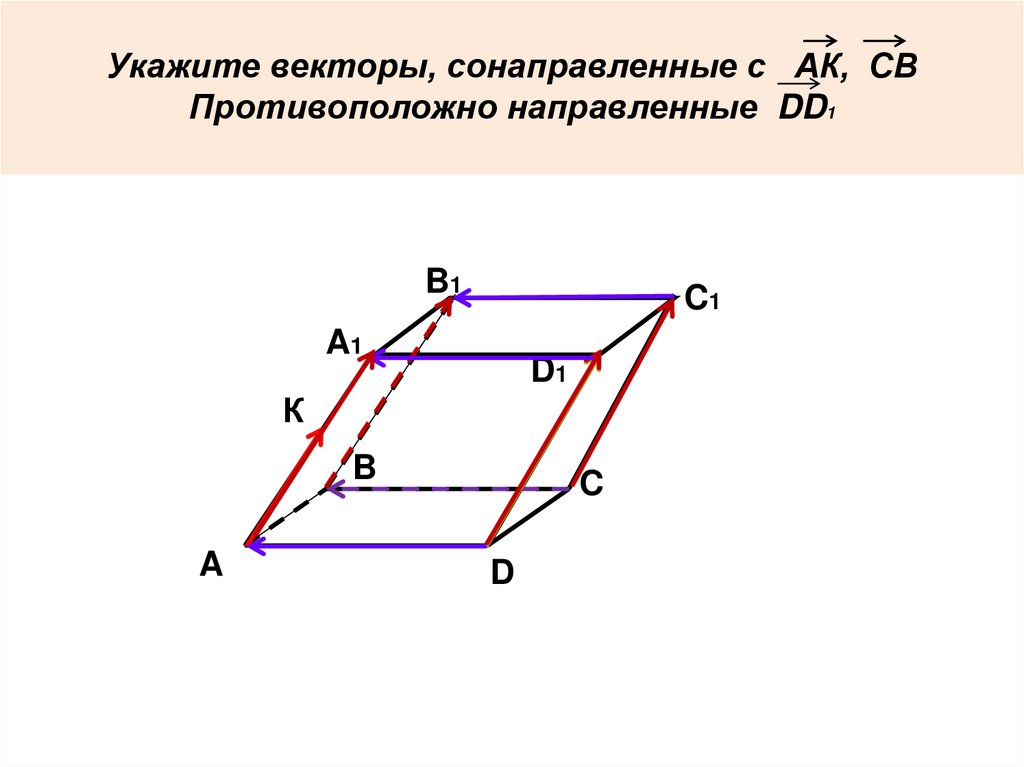
Укажите векторы, сонаправленные с АК, СВ
Противоположно направленные DD1
B1
C1
A1
D1
К
B
A
C
D

8.

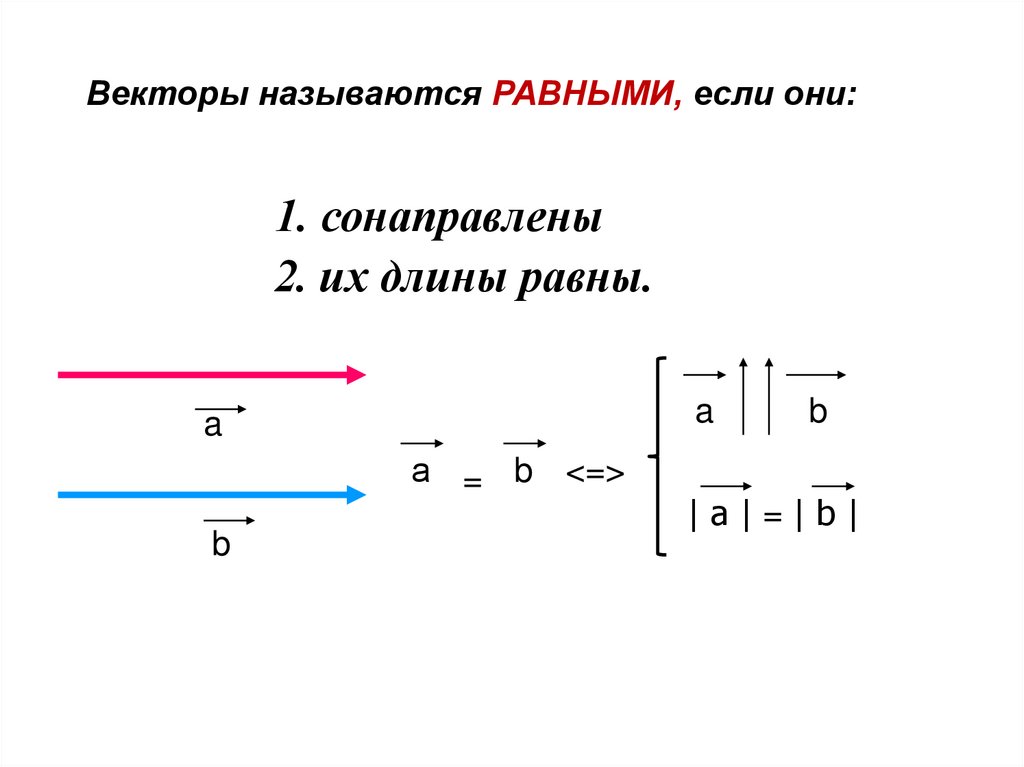
Векторы называются РАВНЫМИ, если они:
1. сонаправлены
2. их длины равны.
a
a
а = b <=>
b
b
|a|=|b|

9.

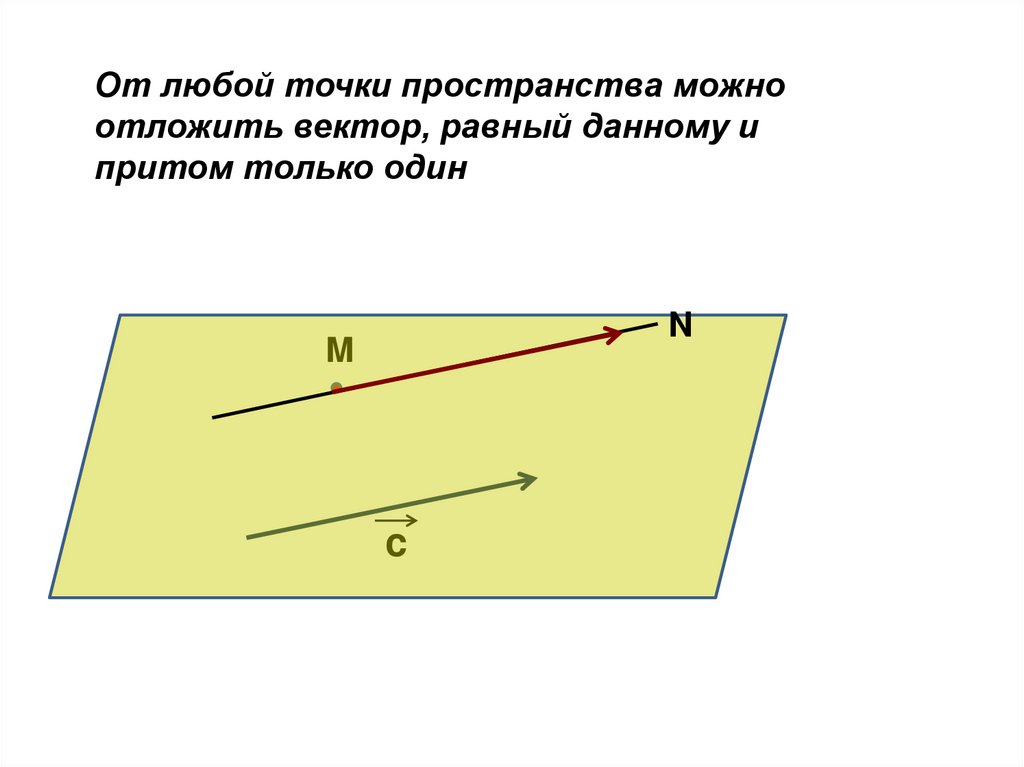
От любой точки пространства можно
отложить вектор, равный данному и
притом только один
N
M
c

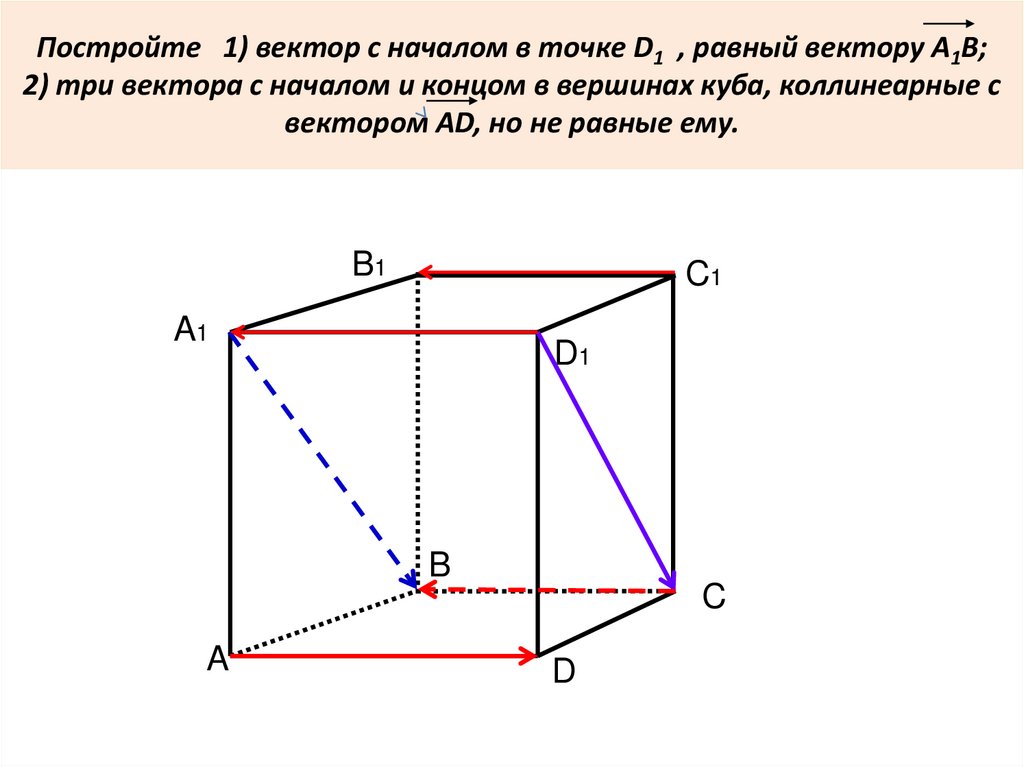
10. Постройте 1) вектор с началом в точке D1 , равный вектору А1В; 2) три вектора с началом и концом в вершинах куба, коллинеарные

с
вектором AD, но не равные ему.
B1
C1
A1
D1
B
A
C
D

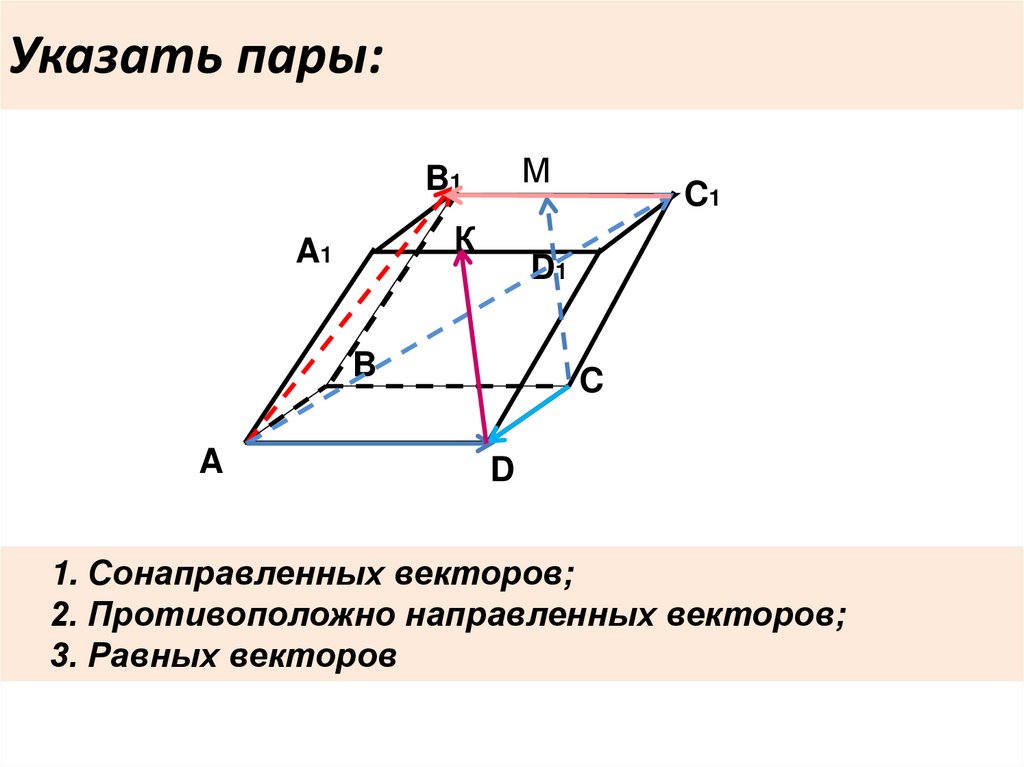
11. Указать пары:

М
B1
К
A1
D1
B
A
C1
C
D
1. Сонаправленных векторов;
2. Противоположно направленных векторов;
3. Равных векторов

12. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ

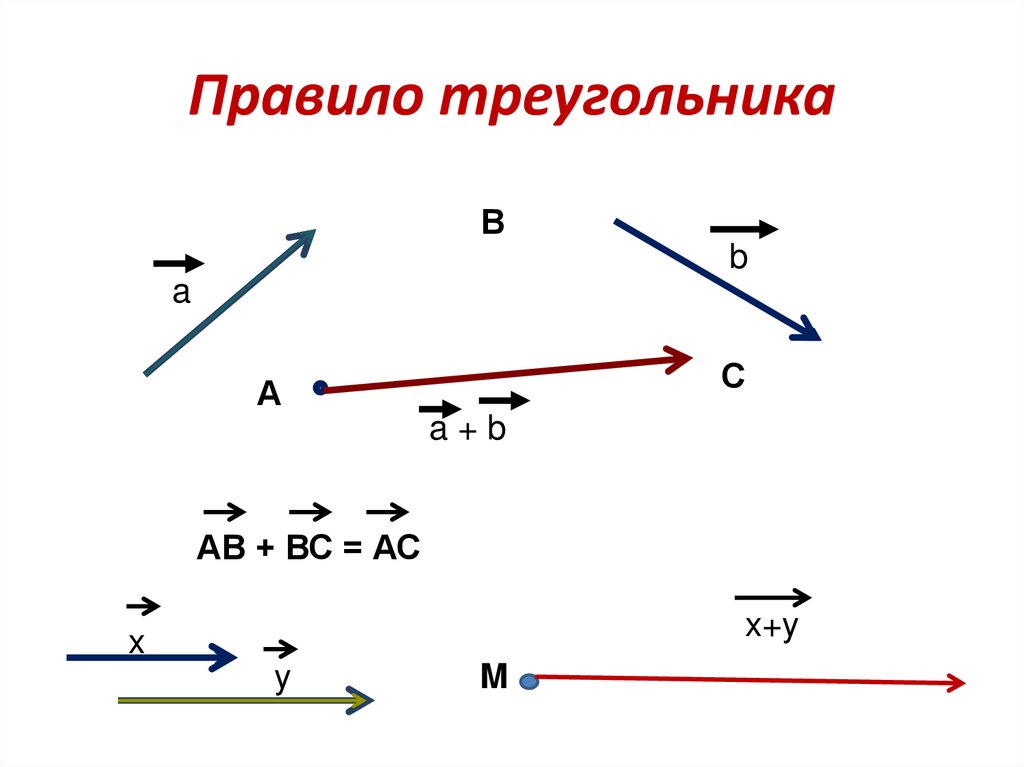
13. Правило треугольника

В
b
a
С
А
a+b
АВ + ВС = АС
x+y
x
y
M

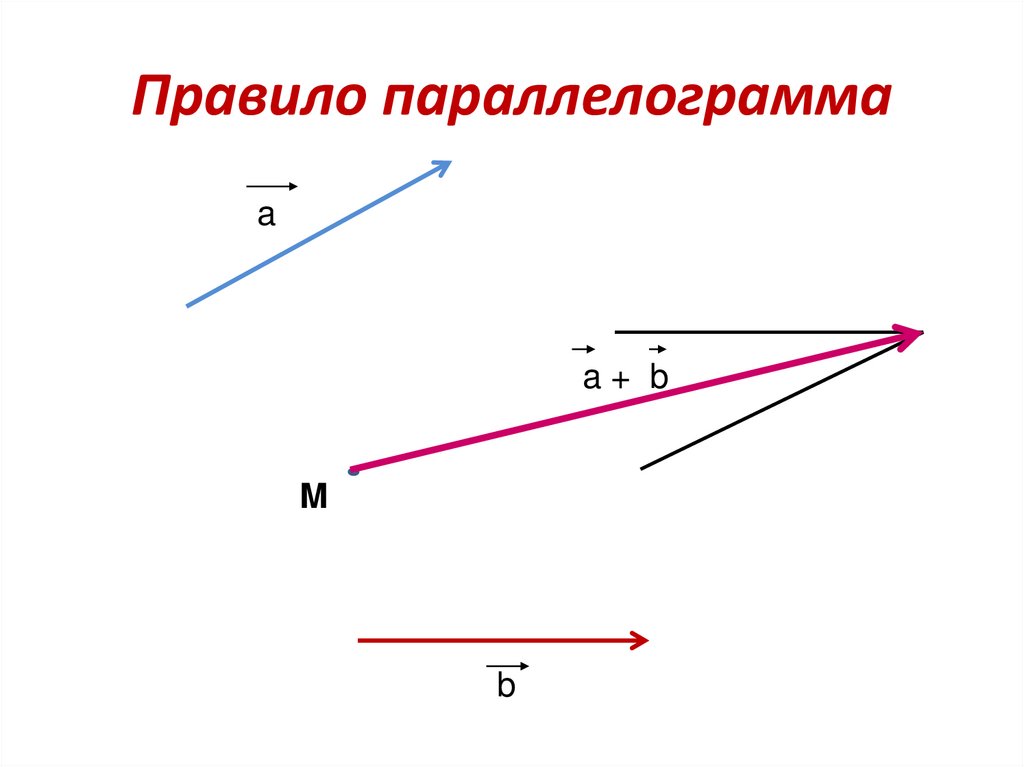
14. Правило параллелограмма

a
a+ b
M
b

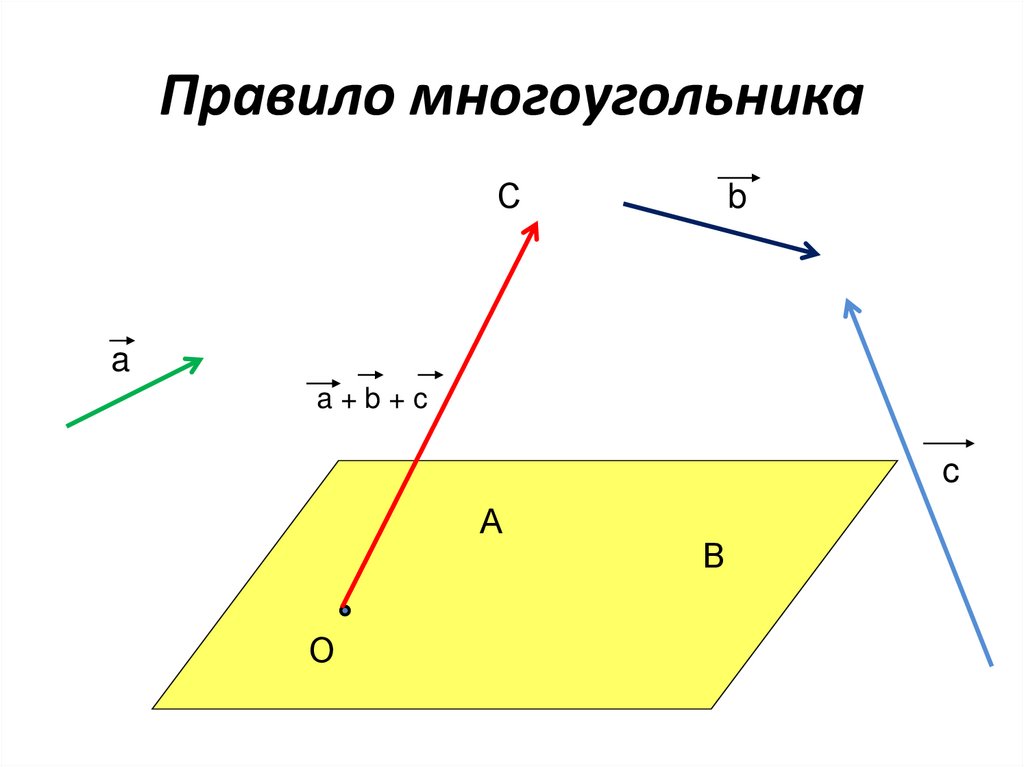
15. Правило многоугольника

С
b
a
a+b+c
c
А
О
В

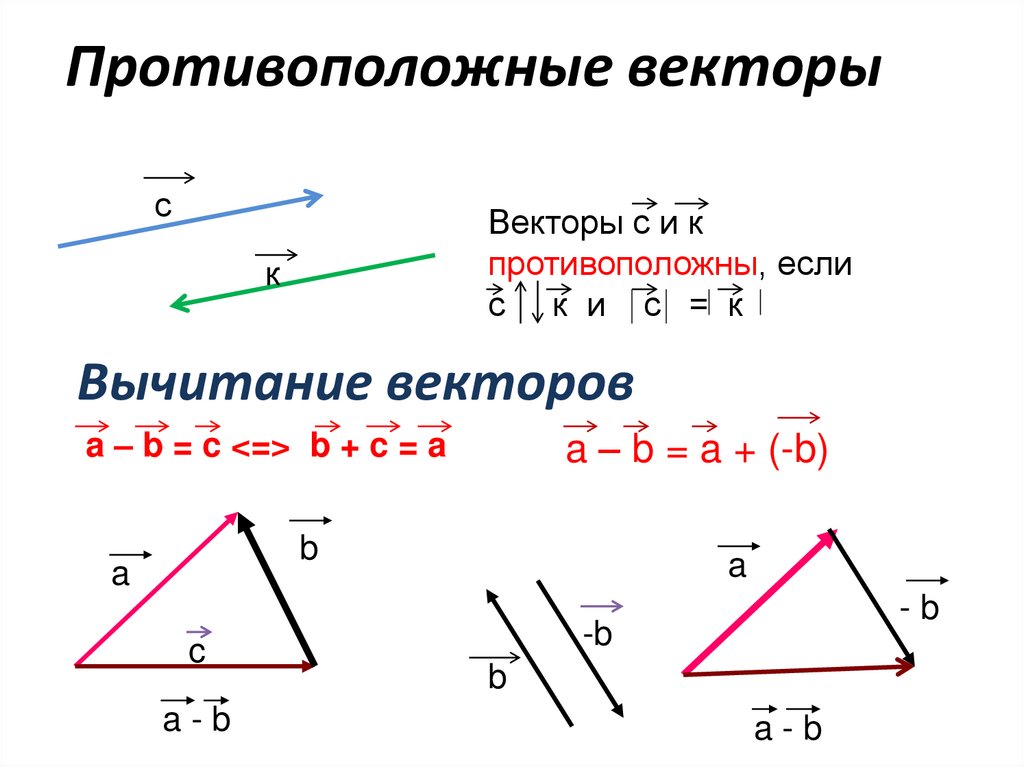
16. Противоположные векторы

с
Векторы с и к
противоположны, если
с к и с = к
к
Вычитание векторов
a – b = c <=> b + c = a
a – b = a + (-b)
b
a
c
a-b
a
-b
-b
b
a-b

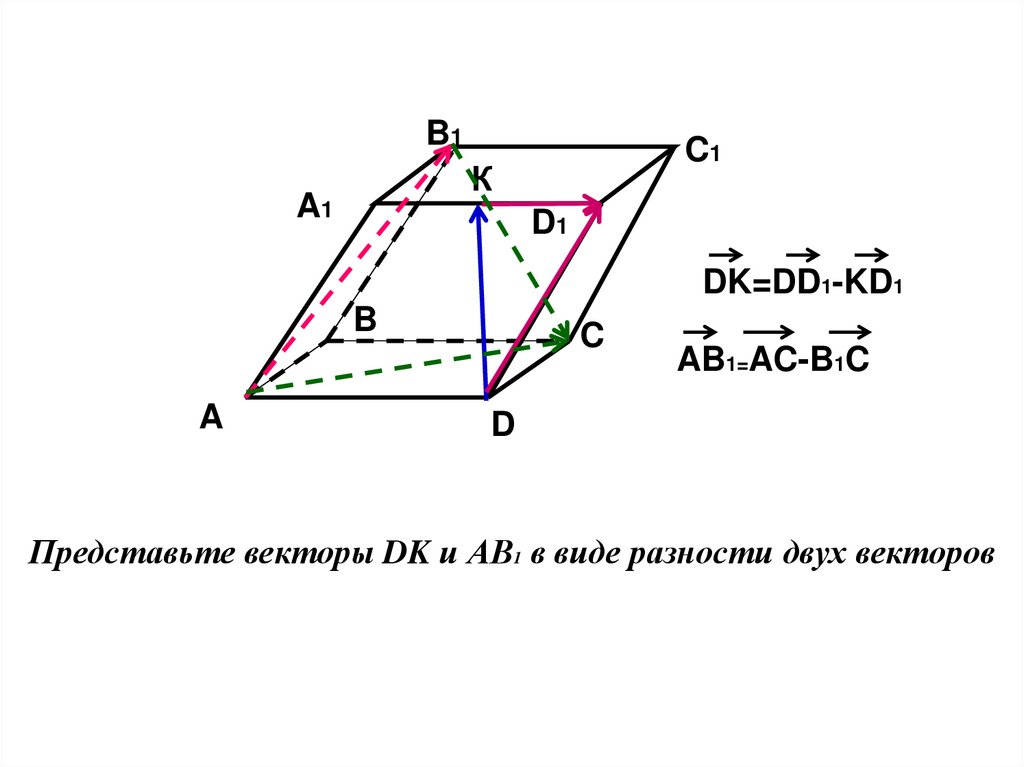
17. Представьте векторы DK и АВ1 в виде разности двух векторов

B1
C1
К
A1
D1
DK=DD1-KD1
B
A
C
AB1=AC-B1C
D
Представьте векторы DK и АВ1 в виде разности двух векторов

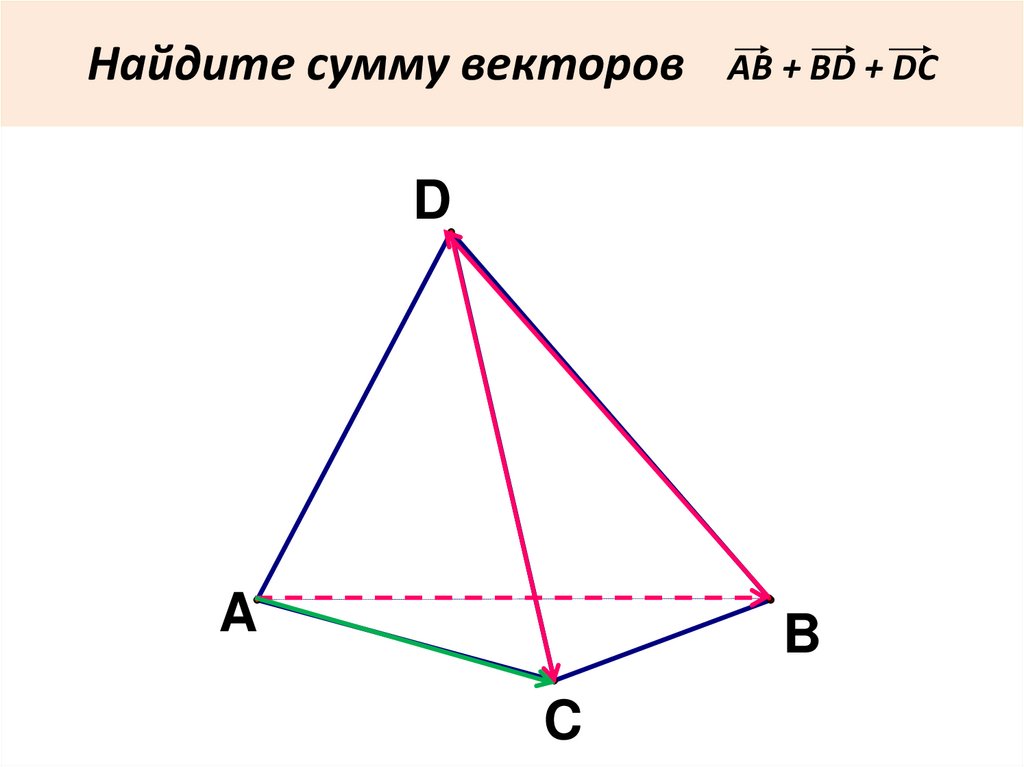
18. Найдите сумму векторов АВ + ВD + DC

D
A
B
C

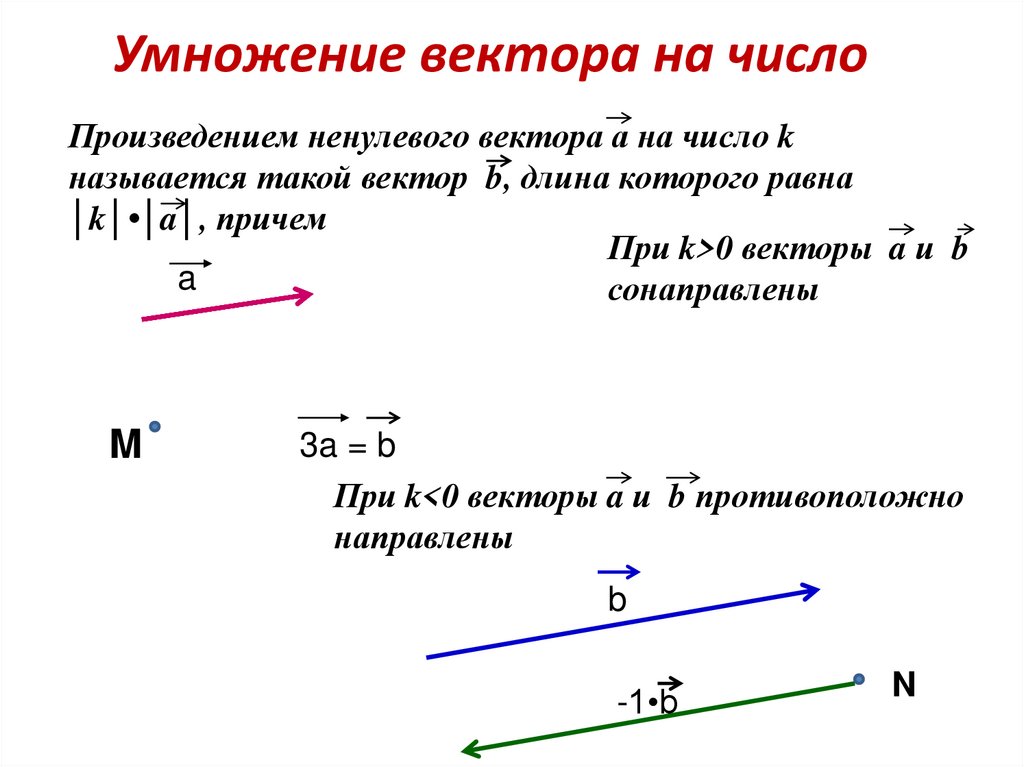
19. Умножение вектора на число

Произведением ненулевого вектора а на число k
называется такой вектор b, длина которого равна
│k│•│a│, причем
При k>0 векторы a и b
a
сонаправлены
M
3a = b
При k<0 векторы a и b противоположно
направлены
b
-1•b
N

20. Законы сложения и умножения вектора на число

1.
2.
3.
4.
5.
а + b = b + а (переместительный)
(а + b) + с = а + (b + с) (сочетательный)
(k n) a = k (n a) (сочетательный)
k (a + b) = ka + kb (распределительный)
(k + n) a = ka + na (распределительный)

21.

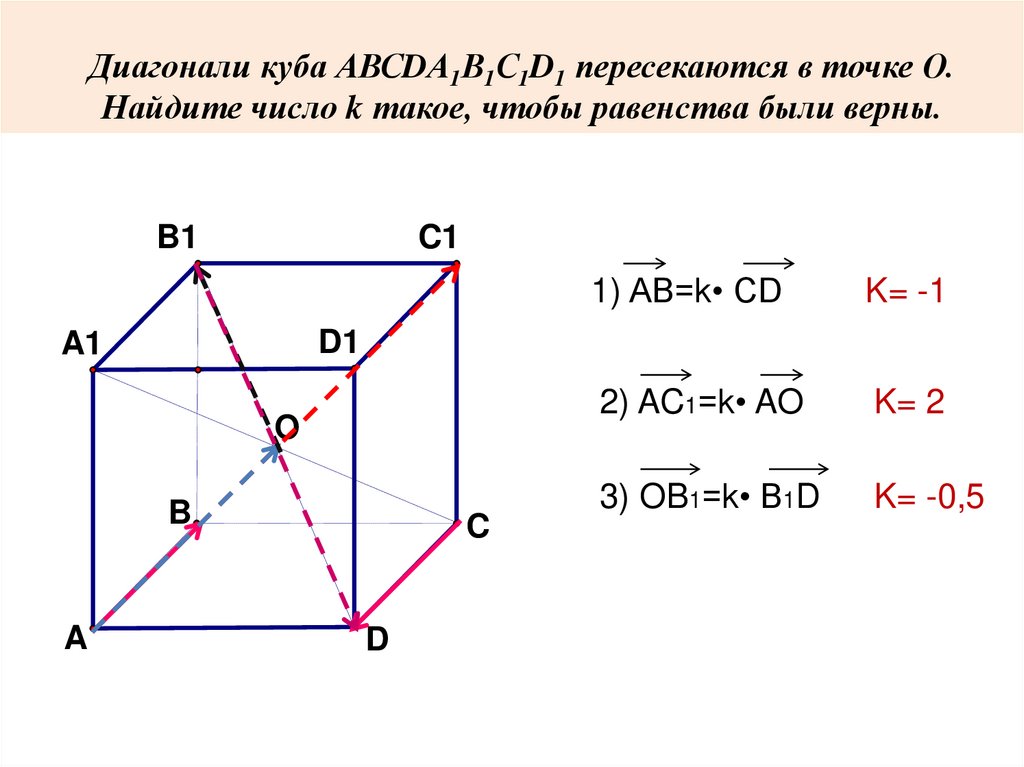
Диагонали куба АВСDА1В1С1D1 пересекаются в точке О.
Найдите число k такое, чтобы равенства были верны.
B1
C1
K= -1
2) AC1=k• AO
K= 2
3) OB1=k• B1D
K= -0,5
D1
A1
O
B
A
1) AB=k• CD
C
D