Векторы на плоскости

1. Тема урока:

2. План.

1.Историческая справка.
2.Определение вектора.
3.Нулевой вектор.
4.Длина вектора.
5.Коллинеарные векторы.
6.Виды коллинеарных векторов.
7.Противоположные векторы.
8.Равные векторы.
9.Откладывание вектора от данной точки.

3. Историческая справка

• Термин вектор (от лат. Vector –
“ несущий “) впервые появился
в 1845 г. у ирландского
математика Уильяма
Гамильтона (1805 – 1865) в
работах по построению
числовых систем.

4. Что такое вектор?

Понятие вектора возникает там, где
приходится иметь дело с объектами, которые
характеризуются величиной и направлением:
например, скорость, сила, давление. Такие
величины называются векторными
величинами или векторами.

5. Геометрическое понятие вектора

• ОПР: Отрезок, для которого указано ,
какой из его концов считается
началом , а какой – концом,
называется направленным отрезком
или вектором.

6. Геометрическое понятие вектора

• Направление вектора указывается стрелкой. Точка A
называется началом вектора, а точка B – концом.
• Векторы обозначаются латинскими буквами a, b, c,
…, а также AB, CD, … (на первом месте ставится
начало вектора).
В
Конец
вектора
a
C
c
А
b
Начало
вектора
D

7. Нулевой вектор

• Любую точку плоскости
можно считать вектором.
Такой вектор называется
нулевым.
• Начало нулевого вектора
совпадает с его концом.
• Нулевой вектор
обозначается 0 или СС.
М
MM - нулевой вектор
С
CC - нулевой вектор

8. Длина (модуль) вектора.

• ОПР: Расстояние между началом и концом вектора
называется длиной или модулем вектора.
• Обозначение: |а| или |АВ|.
• Длина нулевого вектора равна нулю.
|0| =0

9.

Задание 1.
Каждая клетка на рисунке имеет сторону,
равную единице измерения отрезков.
A
B
C
a
D
N
|AB| = 5
|CD| = 4
|a| = 5
|NN| = 0

10.

АВ 6
Задание 2.
А
CD 5
C
EF 2,5
F
MM 0
E
B
M
a 13
b 4,5
c 3
D
a
b
c

11. Коллинеарные векторы

ОПР: Два ненулевых вектора
называются коллинеарными, если они
лежат на параллельных прямых или на
одной прямой.
b
Нулевой вектор считается коллинеарным
любому вектору.
a
b
a

12. Задание: укажите коллинеарные векторы

O
b
CD, KF, O, a, b –
коллинеарные
N
D
a
K
O, a – коллинеарные
O, NP – коллинеарные
P
C
m
F
NP, m – не коллинеарные

13. Коллинеарные векторы

• Сонаправленные
• Противоположно
направленные

14.

Сонаправленные векторы
a
b
АА
а в
Два вектора называются сонаправленными,
если они коллинеарные и направлены одинаково.

15.

Противоположно направленные векторы
a
а в
b
Два вектора называются противоположно направленными,
если они коллинеарны и противоположно направлены

16.

Свойства коллинеарных векторов.

17.

b
a
c
b
a
c 0 ,
то a b
если a с, b с,
то a b
c
b
c
если a с, b с,
a
если a с, b с,
то a b

18. Противоположные векторы

Длины равны
Два вектора называются противоположными,
если они противоположно направлены и их длины равны.

19. Равные векторы

a
a
a
a
a

20. ОПР: Ненулевые векторы называются равными, если они сонаправлены и их модули равны. Все нулевые векторы равны друг другу.

a b, если
1.a b
2. a b
Свойство равных векторов.

21.

Задание: найдите равные векторы.
В
a
2
a
С
О
А
1
b
=
b
D
АВСD – параллелограмм.
ВA = CD;
AВ = DC;
CВ = DA;
Найдите еще пары равных векторов.
О – точка пересечения диагоналей.
AD = BC.

22. Откладывание вектора от данной точки

• От любой точки можно отложить вектор, равный
данному вектору, и притом только один.
N
В
а
М
А
M p
N'
p II AB
MN = AB
MN' = AB
p
MN = a

23. Упражнение

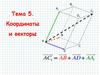
На рисунке 1 изображён параллелепипед
ABCDA B C D
Точки М и К – середины рёбер В С и А D .
Укажите все пары:
1
1
1
1.
1
1
1
1
А) сонаправленных векторов
Б) противоположно направленных векторов
В) равных векторов.

24.

(1)
С1
М
В1
К
D1
А1
В
А
С
D

25. Ответы.

• А)KD и MC ,BC и B C , A D и BC ,
AD и BC
1
1
1
1
1
1
1
1.
• Б)DC и AB , AD и BC , AD и B C ,
AD и A D
1
1
1
1.
• В)DK и MC , AB и CD , AB и AC , B C и BC ,
AD и B C
1
1
1.
1
1

26. Задача 1

Какие из векторов,
изображенных на
рисунке:
1) коллинеарны;
2) сонаправлены;
3) противоположно
направлены;
4) имеют равные длины?
Отложите эти векторы
от одной точки.
d
c
a
b

27.

Задача 2. В прямоугольнике АВСD АВ=3см, ВС=4см,
точка М – середина стороны АВ. Найдите длины векторов.
АВ = 3
В
4
С
ВC = 4
DС = 3
MА = 1,5
3
M
5
СВ = 4
АС = 5
А
D
МC =

28.

Задача 3. В параллелограмме АВСD диагонали
пересекаются в точке О. Равны ли векторы. Обоснуйте
ответ.
С
В
О
А
AВ = DC;
D
ВС = DА;
AО = ОC;
AС = ВD.

29. Задача 4

• На рисунке изображена равнобедренная трапеция
KLMN.
а) Укажите сонаправленные, противоположно
направленные, равные вектора.
б) Укажите векторы, длины которых равны. Равны ли
при этом сами векторы?
L
K
M
N