Similar presentations:
Векторы
1. Векторы
2. Историческая справка
► Термин вектор (от лат.Vector – “ несущий “)
впервые появился в
1845 г. у ирландского
математика Уильяма
Гамильтона (1805 –
1865) в работах по
построению числовых
систем.
3.
Отрезок, для которого указано, какая из егограничных точек считается началом, а какая – концом,
называется направленным отрезком или вектором
► Точка A называется
Конец вектора
В
Вектор АВ
Вектор ВА
А Начало вектора
началом вектора, а
точка B – концом.
Длиной или
модулем вектора
называется длина
отрезка АВ
AB AB
4. Другое обозначение вектора
► Векторы можнообозначать и
латинскими
буквами a, b, c, …
a a
a
c
b
5.
Любая точка плоскоститакже является вектором.
В этом случае вектор называется
нулевым
M
Вектор
MM
Вектор
0
Любое направление можно считать
направлением нулевого вектора.
Длина нулевого считается равной нулю
MM = 0
6.
Назовите векторы, изображенные на рисунке.Укажите начало и конец векторов.
Найдите их длину.
a
A
Вектор AB AB 8
Вектор CD CD 5
C
В
N
Вектор а a 4
D
Вектор NN или 0
0
7.
Понятие вектора возникает там, где приходитсяиметь дело с объектами, которые
характеризуются величиной и направлением:
скорость, сила, давление.
Такие величины называются векторными
величинами или векторами.
8.
При изучении электрических и магнитных явленийпоявляются новые примеры векторных величин.
E
+
Электрическое поле,
создаваемое в
пространстве зарядами,
характеризуется в каждой
точке пространства
вектором напряженности
электрического поля.
На рисунке
изображены векторы
напряженности
электрического поля
положительного точечного
заряда.
9.
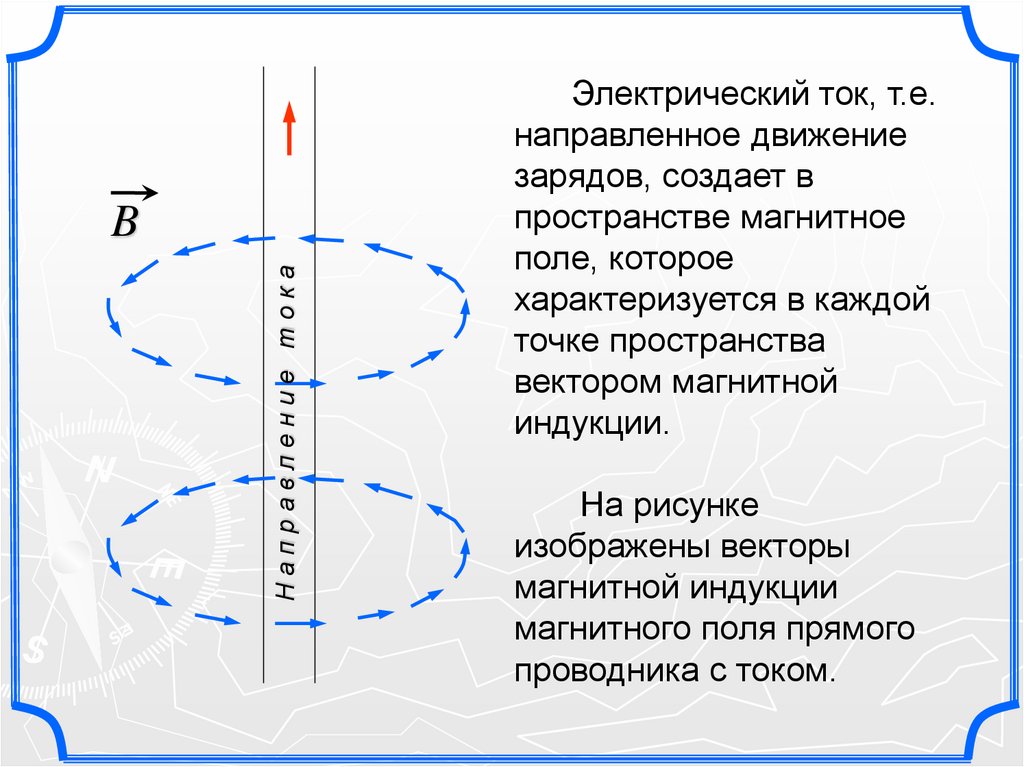
Направление токаB
Электрический ток, т.е.
направленное движение
зарядов, создает в
пространстве магнитное
поле, которое
характеризуется в каждой
точке пространства
вектором магнитной
индукции.
На рисунке
изображены векторы
магнитной индукции
магнитного поля прямого
проводника с током.
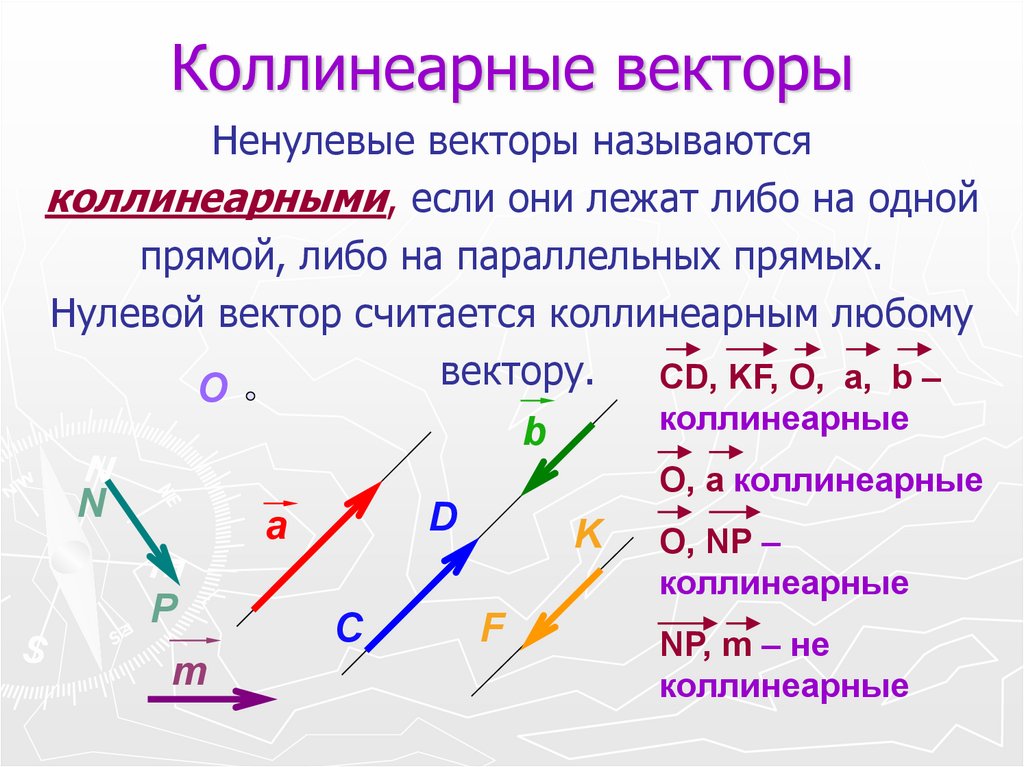
10. Коллинеарные векторы
Ненулевые векторы называютсяколлинеарными, если они лежат либо на одной
прямой, либо на параллельных прямых.
Нулевой вектор считается коллинеарным любому
вектору.
CD, KF, O, a, b –
O
коллинеарные
b
O, a коллинеарные
N
D
a
P
m
C
K
F
O, NP –
коллинеарные
NP, m – не
коллинеарные
11. Коллинеарные векторы могут быть направлены
одинаковопротивоположно
Сонаправленные
Противоположно
направленные
a
C
a ↑↑CD
b ↑↑KF
M
D
F
b
a ↑↓b
K
a ↑↓ KF
Нулевой вектор сонаправлен с любым вектором.
12.
Векторы называются равными,если они сонаправлены и их длины равны.
1
a
b
a = b
2
В
А
С
D
АВСD – параллелограмм.
ВA = CD;
AВ = DC;
CВ = DA;
AD = BC.
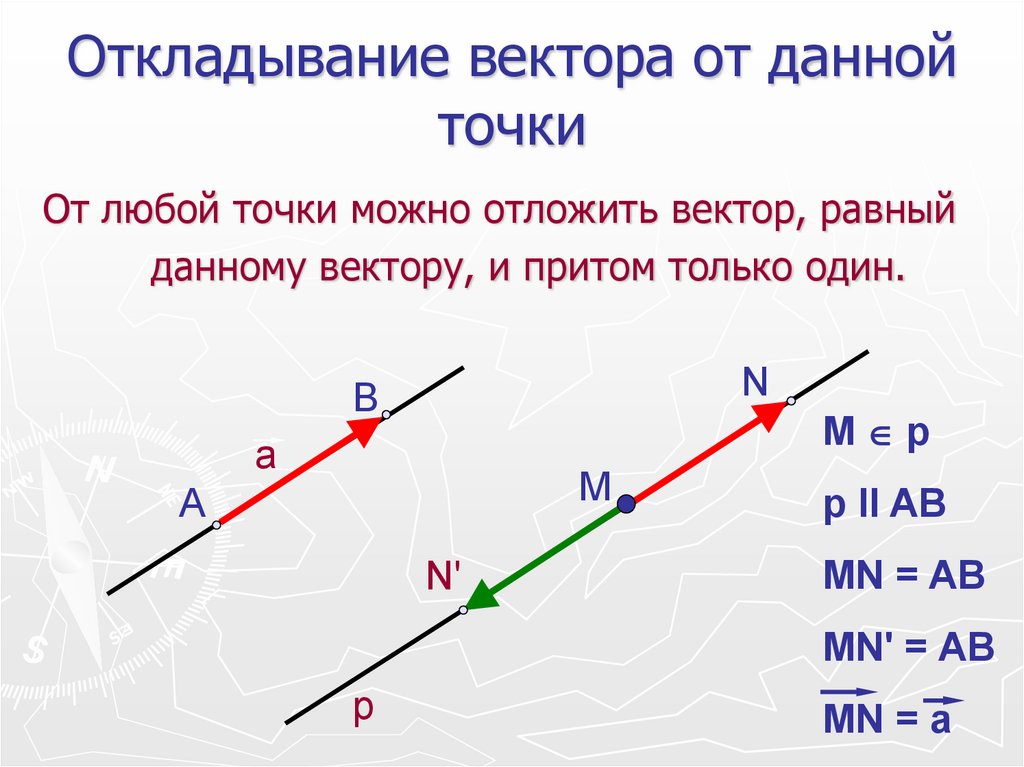
13. Откладывание вектора от данной точки
От любой точки можно отложить вектор, равныйданному вектору, и притом только один.
N
В
M p
а
М
А
N'
p II AB
MN = AB
MN' = AB
p
MN = a
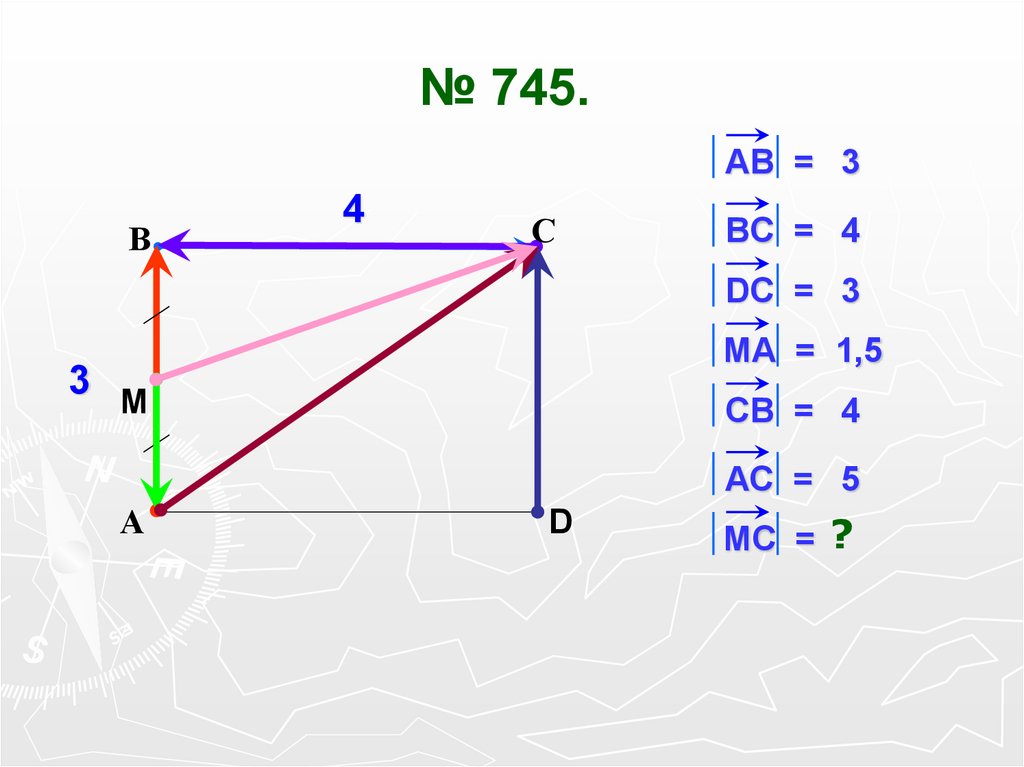
14.
№ 745.АВ = 3
В
4
С
ВC = 4
DС = 3
3
MА = 1,5
M
СВ = 4
АС = 5
А
D
МC = ?
15.
№747
(а)
N
M
P
Q
Коллинеарные:
MN, NM, QP, PQ и MQ, QM, NP, PN
СОНАПРАВЛЕННЫЕ
MN
QM
QP NM
PN MQ
PQ
NP
ПРОТИВОПОЛОЖНО
НАПРАВЛЕННЫЕ
NM
QP
MN
PQ
QM
NP
MQ
PN
16.
В№ 747 (б)
С
D
А
Коллинеарные: AD, DA, BC, CB
СОНАПРАВЛЕННЫЕ
СВ
ВС
DA
AD
ПРОТИВОПОЛОЖНО
НАПРАВЛЕННЫЕ
СВ
AD
ВС
DA
17.
№ 747 (в)G
F
H
Коллинеарных векторов нет
18.
В№ 748
С
О
А
AВ = DC;
D
ВС = DА;
ВС
AВ
DC
AВ = DC
AО = ОC;
DA
AС = ВD.
AC
AO OC
AO = OC
BD
19.
№ 749N
L
S
T
M
K
NL = KL;
KL
NL
MS = SN;
MS
SN
MS = SN
MN = KL;
KL
MN
TS = KM;
TL = KT.
TS
TL
KT
TL = KT
TS
KM
KM
20.
№ 746 (кратко)B
C
5
5
450
A
К
7
12
7
D















 mathematics
mathematics








