Векторы. Понятие вектора

1. Векторы

2. Понятие вектора

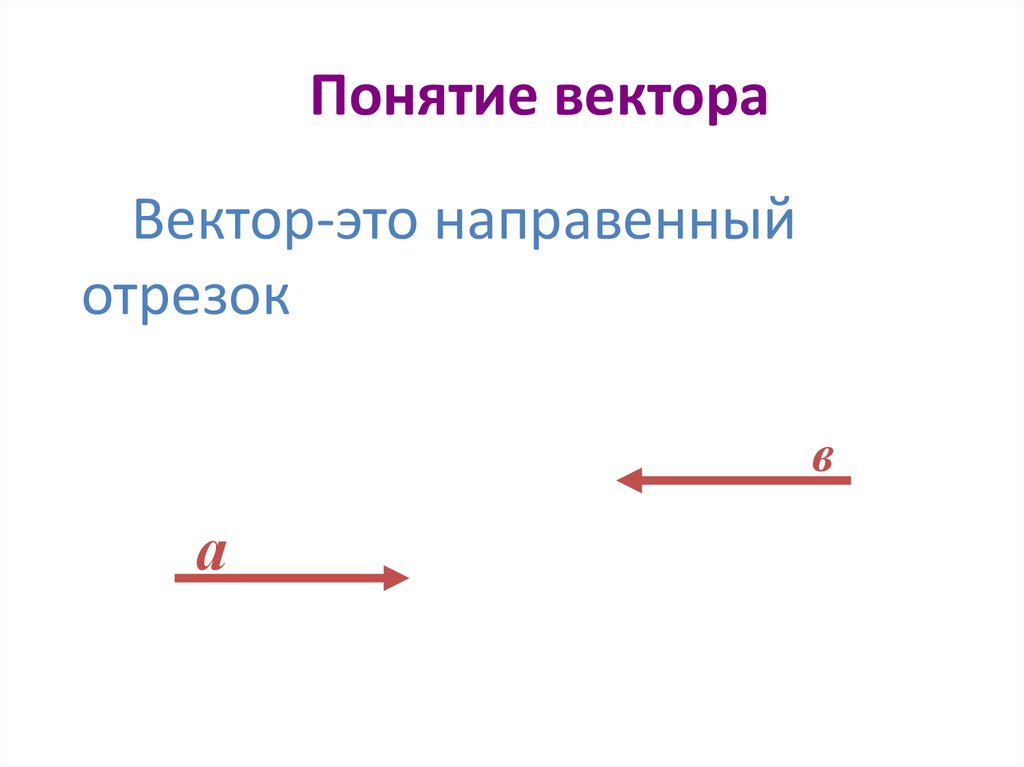
Вектор-это направенный
отрезок
в
а

3. Второе понятие вектора

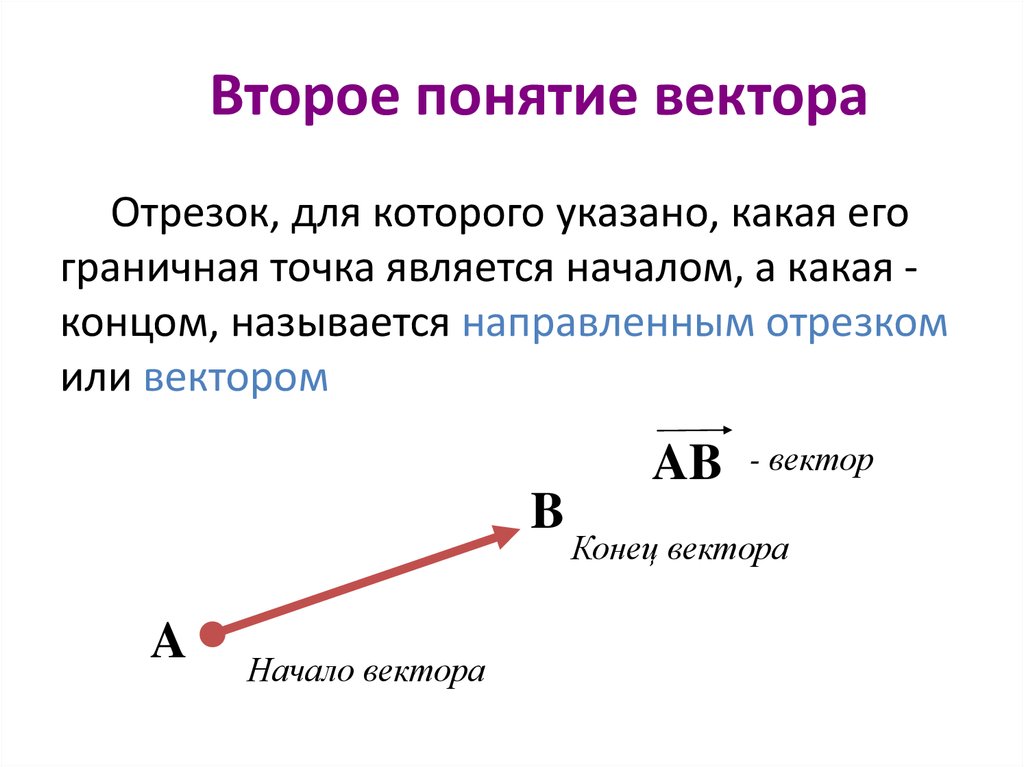
Отрезок, для которого указано, какая его
граничная точка является началом, а какая концом, называется направленным отрезком
или вектором
AB
B
A
Начало вектора
- вектор
Конец вектора

4. Длина вектора

вектор MN или вектор а
N
a
M
Длиной вектора или модулем
не нулевого вектора называется
длина отрезка
|MN| = |a| длина вектора MN
K вектор КК или нулевой вектор
|KK| = 0

5. Коллинеарные вектора

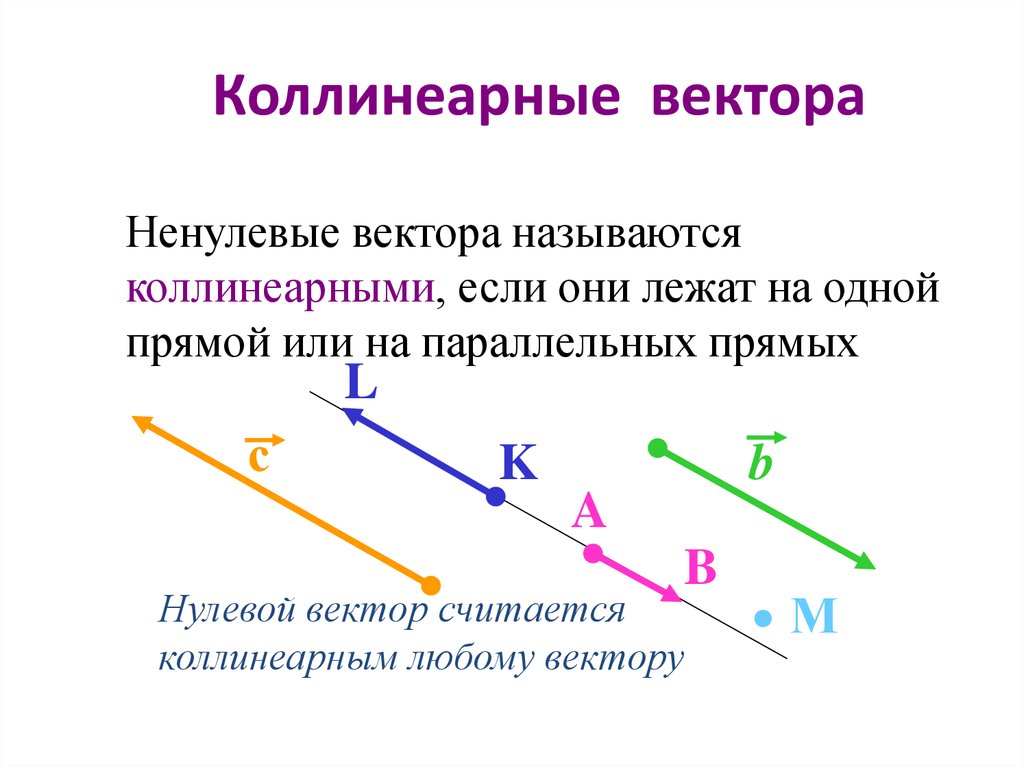
Ненулевые вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых
L
с
K
b
A
Нулевой вектор считается
коллинеарным любому вектору
B
М

6. Сонаправленные вектора

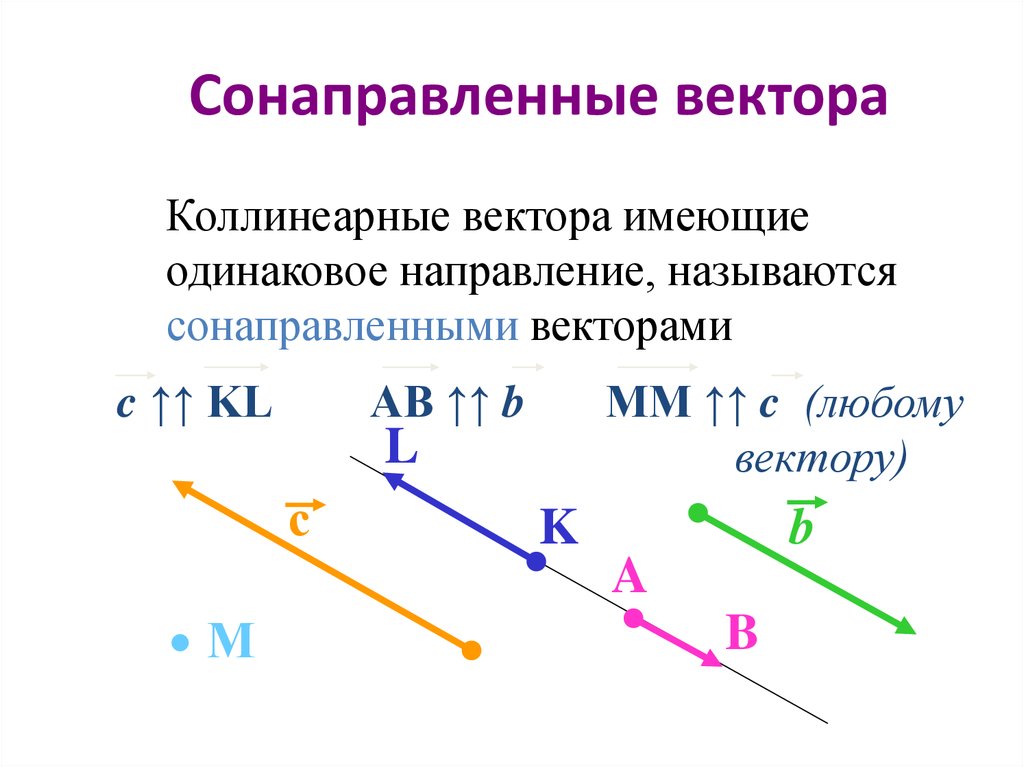
Коллинеарные вектора имеющие
одинаковое направление, называются
сонаправленными векторами
c ↑↑ KL
AB ↑↑ b
MM ↑↑ c (любому
вектору)
L
с
K
b
A
М
B

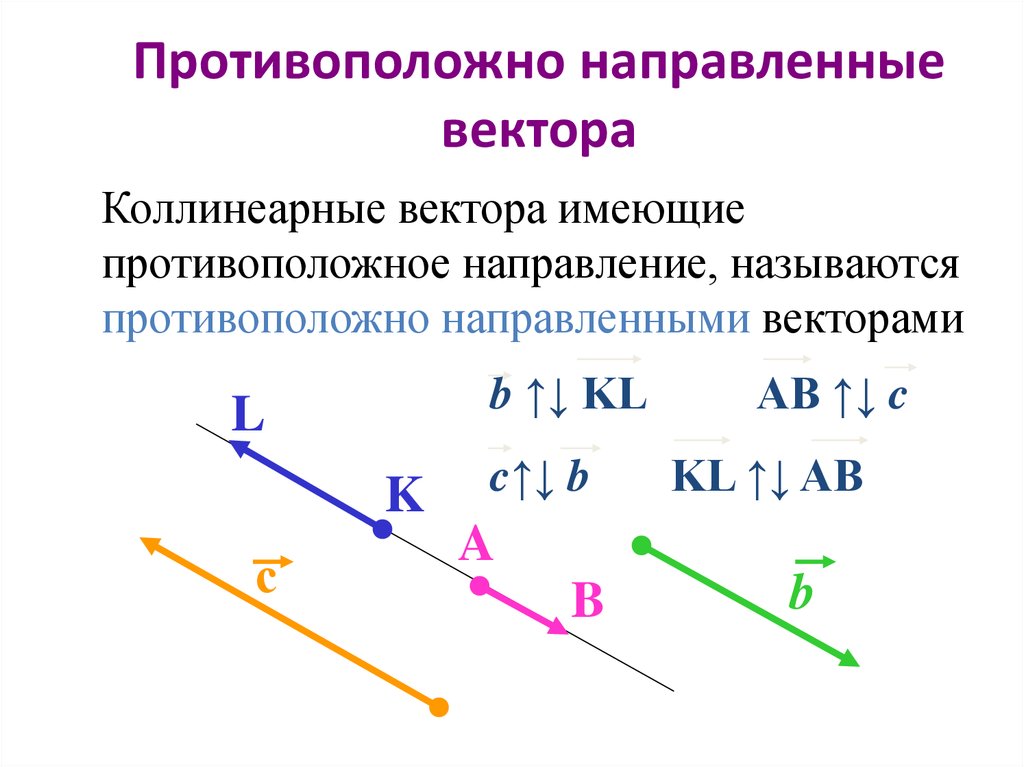
7. Противоположно направленные вектора

Коллинеарные вектора имеющие
противоположное направление, называются
противоположно направленными векторами
b ↑↓ KL
L
K
с
c↑↓ b
AB ↑↓ c
KL ↑↓ AB
A
B
b

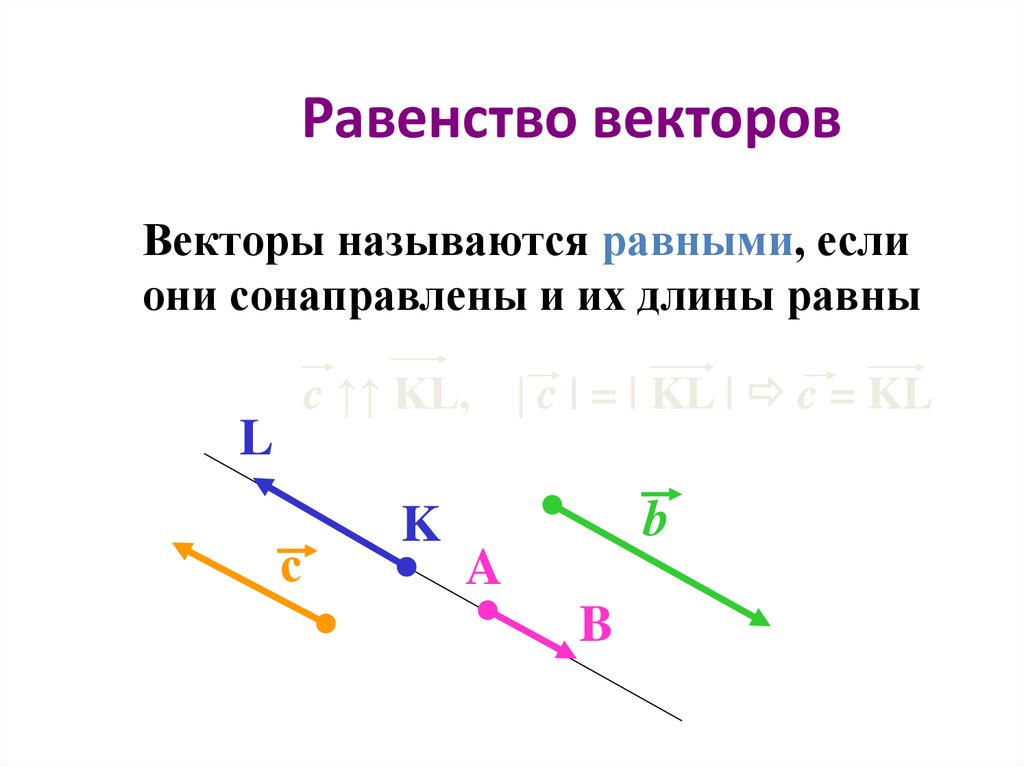
8. Равенство векторов

Векторы называются равными, если
они сонаправлены и их длины равны
c ↑↑ KL, | c | = | KL | c = KL
L
с
K
b
A
B

9. Сложение векторов Правило треугольника

b
Дано: a, b
a
Построить: c = a + b
Построение:
b
с
a
a+b=c

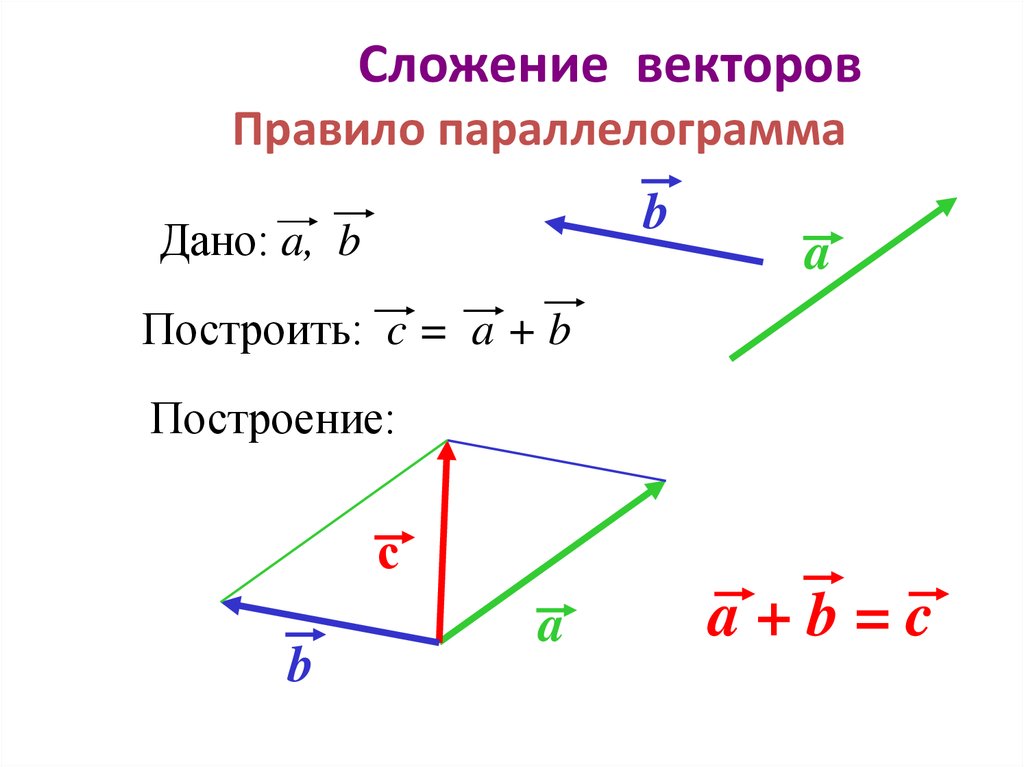
10. Сложение векторов Правило параллелограмма

b
Дано: a, b
a
Построить: c = a + b
Построение:
с
b
a
a+b=c

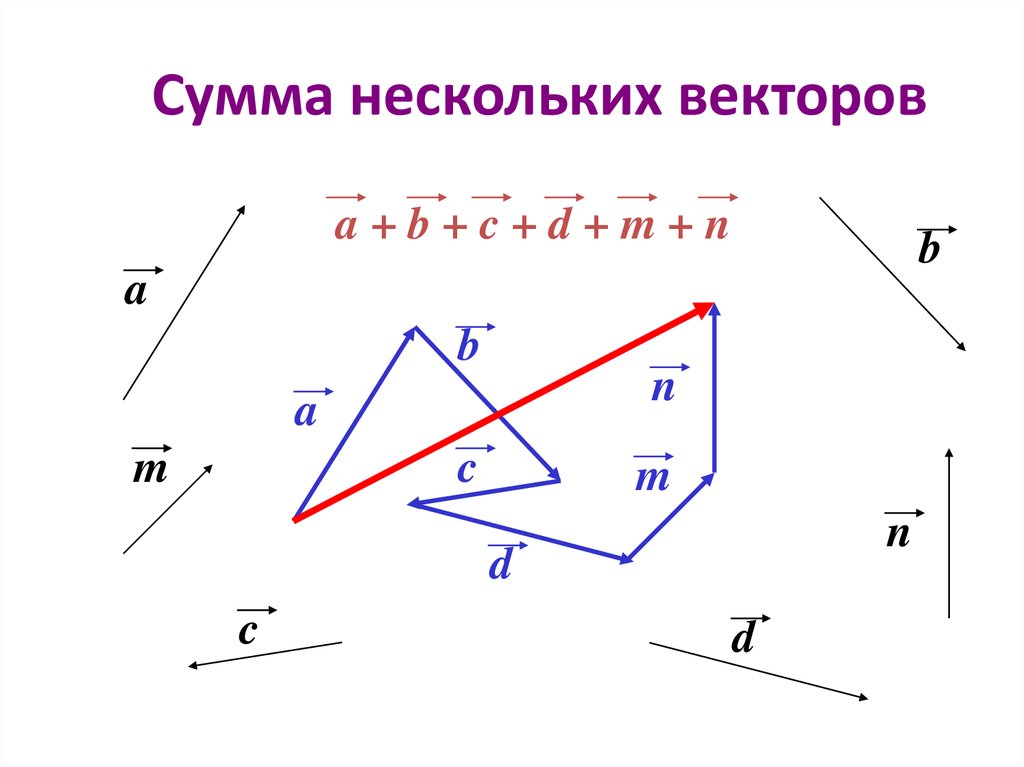
11. Сумма нескольких векторов

a+b+c+d+m+n
b
a
b
n
a
m
c
m
n
d
c
d

12. Вычитание векторов

b
Дано: a, b
a
Построить: c = a - b
Построение:
с
a-b=c
a
b