Граничные условия на границе с черным телом Условием черного тела является

1.

§7.3. Граничные условия на границе с черным телом
Условием черного тела является
a t ,
s 0,
т. е. все падающие на него нейтроны будут поглощаться. Очевидно, что и
при этом условии, как и в случае с вакуумом, вылетевшие нейтроны не
будут возвращаться в среду, поэтому эффективное ГУ можно записать
таким же, как и (40).
Но довольно часто применяется и другая форма ГУ
tr
.
tr
d dx x R
(42)
Для тела конечного размера, в котором диффундируют нейтроны,
возрастает с уменьшением кривизны тела и в предельном случае, когда
радиус кривизны стремится к нулю, равен
R 0
4
3
tr .
(43)

2.

Это доказывается на примере бесконечно тонкого абсолютно
поглощающего стержня ( черного стержня), помещенного в
слабопоглощающую среду. Так как стержень очень тонкий, то поэтому он
не нарушает изотропии углового распределения нейтронов и можно
считать, что уравнение диффузии выполняется всюду. Односторонний ток
нейтронов, падающих на стержень с поверхностью F , с учетом (19) будет
равен
Fi F
4
.
Скорость поглощения равна произведению диффузионного тока I
на F , т.е. результирующему току через эту площадку
( 19 )
FI FD .

3.

Так как сколько нейтронов попадает на стержень, cтолько и
поглощается
F
откуда следует
4
FD ,
4
4 D tr .
3
Таким образом, длина линейной экстраполяции в единицах
транспортной длины меняется в интервале
tr
4
3
Сфера , цилиндр с R 0
0 ,7104 .
Пластина
(44)

4.

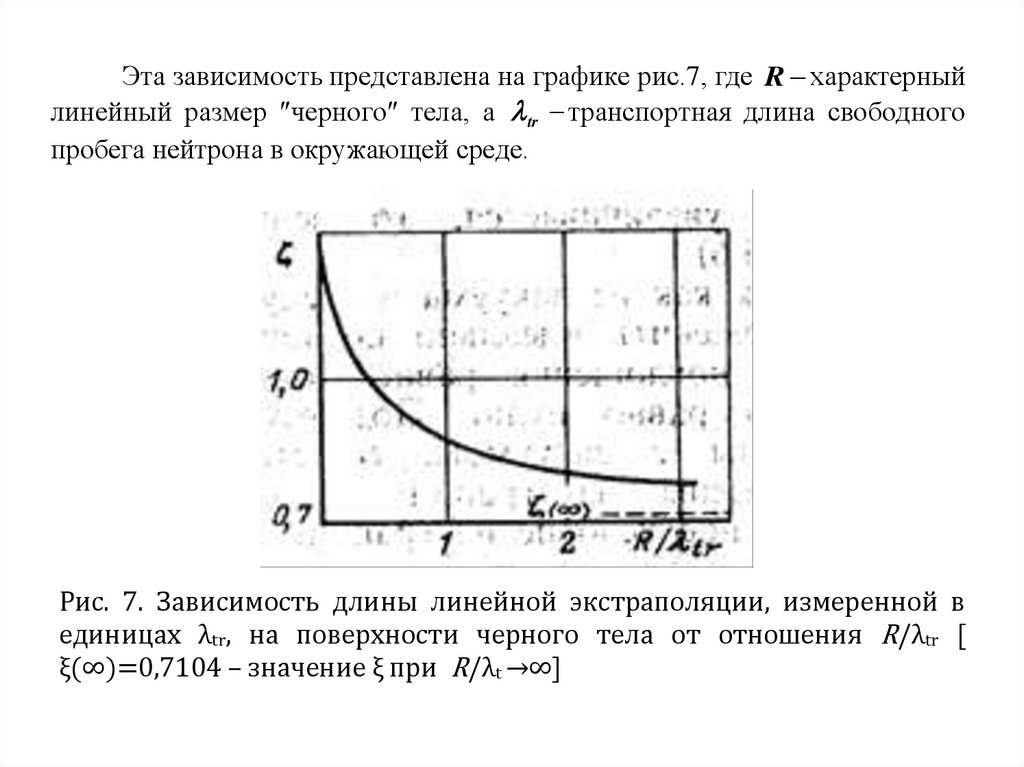
Эта зависимость представлена на графике рис.7, где R характерный
линейный размер черного тела, а tr транспортная длина свободного
пробега нейтрона в окружающей среде.
Рис. 7. Зависимость длины линейной экстраполяции, измеренной в
единицах λtr, на поверхности черного тела от отношения R/λtr [
ξ(∞)=0,7104 – значение ξ при R/λt →∞]

5.

В заключение сделаем 2 замечания:
экстраполированные (эффективные) границы возникают всегда,
когда одна из контактирующих сред либо вакуум, либо черное
тело;
в действительности поток нейтронов равен нулю не на
экстраполированной границе и это условие лишь формальный
математический прием, повышающий точность диффузионного
приближения.

6.

§8. Решения уравнения диффузии в средах с точечным
источником
§8.1. Бесконечная однородная среда
Пусть требуется найти поле моноэнергетических нейтронов,
генерируемых в бесконечной однородной среде точечным изотропным
источником с постоянной скоростью генерации ST , нейтрон / c.
Источник поместим в начало координат.
Уравнение диффузии во всем объеме среды V , кроме точки r=0, есть
D r a r 0 .
С учетом сферической симметрии раскроем лапласиан и после деления
всех членов уравнения на D , получим:
1 2 r
2
r
r 0 ,
2
r
r r
0 r ,
(45)

7.

где 2 a D параметр, определяющий свойства среды. В теории
реактора данное уравнение известно как уравнение диффузии для
неразмножающей среды, о чем говорит знак - .
Граничные условия поставим следующим образом:
1 . 0 r
0 ,
(461)
т.е. поток как материальная субстанция на любом r должен быть
положителен и конечен;
2.
a r dV ST ,
(462)
0
т.е. полное число поглощенных нейтронов в единицу времени равно
скорости их образования – условие баланса для стационарных задач.

8.

Общее решение уравнения (45) известно (смотри в общем списке
таблиц и функций Табл. №6) и имеет вид:
exp r
exp r
.
(47)
C2
r
r
Удовлетворяя это решение первому ГУ, получим уравнение, из которого
следует C 2 0 . Проделав тоже для второго условия, получим
r C 1
a C1
0
exp r
dV ST ,
r
откуда после взятия интеграла найдем константу
S
C1 T
4 D
и закон распределения потока нейтронов
r
ST exp r
.
4 D
r
(48)

9.

ДЗ№5 Получить решение (48).
Решение (48) обобщается на случай произвольного расположения
источника
ST exp r r
r , r
S GT r r ,
4 D
r r
(49)
где GT r r называют диффузионной функцией влияния точечного
источника, которое имеет следующий физический смысл: это есть поток
нейтронов в точке r , обусловленный наличием в точке r точечного
источника единичной интенсивности 1 нейтрон/с.
Другие названия этой функции, встречающиеся в литературе:
точечное диффузионное ядро, функция Грина для точечного
источника.

10.

§8.2. Конечная однородная среда
Рассмотрим источник с интенсивностью ST, помещенный в центре
сферы радиусом R, которая окружена вакуумом. Очевидно, определяющее
уравнение диффузии останется прежним (45), так как приняты та же
сферическая симметрия и тип источника. Следовательно, общее решение
будет прежним, и изменятся только ГУ.
Первое ГУ в центре сферы
1 . r 0
limr 0 4 r I ST .
2
(50)
Это условие означает, что ток нейтронов через сферу как угодно близко
охватывает источник, равен скорости генерации этого источника ST.
Заметим, что согласно закону Фика (22) I D .
Поскольку сфера соприкасается с вакуумом, то второе ГУ
необходимо записать на экстраполированной границе Rэ
2 . r Rэ
Rэ 0 .
(51)

11.

Ход получения решения аналогичен предыдущей задаче и в
результате получим следующий закон распределения плотности
потока нейтронов в сфере
r
ST exp r 1 exp 2 Rэ r
.
4 D
r
1 exp 2 Rэ
(52)
ДЗ№6 Получить решение (52).
ДЗ№7 1. Показать графиком как будут выглядеть потоки
(48) и (52) и объяснить отличия.
2. Что учитывает второй сомножитель в
решении(52).

12.

Сделаем 2 замечания к рассмотренным задачам:
1. Под точечным источником понимают такой источник, размеры
которого малы по сравнению со средней длиной пробега нейтрона в
среде, но больше 0. Поэтому решения (48), (49), (52) не имеют
физического смысла при r 0 или не дают правильного результата
из-за невыполнения условия (15 ).
2. Сравнение решений (48) и (52) с точным решением уравнения
Пайерлса показывает, что хотя при r 0 все же
диффузионное приближение значительно занижает значение
потока в окрестностях источника.

13.

§9. Метод вероятности первых столкновений (ВПС)
§9.1.
Замена
алгебраических
интегрального
уравнения
системой
Замена уравнения Пайерлса уравнением диффузии не единственный
способ упростить задачу и получить простое аналитическое решение.
Другой путь заключается в замене интегрального уравнения системой
алгебраических уравнений. Рассмотрим его подробнее.
Пусть имеется объем V, который может быть разделен на L зон
таким образом, что в пределах каждой зоны сечения остаются
постоянными. Тогда обозначая V i объем i - й зоны (i=0,1,2,...,L-1),
заменяем интеграл по всему объему V в правой части уравнений (33),(34)
суммой интегралов по объемам V i
L 1
r si r S r K r , r dr .
i 0 Vi
(53)

14.

Умножим обе части равенства на полное сечение взаимодействия
нейтрона с ядром зоны j - tj и проинтегрируем по объему V j , изменив
при этом порядок интегрирования:
L 1
tj r dr si dr r tj K r , r dr
i 0
Vj
Vj
Vi
dr S r tj K r , r dr .
Vi
Vj
(54)
Вводя средние по зонам значения потока и объемные скорости
генерации нейтронов
вычислим полное число столкновений tj jV j в объеме V j .

15.

Для этого первый интеграл в правой части (54) умножим и разделим
на r dr , а второй - на S r dr .
Vi
Vi
В результате получим
L 1
tjV j j Vi si i ij S i ijS ,
i 0
где
d
r
r
K
r
tj , r dr
ij i
V
Vj
;
r
dr
Vj
d
r
S
r
K
r
tj , r dr
ijS i
V
Vj
S
r
dr
Vj
.
(55)

16.

До этого момента преобразования не нарушали точности исходного
уравнения Пайерлса.
Однако поскольку r и S r неизвестны, вычислить функции
ij и ijS невозможно.
Поэтому для получения практических результатов необходимо
сделать упрощающие предположения относительно распределения
источников и потока нейтронов в пространстве. Используя самое простое
из них, которое состоит в том, что и S внутри объема V i не зависят от
координат, получают
R
exp t r R dR
tj
0
S
ij ij ij
dr
dr
(56)
2
Vi Vi V j
4 r r

17.

и тогда уравнение (55) примет вид
L 1
tjV j j Vi ij si i S i .
i 0
(57)
Аналогично можно вывести уравнения для других зон, т.е. получить
систему L алгебраических уравнений.
Так как Pij есть вероятность для нейтрона, родившегося в зоне i
испытать первое столкновение в зоне j , поэтому система (57)
представляет собой уравнения метода вероятностей первых
столкновений для решения задач пространственного распределения
нейтронов.

18.

§9.2. Понятие средней хорды
Точность системы (57) и ее эквивалентность исходному
интегральному уравнению Пайерлса полностью определяются точностью
предположения о независимости потоков и распределения источников от
координат.
Чтобы
сформулировать
условие
справедливости
этого
предположения, вводят понятие средней хорды l i , которое
определяется как средний путь, проходимый нейтроном в i-й зоне при
тсутствии в ней рассеяния и поглощения.
Для того, чтобы найти эту величину выделим в бесконечной
однородной среде со следующими свойствами s 0 , a 0 объем V i ,
ограниченный площадью F .

19.

Подсчитаем скорость поглощения, которую с одной стороны можно
записать как
Rai Vi ai ,
но также и через среднюю хорду
8 , 19
Rai 1 exp ai l i
4F ,
где 1 exp ai l i вероятность поглощения на длине l i .
Отсюда приравняв эти выражения и ограничиваясь линейным
членом разложения экспоненты в ряд, получим
l i 4 Vi F .
ДЗ№8 Получить выражение для средней хорды (58).
(58)

20.

Видно, что l i является чисто геометрической характеристикой, не
зависящей от состава зоны, которую иначе называют как средний
возможный путь пробега нейтрона в i-ой зоне.
Тогда условие справедливости предположения о независимости
потоков и распределения источников от координат формулируется как
i ti l i
li
ti
1
(59)
Действительно, чем меньше оптическая толщина каждой зоны,
тем точнее система уравнений. В пределе, при стремлении к нулю
оптической толщины наибольшей зоны система точна.

21.

Реальные размеры зон, обеспечивающие справедливость сделанных
предположений, могут колебаться в зависимости от характера задачи
(значений градиентов), однако последнее условие всегда обеспечивает
приемлемую точность.
Очевидно, что если для какой-либо реальной зоны с постоянным
сечением это условие (59) не выполняется, ничто (за исключением
роста объема вычислений) не мешает разбить ее на части
достаточно малой оптической толщины.