Similar presentations:
Теория переноса ионизирующего излучения
1.
Белорусский государственный университетФизический факультет
ЗАЩИТА ОТ
ИОНИЗИРУЮЩИХ
ИЗЛУЧЕНИЙ
Теория переноса
ионизирующего излучения
2019-2020 уч. г.
2.
Вводные замечанияВо многих случаях экранирования
ионизирующего излучения в веществе экрана
порождается множество частиц вторичного
излучения, что не позволяет применять ранее
использованные аналитические методы.
Строго говоря, это – задача теории переноса
излучения, или транспортной теории
(transport theory)
В наиболее общей форме теория переноса –
это часть статистической физики, в которой
изучается взаимодействие частиц одного
типа (типов) с частицами другого типа (типов)
3.
Вводные замечанияСуществует два основных подхода к
использованию строгих уравнений переноса.
Один из них состоит в использовании
имитационных моделей, основанных на
методах Монте-Карло, описывающих, как
частица излучения мигрирует в среде защиты.
Второй подход состоит в том, что
используются уравнения, которые строго
описывают поле излучения, и чьи решения
дают значения ожидаемого флюэнса или
плотности потока частиц излучения в
веществе экрана.
4.
Детерминистская теорияпереноса излучения
Общий подход к составлению
уравнений переноса излучения
5.
Общая формулировка уравненияпереноса излучения
Для описания поля излучения достаточно
знать распределение объемной
концентрации частиц по энергиям и
направлениям
n p (r , E , t )
С ее помощью определяется распределение
мощности флюэнса (плотности потока
частиц) по энергиям
и направлениям:
( E , r , t ) V ( E )n p (r , E , t )
(1)
где u – скорость частицы. Для фотонов V = c.
Для нерелятивистских нейтронов V c 2 E /E0 n
6.
Общая формулировка уравненияпереноса излучения
Физический смысл ( E , r , t ) :
отнесенный к единице телесного угла и
интервала энергий фотонов или нейтронов
суммарный путь, пройденный в единицу
времени в единице объема частицами
излучения, которые движутся в малом
телесном угле d вблизи направления и
имеющих энергии около E в бесконечно малом
интервале энергий dE.
Именно такое понимание ( E , r , t ) будет
использоваться в дальнейшем для
формулировки уравнений переноса излучения
7.
Уравнение дляn p ( E, r , t )
Уравнение баланса в области объема V,
ограниченной поверхностью площади А:
Скорость
(b) скорость
(a ) мощность
изменения
убыли частиц ИИ
потока частиц
числа частиц
из V через A при взаимодействии
с частицами вещества в V
в объеме V
(c) скорость производства
(d) скорость производства
вторичных частиц с энергией E , частиц источниками
в
объеме
V
движущихся
в
направлени
и
Все выражения определены в узких интервалах
энергий dE и телесных углов d и отнесены к
единичным значениям этих интервалов
(2)
8.
Математическое выражение длялевой части (2)
Скорость
изменения
d
dVn p (r , E , t )dEd
числа частиц dt V
в объеме V
т.к.
dVn p (r , E , t )dEd
V
есть число частиц излучения с энергией E,
движущихся в направлении , отнесенное к
единичному интервалу энергии около E и телесного
угла около .
9.
Левая часть (2), выраженная черезмощность флюэнса
В соответствии с (1)
Скорость
изменения d
dVn p (r , E , t )dEd
числа частиц dt V
в объеме V
1 d
d
dV ( E , r , t )dEd dV ( E , r , t )dEd
V dt V
dl V
где dl = udt – элемент длины траектории
частицы излучения.
10.
Левая часть (2), выраженная черезмощность флюэнса
Однако, часто о траектории частицы говорить
не имеет смысла, поэтому левую часть (2)
лучше представить так:
Скорость
изменения
dV n p (r , E , t )dEd
t
числа частиц V
в объеме V
1
dV
( E , r , t )dEd
u ( E ) t
V
11.
Вычисление слагаемого (а) в (2)(a )мощность
потока частиц dajn ( E , r , t )dEd
из V через A A
где в первом приближении
jn ( E, r , t ) n ( E, r , t )
а n – единичный вектор нормали к
замкнутой поверхности А, ограничивающей
объем V.
12.
Преобразование слагаемого (а)Теорема Остроградского – Гаусса дает:
dajn ( E , r , t ) dan ( E , r , t )
A
A
dV ( ( E , r , t ))
V
Т.к. вектор не зависит от координат, то
подынтегральное выражение превращается
в
производную по направлению вектора
( ( E, r , t )) ( E, r , t )
13.
Окончательный вид слагаемого (а)Поэтому
(a )мощность
потока частиц dV ( E , r , t )dEd
из V через A V
Это слагаемое в русскоязычной литературе
часто называют конвективным членом в
уравнениях переноса. В англоязычной
литературе его называют streaming term или
leakage term
14.
Вычисление слагаемого (b) в (2)Полное макроскопическое сечение ( r , E ) всех реакций взаимодействия частиц излучения с частицами
вещества в объеме V имеет смысл величины вероятности реакций взаимодействия, отнесенной на единицу длины пробега частицы первичного излучения с
энергией Е:
( r , E ) n0 j (r ) j ( E )
j
где суммирование ведется по всем типам j реакций с
частицами вещества, которые способны взаимодействовать
с частицами ионизирующего излучения;
n0 j ( r ) - концентрация
ф
частиц вещества, на которых с
сечением j ( E ) происходит реакция типа j
15.
Вычисление слагаемого (b)Поэтому из физического смысла распреде-
ления мощности флюэнса ( E , r , t ) по
энергиям и направлениям движения
частиц ионизирующего излучения
(b)скорость
убыли частиц ИИ
при взаимодействии
с частицами вещества в V
dV (r , E ) ( E , r , t )dEd
V
(r , E ) d ( r , E )
4
16.
Слагаемое (с) в (2)При взаимодействии частиц ионизирующего из-
лучения с веществом могут порождаться частицы излучения того же типа, что и первичное
излучение.
Если
s
( E E, r )dEd
вероятность того,
что на единице длины пробега,
в направлении , частицы излучения с энергией,
E , образуется частица того же типа с энергией в
интервале dE вблизи E, , движущаяся в узком
интервале телесных
углов d около
направления
17.
Слагаемое (с)(c) скорость производства
вторичных частиц с энергией E ,
движущихся в направлении
s
dV dE d ( E E , r ) ( E , r , t )dEd
V
0
4
Предполагается, что частицы ИИ не
взаимодействуют между собой, поэтому
скорость производства вторичных частиц не
содержит выражения, зависящие от
столкновений частиц ИИ между собой
18.
Слагаемое (d) в (2)(d ) скорость производства
частиц источниками
в объеме V
dVS pV ( E , r , t )dEd
V
где S pV ( E , r , t ) объемная плотность
скорости производства частиц
ионизирующего излучения внешними
источниками, находящимися в объеме V,
отнесенная к единичному интервалу энергий
частиц вблизи E и телесных углов вблизи
направления
19.
Общий вид уравнения переносадля излучения одного вида
Подставим полученные выражения в (2) и
опустим интегрирование по объему, а
также поделим на интервалы энергий dE и
телесных углов d обе части (2):
1
( E , r , t ) ( E , r , t ) (r , E ) ( E , r , t )
u ( E ) t
s
dE d ( E E , r ) ( E , r , t ) S pV ( E , r , t )
0
4
(3)
20.
Уравнение переноса излучениядля частиц одного вида
Вводя полную производную по времени
d
( E , r , t ) ( E , r , t ) u ( E ) ( E , r , t )
dt
t
и учитывая обозначение dl = udt, введенное
ранее, будем иметь:
d
( E , r , t ) (r , E ) ( E , r , t )
dl
s
dE d ( E E , r ) ( E , r , t ) S pV ( E , r , t )
0
4
(3 )
21.
Обобщение на случай частиц ИИразных видов
Будем обозначать вид частиц ИИ прописными
латинскими буквами А, B,…
Тогда вместо (3 ) можно говорить о системе
уравнений, описывающих перенос
смешанного излучения
d
A ( E A , A r , t ) A ( r , E A ) A ( E A , A r , t )
dl A
s
dE B d B AB ( E B E A , B A r ) B ( E B , B r , t )
B 0
4
S pV ( E A , A r , t )
(4)
22.
Особенности терминологииСоставленные уравнения переноса отличаются
от кинетических уравнений Больцмана, описывающих перенос частиц в любом неравновесном
процессе, тем, что данные уравнения не содержат слагаемые, определяемые столкновениями
частиц ионизирующего излучения между собой.
Полагается, что частицы ионизирующего излучения не взаимодействуют между собой при прохождении через вещество.
Поэтому часто уравнения (3), или систему (4)
называют линеаризованными уравнениями
Больцмана
23.
Детерминистская теорияпереноса излучения
Уравнения переноса фотонного
излучения
24.
Фотонное излучение сэнергиями до десятка МэВ
Для фотонного излучения с энергиями фотонов, не
превышающих энергию связи нуклонов в ядре,
(r , E ) n0i (r ){ ph,i ( E ) Z i [ C ,i ( E )
(10)
pp,еi ( E )] pp, Ni ( E )} ph (r , E ) C (r , E ) pp (r , E )
где n0 i ( r ) концентрация атомов элемента типа i в
среде, порядковый номер которого Zi;
E энергия фотонов;
pp (r , E ) n0i (r )[ Z i pp,еi ( E ) pp, Ni ( E )]
i
i
ph,i(E ), C,i(E ), pp,ei(E ), pp,i(E ) – микроскопические
сечения фотоэффекта, комптон-эффекта и образования электрон-позитронных пар в поле электронов и
ядер соответственно для элемента типа i.
25.
Производство вторичныхфотонов
Величина ( E E, r ) в случае чисто фотонного первичного излучения с энергией фотонов, не превышающей энергию отделения нуклона от ядра, может быть представлена в виде суммы четырех слагаемых
s
( E E , r ) C ( E E , r )
s
1
1
pp (r , E )2 ( E E0 e )
ph (r , E ) N ph ( E E r )
4
4
(11)
26.
Производство вторичныхфотонов
C ( E E , r ) - макроскопическое
сечение возникновения комптоновского фотона с энергией в единичном интервале вокруг E , движущегося в единичном интервале
направлений вблизи из фотонов с
энергией E , движущихся в направлении ;
Рассматривается, как правило,
комптоновское рассеяние на электронах;
Когерентным рассеянием (рассеянием
Рэлея) пренебрегается.
27.
Производство вторичныхфотонов
pp (r , E ) - суммарное сечение
образования электрон-позитронных пар в
поле ядер (см. (10); стоящая при нем в
(11) удвоенная дельта-функция выражает
акт аннигиляции, при котором возникают
два фотона с характерной энергией E0e =
= 511 кэВ;
28.
Производство вторичныхфотонов
ph (r , E ) - макроскопическое сечение
фотоэффекта при энергии фотона E ,
N ph ( E E r ) - число фотонов рентгеновской
флуоресценции в энергией, лежащей в
единичном интервале вблизи E , возникших
при фотоэффекте, вызванным фотоном
энергии E .
Излучение фотонов аннигиляции и
рентгеновской флуоресценции считается
изотропным. Поэтому во втором и третьем
слагаемых в правой части (11) стоит 1/4
29.
Переход кУравнения переноса для фотонов часто
удобнее записать через переменную
= E0/E
Которая выражает длину волны фотона в
единицах комптоновской длины волны
частицы с энергией покояE0 (как правило,
электрона).
Причиной является то, что на языке
переменной удобно выражать часть
коэффициентов в уравнении переноса,
определяемую комптоновским рассеянием.
30.
Переход кПри переходе к переменной следует
учесть, что
ES p ( E , r , t ) S p ( , r , t ), S E ( E , r , t ) S ( , r , t );
E (r , E , ) (r , , ), I (r , E , ) I (r , , ).
Уравнение (9) перепишется так:
d
I ( , r , t ) ( r , E ) I ( , r , t )
dl
s
d d ( , r ) I ( , r , t ) S ( , r , t )
0
4
(12)
31.
Переход кВыражение (11) переходит в (индекс
опускаем)
( , r ) C ( , r )
s
1
1
pp (r , )2 ( 1)
ph (r , ) N ph ( r )
4
4
где
(13)
C ( , r ) Z i n0i (r ) Ci ( , )
i
с распределением микроскопического
сечения
комптоновского
рассеяния Ci ( , ) по,
и
32.
Формула дляC ( , r )
Если считать, комптон-эффект происходит на
свобдных электронах, можно использовать
формулу Кляйна – Нишины для
дифференциального сечения. Тогда
s
( , r )
1
[ne (r ) T F ( , ) (1 ) F iso ( , )]
2
где ne (r ) – средняя концентрация электронов,
Т – сечение рассеяния Томсона на электроне
33.
Формулы для F и Fiso3
F ( , )
8
2
( )( 2)
1
F ( , ) pp ( ) ( 1) ph ( ) N ph ( r )
2
iso
Для фотонов с энергией до нескольких сотен
кэВ вклад Fiso пренебрежимо мал.
Тормозное излучение вторичных электронов
также считается малым
34.
Детерминистская теорияпереноса излучения
Уравнения переноса нейтронного
излучения
35.
Общий вид уравнения переносадля быстрых нейтронов
1 d
( E , r , t ) (r , E ) ( E , r , t ) S p ( E , r , t )
u ( E ) dt
s
dE d ( E E , r ) ( E , r , t ) (3 )
0
4
где
M
(r , E ) n0i (r ) i ( E )
i 1
полное макроскопическое сечение всех
реакций взаимодействия нейтронов с ядрами,
36.
Коэффициент рассеяния в уравнениипереноса для быстрых нейтронов
M Li
s
( E E , r ) n0i (r ) ij ( E E , )
i 1 j 0
ij ( E E , ) – дважды дифференциаль-
ное микроскопическое сечение рассеяния
нейтронов на ядре типа i, j – номер уровня
конечного состояния рассеивающего ядра,
j = 0 соответствует упругому рассеянию,
M – число видов ядер в веществе, а
Li +1 – число уровней в ядре с номером i,
включая основное состояние Li = 0.
37.
Источники в уравнении переносадля быстрых нейтронов
Слагаемое S p ( E, r , t ) включает в себя все
процессы производства нейтронов, за
исключением рассеяния, в том числе, и
производства вторичных нейтронов за счет
спонтанного деления, реакций типа ( ,n), ( ,n)
и т.п.
При расчете защиты производство нейтронов
в реакциях деления ядер нейтронами, а также
реакции типа (n,2n) и т.п. можно игнорировать,
но это не допустимо при использовании
уравнений переноса (3 ) при описании
кинетики нейтронов в ядерном реакторе
38.
Источники в уравнении переносадля быстрых нейтронов
Поэтому при расчете
защиты часто можно
считать, что S p ( E, r , t ) не зависит от дважды
дифференциального распределения
мощности
флюэнса нейтронов ( E , r , t ) .
При описании кинетики нейтронов в ядерном
реакторе реакции производства вторичных
нейтронов следует включать в
s
( E E, r )
39.
Для быстрых нейтроновДля быстрых нейтронов имеет место
анизотропия рассеяния.
Поэтому на основании решения задачи о кинематике (вообще говоря, неупругого) рассеяния
нейтронов
ij ( E E , )
ij ( E )
(1 i ) E 1 ij
ij
ij
ij
(
2
n
1
)
f
(
E
)
P
(
)
(
n
n
c
s ( E , E ))
N
n 0
(14)
40.
Для быстрых нейтронов2
2
(
A
1
)
/(
A
1
)
где
i
i
i
а косинусы углов рассеяния
2
2
2
(
E
/
E
)(
A
1
)
(
1
A
)
A
i
i
i ij
ij
с
2 Ai 1 ij
1
E
E Qij Ai
( E , E ) ( Ai 1)
( Ai 1)
2
E
E
EE
а
Qij ( Ai 1)
ij
E Ai
С энергией реакции рассеяния Qij нейтрона на
ij
s
уровне j ядра i. При упругом рассеянии Qi0 = 0.
41.
Коэффициенты разложения пополиномам Лежандра
Коэффициенты разложения fnij по полиномам
Лежандра должны быть получены из
экспериментальных данных или модельных
расчетов, так как не существует хороших
теоретических формул подобно формуле
Кляйна – Нишины для рассеяния нейтронов на
ядрах.
В общем случае считается, что рассеяние при
n > 0 и изотропно в системе центра инерции.
f0ij = 1.
42.
Энергия налетающего нейтронаE
Пределы интегрирования по энергии могут
быть ограничены значением E, т.к. при E > E
ij = 0.
Более того, энергия налетающего нейтрона E
лежит в пределах между
E
ij
max
E
( Ai 1) 2
2
Qij
1
Ai Ai ( Ai 1)
E
ij
min
E
( Ai 1) 2
2
Qij
1
Ai Ai ( Ai 1)
E
и
E
43.
При рассеянии на водородеПри рассеянии на водороде
ij
Emax
Emax
ij
Emin
Emin E
Поэтому интегрирование по энергии в этом
случае может быть проведено в интервале
ij
ij
ij min( E0 , Emin
), ij min( E0 , Emax
)
Где E0 – максимальная энергия нейтронов в
спектре.
Во всех рассмотренных формулах
полагается, что рассеивающее ядро
покоится, что применимо только для быстрых
и эпитепловых нейтронов
44.
Когда можно пренебречьнеупругим рассеянием нейтронов
При энергиях меньше нескольких МэВ
В этом случае уравнение переноса принимает
вид d
dl
M
( E , r , t ) n0i (r ) i ( E ) ( E , r , t )
i 1
i
1 M E / i
S p (E, r , t )
dE n0i (r ) s ( E E )
2 i 1 E
Ai 1 E Ai 1 E
d
( E , r , t )
4
2
E
2
E
где
i ( Ai 1) 2 /( Ai 1) 2
45.
Когда можно пренебречьнеупругим рассеянием нейтронов
и
i
N
(
E
)
i
s
is ( E E )
(
2
n
1
)
f
n ( E ) Pn ( c ( E , E ))
(1 i ) E n 0
а
2
2
( E / E )( Ai 1) ( Ai 1)
c ( E , E )
2 Ai
46.
Случай изотропного рассеянияПри изотропном рассеянии
is ( E )
, i E E E
i
s ( E E ) (1 i ) E
,
0, в остальных случаях
47.
Усредненный учет анизотропиирассеяния
Анизотропия рассеяния приводит к появлению
в материале защиты направлений
преимущественного движения по отношению к
первоначальному направлению движения
нейтронов.
Поэтому нельзя пользоваться средней длиной
свободного пробега нейтронов при
изотропном рассеянии 1 / s (r , E ) .
48.
Усредненный учет анизотропиирассеяния
Вместо нее используют т.н. транспортную
длину, которая обратно пропорциональна
транспортному макроскопическому сечению:
ijs
tr (r , E ) n0i (r ) ijs ( E )(1 s )
(15)
i , js
ijs
где
s – усредненное по всем возможным
направлениям с-системе косинус угла
рассеяния в л-системе.
49.
Усреднение по углам рассеяния в ссистемеУсреднение проводится следующим
образом (индексы i и j опущены):
s
d
d
c
s
(17)
c
а связь между косинусами углов рассеяния
в с- и л-системах
с
2 A( A 1)Q
s
,
A
2
E
1 2 с
1 / 2
(18)
50.
Вычисление sПодстановка (18) в (17) после некоторых
вычислений дает
2
s
3
(19)
Для тяжелых ядер, как видно из табл. 1, (19)
дает
2
s
3A
т.е. стремится к нулю с ростом A. Поэтому
рассеяние нейтронов на тяжелых ядрах
может считаться изотропным
51.
Диффузионное приближение.Закон Фика
Для нейтронов, хаотически движущихся в
веществе защиты в уравнении переноса
необходимо перейти к энергетическому
распределению флюэнса,
проинтегрировав обе части уравнения по
всем направлениям движения нейтронов.
При этом следует принять во внимание,
что в первом приближении
1
jn ( E , r , t ) ( E , r , t )
(n ) ( E , r , t )
tr
52.
Диффузионное приближение.Закон Фика
Тогда, выполняя интегрирование по всем
направлениям движения нейтронов, с учетом
того, что флюэнс хаотически движущихся
нейтронов изотропен
1
( E , r , t )
( E r , t )
4
получим
1
jn ( E r , t ) d jn ( E , r , t )
n ( E r , t )
3 tr
4
53.
Уравнение переноса для дляхаотически движущихся нейтронов
В результате уравнение переноса для тепловых
нейтронов примет вид
1
1
( E r , t )
(
E
r
,
t
)
(
r
,
E
)
(
E
r
, t)
u ( E ) t
3 tr (r , E )
dE s ( E E , r ) ( E r , t ) S pV ( E r , t )
0
где
1
s
(E E r )
d d ( E E , r )
4 4 4
s
Т.о. в этом случае уравнение переноса становится
уравнением второго порядка по пространственным
переменным и приобретает явный параболический
тип.
(20)
54.
Деление ядер нейтронамиДеление ядер нейтронами в системе отсчета,
связанной с центром инерции, можно считать
изотропным. Т.к. делящиеся ядра – тяжелые, то цсистема практически совпадает с л-системой.
Поэтому хорошим приближением является
f
ij ( E )
f
ij ( E E , )
ij ( E E )
4
где ij (E ) - сечение деления нейтроном с энергией E
f
ядра i, находящегося на уровне j, при котором на
один акт деления образуется
ij ( E E )
нейтронов с энергией Е на единичный интервал
энергии
55.
Смыслij ( E E )
Это – распределение числа нейтронов,
образующихся в результате одного акта
деления, а
ij ( E ) dE ij ( E E )
- среднее число нейтронов, приходящееся
на один акт деления
56.
В общем случаеОбщее представление для дважды
дифференциального микроскопического сечения
s
ij ( E E , ) ij ( E )сij ( E ) f ij ( E E , )
где суммирование ведется по всем типам
реакций , характеризуемых сечением ij (E ) , в
которых образуется среднее число мгновенных
с
нейтронов Кij (E ) с энергией E с вероятностью,
f ij ( E E , )
отнесенной к единице энергии E и телесного угла
d
57.
Значениясij
В случае рассеяния
сij0 1
В случае захвата нейтрона (n, ), (n,p), (n, )
и т.п.
сijс 0
В случае деления нейтронов
сijf ij (E )
58.
Учет запаздывающих нейтроновУчет запаздывающих нейтронов в уравнении
переноса нейтронов в размножающей среде,
испускаемых ядрами-эмиттерами, может быть
выполнен через задание мощности силы
источника, отнесенной к единице объема:
1
S pV ( E , r , t )
a na (r t ) a ( E )
4 a
где na ( r t ) – концентрация ядер-предшественников
по энергиям запаздывающих нейтронов a (E ) -
нормированный спектр запаздывающих нейтронов
группы a; суммирование ведется по группам
запаздывающих нейтронов, a – постоянная
распада группы a ядер-предшественников.
59.
Учет запаздывающих нейтроновПри этом уравнение (15) должно быть дополнено
системой уравнений, описывающих кинетику
изменения концентрации ядер-предшественников:
a ( E )
d
k
na (r t ) dE
d ( E , r , t )
dt
g 0
u ( E ) 4
a na (r t )
a
где k – коэффициент размножения нейтронов с среде,
a (E ) –распределение доли запаздывающих
а
нейтронов, отнесенных к группе a, по энергии
нейтронов деления E , образующих ядрапредшественники, дающие вклад в группу a, g –
среднее время жизни поколения нейтронов деления
60.
Учет запаздывающихфотонейтронов
Если фотоны, образующиеся в активной зоне,
могут выбивать нейтроны из вещества, то
объемная мощность силы такого источника
нейтронов определится соответствующим
распределением мощности флюэнса фотонов.
Вместо этого учет запаздывающих
фотононейтронов также можно осуществить,
соответствующим образом в третьем
слагаемом в правой части системы (4)
(продумать эти варианты самостоятельно).
61.
Детерминистскаятеория переноса
излучения
Стационарное уравнение
переноса
62.
Стационарные решенияУравнение переноса
1
( E , r , t ) ( E , r , t ) (r , E ) ( E , r , t )
u ( E ) t
dE d ( E E , r ) ( E , r , t ) S pV ( E , r , t )
s
0
4
если мощность силы
S pV ( E , r , t ) S pV ( E , r )
не изменяется во времени, то частные
решения можно представить в виде
u ( E ) t
( E , r , t ) ( E , r )e
63.
Стационарное уравнениепереноса
Тогда
( E , r ) (r , E ) ( E , r )
(21)
s
dE d ( E E , r ) ( E , r ) S pV ( E , r )
0
4
где
( r , E ) ( r , E )
(22)
Для приближенного решения этого
уравнения применяется несколько широко
распространенных методов, которые будут
рассмотрены позже
64.
Стационарное уравнение переносав диффузионном приближении
В диффузионном приближении
1
( E , r ) (r , E ) ( E , r )
3 tr (r , E )
(23)
dE d ( E E , r ) ( E , r ) S pV ( E , r )
s
0
4
Знак
( r , E ) ( r , E )
Играет важную роль в описании поведения
решений.
65.
Детерминистскаятеория переноса
излучения
Общие свойства решений. Начальные
и граничные условия уравнений
переноса ионизирующего излучения.
Частные случаи
66.
Существование иединственность
При решении уравнения, или системы уравнений
переноса ИИ, необходимо принять во внимание,
что функция
( E , r , t )
может принимать только неотрицательные
значения, и функция непрерывна по
пространственным переменным.
Единственность обеспечивается
соответствующими начальными и граничными
условиями, которые определяются видом
уравнения
67.
Случай однородного стационарногополя излучения.
В бесконечной однородной среде с
равномерно распределенными источниками
распределение мощности флюэнса
стационарного поля по энергиям и
направлениям движения частиц не зависит от
координат и времени:
( E , r , t ) ( E , )
Более того, среда, оказывается, не
обязательно должна быть однородна.
68.
Теорема ФаноFano, 1954
Распределение мощности флюэнса по
энергиям и направлениям в безграничной
среде не зависит от r , если:
(1) состав среды одинаков во всех точках,
но возможны вариации значений
плотности в точке;
(2) Энергетическое и угловое
распределение сил источников
пропорционально локальной средней
плотности (r )
69.
Доказательство теоремы ФаноОсновано на стационарном уравнении переноса
(16) с = 0
( E , r ) (r , E ) ( E , r )
dE d ( E E , r ) ( E , r ) S pV ( E , r )
(16 )
s
0
4
и допущении, что отношения
S pV ( E , r ) S pV
( r , E )
(
E
),
(
E
,
)
(r )
(r )
s ( E E , r ) s
( E E , )
(r )
(24)
Не зависят от r.
Эти условия, очевидно, выполняются для среды,
описанной в формулировке теоремы Фано.
70.
Доказательство теоремы ФаноРазделим (16 ) на (r ) :
1
( E , r ) ( E ) ( E , r )
(r )
(25)
S pV
s
dE d ( E E , ) ( E , r )
( E , )
0
4
Принимая во внимание условия (24), заметим,
что частным решением (25) будет решение
уравнения
S pV
s
( E ) ( E , ) dE d ( E E , ( E , )
( E , )
0
4
(26)
71.
Плоско-параллельная задачаЕсли среда представляет собой
безграничную плиту толщины d, свойства
которой могут меняться лишь в направлении,
перпендикулярном плоскости плиты
(обозначим его осью Oz), то такая задача
называется плоско-параллельной.
Источники распределены в этой плите
равномерно, либо их распределение
неравномерно только в направлении оси Oz.
72.
Плоско-параллельная задачаВ этом случае стационарное уравнение
переноса (16 ) может быть записано в виде
d
( E , z ) ( z , E ) ( E , z )
(27)
dz
s
dE d ( E E , z ) ( E , z ) S pV ( E , z )
0
4
где = cos , а угол отсчитывается от оси
Oz.
Граничные условия определяются на боковых
поверхностях z = 0 и z = d.
73.
Плоско-параллельная задача приизмерении толщин в г/см2
Поделим обе части уравнения (27) на (z)
и введем переменную
z
( z ) ( z )dz
0
Тогда в соответствии с условиями (24),
уравнение (27) примет вид
(см. (25)) ( E , )
( E , x( ))
d
( E , ) ( E ) ( E , )
d
(28)
S pV
s
dE d ( E E , ) ( E , )
( E , )
0
4
74.
75.
Скейлинг поля излученияСтационарное уравнение переноса
( E , r ) (r , E ) ( E , r ) S p ( E , r )
dE d ( E E , r ) ( E , r )
s
0
4
При замене
~
r r
Может сохранить свою форму
относительно некоторого нового
~
~
распределения мощности флюэнса ( E , r )
76.
Скейлинг поля излученияв виде
~ ~
~ ~ ~
~
~
~
~
( E , r ) ( r , E ) ( E , r ) S p ( E , r )
~ ~
~
~s
dE d ( E E , r ) ( E , r )
0
4
Если учесть, что
и положить
~
~
~
~ ~
( r , E ) (r , E ); S p ( E, r ) S p ( E, r )
~
~s
s
( E E, r ) ( E E, r )
77.
Скейлинг поля излученияПри этом решение исходной задачи
заменяется на решение модельной задачи:
~
~
( E, r ) ( E, r )
Этот факт называется скейлингом поля
излучения.
Скейлинг стационарного поля излучения
используется для моделирования процессов
распространения излучения помощью
меньшего по масштабам макета, на котором
могут быть поставлены эксперименты для
проверки теории
78.
Преобразование объемных источников кэквивалентным поверхностным источникам
Пусть V – область, в
которой ищется поле
излучения;
Посмотрим, каким
образом можно заменить
объемные источники,
находящиеся вне этой
области и создающие
часть поля излучения
соответствующим
эквивалентным
поверхностным
источником
79.
Преобразование объемных источников кэквивалентным поверхностным источникам
В каждой точке поверхности,
ограничивающей V, выбирается локальный
базис векторов
к
внешней нормали
поверхности n , и пара векторов y , z ,
произвольно ориентированных в
касательной плоскости.
Если x,y,z – локальные координаты в этом
базисе, то вблизи выделенной точки
поверхности стационарное уравнение
переноса запишется в следующем виде
80.
Преобразование объемных источников кэквивалентным поверхностным источникам
n ( E , r ) y ( E , r ) z ( E , r )
x
y
z
(r , E ) ( E , r ) S V ( E , r ) S a ( E , rs ) ( x)
dE d ( E E , r ) ( E , r )
s
0
4
где S V ( E , r ) - характеризует объемные
источники,
находящиеся внутри объема V,
ам
S a ( E , r ) - характеристика источников,
эквивалентно заменяющих объемные
источники, находящиеся вне области
81.
Преобразование объемных источников кэквивалентным поверхностным источникам
Интегрируя последнее уравнение по x на малом
интервале и устремляя ширину этого интервала к
нулю, получим
S a ( E, rs ) n[ ( E, rs ) ( E, rs )]
где знаками отмечены части флюэнса частиц,
которые вытекают из рассматриваемого объема,
либо попадают в заданный объем.
Часто считают, что ( E , rs ) 0 (извне
интересующей нас области излучение
поглощается), то
S a ( E, rs ) n ( E, rs )
82.
Детерминистская теорияпереноса излучения
Различные формы записи уравнений
переноса излучения
83.
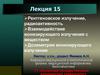
Интегральная форма уравнений переносаизлучения для углового распределения флюэнса
Запишем уравнение переноса излучения (3 ) в
следующем виде:
d
( E , r , t ) (r , E ) ( E , r , t ) q( E , r , t )
dl
(5)
где
s
q ( E , r , t ) dE d ( E E , r ) ( E , r , t )
0
4
S p ( E , r , t )
(6)
84.
Интегральная форма уравнений переносаизлучения для углового распределения флюэнса
Введем новую координатную переменную r
r r l
имеющую смысл радиус-вектора точки, из ко-
торой излучение могло бы придти в точку ,r ,
пройдя прямолинейный
отрезок длины l в на
правлении вектора .
В целях удобства дальнейшего рассмотрения
вместо переменной l возьмем переменную
R = l.
85.
Интегральная форма уравнений переносаизлучения для углового распределения флюэнса
Тогда в (5) надо подставить
r r R
Заметим, что
R
d
exp dR (r R , E )
dR
0
R
(r R , E ) exp dR (r R , E )
0
86.
Интегральная форма уравнений переносаизлучения для углового распределения флюэнса
Поэтому уравнение (5) можно переписать
в виде
R
d
( E , r R , t ) exp dR (r R , E )
dR
0
R
q( E , r R , t ) exp dR (r R , E )
0
87.
Интегральная форма уравнений переносаизлучения для углового распределения флюэнса
Интегрируя полученный результат от 0 до l,
опуская штрих у r , можно получить
( E , r , t )
R
( E , r R , t ) exp dR (r R , E )
(7)
0
R
R
dR q ( E , r R , t ) exp dR (r R , E )
0
0
Это уравнение называется интегральным уравне-
нием для углового распределения флюэнса
88.
Интегральная форма уравнений переноса излучениядля энергетического распределения флюэнса
Проинтегрируем уравнение (7) по всем
направлениям:
( E r , t )
R
d ( E , r R , t ) exp dR (r R , E )
4
0
R
R
d dR q ( E , r R , t ) exp dR (r R , E )
4
0
0
(8)
89.
Интегральная форма уравнений переноса излучениядля энергетического распределения флюэнса
Устремим в правой части R . Тогда первое
слагаемое в правой части (8) устремится к нулю.
Обозначим во втором интеграле r r R
Вводя в первое подынтегральное выражение
второго интеграла множитель
2
R
2 1
r r
представим его в виде
R
R
4 d 0 dR r r 2 q( E, r , t ) exp 0 dR (r R , E)
R
2
90.
Интегральная форма уравнений переноса излучениядля энергетического распределения флюэнса
Рассматривая
R 2 dR d как элемент объема,
записанный в сферических координатах с началом в точке r , (8) можно придать следующий вид
r r
q( E, r , t )
( E r , t ) dV 2 exp dR (r R , E )
r r
0
где в первом интеграле справа интегрирование
производится по всему пространству.
Полученное уравнение называется интегральной
формой уравнений переноса излучения для энергетического распределения мощности флюэнса
91.
Уравнения переноса излученияотносительно энергетического флюэнса
Распределение энергетического флюэнса по
энергиям и направлениям
I ( E, r , t ) E ( E, r , t )
Относительно этой величины уравнение
переноса для одного вида излучения (3 )
d
I ( E , r , t ) ( r , E ) I ( E , r , t )
dl
E s
dE d ( E E , r ) I ( E , r , t ) S E ( E , r , t )
E
0
4
(9)
где S E ( E, r , t ) ES p ( E, r , t ) – энергетическое и
угловое распределение энергии частиц,
испускаемых источником
92.
Смысл коэффициентов, входящихв уравнения переноса (4)
В общем случае необходимо рассматривать
распространение в среде излучения
нескольких видов
Рассмотрим смысл коэффициентов,
входящих в одно из уравнений (4).
При этом он будет различен как для частиц
разного вида, так и для частиц одного вида,
но различных диапазонов энергий, поскольку
в них придется учитывать, начиная с
некоторых порогов энергии, различные
эндоэнергетические реакции
93.
НЕКОТОРЫЕПРИБЛИЖЕННЫЕ МЕТОДЫ
РЕШЕНИЯ УРАВНЕНИЙ
ПЕРЕНОСА
94.
ЭКСПОНЕНЦИАЛЬНОЕ ОСЛАБЛЕНИЕ95.
Случай экспоненциальногоослабление
Приближение экспоненциального
ослабления применимо только к
бесстолкновительному излучению.
В этом приближении стационарное
уравнение переноса (16) без внешних
источников сводится к
o
o
( E , r ) (r , E ) ( E , r ) 0
(29)
т.к., по определению, не рассматриваются
рассеянные частицы
96.
Случай однородной средыПроизводную по направлению
можно представить как производную d/dl
по некоторому параметру l.
Введем переменную r r l
Тогда в однородной среде уравнение (1)
для флюэнса бесстолкновительного
излучения можно свести к
функциональному уравнению
( E )l (30)
o
o
( E, r l ) ( E, r )e
97.
Уравнения типа уравнения (18)При некоторых допущениях можно свести
общее уравнение переноса к уравнению вида
(18).
Если фотоны или нейтроны имеют достаточно
большую энергию, то они рассеиваются, в
основном, в направлении своего
первоначального движения.
Поэтому в интеграле рассеяния в правой части
(16) можно приближенно положить
s
s
( E E , r ) ( E E r ) ( 1) (31)
(“straight-ahead approximation” – приближение
рассеяния вперед)
98.
Приближение рассеяния впередПодстановка (31) в уравнение
(21) без источников дает
( E , r ) (r , E ) ( E , r )
(32)
s
dE ( E E r ) ( E , r )
0
99.
Уравнение для мощности дозыРаспределение мощности дозы по направлениям
движения частиц в точке определяется
соответствующим распределением мощности
флюэнса
R ( r ) d E (r , E ) ( E , r )
0
Поэтому уравнение (27) можно переписать
относительно мощности дозы
R ( r )
s
d E (r , E )[ (r , E ) ˆ ( E r )] ( E , r )
0
(33)
100.
Взвешенный линейный коэффициент рассеяния иэффективный линейный коэффициент ослабления
Здесь введен т.н. взвешенный
коэффициент рассеяния
(
r
,
E
)
s
ˆ ( E r ) d E
ˆ s ( E E r )
(r , E )
0
(34)
Если ввести теперь взвешенный (по дозе)
коэффициент ослабления
~
( r , )
1
s
d E (r , E )[ (r , E ) ˆ ( E r )] ( E , r )
R ( r ) 0
(35)
101.
Экспоненциальное уравнениеослабления для дозы
То можно получить следующее уравнение
для мощности дозы
~
R ( r ) (r , ) R ( r ) 0
(36)
Его формальное решение методом
характеристик
l ~
R ( r l ) R ( r ) exp dl (r l , )
0
(37)
102.
Многогрупповое приближение103.
Основные элементы моделиПрименяется, как правило, к стационарным
уравнениям переноса
Пусть энергии частиц ИИ в веществе лежат в
интервале (0, E0), где E0 – максимально возможная
энергия частиц поля излучения.
Разобьем интервал (0, E0) на ряд смежных
интервалов (Eg, Eg – 1 ), Eg < Eg – 1 ,g = 1,2,…,G.
Введем групповые мощность флюэнса и силу
источника
E g 1
E g 1
g ( r ) ( E , r )dE , S g ( r ) S pV ( E , r )dE
Eg
Eg
104.
Основные элементы моделиВведем групповой полный коэффициент
взаимодействия, g, и групповой
коэффициент рассеяния, sg следующим
образом:
g (r )
1
g ( r )
E g 1
g (r , E ) ( E , r )dE ,
Eg
( r )
s
gg
1
g ( r )
E g 1
Eg
E g 1
dE dE ( E E , r ) ( E , r ),
s
E g
105.
Уравнение переноса вгрупповом приближении
Тогда
g ( E , r ) g (r , E ) g ( E , r )
(38)
G
s
d gg ( r ) g ( r ) S g ( r )
g 1 4
Но, вообще говоря, для того, чтобы задать
g, и sgg , нужно знать решение общего
уравнения, что невозможно.
106.
Уравнение переноса вгрупповом приближении
Систему уравнений (38) можно эффективно
использовать, только, если можно
сформулировать что-нибудь более или менее
правдоподобное про g, и sgg независимо от
мощности флюэнса.
Например, если ( E , r ) W ( E ) ( r ) , то
E
E
1
g (r )
g (r , E )W ( E )dE , Wg W ( E )dE ,
Wg E
(39)
E
g 1
g 1
g
g
1
s
gg ( r )
Wg
E g 1
Eg
E g 1
dE dE ( E E , r )W ( E ),
E g
(40)
s
107.
Модели функции W(E)1. Грубо – W (E) = const для каждой группы.
Тогда в (39), (40) W (E) вообще пропадает.
2. В случае нейтронов деления с энергиями в
несколько МэВ в качестве W (E) может быть
взят спектр нейтронов деления, если только
эти нейтроны и рассматриваются
3. В случае эпитепловых нейтронов
предлагается (Белл и Глестон, 1970)
использовать зависимость W (E) ~E-1.
Аналогичный подход может быть использован
и в диффузионном приближении
108.
Метод моментов (PN-приближение):область применения
Goldstein и Wilkins (1954); Fano, Spencer
и Berger (1959)
Эффективен для отдельных моделей
источников
Точечный
Линейный
Плоскостной
Безграничная среда
109.
Метод моментов (PN-приближение) –основная идея
В системах с выраженной осевой
симметрией угловые зависимости
разложить по полиномам Лежандра.
В более сложных случаях –
разложение по сферическим
функциям
Сохранить слагаемые вплоть до
степени N: N
2n 1
( E , r )
n ( E r ) Pn ( )
n 1 4
110.
Метод дискретных ординат (SN приближение): основные особенностиДискретируется теперь на группы не энергия
а направления движения частиц.
Особенности реализации – для каждой
модели источников
Точечный
Линейный
Плоскостной
Безграничная среда
Методика – та же, что и для многогруппового
подхода в энергетическом диапазоне
111.
ДИФФУЗИОННОЕПРИБЛИЖЕНИЕ
112.
Область применимостиПрименяется, главным образом, к
задачам переноса нейтронов в
материалах биологической защиты
ядерных реакторов и в
материалах, экранирующих
радионуклидные источники.
К защите от излучения нейтронных
генераторов применение
проблематично
113.
Уравнение переноса вдиффузионном приближении
Уравнение переноса в диффузионном приближении
(20) корректно после интегрирования по направлениям
1
1
( E r , t )
(
E
r
,
t
)
(
r
,
E
)
(
E
r
, t)
u ( E ) t
(20)
3 tr (r , E )
d dE d ( E E , r ) ( E , r , t ) S pV ( E r , t )
s
4
0
4
Может быть получено как частный случай уравнения
переноса для осесимметричной задачи в P1приближении.
При этом формула (15) для
tr (r , E ) n0i (r ) ij ( E )(1 sij )
(15)
i, j
непосредственно выводится в этом приближении (см.
выше)
s
s
s
114.
Плоско-параллельная задача для прохождениянейтронов в материале защиты в диффузионном
приближении.
115.
.ПОНЯТИЕ О МЕТОДЕ МОНТЕ –
КАРЛО И ЕГО
ИСПОЛЬЗОВАНИИ В ТЕОРИИ
ПЕРЕНОСА ИЗЛУЧЕНИЯ
116.
Вводные замечанияЕсли можно предсказать точный путь,
который проходит частица, и энергии,
которые она может принимать при
прохождении через вещество в случайно
возникающих взаимодействиях, то
можно рассчитать много полезных величин
путем усреднения по большому числу
отдельных историй движения частицы.
117.
Вводные замечанияНапример, вероятность того, что частица
поглощается в определенном диапазоне
значений ее энергии, может быть оценена
путем вычисления доли частиц с
требуемой энергией, которые заканчивают
свой путь в данном объеме.
В этом и состоит сущность метода МонтеКарло в применении к моделированию
прохождения частиц ионизирующего
излучения через вещество
118.
Вводные замечанияВ методе Монте-Карло треки частиц или,
т.н. истории, генерируются путем
моделирования случайной природы
взаимодействия со средой.
Нет необходимости по сути дела даже
обращаться к уравнению переноса
Возможность применения МК-метода
основано на том, что макроскопическое
сечение есть вероятность события на
единицу длины пробега.
119.
Вводные замечанияВсе, что нужно, это
замкнутые соотношения между
вероятностями, которые управляют длиной
трека отдельной частицы между точками
взаимодействия;
Выбор вида взаимодействия в каждой такой
точке;
Выбор нового значения энергии и нового
направления движения частицы, если
взаимодействие носит характер рассеяния,
либо
Выбор возможного типа производства других
частиц
120.
Вводные замечанияВсе перечисленные выше величины –
стохастические
Для создания выборок их значений
необходимо полное понимание различных
процессов, которые происходят с частицей
с заданного момента ее рождения
источником до момента, когда она либо
поглотится, либо покинет
рассматриваемую систему
121.
Вводные замечанияПроцесс принятия решения о выборе
конкретного значения некоторой
стохастической переменной основан на
выборе случайного числа из однородно
распределенного множества целых чисел,
скажем, от 1 до N.
Это может быть сравнено с процессом
совершения ставок в Монте-Карло –
отсюда и название метода
122.
Основные понятияЦепочка событий, происходящих с
частицей с момента ее испускания
источником до ее поглощения в некотором
объеме, либо выхода из него, называется
историей.
Процесс использования компьютера для
отслеживания заданных историй частиц
может быть выполнен путем, полностью
аналогичным реальному физическому
процессу переноса частицы в веществе
123.
Основные понятияПоглощение, выход частицы из области,
либо любое другое событие может быть
ранжировано путем придания ему
некоторого количества очков,
ставящихся в соответствие
конкретным значениям величин, таких,
как угловые и энергетические
распределения, флюэнса, потока или
поглощенной дозы, после того, как все
истории составлены.
124.
Основные понятияТакой прямой метод моделирования
физической ситуации называется
аналоговым методом Монте-Карло.
Неаналоговый метод Монте-Карло –
процесс используется для решения задачи,
которая физически сильно отличается от
реальной, но приводит к тем же численным
результатам (например, к отклику
детектора), что и основная задача, либо
имеет известное отношение к ней, так что
решение задачи может быть получено
косвенно
125.
Случайные числаДостаточно рассмотреть выбор случайных
значений величины в интервале от 0 до 1.
Это может быть адекватно смоделировано
путем использования случайного значения
целых чисел, лежащих между 1 и N,
каждое из которых затем делится на N.
В результате получается множество
значений 1/N, 2/N,…, N/N.
126.
Псевдослучайные числаТакие числа неудобно хранить в памяти компьютера
и создавать случайное обращение к ним
Гораздо удобнее просто генерировать
последовательный выбор целых чисел? Равномерно
расположенных между 1 и N и расставленных,
казалось бы, случайно в этом интервале.
Такие числа называются псевдослучайными
числами
Ими заменяют истинно случайные числа
Но их выбор зависит от выбора первого числа, либо
одного из предыдущих чисел последовательности
127.
Псевдослучайные числаГенерация псвевдослучайных чисел связана с
типом используемого компьютера, в частности,
со значением наибольшего целого числа,
которое может быть использовано в данном
компьютере
Поэтому успешность использования
псевдослучайных чисел для моделирования
методом Монте-Карло зависит от конкретного
пакета, задающего генератор случайных чисел
128.
Моделирование непрерывныхраспределений
Пусть ЭВМ генерирует набор случайных
чисел
1, 2, 3,…
принимающих значения на отрезке [0,1].
Тогда вероятность p( i)d i для i оказаться
между i и i + d i есть d i, если i [0,1]
Значит, p( i) = 1.
129.
1 этап решения задачиВыбирается направление движения нейтрона
(фотона, электрона)
Для этого используются 2 первых случайных
числа 1 и 2.
Азимутальный угол, например, равен
= 2 1,
а косинус полярного угла
= 2 2 – 1.
Такой выбор обусловлен изотропностью
источника, т.е. все начальные значения и
равновероятны в своих интервалах.
130.
2 этап решения задачиНаходится место первого столкновения
Если (l) - макроскопическое сечение на
расстоянии l от источника, то вероятность
того, что нейтрон испытает столкновение
между l и l + d l равна
p (l )dl (l ) exp p (l )dl dl
0
l
131.
3 этап решения задачиЕсли выбрано 3, то l можно определить из
уравнения
l
ln 3 p (l )dl
Следовательно,
0
l
d 3 (l ) exp p (l )dl dl
0
и т.к.
p (l )dl p ( 3 )d 3 d 3
то значение l выбрано так, что обеспечивает
правильное распределение p(l).


































































































































 physics
physics