Кинематика сложного (составного) движения точки

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция № 8
Кинематика сложного (составного)
движения точки.
Сложным движением называют такое движение
точки, которое можно представить в виде
геометрической суммы 2-х, 3-х… более простых
движений.
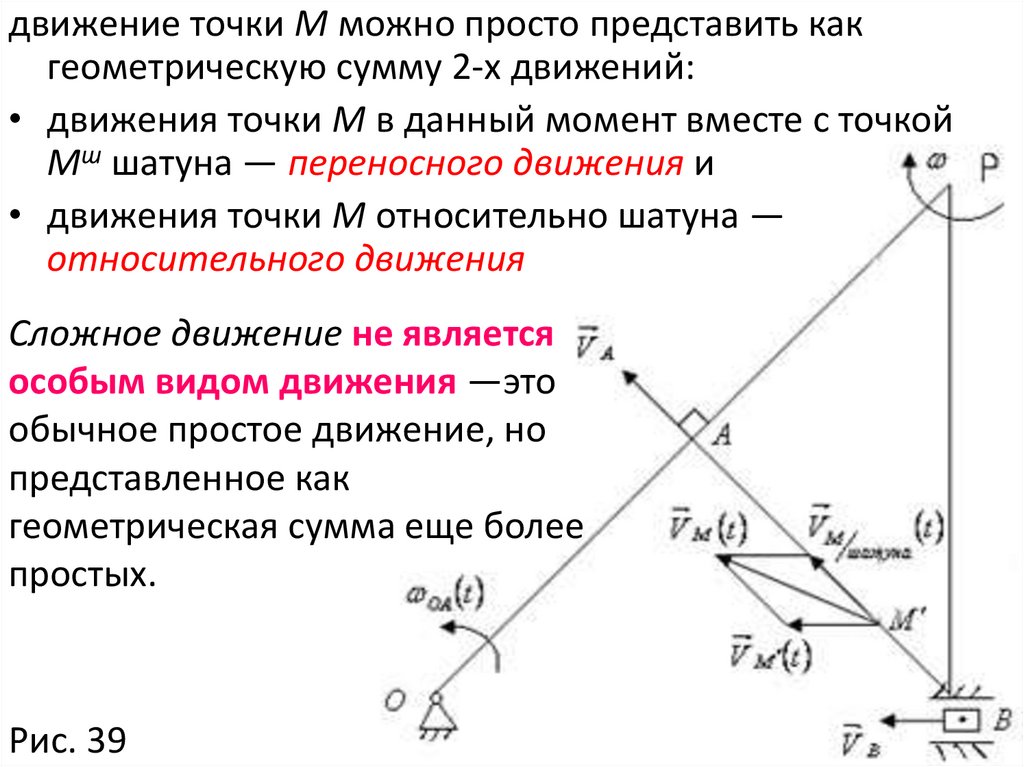
Рассмотрим в качестве примера кривошипно-ползунный
механизм, изображенный на Рис. 39. Здесь точка М
движется по шатуну по какому-то закону. Попытка описать
ее движение в обычной постановке как в К-1 оказывается
чрезвычайно трудной задачей. Гораздо проще можно
рассмотреть ее движение как составное.

3.

движение точки М можно просто представить как
геометрическую сумму 2-х движений:
• движения точки М в данный момент вместе с точкой
Мш шатуна — переносного движения и
• движения точки М относительно шатуна —
относительного движения
Сложное движение не является
особым видом движения —это
обычное простое движение, но
представленное как
геометрическая сумма еще более
простых.
Рис. 39

4.

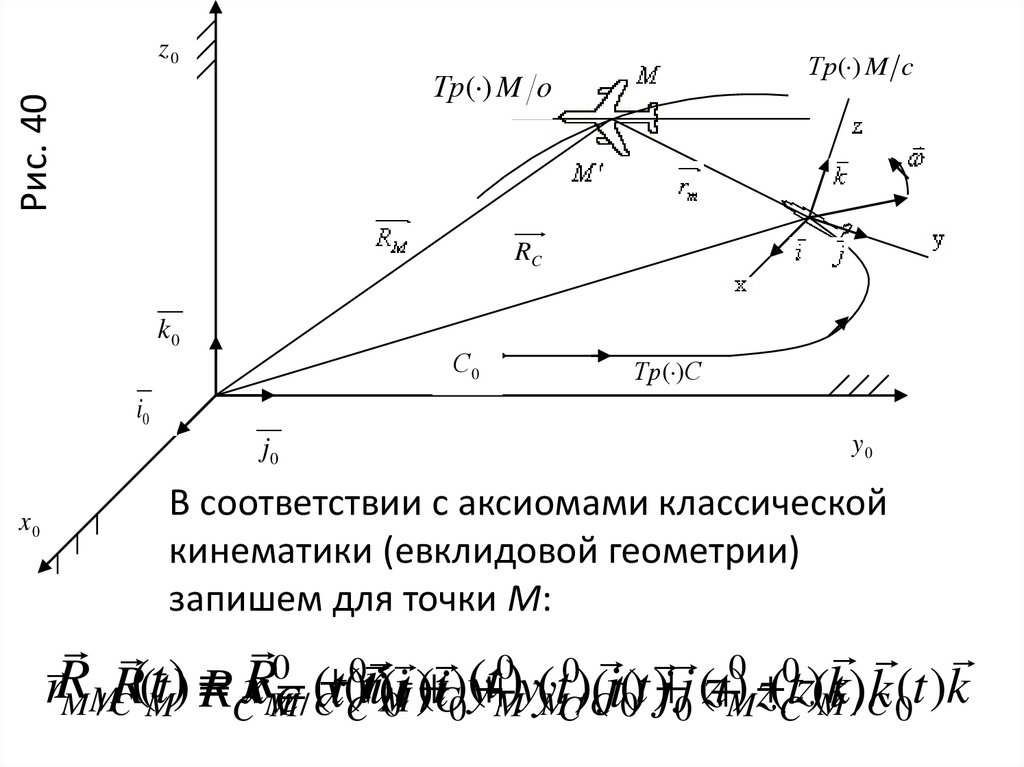
§8.1. Общая постановка задачи о
сложном движении точки.
В физических основах механики выделяют инерциальные
и неинерциальные системы отсчета. Рассмотрим
движение точки М по отношению к 2-м таким системам
координат, представленным на Рис.40. Задачу
представим как задачу о наведении перехватчика на
бомбардировщик противника.

5.

z0
Тр( ) M c
Рис. 40
Тр ( ) M o
RC
k0
С0
Тр ( )С
i0
j0
x0
y0
В соответствии с аксиомами классической
кинематики (евклидовой геометрии)
запишем для точки М:
0 0 0 0 0 0
R
tt)
(
tM)yy(MtC)/ C(jt(0)t )
rMM/ CR((M
RCxRMMC / (C
xt(C)tri)(M
j0j (z tM) z (Ctz)(Mkt )/ Ck 0(t )k
/ tiC0)y
0it )(

6.

Движение точки М по отношению к осям условно
неподвижной инерционной системе координат
( x 0 , y 0 , z 0 ), с началом в точке О, называется
абсолютным движением или просто движением
этой точки.
В соответствии с научной традицией будем все
абсолютные величины метить индексом “а”: Va V , aa a
Движение точки М по отношению к произвольно
движущейся неинерциальной системе отсчета с
началом в точке С (x,y,z ) назовем относительным.
Все относительные величины будем метить индексом “r”
(от французского слова relative — относительный):
Vr V , ar a

7.

Абсолютная и относительная траектории существует
объективно, и мы можем о них говорить.
Переносным движением точки М назовем движение
той точки М΄ подвижного пространства,
связанного с осями подвижной системы координат,
по отношению к неподвижному пространству,
через которую в данный момент проходит
движущаяся точка М.
В соответствии с научной традицией будем все
переносные величины обозначать индексом “е”: Vе , aе

8.

Так как в каждый момент времени движущаяся точка М
проходит через разные точки М΄ подвижного
пространства, которые движутся по разным траекториям
относительно неподвижных осей, то говорить о
переносной траектории, о ее существовании не имеет
смысла. Можно лишь говорить об элементе переносной
траектории, связанном с вектором dS e в данный момент
времени. В целом движение системы координат x,y,z
относительно системы координат x 0 , y 0 , z 0 можно
представить как движение подвижного пространства
сквозь неподвижное.

9.

§8.2. Теорема Бура об абсолютной и
относительной производных
любого вектора по времени.
Пусть задан вектор b bx (t )i (t ) by (t ) j (t ) bz (t )k (t ) (50)
в подвижных осях.
Тогда: абсолютная производная от вектора по
времени будет равна геометрической сумме
его относительной производной и
поворотной компоненты
db d r b
b
dt
dt
(51)

10.

Доказательство:
Вычислим эту производную непосредственно. Тогда
db d
(bx (t ) i (t ) b y (t ) j (t ) bz (t ) k (t ))
dt dt
db
di
dj
dk
bx i bx
by j by
bz k bz
dt
dt
dt
dt
Здесь возникает вопрос о том, какое движение совершают
концы единичных векторов i, j, k и каким образом
можно вычислить производные от них?
Во первых, скорости концов этих векторов
перпендикулярны самим векторам по теореме о
производной от единичного вектора по параметру.

11.

Ясно, что они совершают
вращательное движение с
угловой скоростью e вокруг мгновенной оси,
проходящей через точку С. А раз так, то эти производные
можно вычислить по формуле Эйлера.
di di
dj
dk
i
e i
j
e j k
e k
dt dt
dt
dt
db
bx i e i bx by j e j by bz k e k bz
dt
db
bx i by j bz k e b
dt
Или в компактной форме записи:
db d r b d r b
e b
bx i by j bz k
dt dt
dt
(52)

12.

§8.3. Теорема сложения скоростей.
Выясним вопрос о том, как можно найти скорость точки
по её относительной и переносной скоростям? Для этого
докажем теорему о сложении скоростей. Она
формулируется так:
Абсолютная скорость точки геометрически
складывается из 2-х скоростей — относительной и
переносной.
V Va Vr Ve
(53)

13.

Воспользуемся теоремой Бура. Тогда
dRc dr d r r
Va V
VC
e r
dt
dt
dt
dt
de def dR
r
dr r
Vr
dt
(54)
M
Ve Vc e r Vc VM C ,таким образом
Ve Vc e r
(55)