Интегрирование рациональных иррациональных и тригонометрических функций

1. Интегрирование рациональных иррациональных и тригонометрических функций

Верзилина О.А.

2. Интегрирование рациональных функций

Дробно – рациональная функция
Простейшие рациональные дроби
Разложение рациональной дроби на
простейшие дроби
Интегрирование простейших дробей
Общее правило интегрирования
рациональных дробей

3. Дробно – рациональная функция

Дробно – рациональной функцией называется функция, равная
отношению двух многочленов:
Pm ( x )
f (x)
Qn ( x )
Рациональная дробь называется правильной,многочлен
если степень
степени m
числителя меньше степени знаменателя, то есть m < n , в
многочлен степени n
противном случае дробь называется неправильной.
Всякую неправильную рациональную дробь можно, путем деления
числителя на знаменатель, представить в виде суммы многочлена
L(x) и правильной рациональной дроби:
P( x )
R( x )
L( x )
Q( x )
Q( x )

4. Дробно – рациональная функция

x 5x 9
x 2
4
Привести неправильную дробь к правильному виду:
x 4 5x 9 x 2
3
2
4
3
4x 3
x
2x
x 2x
2x 5 x 9
2x 3 4 x 2
4x 2 5x 9
4x 2 8x
3x 9
3x 6
15
3
x 4 5x 9
x 2
15
3
2
x 2x 4 x 3
x 2

5. Простейшие рациональные дроби

Правильные рациональные дроби вида:
A
x a
A
k
x a
(k 2; k N )
Mx N
2
x px q
V
Mx N
( p 2 4q 0)
x px q
2
k
( p 2 4q 0;
k 2; k N )
Называются простейшими рациональными дробями
, , , V типов.

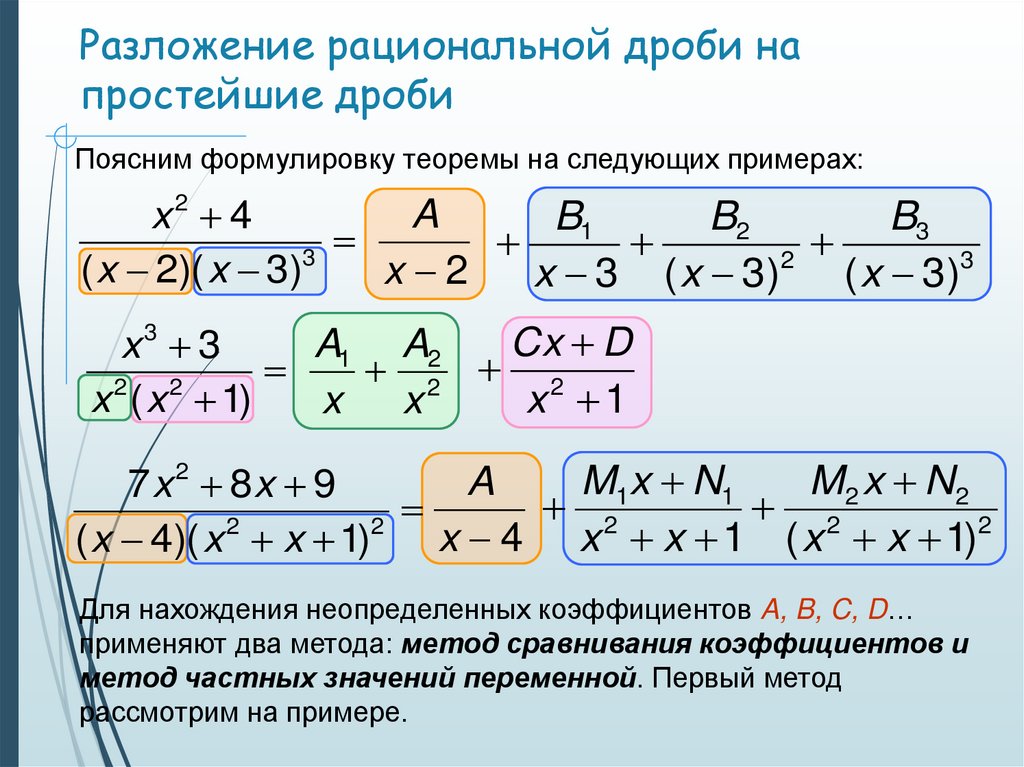
6. Разложение рациональной дроби на простейшие дроби

P( x )
Теорема: Всякую правильную рациональную дробь
,
Q( x )
знаменатель которой разложен на множители:
Q( x ) ( x x1 ) ( x x2 )k ( x 2 p1x q1 )
( x 2 p2 x q2 )s
можно представить, притом единственным образом в виде суммы
простейших дробей:
A
B1
B2
Bk
P( x )
2
k
x x2 ( x x2 )
( x x2 )
Q( x ) x x 1
Cx D
M1x N1
M 2 x N2
2
2
2
2
x p1x q1 x p2 x q2 ( x p2 x q2 )
M s x Ns
2
s
( x p2 x q2 )

7. Разложение рациональной дроби на простейшие дроби

Поясним формулировку теоремы на следующих примерах:
A
x2 4
B3
B1
B2
3
2
( x 2)( x 3)
x 2
x 3 ( x 3)
( x 3)3
Cx D
A1 A2
x3 3
2 2
2
2
x ( x 1)
x 1
x
x
M1x N1
M 2 x N2
A
7x 2 8x 9
2
2
2
2
x 4 x x 1 ( x x 1)2
( x 4)( x x 1)
Для нахождения неопределенных коэффициентов A, B, C, D…
применяют два метода: метод сравнивания коэффициентов и
метод частных значений переменной. Первый метод
рассмотрим на примере.

8. Разложение рациональной дроби на простейшие дроби

Представить дробь в виде суммы простейших дробей:
A 1 Bx3 xC 2
2x 3 x 3
2 2
2
( x 1)( x 2x 5) x x1 1 x x 2 x2 x5 5
2
A( x 2 2x 5) (Bx C )( x 1)
2
( x 1)( x 2Приведем
x 5) простейшие
дроби
Ax 2 2 Ax 5 A Bxк2общему
Cx знаменателю
Bx C 2 x 2 3 x 3
x
2
x1
0
x
Приравняем числители
получившейся и исходной
дробей
A B 2
A 1
2 A C B 3
B 3
коэффициенты
C 2
5 A C Приравняем
3
при одинаковых степенях х

9. Интегрирование простейших дробей

Найдем интегралы от простейших рациональных дробей:
A
d ( x a)
dx
A
A ln x a C
x a
x a
A
k
dx
A
x
a
d ( x a)
k
x a
A x a
k 1
k 1
C
Mx N
x 2 px q dx
Интегрирование дроби 3 типа рассмотрим на примере.

10. Интегрирование простейших дробей

3x 1
3x 1
x 2 2x 10 dx ( x 2 2x 1) 9 dx
x 1 t
3x 1
3(t 1) 1
dx x t 1
dt
2
2
( x 1) 9
t 9
dx dt
3t 2
t dt
dt
3 d t2 9
2
dt 3 2
2 2
2
t 9
t 9
t 9 2
t 9
2
t
2
t 3
2
arctg ln t 9 arctg C
3
3
3
3 2
3
2
x 1
2
ln x 2 x 10 arctg
C
2
3
3

11. Интегрирование простейших дробей

V
Mx N
x px q dx
k
2
p
Интеграл данного типа с помощью подстановки: x
t
2
приводится к сумме двух интегралов:
t dt
dt
M
N1
k
2
2
2
2 k
t a
t a
Первый интеграл вычисляется методом внесения t под знак
дифференциала.
Второй интеграл вычисляется с помощью рекуррентной формулы:
1 2k 3
t
k
2
k 1
k
2
2
k
1
a 2k 2
2(k 1)(t a )
t 2 a2
dt

12. Интегрирование простейших дробей

dt
3 2
(t 1)3
dt
a = 1; k = 3
1 2
arctg t
t 1
dt
2 2 3
t
2
1
2
2
2
2 2 2
2(2 1)(t 1)
t 1
1
t
arctg t
2
2(t 2 1)
2 3 3
t
3
2
2
2
2 3 2
2(3 1)(t 1)
3 1
t
t
arctg t
C
2
2
2
4 2
2(t 1) 4(t 1)

13. Общее правило интегрирования рациональных дробей

Если дробь неправильная, то представить ее в виде суммы
многочлена и правильной дроби.
Разложив знаменатель правильной рациональной дроби на
множители, представить ее в виде суммы простейших дробей
с неопределенными коэффициентами
Найти неопределенные коэффициенты методом сравнения
коэффициентов или методом частных значений переменной.
Проинтегрировать многочлен и полученную сумму
простейших дробей.

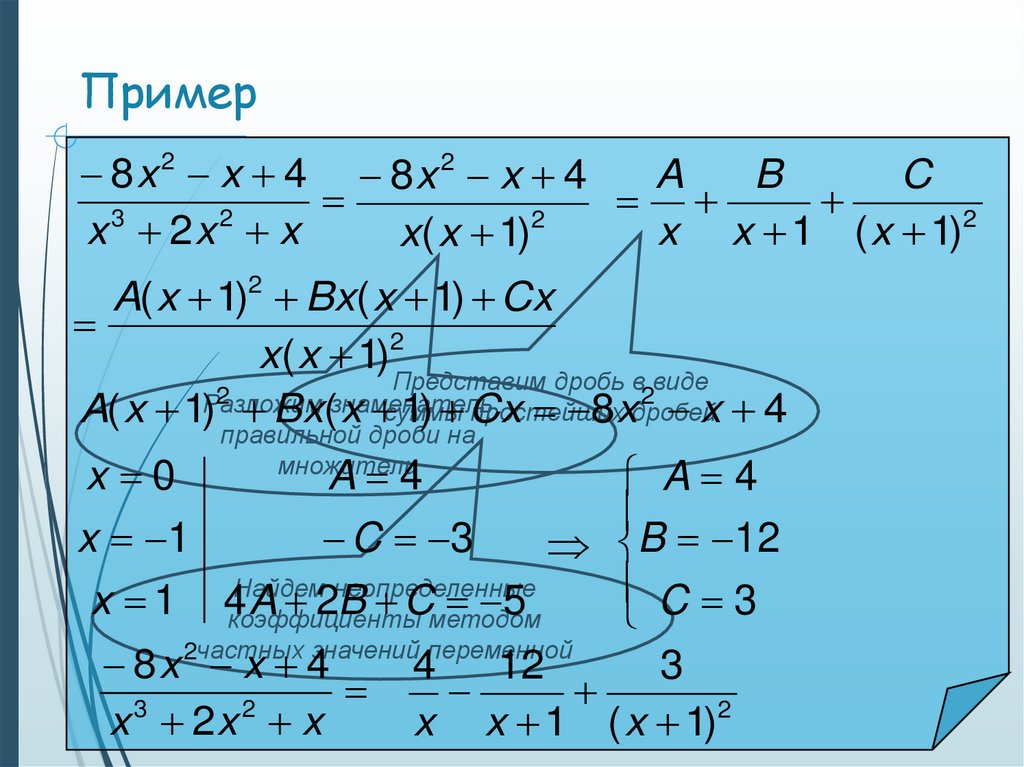
14. Пример

Приведем дробь к
x 5 2x 3 4 x 4
dx
правильному виду.
3
2
x 2x x
x 5 2x 3 4 x 4 x 3 2x 2 x
2
5
4
3
2x 5
x
x 2x x
2x 4 x 3 4 x 4
4
3
2
2x 4 x 2x
3
2
5 x 2x 4 x 4
3
2
5 x 10 x 5 x
8x 2 x 4
2
x 5 2x 3 4 x 4
8
x
x 4
2
x 2x 5 3
3
2
x 2x x
x 2x 2 x

15. Пример

8x x 4 8x 2 x 4
A
B
C
3
2
2
x 2x x
x x 1 ( x 1)2
x( x 1)
2
A( x 1)2 Bx( x 1) Cx
x( x 1)2
Представим дробь в виде
2
2
простейших
A( x 1)Разложим
Bx(знаменатель
x суммы
1) Cx
8 xдробей
x 4
x 0
правильной дроби на
множители
A 4
A 4
x 1
C 3
B 12
Найдем неопределенные
C 3
x 1 4коэффициенты
A 2B Cметодом
5
2частных значений переменной
8x x 4
3
2
x 2x x
4
12
3
2
x x 1 ( x 1)

16. Пример

4 12
3
x 2x 5
dx
2
x x 1 ( x 1)
2
dx
dx
dx
x dx 2 xdx 5 dx 4 x 12 x 1 3 ( x 1)2
2
x3
3
2
x 5 x 4 ln x 12 ln x 1
C
3
x 1

17. Интегрирование тригонометрических функций.

1. Интегралы вида sin kx sin mxdx, sin kx cos mxdx, cos kx cos mxdx
вычисляются с помощью формулы:
1
sin kx sin mx (cos( k m) x cos( k m) x)
2
1
sin kx cos mx (cos( k m) x sin( k m) x)
2
1
cos kx cos mx (cos( k m) x cos( k m) x)
2
,
,
2. Интегралы вида cos m kx sin n kxdx , где хотя бы одно из
чисел m и n – нечетное положительное, k и второе
число – любое, вычисляются подведением под знак
дифференциала.

18.

3. Интегралы вида cos m kx sin n kxdx , где m и n – четные
положительные числа (одно из них может равняться
нулю) k – любое число, вычисляются с помощью форму
понижения степени:
1
1
sin 2 , (1 cos 2 ) , cos 2 (1 cos 2 )
2
2
sin cos
1
sin 2
2
4. Интегралы вида tg m kxdx и ctg m kxdx , где m –
натуральное, k – любое число, вычисляются заменой
переменной: tgkx=z или ctgkx=z.

19.

5. Интегралы вида R(sin x; cos x)dx сводятся к
интегралам от рациональных дробей с помощью
универсальной тригонометрической подстановки
x
tg z
2
x
2tg
2
, откуда sin x
x
1 tg 2
2dz
2
dx
1 z 2
1 z2
cos x
1 z2
x
1 tg
2
cos x
2 x
1 tg
2
2z
sin x
1 z2
2

20. Интегрирование простейших иррациональных функций

1. Интегралы вида
( Ax B)dx
интегрируются так же, как
ax bx c
простейшие рациональные дроби 3 – го вида: в знаменателе
2
выделяются полный квадрат и вводится новая переменная.
ax b n2 ax b
ax b
nk
;
;...;
)dx
cx d cx d
cx d ax b s
t
вычисляются с помощью замены переменной
cx d
,где s – наименьшее общее кратное чисел n1, n2, …, nk; a, b, c,
2. Интегралы вида R( x; n1
d – числа (c и d не равны нулю одновременно).
В частности, корень под знаком интеграла может быть один.

21.

3. Интегралы вида R(x ; a2 , x 2 )dx
,
2
2
R
(
x
;
a
x
)dx
R(x; x a )dx
2
2
вычисляются с помощью тригонометрических
подстановок соответственно:
1. x=a sinz;
dx=a coszdz.
2. x=a tgz;
a sin zdz
dx
2 .
cos z
a
3. x cos z
a dz
.dx cos 2 z

22.

Пример(вычисление с помощью тригонометрических
подстановок).
1 x
dz
dx x tgz ; dx
4
2
x
cos z
2
1 tg 2 z
tg 4 z
dz
cos4 zdz
cos zdz
4
4
3
3
4
tg z cos z
sin z cos z
sin z
3
sin
z
4
sin zd sin z
c
3
1
1
1
2
c
(ctgz ;1 ctg z
; sin z
3
2
x
3 sin z
sin z
1
1 ctg z 1 2
x
2
x 1
) c
x
2
x 1
2
3x 3
3
dz
2
cos z

23.

Спасибо за внимание!!!