Объемы и поверхности тел вращения

1.

ОБЪЕМЫ И
ПОВЕРХНОСТИ ТЕЛ
ВРАЩЕНИЯ
СОСТАВИЛА ПРЕПОДАВАТЕЛЬ
ДАДАТЧЕНКО Т.А.

2.

ПОСТАНОВКА ПРОБЛЕМЫ:
КАКОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
ДОЛЖЕН БЫТЬ ЧАЙНИК ( ПРИ
УСЛОВИИ НЕИЗМЕННОГО
ОБЪЕМА И МАТЕРИАЛА, ИЗ
КОТОРОГО ИЗГОТОВЛЕН
ЧАЙНИК), ЧТОБЫ ВОДА В НЕМ
ОСТЫВАЛА КАК МОЖНО
ДОЛЬШЕ?

3.

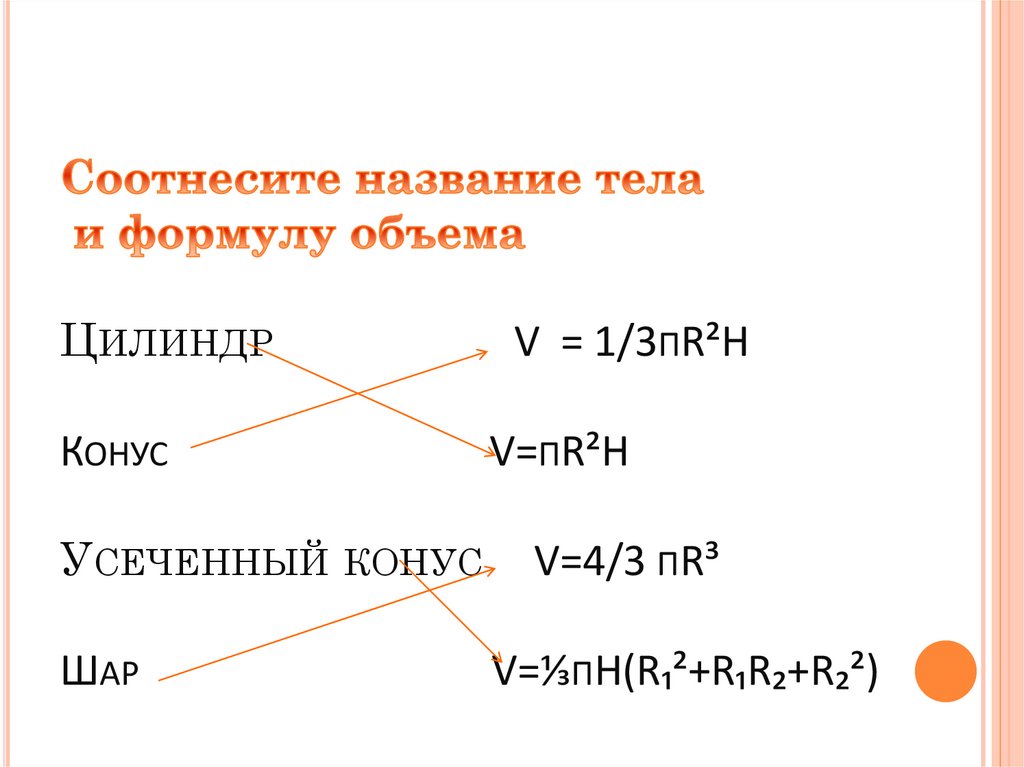
ЦИЛИНДР
V = 1/3ΠR²H
КОНУС
V=ΠR²H
УСЕЧЕННЫЙ КОНУС
ШАР
V=4/3 ΠR³
V=⅓ΠH(R₁²+R₁R₂+R₂²)

4.

ЦИЛИНДР
V = 1/3ΠR²H
КОНУС
V=ΠR²H
УСЕЧЕННЫЙ КОНУС
ШАР
V=4/3 ΠR³
V=⅓ΠH(R₁²+R₁R₂+R₂²)

5.

.
ЦИЛИНДР
S=4ΠR²
КОНУС
S=2ΠRH+2ΠR²
УСЕЧЕННЫЙ КОНУС
S=ΠRL+ΠR²
СФЕРА
S=Π(R₁+R₂)L+ΠR₁²+ΠR₂²

6.

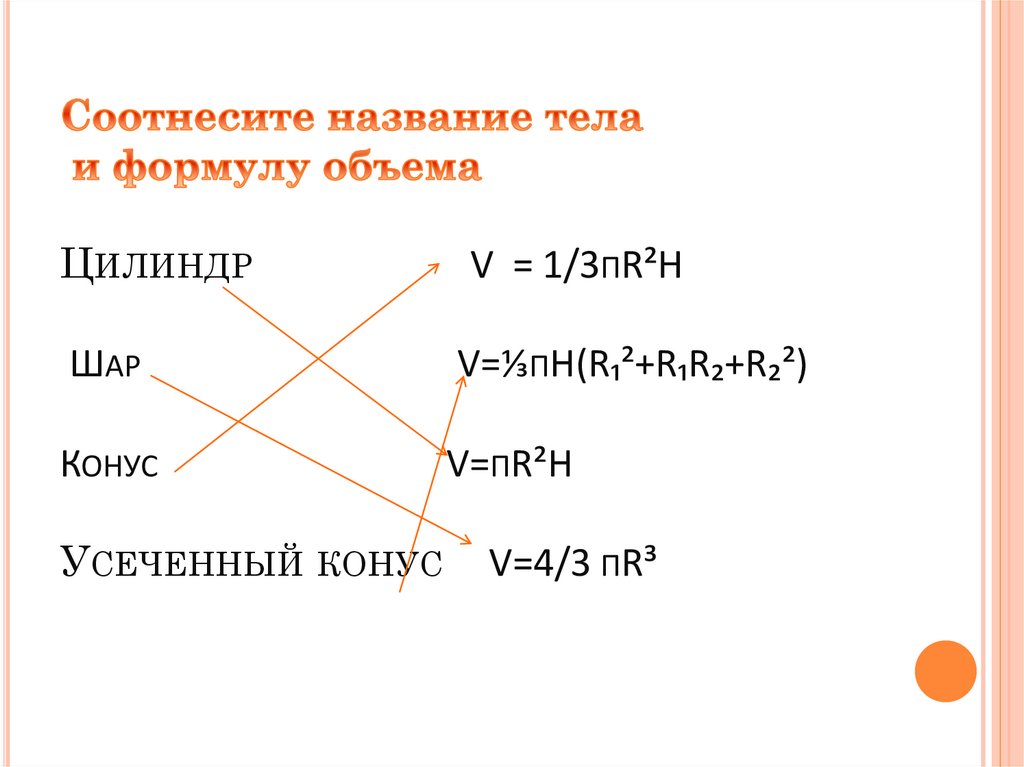
ЦИЛИНДР
V = 1/3ΠR²H
ШАР
V=⅓ΠH(R₁²+R₁R₂+R₂²)
КОНУС
V=ΠR²H
УСЕЧЕННЫЙ КОНУС
V=4/3 ΠR³

7.

ДАНО : V=3Л .
НАЙТИ : S

8.

ДАНО: V=3Л. НАЙТИ : S

9.

ДАНО: V=3Л,
Π=3 ,
H=2 ДМ. НАЙТИ: S

10.

ПЛОЩАДЬ ПОВЕРХНОСТИ
ЧАЙНИКА ШАРОВОЙ ФОРМЫ
РЕШЕНИЕ
V =4/3 π R³ →
3 = 4/3 ∙3 R³ →
3 =4 R³
→
R³ =3/4
→
R³ = 0,75
→
R = 0,9.
S=4 π R²=4∙3∙0,81 = 9,6
Ответ: S = 9,6 дм².

11.

ПЛОЩАДЬ ПОВЕРХНОСТИ ЧАЙНИКА
ПОЛУШАРОВОЙ ФОРМЫ.
V=2/3πR³
3=2/3∙3R³
3=2R³
R³=3/2
R³= 1,5
→
→
→
→
→
R ≈ 1,2.
S = πR²+2πR² = 3πR² ≈ 9 ∙1,44 ≈ 13
Ответ: S = 13 дм ²

12.

ПЛОЩАДЬ ПОВЕРХНОСТИ ЧАЙНИКА
ЦИЛИНДРИЧЕСКОЙ ФОРМЫ
V = π R² H
→
R² =V/(π∙H)
→
R² = 3/(3∙2)=1/2
→
R =√2/2 ≈ 0,7
→
S=2πR²+2πRH=2πR(R+H) →
S=2∙3∙0,7(0,7+2)
→
S=11,3
Ответ: S=11,3 дм²

13.

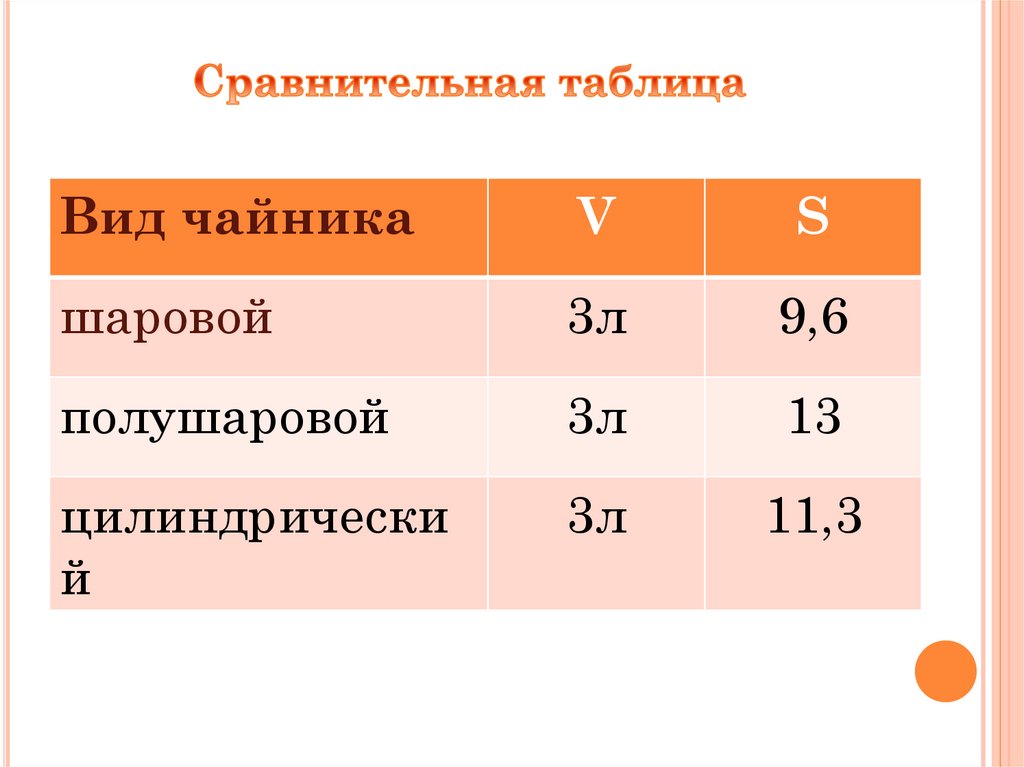
Вид чайника
V
S
шаровой
3л
9,6
полушаровой
3л
13
цилиндрически
й
3л
11,3

14.

Чайник в форме шара
имеет наименьшую
поверхность,
а
значит дольше остается
горячим, то есть остывает
медленнее, чем чайник
любой другой формы.

15.

Почему резервуар чайника быстрее
нагревается и охлаждается, когда
он имеет форму цилиндра?
Почему небольшие капли
жидкости(ртути, дождя, росы)
имеют форму шара?
Почему мыльные пузыри
принимают форму шара?

16.

РОСА НА ЦВЕТАХ

17.

18.

КАПЕЛЬКИ
Принимают сферическую форму за счёт действия сил
поверхностного натяжения. Все молекулы в
жидкости притягиваются друг к другу, но те из них,
которые находятся на поверхности жидкости,
испытывают значительно большее притяжение
внутрь (к молекулам более плотной жидкости), чем
наружу (к молекулам разреженного воздуха).
Поэтому поверхность жидкости ведёт себя подобно
упругой плёнке, охватывающей жидкость со всех
сторон, и стягивающей её.
Поскольку именно сфера является поверхностью с
наименьшей площадью при заданном объёме
(который поверхность должна ограничивать), то
капельки становятся круглыми. Это изменение
формы прекрасно видно при отрыве висящей капли
(в форме капли) и превращение её в шарик в полёте.

19.

МЫЛЬНЫЕ ПУЗЫРИ
Сферой называется поверхность шара. Её не
трудно получить с помощью мыльной воды и
соломинки: опустим соломинку в мыльную
воду, потом вытащим и подуем в нее. И вот уже
летит переливаясь всеми цветами радуги
шарик с тончайшими стенками – сфера. Форма
мыльного пузыря определяется силами
поверхностного натяжения в пленке
поверхностно активного вещества.

20.

Приведите примеры из
практической деятельности,
из жизни, где указанное
свойство имеет применение.