Прямая линия в пространстве

1. Прямая линия в пространстве

Векторное уравнение прямой
Параметрические уравнения прямой
Канонические уравнения прямой
Уравнения прямой, проходящей через две
заданные точки
Общие уравнения прямой
Угол между прямыми
Угол между прямой и плоскостью
Условие принадлежности двух прямых одной
плоскости
Точка пересечения прямой и плоскости

2. Векторное уравнение прямой

3. Векторное уравнение прямой

4. Параметрические уравнения прямой

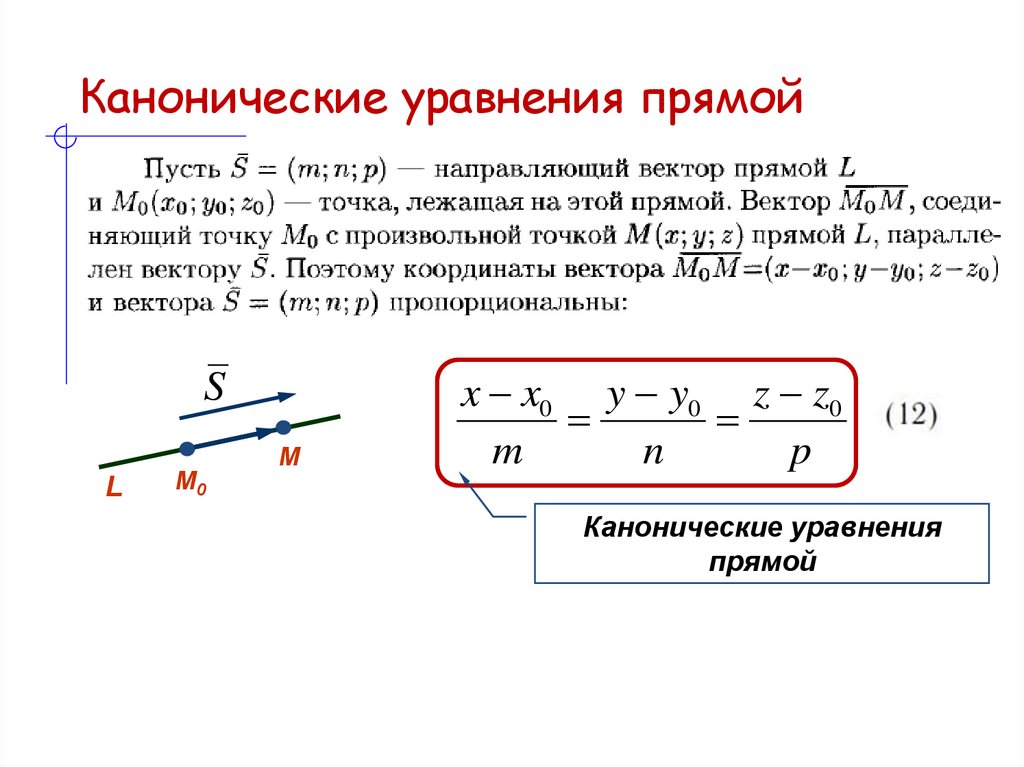
5. Канонические уравнения прямой

S
L
М0
М
x x0 y y0 z z0
m
n
p
Канонические уравнения
прямой

6. Канонические уравнения прямой

7. Канонические уравнения прямой

8. Канонические уравнения прямой

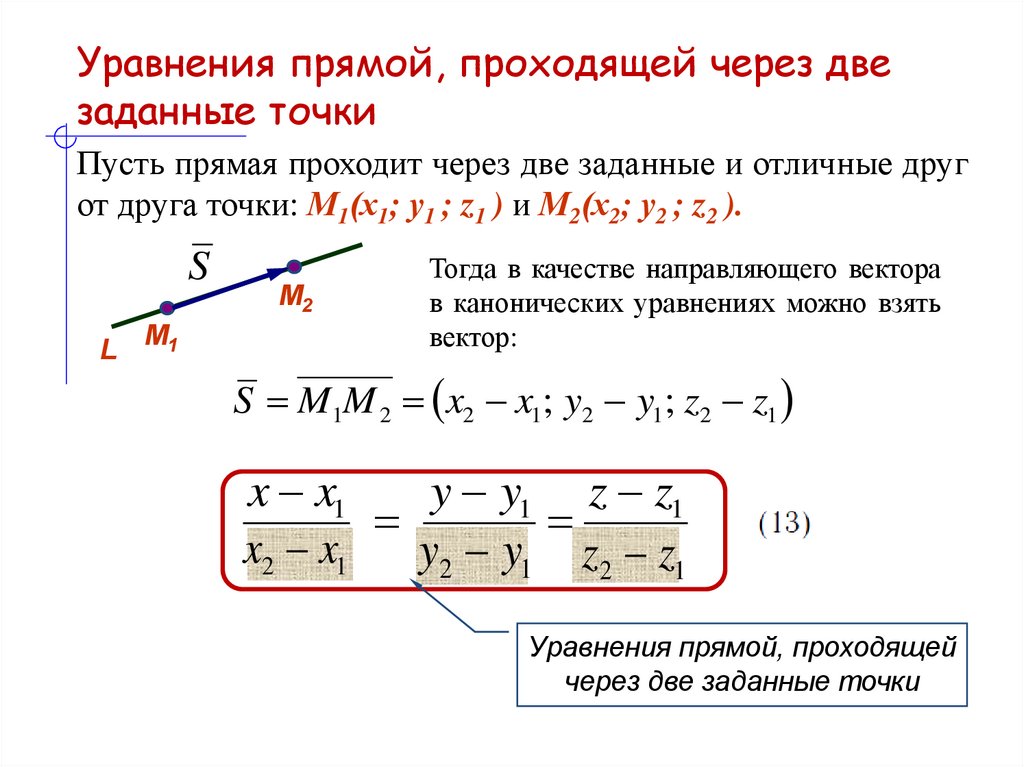
9. Уравнения прямой, проходящей через две заданные точки

Пусть прямая проходит через две заданные и отличные друг
от друга точки: М1(х1; у1 ; z1 ) и М2(х2; у2 ; z2 ).
S
L М1
М2
Тогда в качестве направляющего вектора
в канонических уравнениях можно взять
вектор:
S M1M 2 x2 x1; y2 y1; z2 z1
x x1
y y1 z z1
x2 m
x1
y2 n y1 z2 p z1
Уравнения прямой, проходящей
через две заданные точки

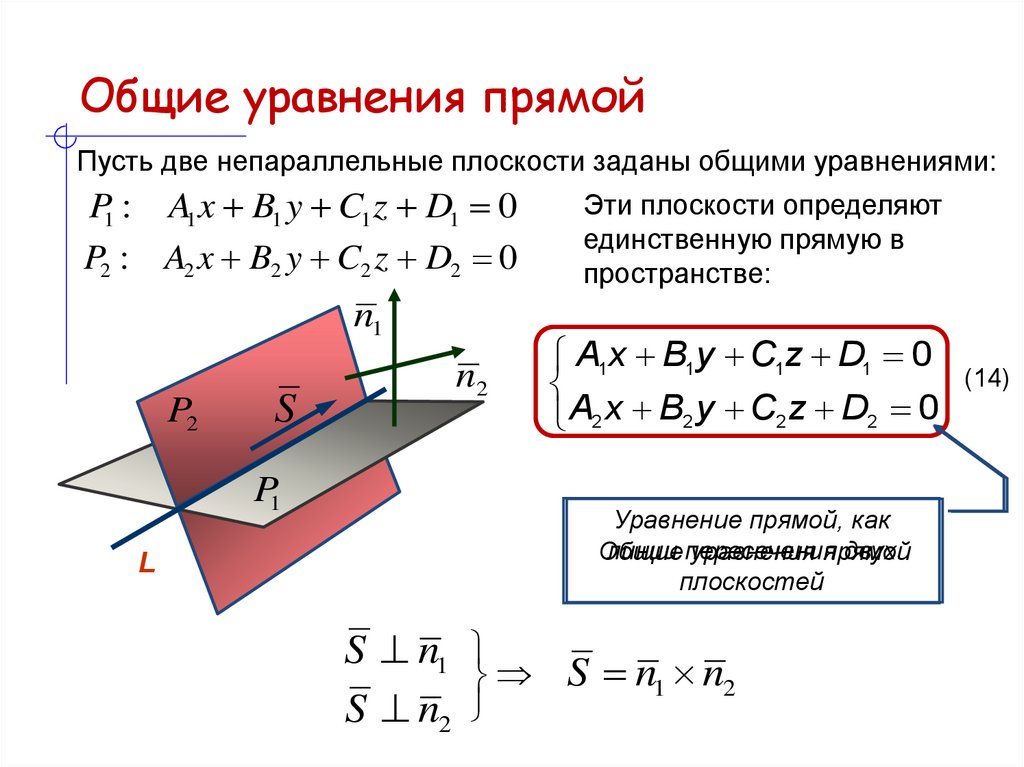
10. Общие уравнения прямой

Пусть две непараллельные плоскости заданы общими уравнениями:
P1 : A1 x B1 y C1 z D1 0
P2 : A2 x B2 y C2 z D2 0
n1
P2
S
P1
L
n2
Эти плоскости определяют
единственную прямую в
пространстве:
A1x B1y C1z D1 0
A2 x B2 y C2 z D2 0
Уравнение прямой, как
линии пересечения
двух
Общие
уравнения прямой
плоскостей
S n1
S n1 n2
S n2
(14)

11. Пример

2x 3y z 2 0
Написать канонические уравнения прямой:
x y z 3 0
Найдем точку, принадлежащую прямой, то есть
удовлетворяющую системе уравнений.
Полагая z равной любому числу, например, z = 0, получим:
x 11
2 x 3 y 2 0
y 8
x y 3 0
Точка M0(11; -8; 0)
принадлежит прямой
Найдем координаты направляющего вектора прямой:
i j k
S n1 n2 2 3 1 4i 3 j k
1 1 1
x 11 y 8
z
4
3
1

12. Угол между прямыми

Пусть две прямые заданы каноническими уравнениями:
x x2 y y2 z z2
L2 :
m2
n2
p2
x x1 y y1 z z1
L1 :
m1
n1
p1
Углом между этими прямыми называется угол между направляющими
векторами к этим прямым.
S1 m1; n1; p1
S2 m2 ; n2 ; p2
cos
S2
S1
L1
L2
L1 // L2
m1 n1 p1
m2 n2 p2
S1 S 2
S1 S2
m1 m2 n1 n2 p1 p2
m12 n12 p12 m22 n22 p22
L1 L2 m1 m2 n1 n2 p1 p2 0

13. Угол между прямыми

14. Угол между прямой и плоскостью

Пусть прямая L задана каноническими
уравнениями:
x x0 y y0 z z0
m
n
p
Плоскость Q задана общим уравнением:
Ax By Cz D 0
Углом между прямой и плоскостью называется угол между прямой и
проекцией этой прямой на плоскость.
2
n
S
Q
L
S n
cos(S , n ) cos( ) sin
2
S n
m A n B p C
m 2 n 2 p 2 A2 B 2 C 2

15. Угол между прямой и плоскостью

m A n B p C 0
m n p
A B C

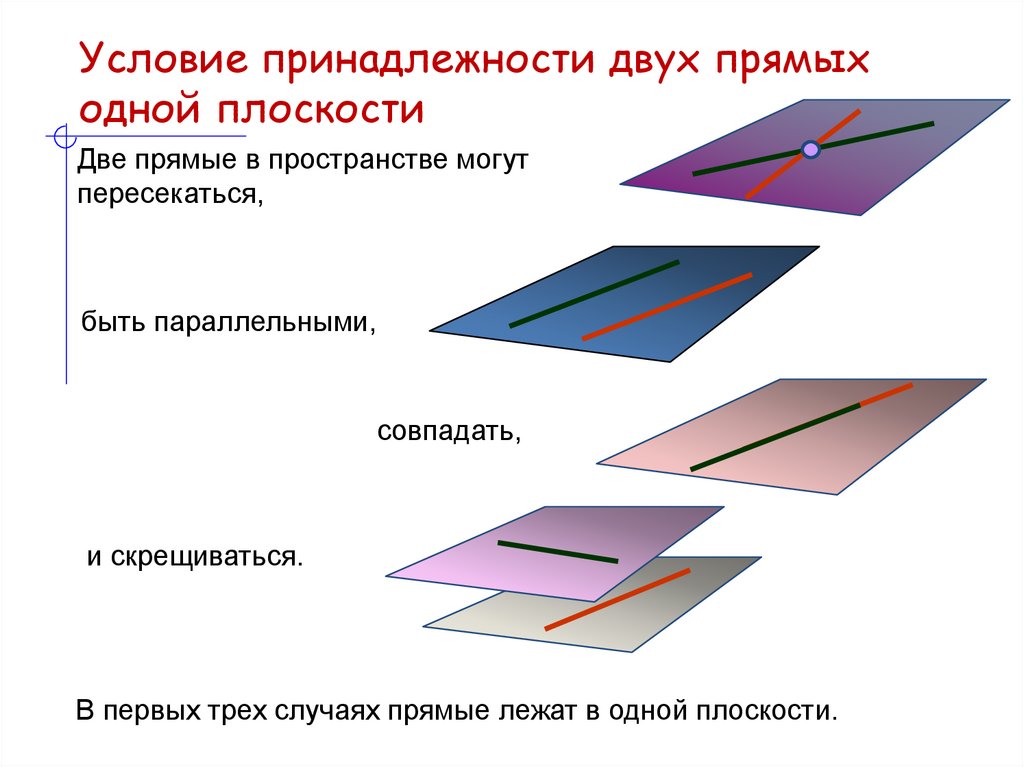
16. Условие принадлежности двух прямых одной плоскости

Две прямые в пространстве могут
пересекаться,
быть параллельными,
совпадать,
и скрещиваться.
В первых трех случаях прямые лежат в одной плоскости.

17. Условие принадлежности двух прямых одной плоскости

Пусть две прямые заданы каноническими уравнениями:
x x1 y y1 z z1
L1 :
m1
n1
p1
x x2 y y2 z z2
L2 :
m2
n2
p2
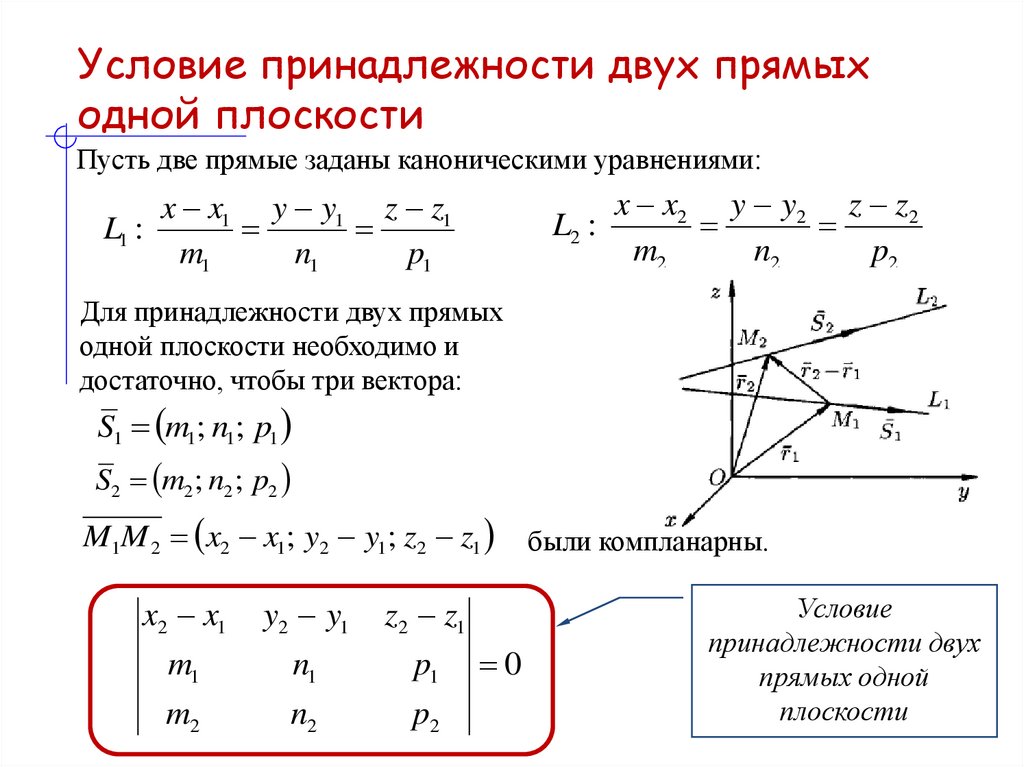
Для принадлежности двух прямых
одной плоскости необходимо и
достаточно, чтобы три вектора:
S1 m1; n1; p1
S2 m2 ; n2 ; p2
M1M 2 x2 x1; y2 y1; z2 z1
x2 x1
m1
m2
y2 y1
n1
n2
z2 z1
p1 0
p2
были компланарны.
Условие
принадлежности двух
прямых одной
плоскости

18. Точка пересечения прямой и плоскости

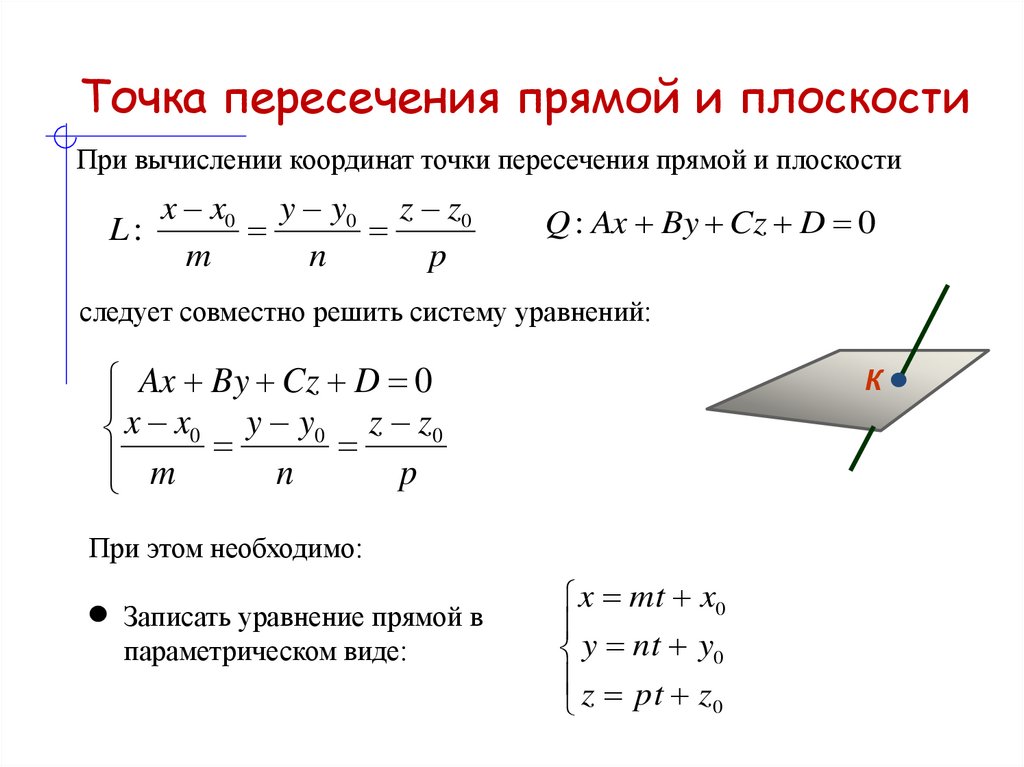
При вычислении координат точки пересечения прямой и плоскости
x x0 y y0 z z0
L:
m
n
p
Q : Ax By Cz D 0
следует совместно решить систему уравнений:
Ax By Cz D 0
x x
y y0 z z0
0
m
n
p
К
При этом необходимо:
Записать уравнение прямой в
параметрическом виде:
x mt x0
y nt y0
z pt z
0

19. Точка пересечения прямой и плоскости

Подставить в уравнение плоскости вместо x; y; z:
A(mt x0 ) B(nt y0 ) C ( pt z0 ) D 0
Решить полученное уравнение относительно t :
Ax0 By0 Cz0 D
t0
Am Bn Cp
Подставить t0 в параметрическое уравнение прямой:
xK mt0 x0
yK nt0 y0
z pt z
0
0
K
K ( xK ; y K ; z K )

20. Пример

Найти точку пересечения прямой и плоскости.
x 1 y z 2
3
5
1
y 5z 6 0
Напишем параметрические уравнения прямой:
Подставим в уравнение плоскости:
5t 5(t 2) 6 0
x 3t 1
y 5t
z t 2
10t 16 0 t 0 1.6
Подставим в уравнения прямой:
x 3 ( 1.6) 1
y 5 ( 1.6)
z 1.6 2
x 3.8
y 8
z 0 .4
K ( 3.8; 8; 0.4)

21. Пример

22. Пример