Similar presentations:
Прямая и плоскость в пространстве
1.
§11. Прямая и плоскость впространстве
п.1. Основные формулы.
1) Расстояние между двумя точками в
пространстве.
M1 ( x1 , y1 , z1 ),
M 1M 2
M 2 ( x2 , y2 , z2 ).
x2 x1 y2 y1 z2 z1 .
2
2
2
2.
2) Деление отрезка в данном отношении.M1 ( x1 , y1 , z1 ),
M 2 ( x2 , y2 , z2 ).
M1M
.
MM 2
x1 x2
x
,
1
y1 y2
y
,
1
z1 z2
z
.
1
3.
п.2. Уравнения плоскости.Составим уравнение плоскости, проходящей
через три данные точки
M1 ( x1 , y1 , z1 ), M 2 ( x2 , y2 , z2 ), M 3 ( x3 , y3 , z3 ).
M2
M1
M3
M
Точка M(x,y,z) принадлежит плоскости тогда и
только тогда, когда векторы
M1 M , M1M 2 , M 1M 3
являются компланарными.
4.
По свойству смешенного произведенияM1M M1M 2 M1M 3 0.
Найдем
M1M ( x x1 , y y1 , z z1 ),
M1M 2 ( x2 x1 , y2 y1 , z2 z1 ),
M1M 3 ( x3 x1 , y3 y1 , z3 z1 ).
Тогда
5.
x x1x2 x1
x3 x1
y y1
y2 y1
y3 y1
z z1
z2 z1 0.
z3 z1
Разложим определитель по первой строке
где
A( x x1 ) B( y y1 ) C ( z z1 ) 0,
y2 y1
A
y3 y1
z2 z1
,
z3 z1
x2 x1
B
x3 x1
x2 x1
C
x3 x1
y2 y1
.
y3 y1
z2 z1
,
z3 z1
6.
Раскроем скобкиAx By Cz Ax1 By1 Cz1 0,
обозначим
D Ax1 By1 Cz1 ,
получим
Ax By Cz D 0
— общее уравнение плоскости.
7.
Вектор, перпендикулярный плоскости,называется нормальным вектором этой
плоскости.
Если плоскость задана уравнением
Ax By Cz D 0,
то вектор
n ( A, B, C )
является нормальным вектором этой
плоскости.
A( x x1 ) B( y y1 ) C ( z z1 ) 0
— уравнение плоскости, проходящей через
данную точку и перпендикулярную данному
вектору.
8.
Уравнениеx x1
x2 x1
x3 x1
y y1
y2 y1
y3 y1
z z1
z2 z1 0
z3 z1
называется уравнением плоскости,
проходящей через три данные точки.
Уравнение
x y z
1
a b c
называется уравнением плоскости, «в
отрезках» (отсекает от координатных осей
отрезки длиной |a|, |b|, |c|).
9.
п.3. Плоскость. Основные задачи.1) Расстояние от точки до плоскости.
M
M ( x0 , y0 , z0 ),
d
: Ax By Cz D 0,
d
| Ax0 By0 Cz0 D |
A B C
2
2
2
.
10.
2) Угол между плоскостями.n2
n1
: A1 x B1 y C1 z D1 0,
: A2 x B2 y C2 z D2 0.
cos
n1 n2
n1 n2
Угол между
плоскостями равен
углу между
нормальными
векторами этих
плоскостей.
n1 ( A1 , B1 , C1 ),
n2 ( A2 , B2 , C2 ).
A1 A2 B1 B2 C1C2
A12 B12 C12
A22 B22 C22
.
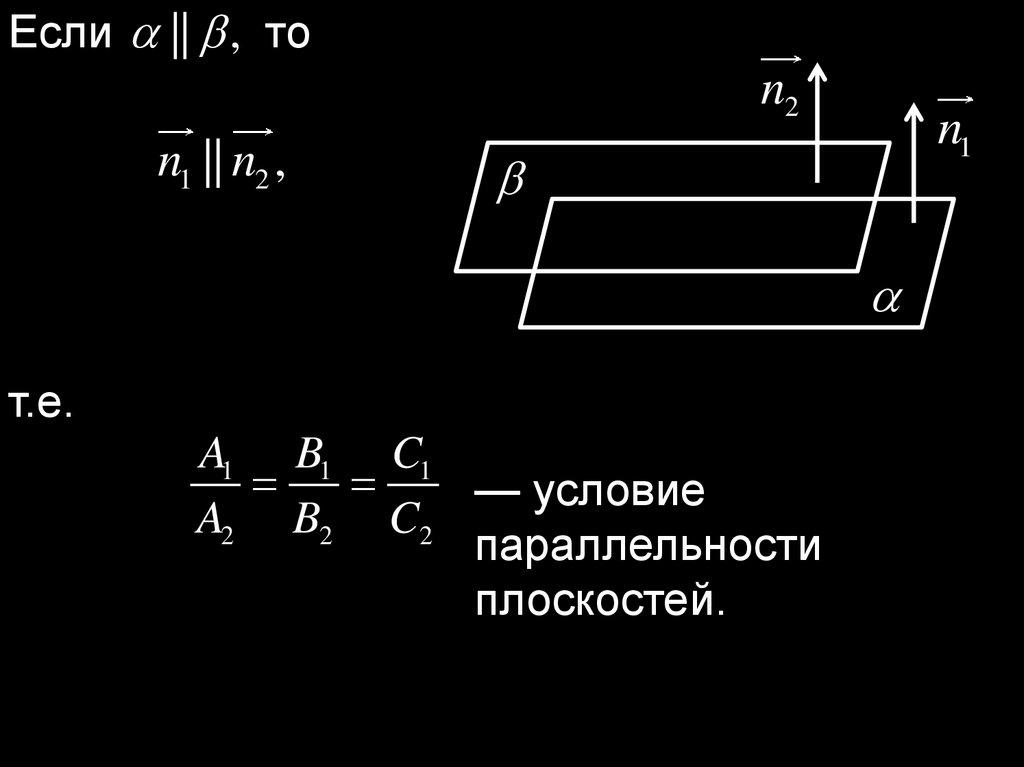
11.
Если || , тоn2
n1 || n2 ,
n1
т.е.
A1 B1 C1
— условие
A2 B2 C2
параллельности
плоскостей.
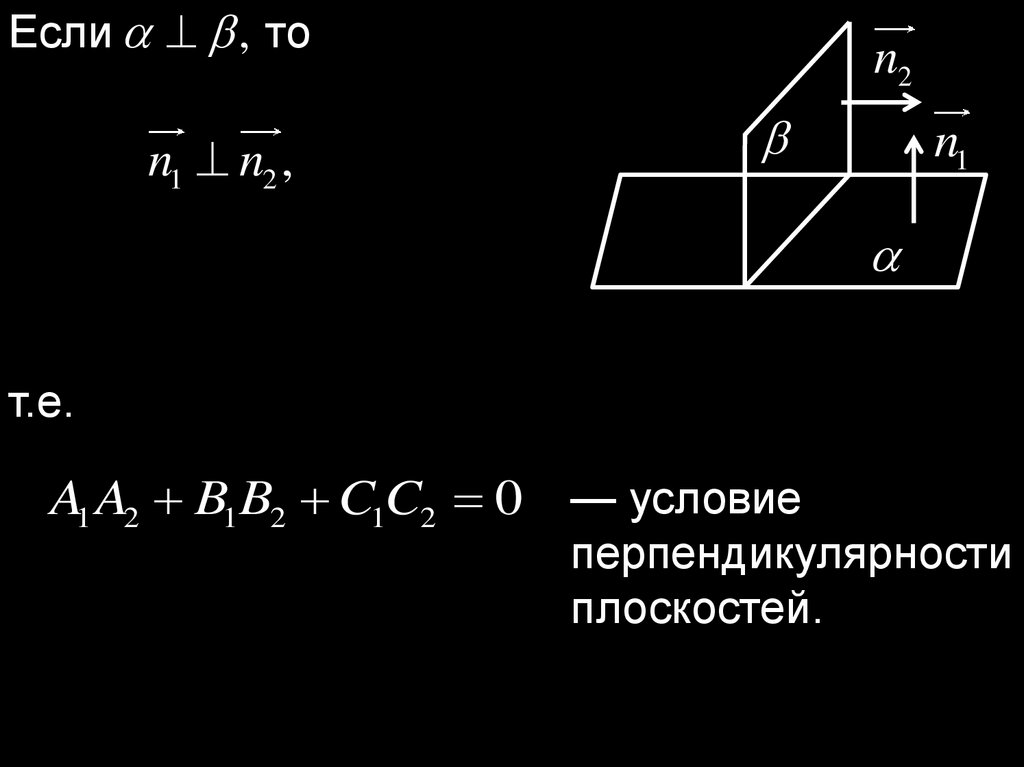
12.
Если , тоn1 n2 ,
n2
n1
т.е.
A1 A2 B1B2 C1C2 0 — условие
перпендикулярности
плоскостей.
13.
Пример. Составить уравнение плоскости,проходящей через точку M(3,2,-1) и
параллельной плоскости
x 2 y 2 z 4 0.
Решение.
Нормальный вектор плоскости x 2 y 2 z 4 0,
n (1, 2, 2),
является нормальным вектором искомой
плоскости.
Тогда требуемое уравнение имеет вид
или
1( x 3) 2( y 2) 2( z 1) 0
x 2 y 2 z 3 0.
14.
п.4. Уравнения прямой.1) Векторное уравнение прямой.
s
z
L
M0
M
O
M 0 ( x0 , y0 , z0 ),
s(m, n, p)
— направляющий
вектор прямой.
Составить
уравнение прямой L.
y
x
Пусть M ( x, y, z ) L.
Тогда OM OM M M .
0
Дано:
0
15.
ОбозначимТак как
то
Тогда
OM r ,
OM 0 r0 .
M 0 M || s,
M 0 M ts.
r r0 ts.
16.
2) Параметрические уравнения прямой.Рассмотрим векторное уравнение
r r0 ts.
Заметим, что
r ( x, y, z ),
Тогда
r0 ( x0 , y0 , z0 ),
x x0 mt ,
y y0 nt ,
z z pt.
0
s (m, n, p).
17.
3) Канонические уравнения прямой.Рассмотрим параметрические уравнения
x x0 mt ,
y y0 nt ,
z z pt.
0
Выразим параметр t из каждого уравнения
x x0
y y0
z z0
t
, t
, t
.
m
n
p
Тогда
x x0 y y0 z z0
.
m
n
p
18.
4) Уравнение прямой, проходящей через дветочки.
M1 ( x1 , y1 , z1 ),
M2
M1
M 2 ( x2 , y2 , z2 ).
В качестве направляющего вектора можно
взять вектор
M1M 2 ( x2 x1 , y2 y1 , z2 z1 ).
Тогда
x x1
y y1
z z1
.
x2 x1 y2 y1 z2 z1
19.
5) Общие уравнения прямой.Прямая в пространстве может быть задана как
линия пересечения двух плоскостей:
A1 x B1 y C1 z D1 0,
A2 x B2 y C2 z D2 0.
Пример. Написать канонические уравнения
прямой, заданной общими уравнениями:
x 2 y z 2 0,
3 y z 1 0.
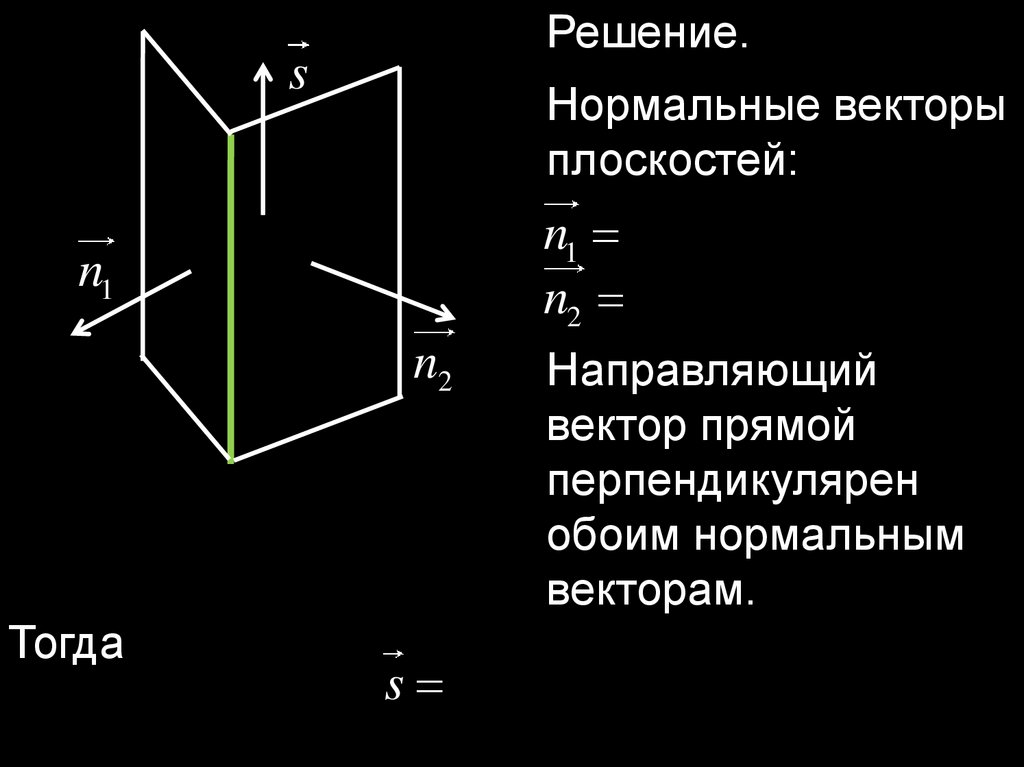
20.
Решение.s
Нормальные векторы
плоскостей:
n1 (1, 2,1),
n2 (0,3, 1).
n1
n2
Тогда
Направляющий
вектор прямой
перпендикулярен
обоим нормальным
векторам.
s n1 n1.
21.
Значит,i
j k
s 1 2 1 i j 3k ,
0 3 1
т.е.
s ( 1,1,3).
Найдем координаты какой-нибудь точки,
лежащей на искомой прямой.
Для этого в общих уравнениях положим,
например, y=0. Тогда
x z 2 0, x 1,
z 1 0; z 1.
22.
Осталось записать уравнения прямой,проходящей через точку
( 1, 0, 1)
с направляющим вектором
s ( 1,1,3).
Получим
x 1 y z 1
.
1 1
3
23.
п.5. Прямая. Основные задачи.1) Угол между прямыми.
Угол между прямыми
L2
равен углу между
s1
направляющими
s2
векторами этих прямых.
L1
x x1 y y1 z z1
L1 :
,
m1
n1
p1
s1 (m1 , n1 , p1 ),
x x2 y y2 z z2
L2 :
. s2 (m2 , n2 , p2 ).
m2
n2
p2
24.
coss1 s2
s1 s2
m1m2 n1n2 p1 p2
m12 n12 p12 m22 n22 p22
.
Если L1 || L2 , то s1 || s2 , т.е.
m1 n1 p1
— условие параллельности
m2 n2 p2 прямых.
Если L1 L2 , то s1 s2 , т.е.
m1m2 n1n2 p1 p2 0 — условие
перпендикулярности
прямых.
25.
2) Расстояние от точки до прямой.M0
z
M1M 0 r1 r0 .
s
M1
r1
r0
O
x
По формуле для
площади
параллелограмма
Sпар ad ,
L
По свойству
векторного
произведения
y
Sпар M1M 0 s .
найдем
d
Sпар
a
r r s
.
1
0
s
26.
Пример. Найти расстояние от точки M(-1,1,2)до прямой
Решение.
x 1 y 2 z
.
2
1
1
r0 ( 1,1, 2).
Прямая проходит через точку
(1, 2,0)
и ее направляющий вектор
(2, 1,1),
т.е.
r1 (1, 2,0), s (2, 1,1).
27.
Тогдаr1 r0 (2, 3, 2),
i
j k
r1 r0 s 2 3 2 5i 6 j 4k ,
2 1 1
r r s 77, s 6,
1
0
77
d
.
6
28.
п.6. Прямая и плоскость. Основныезадачи.
1) Угол между прямой и плоскостью.
n
s
L
Пусть — угол
между прямой и
плоскостью.
Очевидно, что
(n, s)
: Ax By Cz D 0,
x x0 y y0 z z0
L:
,
m
n
p
2
.
n ( A, B, C ),
s (m, n, p).
29.
Тогда| Am Bn Cp |
sin cos(n, s)
.
A B C m n p
Если L || , то s n, т.е.
Am Bn Cp 0 — условие параллельности
2
2
2
2
2
прямой и плоскости.
Если L , то s || n,
m n p
A B C
т.е.
— условие
перпендикулярности
прямой и плоскости.
2
30.
2) Точка пересечения прямой и плоскости.Пример. Найти координаты точки пересечения
прямой
x 1 y 2 z
2
и плоскости
1
1
x y z 2 0.
Решение. Запишем параметрические
уравнения прямой.
Пусть
x 1 y 2 z
t.
2
1
1
31.
Тогдаx 1 2t ,
y 2 t ,
z t.
Подставим в уравнение плоскости
т.е.
1 2t 2 t t 2 0,
1
t .
2
Поэтому координаты точки пересечения
3 1
0, , .
2 2












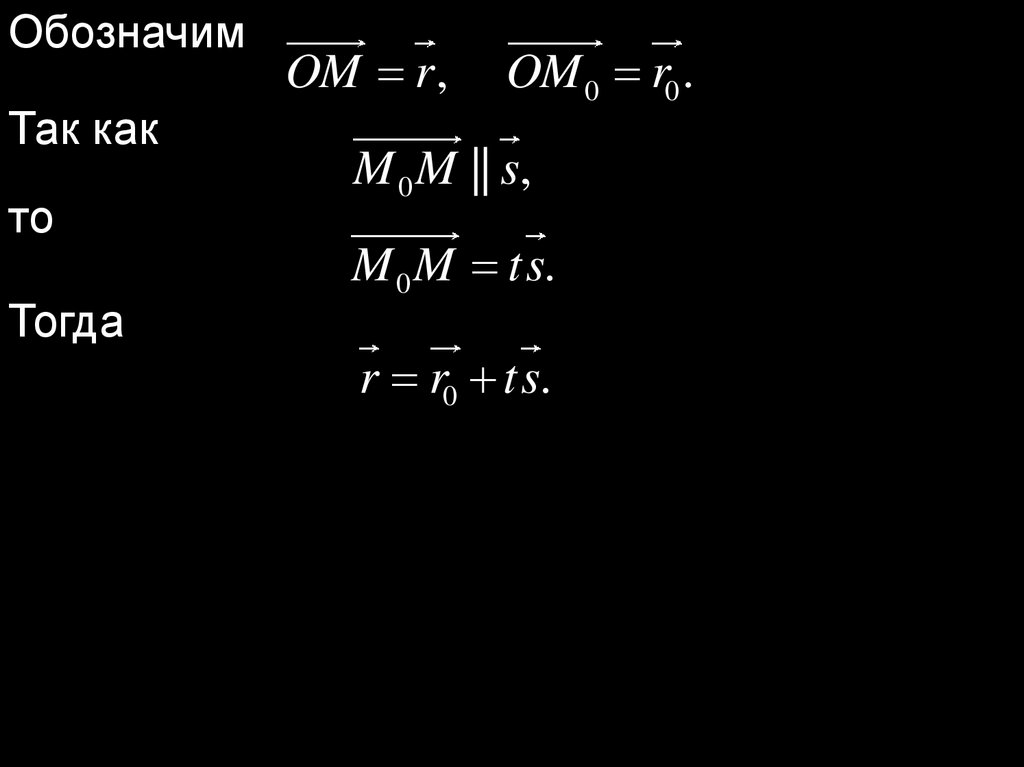










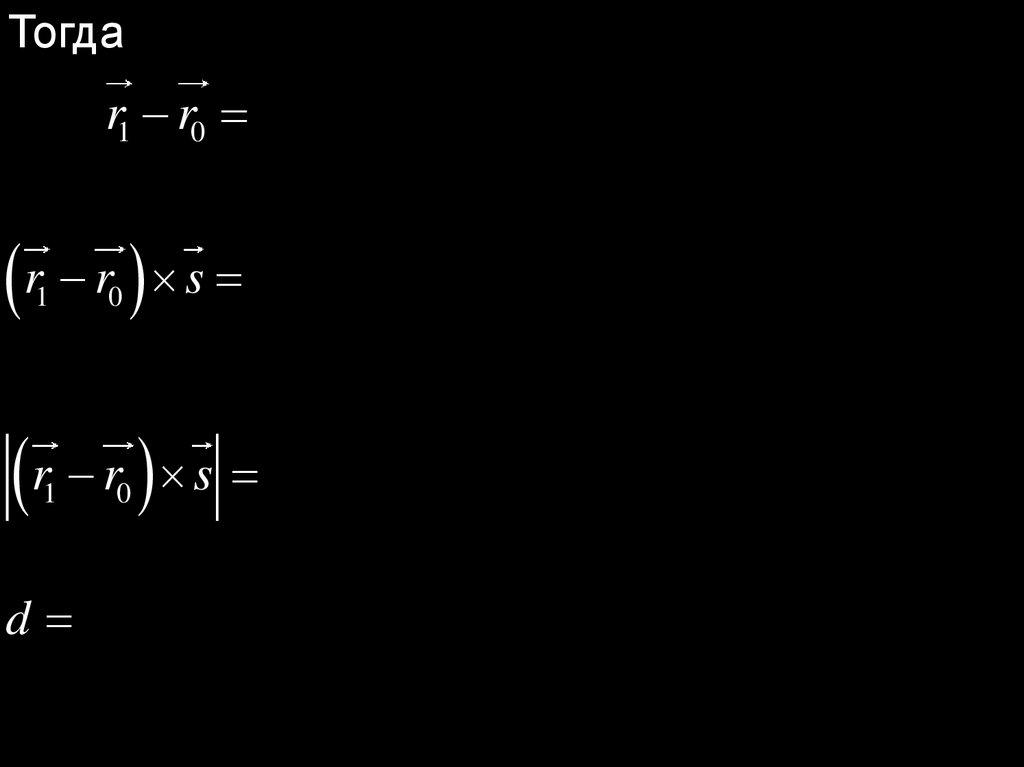




 mathematics
mathematics








