Similar presentations:
Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве
1. Аналитическая геометрия в пространстве
Плоскость и прямая впространстве
2. Плоскость
Основные уравнения плоскости1. Уравнение плоскости, проходящей через заданную
точку M 0 ( x0 ; y0 ; z0 ) перпендикулярно
заданному вектору N A; B; C
N A; B; C
A( x x0 ) B( y y0 ) C ( z z0 ) 0
2. Общее уравнение плоскости
M 0 ( x0 ; y0 ; z0 )
Ax By Cz D 0
N A; B; C
Z
- вектор нормали
c
3. Уравнение плоскости « в отрезках»
x y z
1
a b c
Y
a
X
b
3. Уравнения плоскости
4. Уравнение плоскости, проходящей через тризаданные точки M 1 ( x1 ; y1 ; z1,) M 2 ( x2 ; y2 ; z2 ) и M 3 ( x3 ; y3 ; z3 )
N A; B; C
M ( x; y; z )
M 2 ( x2 ; y 2 ; z 2 )
M 1 ( x1 ; y1 ; z1 )
M 3 ( x3 ; y3 ; z3 )
Условие компланарности векторов
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
M 1M x x1 ; y y1 ; z z1
M 1M 2 x2 x1 ; y2 y1 ; z 2 z1
M1M 3 x3 x1; y3 y1 ; z3 z1
( M 1M M 1M 2 M 1M 3 ) 0
4. Составление уравнений плоскости
1. Составить уравнение плоскости, проходящей через точкуM 0 ( 1;3; 5) перпендикулярно вектору N 3; 2;4
Исходное уравнение:
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Подставляем координаты точки и вектора
3( x 1) 2( y 3) 4( z 5) 0
Раскрываем скобки
3x 3 2 y 6 4 z 20 0
Приводим подобные
3x 2 y 4 z 29 0
Получили общее уравнение плоскости.
5.
2. Составить уравнение плоскости, проходящей через тризаданные точки
M 1 ( 1;3; 5), M 2 (2; 1;0), M 3 (0; 4;7)
В данном случае можно воспользоваться формулой уравнения плоскости,
проходящей через три точки:
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
Подставляем в это уравнение координаты точек и раскладываем
определитель по элементам первой строки
x 1
y 3
z 5
x 1 y 3 z 5
2 1 1 3 0 5 0
3
4
5
0 1 4 3 7 5
1
7
12
13( x 1) 31( y 3) 17( z 5) 0
13x 31y 17z 5 0
0
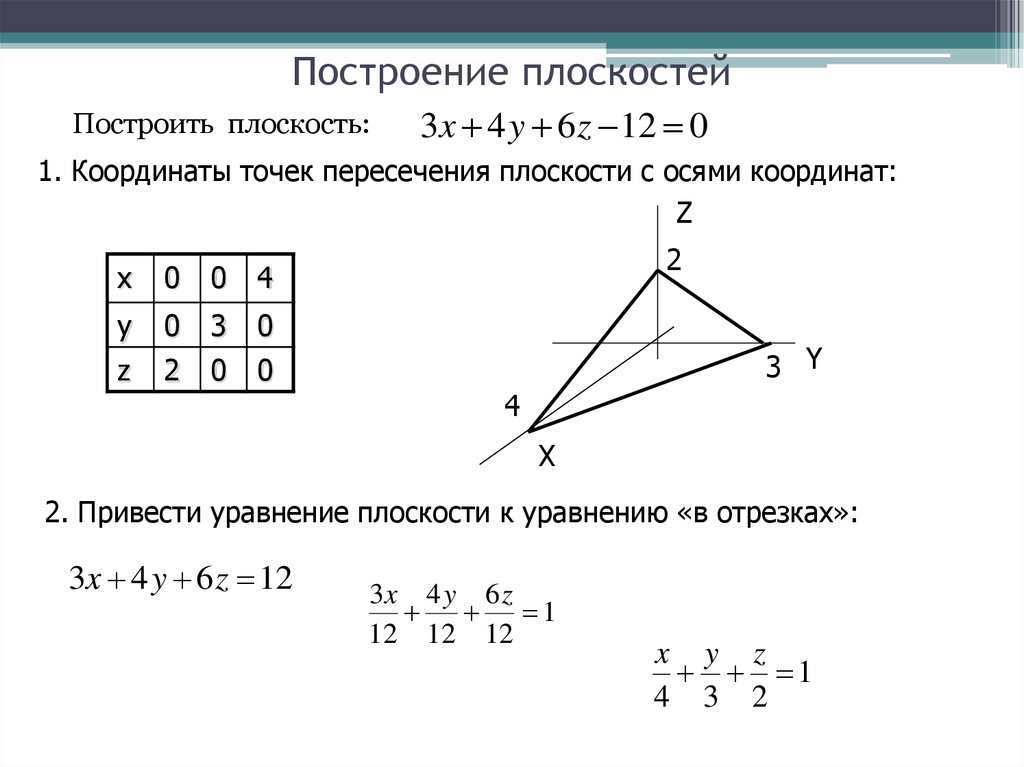
6. Построение плоскостей
Построить плоскость:3x 4 y 6 z 12 0
1. Координаты точек пересечения плоскости с осями координат:
Z
x
0
0
4
y
0
3
0
z
2
0
0
2
3 Y
4
X
2. Привести уравнение плоскости к уравнению «в отрезках»:
3x 4 y 6 z 12
3x 4 y 6 z
1
12 12 12
x y z
1
4 3 2
7. Построение плоскостей
3z 8 02. Построить плоскость
В уравнении отсутствуют две переменные x и y. Такая плоскость
проходит параллельно и оси OX , и оси OY, т.е. она проходит
параллельно координатной плоскости XOY через точку z=8/3 на оси OZ.
Z
8/3
Y
X
0
Аналогично строятся плоскости,
в уравнениях которых отсутствуют
две переменные
8.
• Если в уравнении плоскости отсутствует однапеременная, то плоскость проходит параллельно
той оси координат, переменной которой нет в
уравнении.
• Если в уравнении плоскости отсутствует
свободный коэффициент , то плоскость проходит
через начало координат.
• Если в уравнении плоскости отсутствуют две
переменные, то плоскость проходит параллельно
координатной плоскости, переменных которой
нет в уравнении.
• Уравнения координатных плоскостей
x 0
y 0
z 0
- уравнение плоскости YOZ
- уравнение плоскости XOZ
- уравнение плоскости XOY
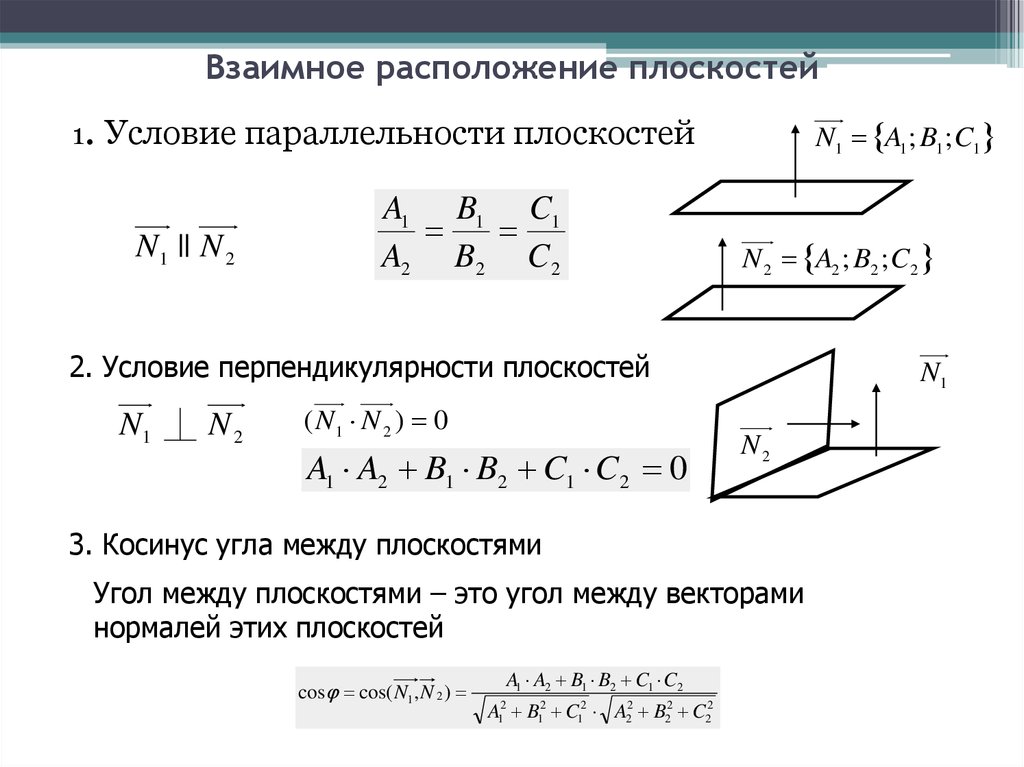
9. Взаимное расположение плоскостей
1. Условие параллельности плоскостейN 1 || N 2
A1 B1 C1
A2 B2 C 2
N1 A1 ; B1 ; C1
N 2 A2 ; B2 ; C2
2. Условие перпендикулярности плоскостей
N1
N2
( N1 N 2 ) 0
A1 A2 B1 B2 C1 C 2 0
N1
N2
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами
нормалей этих плоскостей
cos cos( N1 , N 2 )
A1 A2 B1 B2 C1 C2
A12 B12 C12 A22 B22 C22
10. Расстояние от точки до плоскости
Расстояние от точки M 1 ( x1 ; y1 ; z1 ) до плоскостиAx By Cz D 0 находится по формуле
d
| Ax1 By1 Cz1 D |
M 1 ( x1 ; y1 ; z1 )
d
A2 B 2 C 2
Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
11.
Найти расстояние от точкиM (5; 3; 2)
до плоскости
3x 4 y z 9 0
Используем формулу расстояния от точки до плоскости
d
d
| Ax1 By1 Cz1 D |
A2 B 2 C 2
3 5 4 3 1 ( 2) 9
32 ( 4) 2 ( 1) 2
| 4 |
4
26
26
12. Прямая в пространстве. Основные уравнения
1. Уравнение прямой, проходящей через заданнуюточку M 0 ( x0 ; y0 ; z0 ) параллельно заданному вектору
s m; n; p
x x0 y y0 z z0
m
n
p
- канонические уравнения
s m; n; p - направляющий вектор
2. Параметрические уравнения
x x0 y y0 z z0
t,
m
n
p
s m; n; p
x mt x0
y nt y
0
z pt z0
M 0 ( x0 ; y0 ; z0 )
3. Уравнение прямой, проходящей через две заданные
точки M 1 ( x1 ; y1 ; z1 ) и M 2 ( x2 ; y2 ; z2 )
x x1
y y1
z z1
x2 x1 y2 y1 z 2 z1
s M 1M 2
M 2 ( x2 ; y 2 ; z 2 )
M 1 ( x1 ; y1 ; z1 )
13. Прямая в пространстве. Основные уравнения
4. Общее уравнение прямой в пространствеA1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
Направляющий вектор
i
j
k
s N1 N 2 A1 B1 C1
A2 B2 C 2
s m; n; p
N1 A1 ; B1 ; C1
N 2 A2 ; B2 ; C2
14. Взаимное расположение прямых в пространстве
1. Нахождение угла между прямыми.Прямые в пространстве заданы каноническими уравнениями, поэтому
угол между прямыми – это угол между направляющими векторами
( s1 s2 )
m1m2 n1n2 p1 p2
cos
2
2
s1 s2
m1 n12 p12 m2 n22 p22
s2
s1
2. Проверка условий параллельности и
перпендикулярности прямых
Условие параллельности прямых
s1 || s2
m1 n1 p1
m2 n2 p 2
s2
s1
Условие перпендикулярности прямых
s1
s2
( s1 s2 ) 0
m1m2 n1n2 p1 p2 0
s2
s1
15. Расстояние от точки до прямой в пространстве
Задача о нахождении расстояния от точки M 1 ( x1 ; y1 ; z1 )до прямой x x0 y y0 z z0
m
n
p
На векторах
M 0 M1 x1 x0 ; y1 y0 ; z1 z0
И s m; n; p строим
M 1 ( x1 ; y1 ; z1 )
d
параллелограмм. Высота этого
параллелограмма
–
искомое
расстояние.
s
M 0 ( x0 ; y0 ; z0 )
Высоту находим как отношение площади параллелограмма к длине
основания. Площадь параллелограмма – это модуль векторного
произведения векторов, а длина основания – это длина вектора
d
M
0
M1 s
s
s
16.
Найти расстояние от точки M ( 1;4; 2)до прямой x 2 y 4 z
3
5 1
Искомое расстояние – это высота
параллелограмма, построенного на
векторах
M ( 1;4; 2)
d
s 3; 5;1
s 3; 5;1
и
M 0 M 3;8; 2
M 0 (2; 4;0)
Площадь параллелограмма находим, используя векторное произведение
i
S s M 0M 3
3
j
5
8
k
1 2i 3 j 9k
2
s 3; 5;1
s 32 ( 5) 2 12 35
S
94
d
Расстояние от точки до прямой
35
s
Длина основания – это длина вектора
2 2 32 9 2 94
17. Взаимное расположение прямой и плоскости в пространстве
1. Условие параллельности прямой и плоскостиN A; B; C
s m; n; p
s
( N s) 0
N
Am Bn Cp 0
2. Условие перпендикулярности прямой и плоскости
s m; n; p
N A; B; C
N || s
A B C
m n p
18. Взаимное расположение прямой и плоскости в пространстве
3. Нахождение угла между прямой и плоскостьюs m; n; p
N A; B; C
Углом между прямой и плоскостьюугол между этой прямой
и ее ортогональной проекцией на
эту плоскость
Из уравнений прямой и плоскости
известны направляющий вектор
прямой и вектор нормали плоскости.
Угол между этими векторами -
cos sin
Так как в сумме углы дают 90 градусов, а значит
Поэтому при нахождении угла между прямой и плоскостью находят
не косинус, а синус угла. Так как синус угла между прямой и плоскостью
может быть только положительным, то:
| ( N s) |
| Am Bn Cp |
sin
2 2 2
2
2
2
N s
A B C m n p
19. Решение типовых задач
1. Составить уравнение плоскости, проходящей через точкупараллельно
двум
векторам
и
a 2; 7;5 b 3;0; 4
M 0 ( 1;3; 5)
b
Используем уравнение
N
a
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Координаты точки нам известны. Необходимо найти координаты вектора
нормали. Из рисунка видно, что в качестве вектора нормали можно взять
вектор, являющийся векторным произведением данных в условии задачи
векторов, так как такой вектор перпендикулярен каждому из данных
векторов, а значит перпендикулярен и плоскости.
i
N a b 2
3
j
7
0
k
5 28i 7 j 21k
Итак,
N 28; 7; 21
4
Подставляем все данные в уравнение плоскости
28( x 1) 7( y 3) 21( z 5) 0
4( x 1) ( y 3) 3( z 5) 0
4 x y 3z 8 0
20.
2. Составить уравнение плоскости, проходящей через точку M (2; 1;5)4 x y 3z 2 0
перпендикулярно двум плоскостям
x 2 y 5z 3 0
N
N1 4; 1;3
N 2 1;2; 5
Основное уравнение:
A( x x0 ) B( y y0 ) C ( z z0 ) 0
M
Для составления уравнения плоскости есть точка M (2; 1;5) .
Вектором нормали может являться вектор, равный векторному
произведению векторов нормалей данных плоскостей.
i
j
N N1 N 2 4 1
1
2
k
3 i 23 j 9k
5
Остается только подставить
все данные в уравнение.
21.
3. Составить уравнение плоскости, проходящей через точкуM (2; 1;3)
перпендикулярно прямой x 1 y 2
z
5
3
4
Основное уравнение плоскости
s
N
M
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Из рисунка видно, что в качестве
вектора нормали плоскости можно
взять направляющий вектор прямой
N s {5;3; 4}
Таким образом, для составления уравнения плоскости есть все данные:
координаты точки и вектора нормали
5( x 2) 3( y 1) 4( z 3) 0
5x 3 y 4 z 5 0
22.
4. Составить уравнение плоскости, проходящей через точку M (4; 2; 1)и отсекающую на осях координат одинаковые отрезки
Для решение задачи используем уравнение плоскости «в отрезках»
x y z
1
a b c
Отрезки на осях одинаковые, поэтому
x y z
1
a a a
или x y z a
Для нахождения a подставляем в это уравнение координаты
точки M
4 2 1 a
a 1
Итак, уравнение плоскости: x y z 1
23.
5. Составить уравнение прямой, проходящей через точку M ( 3; 1;5)параллельно оси OY.
В качестве направляющего вектора можно использовать любой вектор,
параллельный оси OY. Самый простой вектор – это единичный вектор оси OY
s j 0;1;0
Канонические уравнения прямой
x 3 y 1 z 5
0
1
0
6. Составить канонические уравнения прямой, проходящей через две
точки M (3; 2;0) и M (0;6; 4)
1
2
В качестве направляющего вектора можно использовать вектор,
соединяющий эти точки.
s M 1M 2 3;8; 4
Уравнения прямой:
x 3 y 2
z
3
8
4
! Использовать можно координаты любой точки
24.
7. Составить уравнение прямой, проходящей через точку M ( 3;5; 2)перпендикулярно плоскости 4 x y 3z 1 0
Канонические уравнения прямой
s
M
x x0 y y0 z z0
m
n
p
N
Из рисунка видно, что в качестве
направляющего вектора прямой можно
взять вектор нормали плоскости
s N {4; 1;3}
Таким образом, для составления уравнения прямой есть все данные:
координаты точки и направляющего вектора
x 3 y 5 z 2
4
1
3






















 mathematics
mathematics








