Мат.стат практика №9

1.

Основы математической
статистики
Практическое занятие №9
Тема
1.
Исследование
зависимости
между
случайными
величинами. Ковариация и парный коэффициент корреляции
Тема 2. Линейная регрессия

2.

Основы математической статистики
Практическое занятие №9
Одним из способов изучения зависимостей между величинами
является построение графиков. На координатных осях в заданном масштабе
откладываются значения величин и на координатной плоскости или в
координатном пространстве получают серию точек, каждая из которых
фиксирует совместное наблюдение нескольких признаков. Пусть имеется
серия парных наблюдений значений величин X и Y. По этим данным можно
построить график, вид которого будет зависеть от характера зависимости
между X и Y.
2

3.

Основы математической статистики
Практическое занятие №9
Для случая I можно сказать, что
зависимость между X и Y скорее всего
отсутствует.
Для случая III можно уверено
сказать,
что
существует
четкая
функциональная (однозначно описываемая
некоторой функцией) зависимость.
Во II случае можно предполагать,
что зависимость между X и Y имеет место,
однако описать эту зависимость с помощью
Рисунок 1 – Возможные типы зависимости
некоторой функции можно лишь примерно.
между двумя переменными
Такая зависимость может быть названа
стохастической или вероятностной. Она не
всегда может быть в явном виде установлена
на графике и должна быть оценена с помощью
специальных статистических процедур.
3

4.

Основы математической статистики
Практическое занятие №9
Пусть – x1 y1; x2 y2 ; x3 y3;...; xn yn выборка парных наблюдений объема n. Случайные
величины x и y имеют нормальный закон распределения. Для них рассчитаем
средние значения и стандартные отклонения.
Введем показатель совместной изменчивости двух величин x и y, называемый
корреляционным моментом. Под корреляционным моментом понимается
математическое ожидание произведения отклонений случайных величин x и y от
их центров распределения:
M [( x m( x ))( y m( y ))]
где m(x) и m(y) математические ожидания случайных величин x и y.
Оценкой математических ожиданий являются выборочные средние значения.
Несмещенной оценкой корреляционного момента является ковариация. Чтобы
получить ковариацию рассчитаем сначала центрированную сумму смешанных
произведений, а затем дадим оценку ковариации:
n
SPxy
SPxy ( xi x )( yi y )
cov xy
n 1
i 1
4

5.

Основы математической статистики
Практическое занятие №9
Ковариация характеризует степень совместной изменчивости величин x и y,
подобно дисперсии, характеризующей степень изменчивости одной
случайной величины.
Коэффициент корреляции может быть рассчитан
ковариации к произведению стандартных отклонений:
rxy
как
отношение
cov xy
sx s y
Более простая, но менее наглядная процедура расчета коэффициента
корреляции сводится к вычислению нецентрированной суммы смешанных
произведений и среднего смешанного произведения. После этого
вычисляется коэффициент корреляции:
1 n
xy xi yi
n i 1
rxy
xy x y
sx s y
По существу коэффициент корреляции является стандартизированной
оценкой ковариации.
5

6.

Основы математической статистики
Практическое занятие №9
Величина r играет чрезвычайно большую роль в статистических исследованиях.
Его значения заключены в интервале между +1 и –1. В реальных условиях
коэффициент корреляции не бывает равен единице (или минус единице) и
характеризует степень статистической связи между свойствами х и у.
Чем ближе по абсолютной величине r к единице, тем сильнее связь между
свойствами; она может быть положительной (r > 0) и отрицательной (r < 0).
Таким образом, коэффициент корреляции является мерой линейной
зависимости между двумя величинами. Для оценки нелинейных зависимостей
он непригоден.
Полученное значение выборочного (по результатам исследования выборки)
коэффициента корреляции является точечной оценкой его истинного
значения. Распределение выборочного коэффициента корреляции описывается
особым законом и асимптотически стремится к нормальному распределению
при увеличении длины выборки.
6

7.

Основы математической статистики
Практическое занятие №9
Введем новую случайную величину:
t
r n 2
1 r2
Эта величина имеет распределение Стьюдента и может быть использована для
проверки нулевой гипотезы: H0: r 0 при альтернативе H1: r 0.
Нулевая гипотеза отвергается, если t t , n 2 ,
где t , n 2 – табличное критическое значение критерия Стьюдента для уровня
значимости α и n-2 степеней свободы, n – число пар наблюдений в выборке.
7

8.

Основы математической статистики
Практическое занятие №9
Для
n ≥ 40 стандартная ошибка коэффициента корреляции может быть
рассчитана по следующей формуле:
1 r2
r
n
а величина t - критерия: t r / r
Если рассчитанный критерий превысит табличное значение критерия
Стьюдента для заданного уровня значимости α и n-2 степеней свободы,
нулевая гипотеза о равенстве коэффициента корреляции нулю отвергается.
8

9.

Основы математической статистики
Практическое занятие №9
Коэффициент корреляции является показателем линейной зависимости между
переменными. Он позволяет описать линейную зависимость в виде уравнения
регрессии типа y a bx.
Статистический
характер
зависимости
между
переменными
позволяет
построить две прямых регрессии. Прямые регрессии y на x и x на y имеют вид:
y y r
Sy
Sx
( x x)
x x r
Sx
( y y)
Sy
Это в общем случае две разных прямых, пересекающихся в точке с
координатами x , y . Если коэффициент корреляции равен единице прямые
регрессии совпадут и будет иметь место функциональная зависимость y
от x, когда каждому значению x отвечает одно значение y.
9

10.

Основы математической статистики
Практическое занятие №9
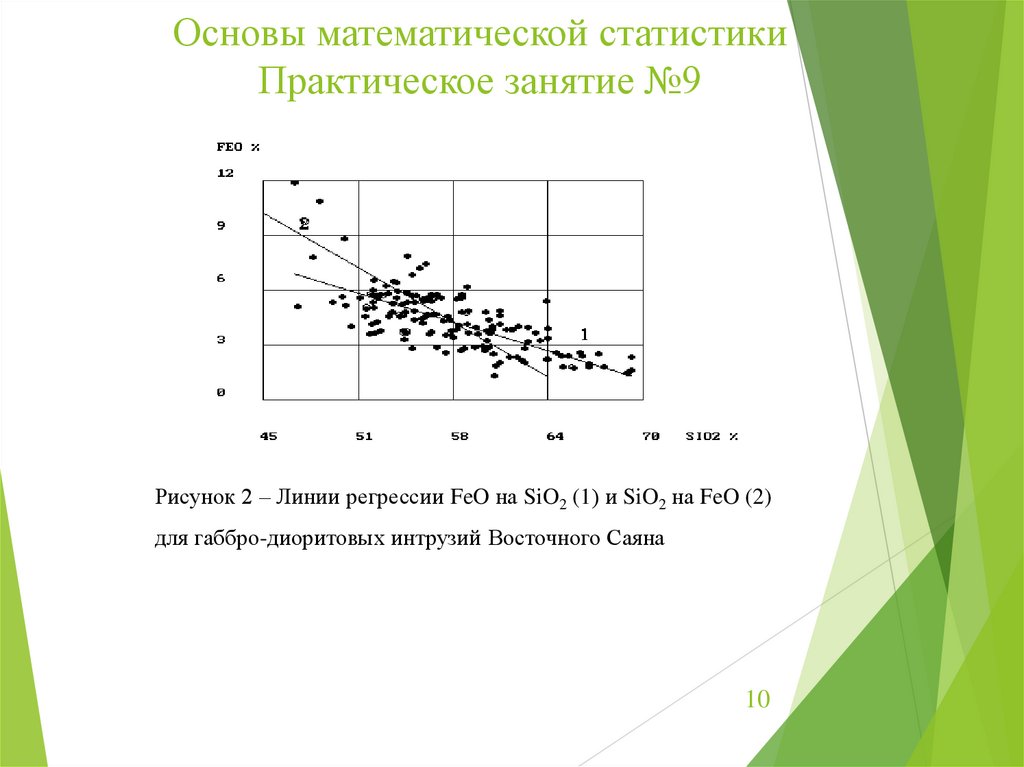
Рисунок 2 – Линии регрессии FeO на SiO2 (1) и SiO2 на FeO (2)
для габбро-диоритовых интрузий Восточного Саяна
10